1 Introduction

The current generation of nanolithography machines uses extreme ultraviolet (EUV) light to enable the printing of ever smaller features. To generate EUV radiation, a laser-produced plasma (LPP) is created by focusing high-energy laser pulses onto liquid micro-droplets of tin, where line emission from highly charged ions in the plasma produces the desired 13.5 nm light [1,2,3,4,5,6]. Some such laser pulses also induce strong shock waves on the metal droplets, causing them to deform hydrodynamically and, for the most intense pulses, undergo explosive cavitation [7,8,9,10].

In the most efficient EUV generation schemes, two incident pulses are typically used. The first pulse is used to deform the droplet in a controlled way, to produce a tin target with a desirable spatial density distribution for more efficient light coupling and plasma generation by a second pulse. That target shape is subsequently irradiated by the second, more energetic pulse, creating an EUV-emitting plasma. Understanding and controlling the expansion induced by the first pulse is an important step in producing an optimal target shape.

Prior works have studied the deformation of liquid tin droplets irradiated by femto- and picosecond laser pulses [7, 8, 11,12,13]. A general observation is that irradiation by such ultrashort pulses leads to the generation of intense pressure waves inside the droplet, resulting in shock-wave-driven phenomena such as cavitation and spallation, and associated explosive fragmentation. This behaviour is strikingly different from the dynamics induced by longer pulses with nanosecond duration, where the droplets mainly deform hydrodynamically into thin disks, driven by plasma pressure [10]. Recent evidence suggests that a droplet fragmented into a cloud of small particles, as one can obtain when using ps pulses, could be a favourable target for EUV generation [14, 15].

In the first part of this paper, prior studies by the authors on laser-induced cavitation of tin microdroplets are expanded to the case of irradiation by femtosecond pulses. The effects of laser pulse energy and duration on droplet deformation are examined, as it was established in [7, 10] that these parameters play an important role in various aspects of droplet deformation. In the second part, the effect of the polarization of the laser pulses on droplet deformation is studied. Results in literature have only addressed the case where the incident laser beam is circularly polarized. For that case, the absorption profile on the droplet surface is cylindrically symmetric. Using a linearly polarized incident beam instead leads to asymmetric shock waves in the droplets, creating unique target shapes. These unique absorption profiles and consequent shock waves affect the spatial distribution of the material ablated from the front of the droplet as well as the shape of the spallation front, i.e. the liquid material ejected from the back of the droplet along the laser propagation direction. As this liquid debris poses risks to the delicate equipment inside the machine, accurate understanding on how to minimize and manage its presence is a key part of EUV nanolithography machine design. Understanding how to break the typical cylindrical symmetry in a controlled way could be a significant addition to current debris management solutions. To complement these studies, smoothed-particle hydrodynamics (SPH) simulations were used to calculate the propagation of cylindrically asymmetric shock waves in a liquid droplet, having shown qualitative agreement with the experimental results.

2 Experimental setup

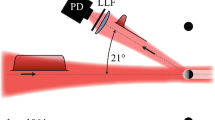
The interaction chamber and the laser system used in this study have previously been described in detail [7, 16]. A schematic overview of the experiment is shown in Fig. 1. The droplet generator is operated in a vacuum chamber (10\(^{-7}\) mbar), holding a reservoir of tin above the center of the chamber at a temperature of 260 °C, well above its melting point of 232 °C. Liquid tin is pressured through a 6.5-\(\upmu\)m nozzle, producing a multi-kilohertz train of 15- or 23-\(\upmu\)m radius droplets of 99.995% purity tin. The droplets pass a horizontal light sheet produced by a helium–neon laser, while the scattered light recorded is by a photomultiplier tube. This signal is used to trigger the laser system at a reduced repetition rate of 10 Hz.

Fig. 1
figure 1

Simplified top-view diagram of the experimental setup. A combination of a thin-film polarizer (TFP) and half-wave plate \((\lambda /2)\) is used to control pulse energy. BD beam dump, FC Faraday cup, FL \(f = +500\) mm focusing lens. Inset: Shadowgraph of a tin droplet after laser irradiation (laser incident from the left side), highlighting the regions of interest of the different processes discussed in the text

Full size image

The laser pulses are generated in an optical parametric chirped pulse amplifier (OPCPA), comprising 3 KTA crystals pumped by a Nd:YAG amplifier at 1064 nm and seeded by a commercial fiber oscillator and amplifier at 1550 nm. The OPCPA system produces pulses with energies up to 10.5 mJ that can be compressed to a minimum pulse duration of 220 fs [16]. The pulse duration is varied by changing the distance between a pair of transmission gratings that make up the compressor. The laser energy is adjusted with a combination of a half-wave plate and polarizer. The polarization is then adjusted using an additional half-wave plate and a quarter-wave plate, allowing for circular as well as adjustable linear polarization. The beam is focused to a Gaussian spot with a diameter of 80 \(\upmu\)m (FWHM), using a 500 mm focal length plano-convex lens. For a 5 mJ pulse, this results in laser fluences of 66 and 62 J/cm\(^{2}\) for droplets with radii of 15 and 23 \(\upmu\)m, respectively. Although the surface cross-section and thus the total absorbed laser energy changes with droplet radius, having similar fluences on both droplet radii allows for comparisons between the data sets.

Time-resolved shadowgraphy was used to capture the temporal evolution of the droplet [7]. A single, temporally and spatially incoherent, \(560 \pm 10\) nm wavelength, 5-ns-long light pulse illuminated the droplet at 90° from the input laser direction, in the plane of incidence of the laser. A long-distance microscope equipped with a CCD camera recorded the backlit droplet with a resolution of 4 \(\upmu\)m. The temporal dynamics of the process were captured by recording shadowgraphy images at different time delays after laser incidence on the droplet.

3 Results and discussion

Fig. 2
figure 2

Shadowgraphy images of tin micro-droplets (23 \(\upmu\)m initial radius), taken at various time delays after laser irradiation (noted above the figure). Pulse energies of 5 mJ (a) and 1 mJ (b) are shown, for various pulse durations (indicated on the left of the figure). Laser spot size: 80 \(\upmu\)m (FWHM)

Full size image

Upon irradiation by an ultrashort laser pulse, three main processes are induced in the tin droplet, which are ablation, cavitation and spallation. Each of these processes leads to characteristic deformations that can be tracked by shadowgraphy. The inset to Fig. 1 shows the response of an initially spherical tin droplet to irradiation by an ultrashort laser pulse. Upon laser impact, a thin layer of tin is rapidly ablated, and the ablated material can be seen travelling backwards in the direction of the laser source. When ultrashort pulses are used, the laser energy is deposited over a duration comparable to the electron–phonon coupling timescale (\(\sim\) ps), much shorter than hydrodynamical timescales (\(\sim\) ns). This fast energy deposition leads to a high-pressure shock wave that converges towards the center of the droplet. This shock wave consists of a strong compression wave, followed by a rarefaction wave. As the shock wave focuses near the droplet center, the increased negative pressure of the rarefaction wave may result in rupturing of the liquid structure and formation of a rapidly expanding cavity [7, 8, 11, 17]. This cavitation process leads to the expansion of the droplet into a spherical shell. The morphology and temporal dynamics of this expansion are dependent on laser parameters such as energy and pulse duration.

After passing through the center of the droplet, the shock wave propagates towards the back surface of the droplet. Upon reflection from this surface, the compression wave converts into a back-propagating rarefaction wave, which overlaps with the trailing rarefaction part of the incident shock wave close to the surface. The negative pressure caused by this combination of shock waves can exceed the tensile strength of the material, leading to spallation, i.e. the ejection of a sheet of liquid from the back surface [11].

The scope of the present work was to investigate the influence of laser parameters in the ultrashort pulse regime on the droplet deformation, focusing on the three phenomena described above. First, the effects of energy and pulse duration were studied, using circularly polarized light. Circular polarization results in a cylindrically symmetric absorption profile on the irradiated surface, in turn leading to cylindrical symmetries for the processes described above. Following this, incident pulses with linear polarization were used, leading to a breaking of the absorption symmetry. This geometry gives rise to asymmetric shock waves and subsequent deformation processes, which were studied through experiments and simulations.

3.1 Effect of laser pulse energy and duration on droplet deformation

Fig. 3
figure 3

a Temporal evolution of the cavitation shell a 23-\(\upmu\)m-radius droplet, after irradiation by a 5 mJ, 200 fs pulse. The solid black line is the result of a linear fit to the data points highlighted in red. The slope of this fit is used to determine \(\dot{R} (t=0)\); b for 1 mJ pulses, \(\dot{R} (t=0)\) is not dependent on pulse duration; c for 5 mJ pulses, \(\dot{R} (t=0)\) decreases for longer pulses. This is seen for both droplets sizes used: \(R_0=15\,\upmu\)m (pink circles) and \(R_0=23\,\upmu\)m (yellow diamonds)

Full size image
Fig. 4
figure 4

Top: Demonstration of the \(R_0\) scaling for 1 ps pulses, as both data sets collapse neatly to a power law curve when multiplied by their corresponding initial droplet radius. Bottom: The power law exponent \(\alpha\) decreases for longer pulses, indicating that cavitation dynamics are more sensitive to energy for shorter pulses

Full size image

Figure 2 shows the response of a tin droplet to irradiation by ultrashort laser pulses using circularly polarized light. The figure shows a time lapse series of images recorded at increasing time delays (ranging from 0.25 to 2.5 \(\upmu\)s) after the laser pulse impacts at \(t=0\) s, for pulse energies of 5 and 1 mJ (Fig. 2a, b, respectively), and for pulse durations of 220 fs, 1 ps and 10 ps. In these images, clear droplet deformation as described above are observed. In all images, a shell of ablated material traveling back from the laser-facing side can be seen, as well as a spherical expansion of the liquid due to cavitation. For a pulse energy of 5 mJ, (Fig. 2a) clear spallation is also observed, initially forming a bubble-like shell on the back side of the droplet (i.e. the side opposite to where the laser impacts). At later times, this bubble breaks up into a large number of microparticles. For even later times, also the cavitation expansion leads to fragmentation of the thin shell. At the lower energy (Fig. 2b), the spallation is not observed, likely because the laser-generated shock wave is not sufficiently strong to exceed the material’s tensile strength. One observation is that these deformations only weakly depend on the pulse duration in this regime. While at higher energies some differences are apparent, at lower energies the target shapes are strikingly similar even for a pulse duration variation by a factor \(\sim\) 45. This is in line with predictions by prior authors [11].

3.1.1 Cavitation dynamics

To analyze the cavitation dynamics, a series of time-delayed shadowgraphy images was recorded. The radius R(t) of the cavitation shell was tracked as a function of time using an image processing algorithm. Figure 3a shows an example of such radius tracking, indicating a linear time dependence of R(t). The determination of R(t) is complicated at early times (\(t<0.5\,\upmu\)s) by the presence of the dense ablation front, and at late times (\(t>2\,\upmu\)s) by fragmentation of the shell. Therefore, the expansion velocity \(\dot{R}\) was determined by fitting a linear function to the intermediate times where the shell is clearly distinguishable and not yet fragmented.

Looking at the effects of pulse duration on the expansion velocity, it was found that for low energies (1 mJ in Fig. 3b), the expansion velocity is not clearly dependent on pulse duration, while for higher energies (5 mJ in Fig. 3c), there is a significant decrease in velocity towards longer duration pulses. These trends are seen for both initial droplet sizes.

The influence of incident laser energy on the expansion speed (at constant pulse duration) was also investigated, and shown in Fig. 4a. In previous work, such a measurement was already performed for a single pulse duration of 15 ps [7], and that study was now expanded to a range of shorter pulse durations. Similar to that previous work, by scaling each data sets by its corresponding initial droplet radius \(R_0\), the data for different droplet sizes collapses onto a single power-law curve (Fig. 4b). This scaling behaviour originates from the relation between the magnitude of the induced shock wave and the irradiated droplet area, which is proportional to \(R^2\), combined with the fact that the expansion is hindered by the mass of the droplet proportional to \(R^3\), which results in a \(R^{-1}\) scaling.

The energy dependence of the scaled expansion velocity is well expressed by a power-law function \(R_0 \times \dot{R} (t=0) = A \times E^\alpha\), for all pulse durations used. This power-law description was previously observed for longer pulses [7], where a value \(\alpha =0.46\) was reported, using 15 ps pulses at 1064 nm wavelength. This power-law description is found to extend to ultrashort pulses below 1 ps. Notably, the power-law exponent \(\alpha\) decreases as a function of pulse duration, as shown in Fig. 4c. In practical terms, this means that as the pulse duration increases, the shell expansion velocity scales less strongly with pulse energy.

When observing the spallation dynamics, at higher energies the process is again found to be less violent for longer pulses. At 1 mJ energy, no significant spallation is observed. At 5 mJ pulse energy, as the pulse duration increases, the spallation front expands more slowly and holes form in the shell at a later time (compare images at delay times 0.5 and 1 \(\upmu\)s in Fig. 2a).

Fig. 5
figure 5

a Velocity of the ablation front for a laser pulse energy of 1 mJ. The velocity is largely independent of pulse duration and droplet diameter. b Ablation front velocity at laser pulse energy of 5 mJ. A significant dependence on both pulse duration and droplet diameter is found

Full size image

3.1.2 Ablation dynamics

The velocity of the ablation front is measured in a similar way to that described above for the cavitation, tracking the displacement of the ablation front as a function of time through image processing and fitting a linear function. This measurement was performed for a range of pulse durations at two different energies, of which the results are shown in Fig. 5. Similar to what was observed for the cavitation dynamics, at low energy the ablation front velocity is not clearly dependent on pulse duration, while for higher pulse energies there is a significant decrease in velocity for increasing pulse duration. Another observation that follows from Fig. 5 is that the ablation front velocity is the same for both droplet diameters used in the experiment, while at higher energies there is a significant increase for the smaller droplets.

Furthermore, in some measurements, a sharp higher density edge in the ablation front is observed. This is best seen in Fig. 2, for 5 mJ pulses at 0.5 and 1 \(\upmu\)s delays. This sharp edge has been described as a two-phase liquid–gas mixture [18, 19]. The ablation front becomes increasingly visible as the pulse energy increases at fixed pulse duration, while at fixed laser energy, the front becomes more apparent for longer pulses. This variation was not yet observed in measurements using longer 15 ps pulses at 1064 nm, where this edge was visible for all pulse energies [7].

Fig. 6
figure 6

Ion time-of-flight traces recorded using a Faraday cup for different incident laser pulse parameters. An increase in ion flux is observed, at 30\(^\circ\) from the incident beam, for increasing pulse duration at fixed energy

Full size image

3.1.3 Discussion on deformation scalings

These changes in ablation front and cavitation velocity with pulse duration can be explained by the increased influence of the generated plasma on the expanding material. As the incident energy per unit area on the droplet surface is almost identical for both droplet diameters, and ablation can be considered to be due to local heating, the droplet diameter should not influence the ablation front velocity in the absence of any other effect. However, the laser intensities used are sufficiently high to produce plasma, and the presence of a finite plasma density at the laser facing side would impact the observed deformation, since this plasma would exert a pressure on the deforming and ablated material passing through it.

Both the ablation front and the cavitation experience a drag when expanding into a plasma, which leads to a reduction in expansion velocity that scales with plasma density. To quantify the amount of plasma generated by the different laser pulses, a Faraday cup (FC) is placed on the target chamber at an angle of 30° with respect to the incident laser beam (in the backward direction). The FC records a time-of-flight trace of the ions emitted from the target after laser impact, as shown in Fig. 6. The charge detected by the FC allows a comparison of the amount of plasma generated for different laser parameters.

As expected, the FC data show that the amount of plasma-related current produced by the laser sharply increases with pulse energy. But from these measurements, it also becomes clear that the amount of produced plasma increases with incident pulse duration. The increased current and shift towards shorter time-of-flight seen in Fig. 6 for increasing pulse duration indicate that longer pulses lead to a higher density and higher temperature plasma upon impact. A possible reason for this scaling may be that on the timescale of the electron–phonon coupling, which is several picoseconds for most metals, lattice heating and subsequent evaporation and plasma formation start to occur, leading to a significant increase in absorption. As a result, longer pulses will be more effective in depositing energy into the material. This increased plasma density explains the formation of a more distinct front in the ablation plume for both higher energies and longer pulses. It also explains the reduction of ablation and cavitation velocity for longer laser pulses: as such pulses produce more plasma, the drag on the expanding material increases. At low incident energy (\(E=1\) mJ), the FC data indicate that little plasma is formed, which would not produce a significant force on the expanding material, which explains the absence of an effect in Figs. 3b and 5a. The appearance of the dependence of droplet diameter is also explained from the plasma perspective. Larger droplets absorb a larger fraction of the incident beam simply by increased geometrical overlap with the laser focus, but also have lower local surface curvature. As ultrafast-laser-induced plasma expansion is strongly directional and oriented perpendicular to the surface [20, 21], a stronger surface curvature leads to a faster reduction in plasma density as a function of distance from the surface. Therefore, at constant laser energy and focal spot size, a larger droplet will experience more plasma pressure counteracting its deformation, both in expansion and ablation.

3.2 Polarization-controlled droplet deformation

Several papers have covered the topic of ultrafast laser-droplet interaction, including the role of laser-driven shock waves in the deformation dynamics [7, 8, 11]. To the best of our knowledge, all used circularly polarized light. The use of a circular incident laser polarization leads to an absorption profile that is cylindrically symmetric around the beam propagation axis. This symmetry can be broken using linearly polarized light. That may result in a detectable effect on the generated shock wave dynamics, which is the scope of the present investigation.

Fig. 7
figure 7

Absorption coefficient mapped onto the laser-facing surface of a spherical droplet, for linear and circular incident laser polarization. The beam is taken to have a 2D Gaussian spatial distribution with an 80 \(\upmu\)m radius (FWHM) for all cases. The droplet radius is indicated above each profile

Full size image

Absorption and reflection profiles can be calculated with the Fresnel equations. For a curved surface, the incident polarization state must locally be decomposed into s- and p-polarization with respect to the plane of incidence on each point of the curved surface. For clarity, the polarization of the incoming laser beam will be labelled as vertical or horizontal (perpendicular or parallel to the surface of the optical table, respectively) and s and p nomenclature will be used when referring to the droplet surface.

Fig. 8
figure 8

Effects of laser polarization on droplet expansion at various delays after laser irradiation, for laser energies of 5 mJ (a) and 1 mJ (b). Pulse duration of 220 fs for all cases. The polarization state is indicated on the left of each row. Initial droplet radius: 23 \(\upmu\)m, laser spot size: 80 \(\upmu\)m (FWHM)

Full size image
Fig. 9
figure 9

Cavitation expansion velocity for different polarizations for droplets with \(R_0=23\,\upmu\)m (a) and \(R_0=15\,\upmu\)m (b). Pulse energy of 5 mJ for all cases

Full size image

This decomposition into s- and p-polarization and the resulting absorption profiles can be analytically derived. Figure 7 shows the profiles of the absorbed energy on the droplet, for both linear and circular polarization. This calculation follows the procedure described above, assuming an 80 \(\upmu\)m FWHM Gaussian beam incident on a droplet with a radius of 15 \(\upmu\)m (left) and 23 \(\upmu\)m (right). The most noteworthy feature in the absorption profile for linear polarization is the clear cylindrical symmetry breaking, featuring zones of high and low absorption at edges along and opposite to the polarization axis, respectively.

When using linearly polarized pulses incident on tin droplets, the resulting absorption inhomogeneity produces drastic changes in the droplet expansion and in the shapes of the spall and ablation front, as shown in Fig. 8. In this figure, shadowgraphs at different time delays are shown for circular, horizontal and vertical polarizations, respectively. The pulse duration is 220 fs, and the incident energies are 5 and 1 mJ (Fig. 8a, b, respectively). As rotating a linear polarization is analogous to rotating the angle of observation of our 90\(^{\circ }\) shadowgraphy system, the shadowgraphs for vertical and horizontal incident polarization can be visualized as the side- and top-view of the same structure.

In these shadowgraphs, differences were observed in the ablation front angle, expansion speed of the cavitation shell, as well as shape of the spall. These differences exist at both energies, but become more apparent in the higher energy measurements. The low-energy data in Fig. 8b highlights the different opening angles of the ablation front, which clearly follow the expected absorption profiles (Fig. 7). For the vertical polarization, there is a Brewster’s angle and thus maximum absorption near the top and bottom of the droplet as seen in the side-view shadowgram, which results in a nearly hemispherical ablation front. For the horizontal polarization, the absorption mostly decreases towards higher angles, resulting in a more backward-directed ablation front. For circular polarization, the ablation front is cylindrically symmetric and shows an angle in between the different horizontal cases. At higher energy (Fig. 8a), these asymmetries become somewhat less apparent because of the increased influence of plasma pressure, but a clear difference in shape of the ablation front is still observed.

At high energy, a marked difference is also observed in the spallation front. As discussed above, spallation occurs when a laser-induced shock wave arrives at the back surface. The initial spatial profile of the shock wave is determined by the local light absorption. After being focused at the center of the droplet and diverging upon further propagation, its spatial profile at the back surface closely follows the initial absorption-driven distribution.

Similar to what is observed for ablation, linear polarization leads to a striking asymmetry in the spallation process. In the plane perpendicular to the polarization direction, the spallation occurs over a limited angular range and is largely forward-directed. In contrast, in the plane parallel to the polarization direction, a much larger angular spread is observed, with sharp lobes near the poles where the light absorption profile was highest.

Fig. 10
figure 10

Comparison between SPH simulations (left) and experimental shadowgraphy images (right). There is a good agreement between the predicted and observed angular extension of the ablation area. A more confined spall is observed for horizontal polarization, as well as structures that resemble the “winglets” for vertical polarization. These simulations cannot account for an expanding cavitation shell (see text). Note the change in scale

Full size image

The expansion speed of the cavitation shows the opposite trend, as the shell expands faster in the plane perpendicular to the input polarization and slower in the parallel plane. Nevertheless, at longer delay time (\(2.5\,\upmu\)s), it can be seen that there is more material expanding perpendicularly to the polarization plane. When a pressure wave propagates from the surface of a sphere towards its center, a larger angle at the surface leads to a tighter focus at the center of the sphere [9]. When the initial pressure profile is elongated along a given axis, the resulting focus will be elongated in an orthogonal direction, leading to an asymmetric initiation of the cavitation process.

Despite the asymmetric conditions, the expansion speed of the cavitation shell continues to be well represented by a power-law of the form \(\dot{R}(t=0) \times R_0 = A \times E^\alpha\), both in the direction parallel and perpendicular to the laser polarization.

Figure 9 compares the cavitation expansion for all polarizations studied, for both droplet radii, as a function of pulse duration for a 5 mJ pulse. The observed asymmetry is found to show a significant decrease with increasing pulse durations. Comparing the expansion velocity of the cavitation shell in the parallel and perpendicular planes for 23 \(\upmu\)m droplets, an asymmetry of 19.4% was measured for 220 fs pulses, which decreases to 7.6% for 10 ps. For 15 \(\upmu\)m droplets, this decrease is lower, going from 23.4% for 220 fs pulses, to 17.8% for 10 ps.

This effect can again be explained through the increased influence of plasma formation towards longer pulse durations. As soon as a dense plasma is present in front of the droplet, the absorption increases strongly and is much less sensitive to polarization and angle of incidence compared to liquid tin droplets [22, 23]. So once this plasma layer is formed, its absorption profile will thus be cylindrically symmetric. Energy transfer into shock waves can still occur, as strong cavitation and spallation are still observed even for much longer pulses, but the resulting shock wave and subsequent deformation dynamics will become much more symmetric compared to the case where plasma absorption is not yet dominant. The asymmetry is more pronounced for smaller droplets, which can readily be explained by the increased influence of the asymmetric absorption as shown in Fig. 7.

To aid in the understanding of the observed dynamics, smoothed-particle hydrodynamics (SPH) simulations were employed, using an in-house developed two-dimensional SPH code following established methods [24, 25]. In SPH, three conservation laws are solved, namely, the continuity equation (conservation of mass), the conservation of particle momentum and the conservation of energy:

$$\begin{aligned}&\frac{\mathrm{D}\rho }{\mathrm{D}t}=-\rho \nabla \cdot {\mathbf {v}} \end{aligned}$$
(1)
$$\begin{aligned}&\rho \frac{\mathrm{D}{\mathbf {v}}}{\mathrm{D}t}=-\nabla p \end{aligned}$$
(2)
$$\begin{aligned}&\rho \frac{\mathrm{D}e}{\mathrm{D}t}+p\nabla \cdot {\mathbf {v}}=Q, \end{aligned}$$
(3)

where D is the convective derivative, \(\rho\) is the mass density, \({\mathbf {v}}\) is particle velocity, p is the pressure, e is thermal energy density of the particles, and Q is the source term. The source term describes the increase in the total energy of the system due to the spatially dependent absorption profile of the laser pulse, calculated using the Fresnel equations, as well as the known spatial profile of the laser (Fig. 7). The temporal shape of the source term is further supplemented with the modeling of energy transfer from electron to lattice via the two-temperature model [26, 27]. In the simulations, the Mie–Grüneisen equation of state for liquid tin is used, following Ref. [11]. The simulations are performed with a circular tin droplet of 3 \(\upmu\)m diameter. Due to the limited computational resources, simulation of the same droplet size as the experiment is impractical. However, hydrodynamic similarity [11] indicates that the dynamics for different droplet sizes are qualitatively similar. Thus, for a qualitative comparison, a smaller droplet size is sufficient.

Figure 10 shows the experimental simulation results in comparison with the experimental data. While the simulations are performed in a 2D geometry and do not account for the influence of plasma, similar trends are observed as seen in the experiment. This agreement provides additional evidence that the spatial distribution of the initial shock wave is the defining parameter for the non-cylindrically symmetric dynamics. Both the ablation front and spall are more confined in the direction perpendicular to the input polarization and wider along the polarization direction, when compared to circular polarization case. It should be noted that in a 2D geometry, cavitation effects are expected to be underestimated due to the lower ratio between surface area and focal volume in a 2D geometry compared to a more realistic 3D case. However, ablation and spallation are mainly determined by the local shock wave at the droplet surface, which can be expected to show similar behaviour in 2D and 3D models. Therefore, only qualitative agreement is sought in this simulation effort, and especially the shape of ablation and spallation fronts are to be compared here.

4 Conclusions

The effects of pulse energy and duration on the shock-wave-driven expansion dynamics of liquid tin micro-droplets irradiated by ultrashort laser pulses have been reported in this work. The initial cavitation expansion velocity as well the velocity of the ablated material are found to decrease as a function of pulse durations, in situations where the pulses are sufficiently intense to produce significant plasma density. Using linearly polarized laser pulses, non-symmetric shock waves were produced in the droplets, leading to non-symmetric droplet deformation dynamics and uniquely shaped targets. Lastly, 2D SPH simulations show a qualitative agreement with the experimental results, highlighting the role of shock waves in the laser-driven deformation dynamics, and indicating that the non-cylindrically symmetric pressure wave launched from the surface is the main factor for the observed behaviour. The present work further clarifies the influence of ultrashort laser pulses on liquid droplet deformation, and demonstrates a route towards improved control over target pre-shaping in next-generation LPP sources for EUV generation.