Ultrashort-pulsed laser separation of glass-silicone-glass substrates: influence of material properties and laser parameters on dicing process and cutting edge geometry

Abstract

In recent years, ultrashort-pulsed lasers have increased their applicability for industrial requirements, as reliable femtosecond and picosecond laser sources with high output power are available on the market. Compared to conventional laser sources, high quality processing of a large number of material classes with different mechanical and optical properties is possible. In the field of laser cutting, these properties enable the cutting of multilayer substrates with changing material properties. In this work, the femtosecond laser cutting of phosphor sheets is demonstrated. The substrate contains a 230 µm thick silicone layer filled with phosphor, which is embedded between two glass plates. Due to the softness and thermal sensitivity of the silicone layer in combination with the hard and brittle dielectric material, the separation of such a material combination is challenging for both mechanical separation processes and cutting with conventional laser sources. In our work, we show that the femtosecond laser is suitable to cut the substrate with a high cutting edge quality. In addition to the experimental results of the laser dicing process, we present a universal model that allows predicting the final cutting edge geometry of a multilayer substrate.

1 Introduction

Material processing with ultrashort-pulsed lasers is of particular interest because of the high flexibility and the broad field of applications. Due to the high peak intensities and the short laser-material interaction time offered by such systems, a wide range of material classes can be processed with minimal thermal stress and high precision.

Therefore, ultrashort-pulsed lasers show a high potential for processing substrates with changing material properties such as phosphor sheets. In the lighting industry, the phosphor material is usually embedded in epoxy or resin and directly applied to the LED. When using “remote phosphor” or preforms where the phosphor is embedded in solid material in the form of wafers or sheets, the material must be subjected to a cutting process. When using ceramic or crystalline phosphors, conventional sawing methods used in the semiconductor industry can be applied. In the case of sheets, where the phosphor is embedded in a silicone matrix positioned between two glass plates, the cutting methods are very limited due to the different mechanical properties of the panel materials. The choice of a laser cutting method is promising because of the contactless ablation process. The femtosecond laser as a cutting tool for semiconducting [1, 2] and dielectric materials [3,4,5] is already well documented in the literature and shows good results regarding process quality. To our knowledge, laser processing of both phosphor-filled silicon materials and phosphor sheets is not documented in the literature. However, the laser processing of silicone materials such as PDMS is being intensively investigated [6,7,8]. In principle, the processing of silicone shows good results, but only in a very low power and fluence regime compared to glass to avoid thermal damage. However, in order to efficiently cut the material combination with glass, a parameter window must be found in which the silicone is not damaged, but in which an adequate cutting of the glass plates is also possible.

In this work, we demonstrate the femtosecond laser dicing of a sandwich system (phosphor sheet) with high cutting edge quality. In a first step we investigated the possible ablation depth and quality in a single line cutting approach. Since a saturation process of the ablation depth does not allow the complete separation of the substrate, a multiline approach is investigated. By placing several parallel cutting paths it is possible to extend the cutting channel to allow a complete separation of the substrate. In order to predict the cutting edge geometry, a simple calculation is applied to examine the ablation saturation during laser cutting or drilling. In the literature one usually finds numerical models for calculating the groove geometry. In the model presented by Vázquez de Aldana [9] the influence of diffraction of the incident pulse at the entrance of the channel as well as reflections at the channel walls for calculating the crater shape is considered. In [10] the crater shape can be determined by a model which takes into account the time and space dependent optical properties of highly ionized dielectrics. A quantum treatment is used to determine free electron heating and free electron relaxation time in dense plasma. The calculation presented in this work is based on the drop of the laser fluence down to the threshold value at a certain inclination of the cutting edge. This simple correlation allows the calculation of the final crater profile after ablation saturation has occurred. This is sufficient for the determination of the cutting geometry, since the high number of scan repetitions during the cutting process leads to a geometry that already approaches the saturation range. Additional the model can be applied to the multilayer system and thus allows to calculate the complete cutting edge geometry. A subsequent comparison with the experimental results shows the high agreement with the calculated values.

2 Materials and methods

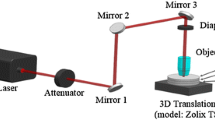
For the experiments, a sheet from PhosphorTech with a total thickness of 640 microns was used. The phosphor, embedded in a silicone matrix, is placed between two glass plates and has a thickness of 230 microns. The laser used was a Spirit^® from Spectra-Physics Rankweil, a femtosecond laser with a maximum output power of 30 W and a pulse duration of 330 fs. The laser was operated at its second harmonic with a wavelength of 523 nm. The beam was manipulated using a galvo-scanner and an f-theta lens with a focal length of 170 mm. The focal diameter of the beam as well as the multipulse ablation threshold of the glass and silicone, respectively, was measured using the method of Liu [11]. The beam diameter was 21 µm. The threshold fluence is 1.5 J/cm² for the glass and 0.6 J/cm² for the silicone. A number of 100 pulses were applied for each data point in the Liu plot to avoid accumulation effects since the threshold fluence value changes from the single pulse up to the multipulse ablation regime.

To develop optimal cutting parameters, straight test lines with variable parameter settings were cut across the edge of the sample. The length of the cutting lines was 20 mm to avoid a temperature rise in the adjacent bulk material caused by heat accumulation. The cross section of the cut was examined by optical microscopy of the front surface as illustrated in Fig. 1. Single line cutting experiments (see Fig. 1A) as well as cutting with multiple parallel lines (see Fig. 1B) were performed to find out an optimal parameter setting for separation of thick multilayer substrates.

Fig. 1

Schematic drawing of the setup for cutting tests with single (A) and multiple cutting lines (B). The cuts were placed across the edge of the sample. This enables examination of the results by optical microscopy on the left sidewall

For the multiline cutting, experiments with up to 15 parallel lines were applied. The ideal line spacing for this approach will be determined experimentally in this work. The parallel line pattern was repeated N times to achieve the required cutting depth. In each repetition, the pattern was reproduced without lateral offset so that every individual cut is positioned exactly in the trench of the previous one.

Since cutting with a single line scan resulted in narrow grooves with a high aspect ratio, the sample was embedded in resin and polished to obtain reliable depth measurements. In case of multiple line cutting experiments, no sample preparation was necessary. The morphology of the laser treated sample was examined by scanning electron microscopy.

3 Theory

In this section, a simple model is presented which allows the calculation of the final groove shape for single as well as for multiple line cutting with an ultrashort pulsed laser and a Gaussian intensity profile. The model assumes that the ablation threshold was reached along the final cutting edge geometry. For this reason, the agreement between model and experiment is at its maximum when the cutting process at the respective area of the edge already shows a significant reduction in cutting efficiency or has already stopped.

At the beginning of the cutting process with a Gaussian beam, the incident laser hits a flat surface and a groove evolves resembling the beam fluence profile. The fluence profile in the focal plane is given by

$$ F\left( r \right) = F_{0} e^{{\frac{{ - 2r^{2} }}{{w_{0}^{2} }}}} $$

(1)

where F₀ is the maximum fluence in the center of the beam and w₀ is the beam radius. The focal plane is positioned at the sample surface. For subsequent cutting steps, the inclination angle of the laser beam is changing depending on the position within the laser spot, except the beam center where the normal incidence remains. Consequently, the laser pulse energy is projected to an increased surface area within the cutting groove leading to a decrease of the laser fluence given by

$$ \cos \alpha = \frac{A}{{A_{\text{proj}} }} \to F_{\text{proj}} = F\cos \alpha $$

(2)

with α representing the inclination angle. For increasing number of cutting repetitions, the inclination angle further increases. Consequently, the ablation rate decreases and finally stops when the projected fluence reaches the ablation threshold value of the material. The corresponding inclination angle is given by

$$ \alpha_{\text{th}} = \arccos \frac{{F_{\text{th}} }}{F\left( r \right)} $$

(3)

For applications where the separation of thicker substrates must be realized, the cutting depth can be increased significantly by applying several parallel cutting paths with a line distance smaller than the beam diameter. The resulting fluence profile equals a tophat, which results in a constant inclination angle given by

$$ F\left( r \right) = F_{0} = {\text{const }} \to \alpha_{\text{th}} = \arccos \frac{{F_{\text{th}} }}{{F_{0} }} = {\text{const}} . $$

(4)

In Fig. 2 the fluence profiles and the resulting calculated crater shapes are shown for a Gaussian beam (single line cutting) and a tophat shape (multiline cutting), respectively. The crater profile for single line cutting is in accordance to results presented by Kalupka et al. for single line ablation of borosilicate glass using a Ti:Sapphire laser [12].

Fig. 2

Calculated crater shape given by the inclination angle where the projected fluence reaches the multipulse ablation threshold value for a Gaussian and a tophat profile, respectively

The threshold fluence of 1.5 J/cm² corresponds to the value determined by the Liu method. In order to be able to demonstrate the crater shape in the diagram in scale, a much smaller fluence was assumed than for laser cutting. For this reason, a value of 3 J/cm² was chosen for the calculation, resulting in a crater angle of 60°. The area of constant laser fluence is highlighted in both panels. The threshold fluence and the corresponding cavity edges are pointed out by arrows. The Gaussian fluence profile results in a curved cavity which tapers to the deepest point at the fluence maximum in the beam center. The final cutting groove profile shows very well the cutting depth limitations of single line cutting with a focused Gaussian beam. Due to the v-shaped bottom of the cavity, the cutting process stops because of the drop of the projected fluence value. This limit is, according to the calculations above, solely determined by the ratio of the laser fluence and the ablation threshold of the material to be ablated.

The cross-section of the groove for the tophat profile is identical in the outer areas due to the Gaussian slope whereas a v-shaped groove forms within the constant fluence region. Here, the sidewall of the cavity is a straight line with, according to Eq. 4, with a groove angle of 60° for the selected parameter values. The possible cutting depth can be easily approximated by using trigonometric calculations.

In addition, the model can be used very well to calculate kerf geometries when cutting a multilayer stack with changing material properties. As described in the model, the inclination of the kerf depends on the ratio of the ablation threshold to the fluence used. If a substrate is processed which consists of layers with different threshold fluences, the cutting edge also shows a changing inclination as described in the model. In this article a material combination is cut, which is very well suited for the demonstration of this fact, since the ablation thresholds differ to such an extent that a significant change of the edge inclination can be observed.

4 Results and discussion

In a first step, single line cutting experiments with different output power or number of scan repetitions were performed. The maximum laser power was limited to 6 W at a repetition rate 250 kHz. Previous studies have shown that at higher fluence values the silicone has already been damaged in the form of bubbles and carbonization. The cutting speed was two meters per second. The results for the groove depth as a function of scan repetitions can be seen in Fig. 3 for three values of laser output power.

Fig. 3

Single line cutting depth depending on the scan repetitions for three different values of output power

The three curves show a similar trend where the depth increases approximately linearly within the first 70 repetitions. For increasing numbers, the cutting depth shows a saturation effect and the cutting efficiency decreases significantly for repetitions higher than 150. At 500 a maximum depth of approximately 100 µm can be achieved at an output power of 6 W. A further increase of power was not possible due to damages within the silicone layer. Figure 4 shows images of cutting cross-sections after sample preparation with varying number of scan repetitions from the experiments done with an output power of 3 W. Panel a shows the profile after 20 scan repetitions. The shape of the shallow cut still follows the Gaussian fluence profile of the laser beam. After 50 repetitions (panel b) it already converges toward the final shape corresponding the inclination angle for the projected fluence reaching the threshold value for ablation. Further repetitions (70 for panel c, 100 for panel d) result in minor changes of the groove shape close to the surface of the substrate but in an increase of cutting depth by the formation of a thin tapered cut. Panel e shows a magnified image of panel c where the calculated final crater shape (see Eq. 3) is superimposed. The comparison shows a high agreement of the theoretical curve with the experimental result in the upper range where the projected fluence has already reached the ablation threshold. Further scan repetitions would lead to an extension of the cut and to a further approximation to the final crater shape.

Fig. 4

Panels a–d show cross-section of the laser cut glass substrate processed with a laser output power of 3 W and 20, 50, 70 and 100 laser passes, respectively. The image in panel e shows the groove cut with 70 passes superimposed with the calculated final crater shape. It shows a high agreement of the theoretical curve with the experimental result in the upper range where the projected fluence has already reached the ablation threshold

Since the maximum cutting depth by a single line scan is limited to approximately 100 microns, a full cut of the phosphor sheet is not possible. Using a bigger laser spot may be an option for an increased cutting depth but for substrates with a thickness of several hundreds of micrometers, a multiline approach, where the cut is done by several parallel lines, is a suitable method.

In a first step, the ideal line spacing was determined for multiple-line cutting. For this purpose, cutting tests with different line spacings were carried out. Afterward the sample was embedded in resin and polished on the front side to measure the maximum crater depth. Figure 5 shows the crater depth in dependence of the line spacing. The laser power used was 1.04 W at a repetition rate of 250 kHz. The cutting of 5 parallel lines was repeated for 700 times to ensure that the edge shape has already reached its final geometry. The value for which the line spacing corresponds to the beam radius (w₀ = 10.5 µm) is highlighted as a vertical dashed line.

Fig. 5

Cutting depth as a function of the line distance

A line spacing higher than 12 microns leads to a significant drop of the cutting depth, because at these distances the kerf starts to be divided into its individual cuts. The maximum cutting depth can be reached at a value of 12 µm but the very large line distance leads to a slightly wavy cutting edge. A further reduction of the line spacing produces straight cut edges but with the disadvantage that the smaller the value is chosen, the faster the saturation depth is reached caused by the much narrower kerf. As a good compromise a line distance of 10 µm (highlighted with a red dotted circle) was chosen for the following multiline cutting experiments, which corresponds to a value just below the beam radius. This leads to straight cutting edges with a sufficient yield of groove depth compared to the number of cuts.

For the multiline cutting, experiments with 5, 10 and 15 parallel lines with the before determined distance of 10 micrometers were applied to achieve the required cutting depth. In this experiment up to 400 repetitions were performed. Results are shown in Fig. 6. The length of the y-axis of the plot equals the total sample thickness and the glass-silicone interfaces are visualized by horizontal lines and serve as a guide for the eye.

Fig. 6

Cutting depth achieved by laser cutting with multiple lines. With 15 parallel lines it is possible to cut through the first two layers without saturation effects

In case of 5 parallel lines the groove depth saturates within the first glass plate at a depth of 170 microns at 400 scan repetitions. Increasing the number of parallel cutting lines to 10 enables a full cut of the first glass plate as well as the whole phosphor/silicone layer. At a depth of about 180 microns within the glass plate a decrease in ablation rate is already evident but the much lower fluence threshold as well as the higher ablation rate of the silicone enables cutting to the next glass-silicone interface where the cut stops. To enable cutting of the second glass plate, a further increase of the cutting lines up to 15 was necessary. Here, the first glass plate was cut through after approximately 110 scan repetitions. After 200 scans, the silicone was also cut through without any saturation effect of the ablation rate for both layers and the second glass plate shows a groove depth of 13 microns. At the final value of repetitions, the cut stops at a residual thickness of 40 microns. The phosphor sheet can now be broken very easily for a complete separation of the individual substrate dies.

An optical microscope image of the cutting cross-sections for the experiments with 15 parallel lines is shown in Fig. 7. Like the single line results, the cross section of the cutting groove resembles the fluence profile of the laser in the beginning of the process. Since the fluence profile can be estimated as a quasi-top hat, the cutting line shows a flat ground surface for repetitions up to 100. In this regime, geometrical issues do not affect the maximum laser fluence. The focal position of the laser is kept constant at the sample surface during the whole cutting process. Since the Rayleigh length (focal length) for a beam with w₀ = 10.5 µm and a wavelength of λ = 523 nm is 662 µm, there is also no significant fluence drop caused by defocus within the first glass layer. This can explain the constant cutting rate which was observed in the discussion of Fig. 6. After 200 repetitions, the cutting process already reached the lower glass plate. The difference of the groove angle of glass and silicone is evident which is attributed to the difference in ablation threshold values. The cutting edge of the upper glass plate is bent during the cutting process, but it already converges to its final straight shape after 400 repetitions.

Fig. 7

Optical microscope image of the cutting cross-sections corresponding to the results shown in Fig. 2 for 15 cutting lines

The final straight cutting line can be clearly seen in the left image of Fig. 8 which shows an SEM image of a separated phosphor sheet dye. The measured cutting angle for each layer is displayed on the left edge where the laser entrance side was from the thicker glass layer in accordance to the depth measurements shown in Fig. 6. Calculating the inclination angle using Eq. 4 results in an angle of α = 79.96° for the first layer which is in absolute agreement with the experimental results. Since the silicone as well as the lower glass layer is in the range and above the Rayleigh length of the beam, respectively, the fluence was corrected using Gaussian beam calculations for an exact calculation of the theoretical inclination angle value. The calculated beam radius at the first glass-silicone interface is 11.6 µm and the resulting fluence is 7.1 J/cm². This leads to an inclination angle of 85.15° which again equals the measured value.

Fig. 8

Left: SEM image of the laser-cut phosphor sheet. On the left side of the sheet the measured cutting angle for each layer is displayed. Here, the laser entrance side of the cut was at the thicker glass plate corresponding to the measurements in Fig. 5. The facing surface (cut from the other side) demonstrates a high-quality cut for all three layers; right: SEM image of the three layers with corresponding EDX analysis. Debris deposit at the areas of individual silicone layers results from the cutting process of the final glass layer

The beam radius further increases and is 12.6 µm at the next silicone-glass interface at a distance of 440 µm from the sample surface. The corresponding laser fluence is 6 J/cm² and results in an inclination angle of 75.5° which is very close to the value observed in the experiment.

The cutting edges, which can be seen in the SEM image from the front, were cut from the bottom of the sheet. For this reason, the thin breaking area after separation can be seen on the upper edge. The cutting areas show high quality cuts for both materials. The edges as well as the sidewalls of the glass layers are very smooth and show no evidence of cracking, chipping or melting. Even the four individual silicone layers are visible, which were deposited during the manufacturing process of the phosphorus layer. They show melt-free cut edges, but their roughness is much higher compared to the laser-cut glass edge. For this reason, deposits appear to form more easily. These can be seen in the areas between the individual silicone layers in the form of small islands. The EDX analysis (see Fig. 8; right panel) shows highly elevated silicon signals in these areas, suggesting that the material is machining residue from the lower glass plate.

5 Conclusions

In this work, we demonstrate the femtosecond laser dicing of a sandwich system (phosphor sheet) with high cutting edge quality. By placing several parallel cutting paths, it is possible to separate the substrate down to a narrow remaining breaking edge. This is the most suitable process in terms of application, as a complete cut through would require further scan repetitions. Breaking allows easy separation of the dyes after the cutting process with a consistently high edge quality.

To predict the cutting edge geometry, a simple model is used to investigate the ablation saturation during laser cutting or drilling. This is sufficient for the determination of the cutting geometry, since the high number of scan repetitions during the cutting process leads to a geometry that is already approaching the saturation region. The model was applied to the multilayer system and thus allowed the calculation of the complete cutting geometry. A subsequent comparison with the experimental results shows the high agreement with the calculated values. Both the calculated and the measured value for the first glass plate were 80°. Since the ablation threshold of the silicone is lower than that of the glass, the sidewall is steeper with a calculated angle of 85.15°. This also corresponds very well to the measured values of 85°. Due to the reduced fluence in the area of the lower glass plate, the calculated value of the sidewall has dropped to 77°, which corresponds very well with a measured angle of 75°. The deviation of 2° is probably due to the fact that in a deep trench with a increasing aspect ratio, processes such as scattering at debris particles already play a role. This should be taken into account for cuts with higher aspect ratio.