1 Introduction

The phonon density of states (pDOS) constitutes a fundamental characteristics of a solid. Nowadays, for Fe the method of nuclear inelastic scattering (NIS) of synchrotron radiation can be used to measure this quantity [1]. This method also allows to study the changes of the pDOS in situations relevant for applications, such as in fatigue test used in materials science [2].

From the theoretical side, the pDOS of ideal crystals has been studied for long and is well understood [3]. However, real materials have defects, which render the calculation of the pDOS more complicated [4, 5]. For extended defects, such as dislocations or grain boundaries, atomistic simulations based on molecular dynamics can be used to calculate the pDOS of materials [6, 7].

Physical phenomena involving phonons are very often investigated via inelastic neutron scattering. This technique however is restricted to large sample volumes. Synchrotron based NIS is able to deliver the pDOS not only of \(^{57}\)Fe containing samples but also of single micrometer-sized objects, thin films and even monolayers. This motivates the present study which paves the way for future investigations of defects and grain boundaries in micro- and possibly nano-objects.

In this study, we present experimental data of the pDOS of Fe obtained by NIS. The data focus on the changes of the pDOS induced by straining an Fe sample. To analyze the data, we use molecular dynamics data of the pDOS in homogeneously strained Fe, on the basis of previous theoretical analyses [8]. The comparison will allow us to interpret the changes induced by strain and to discuss the origin of the remaining differences between experiment and simulation.

2 Experimental method

The NIS experiments were carried out at PETRA III, DESY in Hamburg, Germany, more specifically, at the “High Resolution Dynamics Beamline P01” [9]. The incoherent inelastic signal was detected in-situ by using avalanche photodiode detectors mounted in close proximity, ca. 1 cm above the sample. By means of an appropriate monochromator setup [10], the incident synchrotron radiation energy was tuned from \(-20\) meV to 50 meV around the resonance energy of 14.4 keV using a step size of 0.25 meV and 4 s per point. The energy resolution was ca. 1.1 meV. After subtraction of the elastic line and data normalization, the evaluation of the experimental density of phonon states was performed using the program ISDOS10, Version10, written by Sergeev [11].

Fig. 1
figure 1

Experimental setup for in-situ synchrotron radiation measurements during tensile loading

Full size image
Fig. 2
figure 2

Change of the pDOS of Fe under strain obtained by in-situ NIS experiments. The inset shows experimental error bars in the peak region of the pDOS

Full size image
Fig. 3
figure 3

Change of the pDOS under strain, simulation results

Full size image
Fig. 4
figure 4

Change of the peak heights in experiment and simulation under strain: a longitudinal peak, b first and c second transverse peak

Full size image
Fig. 5
figure 5

Change of the minima in experiment and simulation under strain: a first and b second minimum

Full size image
Fig. 6
figure 6

Extraction of velocity of sound from the pDOS according to Refs. [13, 18]. Data taken from the in-situ NIS experiment at 0% strain

Full size image

In contrast to previous experiments [2], the external strain was applied using an in-situ tensile test module “Deben Microtest 300N” with a maximum force of 300 N, see Fig. 1. The displacement of the specimen was measured with an inductive measurement cell. The initial gauge length between the clamping sections was 10 mm. The traverses of the module were constantly moved with 0.1 mm/min until a displacement of 1 mm and 2 mm was achieved, which corresponds to a total strain of 10% and 20% respectively. The exact traverse position was held constant at the mentioned displacements during the whole measurement.

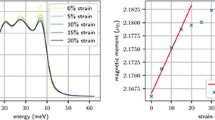
Using this method, we obtain the pDOS, g(E), for an unstrained sample and for strain values of 10% and 20%, see Fig. 2. In this study, the pDOS is always shown in a normalized form, \(\int g(E) \; dE =1\).

3 Results and discussion

To analyze and interpret the changes of the pDOS under strain, we calculate data for the pDOS of Fe using molecular dynamics simulation.These data were obtained in a way as described in [8] for a polycrystalline (pc) Fe sample with a grain size of around 10 nm; the sample contains around \(N=250{,}000\) atoms. The strained sample was produced with a strain rate of \(10^{10}\) s\(^{-1}\). The pDOS was evaluated from the velocity autocorrelation of the Fe atom vibrations at a temperature of 300 K. The velocity autocorrelation function is calculated for times up to 50 ps, corresponding to an energy resolution of 0.08 meV. It was convoluted with a gaussian of width 0.632 ps in order to reduce noise within the signal. Meyer et al. [8] also studied the influence of the interatomic interaction potential on the pDOS, which was found to be surprisingly large. The potential by Ackland et al. [12] was found to show the closest agreement with experimental data and was therefore used in the present study. For the present evaluation, the crystal relaxation after straining was increased from 10 to 50 ps; as a result, an improved resolution in particular for low-frequencies was obtained as compared to the data published recently.

Figure 3 shows the results, which we will discuss and compare to the experimental data. While the simulational results were obtained also for strains of 5% and 15%, for better visibility only the data for 0%, 10%, and 20% are shown. The most important changes induced by strain are localized in the peak region. The pDOS is characterized by three peaks. The two lower-frequency peaks, at around 22.5 and 27 meV, are mainly due to transverse phonon modes and will therefore be denoted as the transverse peaks. The high-frequency peak, at 36 meV, lies above the frequencies of transverse phonon modes and is hence due to longitudinal modes; it will be denoted as the longitudinal peak. The peak heights will be denoted by P\(_{{\mathrm{T}} 1}\) and P\(_{{\mathrm{T}} 2}\) and P\(_{\mathrm{L}}\), respectively. In order to characterize the changes induced by strain on the pDOS, these heights will all be normalized to their values at zero strain.

Analogously, the minima between the peaks will be denoted as the first minimum (at around 24 meV) and the second minimum (at around 32 meV).

Quite generally, the peak heights decrease under the strain, both in experiment (Fig. 2) and in the simulation (Fig. 3). Since error bars in the experimental data are quite large, we base our discussion mainly on the evolution of the simulational data under strain. The most pronounced changes occur in the longitudinal peak. They are quantified in Fig. 4a. The change in P\(_{\mathrm{L}}\) is considerably more pronounced in the simulated sample than in experiment; we consider that this is due to the larger grain size of the experimental sample. In previous work [8], it was shown that the P\(_{\mathrm{L}}\) decrease correlates linearly with an increase in dislocation density in the material.

The first transverse peak P\(_{{\mathrm{T}} 1}\) is only slightly affected by strain, see Fig. 4b. Here, both in experiment and in simulation, the maximum changes in P\(_{{\mathrm{T}} 1}\) peak height amount to only around 2%. The second transverse peak P\(_{{\mathrm{T}} 2}\) shows more pronounced changes and the evolution of the simulated peak height closely resembles that of the experimental height. In experiment, in particular the broadening of P\(_{{\mathrm{T}} 2}\) under strain is clearly visible.

The physical reason for the decrease of the peak heights lies in a depopulation of mid-frequency modes in the strained samples due to defect formation [8]. The modes are redistributed from the mid-frequency region to the high- and low-frequency tails. This effect is particularly clearly seen in the simulated spectra which feature the increase in the tails of the pDOS well, since the changes in the peak heights are more pronounced.

The changes in the minima between the peaks are quantified in Fig. 5. Changes here are smaller than in the peak heights. This is due to the near cancellation of two effects: (1) phonon modes are redistributed away from the mid-frequency region, depleting also the minima; (2) the broadening of the transverse and longitudinal peaks visible in Figs. 2 and 3 re-populates the minima. Overall, the experimental data—and for P\(_{{\mathrm{T}} 2}\) also the simulational data—is uncertain even of the sign of the change in the minima height. Hence an analysis of the minima does not appear to be useful for analyzing the strain-induced changes in the pDOS.

At low frequencies, below around 20 meV, the pDOS features a quadratic increase, which can be characterized as [13]

$$\begin{aligned} g(E) = \frac{V}{2 \pi ^2 \hbar ^3 v_D^3} E^2 , \end{aligned}$$
(1)

where V is the atomic volume and \(v_{\text {D}}\) is the Debye velocity of sound, see Fig. 6. The data allow us to extract a value of \(v_{\text {D}} = 3.49\) km/s. This region of long-wavelength vibrations is thus determined by the elastic constants of the material. The experimental spectra show no change in this region under strain. The simulation data, however, show an increase of the spectra in this region which originates from an elastic stiffening of the material under strain.

Table 1 Thermodynamic parameters extracted from a the experimental and b the calculated pDOS. In the experimental data, the value in brackets indicates the uncertainty of the last digit
Full size table

The pDOS allows to evaluate basic thermodynamic parameters (per atom) [1, 14, 15], such as the internal vibrational energy, U, the specific heat at constant volume, \(c_{\text {V}}\), and the vibrational entropy, S. The data are listed in Table 1 and feature a considerable decrease of force constant and energy with strain. Such a decrease has already been seen previously [2] where, however, no in-situ experiments could be performed. The mean phonon energy, G, is proportional to the Debye temperature, \(T_{\text {D}}\), via \(k_{\text {B}} T_{\text {D}}=(4/3)G\), where \(k_{\text {B}}\) is Boltzmann’s constant. The experimental data obtained for 0% strain are in good agreement with previous measurements on \(\alpha \)-Fe [2, 16]. For increased tensile strain, we observe a small decrease of the mean phonon energy, the total vibrational energy, and—consistently—an increase in the vibrational entropy. This lowering of the mean vibrational frequencies is accompanied by a decrease of the force constant; this latter aspect is the only feature that is clearly outside the error bars in the experimental data. We conclude that the integral changes in the pDOS under strain can be characterized as a mode redistribution towards lower frequencies. This aspect coincides with our previous analysis of the changes induced by mechanical fatigue in an ARMCO iron sample [2].

(a)

strain

\(f_{\text {L}}\)

\(\sqrt{x^2}\) (Å)

\(U_{\text {vib}}\) (meV)

\(c_{\text {v}}\) (\(k_{\text {B}}\))

\(S_{\text {vib}}\) (\(k_{\text {B}}\))

G (meV)

D (N/m)

0%

0.79(1)

0.115(3)

84(3)

2.72(3)

3.14(9)

26.9(1)

170(5)

10%

0.79(1)

0.113(3)

84(3)

2.73(3)

3.14(9)

26.8(1)

166(5)

20%

0.79(1)

0.114(3)

84(3)

2.74(3)

3.15(3)

26.5(5)

160(5)

(b)

strain

\(\sqrt{x^2}\) (Å)

\(U_{\text {vib}}\) (meV)

\(c_{\text {v}}\) (\(k_{\text {B}}\))

\(S_{\text {vib}}\) (\(k_{\text {B}}\))

G (meV)

D (N/m)

0

0.155

84.84

2.711

3.203

27.18

180.4

5

0.162

84.79

2.713

3.227

27.04

179.3

10

0.166

84.78

2.713

3.233

27.02

179.1

15

0.164

84.75

2.714

3.243

26.94

178.4

20

0.166

84.75

2.715

3.250

26.91

178.2

In simulation—and less pronouncedly also in experiment—an increase of the high-frequency tail of the pDOS with strain can be observed. It is caused by the production of extended defects, which also populate high-frequency modes [8]; this is in contrast to the well-understood action of vacancies, which lead to a decrease of the pDOS at high frequencies [17].

The effects of tensile strain are more clearly seen in the simulation than in the experiment, primarily because the error bars in the experiment are unavoidably quite large. Thus, differences between experiment and simulation cannot be clearly identified. These could however exist, caused by the different grain size (10 nm in simulation vs around 10 \(\upmu \)m in experiment) and strain rate (\(10^{10}\) s\(^{-1}\) vs \(1.7 \times 10^{-4}\) s\(^{-1}\)). The values used in simulation are typical of molecular dynamics simulation, and cannot be changed by the many orders of magnitude necessary to reach experimental conditions.

4 Conclusions

We conclude that simulation shows qualitatively the same features as experiment, but in a more pronounced manner. The depopulation of the modes are most clearly observed in the changes in peak height, where the effect is most pronounced for the longitudinal and the second transverse peaks.

Under strain, the pDOS of pc Fe samples changes in a characteristic way by a decrease in the peak heights of the spectra. These feature a redistribution of phonon modes away from the mid-frequency region towards the tails of the distribution and are caused by defect production under the high strain levels. The changes of the thermodynamic parameters in the sample are characterized by a decrease in the mean phonon frequency and a concomitant decrease in the force constant.

In the future, it appears interesting to use samples prepared with various initial microstructures (such as grain sizes) and to measure the changes induced in these samples by tension. Also, the effect of temperature on the results might be studied, since, e.g., the occurrence of various dislocation types will be affected.