1 Introduction

Since the first Direct Laser Write (DLW) waveguides were demonstrated in 1996 [1], there has been an ever-increasing uptake of the technology for photonic applications. A particularly attractive feature is the ability to fabricate devices in three dimensions, opening the door to new 3D architectures such as photonic lanterns [2], tritters [3], tunable circuits [4], and high-density space-division multiplexing in telecommunications [5]. The technology is progressing to the point that it is now required to write waveguides over depth ranges greater than several hundred micrometers, for structures such as waveguide arrays [6,7,8].

The critical issue of writing waveguides over a large depth range is spherical aberrations (SA). The refractive index mismatch between air and the substrate leads to a varying degree of refraction for rays incident at different angles, having previously been focused by a microscope objective. For moderate/high numerical aperture (NA) microscope objectives (NA \(\ge 0.4\) [9]), this leads to significant SA, which distorts the focal volume, with a large degree of axial elongation. Spherical aberrations increase with increasing NA, focusing depth, and refractive index of the substrate. For DLW waveguides, moderately high NA lenses are required to achieve sufficient peak intensities, and to reduce the ellipticity and the size of the focal volume, while the use of oil immersion objectives to eliminate the refractive index mismatch is not applicable for writing deep waveguides due to the short working distance of these lenses [10,11,12,13,14,15,16].

In general, the shape of the focal volume can be designed with the help of beam shaping. The slit beam shaping technique [17] with a physical slit aperture has already been applied for waveguide writing in the low and high repetition rate regime for several glasses [18,19,20,21] to improve the performance of shallow waveguides. Astigmatic focusing may also be employed for a similar effect [22, 23], while the multiscan technique [2, 20, 24] also allows control of the waveguide shape. However, to overcome the problem of depth-related focus distortion, the correction of SA is crucial. Microscope objectives with adjustable SA compensation [11] could be utilized, although this becomes practically difficult for large 3D waveguide networks. Aberration correction by liquid crystal spatial light modulators (LC-SLMs) [25, 26] has several advantages, including higher accuracy and flexibility, and particularly that the LC-SLM may be used simultaneously with slit beam shaping for writing deep waveguides [16].

For low laser pulse repetition rates, the structural modifications induced by DLW closely match the shape of the laser focus, such that any distortion adversely affects the waveguide with particular reference to the mode profile. We have previously demonstrated the benefits of aberration correction for 3D waveguide writing in such a regime [16], and here, we extend the work to explore the consequences at higher pulse repetition rates in the heating regime. While the negative impact of SA on DLW in the heating regime was noted by Eaton et al. [27], who showed an increase in the mode field diameter with increasing writing depths, Fernandez et al. [28] demonstrated that SA can actually aid high repetition rate DLW in some circumstances by driving laser-induced ion migration [18, 29].

Much attention has recently been paid to DLW in the borosilicate glass Eagle 2000 from Corning [30,31,32], whose properties include a comparatively low bandgap, low melting point, and low thermal diffusivity, which are beneficial for the formation of high-quality waveguides in the high repetition rate regime [14]. Consequently, we chose Eagle 2000 as the material for our study on aberration effects during waveguide writing in the heating regime, using a frequency-doubled femtosecond laser (515 nm) with pulse repetition rate of 1 MHz. Having demonstrated the negative impact of aberration on waveguide formation, we subsequently use an LC-SLM for aberration correction, enabling the fabrication of low-loss single-mode waveguides over a depth range greater than 1 mm.

2 Experimental setup

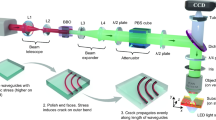
Waveguides were written with a regeneratively amplified Yb:KGW laser (Pharos SP-06-1000-PP; Light Conversion), delivering 168 fs laser pulses at a repetition rate of 1 MHz with a central wavelength of 1030 nm, which was frequency doubled to 515 nm. The beam was expanded and was directed on to an LC-SLM (Hamamatsu Photonics X10468). The LC-SLM was imaged in a 4f configuration onto the pupil plane of a microscope objective (20 \(\times\); Zeiss Plan Neofluar; 0.5 NA), which had internal correction for SA corresponding to 170 \(\upmu\)m depth in common glass (coverslip correction). The workpiece was moved perpendicular to the laser beam (transverse writing geometry) during fabrication with a three-axis translation stage [AEROTECH; ABL 10100LN (x, y) and ANT95-3-V (z)].

The laser pulses were focussed inside the borosilicate glass (Corning Eagle 2000) specimen (\(20\times 20\times 1.15\, \mathrm {mm}^3\)) at various depths from 170 \(\upmu\)m down to 1000 \(\upmu\)m. Due to the comparatively low bandgap of the glass (4.0 eV [14]), we assume that a two-photon absorption at wavelength 515 nm (2.4 eV) was the initial ionization mechanism followed by avalanche ionization. The refractive index at the laser wavelength was estimated with Cauchys equation to be 1.511, very close to that of coverslip glass.

Fig. 1
figure 1

Theoretical simulations of the focal intensity distribution for focusing at different depths. The propagation direction is along the positive z-direction. The brightness is normalized for each image, while the peak intensity ratio relates the peak intensity to that at the aberration-free depth of 170 \(\upmu\)m

Full size image

After fabrication, the two relevant surfaces of the specimen were polished to reveal the waveguide and improve the surface quality to achieve lower coupling losses. 777 nm laser light from a polarization maintaining single-mode fiber was butt-coupled into the waveguide without any immersion fluid to record the near-field mode of the end facet, using a long-working distance microscope objective and a CCD camera. In addition, the throughput of the waveguides was determined by coupling the light into a power meter. All values reported are for total throughput of the waveguides, not taking into account either Fresnel reflections at the fiber–glass interface or coupling losses due to mode-mismatch between fiber and waveguide.

3 Experimental results

3.1 Waveguides at 170 \(\upmu\)m depth

Since the microscope objective used for the experiments had an internal aberration correction for a 170 \(\upmu\)m coverslip with refractive index close to that of the Eagle 2000 glass, waveguide fabrication in this depth can be considered as aberration-free. Consequently, the LC-SLM was not used for experiments at this depth. The highest throughput achieved at this depth was used as a benchmark for waveguides written in deeper depths. To identify the writing parameters of feed rate and pulse energy for this benchmark, two subsequent studies were carried out. In the first one, a coarse gradation of both parameters was applied to locate the process window. Afterwards, a finer gradation was used to achieve a more detailed characterization of the previously located process window. The optimum conditions for our application were, thus, determined as a feed rate of 2 mm/s and pulse energy of 80 nJ (measured after the objective lens). Eleven waveguides written with this combination all showed guided throughput > 84% over a 20 mm chip.

3.2 Deep waveguides without aberration correction

To investigate the impact of SA on the quality of a waveguide, we wrote waveguides at different depths without using the LC-SLM for aberration correction. Since, for our application, the process window was greatest for a feed rate of 2 mm/s, the deep waveguides were written with this constant value. Before setting the range for the variation of pulse energy, we simulated the intensity distribution of the focal region for all investigated depths (Fig. 1). We modeled the aberration using the analytic function [15, 33]:

$$\begin{aligned} \phi _{\mathrm {SA}} = \frac{2\pi d}{\lambda } \left( \sqrt{n_2^2 - (\rho \mathrm {NA})^2}-\sqrt{n_1^2 - (\rho \mathrm {NA})^2}\right) , \end{aligned}$$
(1)

where \(\lambda\) is the wavelength of the fabrication laser, \(\rho\) is the normalized objective lens pupil radius, NA is the associated numerical aperture, and \(n_1\) and \(n_2\) are the refractive indices of air and glass respectively. We note from Eq. 1 that the phase aberration is larger and, hence, the focal distortion stronger, for the frequency-doubled wavelength as opposed to the fundamental wavelength of the laser. This can be understood, since the refraction at the surface creates a path length difference which is relatively insensitive to wavelength. Thus, in the absence of aberration correction, it would be better for 3D photonic circuits to use a longer wavelength fabrication laser and reduce the aberration effects.

Fig. 2
figure 2

a Transmission throughput as a function of laser writing pulse energy, for waveguides fabricated at different depths below the glass surface at a feed rate of 2 mm/s. b Transmission microscope image and c near-field mode profile of the guiding structure fabricated with 160 nJ at a depth of 450 \(\upmu\)m

Full size image

The peak intensity ratio is defined as the simulated peak focal intensity of the respective depth divided by the peak intensity of the aberration-free depth. From Fig. 1, we can see that, at a depth of 250 \(\upmu\)m, the aberration is expected to modestly reduce the peak intensity, but does not significantly alter the focal dimensions. However, going deeper into the glass leads to a rapid reduction in peak intensity and severe focal distortion.

We examined the effect of writing waveguides at different depths without aberration correction. The pulse energy was varied to ascertain whether there was a process window in which the aberration did not prevent the fabrication of low-loss single-mode waveguides. The minimum pulse energy at every depth was set as 80 nJ, corresponding to the optimum in the absence of depth-dependent aberration. The pulse energy was then varied at each depth in a range up to a maximum value where the peak intensity predicted by theory for the aberrated focus (Fig. 1) corresponded to the peak intensity at the aberration-free depth of 170 \(\upmu\)m. This was not possible for every depth, since the pulse energy after the objective was limited to 250 nJ.

For the 250 \(\upmu\)m depth, single-mode waveguides with throughput 81% could be achieved. The process window was slightly shifted to higher pulse energies due to the focus distortion. For all other depths, guiding structures with > 65% throughput could be formed. As expected, the throughput maximum was shifted to higher pulse energies for increasing depths. However, as the throughput increased, the guiding structure always comprised multiple guiding regions stacked above each other, as shown in Fig. 2. This can be understood from inspection of microscope images of the end facet for the waveguides, also in Fig. 2, showing a large axial elongation in the written structures, which is related to the focal distortion generated by the spherical aberration, as predicted theoretically Fig. 1. We note that the depth window for single-mode waveguide operation is extended by fabricating weaker waveguides at lower pulse energy, but the aberration is still present and leads to a severely elongated mode shape and associated high coupling loss to optical fiber. Thus, we can see that the aberration cannot be circumvented by varying the pulse energy in the cumulative heating regime and, therefore, limits the depth range for devices if identical waveguides are required.

3.3 Deep waveguides with aberration correction by an LC-SLM

Having demonstrated the negative impact of SA, we now want to show experimentally that we can compensate the SA with the help of an LC-SLM and achieve the quality of the benchmark waveguides for several depths down to 1000 \(\upmu\)m. A predictive aberration correction was applied following the procedure as outlined in Ref [15], where we note that the aberration correction protocol is the same for laser processing in both the high and low pulse repetition rate regimes. The depth focused inside the glass d is used to calculate the appropriate phase compensation in the pupil of the objective lens \(\phi _{\mathrm {SA}}\) using Eq. 1. The component of \(\phi _{\mathrm {SA}}\) which corresponds to a pure spherical defocus was removed to increase the bandwidth of the SLM, as described in Ref. [15], such that the actual fabrication depth was \(n_2 d\), while d corresponded to the physical translation distance. This process yielded the phase masks displayed in the third row of Fig. 3a. To ensure the phase correction was optimum at each depth, a further aberration correction step was applied following a sensorless adaptive optics scheme [34]. Varying magnitudes of low-order Zernike modes (up to and including the fourth radial degree) were added to the depth correction phase and displayed in sequence on the SLM, while experimentally observing the threshold pulse energy required for fabrication. The magnitude of each Zernike mode which minimized the threshold pulse energy was added to the final correction phase and then applied to the SLM [26].

Fig. 3
figure 3

a Transmission microscope images of the end facet (top row) and near-field mode profile (second row) for waveguides written at different actual depths d beneath the glass surface. A pulse energy of 70 nJ was used for fabrication at every depth. Also shown on the third row is the phase mask corresponding to the correction of the depth-induced spherical aberration. The bottom row shows the SLM display used for aberration compensation at each depth, where the active circle corresponds to the area of the device conjugate to the objective pupil and displays the phase mask shown in the third row. In addition, a background phase is added to compensate for system aberrations, while the pupil phase is further optimized to minimize the fabrication threshold pulse energy. b Transmission microscope images showing the reliable fabrication of pairs of uniform waveguides using a single pulse energy through the entire depth of the workpiece

Full size image

Figure 3 shows microscope images of waveguides fabricated at different depths through the thickness of the glass workpiece using aberration compensation. The optimum pulse energy for waveguide fabrication was reduced slightly to 70 nJ relative to the experiments in Sect. 3.1, since the SLM was effective in removing system-related phase aberrations. A pulse energy of 70 nJ and feed rate of 2 mm/s were subsequently used at every depth. There was no discernible depth dependence to the structural modification when viewing the end facet of the waveguides in a transmission microscope. The near-field mode profile is also shown at each depth, for guided light of 777 nm. The waveguides supported just a single mode irrespective of depth, and there was minor variation in the mode size and ellipticity. This uniformity in the structural change while using a constant pulse energy for the fabrication indicates that we achieved good correction of the depth-dependent aberration.

The transmission microscope image in Fig. 3b further emphasizes the uniformity of the fabrication with the aberration compensation. It was, thus, possible to fabricate uniform waveguides through the entire depth of the workpiece without changing the fabrication parameters of feed rate and pulse energy.

Fig. 4
figure 4

Plot of the transmission throughput and mode ellipticity as a function of depth for waveguides fabricated with adaptive aberration compensation

Full size image

Figure 4 plots the transmission throughput and mode ellipticity of the aberration-corrected waveguides as a function of depth in the glass. The mode size was plotted by fitting a Gaussian function to each axis of the near-field mode profile and displaying the 1/e value. There was minor change in the mode size as a function of depth and no obvious trend, but, importantly, the ellipticity of the mode remained approximately constant, showing no clear evidence of elongation along the fabrication optical axis z from depth-dependent spherical aberration. Likewise, there was no discernible difference in transmission of the waveguides as a function of depth for the aberration-corrected waveguides, and any variation was within typical fabrication bounds.

4 Conclusion

In conclusion, we have demonstrated that depth-dependent spherical aberration limits the performance of direct laser written waveguides fabricated in the cumulative heating regime, using a laser pulse repetition rate of 1 MHz. The minimum achievable propagation loss is increased at a distance of just 80 \(\upmu\)m from the optimum depth, while waveguides written deeper in the workpiece became increasingly multimode. We note that using the frequency-doubled beam for the fabrication likely exacerbates the depth dependence, since the phase aberration is stronger than using the fundamental wavelength of the amplified laser. We have additionally shown though that predictive aberration correction with adaptive optics is successful for the fabrication of uniform single-mode waveguides at any depth in the workpiece. This is crucial when fabricating complex waveguide lattices [35] and holds promise for a wide range of three-dimensional photonic circuits.