Abstract
Optical-lattice-like waveguides were fabricated in a z-cut lithium niobate crystal by an 11-MHz-repetition-rate pulsed laser. Two simple approaches based on varying the inscribing pulse energy in accordance with the position of the tracks were implemented to enhance the inscription results. Low propagation losses were observed in the visible and near-infrared parts of the spectrum. The minimum losses of less than \((0.4\pm 0.1)\) dB/cm and \((3.5\pm 0.2)\) dB/cm for transverse electric and transverse magnetic polarized light, respectively, in the fundamental guiding mode at \({1550}\hbox { nm}\) were achieved after heat treatment at \({350}\,^{\circ }\hbox {C}\) for three hours, and were preserved up to \({700}\,^{\circ }\hbox {C}\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Lithium niobate (LN) offers incredible versatility as a substrate for integrated photonics (IP) platforms owing to its wide range of transparency, high second-order nonlinearity and commercial availability [1]. Recently, a number of LN-based IP devices have been demonstrated, such as electro-optic modulators [2] and various types of frequency-mixing devices [3], which show a potential for applications in high-speed optical communication interconnects, on-chip sensors and quantum photonics. Among the various micro-machining techniques of photonic waveguides, such as proton exchange, titanium in-diffusion, iron implantation and dry etching, the femtosecond (fs)-laser inscription method is considered to offer improved versatility in the choice of processed materials and greater flexibility in creating micro-structures in the three-dimensional space [4].
In general, fs-laser written waveguides in LN can be categorized into three groups depending on the mechanism of optical guiding: positive refractive index (RI)-induced [5,6,7], stress-induced [8,9,10], and depressed-cladding waveguides [11,12,13,14,15,16,17]. The focus of the present study is on the fabrication and optimization of waveguides of the third type, which present a number of advantages over the first two types, including unmodified properties of the waveguide core, low polarization dependence, high thermal stability and, especially, output-profile controllability. While several studies have reported on waveguide inscription in LN using low-repetition-rate (LRR) fs-laser systems [11,12,13,14,15,16], to date the inscription by high-repetition-rate (HRR) fs lasers has been less explored. HRR laser systems enable significantly shorter processing times compared to their LRR counterparts. This is especially advantageous to the fabrication of complex structures and large-scale commercial production. It is also noteworthy that the energy efficiency of HRR systems can be twice as large as that of LRR systems owing to the heat accumulation effect [18]. Recently, Bhardwaj et al. demonstrated depressed-cladding waveguides based on the usual circular packing geometry in a x-cut LN crystal with impressively low losses of 0.56 dB/cm and 0.51 dB/cm for TE (perpendicular to optical axis) and TM (parallel to optical axis) polarized light, respectively, at 1550 nm [17]. While an HRR laser (200 kHz at 1030 nm) was used for inscription, thermal treatment of the fabricated waveguides, which has been demonstrated by Nguyen et al. [16] to improve the anisotropic guiding properties of a waveguide, was not included in their study.
In this work, we fabricated depressed-cladding waveguides with a hexagonal optical-lattice-like structure in z-cut LN samples. This packing geometry was recently shown numerically by Karakuzu et al. to offer low-loss waveguide operation over a wide spectral range [19]. We systematically explored the effects of operational parameters such as the laser pulse energy, the speed and direction of translation stage movement, and the beam focus depth inside the samples on the inscription process, which have not been comprehensively studied in the HRR regime yet, as well as the effects of post-fabrication heat treatment. Ultimately, we demonstrated that HHR fs-laser micro-machining can effectively be used to attain depressed-cladding waveguides featuring low losses and single-mode guiding for both the TE and TM polarization states in LN. Our results revealed not only that thermal annealing brings about a notable enhancement of the optical guiding performance in both orthogonal polarizations, but also that waveguides inscribed by an HRR laser feature higher thermal stability than LRR-laser-modified structures [7, 16]. The observed waveguide’s tolerance to high temperature annealing is promising for applications requiring extreme working conditions. Preliminary findings of this research were published in [20]. In this paper, we report on the study of the effects of higher-temperature annealing on the fabricated waveguides, which gives insight into the optical guidance and physical morphology of laser-inscribed structures after intense thermal treatment. Further, we discuss in detail some challenges faced by the current fs-laser inscription technology, such as the inscribing pulse energy degradation due to spherical aberration and the focus splitting effect originating from the birefringence of the host material, and the measures that can be taken to minimize such effects. Finally, we provide an interpretation of the anisotropic guiding behavior of the fabricated waveguides based on our observations as well as previous theoretical and experimental studies.
2 Experimental setup and methodology
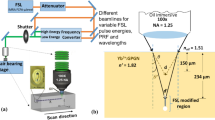
The inscribing laser was a Ti:sapphire oscillator system (Femtosource Scientific XL) that delivered an output beam at 790-nm central wavelength and 11-MHz repetition rate. The pulse duration was adjusted to 66 fs, corresponding to a spectral width of approximately \({25}\hbox { nm}\). The three-dimensional translation system (Aerotech) used for inscription comprised a two-dimensional air-bearing stage (ABL10050) for the x and y directions, which enabled precise movement of the samples transversely to the laser beam, and a linear mechanical stage (ATS100) for the z direction, enabling accurate positioning of the focusing objective relative to the samples along the direction of the laser beam. The motion of the stages was controlled via commercial Aerotech software, providing functions for setting the writing speed and executing external programs to operate the optical shutter and the laser power attenuator. A 100x microscope objective (oil-immersion, \(n = 1.518\)) with a numerical aperture (NA) of 1.25 was used to focus the circularly polarized beam beneath the polished surface of \(5\%\)-Mg-doped z-cut LN wafers. We found that the use of this high-NA micro-objective combined with keeping the pulse energy below the threshold for self-focusing could effectively prevent filamentation of the inscribed structures. To minimize the depth-dependent focus-splitting effect originating from the uni-axial birefringence of LN [21], we chose to write our waveguides close to the sample surface (in the depth range of 35 to \({130}\,\upmu \hbox {m}\)). The elongation of the modification tracks caused by spherical aberration, which is usually regarded as being problematic, was in fact found useful here to bridge the separated modified areas resulting from focus splitting. Although the cross-sectional shape of individual tracks was elliptic, it was possible to carefully adjust the vertical and horizontal spacing between them within the hexagonal lattice geometry to achieve an output mode-field with a nearly circular symmetry. Furthermore, by maintaining the laser pulse energy density constant and above the heat-accumulation threshold, we could produce tracks with a smooth profile and high RI contrast without needing any advanced aberration-correction techniques, such as spatio-temporal focusing [22] or adaptive optics [23, 24], which would add cost and complexity to the fabrication process.
Figure 1 shows an example of a waveguide cross section, where the array of circles represents the disposition of the modification tracks. Each waveguide comprised 84 tracks precisely arranged in an optical-lattice-like packing geometry with four hexagonal layers. The tracks were damage tracks and were inscribed via a single scan along the LN crystalline x-axis. The order of writing was from high to low row-index (m) tracks to avoid overlap between inscribed tracks and the laser beam path. Preliminary trials indicated that a track separation (d) between \({9}\,\upmu \hbox {m}\) and \({12}\,\upmu \hbox {m}\) is optimal in that the tracks are neither so densely packed to induce structural defects nor so loosely packed to produce multi-mode optical confinement. In the present study, we used the value d of \({9.9}\,\upmu \hbox {m}\), along with a vertical separation between track rows of \({6.0}\,\upmu \hbox {m}\), which is the nearest integer multiple of the step size of the vertical translation stage in our setup able to realize a nearly circular mode field.
While the effect of spherical aberration on the shape of the modification tracks was not problematic in this study, the dependency of the laser energy density on the inscription depth resulting from longitudinal focus spreading, which can cause a decline of the laser-induced RI change with increasing depth [23, 24], is needed to be addressed to ensure homogeneity of the optical cladding across the waveguide cross section. In fact, in the stage of parameter testing we noticed that a suitable increase of the input pulse energy with the inscription depth would suffice to compensate the energy density degradation in the irradiated regions and, thus, lead to strengthened cladding effects of the resulting waveguide and, hence, a more vertically symmetric output intensity profile. To test this assumption, a set of waveguides (named Group B) were fabricated by linearly varying the laser pulse energy with the inscription depth and compared with a reference waveguide set (Group A) for which the pulse energy was fixed. We also fabricated waveguides with a radial variation of the pulse energy (Group C) to examine the effects of different cladding RI distributions on light guiding, which was previously studied numerically [19]. Within the pulse-energy-variation schemes mentioned above, the energy \(E_{m,n}\) allocated to the machining of a track of vertical position m and radial position n (see Fig. 1) can be described by
where the values of the energy-increase steps \(\varDelta E_\mathrm{d}\) and \(\varDelta E_\mathrm{r}\), initial pulse energy \(E_0\), and parameter p, given in Table 1 for the different groups of waveguides, were chosen based on the empirical grounds of our experimental observations.
After waveguide inscription, the LN wafers were diced to a width of \({2.35}\hbox { cm}\) (waveguide length) and side polished to the optical grade. An optical microscope was used to photograph the waveguides and individual inscription tracks in the differential-interference-contrast (DIC) and bright-field modes. Several track’s top-view images recorded at slightly different focus distances were used to calculate the cumulative phase profiles of individual tracks at \({530}\hbox { nm}\) by the IATIA commercial software using the quantitative phase microscopy (QPM) method. The RI change profiles of the tracks (with respect to the non-irradiated areas) were thereby reconstructed. From a track’s RI distribution, we retrieved the differences between the negative peak located close to the center of the irradiated area and the adjacent positive humps at different positions along the track. The average of these RI differences will be hereafter referred to as the RI contrast \((\varDelta n)\) of a track.
The light sources for waveguide characterization included three QPhotonics fiber-coupled laser diodes (of central wavelengths \(\lambda _0 = 1064\), 1456 and 1547 nm), an ILX Lightwave laser diode (\(\lambda _0 = 1310\) nm) and a Fianium SC450-4 supercontinuum source which operated with three bandpass filters from Semrock (\(\lambda _0 = 531\), 700 and 840 nm). The beam from the source was coupled into the waveguide being investigated by a conventional fiber butt-coupling setup, and the waveguide output was collimated by a microscope objective and measured by either a photodetector (Newport) or an InGaAs camera (Goodrich). The propagation loss \((\alpha )\) was estimated by subtracting the double-Fresnel loss and the loss due to mode mismatch from the insertion loss. The mode-mismatch loss was evaluated as the overlap integral of the measured electric fields in the waveguide and coupling single-mode fiber.
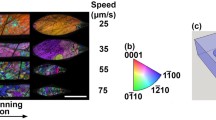
RI contrast, and cross-sectional height and width of individual tracks versus (a) laser pulse energy, (c) translation speed, and (d) focus depth. (b) DIC images of track’s cross sections selected from subplot (a), showing a ‘quill pen’ structure. This figure is adapted from [20]
Heat treatments of the waveguides were performed at six temperatures: 250, 350, 500, 700, 850 and \({950}\,^{\circ }\hbox {C}\) in an incremental order by using an open-air furnace. The annealing duration time was set to three hours for each temperature, excluding heating-up (at \({1}\,^{\circ }\hbox {C/s}\)) and cooling-down (at \({3}\,^{\circ }\hbox {C/s}\)) periods. The optical characteristics of the waveguides were thoroughly tested after each thermal annealing step.
3 Results and discussion
3.1 Effects of operational parameters
Figure 2a shows the RI contrast and cross-sectional dimensions of individual tracks inscribed with a writing speed of 10 mm/s and varying laser pulse energy at a depth of approximately \({85}\,\upmu \hbox {m}\). The following linear equation can be fitted to the observed dependence of the RI contrast on the pulse energy:
where \(k[-x,+x] = [2.71, 2.44]\times 10^{-2}\hbox { nJ}^{-1}\) represents the increasing rate of negative RI contrast, and \(E_\mathrm{th}[-x,+x]=[11.09, -0.59]\) nJ is the energy threshold for generation of the RI modification. Slight differences in the parameter values between the negative and positive x translation directions suggest that the tracks experienced the nonreciprocal writing phenomenon, which was previously reported by Yang et al. [25] using an LRR fs-laser system (250-kHz at 1064 nm). However, Yang’s results revealed a direction-dependent behavior only for the tracks written along the y-axis, whereas our observation concerns the x-axis translation. The track’s cross sections shown in Fig. 2b exhibit the so-called ‘quill pen’ structure, which plausibly stemmed from an-isotropic trapping of the electron plasma by a tilted front of the inscribing laser pulse [26]. It is noteworthy that we did not observe significant differences in track sizes in relation to the translation direction. The average height-to-width ratios were 4.4 and 4.6 for the \(-x\) and \(+x\) directions, respectively. These ratios tended to decrease with increasing pulse energy.
Figure 2c, d illustrates the dependence of the track’s properties on the translation speed and the focus depth. It can be seen that within the range of moderate translation speeds (from 5 mm/s to 20 mm/s), the track’s properties did not change significantly with varying speed. This reflects a distinctive feature of the RI modifications for laser writing in the heat accumulation regime. By contrast, both the RI contrast and cross-sectional dimensions showed noticeable increase/decrease with increasing translation speed at the low/high speeds. Furthermore, the track’s properties were largely preserved within the range of variation of the focus depth from \({50}\,\upmu \hbox {m}\) to \({110}\,\upmu \hbox {m}\) (which is assumed to be the depth range sustaining minimum aberration of the focusing objective). Figure 2d also highlights that for beam focusing beyond this optimal depth range the tracks generated by low pulse energies suffered more from drops in both RI contrast and size of the damage area. Actually, we can see in Fig. 3 that from a depth of approximately \({110}\,\upmu \hbox {m}\), the combination of the effects of focus splitting and track’s elongation impacted significantly the cross-sectional morphology of the tracks, with the development of vertical splitting in the tracks written with low pulse energy and the presence of a non-damage tail (dashed boxes) in the high-energy-generated structures. It is worth noting that the focus splitting effect was observed here at deeper (4-5 times) inscription depths than those reported by Zhou et al. using a focusing objective (oil) of 1.45-NA and linearly polarized LRR fs-laser pulse [21].
3.2 Optical guiding properties before heat treatment
Characterization of unannealed waveguides. a Propagation losses (top) and MFD (bottom) of Group A, B and BX waveguides versus initial pulse energy \(E_0\). b Cross-section’s DIC images and TE near-field intensity profiles of waveguides fabricated with different pulse-energy variation schemes. \(\lambda ={1550}\hbox { nm}\). This figure is adapted from [20]
Figure 4 summarizes the results of the characterization of the different groups of fabricated waveguides before heat treatment. As can be seen in Fig. 4a, the guiding properties of the waveguides were highly sensitive to both the laser pulse energy and the speed of writing. The increase in track’s RI contrast induced by higher pulse energy tended to reduce both the waveguide propagation losses \((\alpha )\) and mode-field diameter (MFD). However, for pulse energies above 50 nJ, the effects of high-energy-driven defects and strong stress field (originating from lattice defects and amorphization) came into play, thus worsening the propagation loss for both light polarization states. The inferior guiding performance of the waveguides in Group BX as compared to Groups A and B waveguides can be ascribed to the higher track roughness and stronger induced stress field that were typically observed for the tracks written at low translation speeds. These results, therefore, substantiate the importance of operational parameter optimization for the inscription of good-quality waveguide structures.
It is apparent in Fig. 4a that the optical guidance of the fabricated waveguides was polarization dependent, with the loss in the TE polarization state being significantly lower than that in the TM state across the range of pulse energy studied. There are two possible explanations for this behavior: the anisotropic piezo-optic (APO) RI change generated by the stress field surrounding the inscribed tracks, and the modal radiation leakage (MRL) effect due to orthogonal polarization mode coupling. The APO effect was mentioned by Burghoff et al. [8] to describe the guiding mechanism of their Type-II dual-track waveguides, in which the optical guiding zone located between two parallel tracks (stress-field overlapping area) was able to support only the beam with TM polarization. The observed leakage of the TE-polarized beam was explained to result from anisotropic conformation changes of lattices located on the sides of the modification tracks. In other words, a compressing stress along the horizontal axis would cause a negative RI change in the TE polarization (leaky mode), whereas a tension along the vertical axis would lead to a positive index change in the TM polarization (guided mode). A similar idea was later applied to depressed-cladding waveguides of a circular packing geometry by Nguyen et al. [15], but the stress-field effect, which mainly concerned the cladding region (rather than the guiding core), was suggested to suppress light confinement in the TM polarization and enhance light guidance in the TE polarization. However, it remains questionable whether the APO effect can explain the anisotropic behavior of waveguides post-processed by thermal annealing, which entails removal of both residual defects and stress (see Sect. 3.3). On the other hand, it is well known that waveguide modes polarized along the axis of lower RI (TM mode in LN) usually suffer from MRL if the birefringence of the host material is sufficiently high compared to the core-cladding RI contrast and the beam propagation direction is not perfectly parallel to any principle axis of the material [27]. Several numerical approximations have been developed to relate the polarization dependence of light confinement to the MRL effect in LN waveguide platforms see, for instance, the work of Burns et al. dealing with Ti-diffused waveguides in x- and y-cut wafers [28]. Because the MRL effect is unlikely to be sensitive to heat treatment and the polarization dependence of light confinement persisted in our waveguides after annealing (see Fig. 6), we believe that MRL was the dominant factor influencing this anisotropic guiding behavior.
The waveguide of type B05 featured the best optical guiding properties with: \(\alpha _{\tiny {\text {TE}}} = (1.8\pm 0.1)\) dB/cm \(\alpha _{\tiny {\text {TM}}} = (5.0\pm 0.2)\) dB/cm and \(\hbox {MFD} = (23.6\pm 1.2)\,\upmu \hbox {m}\), which were slightly enhanced relative to the A05-type waveguide written at the same but constant pulse energy: \(\alpha _{\tiny {\text {TE}}} = (2.0\pm 0.2)\) dB/cm, \(\alpha _{\tiny {\text {TM}}} = (5.6\pm 0.2)\) dB/cm and \(\hbox {MFD} = (24.1\pm 1.2) \,\upmu \hbox {m}\). This can be explained by looking at Fig. 4b: the modified tracks on the upper and lower rows of B05 were more consistent in size and modification strength as compared to A05, which therefore led to higher and more symmetric light confinement. Although Group B waveguides did not show significant performance improvement over Group A waveguides in terms of propagation losses, which in fact tended to become worse in the high-energy inscription regime (Fig. 4a), their more circular mode-field entailed less coupling loss when connecting them to conventional circular-cross-section optical fibers. In comparison to A05 and B05, the waveguide of type C02 shown in Fig. 4b featured larger MFD, which can be explained by the lower RI contrast and smaller size of the tracks inscribed in its inner layers, but only slightly increased propagation losses (see Fig. 6), presumably owing to a higher track smoothness. Similar behavior was displayed by the other Group C waveguides. This observation suggests that the radial pulse-energy variation scheme can effectively be used to control the size of the waveguide’s guiding intensity profile. However, further optimization of the operational parameters would still be required to achieve the low confinement losses shown in Karakuzus numerical study [19]. The observed mode-field profiles showed that the fundamental guiding mode was the dominant mode excited in all waveguides presented in this study. Slight tuning of the relative coupling-stage positions only resulted in minor changes of the mode shape and circularity, but did not lead to the emergence of higher-order modes.
3.3 Effects of heat treatment
We assessed the impact of heat treatment on the tracks shown in Fig. 2a and written with the -x translation direction. The results are summarized in Fig. 5a and highlight that the behavior of the track’s RI contrast in response to thermal annealing was sensitive to the inscribing pulse energy. The RI contrast of tracks generated with low pulse energies (\(<{53}\hbox { nJ}\), dashed lines) progressively increased with the first three annealing temperatures (250–\({500}\,^{\circ }\hbox {C}\)), but it began to lessen at \({700}\,^{\circ }\hbox {C}\) and it had nearly faded at \({950}\,^{\circ }\hbox {C}\). On the other hand, the RI contrast of tracks inscribed by high pulse energies (\(>{53}\hbox { nJ}\), solid lines) continued to increase up to the very high temperature of \({700}\,^{\circ }\hbox {C}\). After this temperature, it showed a declining trend as with the case of low-energy written tracks. It is worth noting that these features are markedly different from those described in the work of Nguyen et al. [16], in which an LRR (1 kHz at 795 nm) fs-laser was used and the RI contrast of the tracks immediately declined after the first thermal annealing stage at \({260}\,^{\circ }\hbox {C}\). Hence, our results reveal the ability of HRR fs-laser systems to fabricate highly thermally stable optical structures. This also provides an indication of the nature of some hardly reversible material modifications, such as amorphization, crystallization, and chemical composition changes, which are plausibly driven by the heat accumulation effects and feature only in this regime of multiple pulse interactions.
Figure 5b shows the cross sections of the B07-type waveguide before and after thermal annealing. It can be clearly seen that some areas of the induced stress field and the non-damage modifications were largely erased after heat treatment at 250 and \({350}\,^{\circ }\hbox {C}\), and seemed vanished after treatment at \({700} \,^{\circ }\hbox {C}\). A similar observation was made by Burghoff et al. [7]. However, the employment of a lower temperature (\({200}\,^{\circ }\hbox {C}\)) and a shorter annealing time (30 minutes) in their work sufficed to wipe out the positive ordinary RI humps around the damage tracks generated by an LRR fs-laser (1 kHz at \({800}\hbox { nm}\)). A few shallow surface cracks were observed in the cladding region of our waveguides, which are attributed to the non-uniform expansion/contraction of the exposed/unexposed areas during the heat treatment. These cracks appeared to have no noticeable effect on the guidance of light mainly occurring in the waveguide’s core.
Fig. 6 demonstrates the remarkable enhancement of the optical guiding performance for both TE and TM polarized light at \({1550}\hbox { nm}\) afforded by the thermal annealing process, especially by the first two stages. The propagation losses reached their minimum values after annealing at \({350}\,^{\circ }\hbox {C}\), and underwent only slight growth with increasing temperature up to \({700}\,^{\circ }\hbox {C}\). The lowest propagation losses of less than \((0.4\pm 0.1)\) dB/cm and \((3.5\pm 0.2)\) dB/cm for the TE and TM polarization states, respectively, were achieved from the B07 waveguide. These losses were calculated from the measured insertion loss of \({3.7}\hbox { dB}\), the mode-mismatch loss of approximately \({1.6}\hbox { dB}\), and the double-Fresnel loss estimated at \({1.3}\hbox { dB}\). The improvement in guiding properties engendered by thermal annealing can be explained as the result of both enhanced light confinement owing to an increased overall RI contrast, weakened induced stress field and reduced transient defects. It is remarkable that the B05-type waveguide, which showed the best optical guiding properties before heat treatment (Sec. 3.2), also experienced enhanced optical guidance as a result of annealing, but to a lower degree than the B07 waveguide, which was fabricated with higher-energy pulses. This means that in order to make waveguides with minimal propagation losses, consideration to the thermal annealing effects should be given at the initial stage of inscription parameter selection. The MFD exhibited a similar evolution with varying annealing temperature, but it started to increase earlier, just after the second annealing step. The light confinement in the TE polarization noticeably diminished after annealing at \({850}\,^{\circ }\hbox {C}\) and began to vanish at \({950}\,^{\circ }\hbox {C}\), which is close to the Curie temperature of LN at around \({1140}\,^{\circ }\hbox {C}\), in some waveguides inscribed by low pulse energy. Interestingly, these waveguides continued to confine light in the TM polarization even after such high-temperature treatments.
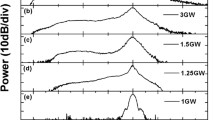
Propagation losses and MFD of the B06 waveguide after annealing at \({350}\,^{\circ }\hbox {C}\) versus wavelength. This figure is adapted from [20]
Figure 7 shows the wavelength dependence of the guiding properties of the B06 waveguide after annealing at \({350}\,^{\circ }\hbox {C}\). While the propagation loss in the TE polarization mode remained approximately constant across the wavelength range being studied, the loss in the TM mode showed a sudden increase in the proximity of the boundary between the visible and near-infrared regions, notwithstanding that the fundamental guiding mode was still observed. This phenomenon likely relates to waveguide’s structural features, such as laser-induced gratings or, in general, quasi-periodical non-uniformities at the boundaries of the guiding region, which would respond differently to the portions of degenerated coupled extraordinary- and ordinary-polarized fields for different wavelengths of the input beam. The MFD in both TE and TM polarizations tended to increase with increasing wavelength in the visible portion of the spectrum and then slightly decreased when the wavelength approached \({1550}\hbox { nm}\).
4 Conclusions
We have reported on the fabrication and optimization of optical-lattice-like depressed cladding waveguides in z-cut LN. The optimized waveguides featured low propagation loss for the TE polarization state and moderate loss in the TM polarization. Fundamental mode guidance was observed across a wide portion of the spectrum from visible to near infrared. Two recently proposed approaches based on varying the inscribing laser pulse energy in accordance with the position of the tracks were deployed in the fabrication process, which led to the enhancement of waveguide’s confinement intensity distribution symmetry, and also offered an alternative way of adjusting the mode-field size. The heat treatment of the fabricated waveguides revealed an interesting feature of the damage tracks generated by an HRR fs-laser: the RI contrast is enhanced by annealing and remains stable under high temperatures, opposed to the track degradation that typically occurs in the case of LRR-laser inscription. This high thermal stability of the fabricated waveguides is ascribable to the virtually irreversible material modifications induced by HRR fs-laser writing. The low attenuation and high thermal stability of our waveguides suggest promising applications in telecommunications, nonlinear integrated optics, and harsh environment sensors.
References
L. Arizmendi, Phys. Status Solidi A 201(2), 253 (2004)
C. Wang, M. Zhang, B. Stern, M. Lipson, M. Lončar, Opt. Express 26(2), 1547 (2018)
R. Luo, H. Jiang, S. Rogers, H. Liang, Y. He, Q. Lin, Opt. Express 25(20), 24531 (2017)
S. Gross, M.J. Withford, Nanophotonics 4(3), 332 (2015)
R. Thomson, S. Campbell, I. Blewett, A. Kar, D. Reid, Appl. Phys. Lett. 88(11), 111109 (2006)
A.H. Nejadmalayeri, P.R. Herman, Opt. Express 15(17), 10842 (2007)
J. Burghoff, H. Hartung, S. Nolte, A. Tünnermann, Appl. Phys. A 86(2), 165 (2007)
J. Burghoff, S. Nolte, A. Tünnermann, Appl. Phys. A 89(1), 127 (2007)
J. Burghoff, C. Grebing, S. Nolte, A. Tünnermann, Photon-assisted synthesis and processing of functional materials. Appl. Surf. Sci. 253(19), 7899 (2007)
Y. Liao, J. Xu, Y. Cheng, Z. Zhou, F. He, H. Sun, J. Song, X. Wang, Z. Xu, K. Sugioka, K. Midorikawa, Opt. Lett. 33(19), 2281 (2008)
R. He, Q. An, Y. Jia, G.R. Castillo-Vega, J.R. Vázquez de Aldana, F. Chen, Opt. Mater. Express 3(9), 1378 (2013)
S. Kroesen, W. Horn, J. Imbrock, C. Denz, Opt. Express 22(19), 23339 (2014)
J. Lv, Y. Cheng, J.R. Vázquez de Aldana, X. Hao, F. Chen, J. Lightwave Technol. 34(15), 3587 (2016)
J. Lv, Y. Cheng, Q. Lu, J.R. Vázquez de Aldana, X. Hao, F. Chen, Opt. Mater. 57, 169 (2016)
H.D. Nguyen, A. Ródenas, J.R. Vázquez de Aldana, J. Martínez, F. Chen, M. Aguiló, M.C. Pujol, F. Díaz, Opt. Express 24(7), 7777 (2016)
H.D. Nguyen, A. Ródenas, J.R. Vázquez de Aldana, G. Martín, J. Martínez, M. Aguiló, M.C. Pujol, F. Díaz, Opt. Express 25(4), 3722 (2017)
S. Bhardwaj, K. Mittholiya, A. Bhatnagar, R. Bernard, J.A. Dharmadhikari, D. Mathur, A.K. Dharmadhikari, Appl. Opt. 56(20), 5692 (2017)
M. Dubov, S. Boscolo, D.J. Webb, Opt. Mater. Express 4(8), 1708 (2014)
H. Karakuzu, M. Dubov, S. Boscolo, Opt. Express 21(14), 17122 (2013)
T. Piromjitpong, M. Dubov, S. Boscolo, in SPIE Photonics Europe (SPIE, 2018), vol. 10684, pp. 11
G. Zhou, A. Jesacher, M. Booth, T. Wilson, A. Ródenas, D. Jaque, M. Gu, Opt. Express 17(20), 17970 (2009)
F. He, H. Xu, Y. Cheng, J. Ni, H. Xiong, Z. Xu, K. Sugioka, K. Midorikawa, Opt. Lett. 35(7), 1106 (2010)
B.P. Cumming, A. Jesacher, M.J. Booth, T. Wilson, M. Gu, Opt. Express 19(10), 9419 (2011)
C. Mauclair, A. Mermillod-Blondin, N. Huot, E. Audouard, R. Stoian, Opt. Express 16(8), 5481 (2008)
W. Yang, P.G. Kazansky, Y.P. Svirko, Nat. Photonics 2, 99 (2008)
P.G. Kazansky, W. Yang, E. Bricchi, J. Bovatsek, A. Arai, Y. Shimotsuma, K. Miura, K. Hirao, Appl. Phys. Lett. 90(15), 151120 (2007)
M. Lu, M.M. Fejer, J. Opt. Soc. Am. A 10(2), 246 (1993)
W. Burns, S. Sheem, A. Milton, IEEE J. Quant. Electron. 15(11), 1282 (1979)
Acknowledgements
T. Piromjitpong acknowledges the financial support from the Royal Thai Government.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Piromjitpong, T., Dubov, M. & Boscolo, S. High-repetition-rate femtosecond-laser inscription of low-loss thermally stable waveguides in lithium niobate. Appl. Phys. A 125, 302 (2019). https://doi.org/10.1007/s00339-019-2609-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00339-019-2609-6