Abstract
In laser machining with ultrashort laser pulses unwanted X-ray radiation in the keV range can be generated when a critical laser intensity is exceeded. Even if the emitted X-ray dose per pulse is low, high laser repetition rates can lead to an accumulation of X-ray doses beyond exposure safety limits. For 925 fs pulse duration at a center wavelength of 1030 nm, the X-ray emission was investigated up to an intensity of 2.6 × 1014 W/cm2. The experiments were performed in air with a thin disk laser at a repetition rate of 400 kHz. X-ray spectra and doses were measured for various planar target materials covering a wide range of the periodic table from aluminum to tungsten. Without radiation shielding, the measured radiation doses at this high repetition rate clearly exceed the regulatory limits. Estimations for an adequate radiation shielding are provided.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
During the past years material processing using ultra-short laser pulses has undergone a considerable development. This development was initiated by the invention of novel laser technologies, as e.g. the thin disk lasers [1]. The thin disk laser technology delivers high stable output power in the range of several 10 W up to several 100 W, with pulse durations below 1 ps at repetition rates of several 100 kHz. These high repetition rates make laser processing quick, cost-effective, and thereby more attractive for industrial applications. For that different ultra-fast laser processing strategies are employed. For an optimum laser ablation efficiency along with high machining precision, fluences of about ten times the ablation threshold are used [2,3,4]. An optimum processing window around 1 J/cm2 was found for steel. Glasses require higher fluences ranging up to ∼ 30 J/cm2 [5]. However, in alternative sequential processing strategies it might be beneficial to increase the removal rate via much higher fluences in a first roughing step. In the subsequent finishing step at lower fluence the required surface quality is realized [6]. Hence, to regard the full hazard potential the highest achievable fluence with the used laser system must be considered as realistic scenario. In this work, a maximum laser fluence of 255 J/cm2 was reached, corresponding to a peak intensity of 2.6 × 1014 W/cm2 taking into account the temporally Gaussian pulse shape.
At high laser intensities energy can be transferred to electrons by means of laser plasma interaction. The energy, which can be transferred to a plasma electron, depends on the mechanism dominating the laser plasma interaction. If the kinetic energy of the plasma electrons becomes high enough, characteristic X-ray radiation and Bremsstrahlung can be generated by interaction with the target material. In an intensity range of 1013–1014 W/cm2, the generation of dose relevant X-ray radiation is very inefficient and the emitted dose per pulse is low. Therefore, laser safety in terms of radiation hazard in the intensity region from 1013 to 1014 W/cm2 was addressed only in rudimentary form so far. Bunte et al. pointed out a possible danger when using a 30-fs laser system operated at 1 kHz repetition rate with an intensity above 1014 W/cm2 for processing of copper [7]. However, in laser material processing with high repetition rates, the low X-ray radiation dose per pulse can accumulate over time, leading to a dose high enough to be hazardous for the operating staff. For safety precautions, a detailed knowledge of the emitted radiation dose and its spectral distribution is required. For this purpose, the spectral X-ray emission and the generated dose in laser material processing at intensities up to 2.6 × 1014 W/cm2 was investigated in the present work. It will be shown that the dose relevant X-ray emission in laser material processing at intensities up to 2.6 × 1014 W/cm2 with a pulse duration of 925 fs and at a wavelength of 1030 nm is restricted to an energy range below 30 keV.
2 Experimental
2.1 Optical setup
The experiments were performed using a TRUMPF laser system (TruMicro 5050 femto edition). The laser delivers high-contrast pulses (no pedestal, no pre-pulse) with 925 fs pulse duration at a laser center wavelength of 1030 nm. The maximum repetition rate of the laser system was 400 kHz, the maximum single pulse energy was 100 µJ, resulting in an average laser power of 40 W. The collimated output beam of the laser with a diameter of about 5 mm was expanded by a factor of 2 in diameter and directed onto a Galvanometer scanner head (hurrySCAN II 14, SCANLAB GmbH), which was connected to the controller unit of the TRUMPF laser system (cp. Fig. 1). The laser beam was focused in air onto the sample by means of an F-Theta lens with a focal length of 56 mm. The angle of incidence of the laser beam onto the sample plane was 0°. The focal beam diameter (1/e2) was determined by the D2-method [8] and set to 2w0 = 10 ± 1 µm, resulting in a maximum intensity of 2.6 × 1014 W/cm2.
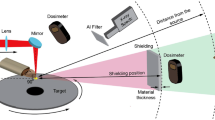
Experimental setup used for X-ray dose measurements. Shown is the optical beam path, the scanner head, the sample stage and the arrangement of the detector systems. In all measurements the CdTe spectrometer and the dosimeters (OD-02 and DIS-1) were positioned at the same angle vertical to the target surface. In the horizontal plane, the dosimeters were placed under an angle of about 12° to the scan direction, whereas the CdTe spectrometer was oriented parallel to the scan direction. The setup is enclosed by a radiation protection housing shielded with 1 mm Pb. To prevent secondary emissions, the wall of the housing and all other potential sources of secondary emission were covered with PMMA and aluminum
Technical grade planar samples of pure tungsten, carbon steel (S235JR), an aluminum alloy (AlMgSi), and alumosilicate glass (Gorilla glass) were investigated. The samples were mounted on a 5-axis stage. This stage allows the alignment of the sample horizontally and to position it in height with an accuracy of < 5 µm. For dose measurements the samples were irradiated over 5 s using a scan speed of 1000 mm/s. The X-ray radiation dose was accumulated in the experiment. From the accumulated dose, the dose rate was calculated. Debris emitted during the laser ablation was continuously removed by an exhaust system. The selected scan field area was 10 mm × 10 mm. Within the scan fields, lines with a spacing of 20 µm were written in a direction, away from the X-ray detectors, with the linear polarization of the laser beam parallel to the lines. In this arrangement, the highest dose values were obtained. Since the planarity of the samples (rolled metal sheets) was rather low, measurements were performed at different sample positions. The highest dose was finally selected from the entire set of dose measurements. This highest dose can be regarded as “worst case” scenario. In case of tungsten, the highest dose values were obtained after repeating the scan process several times at the same area. In case of steel, the aluminum alloy, and Gorilla glass, the highest dose values were obtained in the first scan.
2.2 X-Ray dose measurements
X-Ray radiation was measured using different detection systems. For dose measurements, a highly sensitive ionization chamber (OD-02, STEP GmbH), an electronic Direct Ion Storage (DIS) memory cell (DIS-1, Mirion Technologies GmbH) and thermoluminescence dosimeters (MCP-N, RadPro International GmbH) were applied. The thermoluminescence dosimeters were read out manually (TLDcube, RadPro International GmbH).
Different operational quantities are in use to define human-body protection quantities in an external radiation field. With the ionization chamber used in this work, the ambient dose equivalent H*(10) and the directional dose equivalent H′(0.07) can be measured. The ambient dose equivalent H*(10) is the operational quantity for area monitoring. It is the dose equivalent at a depth of 10 mm in a 30-cm diameter sphere of unit density tissue (ICRU-sphere, International Commission on Radiation Units and Measurements). The ICRU-sphere is a sphere with a density of 1 g/cm3 and a mass composition of 76.2% oxygen, 11.1% carbon, 10.1% hydrogen, and 2.6% nitrogen. The directional dose equivalent H′ (0.07, Ω) is the operational quantity for the determination of the dose to the human skin and is measured at a depth of 0.07 mm in the ICRU-sphere. The quantity Ω denotes hereby the angle of incidence of the X-ray radiation to the sphere.
The DIS-1 dosimeter is a personal dosimeter, which yields the personal dose equivalents Hp(10) and Hp(0.07). These operational quantities are used for monitoring the exposure dose of an individual. For X-ray photon energies below 50 keV, the measured personal radiation dose (with a dosimeter calibrated on a slab phantom to simulate the human torso) and the ambient radiation dose deliver almost identical values and a ratio of H*(10)/Hp(10) = 1 and H′(0.07,0°)/Hp(0.07) = 1 can be used to compare these operational quantities [9, 10]. For dose limits, most countries adopt the recommendations of the ICRP (International Commission on Radiological Protection). Dose limits for members of the public are 1 mSv/a effective dose, controlled by the dose equivalents at a depth of 10 mm, and 50 mSv/a for the exposure of the skin [11]. For working personal, the dose limits must be related to the occupational exposure time per year. Note that the regulatory radiation limits for working personal can differ from country to country.
The DIS-1 dosimeter and the TLDs are both passive dosimeters, which accumulate the radiation dose. Passive dosimeters are recommended for pulsed X-ray radiation, since a saturation, which would lead to an underestimation of the radiation dose, can be ruled out using this dosimeter type. However, the latter does not mean, that active dosimeters, as the OD-02 are not suited for measurements of pulsed radiation, as will be shown below. If the X-ray dose per pulse is low enough to not saturate the dosimeter, even active dosimeters can yield reliable results. Since passive dosimeters must be read out manually after each measurement, they are not convenient in practical use, e.g. if measurements must be repeated many times, to align a radiation source. For that reasons, all measurements were performed using the OD-02 in an “accumulation mode”, which delivers a resolution of 0.01 µSv in H′(0.07). The resolution delivered by the DIS-1 is 10 µSv in Hp(0.07). The reliability of the OD-02 dosimeter was ensured in all measurements by comparing the accumulated doses collected by the OD-02 over an extended period of time with the simultaneously accumulated doses collected by the passive dosimeter systems. In Fig. 2 the comparison of the doses accumulated by the passive dosimeter DIS-1 and the active dosimeter OD-02 is shown. In addition, selective accumulated doses collected with the TLDs are also displayed. A linear dependence between the accumulated doses collected by the OD-02 and the accumulated doses collected by the passive dosimeters was observed. In this way, the reliability of the OD-02 up to the highest measured dose rates was verified in the experiment. All detectors were calibrated by the manufacturer and by using radiation standards of the Physikalisch-Technische Bundesanstalt (PTB, Braunschweig, Germany).
Comparison of the accumulated doses, which were simultaneously collected by the active dosimeter OD-02 and by the passive dosimeter DIS-1. In selected measurements additionally TLDs were applied. The linear least-squares fit gives a slope of 1, which confirms that, regardless of its active measurement principle, the measurements with the OD-02 are reliable here
2.3 Measurement of spectral X-ray emission
For the selection of an instrument for spectral X-ray emission measurements, the specific experimental conditions in laser material processing must be considered. Appropriate instruments for spectral measurements of pulsed plasma radiation in a dose relevant photon energy range above 2 up to 50 keV are efficient broadband X-ray crystal spectrometers [12, 13], single photon counting semiconductor detectors [14] and TLD based spectrometers [15]. Considering the specific requirements in laser material processing, a single photon counting CdTe spectrometer (X-123CdTe Spectrometer, 3 × 3 × 1 mm3, 100 µm Be window, Amptek Inc.) was selected for the spectral measurements in this work. The CdTe spectrometer tolerates changes of the position of the radiation source during the scan process, it allows to collect a complete spectrum within the scanning time of several seconds, and the high stopping power of CdTe provides a detection efficiency of nearly 100% over a broad energy range up to photon energies of 50 keV. Even though these detectors are ideally suited for the requirements in this work, the detector type has some disadvantages, e.g. its vulnerability to pile-up. This effect arises, if multiple X-ray photons hit the single photon detector in the time frame of the processing time and are registered as one single photon with higher energy. Because of the moving plasma spot in the scan process, no X-ray collimator could be employed in the measurements to reduce the pile-up, since a collimator would lead to an underestimation of the emitted photon flux. Therefore, to minimize the pile-up, the CdTe spectrometer was operated at a large distance of 64.5 cm to the laser-generated plasma. In addition, the radiation per pulse was attenuated by aluminum foils placed in front of the X-ray detector. The thickness of the aluminum foils was determined from the attenuation using a 55Fe and a 109Cd radiation standard (PTB). Measurements were performed with aluminum foil thicknesses up to 362 µm. Another characteristic feature of CdTe spectrometers, which must be considered in quantitative X-ray spectroscopy, is an unavoidable background continuum appearing in the spectrum with a step close to intense emission lines. This step-like background with increased count rates at the low-energy side of the emission lines arises from energy degrading effects, e.g. by Compton scattering and incomplete charge collection [16]. The X-ray emission lines itself can be approximated by Gaussian shaped peaks in an energy range below 15 keV [17]. As will be shown in Sect. 3.3, the Bremsstrahlung continuum can be approximated by a Maxwellian distribution. If these contributions to the spectrum are known, the background continuum can be estimated and eliminated from the measured spectrum. The latter was done in the present work. Since the evaluated background continuum was vanishingly low in the spectral region of interest, it was neglected in the evaluation process described in Sect. 3.3. Calibration of the energy scale of the detector was done by radiation standards of PTB and by the known emission line energies of the investigated target materials.
3 Results and discussion
3.1 Dependence of dose rates on detection angle
In a first step, the angular distribution of the dose was determined in the experiment. The distance from the X-ray emitting plasma source to the OD-02 dosimeter was set to 420 mm in all measurements. This is a typical distance between the laser-plasma source and the torso of an operator. The range of detection angles for which the detector volume of the OD-02 was completely exposed to X-rays was geometrically restricted by the scanner head and the size of the target. In Fig. 3 the collected dose rates Ḣ′(0.07) in dependence on the detection angle vertical to the target plane are shown for steel S235JR and tungsten at an intensity of 2.6 × 1014 W/cm2.
As can been seen in Fig. 3, the emitted X-ray dose strongly depends on the detection angle. The angle at which the highest X-ray dose rates can be found was determined to about 29° with respect to the sample plane.
3.2 Dependence of dose rates on the material
Tungsten (Z = 74), steel (Z = 26), aluminum alloy (Z = 13), and Gorilla glass were investigated. The atomic number Z of these materials covers a wide range of the periodic table. The selection represents common used materials in the laser-based industrial fabrication process [18]. Doses of the directional dose equivalent H′(0.07) were measured with the ionization chamber dosimeter OD-02 at a fixed distance of 420 mm and a fixed detection angle of 29°. The related dose rates Ḣ′(0.07) are displayed in Fig. 4 as function of the laser peak intensity. The intensity was varied in the experiment by tuning the single pulse energy of the laser.
Measured dose rates Ḣ′(0.07) in dependence on the target material and the incident laser peak intensity. Different target materials were investigated (tungsten, steel S235JR, an aluminum alloy, and Gorilla glass) using the ionization chamber dosimeter OD-02 at a distance of 420 mm in air. The intensity was varied between 2.6 × 1013 and 2.6 × 1014 W/cm2 by tuning the laser pulse energy
Figure 4 shows an increase of the dose rate with rising laser intensity. Furthermore, a tendency of increasing dose rates with increasing atomic number Z can be observed at a fixed intensity. The lower dose rates measured for Gorilla glass in comparison to the aluminum alloy can be explained by the lower concentration of aluminum in Gorilla glass.
The measured dose rates in Fig. 4 clearly exceed the radiation safety limit for skin dose, which is 50 mSv/a for members of the public (25 µSv/h @ 2000 h operation time per year) [11]. The maximum dose rate Ḣ′(0.07) measured at the highest intensity was 163 mSv/h. This dose rate exceeds the allowed regulatory radiation limit by a factor of about 6.6 × 103. This highest measured dose rate corresponds to a single pulse dose of 0.1 nSv.
3.3 Dependence of spectral X-ray emission on the material
A comparison of the spectral X-ray emission for the investigated target materials at the highest laser intensity of 2.6 × 1014 W/cm2 is shown in Fig. 5. The spectra in Fig. 5 were collected at the distance of 64.5 cm from the laser ablation spot, with a 362 µm thick aluminum foil placed in front of the spectrometer. In the low photon energy range, the spectra are strongly attenuated by the filter absorption and the absorption in air. The accumulated counts visible at lowest photon energies can be therefore attributed to the step-like background continuum mentioned in Sect. 2.3. The spectral distribution of the plasma emission consists of two parts: the characteristic lines (visible for tungsten, discriminated by the aluminum filter and the absorption in air for steel S235JR) and a Bremsstrahlung continuum. The Bremsstrahlung continuum can be approximated with a Maxwellian distribution of the form [19]:
X-Ray spectra in air measured with the CdTe spectrometer at a laser intensity of 2.6 × 1014 W/cm2 at a distance of 64.5 cm from the laser ablation spot. In the measurement a 362 µm thick aluminum foil was placed in front of the detector. Shown are spectra recorded with tungsten, steel S235JR, and an aluminum alloy as target material. The black curves are calculated Maxwellian distributions
where \({k_{\text{B}}}=8.6~ \times ~{10^{ - 5}}{{{\text{eV}}} \mathord{\left/ {\vphantom {{{\text{eV}}} {\text{K}}}} \right. \kern-0pt} {\text{K}}}~\) and 1 eV ≙ 1.2 × 104 K, E denotes the X-ray photon energy, kB is the Boltzmann constant, and Te is the electron temperature, by convention expressed in keV. It can be seen in Fig. 5, that for the different investigated materials the spectral distribution (curve shape) varies much less than the number of emitted X-ray photons (area below the curves). While the area below the measured curves clearly increases with the atomic number Z, the shape of the measured photon energy distribution remains almost constant. The Maxwellian distribution describes well the measured curves. Only at the high-energy tail a deviation from the calculated Maxwellian distribution is observed, which can be explained by a pile-up. For tungsten, the deviation of the calculated Bremsstrahlung spectrum from measured data is most pronounced.
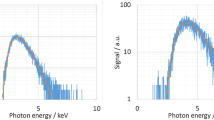
A simple approach was used to estimate the spectral photon flux emitted by the laser plasma from the measured spectra. The latter was done by combining two spectra, which were recorded at nearly the same dose rate, but with different aluminum filter thickness and, therefore, different pile-up contributions. As a result, a spectrum with low pile-up was obtained, without losing the spectral information in the low-energy channels of the CdTe spectrometer due to the strong attenuation by filters or the absorption in air at large distances. In a first step, the spectra were corrected for the detector efficiency given by the manufacturer, and the attenuation of the spectral emission due to filters and absorption in air was eliminated from the two spectra using tabulated mass attenuation factors [20]. The high-energy tail of the spectrum, which was less attenuated and, therefore, more affected by pile-up, was replaced by the high-energy tail of the stronger attenuated spectrum with lower pile-up contribution. To combine both spectra, the less attenuated spectrum was scaled in amplitude until both spectra exhibit the same count rates in the overlapping region. By this procedure, losses due to pile-up could be compensated in the less attenuated spectrum. In the energy range, where no counts were accumulated in the spectra (absorption in air and by filters), the spectrum was filled up with an appropriate Maxwellian distribution fitting the whole spectrum. Consequently, the combined spectrum represents the energetic distribution of the emitted X-ray photons in vacuum extrapolated to low photon energies. In Fig. 6 the two tungsten spectra with different filter attenuation and the combined spectrum are shown. The upper spectrum in the right of Fig. 6 was taken with a 45 µm thick aluminum filter in front of the CdTe spectrometer, the lower spectrum with a 362 µm thick aluminum filter. The grey dashed curve represents the calculated Bremsstrahlung continuum estimated by a Maxwellian distribution with an electron temperature Te of 1.76 keV. As seen in Fig. 6, no counts were collected by the CdTe spectrometer at photon energies above 30 keV.
Displayed is the combined spectrum in vacuum (left), which was constructed from the two measured emission spectra at the right. The measurements were performed in air with tungsten as target material at the highest intensity of 2.6 × 1014 W/cm2 at the distance of 64.5 cm. The upper spectrum at the right is attenuated by 45 µm thick aluminum foil, the lower spectrum by 362 µm thick aluminum foil. The combined spectrum was extrapolated to lower X-ray photon energies by a Maxwellian distribution (grey dashed line)
The spectral X-ray photon flux can be estimated from the combined spectrum assuming, that the accumulated counts in the spectrum represent the number of photons emitted into the solid angle, which is covered by the CdTe spectrometer area at the distance of 64.5 cm. In Fig. 7 the calculated photon flux ΦΕ for tungsten is displayed for two different propagation distances in air (100 and 420 mm). The distance of 100 mm was chosen because of its relevance for radiation-protection, the distance of 420 mm was chosen to compare the results with the performed dose measurements presented in this work.
Spectral X-ray photon flux ΦΕ for tungsten calculated in air at the highest intensity of 2.6 × 1014 W/cm2 at two distances (100 and 420 mm). Additionally, the photon flux calculated from the Maxwellian distribution in Fig. 6 is shown (grey dashed line)
Using the spectral photon flux ΦΕ the dose rates as function of photon energy can be calculated [21, 22]. For the calculation of the spectral dose rates for tungsten shown in Figs. 8 and 9 conversion factors in vacuum were taken from [21]. Integration over the curves in Figs. 8 and 9 yields the dose rates Ḣp(0.07) and Ḣp(10) (cp. Table 1). The calculated dose rate Ḣp(0.07) in air at a distance of 420 mm was determined to 156 mSv/h and corresponds well to the dose rate of 158 mSv/h in H′(0.07), which was simultaneously measured with the OD-02 dosimeter for the spectra displayed in Fig. 6. Since in an energy range < 50 keV the personal radiation dose and the ambient radiation dose can be set equal [9, 10], the dose rates in Table 1 also present the quantities Ḣ′(0.07) and Ḣ*(10). All the dose rates in Table 1 clearly exceed the regulatory limits.
Spectral dose rate Ḣp(0.07) for tungsten at the highest intensity of 2.6 × 1014 W/cm2 at two distances (100 and 420 mm) calculated in air from the spectral X-ray photon flux ΦΕ in Fig. 7. Additionally, the spectral dose rate Ḣp(0.07) calculated from the Maxwellian distribution in Fig. 7 is shown (grey dashed line)
Spectral dose rate Ḣp(10) for tungsten at the highest intensity of 2.6 × 1014 W/cm2 at two distances (100 and 420 mm) calculated in air from the spectral X-ray photon flux ΦΕ in Fig. 7. Additionally, the spectral dose rate Ḣp(10) calculated from the Maxwellian distribution in Fig. 7 is shown (grey dashed line)
Based on the spectral dose rates in Figs. 8 and 9, the estimation of dose rates at photon energies above 30 keV can be refined. For both operational dose quantities H′(0.07) and H*(10) dose rates in air of 0.7 µSv/h at 100 mm and 0.04 µSv/h at 420 mm can be estimated for the photon energy range above 30 keV by integration over the spectral dose rates calculated from the Maxwellian distribution.
3.4 Radiation protection
In Sect. 3.2 it was shown that the measured radiation dose at high-laser repetition rates can exceed the regulatory exposure limits for members of the public (25 µSv/h for the exposure of the skin and 0.5 µSv/h effective dose @ an operation time of 2000 h per year) even at relative low laser peak intensities between 1013 and 1014 W/cm2. Furthermore, it was shown in Sect. 3.3, that for the used laser system the dose relevant X-ray emission in the investigated intensity range is limited to photon energies below 30 keV. Since the radiation dose exceeds the regulatory limits, an adequate radiation shielding should be used. To estimate an adequate shielding, the attenuation factor of the shielding material for the incident radiation must be known. That attenuation factor can be evaluated by dividing the dose obtained from the non-attenuated photon spectrum by the dose obtained from the calculated photon spectrum behind a specific shielding material of a certain thickness.
In Fig. 10 attenuation factors for three different shielding materials (Fe, Al, SiO2) are displayed. These attenuation factors were calculated in air for a distance of 420 mm to the ablation plasma spot. It can be seen that a steel plate of 0.5 mm thickness can reduce the X-ray radiation dose of H′(0.07) in air by a factor of 106 and in H*(10) by a factor of 104. Consequently, a steel plate of 0.5 mm thickness placed at the distance of 420 mm to the plasma can reduce effectively the highest measured X-ray radiation dose rate Ḣ′(0.07) of 163 mSv/h and the calculated dose rate Ḣ*(10) of 680 µSv/h to a level below the regulatory radiation limits, assuming an exposure time of 2000 h per year. Here, it must be noted that other laser wavelengths or pulse durations at the same laser intensity (e.g. also in the ps range), another than a perpendicular laser incidence and pre-pulses can lead to higher dose rates and that the calculated radiation shielding must be modified in these cases. Furthermore, it must be underlined that the limited planarity and the surface quality of our targets (as being present during industrial machining processes), i.e. the “worst case” in the presented measurements cannot be adopted to highly planar samples with deviating surface quality. Therefore, the thicknesses of the radiation shielding material should be chosen rather generous, e.g. in the range of 1 mm for steel.
Calculated shielding attenuation factors for H′(0.07) and H*(10) in air. The calculations were performed at the distances of 420 mm from the laser ablation spot for the highest intensity of 2.6 × 1014 W/cm2 with tungsten as target material and for different thickness of shielding materials (iron, aluminum, and SiO2)
4 Conclusions
In summary, we have presented X-ray dose measurements in air at a distance of 420 mm to the laser ablation spot using a 400 kHz repetition rate 925-fs laser system at 1030 nm wavelength. The measurements were performed on tungsten, carbon steel (S235JR), an aluminum alloy (AlMgSi), and alumosilicate glass (Gorilla glass) as target materials. Up to laser intensities of 2.6 × 1014 W/cm2, the dose relevant X-ray emission is limited to photon energies below 30 keV. The highest measured X-ray dose rate Ḣ′(0.07) of 163 mSv/h obtained with tungsten as target material corresponds to a single pulse dose of 0.1 nSv. A radiation protection shielding of 1 mm thick steel is suggested here for the used laser system.
References
A. Giesen, H. Hügel, A. Voss, K. Wittig, U. Brauch, H. Opower, Scalable concept for diode-pumped high-power solid-state lasers. Appl. Phys. B 58, 365–372 (1994)
B. Neuenschwander, B. Jaeggi, M. Schmid, G. Hennig, Surface structuring with ultra-short laser pulses: basics, limitations and needs for high throughput. Phys. Procedia 56, 1047–1058 (2014)
J. Schille, L. Schneider, U. Loeschner, Process optimization in high-average-power ultrashort pulse laser microfabrication: how laser process parameters influence efficiency, throughput and quality. Appl. Phys. A 120, 847–855 (2015)
S. Russ, R. Gebs, L. Bauer, U. Keller, T. Meyer, J. Roller, B. Führa, B. Faisst, Shorter than short: how does the pulse duration influence the process efficiency of conductive materials? Proceedings of lasers in manufacturing 2015, p. 161, (2015)
J. Bliedtner, C. Schindler, M. Seiler, S. Wächter, M. Friedrich, J. Giesecke, Ultrashort pulse laser material processing. Laser Tech. J. 13, 46–50 (2016)
G. Eberle, C. Dold, K. Wegener, Laser fabrication of diamond micro-cutting tool-related geometries using a high-numerical aperture micro-scanning system. Int. J. Adv. Manuf. Technol. 81, 1117–1125 (2015)
J. Bunte, S. Barcikowski, T. Püster, T. Burmester, M. Brose, T. Ludwig, Secondary hazards: particle and X-ray emission. Top. Appl. Phys. 96, 309–320 (2004)
J.M. Liu, Simple technique for measurements of pulsed Gaussian-beam spot sizes. Opt. Lett. 7, 196–198 (1982)
International Commission on Radiological Protection: 2010, in Conversion Coefficients for Radiological Protection Quantities for External Radiation Exposures, Publication No. 116. Annals of the ICRP, Vol. 40 (2–5)
T. Otto, Personal dose-equivalent conversion coefficients for 1252 radionuclides. Radiat. Prot. Dosimetry. 168, 1–10 (2016)
International Commission on Radiological Protection: 1990, in Recommendations of International Commission on Radiological Protection, Publication No. 60. Annals of the ICRP, Vol. 21 (Pergamon Press, Oxford and New York, 1991)
H. Legall, H. Stiel, M. Schnürer, M. Pagels, B. Kanngießer, M. Müller, B. Beckhoff, I. Grigorieva, A. Antonov, V. Arkadiev, A. Bjeoumikhov, An efficient X-ray spectrometer based on thin mosaic crystal films and its application in various fields of X-ray spectroscopy. J. Appl. Crystallogr. 42, 572–579 (2009)
M. Gerlach, L. Anklamm, A. Antonov, I. Grigorieva, I. Holfelder, B. Kanngießer, H. Legall, W. Malzer, C. Schlesiger, B. Beckhoff, Characterization of HAPG mosaic crystals using synchrotron radiation. J. Appl. Crystallogr. 5, 1381–1390 (2015)
S.M. Gruner, E.F. Eikenberry, M.W. Tate, Comparison of X-ray detectors. In: Rossmann MG, Arnold E (eds) International Tables for Crystallography Volume F: Crystallography of biological macromolecules. International Tables for Crystallography, vol F. (Springer, Dordrecht, 2006), pp. 143–147
R. Behrens, H. Schwoerer, S. Düsterer, P. Ambrosi, G. Pretzler, S. Karsch, R. Sauerbrey, A thermoluminescence detector-based few-channel spectrometer for simultaneous detection of electrons and photons from relativistic laser-produced plasmas. Rev. Sci. Instrum. 74, 961–968 (2003)
R. Gunnink, R. Arlt, Methods for evaluating and analyzing CdTe and CdZnTe spectra. Nucl. Instrum. Methods Phys. Res. Sect. A 458, 196–205 (2001)
R.H. Redus, J.A. Pantazis, T.J. Pantazis, A.C. Huber, B.J. Cross, Characterization of CdTe detectors for quantitative X-ray spectroscopy. IEEE Trans. Nucl. Sci. 56, 2524–2532 (2009)
O.H. Heckl, C. Siebert, D. Sutter, J. Kleinbauer, D. Bauer, Perfect precision in industrial micro machining. Laser Tech. J. 9, 42–47 (2012)
D. Salzmann, Atomic Physics in Hot Plasmas (Oxford University Press, New York, 1998)
B.L. Henke, E.M. Gullikson, J.C. Davis, X-ray interactions: photoabsorption, scattering, transmission, and reflection at E = 50–30000 eV, Z = 1–92. Atomic Data Nucl. Data Tables 54, 181–342 (1993)
K.G. Veinot, N.E. Hertel, Personal dose equivalent conversion coefficients for photons to 1 GeV. Radiat. Prot. Dosimetry. 145, 28–35 (2011)
International Commission on Radiation Units and Measurements (ICRU), Conversion coefficients for use in radiological protection against external radiation. ICRU report 57 (1998)
Acknowledgements
The authors gratefully acknowledge financial support by the German Federal Ministry for Education and Research (BMBF) in the funding program Photonics Research Germany under contract number 13N14249. We would like to thank Simone Russ and Marc Sailer (both TRUMPF Laser GmbH) for experimental support and Dr. David Heisenberg (TRUMPF GmbH) for valuable discussions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Legall, H., Schwanke, C., Pentzien, S. et al. X-ray emission as a potential hazard during ultrashort pulse laser material processing. Appl. Phys. A 124, 407 (2018). https://doi.org/10.1007/s00339-018-1828-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00339-018-1828-6