Abstract
A two-dimensional thermomechanical finite element (FE) model of laser surface glazing (LSG) has been developed for H13 tool steel. The direct coupling technique of ANSYS 17.2 (APDL) has been utilised to solve the transient thermomechanical process. A H13 tool steel cylindrical cross-section has been modelled for laser power 200 W and 300 W at constant 0.2 mm beam width and 0.15 ms residence time. The model can predict temperature distribution, stress–strain increments in elastic and plastic region with time and space. The crack formation tendency also can be assumed by analysing the von Mises stress in the heat-concentrated zone. Isotropic and kinematic hardening models have been applied separately to predict the after-yield phenomena. At 200 W laser power, the peak surface temperature achieved is 1520 K which is below the melting point (1727 K) of H13 tool steel. For laser power 300 W, the peak surface temperature is 2523 K. Tensile residual stresses on surface have been found after cooling, which are in agreement with literature. Isotropic model shows higher residual stress that increases with laser power. Conversely, kinematic model gives lower residual stress which decreases with laser power. Therefore, both plasticity models could work in LSG for H13 tool steel.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
H13 tool steel is predominantly utilised in tooling industries especially forging tools, die casting moulds (Cu, Al alloys casting), extrusion dies, moulds for glass industry, etc. This material offers a good combination of hardness and toughness at working temperature. However, because of simultaneous thermal and mechanical effects caused by the abrasion of high-velocity molten metals during casting, the conventional H13 tool steel mould experiences softening, erosion and thermal fatigue, etc. Thus, the tool life decreases drastically [1]. It is reported that the service life of H13 tool steel mould for aluminium casting is maximised up to 180 thousands cycles through 21 times in-service repairing the crack surfaces of the mould by welding [2]. Different surface modification techniques such as PVD, CVD, and laser surface modifications have been adopted to overcome the problem [3].
Nowadays, laser surface modification techniques are quite popular because of its manifold advantages. Laser processes are very fast and energy efficient. The high-energy density and localised heat from laser beam provide very high cooling rates and heat sink resulting into self-quenching. It enhances surface properties with higher hardness, wear resistance, and fatigue strength over conventional process (welding, PVD, CVD, etc.). However, it also induces residual or thermal stresses in surface and sub-surface regime, which is not desirable [4]. Researchers are trying various types of laser surface modification techniques such as laser surface melting/glazing (LSM/LSG), laser transformation hardening, laser cladding (LC), selective laser sintering (SLS), and direct metal deposition (DMD) [5,6,7,8]. Among those processes, SLS, LC or DMD can be used as both forming and repairing processes where similar or different materials are added externally on top of a substrate mostly in powder form. On the other hand, surface is encountered solely heat treatment in the LSM, LSG and laser transformation hardening processes which alter the structures and improve properties of the surface from the bulk material. All laser surface modification processes provide high cooling rates and induce residual stress. For example, Telesang et al. reported the 45% higher hardness and high compressive stress achieved in clad surface after LC of H13 tool steel on same substrate. He compared the surface hardness and residual stress between continuous wave (CW) and pulse mode of fibre-coupled diode laser in his experiment. Pulse laser induced higher compressive stress and higher hardness resulting into good wear and fatigue resistance on the restored surface of H13 tool steel substrate [9]. On the other hand, a minimal tensile residual stress on fused surface was reported in SLS of H13 tool steel sample treated with Nd:YAG (Neodymium–Yttrium Aluminium Garnet) laser by Ibraheem et al. [5]. In another work, Telesang et al. found the compressive residual stress induces on surface for surface hardening of H13 tool steel using CW diode laser. However, the stress turned into tensile residual stress when surface melting occurred [3]. It is noted that the surface properties and residual stress varied in magnitude and type for different laser modification techniques. Moreover, they differed with various laser parameters such as laser power, scanning speed, beam diameter, pulse frequency, powder flow rates, and wavelength depending on types and modes of laser beam. Therefore, it is important to optimise the process parameters to get best out of the laser processes according to service requirements. Due to the complex nature of underpinned physics and many controlling parameters of laser techniques, conducting experiments of those processes cost a lot of time and efforts. Regarding the fact, simulation and modelling of laser surface modification processes offer the best way of optimising the process and predicting residual stress [10,11,12].
For last few years, through modelling and simulation, scientists have been trying to predict the residual stresses in laser surface modification techniques of different materials (metals and alloys) and correlating with process parameters [13,14,15]. For instance, a 3D modelling of SLS of H13 tool steel predicting residual stress was carried out by Ibraheem et al. using ANSYS code. Small tensile residual stress was predicted in his work on the surface of fused H13 tools steel powder which agreed with the experimental strain measurement [5]. Yilbas et al. modelled laser heating of aluminium metal surface to predict residual stress using ANSYS FEA software. The development of compression stress field below the surface was reported here. A direct coupling method of thermal and structural analysis was applied by ANSYS in this work [13]. In direct coupling technique, single finite element analysis is conducted for accomplishing both thermal and structural process simultaneously using direct coupling element. ANSYS has this special and efficient feature of analysing thermal stress [16]. Simulation of laser engineered net shaping (LENS) deposition of H13 tool steel was conducted to predict residual stress using FEM in SYSWELD by Talukder et al. [17]. In laser modification treatments the surface hardness increases. Hardening is induced by the plastic flow or strain hardening in materials. In metals and alloys, yield strength is evolved due to plastic flow. It was reported that the evolving yield strength in strain hardening can follow three possible mechanisms: (1) linear isotropic hardening, (2) kinematic hardening and (3) mixed hardening [18]. Therefore, it is important to know the material behaviour in evolving yield phenomenon to correctly model residual stress of laser modification treatments. In literature, use of both isotropic and kinematic models has been observed. Yilbas et al. modelled residual stress using ABAQUS FEM code of laser surface melting with aluminium composite. He considered the workpiece as an elastic body and used isotropic hardening to model rate-independent plasticity with temperature-dependent yield strength [19]. In another work of laser cladding by Paul et al., ABAQUS FEA software was used to model residual stress in H13 tool steel clad and substrate. A kinematic hardening model with von Mises yield criterion was used to calculate plastic strain in this model. Although the prediction values gave rise to up to 25% error with experimental data, but the trend in stress distribution was in agreement [20]. Li et al. also followed kinematic hardening rule in predicting stress distribution of laser surface melting of 42CrMo4 steel in SYSWELD commercial FEA code [14, 21]. Throughout the literature no numerical modelling work has been found particularly for LSG of H13 tool steel. In LSG, utilising high beam intensity from laser heat source, the surface temperature is raised up to melting point of the material followed by a sharp cooling. This leads to a thin, hard, semi-crystalline modified surface layer on top of the bulk material. The benefit of using LSG is that no additional material needs to add externally. The use of higher energy density (106–109 Wm− 2) and shorter interaction or residence time (10− 4 s) differ LSG from other laser melting processes, which results in very high cooling rates (104–108 Ks− 1) [22]. This higher rate of cooling causes amorphisation making surface very hard and resistant to softening at elevated temperature, while simultaneously developing residual stress in modified zone [4, 23,24,25,26].
In this study, a 2D FE thermomechanical model of LSG for H13 tool steel has been developed in ANSYS APDL 17.2 software. The model predicts temperature history, temperature change rate/thermal cycle and residual stress for two laser power 200 and 300 W with constant 0.2 mm beam width and 0.15 ms residence time. Residence time is defined by the period for what the laser beam irradiates the material surface. It is calculated by dividing beam width with scanning speed of laser beam. However, in this model, the laser heat source has been considered as a stationary line heat source, where the line is equal to the beam diameter 0.2 mm. Direct coupling and transitional mapped meshing features of ANSYS have been used for simulating the thermomechanical effect in LSG for better accuracy, see Sect. 2. The residual stress has been analysed based on temperature gradient approach [27]. This residual stress developed in LSG is the stress induced for thermal strain in the absence of any external force. It is not only important to know the distributions of residual stresses in modified surface during LSG, but also need to understand how material flow behaviours affect the thermal stresses and surface hardening. Therefore, two separate hardening or plasticity models, isotropic and kinematic, have been utilised to calculate the plastic flow induced by the thermal residual stress. The results will be compared for laser power and between two plasticity models.
2 Models and methodology
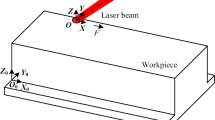
The schematic representation on LSG process with circular cross-section of a cylindrical sample is illustrated in Fig. 1. In this figure, the stationary laser beam irradiates the surface of the cylindrical sample, which is considered as a line heat source for 2D model. The transient thermomechanical model has been analysed for 200 W and 300 W laser power with constant 0.2 mm beam width and 0.15 ms residence time.
2.1 Mathematical formulation
The governing equation of the thermal analysis of LSG is defined by 1st law of thermodynamics and Fourier heat conduction equation. Equation 1 expresses the underpinned thermal phenomena in this process, where no heat generation inside the sample is assumed on the application of the stationary laser heat source. Therefore, the heat generation and velocity terms are ignored in Eq. 1.
where ρ(T), CP(T) and k(T) represent temperature-dependent density, specific heat and thermal conductivity, respectively. Qlaser is the heat flux from the laser beam applied on the surface. The laser beam has been considered as a line heat source of constant heat flux estimated from the Eq. 2.
In Eq. 2, Plaser is the laser power, r0 is the radius of laser beam. A is the absorption coefficient of material for the laser light which has been taken 0.3 for H13 tool steel [24]. The laser beam is assumed as continuous wave (CW) mode. The value of absorption coefficient is taken considering the laser beam as CO2 laser of 10.6 μm wavelength from the literature. Initially, the entire temperature of circular model has been kept at 25 °C or 298 K when time t = 0. The heat loss due to convection and radiation has been ignored, as the time duration is very short (0.15 ms) and a small melt pool is created locally with 0.2 mm beam width.
The high heat flux of laser beam and short interaction or residence time cause very high cooling rates in LSG process. Therefore, it results into higher residual stress in the modified surface area. The residual stress is induced generally due to thermal gradient between the heated zone and cold bulk material, and that is why it is addressed as thermal stress. Developing thermal stress in LSG is complex phenomena. Many factors such as temperature gradient effects, material constraints (stiffness, bonding) and phase transformation within fraction of seconds are involved in inducing stress [14, 28]. The phase transformation effect on thermal stress development is out of scope in this study. Therefore, the nature of residual stresses can be explained by the temperature gradient mechanism explained in [27, 29]. Figure 2 shows a brief demonstration of the stress–strain relationship based on temperature gradient.
Schematic demonstration of thermal stress development due to thermal strain in temperature gradient mechanism (a) during heating and (b) during cooling [27]
Due to the temperature gradient and material constraint around the laser heated area, the total strain developed in the system is expressed as Eq. 3.
In Eq. 3 the total strain εtotal consists of thermal (εth), elastic (εel) and plastic (εpl) strains. Thermal strain is calculated utilising coefficient of thermal expansion and temperature gradient. The elastic part follows the linear relationship of stress–strain (Hook’s law) and plastic strain is calculated using bilinear rate-independent Mises plasticity [14]. In this study, both isotropic and kinematic hardening rule have been applied separately for determining plastic strain and compare the effects on thermal stress. In the theory of isotropic hardening phenomenon, the yield surface in deviatoric stress space evolves in size but the centre of the surface does not displace. This means, in uniaxial tension–compression, the material yields in same magnitudes for both tension and compression loading. On the other hand, for kinematic hardening phenomenon, material yields at less magnitude during compression loading than being loaded in tension. In this case, the yield surface remains in same size but translates in the stress space which is called Bauschinger effect. The von Misses yield criteria during isotropic and kinematic hardening take the following forms, respectively, written in Eqs. 4 and 5. For more to read about the theory, see [30].
For isotropic hardening,
For kinematic hardening,
In Eqs. 4 and 5, σ s is initial yield strength, σ e is von Misses stress, σ f is the new yield stress evolving due to the plastic strain increment ε ij p, and σ ij is called the back stress which resulted in because of the translation of yield surface in kinematic hardening. In practical cases, most metals and alloys show combined behaviour in case of plastic deformation [30].
2.2 Numerical formulation
The circular cross-section of the cylindrical sample has been taken as the geometry for the transient 2D FE thermomechanical model. The diameter of the circular section is 10 mm. ANSYS APDL 17.2, a commercial finite element package has been utilised to calculate temperature profile, thermal history and residual stress from this model. The direct coupling technique has been used to create the thermomechanical effect. In coupling method, the output temperature distribution of thermal analysis is used as input for structural analysis as thermal loads. Plane223 element type is selected for the FE model. This element type has direct coupling effect where the thermal and structural both analyses are run simultaneously which saves simulation time. Plane223 is a higher order element with eight nodes and up to four degrees of freedom. Higher order element means it has middle nodes which can calculate very small deflection with better accuracy and useful for meshing non-linear geometry such as circle or cylinder. It is compatible for simulating elastic, plastic deformation and large deflection of metals and alloys. The circular geometry has been meshed using quadratic shaped of Plane223 element. Transitional mapped mesh (TMM) technique has been used to refine the outside area with gradual coarsening towards the centre. TMM technique has twofold advantages: (1) it reduces the total number of elements in the model resulting into reduction of cost and time for meshing (2) through refinement, TMM ensures more accuracy to the average output of the laser irradiated regions in the surface and sub-surface area. The total number of elements in this model is 9444 and nodes are 29,173. The finite element meshed model of circular geometry is shown in Fig. 3. For this transient thermomechanical analysis, the length of the time step has been kept 1 × 10− 6 s considering the short residence time (0.15 ms). The thermal boundary load has been applied as a constant heat flux as presented in Eq. 3. The convection and radiation losses have been ignored as the beam lasts for very brief period and irradiates locally over a tiny small area. For structural boundary condition, the centre of the circular model has been constrained to prevent elemental motion. That means the displacement of central node in both X and Y direction has been set to zero. This simply replicates the clamping effect in practical case of LSG with a cylindrical sample.
Temperature-dependent physical and mechanical properties of H13 tool steel have been input prior to the analysis. The values of density, thermal conductivity, specific heat, coefficient of thermal expansion for H13 tool steel changing with temperature are tabulated in Table 1.
For elastic and plastic phenomena Young’s modulus, Poisson’s ratio, yield strength and tangent modulus of H13 tool steel are also considered. Figure 4 shows how those mechanical properties change with temperature.
Temperature dependent Young’s modulus, Poisson’s ratio, yield strength and tangent modulus of H13 tools steels [32]
3 Results and discussion
3.1 Thermal distribution and temperature change rate
The model creates temperature profile or isotherms due to the conduction heat transfer from the high temperature molten pool to the low temperature bulk. The peak surface temperature can be predicted from these temperature isotherms. The variations in surface temperatures against time are plotted in Fig. 5 for 200 and 300 W laser power with constant 0.2 mm beam width and 0.15 ms residence time. The peak surface temperature at power 200 and 300 W are, respectively, 1603 K and 2459 K at 0.15 ms time. It is observed that at 200 W power the peak temperature remains below the melting point (1727 K) of H13 tool steel, whereas at 300 W it exceeds the melting point. Therefore, to achieve melting point for LSG the laser power should be above 200 W. These surface temperatures at both power levels are same for different hardening models (isotropic and kinematic).
The temperature change rate (dT/dt) is calculated and illustrated against time in Fig. 6. The rate of heating at 200 W power is almost linear over the heating period. However, it slightly varies after 0.124 ms when the surface temperature reaches the melting point (see Fig. 6) at power 300 W. This change might be due to the numerical error, as in ANSYS thermal properties beyond the melting point (1727 K) were kept almost constant for H13 tool steel. Sharp cooling is noticed just after the heat source is removed at 0.15 ms. Temperature drops very quickly almost within 0.003 ms. A large thermal gradient is obvious at that time. After that the rate of cooling gradually decreases because of the reduction in temperature difference between heated area and bulk. From Fig. 6, it is seen that the rates of heating are 1.05 × 107 Ks-1and 2.18 × 107 Ks− 1 for power 200 W and 300W, respectively. The highest cooling rates have been calculated as 6.65 × 107 Ks-1 and 1.51 × 108 Ks− 1 for corresponding laser power 200 W and 300 W.
The high temperature gradient [(1603−298) K = 1305 K, for 200 W and (2459−298) K = 2161 K, for 300 W] and higher cooling rates (6.65 × 107 Ks-1 and 1.51 × 108 Ks− 1) are the indicators of the presence of thermal residual stress in the system.
3.2 Stress and strain
Residual stress has been developed in the surface and sub-surface region due to the large temperature gradient and high rates of heating and cooling. As it is stated earlier that two most principal factors are responsible for the residual stress, one, the strain developed due to thermal gradient and two, the strain developed due to phase transformation [14]. In this study, strain developed due to thermal gradient has been accounted which considers evolution of the volume of material due to the coefficient of thermal expansion. This is called thermal strain which eventually induces elastic and plastic parts of the total strain [19, 27].
Figure 7 illustrates the stress in both X (σ X ) and Y (σ Y ) directions on the surface element where maximum temperatures have been achieved which is in the centre of line heat source. For X axis stress, it is observed that during heating stresses are compressive invariably with power levels and hardening models. After 0.15 ms when cooling starts, these have turned out to tensile stresses (see Fig. 7a). The Y direction stresses (σ Y ) are also in compression during heating time, although they have smaller values than σ X . During cooling, they also transformed to the tensile state, but in a very fluctuating manner (see Fig. 7b).
The reason of the variation of stresses can be correlated with the change of strain in X and Y directions for the LSG process. The total strain for X (ε X total) and Y (ε Y total) directions versus time is illustrated in Fig. 8. Both X and Y directional strain increases initially as heating progresses (see Fig. 8a, b). If strain increases during heating, this indicates the surface material tends to expand outward. But, the surrounding materials do not allow the surface to expand properly. This gives rise to compressive stress in the surface at that time. When cooling initiates, the temperature starts dropping at very high rate. The surface material then starts to shrink which is evident by the reduction of the total strain. Again, the surrounding materials hinder the contraction of the surface causing tensile stress [33]. Although, in uniaxial tensile-compressive loading, if material expands in one direction then the other direction contracts. This phenomenon defines the Poisson’s ratio of materials. But, in this case, the surface material moves in same manner both in X and Y direction, because of the circular shape of the sample. Therefore, sample shape is an important factor on residual stress distribution. ε X total fluctuates during the transition period from heating to cooling. The authors assume that this fluctuation is caused by the material properties input in the analysis. The correct relationship of material properties during transition of solid to liquid transformation is important to know for better accuracy. In case of isotropic hardening, ε X total are lesser than its kinematic counterparts for corresponding laser powers. This indicates that due to higher strain in kinematic plasticity the stress was reduced than its isotropic counterparts based on the theory [30]. ε Y total increases with increased temperature gradient and laser power as the temperature gradient increases with laser power or vice versa. However, the values of ε Y total do not vary with different plastic models (isotropic and kinematic). From the Figs. 7 and 8, a correlation between laser power and plasticity models can be drawn. In isotropic models, with higher laser power higher work hardening occurs in the materials surface for LSG, while in kinematic model material surface more softens due to increasing strain with increasing laser power. Thus, if one knows the material types, depending on its hardening nature the parameters can be optimised in LSG.
Stresses in X direction (σ X ) from surface to centre of the circular model are illustrated in Fig. 9a, b, respectively, both at 0.15 ms time when surface reaches to peak temperature and 0.55 ms time after material cools down. In Fig. 9a, at time 0.15 ms surface reaches to the peak temperature. High thermal strain is developed at that moment and (see in Fig. 8a) the surface experiences compressive stress due to the constraint from the surrounding material. This compressive stress gradually turns into tensile as progressing to the centre from the surface due to the reduction of the thermal gradient as well as thermal strain. Similar trend was reported for laser cladding of H13 tool steel substrate at laser power 2200 W, beam width 3 mm, scan speed 200 mm min− 1 [20]. The highest compressive stress around 330 MPa is achieved for 300 W laser power for both plasticity models. For 200 W, the highest compressive stress is gained at 0.01 mm while it shifts to 0.025 mm for 300 W power (Fig. 9a). This reveals that the depth of heat concentrated zone increases with the increment of laser power. After cooling, the surface gets in tension due to the contraction and the sub-surface region releases stresses. From Fig. 9b, it is observed that the surface stress increases with laser power in case of isotropic model. The highest stress at 300 W reaches to the 2100 MPa which is above the yield stress of H13 tool steel. The reason behind this excessive stress is unknown and needs to verify with experimental study. Whereas in kinematic model, the surface stress after cooling is in small scale and is decreasing with increasing laser power.
3.3 Prediction of crack formation
The equivalent stress, (von Misses stress), is an important indicator to understand the crack formation of the sample surface due to the residual stresses developed during LSG treatment. Figure 10 depicts equivalent von Misses stress of a point on surface (centre of the projected beam, see Fig. 3) over processing time from the model. During heating stresses are growing up to a certain time range which is approximately 0.08–012 ms. For laser power 200 W, the maximum stress developed (around 400 MPa) in the heating period is lower than the power 300 W. After that these stresses, lower down up to 0.15 ms time. When cooling initiates, stresses again start to increase. For isotropic plasticity, the von Misses stress reaches to its higher value and increases with laser power. At 300 W laser power, the von Misses stress goes highest to 2100 MPa which is beyond the material’s yield point. This is an indicator of crack formation in the surface area which needs to be verified with experimental data. For kinematic rule, the behaviour is opposite. At 200 W laser power, the value of von Misses stress is 29 MPa after cooling. With increasing laser power, the value decreases further to 20 MPa. That means the equivalent stresses reduce as cooling progress and lower down as the laser power increases. This indicates that for further increase in laser power the surface may get compressive residual stress in case of kinematic model which is visible in others works for laser surface melting [14, 28]. In cyclic loading like laser surface melting, according to the theory the isotropic hardening model has increased the stress magnitudes due the expansion of the yield surface. In case of kinematic model, the stress has been reduced as the Bauschinger effect accounted due to the shift of the yield surface [34].
4 Conclusion
A 2D thermomechanical finite element (FE) model of LSG for H13 tool steel has been developed using ANSYS APDL 17.2 software. The model has successfully predicted the temperature profile, temperature change rate and residual stress for a circular cross-section of a cylindrical sample of 10 mm diameter. The model output has been analysed for 200 W and 300 W laser power with constant 0.2 mm beam width and 0.15 ms residence time considering the stationary laser beam as a line heat source with constant heat flux. The thermal residual stress has been calculated based on temperature gradient approach. Material plastic flow due to thermal strain has been separately analysed for isotropic and kinematic plasticity models.
For 200 W laser power, the peak surface temperature has been achieved 1603 K which is below the melting point (1727 K) of H13 tool steel. For 300 W, melting has happened and peak surface temperature has reached to 2459 K. Cooling rates have increased from 6.7 × 107 to 1.5 × 108 Ks−1 when laser power has been raised from 200 W to 300 W.
Tensile residual stresses on the surface have been found for both plasticity models. Isotropic model has given higher (2100 MPa) tensile residual stress while kinematic model has produced very low (20 MPa) after cooling. In isotropic, stresses increase with laser power, whereas in kinematic they decrease with increasing laser power. This is indicating the tensile residual stress might transform into compressive stress with further increase of laser power for the kinematic case. The values of residual stresses calculated from the model will be validated in future with experimental work.
References
A. Grellier, M. Siaut, in 6th Int. Tool. Conf, ed. by J. Bergström ed. (Karlstad University, Sweden, 2002), pp. 39–48
M. Muhič, J. Tušek, F. Kosel, D. Klobčar, M. Muhi, J. Tušek, F. Kosel, D. Klob, S. Vestnik, J. Mech. Eng. 56, 351 (2010)
G. Telasang, J. Dutta Majumdar, G. Padmanabham, I. Manna, Mater. Sci. Eng. A 599, 255 (2014)
N. Tamanna, R. Crouch, S. Naher, in 20th Int. ESAFORM Conf. Mater. Form, (AIP Conference Proceedings, Dublin, Ireland, 2017)
K. Ibraheem, B. Derby, P.J. Withers, in (Mat. Res. Soc. Symp.Proc., 2003)
S. Paul, K. Thool, R. Singh, I. Samajdar, W. Yan, Procedia Manuf. 10, 804 (2017)
N.S. Bailey, C. Katinas, Y.C. Shin, J. Mater. Process. Technol. 247, 223 (2017)
S. Oh, H. Ki, Appl. Therm. Eng. 121, 951 (2017)
G. Telasang, J. Dutta Majumdar, G. Padmanabham, M. Tak, I. Manna, Surf. Coatings Technol. 258, 1108 (2014)
M.J. Tobar, C. Álvarez, J.M. Amado, A. Ramil, E. Saavedra, A. Yáñez, Surf. Coatings Technol. 200, 6362 (2006)
J. Romano, L. Ladani, M. Sadowski, Procedia Manuf. 1, 238 (2015)
S.A. Syarifah Nur Aqida, S. Naher, D. Brabazon, Key Eng. Mater. 504–506, 351 (2012)
B.S. Yilbas, A.F.M. Arif, C. Karatas, K. Raza, J. Mater. Process. Technol. 209, 77 (2009)
C. Li, Y. Wang, H. Zhan, T. Han, B. Han, W. Zhao, Mater. Des. 31, 3366 (2010)
S.Z. Shuja, B.S. Yilbas, Opt. Lasers Eng. 51, 446 (2013)
Ansys coupled-field analyses guide, version 17.2, Ansys Inc. (2017), http://support.ansys.com/documentation. Accessed 30 Oct 2017
T.K. Talukdar, L. Wang, S.D. Felicelli, in ASME 2011 Int. Mech. Eng. Congr. Expo. (Denver, Coloradod.), pp. 1–9
I.A. Roberts, C.J. Wang, R. Esterlein, M. Stanford, D.J. Mynors, Int. J. Mach. Tools Manuf. 49, 916 (2009)
B.S. Yilbas, S.S. Akhtar, C. Karatas, H. Ali, K. Boran, M. Khaled, N. Al-Aqeeli, B.J. Aleem, Int. J. Adv. Manuf. Technol. 86, 3547 (2016)
S. Paul, K. Ashraf, R. Singh, in ASME 2014 Int. Manuf. Sci. Eng. Conf. MSEC 2014 Collocated with JSME. 2014 Int. Conf. Mater. Process. 42nd North Am. Manuf. Res. Conf., pp 1–8 (2014)
C. Li, Y. Wang, Z. Zhang, B. Han, T. Han, Opt. Lasers Eng. 48, 1224 (2010)
N.B. Dahotre, Adv. Mater. Process. 35 (2002)
B.H. Kear, E.M. Breinan, L.E. Greenwald, Metals Technology (1979)
S.N. Aqida, Laser surface modification of steel, PhD thesis, (2011)
E. Chikarakara, Laser Surface Modiffications of Biomedical Alloys, PhD theis (2012)
I.R. Kabir, D. Yin, S. Naher, in 19th Int. ESAFORM Conf. Mater. Form., edited by F. Chinesta and E. Abisset-Chavanne, (AIP Conference Proceedings, Nantes, France, 2016), pp. 110003(1–6)
I.A. Roberts, Investigation of residual stresses in the laser melting of metal powders in additive layer, PhD thesis, (2012)
C. Li, Y. Wang, B Han, Opt. Lasers Eng. 49, 530 (2011)
J.P. Kruth, L. Froyen, J. Van Vaerenbergh, P. Mercelis, M. Rombouts, B. Lauwers, J. Mater. Process. Technol. 149, 616 (2004)
J.L. Chaboche, Int. J. Plast. 24, 1642 (2008)
P. Farahmand, P. Balu, F. Kong, R. Kovacevic, in ASME 2013 Int. Mech. Eng. Congr. Expo (San Diego, California, 2015), pp. 1–12
S. Zekovic, R. Dwivedi, R. Kovacevic, in the proceedings of Solid Freeform Fabrication Symposium (Austin, Texas, USA, 2005), pp 338–355
N. Tamanna, R. Crouch, I. R. Kabir, S. Naher, Appl. Phys. A Mater. Sci. Process. 124, 202 (2018)
S.K. Velaga, S.A. Kumar, A. Ravisankar, S. Venugopal, Int. J. Press. Vessel. Pip. 150, 72 (2017)
Acknowledgements
The work described in this paper has been supported by INTACT project of Erasmus-Mundus (Grant agreement reference: 2013–2829/001-001-EM Action2-Partnerships), and Department of Mechanical Engineering and Aeronautics of City, University of London. The authors are grateful enough to Professor Ranjan Banerjee for the valuable discussion when developing the FEM model.
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kabir, I.R., Yin, D., Tamanna, N. et al. Thermomechanical modelling of laser surface glazing for H13 tool steel. Appl. Phys. A 124, 260 (2018). https://doi.org/10.1007/s00339-018-1671-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00339-018-1671-9