1 Introduction

The electromagnetic parameters of materials determine the characteristics of electromagnetic wave when the electromagnetic wave propagates in it. The test methods of the electromagnetic parameters vary a lot. Different shapes, structures and physical properties of the test samples are required when different methods are adopted. Generally, the testing methods can be divided into two broad categories: network parameters method [1,2,3,4,5] and resonance method [6,7,8].

With the rapid development of high-power microwave, whether the microwave properties of the materials will change or not under strong electromagnetic environment attracts attention of researchers. It is found that \({\text{SiO}}_2\) nanoparticles dispersed in liquid polymethylsiloxane exhibit unique optical nonlinearity in low-intensely visible radiation fields [9]. Transient response of dielectric materials under ultrafast laser radiation is studied and a dynamical observation on the development of electron–hole plasmas is presented [10]. Researches have demonstrated that the dielectric constant of ferroelectric materials changes nonlinearly along with the changes of external electric field, which is the characteristic of ferroelectric materials themselves [11, 20]. However, those studies were carried out under dc or low-frequency electromagnetic field conditions [11,12,13,14,15,16,17,18,19,20,21].

Indium phosphate (InP) is a kind of direct band gap compound semiconductor, which is widely used in microwave and optoelectronic devices. Existing studies demonstrate that heavy ion irradiation can change the structure of the material [22, 23], which may affect the physical properties of the material [24,25,26]. The radiation characteristics of InP has been explored [27,28,29,30,31,32]. However, these researches mainly focus on experiment, which lacks theoretical explanation.

This paper studies the dielectric property of microwave semiconductor materials, under the environment of strong microwave electromagnetic field in a compressed rectangular cavity. In order to create a strong strength of electromagnetic field, the exciting power signal should be coupled into the cavity with low reflection and less energy be coupled out to the load, which makes most energy stay in the cavity. The test system is established in Sect. 3. During the experiment, the dielectric property of InP with a nonlinear behavior is found under the strong electromagnetic environment. We analyze that the nonlinear behavior of the dielectric property of InP is not the thermal nonlinearity but nonlinear behavior of material itself. As far as we know, this is the first time that the dielectric property of InP is studied under a strong electromagnetic field in microwave band.

2 Cavity design

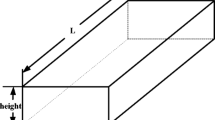
Different from the conventional rectangular cavity, a compressed rectangular cavity is designed in this paper. Firstly, a normal \({\text {TE}}_{102}\) rectangular cavity is modeled in HFSS, which works at the frequency around 2.45 GHz and it has a width of 83.36 mm and height of 43.18 mm. Secondly, in order to increase the local electric field strength in the cavity, we compress the height of the rectangular cavity where the length is \(\lambda _g /4.\) Here \(\lambda _g\) is the waveguide wavelength. The structure schematic of the compressed cavity is given in Fig. 1. The compressed rectangular cavity keeps the same \({\text {TE}}_{102}\) model and the same resonant frequency, as we change the length of the cavity. The length of the compressed rectangular is 155 mm and the height of the compressed part d is 10 mm.

Based on the calculated sizes, a model of the \({\text {TE}}_{102}\) compressed rectangular cavity is built and simulated by HFSS. The resonance curves of the compressed cavity and the simulated results are shown in Fig. 2.

According to the transmission curve, the load quality factor is calculated through the following formula [19]:

$$\begin{aligned} Q_{\rm{L}}=\frac{1}{\text {BW}}, \end{aligned}$$
(1)

where

$$\begin{aligned} {\text {BW}}=\frac{\Delta f_{1/2}}{f_0}. \end{aligned}$$
(2)
Fig. 1
figure 1

The compressed rectangular cavity structure schematic

Full size image

In Eq. (2), \(f_0\) is the resonant frequency and \(\Delta f_{1/2}\) is the half-power bandwidth. Figure 2 shows that the half-power bandwidth is 0.0003 at the resonance point of 2.458 GHz. From (1) and (2), the loaded quality factor \(Q_{\rm{L}}\) of 8193 can be derived. This value is appropriate for the experiment.

Fig. 2
figure 2

Simulated results of transmission and reflection characteristics of the compressed rectangular cavity

Full size image
Fig. 3
figure 3

Electric field distribution inside the compressed cavity

Full size image
Fig. 4
figure 4

A line through the compressed part with a length as the same length of the cavity, which used to see the field strength changes in the cavity

Full size image

Figure 3 shows the electric field distributed inside the compressed cavity. From the field distribution, it is easy to see that the field strength at the compressed region is stronger than any other place in the cavity. In order to check the accurate field distribution in the cavity, a line through the compressed part with a length of the same as the cavity length is drawn in the HFSS model, as shown in Fig. 4. Then, the electric field strength along the line is shown in Fig. 5. From the field strength curve, it is obvious that the strongest electric field in the cavity lies at the compressed part. With a proper compression, about twice or more times stronger electric field strength is obtained at the compressed part than the electric field strength at the normal cavity.

Fig. 5
figure 5

Simulated electric field strength along the line

Full size image

Through the calculation and simulation, the compressed cavity is suitable for our test system, which created a strong electric field with an appropriate power being injected in. Changing the input power could change the strength of the electromagnetic field in the cavity. The compressed rectangular cavity is fabricated and coated with silver as presented in Fig. 6.

Fig. 6
figure 6

Photograph of the compressed rectangular cavity

Full size image

3 The test system

Based on the compressed rectangular cavity designed in Sect. 2, a model of the nonlinear properties of microwave material test system is established, which is shown in Fig. 7. The VNA acts as a microwave source, whose frequency is the same as the resonance frequency of the cavity and its power can be changed continuously. The isolators protect the VNA and power amplifier by reducing the reflections. The amplifier with a maximum output power of 50 dBm is used to extend the power of the microwave source. In order to let more energy be coupled into the cavity, the amplified signal is input into the compressed cavity through a loop, where the magnetic field strength is the strongest. In addition, the probe is placed at a point where the electromagnetic field is rather low, and it couples with small amounts of energy for analysis. Through an attenuator, signals are collected and shown on the VNA. The material under test is inserted at the compressed part of the cavity through a quartz tube. The test system utilized is shown in Fig. 8.

4 Experiment and analysis

In the paper, measurement is performed on InP, a kind of very important microwave semiconductor material. The InP sample is loaded in a quartz tube for the convenience of the test and inserted in the cavity at the compressed part where the electric field strength is strongest in the cavity. Before testing, the effects of the quartz tube should be excluded. In other words, we want to make sure that the nonlinear phenomenon is caused by the InP itself rather than the quartz tube. Therefore, the quartz tube is tested first.

Fig. 7
figure 7

Model of the nonlinear property of microwave material test system

Full size image
Fig. 8
figure 8

Photograph of the test system

Full size image

Firstly, the quartz tube is put at the compressed part of the cavity and a low output power signal, −15 dBm, is given by the VNA. The transmission curve is obtained, which is the black as shown in Fig. 9. Then the output power of the VNA is increased to 0 dBm and the transmission curve is gotten, which is the red as shown in Fig. 9. The red curve is marked and held for about 10 s. After that, we set the output power of the VNA back to −15 dBm. The transmission curve is obtained again and it is the blue curve as shown in Fig. 9. In order to look at the changes more clearly, Fig. 9 is enlarged at the resonant point, which is shown in Fig. 10. From the curves, the resonant frequency has no changes while the output power of the VNA is changed.

Fig. 9
figure 9

Test curves of the quartz tube

Full size image

According to the perturbation theory [19], as is presented in (3) and (4), the real part of dielectric constant is the reason of the resonant frequency shift and the imaginary part causes the change of the quality factor of the cavity. Thus, considering the resonant frequencies of the resonance curves of the cavity loaded with the quartz tube under different power levels are still the same, we conclude that the real part of dielectric constant of the quartz tube has no nonlinearity in the given strong electromagnetic field environment. Therefore, the quartz tube can be used for the InP test.

$$\begin{aligned} \frac{\omega -\omega _0}{\omega _0}=-\varepsilon _0(\varepsilon '-1)\frac{\int _\Delta {\bf {E}}\cdot {\bf {E}_0}^*{\rm {d}}V}{4W} \end{aligned}$$
(3)
$$\begin{aligned} \frac{1}{Q}-\frac{1}{Q_0}=\varepsilon _0\varepsilon ''\frac{\int _\Delta {\bf {E}}\cdot {\bf {E}_0}^*{\rm {d}}V}{4W}, \end{aligned}$$
(4)

where \(\omega \) and \(\omega _0\) are the angular resonant frequency before and after the perturbation. Q and \(Q_0\) are the quality factor before and after the perturbation. \({\bf {E}}\) and \({\bf {E}_0}\) are the electric field strength before and after the perturbation in the cavity. W is the total store energy in the cavity. And \(\varepsilon ',\) \(\varepsilon ''\) is the real and imaginary part of the dielectric constant.

After excluding the influence of the quartz tube on test results, we put the InP sample inside the tube, and place it at the compressed part of the cavity. The steps of the quartz tube experiment are repeated, and the test results are shown in Fig. 11. Parts of the resonant curves at the resonant point are enlarged, which are shown in Fig. 12.

Fig. 10
figure 10

Enlarged view of the resonant part of the curves in Fig. 9

Full size image
Fig. 11
figure 11

Test curves of InP

Full size image
Fig. 12
figure 12

Enlarged view of the resonant part of the curves in Fig. 11

Full size image

In Fig. 11, the black curve and the red curve are obtained at the output power level −15 and 0 dBm, respectively. It is found that the resonant frequency changes while the output power of the VNA changes from −15 to 0 dBm. After setting back the output power to −15 dBm, the resonant curve is the blue one as shown in Fig. 11. It is easy to see that the blue curve is basically coincident with the black one. According to Eq. (3) given above, we can draw the conclusion that the dielectric constant of the InP has changed under different microwave source power levels. What is more, in Fig. 12, parts of the red curve are deformed. For two reasons, we attribute this phenomenon to the inherent nonlinear property of InP rather than the microwave heating.

On the one hand, dielectric loss is used to describe the degree of microwave absorption of the materials [31]. The bigger the loss is, the faster the microwave is absorbed. The dielectric loss of the InP sample under test is measured by the perturbation method with a cylindrical cavity, which is about \(1.3\times 10^{-4}.\) It means that it needs time to heat the InP sample as the dielectric loss is very small. However, in the experiment, the transmission curves change immediately with the change of the output power of the VNA. The curves change time can be ignored. This shows that the dielectric property changes before the InP sample is heated. It can be concluded that the resonant frequency changes because of the change of the dielectric field strength in the cavity rather than the microwave heating.

On the other hand, in the experiment, the output power of the VNA remains at 0 dBm for 10 s. Assume that the InP sample has been heated and the heating causes the nonlinear phenomenon in the meantime. The thermal conductivity of InP is only 0.7W cm\(^{-1}\) K\(^{-1},\) which means that the heat dissipation of the InP sample is not very good. Therefore, the heat of the InP sample would not dissipate so quickly even though InP is heated during the experiment. If we change the output power of the VNA, the red curve will not change much. That is to say, the blue curve would not be coincident with the black curve before the heat is dissipated. However, in the experiment the red curve changes to the blue curve immediately after we change the output power of the VNA from 0 to −15 dBm. All this proves that the assumption is not valid. Therefore, we believe that InP shows nonlinear dielectric property under strong electromagnetic field environment.

In order to further address the conclusion that the nonlinear behavior of the dielectric property of InP is not the thermal nonlinearity but nonlinear behavior of material itself, two additional experiments are added for comparison. In the experiment, the output power of the VNA changes very quickly from −15 to 0 dBm. Then, the red curve is marked and held for about 30 s, 2 min, respectively. The experimental results are shown in Figs. 13 and 14.

Fig. 13
figure 13

Test curves of InP, as the output power of the VNA is held on at 0 dBm for 30 s

Full size image
Fig. 14
figure 14

Test curves of InP, as the output power of the VNA is held on at 0 dBm for 2 min

Full size image
Fig. 15
figure 15

Samples of InP under test

Full size image

In Figs. 13 and 14, it is easy to see that the blue curve cannot be coincident with the black one any more when the holding time is increased. In other words, the InP has been heated during the holding time, and the effect will be more significant with the holding time is longer. On the other hand, in Figs. 13 and 14, the frequency deviation between the red curve and the black curve is almost five times larger than the frequency deviation between the blue curve and the black curve. This means that by heating it is not possible to change the resonant curve from black to red curve in a very short time in the experiment. Therefore, we draw the conclusion that it is the inherent nonlinear property of InP that causes the nonlinear phenomenon in microwave band. Samples of InP and the quartz tube are shown in Fig. 15.

5 Conclusion

In this paper, we develop the compressed rectangular cavity through compressing the height of a normal rectangular cavity, and a strength of electric field about \(6\times 10^4\) V/m at the compressed region is derived when 1 W power is coupled into the cavity. In test system, a more than 20 W power signal is injected into the cavity. According to the relationships between power and electric field strength, the compressed region acquires a strength of electric field nearly about \(3\times 10^5\) V/m. Through the test, the nonlinear dielectric property of Inp is found under a strong electromagnetic environment, which we estimate is due to the material’s inherent nonlinearity and not caused by microwave heating.