1 Introduction

Since graphene, a two-dimensional graphite, was fabricated by exfoliation from graphite [1], there has been significant research interest in graphene synthesis and graphene properties [2–4]. Numerous works have reported the remarkable properties of graphene, including extraordinary high electron mobility [5], thermal conductivity [6], stiffness and strength [7], as well as large surface area to volume ratio [8], and an unusual electronic structure [9]. However, some of the properties of graphene are not well suited to practical applications, which lead to intense research into new methods of functionalization or property tuning [10].

In applications where the thermal requirements are critical, it is important to regulate the change of the thermal properties. For graphene to be a high-performance thermoelectric (TE) candidate, it is desirable to lower its thermal conductivity as much as possible, which would increase its TE figure of merit [11]. However, it is often the case that the thermal transport properties of graphene are altered as a side effect of tuning other properties. Graphene’s excellent heat transfer properties make it an ideal material for addressing challenges associated with the cooling loads of electric devices [6, 12]. Compared to carbon nanotubes (CNTs), graphene has lower contact resistance and superior thermal heat transfer properties. However, for practical applications, the zero bandgap of pristine graphene must be addressed with proper functionalization. The insertion of impurity or dopant atoms is the most effective method for addressing the bandgap concerns [10, 13]. On the other hand, it can negatively impact thermal conduction properties. Therefore, controlling the impact of impurity on heat transfer [14–16] becomes important for advancing graphene-based technology.

An understanding of the origin of graphene’s high thermal conductivity is challenging because the models of two-dimensional and nanoscale physics are limited. The contribution of phonon scattering to the thermal conductivity is dominant over the electronic contribution [12]. Sadeghi et al. [17] have reviewed current challenges surrounding the thermal transport properties. As regards the heat transport of tuning graphene, investigations of isotope [18], nitrogen [16], and vacancy [19] have been performed. Recently, an elaborate model that corrects the Klemens’ model, which was originally developed for general bulk materials and subsequently adopted for graphene, has been suggested [20].

The silicon-doped graphene has been recently synthesized [21], and density functional theory (DFT) calculation had shown the possibility of enhanced on/off efficiency [13]. It was proposed that bonding stability allows the addition of different atoms bound to Si atoms [22]. In the present study, single-layered graphene with silicon as impurity has been investigated using non-equilibrium MD (NEMD) and equilibrium MD (EMD) to demonstrate the reduction in graphene’s thermal conductivity and the relevant phonon behavior, respectively. MD has already been adopted in investigating the thermal conduction of graphene relating to rectification [14, 23] and thermal property management by controlling chirality, shape, and type of defect [14–16, 24–26]. To evaluate the scattering contributions in the Klemens’ model from the MD results, Callaway type model calculations are conducted. Based on these calculations, additional consideration is given on the long-length behavior of the thermal conductivity.

2 Numerical methods

In classical MD, Newton’s second law is applied to all atoms in the calculation domain, and the force F i , acting on an atom i, is expressed as the gradient of potential energy according to

$$\varvec{F}_{i} = - \sum\limits_{i < j} {\frac{{d\phi_{ij} (r)}}{{d\varvec{r}_{i} }}} ,$$
(1)

where r i is the position vector of the atom i, and the intermolecular potential ϕ ij (r) is given by Tersoff potential model [27, 28]. The potential is used for C–C, Si–Si, and C–Si interactions for silicon-doped graphene in a single form with multiple sets of parameters. All of the parameters used in the current study follow values previously tested and recommended in some applications by Tersoff [27]. The current programs have been validated through tests that reproduce previous results [29, 30]. The Newtonian equation is discretized in time using the Verlet algorithm with a fixed time step of Δt = 0.2 fs for both NEMD and EMD, and both methods have previously been systemically applied to silicon bonds with the Tersoff potential [31].

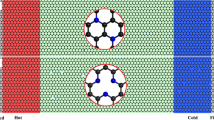
The procedure used by Wei et al. [32] is employed for NEMD calculations, where the half-sized domain, which is used for time-saving purposes, is the only difference from general NEMD calculations. The atomic arrangement of carbon and silicon is depicted in Fig. 1. The length of the model sheets ranges from 10.65 to 63.9 nm, and the width of all the simulated sheets is fixed at 3.9 nm. The silicon atoms are regularly distributed in convenience for the stability of the calculation and the consistent comparison of results for different sheet lengths. This artificial arrangement is not expected to have a significant impact on the results compared with using a random distribution. Five impurity concentrations, ranging between 0 and 10 %, are simulated. Periodic and free boundary conditions are applied in the y and z directions, respectively. The general procedures of NEMD (as described in [31]) are used in the simulations. The atoms start from their initial conditions and undergo the equilibration processes at a temperature of 300 K with 1,000,000 time steps. Then, the sheets are exposed to heat flux by adding and removing kinetic energy at the source and sink.

Fig. 1
figure 1

Atomic distribution for 5 % impurity with carbon atoms in white and silicon atoms in black

Full size image

The thermal conductivity is calculated using Fourier’s law from the resulting temperature gradient and the applied heat flux as

$$q = - k\frac{{{\text{d}}T}}{{{\text{d}}x}},$$
(2)

where heat flux, q, is applied as Δε/A not exceeding 23.0 × 10−5 eV/nm2 for each time step.

The same concentrations are used for both the EMD and NEMD calculations. The DOS calculated using EMD reveals the change of phonon property. The domain for the EMD calculations has x and y dimensions of 10.65 and 11.81 nm, respectively, and the periodic boundary conditions are extended to the x direction to simulate an infinite system. The Fourier transform over velocity autocorrelation function is given by

$$\gamma (\omega ) = \frac{{\langle\sum {v_{i} (t)v_{i} (0)}\rangle }}{{ \langle\sum {v_{i}^{2} (0)}\rangle }},$$
(3)

which is considered to be equivalent to the DOS [33].

3 Results and discussion

After a sufficient number of time steps to adapt to the heat flux, steady temperature profiles are established. Figure 2 presents a temperature profile obtained at a 63.9-nm-long pure graphene sheet subjected to a thermal energy of 15.3 × 10−5 eV/nm2. With the exception of the regions near the sink and source, a linear profile is generated, from which the thermal conductivity can be calculated.

Fig. 2
figure 2

Temperature profile for the 63.9-nm-long pure graphene subjected to thermal energy of Δε/A = 15.3 × 10−5 eV/nm2

Full size image

The thermal conductivity values calculated for all conditions are shown in Fig. 3. The thermal conductivity increases with increasing sheet length, as expected because the phonon mean path depends on the sheet dimension. This can simply be explained using kinetic theory,

$$k = \frac{1}{3}cv_{p} \quad l = \frac{1}{3}cv_{p}^{2} \tau ,$$
(4)

where c, v p , l, and τ represent specific heat, phonon velocity, mean free path, and scattering time, respectively. As the impurity level of the graphene increases, the conductivity decreases.

Fig. 3
figure 3

Size-dependent thermal conductivities obtained from NEMD calculations for pure and impure graphenes

Full size image

Because of the extremely large computational cost, most of MD calculations employ an extrapolation scheme to estimate the bulk thermal conductivity based on smaller scale simulations, where Matthiessen’s rule has been favored. In this case,

$$1/l_{\text{eff}} = 1/L + 1/l_{\infty } ,$$
(5)

where the free path of infinite size l ∞ and the free path confined by distance between sink and source L contribute to the effective free path of finite length l eff. According to the NEMD procedure, the effective conductivity approaches the bulk conductivity as 1/L approaches zero (i.e., at the infinite length). Thus, the inverse relationship shown in Fig. 3 facilitates the estimation of infinite conductivity k ∞. For the pristine graphene sheet, the extrapolation gives k ∞ = 774 W/mK, which is in agreement with recent NEMD calculations on the same potential model [16, 32, 34]. The large deviation from linearity at the maximum concentration (10 % silicon atoms) is related to the resolution of conductivity, i.e., the conductivity value is so small that the inverse value appears large.

The conductivity reduction ratios compared to pure infinite sheet, which is calculated from Eq. (5), are presented in Fig. 4. A drastic reduction in the thermal conductivity is observed. A 2 % impurity concentration results in more than an 80 % reduction, while a 10 % impurity concentration reduces the conductivity to <2 % of that in pure graphene. These reduction rates are larger than those obtained by simple mass substitution of isotopic atoms [18] or by nitrogen doping of graphene [16].

Fig. 4
figure 4

Thermal conductivity ratios estimated by Eq. (5)

Full size image

Using the NEMD model, an accurate fitting scheme is necessary to estimate the bulk thermal conductivity other than Eq. (5). There are three conjectures on the behavior of the thermal conductivity: (1) As in MD simulation, the bulk thermal conductivity is usually estimated by the Matthiessen’s rule preferred in general bulk (three dimensional) materials , which assumes a finite k at infinite length [31, 32]; (2) the k diverges in lower dimensions especially with logarithmic law (log dependence) for two dimensional lattices, which, in graphene, is known to be valid up to L < ~9 μm, and then diverges [35]; and (3) the k follows log dependence when L is smaller than about 100 μm, and for longer L, it converges when the thermal transport reaches the diffusive regime [36].

Barbarino et al. [37] calculated the thermal conductivity for the graphene whose length is in the range of 0.83–100 μm using approach-to-equilibrium MD (AEMD) with the reactive empirical bond order (REBO) potential, which can accommodate a large computational domain size with relatively shorter computing time. Their results support the third conjecture mentioned above.

We assumed Matthiessen’s rule to estimate k ∞, which is turn out to be 774 W/mK. This is much smaller value compared to experimentally observed literature value of about 3000 W/mK [38, 39]. However, if we use the size dependence proposed by Barbarino et al. for fitting, instead of Matthiessen’s rule, the thermal conductivity becomes about 2700 W/mK. The k/k (100 mm) at 60 nm is 0.1, and its value is 0.6 at about L = 3 mm where most experimental data are available; thus, 6 times of our k = 440 W/mK at L = 60 nm yields about 2700 W/mK.

The DOS for the same configuration and concentration rate as in the NEMD cases is also obtained using EMD calculations. The calculated DOS of pure sheet is consistent with the dispersion curve obtained from Boltzmann transport calculations using the same original potential [40, 41]. Figure 5 presents the dispersion curve obtained from Boltzmann transport calculations and the DOS obtained from the EMD. Most of the singular points in DOS shown in Fig. 5 correspond to the frequencies of the symmetric points in the dispersion curve. Each of six phonon branches causes a high DOS peak at the M points. The nonzero and higher DOS at zero frequency (Γ1–3 point) is related to the quadratic dispersion relation of out-of-plane phonon modes, which is a direct consequence of the two dimensionality of graphene [42]. At K 1–2 where the optical and acoustic modes are contacted, the valley between the two M peaks is formed. This is analogous to the electronic band structure, where a zero bandgap is formed by the contact.

Fig. 5
figure 5

Dispersion curve obtained from the Boltzmann transport equation [40, 41] and DOS obtained from the present MD calculations for a pure graphene sheet

Full size image

The DOS for the pristine and impure graphenes is presented in Fig. 6. To allow the DOS calculated for the different impurity concentrations to be compared, the frequency, ω, has been corrected to adjust for the mass changes that result from the replacement carbon with silicon atoms [15], using

$$\omega_{0} /\omega_{d} = \sqrt {f_{d} (m_{d} /m_{0} ) + (1 - f_{d} )} ,$$
(6)

with subscripts 0 and d denoting the host and dopant fraction, respectively. Without the correction, the real confinement frequency is reduced from 73 GHz for the pure case to 70 GHz at 10 % impurity concentration.

Fig. 6
figure 6

DOS obtained from the present MD calculations with frequency corrected by Eq. (6). From top to bottom: 0.00, 0.63, 1.25, 5.00, and 10.0 % silicon concentrations

Full size image

The most remarkable change in the DOS distribution is that the increased concentration rate reduces or broadens all of the M point peaks of the pure sheet. In Adamyan’s calculations [43] for sheets doped with aluminum atoms, which have a mass comparable to silicon atoms, the peaks are lower near the van Hove singularities. Generally, peak broadening indicates that the scattering rates increase [33, 44] for all phonons.

The contraction of the frequency regime, as shown in Eq. (6), suggests that the effect of the phonon velocity being reduced by the impurities can account for only a limited or small portion of the full conductivity reduction [see Eq. (4)]. Hence, the distribution of DOS indicates that the primary source of the reduction is the increased scattering rate. Both calculation models predict that the additional peaks arise at the same frequencies, K 1–2 and K 4–5. These additional peaks accompany the splitting of the intersected modes, which is analogous to the bandgap opening in the doped graphene [43, 45]. It has been suggested that the shapes of the additional peaks are the result of optical phonons that occupy a narrow band with relatively low phonon group velocity [45]. This conversion of peaks into modes that do not contribute to the heat transport could enhance the reduction in thermal conductivity. At the maximum concentration in Fig. 6e, the DOS is significantly different from the lower concentration models in that the peaks disappear and the gap separating the in-plane acoustic modes from the other modes is bridged because of the growth of the additional distribution.

The cause of imperfect scattering due to defects in the crystalline structure can be analyzed with a few constituent elements in the Rayleigh scattering model, as shown by Klemens [46]. When adjusted to two-dimensional material, such as graphene [47], the phonon relaxation time is given by

$$\tau_{\text{pd}} = \frac{{24\pi c_{d} \omega^{3} }}{{\omega_{{p,{ \hbox{max} }}}^{2} }}\left\{ {S_{1}^{2} + (S_{2} + S_{3} )^{2} } \right\},$$
(7)

where c d is the concentration of defect atom. The elemental parameters S 1, S 2, and S 3 are related to differences in mass, velocity, and radial spacing, respectively [46]. For example, S 1 accounts for only mass changes, such as in isotopes. While the first term is the contribution of pure mass change, the latter two are commonly derived from the change of interatomic force. The scattering rate is larger than the simple mass change when the change of the interatomic force involves different atomic species. Hence, the conductivity of graphene doped with heavy atoms such as silicon is lower than that of enriched isotope or of graphene doped with lighter atoms.

Figure 7 shows the instantaneous atomic arrangements. Even in the pure sheet, graphene has intrinsic ripples on the order of one nanometer, which is comparable to that of real suspended graphene [48]. The level of perturbation is getting higher than the natural ripple (Fig. 7a) (for pure graphene) with increasing silicon concentration. This perturbation occasionally results in irregular twisting of the smooth ripples. Non-planar shapes such as ripples and areas of high curvature can cause reduced thermal conductivity [49]; reductions by folding [50] and curvature [16] have been reported. While the large-scale irregular ripples occur when the impurity concentration is relatively high, as shown in Fig. 7, another source of strain induced by the change of bond type is present at even low impurity concentrations.

Fig. 7
figure 7

Atomic arrangements of graphene with different concentrations. a 0.00 % Si, b 1.25 % Si, c 10.00 % Si

Full size image

Figure 8 depicts tetrahedra comprised of four atoms. The tetrahedra comprised of four carbon atoms, i.e., those that do not include a Si impurity atom, are planar and show a propensity for sp2 bonding, as shown in Fig. 8a. The average bond angle and length are 120.0° and 0.146 nm, respectively, which are typical sp2 values. When the silicon impurity is at the center of the tetrahedra, with carbon neighbors, as shown in Fig. 8b, tetrahedra are no longer within two-dimensional plane, as the silicon atoms rise or sink away from the plane formed by the three adjacent carbon atoms. The average bond angle and length for every Si–C bond for all of the impure cases are 102.3° and 0.176 nm, respectively. These values indicate that the silicon impurity converts the two-dimensional sp2 bonds into sp3 bonds. The sp3 bond induces an increase in out-of-plane motion, and its disturbance to in-plane heat transfer is well known [51]. It is acknowledged that the addition of sp3 bonds reduces the in-plane thermal conductivity of graphene [52, 53]. Even a simple substitution of the bond type without the insertion of the impurity [52] can lead to a large reduction, of a similar order of magnitude to that which results from nitrogen doping [16], when sp2 orbitals are preserved in N–C bonds of the N-doped graphene. The thermal conductivity reduction due to either simple sp3 substitution or of lighter atomic substitution is commonly about 77 % at 5 % impurity concentration as in the references [16, 52]. The effect of sp3 replacement on pure strain (S 3) is expected to be negligible for interstitial silicon compared with large mass substitution of a vacancy [54]. The second term, S 2, which indirectly reflects changes in the intermolecular angle and distance due to the strain, for example, in Tersoff model, is expected to have a contribution comparable to the mass effect.

Fig. 8
figure 8

Tetrahedra consisting of a central atom and its three carbon neighbor atoms. The central atom is a carbon and b silicon

Full size image

Callaway type calculations are performed using the same constituent models and calculation parameters as Alofi and Srivastav [47]. In Fig. 9, the solid symbol indicates the results obtained from the calculation and open symbol denotes the data obtained by the MD simulation. The conductivity values from the MD calculations are rescaled by half for comparison. The length dependence shown in Fig. 9a for pure graphene agrees with the recent reports that the thermal conductivity increases logarithmically but converges at a large (millimeter) scale [37]. The parameter S in the Klemens’ imperfection model is determined from the thermal conductivity values of MD simulations. The mass parameter S 1 that results from the mass change is fixed because of the known mass of silicon, but non-mass terms, S 23 = S 2 + S 3, are difficult to measure and are therefore calculated by fitting the thermal conductivity, which is obtained from the present MD calculation. In particular, at a moderate concentration of 0.63 %, the value of S 23 = 0.15 gives the best fit to the thermal conductivity [a curve with open circle symbol in Fig. 9b]. While the mass parameter S 1 is 0.38 at 0.63 % of silicon atoms, the S 23 parameter is related to the change of intermolecular force and its resultant strain. The value S 23 = 0.15 is used for all of the impurity ratios. This choice of parameters is valid for the low concentrations, as shown in Fig. 9b, which demonstrates that the focused length scale is close to the range of MD calculation. At moderate concentrations, the mass effect (S 1 = 0.38) is larger than or comparable to non-mass effect (S 23 = 0.15). This is because the mass of the silicon atom is nearly two times larger than the mass of the host atom. In the Callaway type model calculation, the reduction ratios in long-length limit are increased compared with those for the small sizes. According to Eq. (5), the thermal conductivity at 0.63 % impurity is 28 % of the pristine graphene, as shown in Fig. 4; this ratio decreases to 22 % at 10 μm in the Callaway model. The same tendency is found for the isotopic defect; some MD calculations [26, 55] based on the small size have reported to underestimate the reduction in comparison with experimental and theoretical values [18, 36].

Fig. 9
figure 9

Length dependence of thermal conductivity calculated using the Callaway type model (solid line). For impure graphene, S 23 = 0.15 is used. a L < 100 μm b L < 10 μm with MD data (dashed line)

Full size image

For higher concentrations, the value of S 23 = 0.15 fitted for moderate concentration does not sufficiently account for the reduction in the thermal conductivity. The predicted thermal conductivity is smaller than that predicted using MD, and the deficiency in S is not negligible. A new kind of scattering model is needed to describe the effect of the irregular ripple, as shown in Fig. 7c. The strain evaluated for the sp3 bond follows the Klemens’ scattering formula, as shown in Fig. 7b. In this case, every defect has the same strain rate and interatomic relation, so the defect density is proportional to the scattering rate, which the Klemens’ model also implies. However, the ripple, which is not subject to a single point defect, requires an understanding of the principle of formation and the resultant effect on thermal transport.

4 Summary and conclusions

Molecular dynamics simulations are performed to investigate the effect of silicon impurity on the thermal conductivity of graphene sheets. The results obtained are in good agreement with previously published phonon property calculations. NEMD reveals a drastic reduction in thermal conductivity with even a small concentration of silicon impurity. The calculations show that only 0.63 % atomic replacement decreases the thermal conductivity to 30 % of that of pure graphene. Impurity concentrations of 3 % reduce the conductivity to less than one-tenth of the pure graphene conductivity. These results suggest that silicon impurity is more effective at reducing the conductivity than the isotopic dopant; experiments have shown that the thermal conductivity of graphene isotopically enriched with 1.1 % of 13C is reduced to 63 % of pure graphene [18]. Further, our results suggest that silicon impurity is superior to nitrogen doping, which has been observed to reduce the thermal conductivity to 30 % of pure graphene at of 3 % nitrogen impurity [16]. For higher silicon concentrations, the present NEMD shows that the conductivity decreases to 1.7 % of the pure graphene conductivity at 10 % silicon. The reduction rate may increase when the logarithmic length dependence is applied, which has been recently supported by experiments and calculations.

The DOS obtained from EMD calculations shows the phonon properties expected in the presence of crystalline imperfectness. The peak broadening or reduction becomes more significant at higher concentration, which is related directly to the reduction in phonon heat transfer. The broadening implies an increase in the scattering rate, which results in a reduction in thermal conductivity. The increase in scattering by imperfection is shared with all of the acoustic and optical branches of phonons.

From the scattering time model analysis, it can be seen that the contribution of the mass element (S 1) of the silicon impurity plays a significant role in reducing the conductivity, especially at a moderate concentration. The non-mass effect comes from the change of the sp2 C–C bonds to the sp3 Si–C bonds. For high impurity concentrations, the shape of the graphene is severely distorted and the irregularity of the ripples increases, which could contribute to the reduction in conductivity. We propose that the ripples have a different scattering source than that which is normally modeled in Klemens’ formula.