Design and characterization of arrayed waveguide gratings using ultra-low loss Si₃N₄ waveguides

Abstract

Planar waveguides with ultra-low propagation loss are necessary for integrating optoelectronic systems that require long optical time delay or narrowband optical filters. In this paper, we review an ultra-low loss planar waveguide platform that uses thin (<150 nm) Si₃N₄ cores and thick (>8 μm) SiO₂ cladding layers. In particular, we discuss the performance of arrayed waveguide gratings (AWGs) fabricated with the platform. We propose the use of a practical design method that takes the statistical nature of worst-case crosstalk into account. We also demonstrate the measurement of amplitude and phase error distributions in an AWG using an optical backscatter reflectometer. We show that the waveguides have phase errors small enough to achieve AWG crosstalk below −30 dB, while crosstalk below −40 dB should also be possible with optimization of the component design.

1 Introduction

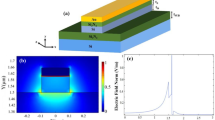
Figure 1 shows a schematic cross-section of an ultra-low loss (ULL) Si₃N₄ waveguide. The stoichiometric Si₃N₄ core layer is deposited via low-pressure chemical vapor deposition onto a 15-μm-thick silicon dioxide layer that is wet-thermally grown on 200 mm silicon substrates. The cores are dry-etched, and a thin encapsulating oxide layer is then deposited and planarized with chemical mechanical polishing. The waveguides are annealed for several hours at 1,050 °C to densify the encapsulating oxide and drive impurity hydrogen out of the film. At this stage, a silicon dioxide upper cladding may be deposited (as shown in Fig. 1) or bonded to the wafer (as discussed in [1]). For applications requiring active devices, a thin device silicon layer may be bonded instead [2].

Fig. 1

Cross-section of the waveguide structure characterized and discussed in this work. The fundamental TE mode simulated at λ ₀ = 1,550 nm is shown

Due to their thin and wide core geometries, these ULL Si₃N₄ waveguides have favorably low propagation loss over a large range of minimum bend radii extending from 20 μm to 7.5 mm (depending on the core thickness) [3]. Furthermore, the recent integration of active hybrid silicon devices [4] makes ULL Si₃N₄ components promising for the integration of optoelectronic systems requiring long propagation lengths, such as those typically achieved in single-mode fiber [3]. Though previous papers focused on the favorable amplitude characteristic of the waveguides, many target applications also require a good phase characteristic, such that the accumulation of phase errors with propagation in the waveguide is minimal [5]. Since the thin ULL Si₃N₄ waveguides are more sensitive to core thickness fluctuations than lower-index-contrast platforms having thicker cores, the waveguide fabrication requirements to achieve a good phase characteristic are stricter, and the extent to which these requirements are met by the platform should be investigated.

In this work, we present such an investigation into the phase characteristic of ULL Si₃N₄ waveguides. In doing so, we characterize an AWG fabricated with the platform, since such components are important to many applications and are also highly sensitive to waveguide phase errors [5]. In the next section, we review the modeling and measurement of the AWG transmission spectrum, including the effects of amplitude and phase errors. We then discuss a method of calculating the worst-case crosstalk of an AWG due to such errors. The method, which was originally applied to phased array radar, takes into account the random nature of the phase errors present in all waveguides. Finally, we directly measure the phase errors in the AWG’s arrayed waveguides with a simple setup using an Optical Backscatter Reflectometer (OBR).

2 Ultra-low loss Si₃N₄ arrayed waveguide gratings

Figure 2a shows the mask layout for the eight-channel AWG discussed in this work. The AWG, which has a 14.4 mm² footprint, has free propagation regions with 434 μm Rowland radius, 61 arrayed waveguides, and an array waveguide length increment of 53.609 μm (grating order, m = 50). As shown in Fig. 2b, half of this length increment is achieved with one bent and two straight waveguides, as the structure is symmetric about the vertical axis. The center (or average) arrayed waveguide length is 6.643 mm, and the minimum bend radius is 1.33 mm.

Fig. 2

a The mask layout for the AWG discussed in this work. b The bend radii and the lengths of the first (s ₁ ) and second (s ₂ ) straight waveguides in the array of the AWG in (a)

Figure 3a shows the fiber-to-fiber transmission spectra of the AWG measured with a tunable laser. As discussed in [4] and seen in the figure, the worst-case crosstalk for the design is −33.5 dB. The component has an estimated on-chip loss of 0.9 dB. The propagation loss in the single-mode waveguides was measured to be 3 dB/m, which is negligible over the 6.643 mm of propagation. So the main contributions to on-chip loss are diffraction into the m ± 1 grating orders, which is estimated to be 0.53 dB from (9) in [6], and loss at the transition between the free propagation region and arrayed waveguides. The gap between array waveguides is 400 nm at the transition, giving an estimated loss of 0.34 dB if one assumes that all optical intensity outside of the arrayed waveguide cores is lost.

Fig. 3

a The measured transmission spectrum of the AWG. b The transmission spectrum modeled using the mode solutions of the structure in Fig. 1 and (2)

It is well known that the transmission spectrum of an AWG can be modeled as [7–9]:

$$ G\left( \lambda \right) = \mathop \sum \limits_{n = 0}^{{N_{a} - 1}} A_{n} { \exp }\left\{ {jn\frac{2\pi }{{\lambda_{0} }}\left[ {n_{{{\text{eff}},{\text{a}}}} \left( \lambda \right) \Updelta L - n_{\text{eff,FPR}} \left( \lambda \right){\text{d}}_{\text{a}} \sin \theta } \right]} \right\} = \mathop \sum \limits_{n = 0}^{{N_{a} - 1}} A_{n} {\text{exp}}\left( {jn\mu } \right) $$

(1)

where A _n is the intensity in array waveguide n, n _eff,a is the effective index of the array waveguide, ΔL is the length increment in the array, n _eff,FPR is the effective index in the free propagation region, d_a is the center-to-center array waveguide spacing at the free propagation interface, and θ is the receiver waveguide angle. Figure 3b shows the spectrum modeled for the structure using the mode solutions (like that in Fig. 1) in (1). The sidelobe level in the simulated spectrum, which determines the worst-case crosstalk, receives a negligible contribution due to truncation of the approximately Gaussian far-field at the array waveguide aperture [10]. Phase errors in optical paths 0 through (N _a − 1) make up the dominant contribution. The standard deviation of the phase errors in the optical paths can be estimated using (A2) in [11]. In our model, refractive index fluctuations are assumed to be zero, while the sidewall and surface roughness parameters are fit to be [L _c (nm), σ (nm)] = [30, 4] and [30, 0.5], respectively. The surface fluctuations in the free propagation region are assumed to be equal to those in the arrayed waveguides. The calculated estimate for the standard deviation of the phase errors is then σ _ϕ  = 0.0607 rad. By adding error terms to (1) as in [7]:

$$ G\left( \mu \right) = \mathop \sum \limits_{n = 0}^{{N_{a} - 1}} A_{n} \left( {1 + \delta_{n} } \right) { \exp }\left( {j\phi_{n} } \right) { \exp }\left( {jn\mu } \right) $$

(2)

where δ _n is the amplitude error and φ _n is the phase error, the general effect on the spectral sidelobe level is included in the model. In Fig. 3b, all δ _n are equal to zero while φ _n are generated from a normal distribution having zero mean and a standard deviation equal to 0.0607 rad.

3 Calculating worst-case crosstalk

Equation (2) can be used to estimate the crosstalk in an AWG design due to random amplitude and phase errors in the optical paths. However, since the errors are random from one component to another, the worst-case crosstalk varies when calculating (2) many times with different sets of random errors. In a fabrication run of many AWGs, this fluctuation would also be experimentally observed. In [5], Okamoto gives an empirical expression relating phase errors to crosstalk that fits well to his experimental data:

$$ {\text{XT}}\sim 20{ \log }_{10} \left( {\frac{{\delta n_{\text{c}} L_{\text{ctr}} }}{{\lambda_{0} }}} \right)\sim 20{ \log }_{10} \left( {\frac{{\sigma_{\phi } L_{\text{ctr}} }}{2\pi }} \right) $$

(3)

where δn _c is the effective index fluctuation, λ ₀ is the free-space wavelength, and L _ctr is the length of the center waveguide in the array. For the structure in this work, using σ _ϕ = 0.0607 rad in (3) gives a crosstalk of −36.15 dB. Yet Okamoto also states that the expression should be proven analytically. Furthermore, since the knowledge of the phase and amplitude errors is statistical, an expression that gives the probability of achieving a certain worst-case crosstalk is also desired. In [7], Hsiao derives such an expression for the probability of a worst-case sidelobe level in a linear-phased array radar, and we can directly apply his derivation to the spectral sidelobes of an AWG:

$$ P\left( {S < S_{L} } \right) = \mathop \int\limits_{0}^{{S_{L} }} \frac{S}{{\sigma^{\prime 2} }}{ \exp }\left( { - \frac{{S^{2} + 1}}{{2\sigma^{\prime 2} }}} \right)I_{0} \left( {\frac{S}{{\sigma^{\prime 2} }}} \right){\text{d}}S $$

(4)

where

$$ \sigma^{\prime 2} = \frac{{\frac{1}{2}\left[ {1 + \sigma_{\delta }^{2} - \varPhi \left( 1 \right)^{2} } \right]\mathop \sum \nolimits_{n} A_{n}^{2} }}{{\varPhi \left( 1 \right)^{2} \left[ {\mathop \sum \nolimits_{n} A_{n} \cos \left( {n\mu } \right)} \right]^{2} }} $$

(5)

$$ \varPhi \left( 1 \right) = { \exp }\left( { - \frac{{\sigma_{\phi }^{2} }}{2}} \right) $$

(6)

and where S is the sidelobe level normalized to the designed sidelobe level ${\text{i}}.{\text{e}}.\text{ }\left( {S = \frac{{S_{{({\text{array \; errors}})}} }}{{S_{{({\text{no \; array \; errors}})}} }}} \right)$, I ₀ is the modified Bessel function of zero order, σ _δ is the standard deviation of the amplitude errors, σ _ϕ is the standard deviation of the phase errors, and Φ is the characteristic function for the zero-mean normal distribution of the phase errors.

Figure 4a shows the worst-case crosstalk versus probability calculated for the AWG in this work using (4). The curves, shown for various standard deviations of the phase errors while the standard deviation of the amplitude errors is fixed at zero, are calculated by setting (4) equal to a probability on the x-axis and numerically finding the root. As seen in the figure, the expected worst-case crosstalk can vary by as much as 40 dB depending on the component yield desired by the design engineer. Using σ _ϕ  = 0.0607 rad, one finds that the empirical expression (3) calculates the worst-case crosstalk of only 75 % of our fabricated AWG structures, and so (4) should be used if a greater component yield design is desired. Figure 4b shows the worst-case crosstalks versus σ _δ and σ _ϕ achieved with 99 % probability. The figure also shows the results of a 1,000 input Monte Carlo calculation of the worst-case crosstalk generated using (2). The results approach those obtained using Hsiao’s equation and validate its application to AWG design.

Fig. 4

a The maximum crosstalk calculated from (4) versus probability for various values of the phase error standard deviation. b The maximum calculated crosstalk with 99 % probability. The solid line is for phase errors in (4). The dashed line is for amplitude errors in (4). The circular markers are obtained from the Monte Carlo method and (2)

4 OBR characterization of AWGs

As demonstrated in [8, 9], measurement of the amplitude and phase distributions in the optical paths of an AWG can be a useful tool for diagnosing the dominant cause of AWG crosstalk. In [8, 9], Fourier transform spectroscopy is used to accurately measure the distributions in GeO₂-doped silica and InP AWGs. In this section, we use an OBR to measure the distributions [12].

The simple setup, which uses an OBR, an optical circulator, and a polarization controller, is shown in Fig. 5a. In normal operation, an OBR measures an interferogram versus source frequency by interfering the tunable frequency source with the reflection of that source from the device under test (DUT) [12]. Here, a circulator is used so that the interferogram is produced by interference of the source with source transmission through the DUT. This interferogram is obtained by parsing the binary file typically saved and analyzed by the OBR software. The change is analogous to switching from an S₁₁ to an S₂₁ measurement using a vector network analyzer.

Fig. 5

a A schematic of the setup used to measure the amplitude and phase distribution in the array. b The amplitude and c phase versus group delay measured with the setup in (a)

Figure 5b shows the amplitude measured versus group delay. The measurement points obtained from the OBR are shown as red dots. Since the group delay domain data are obtained via a Fourier transform of the frequency domain interferogram, the group delay resolution is set by the frequency sweep range. Since the starting resolution obscures the location of the group delay domain peaks, the interferogram is zero-padded in order to interpolate the group delay domain data and reveal the train of pulses shown as black lines in the data. The pulse peaks are spaced at group delay intervals of:

$$ \tau_{\text{g}} \cong \left( {n_{\text{g,a}} \Updelta L + n_{{{\text{g}},{\text{FPR}}}} {\text{d}}_{\text{a}} { \sin }\, \theta } \right)/{\text{c}} $$

(7)

where n _g,a is the group index of the array waveguides, n _g,FPR is the group index of the free propagation region waveguide, and c is speed of light in free-space. After locating the peak amplitudes in the group delay domain, the phase measured at those group delay locations gives the phase distribution as shown in Fig. 5c.

The circular markers in Fig. 6a show the normalized linear amplitude distribution measured in the array. The red line shows the expected distribution calculated for a Gaussian approximation to the waveguide mode at the free propagation region. The best approximate Gaussian is obtained by maximizing the overlap integral of the simulated TE mode field with that of a 2D Gaussian, giving a divergence θ ₀ = 8.461° in the free propagation region. In the edge arrayed waveguides having amplitude too low to be measured, the Gaussian approximation is used as denoted by triangular markers.

Fig. 6

a The measured (circular markers) and calculated (red line and triangular markers) amplitude distribution in the AWG array. b The measured (circular markers) and calculated (triangular markers) phase errors in the array. The red line shows the simulated phase errors due to the different bend radii and different lengths of bend mode propagation in the array

The circular markers in Fig. 6b show the phase error distribution measured in the array. The simulated red line shows the slowly varying error due to the different bend radii and lengths of bend propagation in the array (as shown in Fig. 2b). Subtracting out this slowly varying error, the measured standard deviation of the phase errors is 0.056 rad. The triangular markers at the array edges are calculated by adding the simulated slowly varying error to phase errors randomly generated from a normal distribution of zero mean and 0.056 rad standard deviation.

Finally, we show a single measured channel in Fig. 7 along with the transmission spectrum calculated from the distribution in Fig. 6 using (2). The agreement between the measured and calculated spectra validates the measurement method, but we note that even better agreement was obtained by Yamada et al. [9] using a corrected Fourier transform spectroscopy method in. If σ _δ is set equal to zero, the sidelobe level does not change, indicating that phase errors contribute the most to the measured sidelobe level. The dotted blue line in Fig. 7 shows the channel spectrum calculated when σ _ϕ is set to zero. The new sidelobe level is limited by the amplitude errors that are apparent in Fig. 6a. This indicates that crosstalk less than −40 dB should be possible through a reduction of σ _ϕ in the structure. From Fig. 4b, we estimate that a σ _ϕ of 0.02 rad should enable a crosstalk less than −40 dB in 99 % of the fabricated components. A lower σ _ϕ can be achieved through further optimization of the AWG layout to decrease the average propagation length in the array.

Fig. 7

A single channel of the AWG measured with transmission and OBR reflection methods. The channel calculated from the amplitude and phase error distribution from Fig. 6 is also shown (green dashes). The blue dotted line shows the channel crosstalk improvement obtained from eliminating all phase errors

5 Conclusions

Ultra-low loss Si₃N₄ waveguides enable optical filtering components with very low on-chip loss. Furthermore, the higher refractive index core material allows for a wide range of minimum bend radii, such that smaller component footprints are possible compared to lower contrast materials. In this work, we investigated the performance of a single AWG device in order to also investigate the phase characteristics of the ULL Si₃N₄ waveguides. In doing so, we proposed the use of a phased array radar design equation for the practical design of AWGs with desired worst-case crosstalk. We also demonstrated another way to measure the amplitude and phase error distributions in an AWG using an OBR. Finally, we concluded that the ULL Si₃N₄ components should be able to match the best-in-class crosstalk performance of larger and lower-index-contrast cores with some refinement of the component layout.