Introduction

Coral populations worldwide are sensitive to a range of biotic and abiotic pressures (Riegl 2020), many of which will be exacerbated by future climatic change and human exploitation (Wolff et al. 2018; Riegl and Glynn 2020). Subsequently, the future status of coral reef ecosystems relies on the resilience of coral populations, specifically their capacity to endure, and recover from, increasingly frequent disturbance events (Holling 1973). Accordingly, a resilience-orientated focus is becoming commonplace in reef management (Mcleod et al. 2019, 2021), necessitating an ability to predict the responses of coral populations to varying biotic and abiotic regimes (Lam et al. 2020). Yet, a limited understanding for the dynamics underpinning coral population performance and resilience still hinders our capacity to recognise and manage the climate induced reassembly and/or collapse of coral reef ecosystems (Bellwood et al. 2004; Edmunds and Riegl 2020).

Although limited, the application of demographic theory within coral research is not a novel concept (Edmunds et al. 2014). Structured population models offer insight into how the state of individuals (typically their size, age, or developmental stage; Caswell 2001) arbitrates their survival and reproduction and how these fitness components in turn shape the overall responses of populations to local biotic and abiotic conditions (Box 1; Benton et al. 2006). Understanding how patterns in the survival, progression (i.e. growth), retrogression (i.e. negative growth, shrinkage; Salguero-Gómez and Casper 2010), and reproduction of individual colonies, influence population-level characteristics will improve effective management (Riegl et al. 2018; Brito-Millán et al. 2019a; Madin et al. 2020; Pisapia et al. 2020). Appropriately, state-structured demographic approaches are being increasingly utilised to quantify the mechanisms supporting or preventing the persistence and revival of disturbed coral communities (e.g. Kayal et al. 2018; Cant et al. 2021c). Accordingly, there is a growing appreciation for how the size structure of coral populations influences their dynamics and endurance (Bak and Meesters 1998, 1999; Anderson and Pratchett 2014; Dietzel et al. 2020; Lachs et al. 2021), with recent appeals for efforts to be concentrated towards gauging the resilience of coral communities (Pisapia et al. 2020). However, we argue here that the contemporary application of state-structured demographic tools in evaluating the viability of coral populations, and their communities, does not reflect our need to anticipate their resilience.

Box 1 Scaling from individuals to communities
Full size table
Fig. 1
figure 1

Records of survival, size, and reproductive output, collected from tagged coral colonies over time, can enhance our understanding of population trajectories and, when collected across multiple populations, can be used to predict community reassembly under future climate scenarios. Here, subscript notation is used to reflect how the changing state of individuals corresponds with changes in individual-level characteristics. In this schematic the state of individuals refers to colony size and thus the growth (g) of individuals between size x and y is expressed as gyx

Full size image

Prevailing knowledge of coral population dynamics centres around long-term (i.e. asymptotic) population characteristics (Box 2), with measures of long-term population growth rate (λ) often used for projecting the viability of coral assemblages (e.g. Foster and Foster 2013, 2018; Edmunds 2015, 2020; Riegl et al. 2017; Kodera et al. 2020; Cant et al. 2021c; Shlesinger and van Woesik 2021). Indeed, the same is true across ecological theory, with our understanding of population dynamics focused on asymptotic population characteristics (Morozov et al. 2020). Quantifying the asymptotic characteristics of various populations presents a valuable comparative tool for exploring abiotic tolerances (Beissinger and Westphal 1998). Yet, for populations to realise their asymptotic potential, they require the persistence of stable conditions over extended timescales (Caswell 2001). In reality, though, seasonality exposes populations to periodic abiotic shifts, whilst predation, human exploitation, or storm and fire events generate recurrent and instantaneous disturbances. These short-term abiotic and biotic disturbances ensure that natural environments rarely exist at a stable equilibrium (Williams et al. 2011; Hastings et al. 2018). Consequently, evaluating the resilience and viability of populations requires an understanding for how the dynamics of populations manifest across timescales more representative of the disturbance cycles to which they are exposed (Hastings 2010). Here, we discuss why greater commitment towards quantifying the short-term, or transient, dynamics of coral populations is therefore required to enhance our capacity for anticipating the future resilience of coral reef ecosystems.

Box 2 The status of demographic tools within coral research
Full size table
Fig. 2
figure 2

The cumulative number of studies that explicitly explore the state-structured demographics of coral populations as identified by our search for the term coral* AND demograph* across the peer-reviewed literature within the SCOPUS database. The colour scale differentiates between studies that focus on only investigating patterns in colony survival, growth, and/or reproduction, and those that present estimates of either deterministic population growth (λ), stochastic asymptotic characteristics (λs), or transient population characteristics

Full size image

Transient versus asymptotic population dynamics

Structured population models characterise and define the trajectories of populations according to the individual-level allocation of resources towards survival, changes in size (or the state of interest), and reproduction. Populations can be structured according to the distribution of their individuals across some state variable, be that age (Leslie 1945), developmental stage (Lefkovitch 1965), size (Easterling et al. 2000), or a combination (Caswell et al. 2018). The transition of individuals across state classes is, in turn, mediated by selection gradients that emerge from the state-specific patterns of survival, development, and reproduction (Groenendael et al. 1988; van Tienderen 2000). In state-structured demography, patterns across these vital rates can subsequently be condensed into a population projection matrix (A), with each matrix element (aij) expressing the expected transition of individuals into state class i from state class j during the time interval t to t + 1, or the per-capita a/sexual contributions of state j individuals into state class i during that same interval (Caswell 2001). This population matrix can then be used to project the size (N, number of individuals) and structure (n, number of individuals in each state) of a population:

$${N}_{t+1}= \sum \bf{n}_{t+1}=\sum \bf{A}{\bf{n}}_{t}$$
(1)

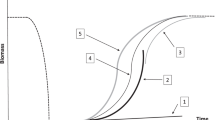
Within a stable environment, the state structure of a population is expected to converge towards its stationary equilibrium, after which the state relative composition of the population will remain constant (Caswell 2001). At its stationary equilibrium, therefore, the size of a population is expected to change at a constant rate through time, termed its asymptotic population growth rate (λ; Caswell 2001). This value of λ, for any state-structured population, is equal to the dominant eigenvalue of its corresponding population matrix A and exists on a non-negative scale reflecting the proportional growth (λ > 1), decline (λ < 1), or demographic equilibrium (λ = 1) of a population over time. For their stable structure to manifest, however, populations typically require time in a constant environment to allow the state distribution of their individuals to converge towards its equilibrium state without displacement by local disturbances (Fig. 3; Bierzychudek 1999). Yet, populations are rarely exposed to stable conditions or equilibria (Hastings 2001, 2004; Williams et al. 2011), and the vital rate patterns used in constructing population projection matrices are themselves not consistent and contingent on the environmental conditions in which they are observed (Benton and Grant 1996; Boyce et al. 2006). Moreover, as populations change in size their dynamics are subject to density–dependant regulation (Engen et al. 1998; Lande et al. 2003). The dynamics of populations are, therefore, expected to vary over time as environmental conditions change (Tuljapurkar and Orzack 1980; Tuljapurkar 1989).

Fig. 3
figure 3

At stationary equilibrium, populations are expected to change size at a constant rate, termed their asymptotic growth rate (λ). However, to display asymptotic characteristics, populations need a stable state structure and so require time at equilibrium to enable the development of this stable structure. In the absence of a stable state structure, populations will display varying growth rates as they converge towards asymptotic expectations, even within equilibrate environments. Note that, although in this schematic the populations growth rate is increasing towards its asymptotic trajectory, estimates of λ can also reflect asymptotic decline

Full size image

The perpetual instability generated by regular disturbances ensures that populations rarely attain their asymptotic trajectories (Hastings 2001; Hastings et al. 2018). Natural environments persist within a non-equilibrate condition maintaining populations within a transient state during which their trajectories can radically differ from asymptotic expectations (Stott et al. 2010, 2011; Hastings et al. 2018). Anticipating the future condition and endurance of populations thus requires an awareness for their transient characteristics (Ezard et al. 2010). Transient shifts in the state structure of populations can elevate (amplification) or diminish (attenuation) their growth rates relative to asymptotic projections (Townley et al. 2007). Equally, for populations existing in a transient state, there is a natural tendency for their state structure to converge towards a stable distribution (Caswell 2001). Intuitively, with population resilience comprised of the attributes of resistance (the ability to withstand disturbances), compensation (the ability to benefit from disturbances) and recovery (the speed and ability to reattain stationary equilibria), the transient dynamics of populations therefore represent quantifiable measures of these features of resilience (Box 3; Hodgson et al. 2015; Capdevila et al. 2020).

Box 3 Measuring transient population characteristics
Full size table
Fig. 4
figure 4

Various measures exist for quantifying transient population characteristics. Disturbances (*) disrupt the structural composition of populations forcing them into a transient phases during which their trajectories will deviate from asymptotic expectations (λ, dashed line). The response of a population during this transient phase is contingent on their capacity for amplification (increases in population growth) and attenuation (declines in population growth). Using the measures of reactivity and maximal amplification (describing the initial, and maximum, increase in population growth rate during transient conditions) ecologists can quantify the relative amplification potential of natural populations. Alternatively, the measures of first-step attenuation and maximal attenuation can be used to describe the initial, and maximum decline in population growth rate during transient conditions. Meanwhile, damping ratio estimates describe the time required for a perturbed population to reobtain a stable equilibrium. Accordingly, by revealing the capacity for populations to grow (compensation), avoid declines (resistance), and/or recover following a disturbance event, these transient metrics present ecologists with measures of population resilience

Full size image

Transient dynamics and the resilience of coral communities

Transient demographic approaches present an effective tool for explicitly evaluating the resilience of natural populations (Capdevila et al. 2020). Indeed, such approaches have proven instrumental in our understanding of the establishment of populations within new and variable environments (Iles et al. 2016; McDonald et al. 2016, 2017; Jelbert et al. 2019). Exploring the transient dynamics of coral populations can thus enhance our understanding regarding the future diversity, condition, and resilience, of coral communities. Globally, coral communities are being exposed to increasingly recurrent thermal stress events, at frequencies soon expected to exceed the recovery time required by most coral species (Hughes et al. 2018; Sully et al. 2019). Presently, considerable value is placed on classifying coral species according to their morphological and functional traits, with the subsequent categorisation of coral taxa offering proxies for the vulnerability of various coral communities to said recurrent stress events (Darling et al. 2012, 2019). Quantifying the relative affinities of different coral populations for demographic recovery presents the opportunity for justifying these assumptions; helping to distinguish the species and populations most vulnerable and or resilient to projected recurrent disturbance regimes.

Equally, the amplification and attenuation characteristics of populations simultaneously reflect their stability following a disturbance. Distinguishing between the differential attributes of compensation and resistance in different populations is important for managing the future condition of biological communities (Capdevila et al. 2020). Assessments of coral communities following repeated disturbances have demonstrated divergent shifts in species compositions (Adjeroud et al. 2009; Pratchett et al. 2011, 2020). With knowledge of the capacity for various coral populations to undergo demographic amplification or for avoiding demographic attenuation, we can begin to forecast and anticipate the reassembly of coral communities, thereby improving the effectiveness of adaptive reef management. Indeed, Sandin and McNamara (2012) and Brito-Millán et al. (2019b) demonstrate how the transient characteristics of coral populations determine the resilience of their wider reef communities to algal phase shifts. Importantly, these contributions to our understanding of transient dynamics within coral environments advocate for a consideration of spatial interactions within assessments of coral population dynamics. Spatial interactions between individual corals impacts upon their fitness characteristics (Buss and Jackson 1979; Idjadi and Karlson 2007; McWilliam et al. 2018), yet the exact role these spatial interactions play in defining the performance of coral populations remains unresolved (Alvarez-Noriega et al. 2018). Ultimately, assessing the combined influence of state-structured demography and spatial interactions (e.g. Adler et al. 2010; Chu and Adler 2015) upon the performance, and resilience, of coral populations represents an important and worthwhile endeavour.

Alternatively, a disturbance does not necessarily imply a negative impact, merely a change to a system (Pickett and White 1985). Disturbances to the structure of populations can be brought about by the cessation of a continuous pressure (e.g. Götz et al. 2008), changes in resource availability (e.g. Goldstein and Steiner 2020), or their introduction into a novel environment (Jelbert et al. 2019). With the ability of natural populations for undergoing demographic compensation underpinning their capacity for exploiting changes in their local environment (Jelbert et al. 2019), the transient dynamics of populations can offer insight into their invasive potential (Iles et al. 2016). Demographic compensation mediates the persistence of coral populations established along coastlines characterised by increased abiotic variability (Cant et al. 2021a, b). Predicting and quantifying demographic compensation within coral populations will, therefore, aid in forecasting the winners and losers in reef communities targeted by conservation and restoration initiatives, or those undergoing climate induced range shifts. To illustrate this potential, we provide an example evaluating the performance of a subtropical coral population in Eastern Australia (Box 4).

Box 4 Transient dynamics in Pocillopora aliciae: an empirical example
Full size table
Fig. 5
figure 5

Describing how size mediated patterns in survival, growth, fragmentation, and recruitment, determine the transition of individual colonies during the time interval t to t + 1, we used an IPM to evaluate the condition and viability of a Pocillopora aliciae population. Repeated surveys of individually tagged colonies were used to document the survival, growth, fragmentation, and recruitment characteristics of individuals colonies, and how these patterns are influenced by colony size. By condensing these individual-level patterns into a probability density kernel our IPM subsequently translates the transition of P. aliciae individuals across a continuous size spectrum into measures of both asymptotic and transient population characteristics

Full size image
Fig. 6
figure 6

The asymptotic and transient dynamics of Pocillopora aliciae within the Solitary Islands forecast very different outlooks for this subtropical population. (a) Estimates of long-term population growth correspond with a rapid temporal decline in population size; a trajectory that persists irrespective of population structure, as illustrated by comparisons between forecasts involving a population in which individuals are distributed evenly across the size spectra (black), a population with a structural bias towards larger sized individuals (red; >80% of individuals larger than median size), and a population with a structural bias towards smaller sized individuals (blue; >80% of individuals smaller than median size). (b) Meanwhile, the transient characteristics of the population indicate it to possess the capacity for elevating its growth rate, relative to long-term expectations (λ, dotted line), following a disturbance. However, the magnitude of this increase is dependent on initial population structure, with the increased prevalence of smaller-sized colonies reducing population reactivity (\(\overline{\rho }\)), and driving population attenuation (diminished growth rate relative to λ). Across both panels shaded regions correspond with the confidence bounds associated with each projection

Full size image

Complexities in the modelling approaches used to explore the dynamics of natural populations have resulted in these techniques remaining largely overlooked within coral research (Edmunds et al. 2014). Indeed, parametrising the demographic models needed to quantify population characteristics requires considerable amounts of data (Ellner et al. 2002). Although, despite the data demanding nature of state-structured demographic models, the collection of the necessary data regarding the survival, transitions in size, fragmentation, and recruitment, of individual coral colonies is possible alongside current reef monitoring efforts (Edmunds and Riegl 2020). Furthermore, new techniques for analysing the demographic characteristics of populations structured by a continuous state variable like size (Integral Projection Models; Easterling et al. 2000) have reduced the data demands of demographic assessments (Ramula et al. 2009). As a result, IPM frameworks are growing in popularity throughout coral research (see Bruno et al. 2011; Madin et al. 2012; Zychaluk et al. 2012; Elahi et al. 2016; Kayal et al. 2018; Precoda et al. 2018; Lord et al. 2020; Cant et al. 2021c; Carlot et al. 2021). Finally, studying the dynamics, particularly the transient characteristics, of coral populations is made increasingly accessible by the development of demographic analysis packages such as popdemo (Stott et al. 2012) within open-source programs like R (R Core Team 2019).

Forecasting the resilience of coral populations presents a major challenge for the future conservation of various reef communities (Lam et al. 2020). Currently, we lack the mechanistic insight into the resilience and response of coral populations to disturbance necessary for predicting the future reassembly and persistence of coral communities given increasingly recurrent disturbances. It is not our intention to dismiss previous efforts to evaluate the dynamics of coral populations using asymptotic characteristics. The asymptotic characteristics of populations present a useful tool in exploring the relative tolerances of differing populations (Beissinger and Westphal 1998) and have proven valuable in the management of threatened populations (Johnson et al. 2010). We have illustrated, however, that for evaluating and forecasting the responses of coral assemblages to disturbance and changing environments, asymptotic characteristics do not represent measures of population resilience (Hastings et al. 2018). Instead, we advocate for greater a focus towards investigating the transient dynamics of coral populations that more accurately reflect their dynamics within natural environments (Ezard et al. 2010). Evaluating coral reef community resilience using the framework of transient demographic theory will provide a new effective lens on the temporal and spatial nature of coral reef resilience, a view that will transcend current approaches of conducting single reef assessments to determine resilience (Maynard et al. 2015; McLeod et al. 2021).