Abstract
Reconstructing the topography of shallow underwater environments using Structure-from-Motion—Multi View Stereo (SfM-MVS) techniques applied to aerial imagery from Unmanned Aerial Vehicles (UAVs) is challenging, as it involves nonlinear distortions caused by water refraction. This study presents an experiment with aerial photographs collected with a consumer-grade UAV on the shallow-water reef of Fuvahmulah, the Maldives. Under conditions of rising tide, we surveyed the same portion of the reef in ten successive flights. For each flight, we used SfM-MVS to reconstruct the Digital Elevation Model (DEM) of the reef and used the flight at low tide (where the reef is almost entirely dry) to compare the performance of DEM reconstruction under increasing water levels. Our results show that differences with the reference DEM increase with increasing depth, but are substantially larger if no underwater ground control points are taken into account in the processing. Correcting our imagery with algorithms that account for refraction did not improve the overall accuracy of reconstruction. We conclude that reconstructing shallow-water reefs (less than 1 m depth) with consumer-grade UAVs and SfM-MVS is possible, but its precision is limited and strongly correlated with water depth. In our case, the best results are achieved when ground control points were placed underwater and no refraction correction is used.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Coral reefs are complex and highly biodiverse ecosystems that are put at risk by increasing stresses from both local and global factors (Fine et al. 2019). In turn, they provide several ecosystem services amounting to nearly 200,000 US dollars per acre per year (Costanza et al. 2014). Natural hazards and anthropogenic pressures affect small islands’ coastlines and the underwater marine environment surrounding them (Kench and Brander 2006; Duvat and Magnan 2019; David and Schlurmann 2020). In the face of climate change, the increase in ocean temperatures is forecasted to lead to more extensive coral bleaching (Skirving et al. 2019), causing increased coral mortality (Hédouin et al. 2020). As coral reefs play an important role in the protection of low-lying islands from waves and wave energy (Ferrario et al. 2014), it is important to develop and assess the effectiveness and precision of new and low-cost techniques to monitor the evolution of reef areas over time. To this end, remote sensing from satellites or laser scanners and echo sounders are often employed to analyze the status and temporal evolution of beaches and marine environments (Klemas 2011; Colbo et al. 2014; Hedley et al. 2018; Panagou et al. 2020).
Single-Beam Echo Sounder (SBES) or Multibeam Echo Sounder (MBES) sonar determine water depths by transmitting sound pulses into water. Survey grade MBES cover areas with a sensor covering a lateral area of \(120^\circ - 150^\circ\) to record bathymetry with a vertical resolution of \(<1\%\) of the water depth (Colbo et al. 2014). However, survey-grade echo sounders depend on vessel draft and are usually not suitable for shallow waters (\(< 4\)–5 m depth, Leon et al. 2015; David and Schlurmann 2020). Consumer-grade SBESs—for example used by fishers—have a smaller immersion depth but recorded water depths vary between centimeter to lower decimeter scale compared to ground-truth water depths (Bandini et al. 2018). Furthermore, SBESs record punctual measurements and thus do neither provide an areal overview of the surveyed marine area, nor color information for mapping of the site, which is particularly relevant in coral reefs.
Other bathymetric survey methods are operated from the beach: Terrestrial 60 Laser Scanning (TLS) can record topography and bathymetry from a single device. The error of underwater measurements increases with distance to the device. Here, the measuring error is equal to the measured water depth for distances \(\gtrsim 15\,\hbox {m}\) (Panagou et al. 2020).
A further method to derive bathymetries of coastal zones is to observe nearshore wave propagation and transformation, both by radar (Borge et al. 2004; van Dongeren et al. 2008) and video (or high-frequency image) recording devices (Aarninkhof et al. 2005; Holman et al. 2013). Radar-based depth inversion methods require stationary installed devices and process data in the order of days (Chernyshov et al. 2020; Gawehn et al. 2020). In contrast, UAV-borne video data uses mobile equipment that can be controlled remotely. But in this case, operating times are limited, as they depend on battery capacities (Bergsma et al. 2019). Still, both techniques are especially valuable on sandy shores with turbid waters.
In clear waters however, aerial imagery has been applied to directly survey underwater topography or bathymetry. For example, recent studies, employing UAV-borne Light Detection and Ranging (LiDAR), achieved centimeter accuracy for riverine waters of less than 2 m depth (Mandlburger et al. 2020). When using UAV-borne LiDAR measurements, bathymetric reconstruction is independent of surface texture. This leads to a more robust outcome compared to photogrammetric methods (Mandlburger 2019). However, LiDAR-based data struggle with “too shallow” waters or increased hydrodynamic activity, such as whitecaps of broken waves (Klemas 2011; Leon et al. 2015). A major issue with UAV-borne LiDAR is that drone platforms carrying the devices are usually larger and have a high take-off weight, which often requires a higher-level drone operations permits. A more common way to employ UAV-borne data is therefore to use consumer-grade drones, collecting aerial photographs and processing them with the SfM-MVS reconstruction approach afterward. SfM-MVS merges photogrammetric principles with advances in 3D computer vision algorithms (Carrivick et al. 2016).
The SfM-MVS methods use aerial imagery to create precise and accurate three-dimensional DEM of coastal areas (Murfitt et al. 2017; Casella et al. 2020; Talavera et al. 2020). However, reconstructing coastal areas with SfM-MVS techniques is mostly limited to dry beach areas. Thorough planning in advance helps to identify the potentials and limitations under the given circumstances on site and to manage expectations of the achievable outcome (Joyce et al. 2019). SfM-MVS techniques have been applied widely to reconstruct coastal topography with centimeter accuracy (see for example Casella et al. 2016; Murfitt et al. 2017; Casella et al. 2020; Talavera et al. 2020). As for underwater imagery, three-dimensional photogrammetric models facilitate to study changes in coral reefs (Storlazzi et al. 2016; Rossi et al. 2019; Carlot et al. 2020). Using airborne images to analyze underwater environments requires (a) calm water surfaces, (b) is dependent on the Secchi depth (visibility by means of turbidity) and (c) is dependent on surface textures of underwater areas (Mandlburger 2019). Within the water column, light is continuously attenuated through absorption and scattering along the optical path (Chirayath and Earle 2016; Chirayath and Li 2019). Bathymetric reconstruction in calmer and deeper waters with user grade UAVs (and without LiDAR sensors) is possible, but is characterized by large uncertainties and becomes more challenging with increasing water depths and hydrodynamic activity (Casella et al. 2017). But the biggest challenge of UAV-borne photogrammetry on coasts is to include and exploit recordings of both, surface and underwater images from aerial imagery, because light refracts on the water surface (Casella et al. 2017; Dietrich 2017; Mandlburger 2019). Refraction of light on the water surface is explained by Snell’s Law. Using Snell’s Law directly on submerged riverine areas of the reconstructed DEMs already reduces the error, while site specific calibrations can further improve results (Shintani and Fonstad 2017). Other approaches consider camera parameters and viewing angles in their refraction correction and improve the reconstruction precision to be about \(0.02\%\) of the flying altitude (Westaway et al. 2000; Woodget et al. 2015; Dietrich 2017). Recently, machine-learning algorithms have emerged, correcting consumer-grade UAV data of submerged areas with a corresponding subset of accurate point clouds from LiDAR measurements (Agrafiotis et al. 2019, 2020). This approach is similarly accurate than more sophisticated refraction correction based on Snell’s Law.
Through-water photogrammetry depends on calm water surfaces, as surface undulations further disturb the SfM-MVS process beyond the aforementioned effects. Further adverse effects from surface undulations include unwanted reflection of sunlight on the water surface—also known as sun glare—(Overstreet and Legleiter 2017; Muslim et al. 2019) and light effects on the seafloor. These light effects are caused by wave crests, which act as fluid lenslet. However, fluid lenslets also facilitate magnification of the seafloor in certain areas and benefit its three-dimensional reconstruction when using high-framerate multispectral videos (Chirayath and Li 2019). At the time of writing though, such fluid lensing algorithm is not publicly available, while readily available platforms are about ten times more expensive than user-grade UAVs (Chirayath and Earle 2016).
This study stems from a project dealing with sea level rise and associated impacts on small islands (Ratter et al. 2019; David and Schlurmann 2020). The project focuses on obtaining field measurements with aerial surveys to evaluate sediment transport as natural sea level rise adaptation on the Maldivian reef island of Fuvahmulah. While on-land (dry beach) areas were the main objective of the project, this work analyzes data collected on reef flats on Fuvahmulah. Error metrics for varying water depths on reef flats are currently not available (David and Schlurmann 2020). The purpose of this study is therefore to assess the quality of reconstructed underwater topographies (bathymetries) from a SfM-MVS algorithm for different water levels and thus to utilize this information in future studies. We used a consumer-grade drone to record the intertidal inner reef. We surveyed the same area in ten flights, with varying water depth conditions. We employed pressure sensors to constantly measure water depths and a Real-Time Kinematic (RTK) Global Navigation Satellite System (GNSS) system to measure the position of Ground Control Points (GCPs) throughout the entire study site with centimeter precision. The GCPs are later used to georeference the three-dimensional model, obtained through the SfM-MVS and Multi-View Stereo (MVS) approach. Surveying starts with the dry reef at low tide and continues as water levels increase with rising tide. In the analysis, the digital reconstruction of the dry reef serves as “accurate” reference topography. Comparing the dry reference DEM with all following DEMs under increasing water depths, we estimate errors of the SfM-MVS algorithm in the bathymetric reconstruction originating from increasing water depth. This study provides error estimates related to three different aligning techniques in the photogrammetric process and evaluates the bathymetric reconstructions calculated with and without the use of publicly available refraction correction algorithms.
Overall, this study aims at (a) assessing the potential and limitation of SfM-MVS algorithms to reconstruct underwater areas; (b) evaluating the benefits of refraction correction in near-shore coastal areas; and (c) increasing confidence in exploiting aerial imagery of clear, shallow waters for bathymetric reconstruction in photogrammetric procedures under field conditions.
Study area, material and methods
Survey site and area of interest
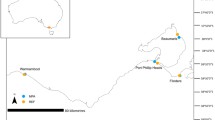
This study was carried out on the reef island Fuvahmulah, one of the most southern islands of the Maldives (Indian Ocean). The island is located about 30 km south of the equator (latitude: \(-0.30^{\circ }\), longitude: \(73.43^{\circ }\), see Fig. 1a. The capital of the Maldives Malé is situated approximately 500 km north of the island, while the distance to the southern tip of the Indian peninsula is about 1025 km (see Fig. 1b). Unlike most other inhabited atolls of the Maldives, Fuvahmulah only consists of one main island and its fringing reef.
This study distinguishes between the survey site and the area of interest: The survey site is the entire area recorded by the UAV. The area of interest focuses on the georeferenced area within the survey site (see Fig. 2).
The survey site is on a shallow, inter-tidal reef on the west coast of Fuvahmulah. The water around Fuvahmulah is clear and provides aerial visibility of the submerged reef bottom—even in depths over 1 m. The study includes ten flights, recorded on March 26th, 2019 between low-tide at around 11:00 and high tide at around 17:30. The tidal range of spring tide in March 2019 was 1.21 m (all tide data from UHSLC; Caldwell et al. 2015). The tidal range on the survey day was 0.76 m, allowing the reef to fall dry at low tide. The water level on the reef \(\Delta h\) is the difference between the first flight and the water level of each subsequent flight, derived from the sea level data (Table 1 summarizes the different water levels and water depths on the study site for each flight). On the survey day, the sky was constantly clear and sunset was at 18:10 (Holmgren et al. 2018, pvlib v0.7.2). Thus, lighting on site only depends on the solar azimuth and zenith (Fig. 1d). For the survey day, the fifth-generation atmospheric reanalysis of the global climate (ERA5) of the Collaboration for Australian Weather and Climate Research (CAWCR) gives a significant off-shore wave height of 0.87 to 1.00 m at \(0^{\circ }\) latitude and \(73^{\circ }\) longitude (C3S 2017), which is at a distance of \(\sim 60\,\hbox {km}\) from Fuvahmulah.
Geographic location and field conditions. Location of a the study site on the island and b of Fuvahmulah within the Indian Ocean; c displays the sea level for the survey based on nearby tide data and water levels measured on site. On March 26th, 2019, the measured data and mean significant wave height on the reef \(H_{s,\mathrm{reef}}\) is recorded by wave gauge SL-20 (see Fig. 2); d sun position on March 26, 2019, throughout the day (orange markers are exemplary times at 07:00 and 10:00 for orientation) at associated flight times (white marker, for exact times, see Table 1)
The aerial surveys cover a distance of about 140–150 m long shore and 70–80 m cross-shore. Four cross-shore zones characterize the survey area: the upper beach is a vegetated beach ridge, fringing the entire island. It hosts palm trees and shrubs (see Fig. 2). A sandy beach of \(\sim 10\,\hbox {m}\) width follows seaside of the vegetated area. The downward sloping coral stone delimits the sandy beach from the fringing coral reef. The coral stone experiences wave run-up and can be considered a natural revetment for the nearby beaches. It is located between about mean sea level and mean high waters. The inter-tidal reef has three longshore sections: On the right side, inhabitants of the island have cut a channel into the reef. The channel provided safe landing for boats before the seaport opened in 2002 (Ratter et al. 2019; David and Schlurmann 2020). This area is constantly submerged and has the highest water depth of the study site. The channel bottom is sandy near the beach but becomes increasingly more rocky seaward. The excavated rocks from the channel construction were dumped adjacent to the channel along the entire reef width and remain there until today. In this longshore area, only the 15 m long inner reef flat section close to the beach is clear of excavated rocks. The remaining reef flat on the left side consist of corals, sand and seagrass. On the landward side of the reef, seagrass grows on the corals and traps sand. Small ponds form in areas which lack seagrass and thus sand cover. These ponds remain submerged for the entire study.
The fringing reef attenuates incoming waves, but the area is still subject to water surface undulations. Sensor SL-20 (see Fig. 2) records the significant wave height—the sensor lies in the inundated channel and measures constantly throughout the entire field survey. The resulting significant wave height on the reef is \(H_s = 0.10\,\hbox {m}\), calculated as the mean of the highest 33 m waves from a zero-crossing analysis.
Survey site, study site and setup. Orthophoto of the survey site on the reef, with reef areas classified according to their landform. The white border shows the study site within the survey site. Round circles show the ground control point (GCP) locations. GCPs paired with pressure sensors have a sensor identifier label below them
The survey site contains 12 uniquely colored and labeled GCPs. These GCPs are made of 0.5 m wide square PVC-tarpaulin sheets. Later, in the SfM-MVS process, the GCPs serve as georeference and scaling of the point cloud and they are used in the bundle adjustment to optimize the image alignment. Therefore, each GCP’s center position is measured with a survey grade GNSS system, being set up as base-rover combination for RTK measurements. Both GNSS devices are Septentrio AsteRx-U receiver combined with a NAVX-3G antenna. The devices measure the GCPs’ position with an accuracy of \(1.24 \pm 0.14\,\hbox {cm}\). An equal distribution of GCPs further supports the alignment quality: four GCPs cover the constantly dry sandy beach, while the remaining eight GCPs lie on the shoreward half of the intertidal reef flat. Seven of the eight reef GCPs are also paired with pressure sensors, measuring the water depth constantly (see Fig. 2). The sampling rate is between 1 Hz and 8 Hz for the four Seametrics PT2X sensors (ID: SL-number, in Fig. 2) and 16 Hz for the three Driesen + Kern P-Log3021-MMC sensors (ID: T-letter, in Fig. 2). The mean water depth \(\overline{h}\) is the average inundation of the reef during each flight, considering measurements from all pressure sensors. In this study, all water depths are measured on-site, while water levels are based on tide data from University of Hawaii Sea-Level Center (UHSLC, Caldwell et al. 2015).
Digital elevation models
A DJI Phantom 4 Pro (V.1) quadcopter records aerial images in ten flights with 25 m altitude from the take-off location. Each flight is considered one survey, as every flight covers the entire survey area. Flight planning is done by DroneDeploy, allowing to record images automatically every 2 s. To record the images, the drone carries a 20 megapixel camera with the camera angle at nadir position (perpendicular to the ground). With these settings, images overlap 80% in the front and 75% on the sides. To further improve three-dimensional reconstruction, all surveys—except number four to six—also contain images of the survey area in non-nadir position (DroneDeploy option 3D Mode turned on). While the first flight of the entire study is the reference flight over the dry reef, all other flights are clustered in four sets with two consecutive flights each—except for the last set containing three consecutive flights (see Table 1). Repeating flights in each set with similar boundary conditions creates redundancy and is meant to compensate for complications, such as deteriorated visibility. The time between the start of each set is about 45–75 min, while within each set, the time between the take-offs is 10–20 min (see Fig. 1c and Table 1).
The aerial images of each flight are the basis for a three-dimensional reconstruction, being carried out with Metashape (v1.5.3 Professional, build 8432; agisoft.com)—a commercial, proprietary software solution by Agisoft LLC (Agisoft 2019) incorporating Structure-from-Motion (SfM, Westoby et al. 2012) and MVS algorithms (in the following referred to as SfM-MVS). The software uses the recorded aerial images of each flight to find clearly distinguishable points in two or more images (tie points; with SfM-MVS). Based on these points, Metashape aligns the cameras. Afterward, the software uses the aligned aerial images to calculate a dense point cloud (with MVS) and then creates three-dimensional models, serving as base for the DEMs and orthophotos. This procedure is carried out for each flight (see Table 1), resulting in ten models. In this study the DEMs of each model have a resolution of 1.36–\(1.76\,\hbox {cm}\ \hbox {px}^{-1}\) and the associated orthophotos have a resolution of 0.68–\(1.31\,\hbox {cm}\ \hbox {px}^{-1}\). The quality setting for each reconstruction step in Metashape are set to high (see Appendix, Table 3 for further information on settings in Metashape). Conventional SfM-MVS techniques make use of self-calibrating bundle adjustment, to accurately handle nonmetric or consumer-grade camera data in photogrammetric processes (Moniwa 1981). But these self-calibrating bundle adjustments are not able to account for radial lens distortion, so that aerial images with almost parallel viewing perspectives contain systematic broad-scale errors in the photogrammetric process—usually referred to as “(vertical) doming”, which has been analyzed by James and Robson (2014). Using simulations of multi-image networks, James and Robson (2014) show that self-calibration, as part of the bundle adjustment process, leads to systematic errors in the DEM and can be mitigated by following practical flight plan solutions: (a) avoiding self calibration (if an accurate camera model is available), (b) taking images with off-nadir camera orientation, (c) estimating the parameter value associated with minimal systematic DEM error using suitably distributed control points (James and Robson 2014; Meinen and Robinson 2020). Other authors showed that the presence and the distribution of GCPs are relevant in reducing the doming effect. In fact, in the area where GCPs are dominant, the elevation difference is an order of magnitude smaller when compared to other regions in the DEM (Nesbit and Hugenholtz 2019; Casella et al. 2020). Camera calibration and correction routines can improve, but not fully diminish systematic errors—especially in peripheral regions of the DEMs (Girod et al. 2017). In this sense, the photogrammetric reconstruction of the reef from images of flight 4 leads to more pronounced doming than observed in any other reconstruction within this study—probably because the survey only contained images recorded in nadir orientation (images in non-nadir position were not collected for flight 4) and sun glint on aerial images affect the photogrammetric process adversely (see Appendix, Fig. 6). Sun glint is another error source in aerial images, impairing the three-dimensional reconstruction of the scene (Overstreet and Legleiter 2017). A polar filter on the camera lens can reduce the effect of sun glint on water surfaces and several techniques for high-resolution UAV imagery exist, using near-infrared wavelengths (700–1000 nm) to account for this effect (Muslim et al. 2019). However, recording information from these wavelengths requires special sensors, usually not being deployed on user-grade UAVs. In flight 4, the sun glint appeared on the upper, north–west facing border in almost all aerial images of the water surface, despite using a polar filter. As a result, sun glint affected the overlapping area between images—and thus the photogrammetric reconstruction—adversely. Due to the obvious and more pronounced vertical errors within the imagery of flight 4, data from this flight will not be considered in the further evaluation of this study. In addition, the SfM-MVS algorithm struggles to provide elevation data in areas being subject to stronger water surface undulations (mostly in the channel, see Fig. 2). At high tide, the pressure sensors record the highest hydrodynamic activity (Fig. 1c). With the SfM-MVS algorithm’s interpolation disabled, 2–4% of the pixels of the flights at high tide (flights 8–10) had no elevation information.
The first flight captures the dry reef and serves as reference case for all following flights. All following flights will record the site under rising tide and thus higher water levels. Acknowledging deviations between coordinates in DEMs and independent measurements (Casella et al. 2020), in this study the dry reef’s DEM is the most exact reconstruction of the reef. Therefore, the resulting deviation DEM (\(\Delta \mathrm{DEM}\)) describes the error made by the SfM-MVS algorithm in underwater areas as:
with the dry reference \(\hbox {DEM}_{\mathrm{surface},1}\) of flight 1 and the gradually inundated topographies \(\hbox {DEM}_{\mathrm{inundated},\mathrm{i}}\). The index i accounts for the subsequent flights 2–10 (see Table 1). Consequently, calculating the deviation between the dry reference DEM and those from an increasingly inundated area reveals the ability of the SfM-MVS algorithm to reconstruct underwater topography for different water levels. Despite that all error metrics derived in this study rely on the reference case \(\mathrm{DEM}_{\mathrm{surface},1}\), the variability among reconstructions from consecutive flights over the dry reef is negligible (for more detailed information on this see Appendix). With regard to \(\Delta \mathrm{DEM}\), negative values mean the SfM-MVS algorithm considers the area to be shallower than the actual dry topography and vice-versa positive values show deeper waters. The raster calculation was carried out in QGIS (version 3.10 LTR “A Coruña” and 3.16 “Hannover”; qgis.org). The software used its internal nearest neighbor algorithm to resample the different DEM resolutions to a common resolution of \(1.8\,\hbox {cm}\,\hbox {px}^{-1}\) in all \(\Delta \hbox {DEM}\)s.
We consider three survey methods that have an impact on the alignment procedure in the photogrammetric process:
-
(a)
The first approach considers the area of interest to be fully accessible and uses all available—even submerged—GCPs in the alignment.
-
(b)
The second approach uses submerged, “wet” GCPs only (see Appendix, Table 4). It considers all DEMs from flight 5 onward, as the reef flat (sandy area with seagrass in Fig. 2) is fully submerged in these cases.
-
(c)
The third approach is done by assuming that only dry areas were accessible (also disregarding the submerged GCPs no.12 in the channel and no. 13 lying in a pond in reconstructions of earlier flights). As the water level increases, GCPs becoming wet are also neglected in the associated alignment (for more information, see Appendix, Table 4).
Furthermore, we also present two different approaches to analyze the error made by the SfM-MVS algorithm in underwater are as:
The first method illustrates the rastered \(\Delta \mathrm{DEM}\)s over the reference flight’s orthophoto, giving a more straightforward overview of the reconstruction error for each survey and its associated reef water level \(\Delta h\) separately (Fig. 3).
Another, more integral approach considers the data of all surveys at once: Since \(\Delta \mathrm{DEM}\) indicates the error made by the SfM-MVS algorithm in underwater areas, pairing the error \(e_{\mathrm{px}}\) of each pixel in every \(\Delta \mathrm{DEM}\) with the pixels’ associated water depth \(h_{\mathrm{px}}\) yields a water depth-dependent representation of the reconstruction error (carried out in python v.3.7.4 with the modules rasterio v.1.1.3 and fiona v.1.8.13 post). Here, the water depth at each pixel \(h_{\mathrm{px}}\) is derived from the pixel’s z-coordinate and it’s mean water depth on the reef \(\overline{h}\) for each flight (see Table 1).
Combining the data from all nine \(\Delta \mathrm{DEM}\)s results in about \(2 - 3 \cdot 10^7\) data points. To illustrate this sheer amount of point data, two-dimensional histograms analyze the error occurrence probability over water depth (Figs. 4, 5 in results). These two-dimensional histograms employ a 5 mm by 1 mm raster (\(h_{\mathrm{px}}\) by \(e_{\mathrm{px}}\)), yielding 1.1 million combinations of \(h_{\mathrm{px}}\) and \(e_{\mathrm{px}}\) (python module: matplotlib, v3.1.3 with function hist2d). The according mean elevation difference \(\overline{e}_h\) combines all \(e_{\mathrm{px}}\) in one water depth h-bin of the histogram as
with \(N_h\) as number of \(e_{\mathrm{px}}\) per h-bin of the histogram. Based on the two-dimensional histograms, a regression function of \(\overline{e}\) summarizes the mean error as function of the water depth h, hence giving a general water depth-dependent error estimate for photogrammetric reconstruction of inundated areas:
with \({\mathcal {O}}\) as order of the regression function, \(m_o\) as estimated coefficients for the regression problem and y as the function’s intercept of the ordinate (python module: scikit-learn v0.21.3, with LinearRegression function for \({\mathcal {O}}=1\) and PolynomialFeatures function for \({\mathcal {O}}>1\)). The coefficient of determination \(R^2\) expresses the regression function’s quality to approximate the mean elevation difference of each bin \(\overline{e}_{h,b}\):
with \(B_h\) as number of bins, \(\overline{e}_{h,b}\) as true value \(\overline{\overline{e}}_h\) in each bin b and \(\mu (h)_b\) as the predicted value of \(\overline{e}_{h,b}\) using the water depth h in the regression function (in Eq. 4, \(\overline{\overline{e}}_h\) is the mean of \(\overline{e}_h\), calculated analogously to Eq. 2 for all bins b of \(B_h\).). If \(R^2=1\), the regression function predicts the mean elevation difference \(\overline{e}_h\) perfectly. \(R^2\) decreases when the relationship worsens and for \(R^2=0\) the regression function disregards any of the provided input features (the \(R^2\)score function comes from the python module scikit-learn version 0.21.3). In this study, the regression functions are valid between the water depth limits \(h=5\,\hbox {cm}\) and \(h=73\,\hbox {cm}\). The lower end is defined by the amplitude a of the significant wave height with \(a = 0.5 H_s\), while the upper end correlates to the maximum water level on the reef \(\Delta h_{max}\) (see Table 1). The root-mean-square error \(\mathrm{RMSE}\) between the regression function and the each pixel’s elevation difference \(e_{\mathrm{px}}\) from the survey is
with \(N_{px}\) as all considered pixels from every \(\Delta\)DEMs (python module: scikit-learn with mean_squared_error function and option \(squared =False\)). In this study, the root-mean-square error measures the quality of the regression function to represent the data. In turn, the regression function itself (Eq. 3) is a metric, expressing the depth-dependent deviation made by the photogrammetric process to reconstruct underwater bathymetry in comparison to “dry” surface topography.
Refraction correction
Snell’s law describes the main challenge and error source of airborne SfM-MVS to reconstruct bathymetry: a submerged object reflects light, traveling to the camera which then records the optical information in an aerial image. However, as the light travels through two media, it refracts at the water surface, altering how inundated areas appear on the image (Woodget et al. 2015; Dietrich 2017). Snell’s law is the mathematical description of underwater objects, appearing to be shallower from outside the water:
with \(n_{\mathrm{air}}\) as refractive index of air (1.0 in Dietrich 2017), \(n_{\mathrm{water}}\) as refractive index of water (1.337 for fresh water in Dietrich 2017), \(\theta _{\mathrm{air}}\) as incident- and \(\theta _{\mathrm{water}}\) as refraction angle (nadir to SfM-MVS point). Snell’s equation accounts for the systematic underprediction of water depths in airborne imagery. Therefore, recent studies used Eq. 6 and presented attempts correcting optical refraction and improving SfM-MVS in underwater areas (Woodget et al. 2015; Dietrich 2017; Chirayath and Instrella 2019). For example, the Python-based, open-source algorithm py_sfm_depth (Dietrich 2017) builds on existing approaches (Woodget et al. 2015) and provides an additional processing step to Metashape. The algorithm reverse-engineers the vertical underwater position of the submerged dense points by applying Snell’s law on the point’s apparent locations. To achieve this, py_sfm_depth uses the information of each point’s cameras (location and orientation) as well as an interpolated, plain water level—similar to the calculation of \(h_{\mathrm{px}}\) in this study. py_sfm_depth is designed for shallow and calm inland waters without using underwater GCPs to align the point cloud (Dietrich 2017). According to the homepage of py_sfm_depth, the refraction correction provides the best outcome with (a) clear water, (b) as few as possible reflections, and (c) minimal water surface ondulations (Dietrich 2020). The homepage also predicts that waves will “increase the ‘noise’ in the SFM point cloud [... and] lead to inaccuracies/errors in the final outputs”. With this in mind, the present study tests the refraction correction algorithm py_sfm_depth for coastal waters under site-specific wave impact with aerial images from flights 6 and 10 (with mean reef water depths \(\Delta h\) of 0.61 m and 0.74 m, see Table 1). The refraction coefficient used within the refraction correction is \(n_{\mathrm{water}}=1.337\) (as suggested by Dietrich 2017). The resulting two-dimensional histograms are based on about \(4.4 - 4.5 \cdot 10^6\) data points (Fig. 5).
Results
As outlined in the methods, this study tests three survey approaches: in the first approach, the reef is accessible and surface, as well as underwater GCPs can be recorded. In the second approach, only underwater GCPs are taken into account in the photogrammetric procedure, while in the third approach only the dry areas are considered to be accessible and thus submerged GCPs are disrespected. The next section presents results from the native workflow with Metashape—both with and without refraction corrected depths. The following section contains the same procedure with refraction corrected models.
Bathymetric reconstruction with submerged and dry GCPs
The first analysis of bathymetric reconstruction assumes that the reef is accessible and underwater GCPs can be recorded. Here, the SfM-MVS algorithm uses all GCPs in the alignment step of the reconstruction. The result is the orthophoto of the reference dry topography, combined with data from all \(\Delta\)DEMs (see Fig. 3). The \(\Delta\)DEMs contain the differences between the dry and submerged reef from two of the ten flights. Following Snell’s Law (Eq. 6), negative values imply the actual, dry reef \(\mathrm{DEM}_{\mathrm{surface}}\) appear to be lower than on the submerged \(\mathrm{DEM}_{\mathrm{inundated},i}\) and vice versa for positive values. In general, the results confirm the initially suggested deviation and underpredicted water depths of submerged areas by Snell's law (Eq. 6). Also, the largest differences between the reconstructions of the dry and wet reef occurs in the deeper channel on the right side. Especially for areas subject to more hydrodynamic activity—especially breaking waves—the SfM-MVS algorithm does not always find matching points, leading to no-data patches in the ΔDEMs (white areas in Fig. 3b and c).
However, the central area of the study site stands in contrast to the general results: The water depth in the shallower area of the DEM is overestimated when not or only slightly submerged (\(\Delta h = 0.274\,\hbox {m}\) and \(0.633\,\hbox {m}\), Fig. 3a and b). This area is slightly shallower than the adjacent areas on the left (see photos in Appendix, Fig. 7). Some rocky outcrops remain above the water level and defining a definite coastline is difficult in this area (see Fig. 3a). But even the DEM with the highest submergence (Fig. 3c) still eventually contains small spots being overpredicted, albeit all rocky outcrops are submerged. Also, the area above the channel is constantly overestimated for all submergence levels. These results show that the SfM-MVS algorithm forces the submerged areas to match the inundated GCPs, negatively affecting adjacent dry areas.
\(\Delta\)DEMs for flight 3, 7 and 9. Difference between the initial, dry DEM and a the submerged DEMs with a \(\Delta h = 0.274\,\hbox {m}\) (flight 3), b \(\Delta h =0.633\,\hbox {m}\) (flight 7), and c \(\Delta h =0.733\,\hbox {m}\) (flight 9) in the study area. Red values indicate shallower water depths in the reconstruction and vice versa blue areas show areas being reconstructed higher than in the reference, dry reef model. Differences range between \(\pm 20\,\hbox {cm}\). The yellow lines are the coastlines, manually extracted from orthophotos and aerial images (see Appendix, Fig. 7)
The results from the orthophotos only give insights into each particular flight. Calculating the specific water depth of each pixel and combining it with the measured difference of water depth gives an integrated view over all flights. This method presents the SfM-MVS algorithm’s performance to reconstruct underwater areas. The test case using submerged GCPs in the alignment phase results in \(30.5 \cdot 10^6\) data points, facilitating a probabilistic estimation of errors (see Fig. 4). For water depths h between 0.05 and 0.73 m the bathymetry is increasingly overestimated by a rate of \(-13.2 \pm 21.7\%\) of the water depth (see Fig. 4a). The corresponding linear function of
describes this trend with the water depth h and a root-mean-square error of \(\mathrm{RMSE} = 0.008 \pm 0.027\,\hbox {m}\) (\(R^2=0.91\)). If only submerged GCPs are considered in the alignment (see Fig. 4b), the function changes to
The function has a root-mean-square error of \(\mathrm{RMSE} = 0.011 \pm 0.025\,\hbox {m}\) with the goodness of fit being \(R^2=0.84\).
If the submerged reef was not accessible, only dry surface GCPs could be used in the alignment. This prevents the SfM-MVS algorithm to force the submerged areas on the GCPs. As the water level increases, the number of GCPs available for aligning decreases. Therefore—and as expected from Snell’s Law (Eq. 6)—the underwater reconstruction for this approach is less accurate and the errors increase to \(-35.2 \pm 13.9\%\) of the water depth for this study (see Fig. 4c, based on \(19.9 \cdot 10^6\) points). The linear function of the regression analysis is
The function yields a root-mean-square error of \(\mathrm{RMSE} =0.030 \pm 0.075\,\hbox {m}\) between 0.05 and 0.73 m water depth (\(R^2=0.86\)).
Performance of underwater reconstruction. The figure combines the occurrence probability of depth differences \(e_{\mathrm{px}}\) between the reference DEM and the submerged DEMs with the associated water depths h in the study area. a illustrates the results for DEMs being aligned with all GCPs, b with DEMs considering only submerged (“wet”) and c only surface (“dry”) GCPs. A linear regression \({\mathcal {O}}=1\) for each case summarizes the scatter plots by giving a function \(\mu (h)\) of the mean deviation in dependence of the depth. The function is valid in the range of 0.05–0.73 m
Refraction correction
Recent attempts successfully corrected water depths from aerial images in riverine environments (Westaway et al. 2000; Woodget et al. 2015), for example with an additional processing step after the alignment (Dietrich 2017).
Using only surface GCPs shows an inverse behavior of the reconstruction error between the corrected and uncorrected DEMs when compared to the previous approach of using all GCPs: with the refraction correction applied, the error is now positive, meaning the correction reconstructs the inundated areas deeper than they are in the reference DEM (Fig. 5). The uncorrected reconstruction, using both surface and underwater GCPs or only underwater GCPs, improves the reconstruction error compared to using only dry, surface GCPs (Fig. 5a, based on \(4.5 \cdot 10^6\) points). However, when using the refraction correction, aligning the point cloud with both surface and underwater GCPs appears counterproductive. The regression analysis approximates the increased error with the function
The function is valid in the range of 0.05–0.73 m with a \(\mathrm{RMSE}\) of 0.194 m (\(R^2=0.98\)). But when using only dry surface GCPs and applying a refraction correction (Fig. 5b, based on \(4.4 \cdot 10^6\) points), the errors remain relatively constant when water depths increase beyond 0.5 m. This is in accordance with the method’s expected error behavior of being dependent on the flying altitude (Dietrich 2017). The regression analysis for the present case approximates the performance with the function
The function yields a root-mean-square error of \(\mathrm{RMSE} =0.271\,\hbox {m}\) for water depths h between 0.05 and 0.73 m (\(R^2=0.84\)).
Performance of underwater reconstruction with refraction correction. The figure combines the occurrence probability of depth differences \(e_{\mathrm{px},\mathrm{corr}}\) between the reference DEM and the refraction corrected, submerged DEMs with the associated water depths h in the study area. a illustrates DEMs considering all GCPs and b the results for DEMs being only aligned with dry surface GCPs. The scatter plots of the refraction corrected DEMs are best summarized by higher order regression functions \(\mu (h)\) with \({\mathcal {O}}>1\). The results are plotted against the linear regression with \({\mathcal {O}}=1\) from Fig. 4a to visualize the error scale compared to the uncorrected reconstruction. The functions are valid in the range of 0.05–0.73 m
Regarding the absolute error of the reconstruction without underwater GCPs and of the refraction corrected reconstruction including submerged GCPs (Figs. 4a, 5a), both methods perform about equally well for water depths between 0.10 and 0.55 m. Beyond depths of 0.55 m the error by the refraction correction stabilizes, while it increases for the uncorrected DEMs.
Therefore, despite being subject to sub-par field conditions, the bathymetric reconstruction benefits from the refraction correction in deeper waters, when no underwater GCPs are used. However, the SfM-MVS algorithm still aligns the bathymetry more exactly with submerged GCPs than correcting an unaligned bathymetry.
Discussion and conclusion
In photogrammetry, when light refracts on the water surface, submerged objects appear distorted on airborne images, leading to falsely estimated water depths in SfM-MVS algorithms. This study quantifies these errors with data from a specially designed field experiment. Our results show the SfM-MVS algorithm underestimates underwater areas by \(13.2 \pm 21.7\%\) (see Fig. 4) of the water depth when both surface and submerged GCPs are used in the optimization process. The result does not significantly improve (\(12.1 \pm 15.3\%\)) when considering only submerged GCPs. But in both cases, reconstruction accuracy of adjacent surface areas decreases with this method. Without using submerged GCPs in the optimization process, the error is at \(35.2 \pm 13.9\%\) of the water depths and the reconstruction benefits from refraction correction in waters deeper than 0.55 m.
In our example, the uncorrected reconstruction leads to underestimated water depths while the corrected reconstruction overestimated the submergence. Despite a varying order \({\mathcal {O}}\) in the approximation of the error function \(\mu (h)\) (see Eq. 3 as well as Figs. 4, 5), future studies should clarify if the reconstruction for water depths up to \(\approx 1\,\hbox {m}\) in general benefit from combining the corrected and uncorrected approach. However, beyond water depths of \(\approx 1\,\hbox {m}\), the uncorrected reconstruction would impair the refraction correction’s relatively stable performance in deeper waters (Fig. 5).
Comparing airborne photogrammetry with other methods to obtain bathymetries (for example LiDAR, echo sounder, etc.) reveals that SfM-MVS algorithms provide good estimates of shallow water depth as well as mapping abilities for clear waters with low hydrodynamic activity. This study, however, uses the approach in more challenging environments and utilizes data recorded under field conditions: The survey was carried out on a sunny day with low winds, which can be considered normal for the late dry season in the Maldives. Also, the off-shore wave height \(H_s\) of 0.88–1.00 m is normal for Fuvahmulah in March, albeit lower than average (David and Schlurmann 2020). The fringing reef attenuates these waves, but the study site still experiences hydrodynamic activity—for example in the form of bores, surges, wave run-up, etc. (Monismith 2007)—which increases as the tide rises. The statistical zero-crossing method used here to calculate \(H_s\) does not consider the smaller surface waves traveling on ondular bores (Sous et al. 2019) but represents the sea state reasonably well compared to qualitative observations on site. Still, waves in the study area affect the results in several aspects:
-
Reconstructing underwater scenes suffers from light effects such as sun glint or reflections on the plain water surface as well as caustics, which are brighter areas from wave-induced fluid lenslets focussing sunlight on the seafloor (Casella et al. 2017; Dietrich 2017; Overstreet and Legleiter 2017; Chirayath and Li 2019; Muslim et al. 2019). If the water surface changes while recording, the incident and reflection angle change in Snell’s Law. As consequence, the SfM-MVS algorithm get ambiguous information on an object’s location and shape, which impairs the reconstruction and can fail to give any information for these areas (see no data areas in Fig. 3).
-
Ambiguous information impacts the refraction correction even stronger than it affects SfM and MVS, since the refraction correction relies stronger on camera position and orientation to emend the appearing depth to the actual depth of each underwater dense point. This ambiguity results in more noise (as described in the manual of py_sfm_depth). In addition, the algorithm py_sfm_depth considers a plain water surface to compute refraction correction. This is not the case in coastal waters, leading to increased errors when compared to riverine environments with calmer water surfaces (compare the results of Dietrich 2017 with this study’s results for the refraction correction in Table 2). This underlines that the quality of the refraction correction highly benefits from calm waters, improving mapping of submerged structures. However, even with waves present, it still enhances the bathymetric reconstruction without underwater GCPs.
-
Water surface undulations also impact the mean water level estimation, used to calculate the water depth h of each pixel in \(\Delta \mathrm{DEM}\), as well as for the refraction correction. Both use an averaged water level derived from the measurements in the study site, neglecting the spatiotemporal variation of h within each flight (compare water levels \(\Delta h\) at sensor SL-20, Table 1). In the absence of water level measurements, the plain water level for the refraction correction could be estimated by sampling the water edge on a river’s bank (Dietrich 2020). However, this post-processing step is less accurate on beaches, because they experience wave run-up. With wave run-up, the coastline is varying and therefore, manual water edge or coastline detection is more difficult and somewhat more arbitrary in coastal areas.
-
In practical terms, the results of this study suggest the best workflow for reconstructing aerial imagery of coastal areas is to separate surface and shallowly submerged areas if sufficient GCPs in inundated areas exist. The bundle adjustment in the SfM-MVS algorithm corrects the sparse point cloud to match the GCPs, having a negative effect on adjacent areas (see Figs. 3, 4a and b, where submerged, wet GCPs affect surface areas negatively and vice versa for Fig. 4c).
The aim of this study was to scrutinize the performance of user-grade UAVs used for topographic reconstruction of coastal areas and associated sediment volumes. Coastal environments consist of surface and underwater areas. SfM-MVS has been successfully used before to create DEMs of dry coastal topography with errors in the order of centimeters (Casella et al. 2020), but through-water photogrammetry is still prone to inaccuracies due to the inherit physical challenges—especially when waves disturb the water surface. Sophisticated approaches use the fluid lensing effect of waves as an advantage to provide high-quality reconstruction of underwater areas (Chirayath and Earle 2016; Chirayath and Li 2019). But such numeric procedure is not (yet) widely available. Other refraction correction algorithms exist, which also aim at improving the precision and accuracy of bathymetric reconstructions from aerial imagery (see Table 2). If complementary, sparse bathymetric measurements from echo-sounding or LiDAR sensors exist, machine learning procedures support SfM-MVS algorithms for submerged areas up to about 15 m water depths in clear water conditions (Agrafiotis et al. 2019, 2020). Without any preparations or post-processing, SfM-MVS algorithm natively facilitates bathymetric reconstruction and aerial mapping of shallowly inundated areas, albeit the reconstruction error increases with water depth and hydrodynamic activity (see Table 2 or Casella et al. 2017; Ye et al. 2016; Shintani and Fonstad 2017; Genchi et al. 2020). However, a confident error metric of standard SfM-MVS has been missing for in field campaigns in coastal surveys or on coral reefs with user-grade UAVs. Therefore, this study quantifies the depth-dependent error in a typical field campaign environment. The results encourage to extent surface (“dry”) beach surveys with conventional UAVs beyond the coastline. The reconstruction improves from adapting aligning strategies, which can already be considered in the planning of the field campaign or pragmatically adapted to the conditions on site. If field conditions do not allow for improved GCP placement, aerial imagery of submerged areas can still be utilized in a SfM-MVS algorithm, but DEMs of these areas contain higher errors. Beyond a depth of 0.55 m, reconstruction of underwater areas further benefits from refraction correction when post-processing the field data. But the reconstruction remains vulnerable to disturbances by waves and sun reflections. In these cases, further correction of the aerial images is required or more advanced techniques, such as fluid lensing, should be considered.
References
Aarninkhof SGJ, Ruessink BG, Roelvink JA (2005) Nearshore subtidal bathymetry from time-exposure video images. J Geophys Res Oceans 110(C6), https://doi.org/10.1029/2004JC002791
Agisoft (2019) Agisoft Metashape User Manual: Professional Edition, Version 1.5. https://www.agisoft.com/pdf/metashape-pro_1_5_en.pdf
Agrafiotis P, Skarlatos D, Georgopoulos A, Karantzalos K (2019) Shallow water bathymetry mapping from UAV imagery based on machine learning. ISPRS Int Arch Photogramm Remote Sens Spat Inf Sci XLII-2/W10:9 – 16, https://doi.org/10.5194/isprs-archives-XLII-2-W10-9-2019
Agrafiotis P, Karantzalos K, Georgopoulos A, Skarlatos D (2020) Correcting image refraction: Towards accurate aerial image-based bathymetry mapping in shallow waters. Remote Sens 12(2), https://doi.org/10.3390/rs12020322
Bandini F, Olesen D, Jakobsen J, Kittel CMM, Wang S, Garcia M, Bauer-Gottwein P (2018) Technical note: Bathymetry observations of inland water bodies using a tethered single-beam sonar controlled by an unmanned aerial vehicle. Hydrol Earth Syst Sci 22(8):4165–4181. https://doi.org/10.5194/hess-22-4165-2018
Bergsma EW, Almar R, Melo de Almeida LP, Sall M (2019) On the operational use of UAVs for video-derived bathymetry. Coast Eng 152. https://doi.org/10.1016/j.coastaleng.2019.103527
Borge JCN, Rodríguez GR, Hessner K, González PI (2004) Inversion of marine radar images for surface wave analysis. J Atmos Ocean Technol 21(8):1291–1300
C3S (2017) ERA5: Fifth generation of ECMWF atmospheric reanalyses of the global climate by the Copernicus Climate Change Service (C3S). https://www.cds.climate.copernicus.eu/cdsapp/home, https://doi.org/10.24381/cds.adbb2d47, Copernicus Climate Change Service Climate Data Store (CDS). Last date of access: 2020-05-31
Caldwell PC, Merrifield MA, Thompson PR (2015) Sea level measured by tide gauges from global oceans—the Joint Archive for Sea Level holdings (NCEI Accession 0019568). Dataset. Version 5.5, NOAA National Centers for Environmental Information,, https://doi.org/10.7289/V5V40S7W
Carlot J, Rovère A, Casella E, Harris D, Grellet-Muñoz C, Chancerelle Y, Dormy E, Hedouin L, Parravicini V (2020) Community composition predicts photogrammetry-based structural complexity on coral reefs. Coral Reefs. https://doi.org/10.1007/s00338-020-01916-8
Carrivick JL, Smith MW, Quincey DJ (2016) Structure from Motion in the Geosciences. John Wiley & Sons Ltd. https://doi.org/10.1002/9781118895818
Casella E, Rovere A, Pedroncini A, Stark CP, Casella M, Ferrari M, Firpo M (2016) Drones as tools for monitoring beach topography changes in the Ligurian Sea (NW Mediterranean). Geo-Mar Lett 36(2):151–163. https://doi.org/10.1007/s00367-016-0435-9
Casella E, Collin A, Harris D, Ferse S, Bejarano S, Parravicini V, Hench JL, Rovere A (2017) Mapping coral reefs using consumer-grade drones and structure from motion photogrammetry techniques. Coral Reefs 36(1):269–275. https://doi.org/10.1007/s00338-016-1522-0
Casella E, Drechsel J, Winter C, Benninghoff M, Rovere A (2020) Accuracy of sand beach topography surveying by drones and photogrammetry. Geo-Mar Lett 40(2):255–268. https://doi.org/10.1007/s00367-020-00638-8
Chernyshov P, Vrecica T, Streßer M, Carrasco R, Toledo Y (2020) Rapid wavelet-based bathymetry inversion method for nearshore X-band radars. Remote Sens Environ 240. https://doi.org/10.1016/j.rse.2020.111688
Chirayath V, Earle SA (2016) Drones that see through waves - preliminary results from airborne fluid lensing for centimetre-scale aquatic conservation. Aquat Conserv Mar Freshwater Ecosyst 26(S2):237–250. https://doi.org/10.1002/aqc.2654
Chirayath V, Instrella R (2019) Fluid lensing and machine learning for centimeter-resolution airborne assessment of coral reefs in American Samoa. Remote Sens Environ 235. https://doi.org/10.1016/j.rse.2019.111475
Chirayath V, Li A (2019) Next-Generation Optical Sensing Technologies for Exploring Ocean Worlds-NASA FluidCam, MiDAR, and NeMO-Net. Front Mar Sci 6:521. https://doi.org/10.3389/fmars.2019.00521
Colbo K, Ross T, Brown C, Weber T (2014) A review of oceanographic applications of water column data from multibeam echosounders. Estuar Coast Shelf Sci 145:41–56. https://doi.org/10.1016/j.ecss.2014.04.002
Costanza R, De Groot R, Sutton P, Van der Ploeg S, Anderson SJ, Kubiszewski I, Farber S, Turner RK (2014) Changes in the global value of ecosystem services. Glob Environ Change 26:152–158
David CG, Schlurmann T (2020) Hydrodynamic Drivers and Morphological Responses on Small Coral Islands - The Thoondu Spit on Fuvahmulah, the Maldives. Front Mar Sci 7:885. https://doi.org/10.3389/fmars.2020.538675
Dietrich JT (2017) Bathymetric Structure-from-Motion: extracting shallow stream bathymetry from multi-view stereo photogrammetry. Earth Surface Process Landf 42(2):355–364. https://doi.org/10.1002/esp.4060
Dietrich JT (2020) py\_sfm\_depth homepage. https://www.geojames.github.io/py_sfm_depth, last accessed: June 3rd, 2020
Duvat VKE, Magnan AK (2019) Rapid human-driven undermining of atoll island capacity to adjust to ocean climate-related pressures. Sci Rep 9(1), https://doi.org/10.1038/s41598-019-51468-3
Ferrario F, Beck MW, Storlazzi CD, Micheli F, Shepard CC, Airoldi L (2014) The effectiveness of coral reefs for coastal hazard risk reduction and adaptation. Nat Commun 5(1), https://doi.org/10.1038/ncomms4794
Fine M, Hoegh-Guldberg O, Meroz-Fine E, Dove S (2019) Ecological changes over 90 years at Low Isles on the Great Barrier Reef. Nat Commun 10(1), https://doi.org/10.1038/s41467-019-12431-y
Gawehn M, van Dongeren A, de Vries S, Swinkels C, Hoekstra R, Aarninkhof S, Friedman J (2020) The application of a radar-based depth inversion method to monitor near-shore nourishments on an open sandy coast and an ebb-tidal delta. Coast Eng 159. https://doi.org/10.1016/j.coastaleng.2020.103716
Genchi SA, Vitale AJ, Perillo GME, Seitz C, Delrieux CA (2020) Mapping topobathymetry in a shallow tidal environment using low-cost technology. Remote Sens 12(9), https://doi.org/10.3390/rs12091394
Girod L, Nuth C, Kääb A, Etzelmüller B, Kohler J (2017) Terrain changes from images acquired on opportunistic flights by SfM photogrammetry. Cryosphere 11(2):827–840
Hedley JD, Roelfsema C, Brando V, Giardino C, Kutser T, Phinn S, Mumby PJ, Barrilero O, Laporte J, Koetz B (2018) Coral reef applications of Sentinel-2: Coverage, characteristics, bathymetry and benthic mapping with comparison to Landsat 8. Remote Sens Environ 216:598–614. https://doi.org/10.1016/j.rse.2018.07.014
Hédouin L, Rouzé H, Berthe C, Perez-Rosales G, Martinez E, Chancerelle Y, Galand PE, Lerouvreur F, Nugues MM, Pochon X, Siu G, Steneck R, Planes S (2020) Contrasting patterns of mortality in Polynesian coral reefs following the third global coral bleaching event in 2016. Coral Reefs 39(4):939–952. https://doi.org/10.1007/s00338-020-01914-w
Holman R, Plant N, Holland T (2013) cBathy: A robust algorithm for estimating nearshore bathymetry. J Geophys Res Oceans 118(5):2595–2609. https://doi.org/10.1002/jgrc.20199
Holmgren W, Hansen C, Mikofski M (2018) pvlib python: a python package for modeling solar energy systems. J Open Source Softw 3(29):884
James MR, Robson S (2014) Mitigating systematic error in topographic models derived from UAV and ground-based image networks. Earth Surface Process Landf 39(10):1413–1420. https://doi.org/10.1002/esp.3609
Joyce KE, Duce S, Leahy SM, Leon J, Maier SW (2019) Principles and practice of acquiring drone-based image data in marine environments. Mar Freshwater Res 70(7):952. https://doi.org/10.1071/mf17380
Kench PS, Brander RW (2006) Response of reef island shorelines to seasonal climate oscillations: South Maalhosmadulu atoll, Maldives. J Geophys Res Earth Surface 111(F1), https://doi.org/10.1029/2005JF000323
Klemas V (2011) Beach Profiling and LIDAR Bathymetry: An Overview with Case Studies. J Coast Res 27(6):1019–1028. https://doi.org/10.2112/JCOASTRES-D-11-00017.1
Leon J, Roelfsema CM, Saunders MI, Phinn SR (2015) Measuring coral reef terrain roughness using ‘Structure-from-Motion’ close-range photogrammetry. Geomorphology 242:21–28. https://doi.org/10.1016/j.geomorph.2015.01.030 (Geomorphology in the Geocomputing Landscape: GIS, DEMs, Spatial Analysis and statistics)
Mandlburger G (2019) Through-Water Dense Image Matching for Shallow Water Bathymetry. Photogramm Eng Remote Sens 85(6):445–455
Mandlburger G, Pfennigbauer M, Schwarz R, Flöry S, Nussbaumer L (2020) Concept and performance evaluation of a novel UAV-borne topo-bathymetric LiDAR sensor. Remote Sens 12(6):986. https://doi.org/10.3390/rs12060986
Meinen BU, Robinson DT (2020) Mapping erosion and deposition in an agricultural landscape: Optimization of UAV image acquisition schemes for SfM-MVS. Remote Sens Environ 239. https://doi.org/10.1016/j.rse.2020.111666
Monismith SG (2007) Hydrodynamics of Coral Reefs. Ann Rev Fluid Mech 39(1):37–55. https://doi.org/10.1146/annurev.fluid.38.050304.092125
Moniwa H (1981) The concept of photo-variant self-calibration and its application in block adjustment with bundles. Photogrammetria 36(1):11–29. https://doi.org/10.1016/0031-8663(81)90006-5
Murfitt SL, Allan BM, Bellgrove A, Rattray A, Young MA, Ierodiaconou D (2017) Applications of unmanned aerial vehicles in intertidal reef monitoring. Sci Rep 7(1), https://doi.org/10.1038/s41598-017-10818-9
Muslim AM, Chong WS, Safuan CDM, Khalil I, Hossain MS (2019) Coral Reef Mapping of UAV: A Comparison of Sun Glint Correction Methods. Remote Sens 11(20), https://doi.org/10.3390/rs11202422, https://www.mdpi.com/2072-4292/11/20/2422
Nesbit P, Hugenholtz C (2019) Enhancing UAV-SfM 3D Model Accuracy in High-Relief Landscapes by Incorporating Oblique Images. Remote Sens 11(3):239. https://doi.org/10.3390/rs11030239
Overstreet BT, Legleiter CJ (2017) Removing sun glint from optical remote sensing images of shallow rivers. Earth Surface Process Landf 42(2):318–333. https://doi.org/10.1002/esp.4063
Panagou T, Oikonomou E, Hasiotis T, Velegrakis AF (2020) Shallow Water Bathymetry Derived from Green Wavelength Terrestrial Laser Scanner. Marine Geodesy 1–21. https://doi.org/10.1080/01490419.2020.1737602
Ratter B, Hennig A, Zahid, (2019) Challenges for shared responsibility - Political and social framing of coastal protection transformation in the Maldives. DIE ERDE J Geogr Soc Berl 150(3):169–183
Rossi P, Castagnetti C, Capra A, Brooks AJ, Mancini F (2019) Detecting change in coral reef 3d structure using underwater photogrammetry: critical issues and performance metrics. Appl Geomat 12(S1):3–17. https://doi.org/10.1007/s12518-019-00263-w
Shintani C, Fonstad MA (2017) Comparing remote-sensing techniques collecting bathymetric data from a gravel-bed river. Int J Remote Sens 38(8–10):2883–2902. https://doi.org/10.1080/01431161.2017.1280636
Skirving WJ, Heron SF, Marsh BL, Liu G, Cour JLDL, Geiger EF, Eakin CM (2019) The relentless march of mass coral bleaching: a global perspective of changing heat stress. Coral Reefs 38(4):547–557. https://doi.org/10.1007/s00338-019-01799-4
Sous D, Tissier M, Rey V, Touboul J, Bouchette F, Devenon JL, Chevalier C, Aucan J (2019) Wave transformation over a barrier reef. Cont Shelf Res 184:66–80. https://doi.org/10.1016/j.csr.2019.07.010
Storlazzi CD, Dartnell P, Hatcher GA, Gibbs AE (2016) End of the chain? Rugosity and fine-scale bathymetry from existing underwater digital imagery using structure-from-motion (SfM) technology. Coral Reefs 35(3):889–894. https://doi.org/10.1007/s00338-016-1462-8
Talavera L, del Río L, Benavente J (2020) UAS-based High-resolution Record of the Response of a Seminatural Sandy Spit to a Severe Storm. J Coast Res 95(sp1):679. https://doi.org/10.2112/si95-132.1
van Dongeren A, Plant N, Cohen A, Roelvink D, Haller MC, Catalán P (2008) Beach Wizard: Nearshore bathymetry estimation through assimilation of model computations and remote observations. Coast Eng 55(12):1016–1027. https://doi.org/10.1016/j.coastaleng.2008.04.011
Westaway R, Lane S, Hicks D (2000) The development of an automated correction procedure for digital photogrammetry for the study of wide, shallow, gravel-bed rivers. Earth Surface Process Landf J Br Geomorphol Res Group 25(2):209–226
Westoby M, Brasington J, Glasser N, Hambrey M, Reynolds J (2012) structure-from-motion photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 179:300–314. https://doi.org/10.1016/j.geomorph.2012.08.021
Woodget AS, Carbonneau PE, Visser F, Maddock IP (2015) Quantifying submerged fluvial topography using hyperspatial resolution UAS imagery and structure from motion photogrammetry. Earth Surface Process Landf 40(1):47–64. https://doi.org/10.1002/esp.3613
Ye D, Liao M, Nan A, Wang E, Zhou G (2016) Research on reef bathymetric survey ofd an UAV stereopair based on two-medium photogrammetry. ISPRS Int Arch Photogramm Remote Sens Spat Inf Sci XLI–B1:407–412. https://doi.org/10.5194/isprs-archives-XLI-B1-407-2016
Acknowledgements
The authors would like to thank Ali Ahmed, Tatiana Ivanova, René Klein, Ibrahim Shiyan (Panda), Zahid as well as Marion and Uwe Zander for their help in the field campaigns. On the Maldives, the authors were supported by the Maldives Meteorological Service (MMS), Fuvahmulah Island Council and Fuvahmulah DIVE School. The authors would also like to thank James T. Dietrich for feedback on his refraction correction routine.
Funding
This study took place in the project “Dealing with change in SIDS: societal action and political reaction in sea level change adaptation in Small Island Developing States (DICES),” Grant No. SCHL 503/17-1 (CGD, NK, PB, TS) and “Holocene sea-level changes in Southeast Asia (SEASchange),” Grant No. RO-5245/1-1 (AR). The projects are framed within the priority program (SPP-1889) regional sea level change and society of the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG). Elisa Casella acknowledges the Leibniz Center for Tropical Marine Research for economical support. Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
CGD planned the survey with input from EC and AR. PB and AR prepared the devices. PB provided the data from the hydrodynamic measurements. CGD, NK and PB carried out the field campaign. CGD and NK post-processed the data with help and advice from EC and AR. CGD prepared the manuscript with the help of NK. EC, AR and TS edited and contributed to the final manuscript. AR and TS designed the research projects in the research program and funded this study.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Topic Editor Mark Vermeij
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Photoscan settings
The study used the SfM and MVS algorithms provided by the software Metashape (v1.5.3 Professional, build 8432; agisoft.com) to calculate three-dimensional DEM of the increasingly submerged reef flat and adjacent beach area. Metashape provides several settings, influencing different stages of the SfM-MVS procedure. Table 3 contains the settings used in Metashape for this study.
Sun glint in aerial images
The method sections shortly touch upon the removal of flight 4 from this study, due to stronger doming than in reconstructions of other flights. Possible reasons are the absence of off-nadir images and strong and structural sun glint on the aerial images. Sun glint in aerial images results in very bright pixels from reflections of sun light on the water surface (Overstreet and Legleiter 2017). Figure 6 shows one aerial image from flight 4, containing sun glint on the upper, northwest facing border of the image process.
Sun glint in an aerial image. Sun glint in one aerial image, recorded within flight 4. This type of sun glint also appears on almost all other aerial images of flight 4, showing the water surface. The sun glint is on the images’ northwest facing border and thus affects image overlapping within the photogrammetric
Reference digital elevation model
All error metrics in this study rely on the first flight serving as reference case. The SfM-MVS software returns a reconstruction error, quantifying the quality of the sparse point cloud to match the GCPs. This error is 5.6 cm in the first reference flight. Since the area does not contain any Independent Control Points (ICPs), there is no accuracy metric for the reconstruction, but it in comparable studies, it is usually within centimeter scale (Casella et al. 2020).
To check the variability of the reconstruction, we used a test flight preceding the experiments of this study. The test flight while the GCPs were placed and the pressure sensors installed, to check the functionality of the UAV and the quality of the preplanned flight. In this test flight, all GCPs were already in place, instead of those on the sandy beach with the numbers 17-20. We did a reconstruction of this flight and compared the resulting reconstruction of the study site to the reconstruction of the first flight. To ensure comparability among both reconstructions, we have not used GCPs 17 to 20 in the reconstruction of flight 1. We then subtracted the DEMs of the test flight from the adapted reconstruction of flight 1, yielding a deviation of \(0.4 \pm 0.5\,\hbox {cm}\) among each other. Both flights were carried out at low-tide. While this test shows that some minor deviations can be expected when reconstructing the same scene with different subsequent flights, we consider these deviations to have no significant influence on our results.
Dry ground control points
In the manuscript, we consider two survey methods, that have an impact on the alignment procedure in the photogrammetric process. The second approach is done by assuming that only dry areas were accessible and as the water level increases, GCPs becoming wet are neglected in the associated alignment. Table 4 contains all GCPs displayed in Fig. 2 and shows whether they have been dry or submerged in the associated flight set and thus if they have been considered in the alignment procedure.
Coastline definition
The manuscript contains an areal overview of deviations between the dry and successively submerged reef in Fig. 3. This figure displays these deviations over the dry reef’s orthophoto and—for better orientation—also shows the manually extracted coast- or waterline associated. We defined the waterline by visual observation from the aerial images such as displayed in Fig. 7.
Visual coastline extraction. An example of aerial images, being used to manually estimate the coastline (yellow lines) in Fig. 3. The images shown here are screenshots from Metashape
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
David, C.G., Kohl, N., Casella, E. et al. Structure-from-Motion on shallow reefs and beaches: potential and limitations of consumer-grade drones to reconstruct topography and bathymetry. Coral Reefs 40, 835–851 (2021). https://doi.org/10.1007/s00338-021-02088-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00338-021-02088-9