Abstract
We consider a variational model for periodic partitions of the upper half-space into three regions, where two of them have prescribed volume and are subject to the geometric constraint that their union is the subgraph of a function, whose graph is a free surface. The energy of a configuration is given by the weighted sum of the areas of the interfaces between the different regions and a general volume-order term. We establish existence of minimizing configurations via relaxation of the energy involved, in any dimension. Moreover, we prove partial regularity results for volume-constrained minimizers in two space dimensions. Thin films of diblock copolymers are a possible application and motivation for considering this problem.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The goal of this paper is to initiate the analytical investigation of variational models for partitions with quasi-minimal surface area, subject to a geometric graph constraint. The admissible configurations of the model that we consider here consist of two phases (i.e., regions of the space with prescribed volume) which are confined by a flat substrate on the bottom side, and by the graph of a Lipschitz function on the upper side. The upper interface between the two phases and the region above them corresponds to a free surface.
The imposition of a graph constraint on the admissible configurations is not new in the mathematical literature and appeared in particular in variational models for epitaxially strained elastic films, see (Bonnetier and Chambolle 2002; Chambolle and Solci 2007; Fonseca et al. 2007; Davoli and Piovano 2019; Crismale and Friedrich 2020); however, to the best of our knowledge this is the first instance where a similar constraint is enforced on a system with multiple phases, and this constitutes the main novelty of this paper.
We are interested in the description of optimal configurations minimizing an energy functional given by the sum of the surface measures of the different interfaces between the phases, possibly with different weights. We also include in the total energy a general volume-order term (allowing, for instance, for possible nonlocal interactions among the two phases); the results in this paper are valid under quite general assumptions on this term, whereas its explicit form would be crucial for the characterization of optimal or equilibrium configurations.
This paper is the first step in the rigorous investigation of the properties of the energy and of optimal configurations of the system. In particular, we discuss the lower semicontinuity properties of the energy, which permits to prove existence of minimizing configurations via relaxation in any dimension. Moreover, we establish several regularity properties of minimizers in dimension two. Further investigations on the fine structure of optimal configurations will be the subject of future work.
A possible application of the variational model that we introduce is the description of equilibrium configurations of thin films of diblock copolymers, see Sect. 1.3 for details.
1.1 The Model
We now pass to an introductory description of the model and of the main results obtained in this paper. For the precise definitions and assumptions, we refer to Sect. 2.
We consider a configuration described by a phase variable u defined in the upper half-space of \(\mathbb R^n\), in general dimension \(n\ge 2\), taking values \(+1\), \(-1\), and 0, representing the two phases \(A_u=\{u=1\}\), \(B_u=\{u=-1\}\), and the region above them \(V_u=\{u=0\}\). For mathematical convenience, we extend u by a fixed value (say, \(u=2\)) also in the lower half-space. Having in mind the application to thin films of diblock copolymers, we will often use the terminology film to denote the region occupied by the two phases \(A_u\cup B_u\), substrate to indicate the lower half-space, and void to indicate the region \(V_u\) above the film.
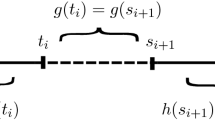
Admissible configurations are those for which the region \(A_u\cup B_u\) is confined in the subgraph of a function \(h_u\) over the flat substrate (see Fig. 1). As customary in this kind of problems, to focus on the effect of the surface energy on the equilibrium configurations, we work with lateral periodic boundary conditions. We also impose the total volume of the film and the ratio between the two constituent phases by means of two mass constraints.
We consider a sharp-interface model in which the short-range interaction energy \({\mathscr {G}}(u)\) of a configuration u is assumed to be proportional to the surface measure of the interfaces between the different phases, with possibly different surface tensions. The interfaces involved are: \(\Gamma _u^{AB}\) (between the two phases inside the film), \(\Gamma ^A_u\), \(\Gamma ^B_u\) (between each phase and the void), and, since also the contact between the film and the substrate costs surface energy, \(S^A_u\), \(S^B_u\) (between each phase and the substrate), \(S_u^V\) (between the substrate and the void).
In addition to the interfacial energy \({\mathscr {G}}(u)\), we consider in the total energy a general volume-order term \({\mathcal {N}}(u)\). For the results contained in this paper, the precise form of this term does not play a role, and the only property that we use is that \({\mathcal {N}}(\cdot )\) is Lipschitz continuous with respect to the symmetric difference of sets, namely
for some constant \(L_{{\mathcal {N}}}\).
Then, the total energy \({\mathscr {F}}(u)\) of a regular configuration u, whose profile is given by a Lipschitz function \(h_u\), writes as
(see Sect. 2 for the precise definition of all the terms involved).
1.2 Main Results
The paper is divided into two main parts, where we study several properties of the energy \({\mathscr {F}}\). In the first part, we focus on its lower semicontinuity with respect to the \(L^1\)-topology, and we identify in Theorem 3.1 the lower semicontinuous envelope \({\overline{{\mathscr {F}}}}\), defined over a larger class of possibly irregular profiles. In particular, the relaxation procedure allows to consider configurations whose free boundary is described by a function \(h_u\) of bounded variation: it then might be unbounded and with jump discontinuities.
The functional \({\overline{\mathscr {F}}}\) has the same form of the original functional \({\mathscr {F}}\), namely it is the sum of a surface energy contribution \({\overline{{\mathscr {G}}}}(u)\) and of the nonlocal interaction \(\gamma {\mathcal {N}}(u)\). Notice that the relaxation affects only the surface part of the energy, as the nonlocal term is continuous with respect to \(L^1\)-convergence. As might be expected, the new surface energy \({\overline{{\mathscr {G}}}}\) has relaxed surface tension coefficients, due to the possibility of reducing the energy by inserting a thin layer of a phase between two other phases (wetting). The non-standard aspect of this procedure is that, due to the additional constraints of the model (namely, the only admissible configurations are subgraphs), not all the possible infiltrations are allowed; this prevents us to apply directly the well-known results about the relaxation of surface energy of clusters in \(\mathbb R^n\), see (Ambrosio and Braides 1990).
Concerning the proof, whereas the liminf inequality follows by a standard argument adapted to our setting (see Proposition 3.7), the construction of a recovery sequence requires extra care (see Proposition 3.8). Indeed, first we approximate a non-regular profile by a Lipschitz one, thanks to a construction by Chambolle and Solci (2007); next, when one of the surface tension coefficients between two phases changes in the relaxation process, we need to approximate the corresponding interface by carefully inserting thin layers of the other phases, preserving both the graph constraint and the mass constraint.
Finally, the existence of a solution to the mass constrained minimization problem for the relaxed functional
where \(0<m<M\), follows by a standard application of the direct method (see Theorem 3.5).
In the second part of the paper, we turn our attention to the study of regularity properties of solutions to (1.2). This is where the main mathematical challenges are, stemming from the fact that admissible competitors have to satisfy the additional condition of being subgraphs. Indeed, if no graph constraint is in force, then partial regularity of minimizing clusters could be obtained by a standard strategy, which would amount to first showing that volume-constrained minimizers are quasi-minimizers of the surface energy, and then to proving an elimination property (see Leonardi 2001) which allows to reduce locally to the case of only two interfaces. Once this is done, partial regularity follows from classical results (see Gonzalez et al. 1983). In our case, though, we cannot apply directly those results, as they require to make arbitrary perturbations, thus possibly exiting the restricted class of admissible configurations. Therefore, we need to perform delicate geometric constructions, and to combine several ideas in order to prove regularity.
We next summarize our main strategy. In Lemma 4.2 we remove the mass constraints by showing that every solution to (1.2) is also a solution to a suitable penalized problem. The proof of this fact follows a rather standard contradiction argument, which amounts to show that if a minimizer of the penalized problem does not satisfy the volume constraint, then it is possible to modify it and reduce its energy—which would be a contradiction—provided that the constant in front of the penalization term is large enough. When there is just one mass constraint and the problem is in the whole space \(\mathbb R^n\), this can be achieved by a suitable rescaling of the minimizer. A refined argument by Esposito and Fusco (2011) shows that the same can be done by a local perturbation of the set, which brings the mass of the perturbed set closer (but not necessarily equal) to the desired mass, reducing the energy at the same time. However, the local variation constructed in Esposito and Fusco (2011) is radial, and is not suitable in our case since the competitor that is constructed in this way might not satisfy the graph constraint. Instead, we perform a local rescaling in the vertical direction, so that the perturbed configuration remains the subgraph of an admissible profile and can be used to contradict the minimality of the starting configuration. Another relevant difference is that in our case two mass constraints are in force; we can however avoid the use of the Implicit Function Theorem (used in arguments like that in (Maggi (2012), Lemma 29.14) and deal with the two constraints one at a time.
The fact that minimizers solve a penalized minimum problem, together with the Lipschitz continuity of the nonlocal energy, immediately implies (see Proposition 4.3) that every solution u to (1.2) is a quasi-minimizer of the surface energy \({\overline{{\mathscr {G}}}}\), in the sense that there exists \(\Lambda >0\) such that
for all admissible competitors v. Notice that in this formulation, admissible competitors do not have to obey the mass constraints, but they still have to satisfy the graph constraint, and thus the regularity of quasi-minimizers does not follow directly from classical results. We denote by \({\mathcal {A}}_{\Lambda ,M}\) the class of quasi-minimizers satisfying the inequality (1.3) and with total mass M, see Definition 4.1. By using (1.3) we then show that \(h_u\) is bounded, see Proposition 4.4.
The next main result, which is proved in Sect. 4.2 through a series of propositions, concerns the regularity of quasi-minimizers in dimension \(n=2\). In view of the previous discussion, it applies in particular to any solution of the minimum problem (1.2).
Theorem 1.1
(Partial regularity in dimension \(n=2\)) Assume that \(n=2\), and that the surface tension coefficients satisfy the strict triangle inequalities
Let \(u\in {\mathcal {A}}_{\Lambda ,M}\) be a quasi-minimizer, according to Definition 4.1. Then, the followings hold.
-
(i)
(Infiltration) There exists \(\varepsilon _0>0\) (depending only on M, \(\Lambda \), and the surface energy coefficients) such that, for any square \({\mathcal {Q}}_r(z_0)\) centered at \(z_0\in \mathbb R^n\) with side length \(r\in (0,1)\), the following implications hold:
$$\begin{aligned} |V_u\cap {\mathcal {Q}}_r(z_0)| < \varepsilon _0 r^2 \quad \quad \Rightarrow \quad \quad |V_u\cap {\mathcal {Q}}_{\frac{r}{2}}(z_0)| = 0, \end{aligned}$$and, if \({\mathcal {Q}}_r(z_0)\) does not intersect the substrate,
$$\begin{aligned} |(A_u\cup B_u) \cap {\mathcal {Q}}_r(z_0)| < \varepsilon _0 r^2 \quad \quad \Rightarrow \quad \quad |(A_u\cup B_u) \cap {\mathcal {Q}}_{\frac{r}{2}}(z_0)| = 0. \end{aligned}$$ -
(ii)
(Lipschitz regularity of the graph) There exists a finite set \(\Sigma \), containing the jump points of \(h_u\), such that \(h_u\) is locally Lipschitz outside \(\Sigma \).
-
(iii)
(Singular set) At the upper end of a jump point of \(h_u\), the graph has a vertical tangent. At the points of \(\Sigma \) that are not jump points of \(h_u\), the left or the right derivative of \(h_u\) is infinite. The graph of \(h_u\) does not contain interior or exterior cusps.
-
(iv)
(Internal regularity of \(\Gamma ^{AB}_u\)) For every \(\alpha \in (0,1/2)\) the interface \(\partial A\cap \partial B\) is a locally a \(C^{1,\alpha }\)-curve in \(\{(x,y)\in \mathbb R^2: 0<y<h_u(x)\}\).
-
(v)
(\(C^{1,\alpha }\)-regularity of the graph) If \(x_0\notin \Sigma \) is such that \((x_0,h_u(x_0))\in \partial ^*A\cup \partial ^*B\), then \(h_u\) is of class \(C^{1,\alpha }\) in a neighborhood of \(x_0\), for every \(\alpha \in (0,1/2)\).
Conditions (1.4) are known to be needed in order to get regularity for minimizing clusters (see Leonardi 2001; White 1996). Indeed, consider the simple case of a flat interface between the phase A and the void V: if for instance one had \(\sigma _{A}=\sigma _{B}+\sigma _{AB}\), then it would be energetically equivalent to insert a thin layer of the phase B between A and V, in such a way that these two phases do not touch anymore. In other words, the strict triangular inequalities are natural conditions to prevent small infiltrations between pair of phases.
The elimination property is well known in the case of minimal clusters (see Leonardi 2001). The idea of the proof is to construct a suitable competitor by filling the minority phase in \({\mathcal {Q}}_r(z_0)\) with one of the other phases. Again, in our case filling \(A_u\) or \(B_u\) by \(V_u\) might lead to a configuration which violates the graph constraint. Therefore, the proof of the infiltration for \(V_u\) (Proposition 4.5) and for \(A_u\cup B_u\) (Proposition 4.6) uses a two-step strategy: first, we prove the elimination property in a semi-infinite strip, where it is possible to fill \(A_u\cup B_u\) with \(V_u\), without violating the graph constraint; then, we show that a minimal configuration having small volume percentage of the void (or of the subgraph) in a cube must necessarily have a small volume percentage of the same in the semi-infinite strip, so that it is possible to conclude by using the first step.
The proof of the Lipschitz regularity follows an idea by Chambolle and Larsen (2003) (see also Fonseca et al. 2007; Fusco and Morini 2012): we show an interior ball condition (see Proposition 4.8), namely that there exists a uniform radius \(\rho _0>0\) such that, for each z on the graph of \(h_u\), it is possible to find a ball with radius \(\rho _0\) tangent to the graph of \(h_u\) only at the point z and contained in the subgraph of \(h_u\). This property implies (Proposition 4.9) that \(h_u\) has only a finite number of jump points, and that \(h_u\) is locally Lipschitz continuous outside a finite set (where the inner ball is tangent to the graph horizontally).
Since in two dimensions the graph \(h_u\) is closed, for each point z on the internal interface between the two phases it is possible to find a ball centered at z that does not intersect the graph, nor the substrate. Therefore, since internal interfaces do not have any graph constraint to satisfy, their \(C^{1,\alpha }\)-regularity follows from classical results (see Remark 4.11).
Finally, the proof of the \(C^{1,\alpha }\) regularity of the graph (Proposition 4.12) is also based on an elimination property for the two sets \(A_u\), \(B_u\) separately. To obtain this, we observe that thanks to the Lipschitz regularity of \(h_u\), for every point \((x_0,h_u(x_0))\in \partial ^*A\cup \partial ^*B\) with \(x_0\not \in \Sigma \) we can find a rectangle such that the graph of \(h_u\) does not intersect its upper and lower sides. This property allows to perform a local perturbation which preserves the graph constraint.
1.3 Application to Thin Films of Diblock Copolymers
We now discuss a possible application of the variational model considered here for the description of the morphology of optimal or equilibrium configurations of thin films of diblock copolymers under some additional assumptions that will be discussed later.
Block copolymers are an important class of soft materials (see Bates and Fredrickson 1999). They are composed by chemically bonded linear chains of monomers. The competition between the repulsion among different subchains and the entropy cost associated with chain stretching is the mechanism behind the extraordinary self-assembly property of block copolymers, that leads to the creation of fascinating patterns exhibiting interesting periodicity properties (see Thomas et al. 1988).
When block copolymers are constrained in a thin film, the landscape of observed configurations can be significantly different from that of the bulk case, due to the influence of film surfaces and the interactions of the blocks with the interfaces. It is indeed observed that in the vicinity of an external interface the microdomains tend to align parallel to that surface (Fredrickson 1987). As noted in the physical literature, “as film thickness decreases, a regime may be encountered where the constraining effects of both interfaces are felt throughout the film and a transition from the bulk, 3D morphology to a 2D thin film morphology may result” (Radzilowski et al. 1996).
An important distinction must be made between unconfined films supported by a solid, flat substrate, where one interface of the film is free, and confined films, where the copolymers and constrained between two hard walls with a fixed thickness. The behavior in these cases is usually illustrated (see Matsen 1997) by considering symmetric diblock copolymers, where the preferred bulk configuration is lamellar: in this case, the copolymer tends to form multilayered structures of lamellae parallel to the interface, in which each period (L) consists of two monolayers. This induces a quantization of the film thickness, which is forced to be a multiple of the natural spacing of the lamellae \(H\approx \frac{kL}{2}\), with k even if the upper and lower surfaces have an affinity for the same component of the diblock copolymer, and k odd if the two surfaces have opposite affinities. However, when the film thickness H and the natural spacing L are not commensurate, this causes compression of the chain of polymers, namely stress in the film, that in the unconfined case is released by locally modifying the thickness of the profile by forming terraces (see Fig. 2, top-right), islands and holes (see Fig. 2, bottom-left); in the confined case, the frustration is relieved by changing the orientation of the lamellae (see Fig. 2, bottom-right).
Besides lamellar configurations, other structures have been observed for asymmetric block copolymers, like for instance spherical (Yokoyama et al. 2000) or cylindrical (van Dijk and van den Berg 1995) mesophases, which show the same phenomena of thickness quantization or change in orientation of the microdomains. See also (Darling 2007) for a review of the possible phases that have been observed and a discussion of their many applications, and (Huang et al. 2021, Fig. 4) for an illustration of the phase diagram in the case of confined films, showing twenty different morphologies depending on the volume fraction and on the film thickness. The possibility of accessing a larger class of equilibrium configurations has been exploited for many applications (see Segalman 2005), ranging from lithography to mass transport. Patterns in thin films of block copolymers have been investigated numerically (see, for instance, Hill and Millett 2017; Lyakhova et al. 2006; Matsen 1997, 1998; Parsons et al. 2017; Stasiak et al. 2012).
Mathematical models aimed at describing the behavior of block copolymers from physics and chemistry can be roughly divided into two categories: (self-consistent) mean fields models (see, for instance, Matsen and Bates 1996; Matsen and Schick 1994) and density functional theory models. A celebrated mean field model for block copolymers was derived by Ohta and Kawasaki in (Ohta and Kawasaki 1986) for the case of diblock copolymers (two monomers) in the strong segregation regime by using several approximations (infinite temperature and thermodynamic limit). It has successfully been used to derive qualitative properties related to both the dynamics and the statics of diblock copolymers. In mathematical terms, the Ohta–Kawasaki is a phase-field model given by the sum of a Cahn–Hilliard-type functional (replaced by a perimeter term in the sharp-interface version) and a nonlocal interaction term. By using a notation similar to the one implemented above, such an energy can be written in the form
where the first term models the short-range interaction between different monomers, related to the surface energy of the interfaces dividing the regions of high concentration of the two monomer species, while the second represents their long-range interaction. The emergence of highly nontrivial pattern configurations at a mesoscopic scale is precisely due to the competition between these two kinds of energies.
The model considered in this paper can be viewed as a variant of the Ohta–Kawasaki model suitable to describe thin films of diblock copolymers in the unconfined case. The two regions \(A_u\), \(B_u\) of an admissible configuration u represent the two phases of the diblock copolymers, and are confined by a solid, flat substrate on the bottom side, while the upper surface is exposed. As a volume-order term \({\mathcal {N}}(u)\) in the total energy, we consider a long-range interaction responsible for the repulsion force between different monomers, and thus acting only on the two sets \(A_u\) and \(B_u\)—see Example 2.3 for the precise definition of \({\mathcal {N}}(u)\). The region above the film (which could be void, air, or a liquid solvent) is modeled as a homopolymer, in the framework of the density functional theory for blends of diblock copolymers with homopolymers derived by Choksi and Ren (2005) (see also Bonacini and Knüpfer 2016; van Gennip and Peletier 2008, 2009 for related studies in the mathematical literature), and it only interacts with the diblock copolymer via the surface energies.
As it can be seen by looking at the Ohta–Kawasaki energy (1.5), surface effects with the exterior are usually neglected in models for block copolymers in the bulk, since they are of several orders of magnitude lower than the other effects considered. When confined in thin films, though, the surface interactions of the two phases with the substrate and with the air (i.e., the additional terms in the energy \({\mathscr {F}}\) compared with (1.5)) become important. This is how, at least heuristically, the change in the energy landscape is justified in the physics literature. Under the additional assumption that the configurations of interest can be described by a graph over the substrate, the model considered in this paper could be of help in the study of such a class of equilibrium stable configurations of block copolymers confined in thin films. We would like to thank the anonymous referees for pointing out that this latter additional assumption is not easily justified from the physical point of view. Indeed, despite the fact that in the physical literature authors refer to the thickness of the film, this does not exclude the possibility of having a film with holes, or arranging with tubes that violate the graph constrain. We were not able to find any paper, either in the physical or in the experimental literature that clearly disregard such possibility.
Finally, we would like to point out that our model is not a dimension reduction model, like that investigated in De Simone et al. (2002).
1.4 Remarks
We conclude this introduction with a few more remarks. The extension to the case of more than two phases is relatively straightforward and the arguments presented here can be directly generalized, at the price of a more demanding notation and of a larger number of different cases to be taken into consideration. It could also be possible to extend our results to different kinds of boundary conditions, or if surface interactions with horizontal walls are presents.
The proofs of the results in this paper follow several well-known arguments used to treat similar problems and most of the techniques are fairly standard. However, the implementation of such ideas in our context, where the graph constraint is in force, poses several additional challenges, mainly due to the need of adapting, and in some cases significantly modifying, the construction of suitable competitors. This is particularly relevant for the construction of a recovery sequence (Proposition 3.8), the local deformation map used in the proof of the penalization argument (Lemma 4.2), and the elimination-type properties (Proposition 4.5 and Proposition 4.12).
The generalization to higher dimensions of the two-dimensional regularity theory for quasi-minimal partitions subject to a graph constraint, developed in Sect. 4.2, is not straightforward and would require new ideas: while we believe that the elimination property might be obtained by refined but similar arguments, the inner ball condition leading to the Lipschitz regularity of the graph is a purely two-dimensional strategy.
Future directions of investigation are the following: firstly, as discussed above, the extension of the regularity results to higher dimensions (in particular in the physical dimension three), and the investigation of finer regularity properties in two dimension; secondly, a description of optimal configurations by means of the Euler–Lagrange equations satisfied by a minimizer, which involve an interplay between the curvature and the nonlocal potential on the regular parts of the interfaces; thirdly, an analysis of the possible singularities (jump points, points where three different interfaces meet, and points where an interface meets the substrate), in particular by deriving rigorously Young’s law for the triple points. Finally, an ambitious task would be to study specific configurations (for instance lamellar patterns with terrace formations) and investigate their stability properties, possibly by means of second variation arguments.
Structure of the paper. The paper is organized as follows. In Sect. 2, we introduce the main notation, the class of admissible configurations and the total energy of the system. In Sect. 3, we compute the relaxation of the energy (Theorem 3.1) and we use this result to prove the existence of minimizing configurations (Theorem 3.5). In Sect. 4, we first show that solutions to the minimum problem (1.2) are quasi-minimizers of the surface energy under a graph constraint (Sect. 4.1), and then we prove Theorem 1.1 on the regularity of quasi-minimizers in dimension two (Sect. 4.2).
2 The Model
2.1 Notation for Functions of Bounded Variation and Perimeters
The profile of the film will be modeled by the (generalized) graph of a periodic function with finite total variation in \((0,L)^{n-1}\) (\(n\ge 2\)), where \(L>0\) is a fixed parameter, and its subgraph will represent the reference configuration of the film. We therefore firstly recall a few notions from the theory of BV-functions (see Ambrosio et al. 2000), in order to fix the notation used in the paper. Given \(h\in L^1_{{{\,\mathrm{loc}\,}}}(\Omega )\), where \(\Omega \subset \mathbb R^{m}\) is an open set (\(m\ge 1\)), its total variation is defined as
and this quantity is finite if and only if the distributional derivative Dh of h is a bounded Radon measure on \(\Omega \). We let \(\mathrm{BV}(\Omega ) :=\{ h\in L^1(\Omega ) \,:\, |Dh|(\Omega )<\infty \}\). If \(h\in \mathrm{BV}(\Omega )\), at each point \(x\in \Omega \) the approximate upper and lower limits
are well defined, where \({\mathscr {L}}^m\) is the m-dimensional Lebesgue measure, \(B_\rho (x)\subset \mathbb R^m\) is the ball centered at x with radius \(\rho \), and \(\omega _m={\mathscr {L}}^m(B_1(0))\). The jump set of h is then defined as the set
and it is well known that \(J_h\) is a \(({\mathcal {H}}^{m-1},m-1)\) rectifiable set, with normal \(\nu _h(x)\) at \({\mathcal {H}}^{m-1}\)-a.e. point \(x\in J_h\).
We also recall that a set \(E\subset \Omega \) has finite perimeter in \(\Omega \) if \(|D\chi _E|(\Omega )<\infty \), where \(\chi _E(x)=1\) if \(x\in E\), \(\chi _E(x)=0\) if \(x\notin E\); the perimeter of E in \(\Omega \) is then defined as
We introduce the essential boundary of E
where, for \(t\in [0,1]\), \(E^t\) denotes the set of points where E has Lebesgue density t. Another relevant subset of the boundary of a set of finite perimeter is the reduced boundary \(\partial ^*E\) (see Ambrosio et al. 2000). At every point of the reduced boundary the measure-theoretic outer normal \(\nu _E\) is defined, the Lebesgue density of E is equal to 1/2, and it is well known that \(\partial _eE\) coincides with \(\partial ^*E\) up to a \({\mathcal {H}}^{m-1}\)-negligible set. We finally recall that a Caccioppoli partition of \(\Omega \) is a finite partition \(\{E_i\}_{i\in \{1,\ldots ,N\}}\) of \(\Omega \), \(N\in \mathbb N\), such that \(\sum _{i=1}^N{\mathscr {P}}(E_i;\Omega )<+\infty \). For a Caccioppoli partition \(\{E_i\}_{i}\), \({\mathcal {H}}^{m-1}\)-a.e. point of \(\Omega \) belongs to one of the sets \((E_i)^1\) or to one of the intersections \(\partial ^*E_i\cap \partial ^*E_j\) (\(i\ne j\)).
2.2 Admissible Configurations
We now describe the class of admissible configurations. Throughout the paper, we will denote by \(x=(x',x_n)\) the generic point in \(\mathbb R^n\equiv \mathbb R^{n-1}\times \mathbb R\), and by \(\mathbb R^n_+:=\mathbb R^{n-1}\times [0,\infty )\). The canonical basis of \(\mathbb R^{n}\) will be denoted by \((e_1,\ldots ,e_{n})\), and the Lebesgue measure on \(\mathbb R^n\) by \(|\cdot |:={\mathscr {L}}^n(\cdot )\). Given \(L>0\), we also set
We assume that the substrate occupies the infinite region
We introduce the class of admissible profiles
The reference configuration of the film is represented by the subgraph of an admissible profile \(h\in {\mathcal{AP}\mathcal{}}(Q_L)\): we denote it and its periodic extension by
respectively. Notice that, as h has finite total variation, the set \(\Omega _h\) has finite perimeter. We also define, for \(h\in {\mathcal{AP}\mathcal{}}(Q_L)\), the free profile
and we denote by \(\Gamma _h^\#\) its periodic extension. Notice that if \(0<x_n<h^-(x')\) then \(x\in (\Omega _h^\#)^1\), while if \(x_n>h^+(x')\) then \(x\in (\Omega _h^\#)^0\); therefore \(\partial _e(\Omega _h^\#\cup S)\) is a subset of \(\Gamma _h^\#\) (and coincides with \(\Gamma _h^\#\) up to a \({\mathcal {H}}^{n-1}\)-negligible set).
The region \(\Omega _h\) occupied by the film is partitioned into two disjoint sets of finite perimeter A, B representing the two phases of the system. We identify these two phases with the level sets of a marker function \(u:\Omega _h\rightarrow \{\pm 1\}\) with bounded variation, so that \(A=\{u=1\}\) and \(B=\{u=-1\}\). As \(\Omega _h\) is in general not an open set, it will be convenient to consider u as a piecewise constant function defined in the full space \(\mathbb R^n\), taking two additional values \(u=0\) and \(u=2\) in the region above the film and in the substrate, respectively. This is made precise by the following definition.
Definition 2.1
(Admissible configurations) Let \(I:=\{\pm 1,0,2\}\). The class \({\mathcal {X}}\) of admissible configurations is the space of functions \(u:\mathbb R^n\rightarrow I\) satisfying the following properties:
-
(i)
\(u\in \mathrm{BV}_{{{\,\mathrm{loc}\,}}}(\mathbb R^n;I)\),
-
(ii)
\(u(x'+Le_i,x_n)=u(x',x_n)\) for all \((x',x_n)\in \mathbb R^n\), \(i=1,\ldots ,n-1\),
-
(iii)
there exists \(h_u\in {\mathcal{AP}\mathcal{}}(Q_L)\) such that \(\Omega _{h_u}^\#=\{u=1\}\cup \{u=-1\}\),
-
(iv)
\(S=\{u=2\}\), where S is the substrate defined in (2.6)
(the previous identities have to be understood in the almost everywhere sense with respect to \({\mathscr {L}}^n\)). The class of regular admissible configurations is defined as
We consider the space \({\mathcal {X}}\) endowed with the \(L^1\)-convergence: we say that a sequence \(\{u_k\}_{k\in \mathbb N}\subset {\mathcal {X}}\) converges in \({\mathcal {X}}\) to \(u\in {\mathcal {X}}\) if \(u_k\rightarrow u\) in \(L^1(Q_L^+)\).
Given an admissible configuration \(u\in {\mathcal {X}}\), we have a partition of the strip \(Q_L^+\) into three sets of finite perimeter, which will be denoted by
and as usual we will denote by \(A_u^\#\), \(B_u^\#\) and \(V_u^\#\) their periodic extensions. Notice that \(A_u\cup B_u=\Omega _{h_u}\) and \(\partial ^*V_u^\#=\Gamma _{h_u}^\#\) (up to a \({\mathcal H}^{n-1}\)-negligible set). In other words, the admissible configurations are just periodic partitions of the upper half-space into three sets of locally finite perimeter A, B, V, with the constraint that \(A\cup B\) is the subgraph of a \(\mathrm{BV}\)-function. The jump set \(J_u\) of u coincides (up to a \({\mathcal H}^{n-1}\)-negligible set) with the union of their reduced boundaries:
with \((u^+(x),u^-(x)) = (i,j)\) (up to a permutation) for every \(x\in \partial ^*\{u=i\}\cap \partial ^*\{u=j\}\).
As we want to consider different values of the surface tension for all the possible different interfaces between the phases, it is convenient to introduce the following notation (see Fig. 1):
and
The set \(S^V_u\) represents the possible region in which the substrate is exposed. In view of (2.12), the disjoint union of these interfaces coincides with the jump set \(J_u\) of u inside the periodicity strip:
with \({\mathcal H}^{n-1}(N)=0\).
2.3 The Energy of Regular Configurations
We now introduce the energy associated with a regular configuration \(u\in {\mathcal {X}_{\mathrm {reg}}}\). This energy will be extended to the whole space \({\mathcal {X}}\) of admissible configurations in Sect. 3 via a relaxation procedure. The total energy is the sum of a surface penalization of the interfaces between the phases, with possibly different surface tension coefficients, and a general volume-order, possibly nonlocal, energy \({\mathcal {N}}(u)\). Here and the rest of the paper we will always assume that \({\mathcal {N}}:{\mathcal {X}}\rightarrow [0,+\infty )\) is a given function satisfying the following property: given a positive constant \(M>0\), there exists \(L_{{\mathcal {N}}}\in (0,+\infty )\), depending on M, such that for all \(u,v\in {\mathcal {X}}\) with \(|\Omega _{h_u}|,|\Omega _{h_v}|\le M\) it holds
Under the previous assumption, we can define the energy of a regular configuration as follows.
Definition 2.2
(Energy) Given positive coefficients \(\sigma _A, \sigma _B, \sigma _{AB}, \sigma _{AS}, \sigma _{BS}, \sigma _S,\gamma >0\), we define the total energy of a regular configuration \(u\in {\mathcal {X}_{\mathrm {reg}}}\) as
By introducing the surface energy density
with \(\Psi (i,j)=\Psi (j,i)\), we can write in a more compact notation an equivalent representation of the energy in terms of the jump set of the piecewise constant function u (see (2.15)):
Example 2.3
(Thin films of diblock copolymer) As discussed in the Introduction, a possible application of the variational model introduced above is in the description of thin films of diblock copolymers. In this case, the sets \(A_u\) and \(B_u\) associated with an admissible configuration \(u\in {\mathcal {X}}\) represent the two phases occupied by the diblock copolymer, and \(V_u\) represents the void (or homopolymer) above the film.
Following (Choksi and Ren 2005) and modeling the phase \(V_u\) as a homopolymer, one can introduce a nonlocal interaction energy \({\mathcal {N}}(u)\) between the two phases \(A_u\), \(B_u\) as follows. For \(u\in {\mathcal {X}}\) we let \({\bar{u}}:=\int _{Q_L^+}u(x)\,\mathrm {d}x= |A_u|-|B_u|\), and we define
where the potential \(\phi _u:Q^+_L\rightarrow \mathbb R\) associated to the configuration \(u\in {\mathcal {X}}\) is the solution to
with periodic boundary conditions on the lateral boundary \(\partial Q_L\times (0,+\infty )\) and zero Neumann boundary condition at the interface \(Q_L\times \{0\}\) with the substrate. By arguing as in (Acerbi et al. (2013), Lemma 2.6), one can check that \({\mathcal {N}}(u)\) obeys the assumption (2.16).
3 Relaxation and Existence of Minimizers
The goal of this section is to compute the lower semicontinuous envelope \({\overline{\mathscr {F}}}\) of the functional \({\mathscr {F}}\) with respect to the convergence in \({\mathcal {X}}\), under a volume constraint: for every \(u\in {\mathcal {X}}\)
In the following theorem, which is proved in Sects. 3.1 and 3.2, we give a representation formula for the relaxed functional \({\overline{\mathscr {F}}}\).
Theorem 3.1
(Relaxation) Assume that \(\sigma _{AB}\le \sigma _A+\sigma _B\). Then, the functional \({\overline{\mathscr {F}}}\), defined in (3.1), is given by
for all \(u\in {\mathcal {X}}\), where
and \({\overline{\Psi }}(i,j)={\overline{\Psi }}(j,i)\).
Remark 3.2
From the proof of Theorem 3.1, it also follows that the representation formula (3.2) continues to hold if we drop the mass constraints in the definition (3.1) of \({\overline{\mathscr {F}}}\).
Remark 3.3
The assumption \(\sigma _{AB}\le \sigma _A+\sigma _B\) prevents the possibility of reducing the energy by inserting of a thin layer of void between the phases A and B. In the diblock copolymer application, this is justified by the fact that the subchains of type A and B are chemically bonded together. In case the opposite inequality holds, the relaxed functional would have a different surface tension (\(\sigma _A+\sigma _B\)) only for the vertical interfaces of \(\Gamma ^{AB}\) connected to the graph.
Remark 3.4
The choice of the \(L^1\) topology is justified by the fact that, in the application we have in mind, we do not consider elastic effects, that would lead to cracks inside the copolymer phases. In case these effects have to be taken into account, a natural topology would be the Hausdorff convergence of the epigraph of the profile, as in Bonnetier and Chambolle (2002), Fonseca et al. (2007); the corresponding relaxed functional would contain additional terms accounting for vertical cracks, connected to the free profile of the film, inside the two phases.
The existence of minimizers of the relaxed functional \({\overline{\mathscr {F}}}\) follows by a standard application of the direct method of the Calculus of Variations. We fix two positive real numbers \(M>0\) and \(m\in (0,M)\), which represent the total volume of the film and the volume of the phase A, respectively.
Theorem 3.5
Existence of minimizers Under the assumptions of Theorem 3.1, the constrained minimization problem
admits a solution. Furthermore, if \({\bar{u}}\in {\mathcal {X}}\) is a solution of the above problem, then
The remaining part of this section is devoted to the proof of Theorem 3.1. Since by assumption (2.16) the term \({\mathcal {N}}\) in the energy is continuous with respect to the convergence in \({\mathcal {X}}\), it is sufficient to compute the relaxation of the surface energy. This is proved, as usual, in two steps: denoting by \({\mathcal {F}}\) the right-hand side of (3.2), in the first step (Proposition 3.7) it is shown that the energy \({\mathcal {F}}(u)\) is smaller than the liminf of the energies of every sequence approximating u; in the second step (Proposition 3.8), we prove the sharpness of the lower bound, constructing a recovery sequence made of regular configurations.
3.1 Lower Semicontinuity
The lower semicontinuity of the interface part of the energy (3.2) follows essentially from the same type of arguments as in Ambrosio and Braides (1990). It is indeed well known (see also White 1996) that, for an isotropic surface energy defined on Caccioppoli partitions of a domain \(\Omega \), where each interface has a cost proportional to its area, the validity of the triangle inequalities between the surface tensions is a necessary and sufficient condition for the lower semicontinuity of the functional. However, in our case we do not deal with generic Caccioppoli partitions, but we have a geometric restriction on the admissible configurations; this is reflected in the fact that the surface tension coefficients \({\overline{\Psi }}(i,j)\) do not satisfy all the possible triangle inequalities, but only those corresponding to actual configurations of the system. For this reason, we cannot directly deduce the lower semicontinuity from Ambrosio and Braides (1990), but the proof is based on the same type of arguments and we will only sketch the main ideas. The main tool is the following lower semicontinuity lemma, whose proof follows easily by adapting the ideas in (Morgan (1997), Proposition 3.1).
Lemma 3.6
Let \(F^1,F^2\subset B_1\) be disjoint sets of finite perimeter with \(F^1\cup F^2 = B_1\), and let \(m>2\). Suppose that, for \(i,j\in \{1,\ldots ,m\}\), \(\lambda _{ij}=\lambda _{ji}\) are nonnegative coefficients such that
For every \(k\in \mathbb N\) let \((F^1_k,F^2_k,\ldots ,F^m_k)\) be a Caccioppoli partition of \(B_1\) into m sets, such that \(F^1_k\rightarrow F^1\), \(F^2_k\rightarrow F^2\), and \(F^i_k\rightarrow \emptyset \) in \(L^1(B_1)\), \(i=3,\ldots ,m\), as \(k\rightarrow \infty \). Then,
Proposition 3.7
Denote by \({\mathcal {F}}\) the right-hand side of (3.2). For every \(u\in {\mathcal {X}}\) and for every sequence \(\{u_j\}_{j\in \mathbb N}\subset {\mathcal {X}_{\mathrm {reg}}}\) such that \(u_j\rightarrow u\) in \({\mathcal {X}}\) there holds
Proof
As already observed, it is sufficient to consider the surface part of the energy, as \({\mathcal {N}}(u)\) is continuous with respect to the convergence in \({\mathcal {X}}\). Without loss of generality we can assume that the sequence \({\mathscr {F}}(u_j)\) is bounded and that the measures  locally weakly* converge in \(\mathbb R^n\) to a positive Radon measure \(\mu \). We need to show that
locally weakly* converge in \(\mathbb R^n\) to a positive Radon measure \(\mu \). We need to show that  . By (Ambrosio et al. (2000), Theorem 2.56) it is sufficient to show that
. By (Ambrosio et al. (2000), Theorem 2.56) it is sufficient to show that
This can be proved by a standard blow-up argument: for fixed \(x\in J_u\), for a suitable sequence \(\rho _k\rightarrow 0^+\) and for a suitable subsequence, we have that the rescaled functions \(v_k(y):=u_{j_k}(x+\rho _k y)\) converge in \(L^1(B_1)\) as \(k\rightarrow \infty \) to the function
and \(\limsup _{\rho \rightarrow 0^+}\frac{\mu (B_\rho (x))}{\omega _{n-1}\rho ^{n-1}} \ge \liminf _{k\rightarrow \infty } \frac{1}{\omega _{n-1}}\int _{B_1\cap J_{v_k}} \Psi (v_k^+,v_k^-)\,\mathrm {d}{\mathcal H}^{n-1}\), so that the claim (3.8) will follow once we prove that
In view of (2.15), in order to show (3.8) we now have to distinguish among six possible cases, depending on which interface contains the point x.
Case 1: \(x\in \Gamma ^A_u\). In this case, in the blow-up limit we have that half of the ball \(B_1\) is filled with the pure phase \(A_u\), and the other half-ball is filled with the phase \(V_u\); that is, up to a permutation \(w^+=1\), \(w^-=0\). Notice that \(x_n>0\) and therefore for k large enough the ball \(B_{\rho _k}(x)\) does not intersect the substrate and can contain only the phases A, B, and V; hence, the rescaled functions \(v_k\) can only take the values \(\{\pm 1,0\}\) in \(B_1\), that is, \(v_k^\pm \in \{\pm 1,0\}\). Since by definition of \({\overline{\Psi }}\) the triangle inequality \({\overline{\Psi }}(1,0)\le {\overline{\Psi }}(1,-1)+{\overline{\Psi }}(-1,0)\) holds and \({\overline{\Psi }}\le \Psi \), the claim (3.9) follows from Lemma 3.6, applied to \(F^1:=\{w=1\}\), \(F^2:=\{w=0\}\), \(F^1_k:=\{v_k=1\}\rightarrow F^1\), \(F^2_k:=\{v_k=0\}\rightarrow F^2\), \(F^3_k:=\{v_k=-1\}\rightarrow \emptyset \).
Case 2: \(x\in \Gamma ^B_u\). This is analogous to the previous case.
Case 3: \(x\in \Gamma ^{AB}_u\). In this case \(w^+=1\), \(w^-=-1\), and since \(B_{\rho _k}(x)\) does not intersect the substrate for k large enough, we have \(v_k^\pm \in \{\pm 1,0\}\). Then, (3.9) follows again by Lemma 3.6 in view of the triangle inequality \({\overline{\Psi }}(1,-1)\le {\overline{\Psi }}(1,0)+{\overline{\Psi }}(-1,0)\), which holds by definition of \({\overline{\Psi }}\) and by the assumption \(\sigma _{AB}\le \sigma _A+\sigma _B\).
Case 4: \(x\in S^A_u\). In this case \(w^+=1\), \(w^-=2\). In principle, all the four phases can be present in a neighborhood of the point x; however, by the geometric constraint the limit interface between the phase A and the substrate S cannot be approximated by the boundary of V. Therefore, in order to apply Lemma 3.6, we first need to get rid of the possible infiltration of the phase V.
We denote by \(A_k:=\{v_k=1\}\), \(B_k:=\{v_k=-1\}\), \(V_k:=\{v_k=0\}\) the phases of \(v_k\) in the upper half-ball \(B_1^+\), and the corresponding interfaces by
Then, we modify \(v_k\) by “filling” the region \(V_k\) with either \(A_k\) or \(B_k\), according to the following rule:
Notice that \({\tilde{v}}_k\rightarrow w\) in \(L^1(B_1)\), and that the partition of the unit ball determined by \({\tilde{v}}_k\) does not contain the phase V. Therefore, using the inequality \(\Psi (1,0)+\Psi (-1,0)\ge \Psi (-1,1)\),
By observing that \({\mathcal H}^{n-1}(S^V_k)\rightarrow 0\) as \(k\rightarrow \infty \), from the previous inequality we obtain
To deduce (3.9) we can now apply Lemma 3.6 to the partition of \(B_1\) determined by \({\tilde{v}}_k\), which contains only the three phases A, B, S and that converges to the configuration where the upper half-ball is filled by A, and the lower half-ball is filled by S. Therefore to apply Lemma 3.6 one only needs to check the triangle inequality \({\overline{\Psi }}(1,2)\le {\overline{\Psi }}(1,-1)+{\overline{\Psi }}(-1,2)\), which holds by definition of \({\overline{\Psi }}\).
Case 5: \(x\in S^B_u\). This is analogous to Case 4, with the roles of phases A and B exchanged.
Case 6: \(x\in S^V_u\). In this case \(w^+=0\), \(w^-=2\), and all the four phases can be present in a neighborhood of the point x. We deduce (3.9) by applying once more Lemma 3.6, since that all the possible triangle inequalities (3.6) hold for \(\lambda _{12}={\overline{\Psi }}(0,2)\) in view of the definition of \({\overline{\Psi }}\). \(\square \)
3.2 Recovery Sequence
The goal of this section is to prove the following result, which combined with Proposition 3.7 completes the proof of Theorem 3.1.
Proposition 3.8
Denote by \({\mathcal {F}}\) the right-hand side of (3.2). For every \(u\in {\mathcal {X}}\) there exists a sequence \(\{u_j\}_{j\in \mathbb N}\subset {\mathcal {X}_{\mathrm {reg}}}\) such that \(u_j\rightarrow u\) in \({\mathcal {X}}\), \(|A_{u_j}|=|A_u|\), \(|B_{u_j}|=|B_u|\), and
Proof
Fix \(u\in {\mathcal {X}}\) and let \(h_u\in {\mathcal{AP}\mathcal{}}(Q_L)\) be the corresponding admissible profile. The proof is divided into several steps (see Fig. 3 for the modifications performed in Step 2, 3, and 4).
Step 1: approximation of \(h_u\) with a regular profile. In this step, we construct a sequence \({\widetilde{u}}_j\in {\mathcal {X}}\) such that \({\widetilde{u}}_j\rightarrow u\) in \({\mathcal {X}}\) and \({\mathcal {F}}({\widetilde{u}}_j)\rightarrow {\mathcal {F}}(u)\), with the additional property that the corresponding profiles \(h_{{\widetilde{u}}_j}\) are smooth. By a diagonal argument, this will allow us, in the following steps, to work under the assumption that the limiting profile is smooth, and to construct a recovery sequence only in this case.
For each \(j\in \mathbb N\) it is possible to find a \(Q_L\)-periodic function \(f_j \in C^\infty (\mathbb R^{n-1})\) such that
and
The proof of the first two statements is contained in Step 1 of the proof of (Chambolle and Solci (2007), Proposition 4.1), while the last statement is proved in (Chambolle and Solci (2007), Remark 4.4). Define the function \({\widetilde{u}}_j: \mathbb R^n \rightarrow \{0,-1,1,2\}\) as
This modification amounts to fill the (small) region in \(\Omega _{f_j}\backslash \Omega _{h_u}\) by the phase A, and to remove the possible parts of the phases A and B outside \(\Omega _{f_j}\) by replacing them with V. Notice that \({\widetilde{u}}_j\in {\mathcal {X}_{\mathrm {reg}}}\) with \(f_j=h_{{\widetilde{u}}_j}\) and
First, we show that
Define the Radon measures \(\mu ^A:=D\chi _{A_u^\#}\), \(\mu ^B:=D\chi _{B_u^\#}\), and, for \(j\in \mathbb N\), define \(\mu ^A_j:=D\chi _{A_{{\widetilde{u}}_j}^\#}\) and \(\mu ^B_j:=D\chi _{B_{{\widetilde{u}}_j}^\#}\). Then, (3.12) and (3.13) yield
and, since \(A_{{\widetilde{u}}_j}\rightarrow A_u\), \(B_{{\widetilde{u}}_j}\rightarrow B_u\), using also the periodicity,
Combining the previous estimates we obtain (3.16) from
where last step follows by (3.11). Next, we claim that
and that
Using (3.16), (3.17), and (3.18), we have
hence
Denote now, for \(\varepsilon >0\), \(Q^\varepsilon :=Q_L\times (\varepsilon ,+\infty )\), and notice that for \({\mathscr {L}}^1\)-almost every \(\varepsilon >0\) we have \({\mathcal H}^{n-1}(J_u\cap \{x_n=\varepsilon \})=0\). For all such \(\varepsilon \), thanks to (3.17) and to (3.21) we obtain
and in turn, arguing as in the proof of (3.16), \({\mathcal H}^{n-1}(\Gamma ^{AB}_{{\widetilde{u}}_j}\cap Q^\varepsilon ) \rightarrow {\mathcal H}^{n-1}(\Gamma ^{AB}_u\cap Q^\varepsilon ).\) Then, for almost every \(\varepsilon >0\)
and similarly \({\mathcal H}^{n-1}(\Gamma ^B_{{\widetilde{u}}_j}\cap Q^\varepsilon )\rightarrow {\mathcal H}^{n-1}(\Gamma ^B_u\cap Q^\varepsilon )\). From these two convergences, (3.19) follows: indeed, if (3.19) fails then for some \(\eta >0\) we would have (using the fact that \({\mathcal H}^{n-1}(\Gamma ^A_{{\widetilde{u}}_j}\cup \Gamma ^B_{{\widetilde{u}}_j})\rightarrow {\mathcal H}^{n-1}(\Gamma ^A_u\cup \Gamma ^B_u)\))
(or the symmetric inequalities with A and B exchanged). This yields
which is a contradiction since \({\mathcal H}^{n-1}(\Gamma ^B_u\backslash Q^\varepsilon )\rightarrow 0\) as \(\varepsilon \rightarrow 0\). This proves (3.19). Finally, by writing
(and similarly for B), we conclude that also (3.20) holds by using (3.16), (3.19), and (3.21).
Thanks to (3.15), (3.16), (3.19), and (3.20) we obtain \({\mathcal {F}}({\widetilde{u}}_j)\rightarrow {\mathcal {F}}(u)\), as desired.
Step 2: the non-exposed substrate. Assume \(v\in {\mathcal {X}_{\mathrm {reg}}}\). We construct a sequence \(\{v_j\}_{j\in \mathbb N}\subset {\mathcal {X}_{\mathrm {reg}}}\) such that
that allows to recover the relaxed coefficients \({\overline{\Psi }}(1,2)\) and \({\overline{\Psi }}(-1,2)\) with the non-exposed substrate in the limit energy, in the sense that
In the case where \(\sigma _{AS}\le \sigma _{BS}+\sigma _{AB}\) and \(\sigma _{BS}\le \sigma _{AS}+\sigma _{AB}\), the relaxed surface tensions \({\overline{\Psi }}(1,2)\) and \({\overline{\Psi }}(-1,2)\) coincide with the original ones \(\Psi (1,2)\) and \(\Psi (-1,2)\); in this case there is nothing to do, and we just take \(v_j:=v\) for each \(j\in \mathbb N\). Assume instead
The only other possible case is \(\sigma _{BS}+\sigma _{AB}<\sigma _{AS}\) and \(\sigma _{BS}\le \sigma _{AS}+\sigma _{AB}\), that can be treated similarly. We need to build a sequence \(\{v_j\}_{j\in \mathbb N}\) satisfying (3.22) and (3.23), which in this case becomes
By standard results on traces of \(\mathrm{BV}\)-functions (for instance, combining Eq. (2.8) and Theorem 2.11 in Giusti (1984)), it is possible to find a sequence \(\{s_j\}_{j\in \mathbb N}\) with \(s_j\rightarrow 0^+\) as \(j\rightarrow \infty \) such that
and since \({\mathcal H}^{n-1}(J_v\cap \{x_n=t\})=0\) for \({\mathscr {L}}^1\)-a.e. t we can also assume
Also note that, since \({\mathcal H}^{n-1}(J_v)<\infty \),
Define the function \(v_j:\mathbb R^n\rightarrow \{0,-1,1,2\}\) as
which satisfies \(v_j\in {\mathcal {X}_{\mathrm {reg}}}\) for each \(j\in \mathbb N\) (since \(h_{v_j}=h_v\)) and \(\Vert v_j - v \Vert _{L^1(Q_L^+)} \le 2 s_j {\mathscr {L}}^{n-1}(Q_L)\), which gives (3.22). This sequence allows to adjust the surface tensions for the substrate: namely, we have by (3.26)
By passing to the limit as \(j\rightarrow \infty \), the first two terms on the right-hand side vanish thanks to (3.27), the third term tends to \(\sigma _{AB}{\mathcal H}^{n-1}(S^B_v)\) by (3.25), and the last term tends to zero by (3.22). Hence, (3.24) follows.
Step 3: the graph. Let \(v\in {\mathcal {X}_{\mathrm {reg}}}\) and \(\{v_j\}_{j\in \mathbb N}\subset {\mathcal {X}_{\mathrm {reg}}}\) be the sequence constructed in the previous step, satisfying (3.22) and (3.23). We want to modify the sequence in such a way to recover the relaxed surface tensions \({\overline{\Psi }}(1,0)\) and \({\overline{\Psi }}(-1,0)\) between the two phases A, B and the void V: more precisely, we want to construct another sequence \(\{w_j\}_{j\in \mathbb N}\subset {\mathcal {X}_{\mathrm {reg}}}\) such that
and
In the case where \(\sigma _{A}\le \sigma _{B}+\sigma _{AB}\) and \(\sigma _{B}\le \sigma _{A}+\sigma _{AB}\), the relaxed surface tensions \({\overline{\Psi }}(1,0)\) and \({\overline{\Psi }}(-1,0)\) coincide with the original ones \(\Psi (1,0)\) and \(\Psi (-1,0)\); in this case there is nothing to do, and we just take \(w_j:=v_j\) for each \(j\in \mathbb N\). Assume instead
The only other possible case is \(\sigma _B+\sigma _{AB}<\sigma _A\) and \(\sigma _B\le \sigma _A+\sigma _{AB}\), that can be treated similarly. In this case the condition (3.30) becomes
Let \(\delta _j\rightarrow 0^+\) and define, for each \(j\in \mathbb N\), the function \(w_j:\mathbb R^n\rightarrow \{0,-1,1,2\}\) by
Note that \(h_{w_j}=(1+\delta _j)h_{v_j}=(1+\delta _j)h_v\) (recalling that \(h_{v_j}=h_v\) for all j, by the construction in Step 2), therefore \(w_j\in {\mathcal {X}_{\mathrm {reg}}}\) and
which yields (3.29). Moreover, by a Taylor expansion
therefore
We get (3.31) by using (3.29) and recalling that, by the construction in Step 2, we have \({\mathcal H}^{n-1}(\Gamma ^A_{v_j})\rightarrow {\mathcal H}^{n-1}(\Gamma ^A_{v})\) and \({\mathcal H}^{n-1}(\Gamma ^B_{v_j})\rightarrow {\mathcal H}^{n-1}(\Gamma ^B_{v})\).
Step 4: the exposed substrate. Let \(v\in {\mathcal {X}_{\mathrm {reg}}}\) and \(\{w_j\}_{j\in \mathbb N}\subset {\mathcal {X}_{\mathrm {reg}}}\) be the sequence constructed in the previous step. We want to modify again the sequence in such a way to recover the relaxed surface tension \({\overline{\Psi }}(0,2)\) of the exposed substrate, that is the interface between the substrate S and the void V: more precisely, we want to construct another sequence \(\{z_j\}_{j\in \mathbb N}\subset {\mathcal {X}_{\mathrm {reg}}}\) such that
and
In the case where \(\sigma _S\le \min \{ \sigma _{AS}+{\bar{\sigma }}_A, \sigma _{BS}+{\bar{\sigma }}_B \}\) there is nothing to do since \({\overline{\Psi }}(0,2)=\Psi (0,2)\), and thus we define \(z_j:=w_j\) for all \(j\in \mathbb N\). Assume that
In this case (3.34) becomes
Note that the other possible cases can be treated similarly (and even more easily).
We fix two sequences \(s^{(1)}_j, s^{(2)}_j\in (0,1)\), for \(j\in \mathbb N\), with \(s^{(1)}_j < s^{(2)}_j\) and \(s^{(1)}_j, s^{(2)}_j\rightarrow 0\) as \(j\rightarrow \infty \), such that, by setting \(L_s:=V_{w_j}\cap \{x_n=s\},\) we have
and
The existence of such sequences can be proved similarly to (3.25), using also the convergence \({\mathcal H}^{n-1}(S^V_{w_j})\rightarrow {\mathcal H}^{n-1}(S^V_v)\) in view of the construction of \(w_j\) in the previous step. We define the function \(z_j:Q_L\times \mathbb R\rightarrow \{0,-1,1,2\}\) (extended by periodicity to \(\mathbb R^n\)) by
Since \(h_{z_j}=\max \{h_{w_j},s_j^{(2)}\}\) we have \(z_j\in {\mathcal {X}_{\mathrm {reg}}}\), and also \(\Vert w_j - z_j \Vert _{L^1(Q_L^+)} \le s_j^{(2)} {\mathscr {L}}^{n-1}(Q_L)\), which yields (3.33). Moreover,
where
Notice that \(R_j\rightarrow 0\) thanks to (3.37). We then obtain (3.35) by passing to the limit in (3.39), using (3.33), (3.36), and the fact that \({\mathcal H}^{n-1}(S^V_{w_j})\rightarrow {\mathcal H}^{n-1}(S^V_v)\).
Step 5: the mass constraint. By combining the constructions in the previous steps and using a diagonal argument, we have that given \(u\in {\mathcal {X}}\), there exists a sequence \(\{z_j\}_{j\in \mathbb N}\subset {\mathcal {X}_{\mathrm {reg}}}\) such that
(see in particular (3.22), (3.29), (3.33) for the convergence of the functions, and (3.23), (3.30), (3.34) for the convergence of the energies). In order to obtain the recovery sequence, we need to restore the mass constraint: denoting by \(|\Omega _{h_u}|=M\), \(|A_u|=m\), we modify the sequence \(\{z_j\}_{z\in \mathbb N}\) and we construct a new sequence \(\{u_j\}_{j\in \mathbb N}\subset {\mathcal {X}_{\mathrm {reg}}}\) such that
and
We first adjust the volume of \(\Omega _{h_{z_j}}\) by a vertical rescaling: namely, we take \(\lambda _j:=\frac{M}{|\Omega _{h_{z_j}}|}\) (notice that \(\lambda _j\rightarrow 1\) as \(j\rightarrow \infty \)) and we let \(h_j:=\lambda _j h_{z_j}\), so that \(|\Omega _{h_j}|=M\). We now need to adjust the volume of \(A_{z_j}\) and \(B_{z_j}\). Let
be the sets obtained by rescaling vertically \(A_{z_j}\) and \(B_{z_j}\) by the factor \(\lambda _j\); notice that \({\widetilde{A}}_j\cup {\widetilde{B}}_j=\Omega _{h_j}\) and therefore \(|{\widetilde{A}}_j|+|{\widetilde{B}}_j|=M\). We also remark that, as \(\lambda _j\rightarrow 1\) and \(A_{z_j}\rightarrow A_u\), \(B_{z_j}\rightarrow B_u\) in \(L^1\), we have \(|{\widetilde{A}}_j|\rightarrow m\), \(|{\widetilde{B}}_j|\rightarrow M-m\) as \(j\rightarrow \infty \).
Suppose to fix the ideas that \(|{\widetilde{A}}_{j}|<m\) (we proceed similarly in the other case). Let \({\bar{x}}\in \Omega _{h_u}\) be a point of density one for \(B_u\). Since \({\widetilde{B}}_{j}\rightarrow B_u\) in \(L^1\), we have
Hence, it is possible to find \(r_0>0\) and \(j_0\in \mathbb N\) such that
Therefore, for every \(j\ge j_0\) (for a possibly larger \(j_0\)) it is possible to find \(r_j\in (0,r_0)\) such that \(|{\widetilde{B}}_{j}\cap B_{r_j}({\bar{x}})|=m-|{\widetilde{A}}_{j}|>0\), since this quantity tends to zero as \(j\rightarrow \infty \). We eventually define
We then have \(h_{u_j}=h_j=\lambda _j h_{z_j}\), so that \(u_j\in {\mathcal {X}_{\mathrm {reg}}}\) and \(|\Omega _{h_{u_j}}|=M\). Moreover, \(A_{u_j}={\widetilde{A}}_{j}\cup (B_{r_j}({\bar{x}})\cap {\widetilde{B}}_j)\), hence \(|A_{u_j}|=|{\widetilde{A}}_j|+|{\widetilde{B}}_j\cap B_{r_j}({\bar{x}})|=m\). Thus (3.42) are satisfied. Finally, also the convergences (3.41) hold, since \(\lambda _j\rightarrow 1\) and \(r_j\rightarrow 0\). \(\square \)
4 Regularity of Minimizers
In this section, we will study the regularity of solutions to the minimum problem
whose existence has been established in Theorem 3.5.
The strategy to prove the regularity of minimizers relies, as it is common in these kinds of problems, on the regularity theory for area quasi-minimizing clusters (see (Maggi 2012, Part IV) and the references therein). Indeed, we will firstly show in Sect. 4.1 via a penalization technique that it is possible to remove the volume constraint in (4.1) by adding a suitable volume penalization to the functional. Furthermore, the term \({\mathcal {N}}(u)\) in the energy behaves as a volume-order term thanks to assumption (2.16). In view of these two properties, it follows that the partition of \(\mathbb R^n\) given by \((A_u,B_u,V_u,S)\), for a solution u of (4.1), is a quasi-minimizer cluster for the surface energy
The precise definition of quasi-minimality in our context is given in Definition 4.1.
Next, in Sect. 4.2 we exploit the quasi-minimality property to obtain the regularity of minimizers in two dimensions stated in Theorem 1.1. Technical difficulties arise from two fronts: on the one hand, we can only compare with clusters that satisfy the constraint of being the subgraph of a function of bounded variation, a fact that poses a severe restriction on the class of competitors. On the other hand, the interfaces between the phases of the cluster are weighted by different surface tension coefficients. The challenges that arise from these two features prevent us to rely on the standard theory quasi-minimizing clusters, and requires ad hoc modifications of the classical proofs. For this reason, we develop a regularity theory only in dimension \(n=2\), since the general dimensional case requires more refined arguments. We also remark that the regularity properties are obtained under the assumption that the surface tension coefficients satisfy a strict triangle inequality (see (4.45)).
4.1 Penalization and Quasi-Minimality
In this section, we show that, in any dimension \(n\ge 2\), every solution to the minimum problem (4.1) is a quasi-minimizer for the surface energy (Proposition 4.3), in the sense of the following definition.
Definition 4.1
(Quasi-minimizer) We say that \(u\in {\mathcal {X}}\) is a quasi-minimizer for the surface energy \({\mathscr {G}}\), defined in (4.2), if there exists \(\Lambda >0\) such that for every admissible configuration \(v\in {\mathcal {X}}\) one has
We denote, for \(\Lambda >0\) and \(M>0\), by \({\mathcal {A}}_{\Lambda ,M}\) the class of all configurations \(u\in {\mathcal {X}}\) such that u is a quasi-minimizer for \({\mathscr {G}}\) with quasi-minimality constant \(\Lambda \), and \(|\Omega _{h_u}|\le M\).
As a first step, we remove the mass constraint in (4.1) by considering a suitable penalized minimum problem, see (4.4). The main idea of the proof is discussed in the Introduction.
Lemma 4.2
(Penalization) Let \(0<m<M<\infty \). Then, there exists \(\Lambda >0\) such that every solution to the constrained minimum problem (4.1) is also a solution to the penalized problem
Proof
Let \(u\in {\mathcal {X}}\) be a minimizer for (4.1), consider a sequence \(\{\lambda _j\}_{j\in \mathbb N}\) with \(\lambda _j\rightarrow \infty \) as \(j\rightarrow \infty \), and \(u_j\in {\mathcal {X}}\) solving the minimum problem
whose existence can be shown arguing as in the proof of Theorem 3.5. We will show that, for j large enough, we have
which will imply that u itself is a solution to (4.5) for j large, as desired.
To prove (4.6), we argue by contradiction and we show that, if at least one of the equalities in (4.6) is not satisfied, then for j large enough it is possible to construct by a local variation a configuration \({\widetilde{u}}_j\in {\mathcal {X}}\) such that \({\mathscr {H}}_{\lambda _j}({\widetilde{u}}_j) < {\mathscr {H}}_{\lambda _j}(u_j)\). The construction of the local variation exploits the same diffeomorphism for both of the mass constraints, applied at different points. In the first part of the proof (Steps 1–4), we thus present the construction of the general diffeomorphism and the corresponding estimates for the change of volume, perimeter, and nonlocal energy under this perturbation. To simplify the notation, in the rest of the proof we will write \(A_j\), \(B_j\), and \(\Omega _j\) in place of \(A_{u_j}\), \(B_{u_j}\), and \(\Omega _{h_{u_j}}\), respectively.
Step 1: Definition of the diffeomorphism. We denote by \(B'_r :=\{ x'\in \mathbb R^{n-1}: |x'|< r \}\) the \((n-1)\)-dimensional ball centered at the origin with radius \(r>0\), and define for \(z\in \mathbb R^n\)
and
We next assume that \(z=0\) and we define a family of local perturbations in C(0, r). Precisely, for \(|\sigma |<r\) we define the map \(\Phi _\sigma :\mathbb R^n\rightarrow \mathbb R^n\) by
The function \(\Phi _\sigma \) is a vertical rescaling with horizontal and vertical cutoff functions. The role of the parameter \(\sigma \) can be seen from Fig. 4. Notice that for \(|\sigma |<r\) the function \(\Phi _\sigma \) is a bi-Lipschitz map and that \(\Phi _\sigma (C(0,s)) = C(0,s)\). Moreover, it holds

where \(\mathrm {Id}_{n-1}\) is the \((n-1)\times (n-1)\) identity matrix,
and
When we will perform a perturbation localized in a cylinder centered at a point \(z\in \mathbb R^n\), we will consider the map \(x\mapsto z+\Phi _\sigma (x-z)\).
Step 2: Estimate of the change in volume. Let \(E\subset C(0,r)\) be a measurable set. We first estimate the maximal change of volume \(\left| |\Phi _\sigma (E)| - |E|\right| \): by using (4.8) and (4.9) we get
Next, we prove more refined estimates on the change of volume of a set E in the upper and lower cylinders \(C^+(0,r)\), \(C^-(0,r)\). We first consider the case \(\sigma >0\). In this case, the followings hold:
-
(i)
For every \(\varepsilon >0\) and \(\sigma \in (0,r)\), if \(|E\cap C^+(0,r)|<\varepsilon r^n\) then
$$\begin{aligned} 0\le |\Phi _\sigma (E\cap C^+(0,r))| - |E\cap C^+(0,r))| \le U(\varepsilon ) |\sigma | r^{n-1}, \end{aligned}$$(4.12)where
$$\begin{aligned} U(\varepsilon ):=\left[ \, 1 - \frac{n-1}{n}\Bigl ( \frac{\varepsilon }{\omega _{n-1}} \Bigr )^{\frac{1}{n-1}} \,\right] \varepsilon . \end{aligned}$$ -
(ii)
For every \(\mu \in (0,\omega _{n-1})\) and \(\sigma \in (0,r)\), if \(|E\cap C^-(0,r)| > \mu r^n\), then
$$\begin{aligned} |\Phi _\sigma (E\cap C^-(0,r))| - |E\cap C^-(0,r))| \le - L(\mu ) |\sigma | r^{n-1}< 0, \end{aligned}$$(4.13)where
$$\begin{aligned} L(\mu ):=\left[ \, \frac{1}{n} -\left( 1-\frac{\mu }{\omega _{n-1}} \right) +\frac{n-1}{n}\left( 1-\frac{\mu }{\omega _{n-1}} \right) ^{\frac{n}{n-1}} \,\right] \omega _{n-1}. \end{aligned}$$
To prove (4.12) we notice that by (4.8) and (4.9), and since \(\sigma >0\),
where \(F_\varepsilon :=B'_{r_\varepsilon }\times (0,r)\) and \(r_\varepsilon :=r(\varepsilon /\omega _{n-1})^{\frac{1}{n-1}}\). Similarly we obtain (4.13) by comparison with \(G_{\mu }:=C^-(0,r)\backslash (B'_{s_{\mu }}\times (-r,0))\), \(s_{\mu }:=r(1-\mu /\omega _{n-1})^{\frac{1}{n-1}}\).
In (4.12)–(4.13) we have written \(|\sigma |\) in place of \(\sigma \) to stress the fact that the same estimates hold also in the case \(\sigma <0\) up to exchanging the roles of \(C^+(0,r)\) and \(C^-(0,r)\), as can be easily checked. Notice that \(U(\varepsilon )\rightarrow 0\) as \(\varepsilon \rightarrow 0\), and that \(L(\mu )\) is strictly positive, and more precisely \(L(\mu )\in (0,\frac{\omega _{n-1}}{n})\) for every choice of \(\mu \in (0,\omega _{n-1})\), with \(L(\mu )\rightarrow 0\) as \(\mu \rightarrow 0\), \(L(\mu )\rightarrow \frac{\omega _{n-1}}{n}\) as \(\mu \rightarrow \omega _{n-1}\).
Step 3: Estimate of the change in perimeter. Given a countably \({\mathcal {H}}^{n-1}\)-rectifiable set \(\Sigma \subset \mathbb R^{n}\), by the generalized area formula (see (Ambrosio et al. 2000, Theorem 2.91)) we have that
where \(\mathrm {d}_x^\Sigma \Phi _{\sigma }:\pi ^\Sigma _x\rightarrow \mathbb R^n\) denotes the tangential differential of \(\Phi _{\sigma }\) at \(x\in \Sigma \) along the approximate tangent space \(\pi _x^\Sigma \) to \(\Sigma \), and the area factor \(J_{n-1} \mathrm {d}_x^\Sigma \Phi _\sigma \) is defined as (see (Ambrosio et al. 2000, Definition 2.68))
(here \((\mathrm {d}_x^\Sigma \Phi _{\sigma })^*\) is the adjoint of the linear map \(\mathrm {d}_x^\Sigma \Phi _{\sigma }\)). In order to estimate (4.15), fix \(x\in \Sigma \) and let \(\tau _1,\dots ,\tau _{n-1}\) be an orthonormal basis for the approximate tangent space \(\pi ^\Sigma _x\). By using (4.8), (4.9), and (4.10), for all \(i,j\in \{1,\dots ,n-1\}\) we have
where \(\Phi _{\sigma }=(\Phi _{\sigma }^1,\ldots ,\Phi _{\sigma }^n)\) and \(\tau _i=(\tau _i^1,\ldots ,\tau _i^n)\) denote the components with respect to the canonical base of \(\mathbb R^n\), and \(w_\sigma (x):=(v_\sigma (x),a_\sigma (x))\). By using the fact that \(|w_\sigma (x)|\le \sqrt{2}|\sigma |/r\) and the general formula \(\mathrm {det}(I+t A) = 1 + t\,\mathrm {trace}(A) + O(t^2)\) as \(t\rightarrow 0\), we get
where \(\big |O\bigl (\bigl (\frac{\sigma }{r}\bigr )^2\bigr )\big | \le C\bigl (\frac{\sigma }{r}\bigr )^2\) for a constant \(C>0\) independent of \(\sigma \), r, and of \(x\in \Sigma \). Therefore by (4.14) we find for \(|\sigma |\) sufficiently small
where \(c_0>0\) is a dimensional constant. This, together with (4.14), yields
Step 4: Estimate of the change of the term \({\mathcal {N}}(\cdot )\). Finally, we estimate the change in the term \({\mathcal {N}}(\cdot )\) of the energy. We note that, by assumption (2.16), it is enough to get an estimate on \(|\Phi _\sigma (E){\bigtriangleup }E|\) for a general set E with finite perimeter. By the same computation as in (Acerbi et al. (2013), Proposition 2.7), writing \(\Phi _{\sigma }^{-1}(x',x_n)=(x',x_n+\phi _\sigma (x_n))\) with \(|\phi _\sigma (x_n)|\le |\sigma |\), for \(f\in C^1(\mathbb R^n)\) we have
Let now \(E\subset \mathbb R^n\) be a set with finite perimeter and let \(\{f_k\}_{k\in \mathbb N}\) be a sequence of smooth functions such that \(f_k\rightarrow \chi _E\) in \(L^1\) and \(\Vert \nabla f_k\Vert _{L^1}\rightarrow {\mathscr {P}}(E)\). Then, also \(f_k\circ \Phi _\sigma ^{-1}\rightarrow \chi _E\circ \Phi _\sigma ^{-1}\) in \(L^1\). Therefore applying (4.17) to the function \(f_k\) and passing to the limit as \(k\rightarrow \infty \) yields
Step 5: General strategy. We can now go back to the main argument of the proof and show that any solution \(u_j\) of the penalized problem (4.5) satisfies the mass constraints (4.6), for j large enough. The idea of the proof is to assume by contradiction that one of the mass constraints in (4.6) is not satisfied, and to construct a perturbation of \(u_j\) in a cylinder C(z, r) by means of the maps \(\Phi _{\sigma _j}\). More precisely, we will choose a point \(z\in \mathbb R^n\), a radius \(r>0\) and scaling coefficients \(\sigma _j\in (-r,r)\) and define
This is a local perturbation inside C(z, r) (the center and the radius will be chosen in such a way that the cylinder does not intersect the substrate S) such that the phases of the new configuration \({\widetilde{u}}_j\) are given by
Thanks to (4.16), (4.18), and (2.16), we get the estimate
where \({\tilde{c}}_0\) depends on the constant \(c_0\) in (4.16) and on the surface tension coefficients. The goal would be then to show that, if at least one of the volume constraints is not satisfied, then it is possible to choose z, r and \(\sigma _j\) so that
for some \(C>0\) independent of j. As \(\lambda _j\rightarrow \infty \), the combination of (4.20) and (4.21) shows that \({\mathscr {H}}_{\lambda _j}({\widetilde{u}}_j)<{\mathscr {H}}_{\lambda _j}(u_j)\) for j large enough, which is a contradiction with the minimality of \(u_j\) in (4.5).
In the next two steps, we will implement the previous strategy. We first observe that, by using u as a competitor in the minimum problem (4.5) and since \({\overline{\mathscr {F}}}(u)<\infty \), we obtain the bounds
Thus, up to a subsequence (not relabeled), we get that \(A_{j}\rightarrow A\) and \(B_{j}\rightarrow B\) in \(L^1\), with \(|A|=m\), \(|B|=M-m\) since \(\lambda _j\rightarrow \infty \). We also have \(\Omega _j\rightarrow \Omega :=A\cup B\). Notice that \(\Omega \) is still the subgraph of an admissible profile.
In the following, given a point \(x_0\in \mathbb R^n\), \(r>0\), and a direction \(\nu = (\nu ',\nu _n)\in {\mathbb {S}}^{n-1}\) with \(\nu _n\ne 0\), we define
and we consider the corresponding cylinder \(C(y_r,r)\). The choice of the point \(y_r\) guarantees, since \(\nu _n\ne 0\), that there exists a constant \(c_\nu >0\), independent of r, such that if \(\nu _n>0\)
while if \(\nu _n<0\)
Notice that the strict positivity of \(c_\nu \) is a consequence of the fact that \(\nu _n\ne 0\).
Step 6: Fixing the total volume. Assume by contradiction that \(|\Omega _j|\ne M\) for infinitely many j. We will consider for simplicity the case \(|\Omega _j|>M\) for all j, as the other case can be treated by a similar argument.
Case 1. Assume that there exists \(x_0\in \partial ^*\Omega \cap \partial ^*B\) such that \(\nu _{\Omega }(x_0)\cdot e_n > 0\) (where \(\nu _{\Omega }\) denotes the exterior normal). We consider the point \(y_r\) and the constant \(c_\nu \) defined in (4.23) and (4.24), respectively, for \(\nu =\nu _{\Omega }(x_0)\) and \(r>0\) to be chosen later.
De Giorgi’s structure theorem for sets of finite perimeter ((Ambrosio et al. 2000, Theorem 3.59)) together with (4.24) ensures that
Therefore, for every \(\varepsilon >0\), the fact that \(\chi _{\Omega _j}\rightarrow \chi _\Omega \), \(\chi _{A_j}\rightarrow \chi _A\) and \(\chi _{B_j}\rightarrow \chi _B\) in \(L^1\) yields the existence of \(r\in (0,1)\) and \(j_0\in \mathbb N\) such that for all \(j\ge j_0\) the following holds:
Moreover, for r small enough we can also guarantee that the cylinder \(C(y_r,r)\) is contained in the upper half-space and does not intersect the substrate. We then choose \(\sigma _j>0\) and consider the perturbation defined in (4.19) centered at the point \(z=y_r\). In view of (4.26), by using (4.12) and (4.13), we get
On the other hand, by (4.11) and (4.27),
Therefore, noting that we can assume \(M<|{\widetilde{\Omega }}_j|<|\Omega _j|\) (it is sufficient to choose \(\sigma _j\) and \(\varepsilon \) small enough), we find
By choosing \(\varepsilon \) sufficiently small, we can ensure that \(U(\varepsilon )+\varepsilon <L(c_\nu )\), which yields (4.21) and leads to the desired contradiction in this case.
Case 2. If the assumption of the previous case does not hold, we can find a point \(x_1\in \partial ^*\Omega \cap \partial ^*A\) such that \(\nu _{\Omega }(x_1)\cdot e_n> 0\). Since \(0<m<M\), it is possible to find a second point \(x_2\in \partial ^* A\cap \partial ^* B\) such that \(\nu _A(x_2)\cdot e_n < 0\).
We will consider the composition of two perturbations of the form (4.19) localized in two disjoint cylinders \(C(y_r^1,r)\) and \(C(y_r^2,r)\), where (see also (4.23))
Let
Note that \(E^1_r\subset C^-(y^1_r,r)\) and that \(E^2_r\subset C^+(y^2_r,r)\). We let \(\mu :=c_{\nu _{\Omega }(x_1)}\), where the constant \(c_\nu \), for a vector \(\nu \), is defined in (4.24). As in the previous case, fixed \(\varepsilon >0\), we can find \(r>0\) and \(j_0\in \mathbb N\) such that for all \(j\ge j_0\) we have
and
By reducing the value of \(r>0\) we can further assume that the two cylinders \(C(y^1_r,r)\) and \(C(y^2_r,r)\) are disjoint and do not intersect the substrate. For a fixed sequence \(\{\sigma _j^1\}_{j\in \mathbb N}\subset (0,r)\), we define a second sequence \(\{\sigma _j^2\}_{j\in \mathbb N}\) as
for each \(j\in \mathbb N\). Notice that \(\alpha \) is independent of r by scale invariance. Then, we consider the configuration \({\widetilde{u}}_j\) obtained by applying to \(u_j\) the composition of the two perturbations \(y_r^1+\Phi _{\sigma ^1_j}(\cdot -y_r^1)\) and \(y_r^2+\Phi _{\sigma ^2_j}(\cdot -y_r^2)\). We denote the sets of the new partition determined by \({\widetilde{u}}_j\) by \({\widetilde{A}}_j\), \({\widetilde{B}}_j\), \({\widetilde{\Omega }}_j={\widetilde{A}}_j\cup {\widetilde{B}}_j\), \(\widetilde{V_j}\).
We first consider the variation of the volume of \(\Omega _j\). By (4.28), and since \(\sigma ^1_j>0\), we can apply (4.12) and (4.13) and obtain
On the other hand, by (4.29) and using (4.11) we find
By combining the two estimates and recalling (4.31), it follows that
Next, we look at the variation of the volume of \(A_j\). We have for \(i=1,2\)
where thanks to (4.30) and (4.11)
Also notice that the choice of \(\sigma _j^2\) in (4.31) guarantees exactly that
Therefore, from (4.33), (4.34), and (4.35), we get
We can now conclude as follows. Similarly to (4.20), we find
where we used (4.22) in the second inequality, and (4.32), (4.36) in the last one. We can therefore choose \(\varepsilon >0\) small enough so that the constant multiplying \(\lambda _j\) is strictly negative; as \(\lambda _j\rightarrow +\infty \), this provides the desired contradiction with the minimality of \(u_j\).
Step 7: Fixing the volume of each phase. In this step, we conclude the proof by showing that \(|A_j|=m\) for j large. Thanks to the previous step, we can assume that \(|\Omega _j|=M\) for all \(j\in \mathbb N\). Suppose by contradiction that \(A_j\ne m\) for infinitely many j. We consider for simplicity only the case \(|A_j|>m\) for all j, as the other case can be treated with similar computations.
Case 1. Assume that there exists \(x_0\in \partial ^* A\cap \partial ^* B\) such that \(\nu _A(x_0)\cdot e_n \ne 0\). We assume to fix the ideas to be in the case \(\nu _A(x_0)\cdot e_n>0\); in the other case, it is sufficient to exchange the roles of the upper and lower cylinders in the computations below. We consider, for \(r>0\) to be chosen, the point \(y_r\) and the constant \(c_\nu \) defined in (4.23) and (4.24), respectively, corresponding to \(\nu =\nu _A(x_0)\).
Fix \(\varepsilon >0\). By De Giorgi’s structure theorem and the convergence \(\chi _{A_j}\rightarrow \chi _A\), there exist \(r>0\) and \(j_0\in \mathbb N\) such that for all \(j\ge j_0\) it holds
and
Moreover, for r small enough we can also guarantee that the cylinder \(C(y_r,r)\) is contained in the upper half-space and does not intersect the substrate. We then choose \(\sigma _j>0\) and consider the perturbation defined in (4.19) centered at the point \(z=y_r\). From (4.38), (4.12), and (4.13), we have
Moreover, from (4.39) and (4.11) we can estimate
Thus, using the fact that \(|\Omega _j|=M\) for all \(j\in \mathbb N\), and that \(m<|{\widetilde{A}}_j|<|A_j|\) (by choosing \(\sigma _j\) and \(\varepsilon \) small enough), we obtain
Therefore, by choosing \(\varepsilon >0\) small enough we get (4.21), as desired.
Case 2. Finally, assume that \(\nu _A(x)\cdot e_n = 0\) for all \(x\in \partial ^* A\cap \partial ^* B\). The construction in this case is similar to the one in Step 6, Case 2. Since \(0<m<M\), we get that there exist \(x_1\in \partial ^* A\cap \partial ^*V\) and \(x_2\in \partial ^* B\cap \partial ^*V\). We let, for \(r>0\), \(y_r^1\) and \(y_r^2\) be the points defined by (4.23) corresponding to the choice of \(\nu _{\Omega }(x_1)\) and \(\nu _{\Omega }(x_2)\), respectively, and
We let \(\mu :=c_{\nu _{\Omega }(x_1)}>0\), where the constant \(c_\nu \), for a vector \(\nu \), is defined in (4.24). As in the previous cases, for fixed \(\varepsilon >0\), we can find \(r>0\) and \(j_0\in \mathbb N\) such that for all \(j\ge j_0\) we have
and
By reducing the value of \(r>0\), we can further assume that the two cylinders \(C(y_r^1,r)\) and \(C(y_r^2,r)\) are disjoint and do not intersect the substrate. For a fixed sequence \(\{\sigma _j^1\}_{j\in \mathbb N}\subset (0,r)\), we define a second sequence \(\{\sigma _j^2\}_{j\in \mathbb N}\) as
for each \(j\in \mathbb N\). Notice that \(\sigma _j^2<0\) and that \(\alpha \) is independent of r by scale invariance. Then, we consider the configuration \({\widetilde{u}}_j\) obtained by applying to \(u_j\) the composition of the perturbations \(y_r^1+\Phi _{\sigma ^1_j}(\cdot -y_r^1)\), \(y_r^2+\Phi _{\sigma ^2_j}(\cdot -y_r^2)\). We denote the sets of the new partition determined by \({\widetilde{u}}_j\) by \({\widetilde{A}}_j\), \({\widetilde{B}}_j\), \({\widetilde{\Omega }}_j={\widetilde{A}}_j\cup {\widetilde{B}}_j\), \(\widetilde{V_j}\).
We first consider the variation of the volume of \(A_j\). By using the last two inequalities in (4.40) and the last inequality in (4.41), together with (4.12), (4.13), (4.11), we get
The choice (4.42) guarantees that
therefore by arguing as in (4.36) we find
and in turn, similarly to (4.37) (using (4.22) (4.43), and (4.44))
We can therefore choose \(\varepsilon >0\) small enough so that the constant multiplying \(\lambda _j\) is strictly negative; as \(\lambda _j\rightarrow +\infty \), this provides the desired contradiction with the minimality of \(u_j\). \(\square \)
The result of Lemma 4.2 together with the Lipschitz continuity assumption (2.16) of the term \({\mathcal {N}}(\cdot )\) easily yields the quasi-minimality of solutions to (4.1).
Proposition 4.3
Let u be a solution to the minimum problem (4.1). Then, u is a quasi-minimizer for the surface energy \({\mathscr {G}}\), according to Definition 4.1.
A standard truncation argument shows that quasi-minimizers are bounded.
Proposition 4.4
(Boundedness) Let \(u\in {\mathcal {A}}_{\Lambda ,M}\). Then, \(h_u\in L^\infty (Q_L)\).
Proof
The boundedness is a consequence of the finiteness of the volume of \(\Omega _{h_u}\) and of the following elimination-type property: there exists \(\varepsilon >0\) and \(t_0>0\), depending on n, \(\Lambda \) and on the surface tension coefficients, such that if \(u\in {\mathcal {A}}_{\Lambda ,M}\) and \(|\Omega _{h_u}\cap \{x_n>{\bar{t}}\}| <\varepsilon \) for some \({\bar{t}}>0\), then \(|\Omega _{h_u}\cap \{x_n>{\bar{t}}+t_0\}| =0\).
To show this, define \(m(t):=|\Omega _{h_u}\cap \{x_n> t\}|\), suppose that \(m({\bar{t}})<\varepsilon \) and notice that for a.e. \(t>0\) it holds \(m'(t)=-{\mathcal {H}}^{n-1}(\Omega _{h_u}^{(1)}\cap \{x_n= t\})\). By comparing with the configuration \(v:=u\chi _{\{x_n\le t\}}\), using the quasi-minimality of u and choosing \(\varepsilon \) small enough, by standard computations one obtains the differential inequality \(m(t)^{\frac{n-1}{n}} \le -Cm'(t)\) for a.e. \(t>{\overline{t}}\), that allows to conclude that \(m(t)=0\) for \(t>{\overline{t}}+C\varepsilon ^{\frac{1}{n}}\) by integration. \(\square \)
4.2 Partial Regularity of Quasi-Minimizers in Dimension 2
From now on, we assume that the dimension of the space is \(n=2\). We also assume that the surface tension coefficients satisfy the strict triangle inequalities
Under these assumptions we will show a series of regularity properties satisfied by a quasi-minimizer u of the surface energy \({\mathscr {G}}\), according to Definition 4.1. Notice that for \(u\in {\mathcal {A}}_{\Lambda ,M}\) we have a uniform bound
for a constant C depending on M, \(\Lambda \) and on the surface tension coefficients. In two dimensions, this bound immediately yields boundedness from above of the film, that is there exists \({\overline{M}}>0\) (depending on M, \(\Lambda \) and on the surface tension coefficients) such that
The first regularity fact that we establish is an elimination property for the empty region above the film, in the spirit of Leonardi (2001).
Proposition 4.5
(Infiltration for V) Let \(u\in {\mathcal {A}}_{\Lambda ,M}\). There exists \(\varepsilon _1>0\), depending on \(\Lambda \), M, and on the surface tension coefficients, such that if for some \(z_0\in \mathbb R^2\) and \(r\in (0,1)\)
where \({\mathcal {Q}}_r(z_0) :=z_0+r{\mathcal {Q}}\) and \({\mathcal {Q}}:=(-\frac{1}{2},\frac{1}{2})\times (-\frac{1}{2},\frac{1}{2})\), then
Proof
Let \({\mathcal {C}}^-:=\bigl (-\frac{1}{2},\frac{1}{2}\bigr )\times \bigl (-\infty ,\frac{1}{2}\bigr )\) and, for \(z_0\in \mathbb R^2\) and \(r>0\), set \({\mathcal {C}}_r^- :=r{\mathcal {C}}^-\), \({\mathcal {C}}_r^-(z_0) :=z_0+{\mathcal {C}}_r^-\). Along the proof, to lighten the notation we will drop the subscript u from the sets (2.11) of the partition determined by u and from the corresponding interfaces (2.13)–(2.14). The proof is divided into two steps.
Step 1: infiltration in strips. We first show that there exists \({\tilde{\varepsilon }}_1>0\), depending on \(\Lambda \) and on the surface tension coefficients, such that for every \(z_0\in \mathbb R^2\) and \(r\in (0,1)\) the following implication holds:
We assume for notation convenience, and without loss of generality, that \({\mathcal {C}}^-_r(z_0)\subset (0,L)\times \mathbb R\); the general case is obtained by periodicity. For \(s\in [0,r]\) we let \(m(s):=| V\cap {\mathcal {C}}^-_s(z_0)|\), so that \(m(r)\le {\tilde{\varepsilon }}_1r^2\) by the assumption. The function m(s) is monotone nondecreasing, with
Fix now \(s\in (0,r)\) such that (4.50) holds and \({\mathcal H}^{1}(J_u\cap \partial {\mathcal {C}}^-_s(z_0))=0\) (notice that \({\mathscr {L}}^1\)-almost every \(s>0\) has this property). We define a competitor by “filling” the empty region in \({\mathcal {C}}^-_s(z_0)\) above the substrate by the phase A or B. More precisely, assume that
and define
(which corresponds to fill the region \(V\cap {\mathcal {C}}_s^-(z_0)\) by the phase A). The proof in the other case, when one has the opposite inequality in (4.51), follows similarly by filling \(V\cap {\mathcal {C}}_s^-(z_0)\) by the phase B.
We then have \(A_{u_s}=A\cup (V\cap {\mathcal {C}}_s^-(z_0))\), \(B_{u_s}=B\), and \(A_{u_s}\cup B_{u_s}\) is the subgraph of an admissible profile; therefore \(u_s\in {\mathcal {X}}\) is an admissible configuration and by quasi-minimality of u we find
Observe now that by (4.51)
where we set \(c_1:=-\frac{1}{2}\max \{\sigma _{AB}-\sigma _B-\sigma _A,-\sigma _A\}>0\) thanks to the strict triangular inequality between the coefficients. Hence,
where we used the isoperimetric inequality in the last inequality, and \(c_2\), \(c_3\) are positive constants depending on the surface tension coefficients. Furthermore, by the geometry of the set V we have \({\mathcal H}^{1}(S^V\cap {\mathcal {C}}_s^-(z_0))\le {\mathcal H}^{1}(V^{(1)}\cap \partial {\mathcal {C}}_s^-(z_0))\), hence
By inserting (4.53)–(4.54) into (4.52) and setting \(c_4:=c_3+2(\sigma _A+\sigma _{AS})\), we find
The previous estimate holds for almost every \(s\in (0,r)\) obeying (4.51), but one can obtain the same estimate also for almost every s satisfying the opposite inequality (with possibly different constants \(c_2\), \(c_4\)). Therefore
Then, by choosing \({\tilde{\varepsilon }}_1>0\) small enough, depending on \(\Lambda \) and on the surface tension coefficients, we obtain that
for a constant \(C>0\) depending only on the surface tension coefficients. From this, it is easy to obtain by integration that \(m(\frac{3}{4}r)=0\), which proves the implication (4.49).
Step 2. We now claim that there exists \(\varepsilon _1>0\) such that
where \({\tilde{\varepsilon }}_1\) is given by the previous step. Once this claim is proved, the conclusion of the proposition follows easily by combining this property with Step 1. Let us now prove (4.55). As before by periodicity we can assume \({\mathcal {Q}}_r(z_0)\subset (0,L)\times \mathbb R\). We denote by \({\mathcal {Q}}'_r(z_0):=z_0 + (-\frac{r}{2},\frac{r}{2})\times \{-\frac{r}{2}\}\) the bottom side of the square \({\mathcal {Q}}_r(z_0)\). We first observe that, by the geometry of the set V, we have
Then (assuming without loss of generality that \(\varepsilon _1<\frac{1}{8}\)) we can find \(\rho \in (\frac{3}{4}r,r)\) such that the two points \(z_0+(-\frac{\rho }{2},-\frac{r}{2})\), \(z_0+(\frac{\rho }{2},-\frac{r}{2})\), on \({\mathcal {Q}}_r'(z_0)\), are not points of density one for V. We then consider the strip \(U:={\mathcal {C}}_{\rho }^-(z_0)\backslash \overline{{\mathcal {Q}}_r(z_0)}\) and, by the choice of \(\rho \), it follows that the lateral boundary of U is outside \(V^{(1)}\), hence

We can further assume that
since this is valid for \({\mathscr {L}}^1\)-almost every \(\rho \in (0,r)\). To continue, we assume that
and we construct a competitor by filling the region \(V\cap U\) by the phase B (the proof in the other case, when one has the opposite inequality in (4.59), follows similarly by filling \(V\cap U\) by the phase A): we define
Since \({\tilde{u}}\in {\mathcal {X}}\) is admissible, by quasi-minimality of u we find, similarly to (4.52),
and in turn, arguing similarly to the proof of (4.53), using the assumption (4.59),
where \(c_1\), \(c_2\) are strictly positive constants depending on the surface tension coefficients. By inserting this inequality into (4.60) we obtain
Now observe that, by the geometry of the set V, we have \({\mathcal H}^{1}(S^V\cap U)\le {\mathcal H}^{1}(V^{(1)}\cap {\mathcal {Q}}_r'(z_0))\); hence from the previous inequality and (4.57) it follows that
Finally, observe that by using the uniform bound (4.46) and the vertical geometry of V we have \(|V\cap U|\le {\overline{M}}{\mathcal H}^{1}(V^{(1)}\cap {\mathcal {Q}}_r'(z_0))\le \varepsilon _1{\overline{M}}r\), so that by inserting this estimate in the previous inequality we obtain
that is, \(|V\cap U| \le C\varepsilon _1^2 r^2\) for some constant \(C>0\) depending on \(\Lambda \), M and on the surface tension coefficients (recall that the bound \({\overline{M}}\) in (4.46) depends only on these quantities). Eventually
provided that we choose \(\varepsilon _1\) small enough. This completes the proof of (4.55). \(\square \)
We also have a dual statement for the region occupied by the film. The proof follows by the same argument used in the proof of Proposition 4.5. However, since we can obtain this result as a consequence of the stronger property proved in Proposition 4.8, we omit the proof.
Proposition 4.6
(Infiltration for \(A\cup B\)) Let \(u\in {\mathcal {A}}_{\Lambda ,M}\). There exists \(\varepsilon _2>0\), depending on \(\Lambda \), M, and on the surface tension coefficients, such that if for some \(z_0\in \mathbb R^2\) and \(r\in (0,1)\) such that \({\mathcal {Q}}_r(z_0)\cap S=\emptyset \) we have
then
Remark 4.7
It is worth to notice that, in the proof of Proposition 4.5 (and also of Proposition 4.6), the constraint of being subgraphs prevents us to construct competitors by means of local variations in a square \({\mathcal {Q}}_r(z_0)\), but imposes to consider the full vertical region below or above the square. Notice also that, if a single set \(\Omega _h\) is a quasi-minimizer of the perimeter in the class of subgraphs, a standard argument (Giusti 1984, Theorem 14.8) shows that it is actually a quasi-minimizer among all possible competitors of finite perimeter, without the constraint (we will exploit this fact in the proof of Proposition 4.12). However, in our case we have a partition of the subgraph into two sets A, B of finite perimeter, and this argument fails due to the presence of different types of interfaces between the phases.
We continue by proving that a quasi-minimizer satisfies an interior ball condition. The proof of this result follows a strategy devised in Chambolle and Larsen (2003) (see also Fonseca et al. 2007; Fusco and Morini 2012) and adapted to our setting. For the reader’s convenience, we report here the details of the main nontrivial technical changes that have to be made. Since we are in dimension 2, the function \(h_u^-\) (see (2.1)) is a lower semicontinuous representative of \(h_u\); in the following it will be convenient to identify \(h_u\) with \(h_u^-\), so that in particular the subgraph \(\Omega _{h_u}^\#\) is an open set. From now on, we work under this convention.
Proposition 4.8
(Interior ball) Let \(u\in {\mathcal {A}}_{\Lambda ,M}\) and let \(\rho _0<\frac{\min \{\sigma _A,\sigma _B\}}{\Lambda }\). Then, for every \({\bar{z}}\in {\Gamma ^\#_{h_u}}\) there exists an open ball \(B_{\rho _0}(z_0)\) such that
Proof
We divide the proof into two steps. To simplify the notation, we drop the subscripts on the various objects depending on u, which is fixed along this proof. We also denote by
where \(h=h_u\) is the profile associated with the configuration u. Recall that, by the convention of identifying h with its lower semicontinuous representative \(h^-\), the set \(\Omega _h^-\) is open.
Step 1. We claim that for every ball \(B_{\rho _0}(z_0)\subset \Omega ^-_h\), where \(\rho _0\) is as in the statement, the set \(\partial B_{\rho _0}(z_0) \cap \Gamma ^\#_h\) consists of at most one point.
Suppose on the contrary that there exists a ball \(B_{\rho }(z_0)\subset \Omega _h^-\), \(z_0=(x_0,y_0)\), such that \(\partial B_{\rho }(z_0) \cap \Gamma _h^\#\) contains at least two points \(a=(x_a,y_a)\), \(b=(x_b,y_b)\), with \(x_a\le x_b\), \(h^-(x_a)\le y_a\le h^+(x_a)\), \(h^-(x_b)\le y_b\le h^+(x_b)\). We will prove that this is not possible if \(\rho \le \rho _0\). By periodicity, we assume without loss of generality that \(B_{\rho }(z_0)\subset (0,L)\times \mathbb R\).
The construction in the proof of Proposition 4.8
We define (see Fig. 5) \(\Gamma _{a,b}\) to be the arc on \(\Gamma _h\) connecting a with b, and \(\gamma _{a,b}\) to be the arc on \(\partial B_\rho (z_0)\cap \{y\ge y_0\}\) connecting a with b. Notice that by construction \(\Gamma _{a,b}\) lies above \(\gamma _{a,b}\). We also let D to be the region enclosed by \(\Gamma _{a,b}\) and \(\gamma _{a,b}\) (i.e., the bounded component of \(\mathbb R^2\backslash (\Gamma _{a,b}\cup \gamma _{a,b})\)). Also let
We construct a competitor by removing the set D from the subgraph \(\Omega _h\): more precisely, we define \({\tilde{u}}:=u\chi _{D^c}\). In this way \({\tilde{u}}\) is an admissible configuration, \(A_{{\tilde{u}}}=A\backslash D\), \(B_{{\tilde{u}}}=B\backslash D\), and the profile \(h_{{\tilde{u}}}\) coincides with h outside \([x_a,x_b]\), and its graph on \([x_a,x_b]\) is given by \(\gamma _{a,b}\). Then, by using the quasi-minimality of u we obtain
hence
To continue, we distinguish between two cases.
Case 1: assume that \(\ell _A\le L_A\), \(\ell _B\le L_B\). In this case we obtain from (4.65)
We estimate the difference \(L-\ell \) as in (Fusco and Morini (2012), Lemma 6.6); we reproduce the argument here for the reader’s convenience. Assume first that h is Lipschitz continuous. Since \(\Gamma _{a,b}\) and \(\gamma _{a,b}\) are the graphs on \([x_a,x_b]\) of h and \(h_{{\tilde{u}}}\), respectively, and \(h(x_a)=h_{{\tilde{u}}}(x_a)\), \(h(x_b)=h_{{\tilde{u}}}(x_b)\), we have
By combining this inequality with (4.66), we see that necessarily \(\rho \ge \frac{\min \{\sigma _A,\sigma _B\}}{\Lambda }\). Therefore, any ball \(B_{\rho _0}(z_0)\subset \Omega _h^-\) can touch the graph \(\Gamma _h^\#\) at most once.
If h is not Lipschitz, then we can approximate h by a sequence of Lipschitz functions \(g_k\) as in (Fusco and Morini (2012), Lemma 6.2), write the previous inequality for \(g_k\) and obtain the same conclusion by passing to the limit.
Case 2: assume that \(\ell _A>L_A\), \(\ell _B\le L_B\) (the other case, \(\ell _A\le L_A\) and \(\ell _B>L_B\), is completely analogous). In this case, thanks to the triangle inequality \(\sigma _A<\sigma _B+\sigma _{AB}\) (see (4.45)), we find by (4.65)
and in turn
One can check that
(this inequality follows essentially by (Maggi (2012), Ex. 15.14)). Therefore, using (4.67) it follows that \(\sigma _B(L-\ell )\le \Lambda |D|\) and in particular (4.66) holds. We can therefore repeat the same argument as in the previous case.
Step 2. By the result in Step 1, the existence of an interior ball at every point of \(\Gamma _h^\#\) can be proved by following the same lines as in (Chambolle and Larsen (2003), Lemma 2) or (Fonseca et al. (2007), Proposition 3.3, Step 2). \(\square \)
As a consequence of the interior ball condition proved in Proposition 4.8, we obtain the Lipschitz regularity of the free profile \(\Gamma _{h_u}^\#\) of a quasi-minimizer u outside a finite set. The proof is an adaptation of the strategy of (Chambolle and Larsen (2003), Lemma 3).
Proposition 4.9
(Lipschitz regularity) Let \(u\in {\mathcal {A}}_{\Lambda ,M}\). There exists a finite set \(\Sigma \subset Q_L\), with \(J_{h_u}\subset \Sigma \), such that \(h_u\) is locally Lipschitz in \(Q_L\backslash \Sigma \) and has left and right derivatives at every point of \(Q_L\backslash \Sigma \), that are, respectively, left and right continuous.
Proof
We denote by \(h:=h_u\) the admissible profile associated with the configuration u. For \(z\in \Gamma _{h}^\#\), we let
where \(\rho _0>0\) is given by Proposition 4.8 and \(\Omega _h^-\) is defined in (4.64). In view of Proposition 4.8, \(n(z)\ne \emptyset \) for all \(z\in \Gamma _h^\#\). Notice also that, if \(\nu \in n(z)\) for some z, then necessarily \(\nu \cdot e_2\le 0\) (or otherwise \(\Gamma _h^\#\) would not be an extended graph). We define the singular set
where \(\pi _x\) denotes the projection on the x-axis, and by \(\Sigma ^\#\) its periodic extension.
Similarly to (Chambolle and Larsen (2003), Lemma 3), one can show that the set n(z) is a closed (possibly degenerate) arc on \(\mathbb S^1\) with length strictly smaller than \(\pi \). In turn, this allows to show that \(\Sigma \) is a finite set with \(J_h\subset \Sigma \), and that h is locally Lipschitz in \(\mathbb R\backslash \Sigma ^\#\). \(\square \)
Remark 4.10
The points in the singular set \(\Sigma \) identified in Proposition 4.9 are of two possible kinds: they are either jump points of the function \(h_u\), or continuity points of \(h_u\) at which the left or the right derivative of \(h_u\) is infinite. At the upper point \((x,h_u^+(x))\) of a jump \(x\in J_{h_u}\), the graph has a vertical tangent. Notice also that the graph of \(h_u\) does not contain cusp points as a consequence of the infiltration property and the inner ball condition (see Step 1 in the proof of Proposition 4.9).
Remark 4.11
Let \(u\in {\mathcal {A}}_{\Lambda ,M}\). Since the set \(\Omega _h^\#=\{(x,y)\in \mathbb R^2: 0<y<h(x)\}\) is open, A is a quasi-minimizer of the perimeter in \(\Omega _h^\#\) in the classical sense. Thus, it is possible to apply standard regularity results (see (Maggi 2012, Theorems 26.5 and 28.1)) to obtain that \(\Gamma ^{AB}_u\) is a locally a \(C^{1,\alpha }\)-curve in \(\Omega _h^\#\) for every \(\alpha \in (0,1/2)\), and that it coincides with \(\partial A\cap \partial B\) in \(\Omega _h^\#\).
Finally, we show that the graph as a better regularity around points of \(\partial ^*A\cup \partial ^*B\). Notice that if \(h_u(x_0)=0\), then \((x_0,h_u(x_0))\notin \partial ^*A\cup \partial ^*B\), or otherwise \(V_u\) would have Lebesgue density zero at that point, which is not permitted by the infiltration property in Proposition 4.5.
Proposition 4.12
Let \(u\in {\mathcal {A}}_{\Lambda ,M}\). If \(x_0\in Q_L\backslash \Sigma \) is such that \((x_0,h_u(x_0))\in \partial ^*A\cup \partial ^*B\), then \(h_u\) is of class \(C^{1,\alpha }\) in a neighborhood of \(x_0\), for every \(\alpha \in (0,1/2)\).
Proof
To simplify the notation, we denote by \(h:=h_u\) the admissible profile associated with the configuration u, and we remove the subscript u from the sets of the corresponding partition. Recalling (4.45), we let
Step 1. Fix \(x_0\) as in the statement and let \(z_0:=(x_0,h(x_0))\). Thanks to Proposition 4.9 we can find \(r_0>0\) (depending on \(x_0\)) such that h is Lipschitz continuous in \((x_0-r_0,x_0+r_0)\), with Lipschitz constant \(\ell \in (0,\infty )\). For \(s>0\), set \(R_s:=z_0 + sR,\) where \(R:=(-1,1)\times (-2\ell ,2\ell ).\) Then,
for all \(s\in (0,r_0)\), where \(\partial ^\pm R_s :=z_0 + (-s,s)\times \{\pm 2\ell s\}.\) Moreover, by possibly reducing the value of \(r_0\), we can also assume that \(R_s\cap S=\emptyset \).
We now prove an infiltration-type property, similar to Proposition 4.5, for the two phases A, B at the point \(z_0\). Precisely, we claim that there exists \(\varepsilon >0\) (depending on \(z_0\)) such that if
for some \(0<r<r_0\), then
The same property holds if the set A is replaced by the set B.
For \(s\in (0,r_0)\) set \(m(s) :=|A\cap R_s|\). Then, for \({\mathscr {L}}^1\)-a.e. \(s\in (0,r_0)\) we have that
and that
We claim that there exist \(C_1,C_2>0\) such that for \(s\in (0,r_0)\) satisfying (4.73) and (4.74), the following differential inequality is true:
Once (4.75) is established, (4.72) will follow by a standard argument by using (4.71) and choosing \(\varepsilon \) sufficiently small, as in the last part of Step 1 in the proof of Proposition 4.5.
We are thus left with proving (4.75). The idea is to construct a suitable competitor and to use the quasi-minimality inequality for u; we have to pay attention that the competitor satisfies the graph constraint. If
then we set (see Fig. 6)
where for a measurable set \(E\subset R_s\) we define
with \(E_x:=\{t\in \mathbb R:\, (x,t)\in E \}\). In the case where
we set instead
Note that the configuration \(v_s=\chi _{A_s}-\chi _{B_s}\) is an admissible competitor for the quasi-minimality inequality in Definition 4.1. In the first case, this follows from (4.70), while in the second case the free profile of the configuration is left unchanged. Denote by \(h_s:Q_L\rightarrow [0,\infty )\) the admissible profile such that \(\Omega _{h_s}=A_s\cup B_s\).
Assume that (4.76) holds, and thus \(A_s\) and \(B_s\) are defined as in (4.77). Then, by an argument similar to (Giusti (1984), Lemma 14.7) one can prove that
Moreover, one can check that

and that
The quasi-minimality of u, together with (4.73), (4.74), (4.81), (4.82), and (4.83), yields
By using (4.69), (4.76), and the isoperimetric inequality, we estimate
By inserting (4.85) into (4.84) we obtain the desired inequality (4.75) in the case where assumption (4.76) holds.
Assume now that (4.79) is in force, and thus \(A_s\) and \(B_s\) are defined as in (4.80). In this case, the quasi-minimality inequality for u yields, using also (4.73) and (4.74),
By using (4.69), (4.79), and the isoperimetric inequality, we estimate (with similar computations as those used to get (4.85))
By inserting (4.87) into (4.86) we obtain the desired inequality (4.75) also in the case where assumption (4.79) holds.
Step 2. We conclude as follows. Let \(x_0\) be as in the statement, and let \(z_0:=(x_0,h(x_0))\in \partial ^*A\cup \partial ^*B\). Assume \(z_0\in \partial ^*B\). Let \(r_0>0\) be as in Step 1, so that h is Lipschitz continuous in \((x_0-r_0,x_0+r_0)\) with Lipschitz constant \(\ell \). Let also \(\varepsilon >0\) be given by Step 1. Then, since \(z_0\in \partial ^*B\cap \partial ^*V\), it is possible to find \(r\in (0,r_0)\) such that \(|A\cap R_r(z_0)|<\varepsilon r^2.\) From Step 1 we get that \(|A\cap R_{r/2}|=0\). This implies that in \(R_{r/2}\) there are only the sets V and B. In particular, we also have \(\partial ^+R_{r/2}\subset B^{(0)}\), \(\partial ^-R_{r/2}\subset B^{(1)}\) (recall (4.70)), and \(B\cap R_{r/2}\) is the subgraph of a function of bounded variation.
Let now \(E\subset R_{r/2}\) be any set of finite perimeter such that \(E{\bigtriangleup }B\subset \subset R_{r/2}\), and let \(E^G\) be the set defined in (4.78). We can test the quasi-minimality inequality with the competitor obtained by replacing the phase \(B\cap R_{r/2}\) by \(E^G\), which is admissible since it satisfies the graph constraint. We therefore find
We observe now that, similarly to (4.81), we have \({\mathscr {P}}(E^G;R_{r/2})\le {\mathscr {P}}(E;R_{r/2})\); moreover (since \(B\cap R_{r/2}=(B\cap R_{r/2})^G\)) we also have
Then, inserting the previous inequalities inside (4.88) we find
for every set of finite perimeter \(E\subset R_{r/2}\) such that \(E{\bigtriangleup }B\subset \subset R_{r/2}\). This shows that B is a quasi-minimizer of the perimeter inside \(R_{r/2}\) in the classical sense, that is without the graph constraint. Thus, the regularity of \(\Gamma _h\cap R_{r/2}=\partial ^*B\cap R_{r/2}\) follows from classical regularity results for quasi-minimizers of the perimeter (see, for instance, (Maggi 2012, Theorems 26.5 and 28.1)). This concludes the proof. \(\square \)
By collecting all the previous statements, we obtain the properties listed in Theorem 1.1.
Proof of Theorem 1.1
The infiltration property (i) follows by Proposition 4.5 and Proposition 4.6. The Lipschitz regularity (ii) and the characterization of the singular set (iii) are proved in Proposition 4.9 and Remark 4.10. The internal regularity of the interface (iv) is discussed in Remark 4.11. The \(C^{1,\alpha }\)-regularity of the graph (v) is proved in Proposition 4.12. \(\square \)
References
Acerbi, E., Fusco, N., Morini, M.: Minimality via second variation for a nonlocal isoperimetric problem. Comm. Math. Phys. 322, 515–557 (2013)
Ambrosio, L., Braides, A.: Functionals defined on partitions in sets of finite perimeter. II. Semicontinuity, relaxation and homogenization. J. Math. Pures Appl. 69(9), 307–333 (1990)
Ambrosio, L., Fusco, N., Pallara, D.: Functions of bounded variation and free discontinuity problems. Oxford Mathematical Monographs, The Clarendon Press, Oxford University Press, New York (2000)
Bates, F.S., Fredrickson, G.H.: Block copolymers-Designer soft materials. Phys. Today 52, 32 (1999)
Bonacini, M., Knüpfer, H.: Ground states of a ternary system including attractive and repulsive Coulomb-type interactions. Calc. Var. Partial Differ. Equ. 55, 114, 31 (2016)
Bonnetier, E., Chambolle, A.: Computing the equilibrium configuration of epitaxially strained crystalline films. SIAM J. Appl. Math. 62, 1093–1121 (2002)
Chambolle, A., Larsen, C.J.: \(C^\infty \) regularity of the free boundary for a two-dimensional optimal compliance problem. Calc. Var. Partial Differ. Equ. 18, 77–94 (2003)
Chambolle, A., Solci, M.: Interaction of a bulk and a surface energy with a geometrical constraint. SIAM J. Math. Anal. 39, 77–102 (2007)
Choksi, R., Ren, X.: Diblock copolymer/homopolymer blends: derivation of a density functional theory. Phys. D 203, 100–119 (2005)
Crismale, V., Friedrich, M.: Equilibrium configurations for epitaxially strained films and material voids in three-dimensional linear elasticity. Arch. Ration. Mech. Anal. 237, 1041–1098 (2020)
Darling, S.: Directing the self-assembly of block copolymers. Prog. Polym. Sci. 32, 1152–1204 (2007)
Davoli, E., Piovano, P.: Analytical validation of the Young-Dupré law for epitaxially-strained thin films. Math. Models Methods Appl. Sci. 29, 2183–2223 (2019)
De Simone, A., Kohn, R., Müller, S., Felix, O.: A reduced theory for thin-film micromagnetics. Comm. in Pure Appl. Math. 55, 1408–1460 (2002)
Esposito, L., Fusco, N.: A remark on a free interface problem with volume constraint. J. Convex Anal. 18, 417–426 (2011)
Fonseca, I., Fusco, N., Leoni, G., Morini, M.: Equilibrium configurations of epitaxially strained crystalline films: existence and regularity results. Arch. Ration. Mech. Anal. 186, 477–537 (2007)
Fredrickson, G.H.: Surface ordering phenomena in block copolymer melts. Macromolecules 20, 2535–2542 (1987)
Fusco, N., Morini, M.: Equilibrium configurations of epitaxially strained elastic films: second order minimality conditions and qualitative properties of solutions. Arch. Ration. Mech. Anal. 203, 247–327 (2012)
Giusti, E.: Minimal Surfaces and Functions of Bounded Variation. Monographs in Mathematics, vol. 80. Birkhäuser Verlag, Basel (1984)
Gonzalez, E., Massari, U., Tamanini, I.: On the regularity of boundaries of sets minimizing perimeter with a volume constraint. Indiana Univ. Math. J. 32, 25–37 (1983)
Hill, J., Millett, P.: Numerical simulations of directed self-assembly in diblock copolymer films using zone annealing and pattern templating. Sci. Rep. 7, 5250 (2017)
Huang, C., Zhu, Y., Man, X.: Block copolymer thin films. Phys. Rep. 932, 1–36 (2021)
Leonardi, G.P.: Infiltrations in immiscible fluids systems. Proc. Roy. Soc. Edinb. Sect. A 131, 425–436 (2001)
Lyakhova, K.S., Horvat, A., Zvelindovsky, A.V., Sevink, G.J.A.: Dynamics of terrace formation in a nanostructured thin block copolymer film. Langmuir 22, 5848–5855 (2006)
Maggi, F.: Sets of Finite Perimeter and Geometric Variational Problems. Cambridge Studies in Advanced Mathematics, vol. 135. Cambridge University Press, Cambridge (2012)
Matsen, M.W.: Thin films of block copolymer. J. Chem. Phys. 106, 7781–7791 (1997)
Matsen, M.W.: Self-assembly of block copolymers in thin films. Curr. Opin. Colloid Interface Sci. 3, 40–47 (1998)
Matsen, M.W., Bates, F.S.: Unifying weak- and strong-segregation block copolymer theories. Macromolecules 29, 1091–1098 (1996)
Matsen, M.W., Schick, M.: Stable and unstable phases of a diblock copolymer melt. Phys. Rev. Letter 72, 1091–1098 (1994)
Morgan, F.: Lowersemicontinuity of energy clusters. Proc. Roy. Soc. Edinb. Sect. A 127, 819–822 (1997)
Ohta, T., Kawasaki, K.: Equilibrium morphology of block copolymer melts. Macromolecules 19, 2621–2632 (1986)
Parsons, Q., Kay, D., Münch, A.: Step evolution in two-dimensional diblock copolymer film, arXiv:1712.01387
Radzilowski, L.H., Carvalho, B.L., Thomas, E.L.: Structure of minimum thickness and terraced free-standing films of block copolymers. J. Polym. Sci. Part B Polym. Phys. 34, 3081–3093 (1996)
Segalman, R.A.: Patterning with block copolymer thin films. Mater. Sci. Eng. R 48, 191–226 (2005)
Stasiak, P., McGraw, J., Dalnoki-Veress, K., Matsen, M.: Step edges in thin films of lamellar-forming diblock copolymer. Macromolecules 45, 9531–9538 (2012)
Thomas, E., Anderson, D., Henkee, C., Hoffman, D.: Periodic area-minimizing surfaces in block copolymers. Nature 334, 598–601 (1988)
van Dijk, M.A., van den Berg, R.: Ordering phenomena in thin block copolymer films studied using atomic force microscopy. Macromolecules 28, 6773–6778 (1995)
van Gennip, Y., Peletier, M.A.: Copolymer-homopolymer blends: global energy minimisation and global energy bounds. Calc. Var. Partial Differential Equations 33, 75–111 (2008)
van Gennip, Y., Peletier, M.A.: Stability of monolayers and bilayers in a copolymer-homopolymer blend model. Interfaces Free Bound. 11, 331–373 (2009)
White, B.: Existence of least-energy configurations of immiscible fluids. J. Geom. Anal. 6, 151–161 (1996)
Yokoyama, H., Mates, T.E., Kramer, E.J.: Structure of asymmetric diblock copolymers in thin films. Macromolecules 33, 1888–1898 (2000)
Acknowledgements
MB is member of 2020 INdAM - GNAMPA project Variational Analysis of nonlocal models in applied science. During the period at Heriot-Watt University, the research of RC was supported by the UK Engineering and Physical Sciences Research Council (EPSRC) via the grant EP/R013527/2 Designer Microstructure via Optimal Transport Theory.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Rustum Choksi.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bonacini, M., Cristoferi, R. Area Quasi-minimizing Partitions with a Graphical Constraint: Relaxation and Two-Dimensional Partial Regularity. J Nonlinear Sci 32, 93 (2022). https://doi.org/10.1007/s00332-022-09852-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00332-022-09852-3