Geometric Control of Two Quadrotors Carrying a Rigid Rod with Elastic Cables

Abstract

This paper presents the design of a geometric trajectory tracking controller for an underactuated multi-body system describing the cooperative task of two quadrotor UAVs (unmanned aerial vehicles) carrying and transporting a rigid bar, which is attached to the quadrotors via inflexible elastic cables. The elasticity of the cables together with techniques of singular perturbation allows a reduction in the model to that of a similar model with inelastic cables. In this reduced model, we design a controller such that the rod exponentially tracks a given desired trajectory for its position and attitude, under some assumptions on initial error. We then show that exponential tracking in the reduced model corresponds to exponential tracking of the original elastic model. We also show that the previously defined control scheme provides uniform ultimate boundedness in the presence of unstructured bounded disturbances.

1 Introduction

The use of aerial robots has become increasingly popular in the last decades due to their superior mobility and versatility in individual and cooperative tasks (Palunko et al. 2012). For instance, aerial robots equipped with manipulators can be utilized for mobile manipulation tasks such as rescue operations and transportation of a cargo. Control design of aerial robots transporting objects has been studied in Maza et al. (2010), Michael et al. (2011), Pereira and Dimarogonas (2019), Pereira and Dimarogonas (2020), Thapa et al. (2020), typically with the goal of having the load track some given trajectory. Several UAVs can be used to transport heavier payloads, thus expanding the capabilities of a single UAV (Gassner et al. 2017). However, each additional UAV adds to the degrees of under-actuation in the system, making control design more difficult.

In aerial transportation, a cable establishes a physical connection between the UAV and the cargo. Geometric nonlinear controllers of multiple quadrotors with a suspended point-mass load were studied in Sreenath et al. (2013) and with a rigid body load in Lee (2014), Wu and Sreenath (2014)—where in particular the cables were modeled as inflexible, inelastic, and massless. In Goodarzi and Lee (2015), the authors model the cables as flexible chains comprised of inflexible, inelastic links with mass. While these works have considered the cable to be inelastic, we are instead motivated by applications where the elasticity in the cable tethers cannot be ignored without compromising the validity of the estimations (Joshi and Rahn 1995). In this paper, we study the problem of two quadrotor UAVs transporting a rigid rod suspended through elastic cables, with the aim of designing a geometric control scheme for the tracking of arbitrary trajectories for the position and attitude of the rod. However, even in the simplest case of a single quadrotor UAV transporting a point-mass load via a massless inflexible elastic cable, as studied in Kotaru et al. (2017) and Wu and Sreenath (2014), the system fails to be differentially flat—making control design a challenging problem. One strategy to fix this is—and that which we utilize here is to reduce the model to the corresponding model with inelastic cables, which is differentially flat, and designing the control scheme in this reduced model. This is accomplished by taking advantage of the fact that elastic cables are typically quite stiff in practice.

The use of geometric controllers in the UAVs literature has been extensively developed in the last years (see, for instance, Chaturvedi et al. (2011), Sanyal et al. (2011), Sanyal et al. (2005), Izadi and Sanyal (2016), Lee (2014), Lee (2015), Lee (2018), Lee et al. (2013), Maithripala et al. (2006), and references therein). In particular, geometric controllers for UAVs as underactuated multi-body systems have been developed in Kobilarov (2014), Kobilarov (2013). In this paper, we propose a coordinate-free form of the equations of motion for the cooperative task, which are derived according to Lagrangian mechanics on manifolds-in particular, via the Lagrange d’Alembert principle for forced systems (Bloch 2015). Working directly on the manifold allows us to avoid potential singularities of local parameterizations (e.g., Euler Angles), generating agile maneuvers of the payload in a uniform manner. In particular, in this work, a geometric control scheme for an underactuated multi-body system taking the form of a geometric PD controller (with additional feedback terms) is designed such that both the rigid rod’s position and attitude track a given desired trajectory exponentially fast.

The main contributions of this work are: (i) the modeling and subsequent derivation of the corresponding equations of motion for the cooperative task of two quadrotor UAVs transporting a rigid rod via inflexible elastic cables. The modeling and dynamics are summarized in Proposition 1. (ii) Reduction of these equations of motion to the case of inelastic cables under the assumption of sufficiently high spring damping and stiffness. This can be considered an extension of the results obtained in Kotaru et al. (2017), which studies the case of a single quadrotor transporting a point mass load via an inflexible elastic cable. The reduced model is shown to be differentially flat in Lemma 1, with the connection points of the cables to the rod and the yaw angles of the quadrotors serving as flat outputs. This is developed in Sect. 3 and employed in Sect. 4 where (iii) we provide a geometric control scheme for the exponential tracking of the load position and attitude to some desired trajectories. The proposed controller is inspired by, and takes a similar form to, that which is found in Lee (2018)—which studies the case of a team of quadrotor UAVs transporting a rigid body with rigid cables. It is important to note that such a controller cannot be applied directly to our problem, as it requires a minimum of 3 UAVs and at least a 2-dimensional rigid body. The major consequences of the rigid rod being a 1-dimensional rigid body come in the description of the attitude—which lies in the unit sphere $S^2$ as opposed to the special orthogonal group $\text {SO}(3)$—and also by the fact that the inertia tensor is singular. Lyapunov analysis is used to determine sufficient conditions for exponential tracking. Theorem 1 then proves the existence of stabilizing gains—for sufficiently small initial errors in the cables—which results in exponential tracking of arbitrary trajectories. We additionally move this control scheme back to the original (elastic) model, where it is shown that the system converges exponentially fast to some neighborhood of the desired trajectory whose size depends upon the spring constant and damping coefficient of the cables. Finally, (iv) we apply the same control scheme in the presence of unstructured bounded disturbances acting on the system. In particular, in Theorem 2 we show that the same control scheme will yield uniform ultimate boundedness in the case of unstructured bounded disturbances acting on the system. Moreover, the ultimate bound can be made arbitrarily small by choosing gains appropriately.

The rest of the paper is structured as follows. In Sect. 2, we model and derive the dynamical system describing the task of carrying and transport a rigid rod between two quadrotors by elastic cables. This is done by constructing the Lagrangian of the cooperative system and subsequently applying the Lagrange d’Alembert principle. Section 3 reduces the dynamical model introduced in Sect. 2 by employing singular perturbation theory techniques. The main results of the work are given in Sects. 4 and 5. We first introduce configuration error functions for each state variable, from which we derive the error dynamics. The geometric controls are constructed in order that the origin is an exponentially stable equilibrium point of the error dynamics. After this analysis, we return to the original model to adequate our geometric control such that trajectories of the original model exponentially track their desired trajectories up to a neighborhood whose size shrinks uniformly with increasing spring stiffness and damping. In Sect. 5, we introduce unstructured bounded disturbances to the reduced model and show that the same control scheme can be applied to achieve uniform ultimate boundedness. Numerical simulations are shown to validate the theoretical results.

Fig. 1

Modeling of the mechanical system describing the cooperative transportation task

2 Modeling and Control Equations

In this section, we model and derive the dynamical system describing the cooperative task between the quadrotors, an underactuated multi-body system. This can be done by constructing the total kinetic and potential energies of the mechanical system describing the cooperative task—in addition to the virtual work done by non-conservative forces—and subsequently using the tools of Lagrangian mechanics on manifolds (Bloch 2015).

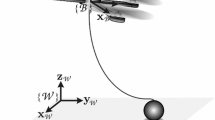
Consider two identical quadrotor UAVs transporting a rigid rod of length $2L_\mathrm{r}$ and total mass $m_\mathrm{r}$ as it is shown in Fig. 1. The rod is considered inflexible and of uniform mass density. Each endpoint of the rod is connected to the center of mass of one quadrotor via a massless inflexible elastic cable of rest length $L_\mathrm{c}$. Note that we consider the rest lengths of both cables to be the same, however this in general will not affect the analysis in the remainder of the paper and can be easily modified to consider cables with different rest lengths.

The basic notation and methodology is fairly standard within the literature and we have attempted to use traditional symbols and definitions wherever feasible. Table 1 provides the symbols and geometric spaces that are used frequently throughout the paper.

Table 1 Nomenclature

The configuration space of the mechanical system is given by

$Q = \underbrace{(S^2 \times \mathbb {R}^3)}_\text {Rigid rod} \times \underbrace{(S^2 \times \mathbb {R})^2}_\text {Cables} \times \underbrace{(\text {SO}(3) \times \text {SO}(3))}_\text {Quadrotor attitudes}$. Hence, we have 17 degrees of freedom—5 degrees corresponding to the rod, 3 degrees for each cable, and 3 degrees for each quadrotor. Observe that the positions of the quadrotors do not appear in the configuration space, as they are uniquely defined in terms of the other state variables due to the holonomic constraint $x_{Q_j} = x_\mathrm{r} + (-1)^j L_\mathrm{r} q_\mathrm{r} - l_j q_j$ for $j = 1,2.$ Meanwhile, we have 8 inputs to the system in the form of two thrust controls $f_1, f_2 \in \mathbb {R}$, corresponding to the total lift force exerted on the quadrotors by the spinning propellers, and two moment controls $M_1, M_2 \in \mathbb {R}^3$, which are related to the torques induced on the quadrotors by the rotating propellers. Thus, the complete systems have 9 degrees of under-actuation. Note also that upon fixing a body frame to each quadrotor such that the vector $\bar{e}_3 = [0, 0, 1]^T$ points in the direction of the applied thrust, we may additionally express the thrust controls $f_j$ via the vectors $u_j=f_jR_je_3\in \mathbb {R}^3$ in the inertial frame for $j = 1,2$. We will utilize this representation frequently throughout the paper. Note that only the quadrotor attitudes and positions are directly actuated by the control inputs. Hence, we will control the load position and attitude (the primary goal of our trajectory tracking problem) indirectly by finding the quadrotor positions and attitudes corresponding to our desired load trajectory.

Remark 1

Observe that, instead of controlling the total thrust and moment, we may choose to control the total thrust of each propeller individually. Such an approach is equivalent under certain assumptions. In particular, we have a correspondence of the form $\begin{bmatrix} f_j&M_j^T \end{bmatrix}^T = K \begin{bmatrix} f_j^1&f_j^2&f_j^3&f_j^4 \end{bmatrix}^T$, where $f_j^k$ is the thrust exerted by the $k^{\text {th}}$ propeller of the $j^{\text {th}}$ quadrotor for $j = 1,2$, and K is a $4\times 4$ matrix (Lee et al. 2010). Under the assumption that the propellers lie in a plane and adjacent propellers spin in opposite directions, K is invertible and so the approaches are equivalent. More general UAVs, such as those with different numbers of propellers (e.g., hexarotors) and those with alternative propeller orientations and altitudes may be considered. In such cases, the results obtained throughout the remainder of the article will similarly apply as long as a similar one-to-one correspondence can be established between the total thrust and moment control pair and the individual thrusts of the propellers. That said, we choose to work with the total thrust control and moment control because they lead to the (very convenient) decoupling of the quadrotor attitude dynamics from the rest of the system dynamics, as will be seen in Proposition 1.

The translational kinetic energy of each quadrotor can be described by $\frac{1}{2} m_\mathrm{Q} ||\dot{x}_{Q_j}||^2$, where $m_\mathrm{Q}$ denotes the mass of the quadrotor. Similarly, the translational kinetic energy of the rod is $\frac{1}{2}m_\mathrm{r} ||\dot{x}_\mathrm{r}||^2$. As the quadrotors and rod are rigid bodies, we further have rotational kinetic energy components in the total kinetic energy. Fixing a body frame to each quadrotor and denoting the angular velocity in this body frame by $\Omega _j\in \mathbb {R}^{3}$, the angular kinetic energy is given by $\frac{1}{2}\Omega _j^T J_\mathrm{Q} \Omega _j$, where $J_\mathrm{Q}$ is a symmetric positive-definite inertia tensor. $\Omega _j$ is defined implicitly by the kinematic equation $\dot{R}_j = R_j \hat{\Omega }_j$, where $\hat{\cdot }: \mathbb {R}^3 \rightarrow \mathfrak {so}(3)$ is the hat isomorphism which maps vectors on $\mathbb {R}^{3}$ to $(3\times 3)$ skew-symmetric matrices

$$\begin{aligned} \Omega = \begin{bmatrix} \Omega _1 \\ \Omega _2 \\ \Omega _3 \end{bmatrix} \mapsto \begin{bmatrix} 0 &{} -\Omega _3 &{} \Omega _2 \\ \Omega _3 &{} 0 &{} -\Omega _1 \\ -\Omega _2 &{} \Omega _1 &{} 0 \end{bmatrix} := \hat{\Omega }. \end{aligned}$$

The angular kinetic energy of the rod is similarly given by $\frac{1}{2} \Omega _\mathrm{r}^T J_\mathrm{r} \Omega _\mathrm{r}$; however, the symmetry of the rod allows us to reinterpret the expression. In particular, we will fix a body frame to one of the endpoints of the rod with $e_1 := q_\mathrm{r}$ as one of the (orthonormal) basis vectors. In this frame, the component of the (body) angular velocity along $e_1$ is identically zero. Moreover, we can describe the inertia tensor explicitly by $J_\mathrm{r}= \begin{bmatrix} 0 &{} 0 &{} 0 \\ 0 &{} \frac{4}{3} m_\mathrm{r} L_\mathrm{r}^2 &{} 0 \\ 0 &{} 0 &{} \frac{4}{3} m_\mathrm{r} L_\mathrm{r}^2 \end{bmatrix}$. From this it is clear that $\frac{1}{2} \Omega _\mathrm{r}^T J_\mathrm{r} \Omega _\mathrm{r} = \frac{2}{3} m_\mathrm{r} L_\mathrm{r}^2 ||\Omega _\mathrm{r}||^2$.

The angular velocity of the rod in the inertial frame is defined implicitly by the kinematic relation $\dot{q}_\mathrm{r} = \omega _\mathrm{r} \times q_\mathrm{r}$ together with the condition that $\omega _\mathrm{r}^T q_\mathrm{r} = 0$, from which it is obvious that $||\dot{q}_\mathrm{r}|| = ||\omega _\mathrm{r}||$. Moreover, for some rotation $R_\mathrm{r} \in \text {SO}(3)$, we have $\Omega _\mathrm{r} = R_\mathrm{r} \omega _\mathrm{r}$, and since the norm of a vector is invariant under the action of $\text {SO}(3)$, we see that $||\Omega _\mathrm{r}|| = ||\dot{q}_\mathrm{r}||$. Altogether, the angular kinetic energy of the rod is given by $\frac{2}{3} m_\mathrm{r} L_\mathrm{r}^2 ||\dot{q}_\mathrm{r}||^2$.

Recall that elements in the tangent space $T_{R}SO(3)$ are identified with elements in $SO(3)\times \mathfrak {so}(3)$ by a left-trivialization. That is, the diffeomorphism $(R,\dot{R})\in T_{R}SO(3)\mapsto (R,R^{-1}\dot{R})=:(R,\hat{\Omega })\in SO(3)\times \mathfrak {so}(3)$ (see Holm et al. (2009) for details). Therefore, after a left trivialization of TSO(3), the tangent bundle of Q can be identified as

$$\begin{aligned} TQ \cong (S^2 \times TS^2 \times \mathbb {R}^3\times \mathbb {R}^3)\times (S^2 \times TS^2 \times \mathbb {R}\times \mathbb {R}) \times (\text {SO}(3)\times \mathfrak {so}(3))^2. \end{aligned}$$

Finally, the total kinetic energy $K: TQ \rightarrow \mathbb {R}$ of the system is given by summing the respective translational and angular kinetic energies of the quadrotors and rigid rod:

$$\begin{aligned} K =\underbrace{\frac{1}{2}m_\mathrm{r} ||\dot{x}_\mathrm{r}||^2 + \sum _{j=1}^{2} \frac{1}{2}m_\mathrm{Q} ||\dot{x}_{Q_j}||^2}_\text {Translational K.E.} + \underbrace{\frac{2}{3} m_\mathrm{r} L_\mathrm{r}^2 ||\dot{q}_\mathrm{r}||^2 + \sum _{j=1}^{2} \frac{1}{2}\Omega _j^T J_\mathrm{Q} \Omega _j. }_\text {Angular K.E.} \end{aligned}$$

Next, we fix a basis for the inertial frame such that $e_3$ is oriented opposite to the direction of gravitational acceleration, in which the total potential energy $U: Q \rightarrow \mathbb {R}$ of the system is given by

$$\begin{aligned} U = \sum _{j=1}^{2}\underbrace{m_\mathrm{Q} ge_3^T x_{Q_j} + m_\mathrm{r} g e_3^T x_\mathrm{r}}_\text {Gravitational P.E.} + \sum _{j=1}^{2} \underbrace{ \frac{1}{2}k(L_\mathrm{c} - l_j)^2,}_\text {Elastic P.E.} \end{aligned}$$

which corresponds to the gravitational potential energies of the quadrotors and the rigid rod, as well as the elastic potential of the cables. As usual, the Lagrangian of the system $L: TQ \rightarrow \mathbb {R}$ is defined by $L:= K - U$.

Note that these controls take the form of non-conservative external forces, so that we must use the Lagrange d’Alembert Variational Principle (see Bloch (2015), for instance)—with controls playing the role of the virtual forces in our system—to obtain our system dynamics from the Lagrangian L. We further wish to add a non-conservative force corresponding to a damping in the elastic cables. In particular, we use the standard model of a damped harmonic oscillator (Joshi and Rahn 1995; Cartmell and McKenzie 2008), used, for instance, in surgical robotic applications (Agrawal et al. 2008), wherein the damping force is proportional to the rate of oscillation of the spring, and is applied in the direction which serves to reduce the amplitude of the oscillations. It should be noted that this model may fail in the case of high oscillation rates—in which nonlinear velocity dependent terms may begin to dominate. Throughout the paper, we will assume implicitly that we remain in the low-velocity regime. This in part is justified by the assumption that the spring constant k and damping coefficient c are large, which naturally prevents this extreme behavior.

Note also that the fact that the inertia tensor of the rigid rod is singular give rise to a cyclic variable in the Lagrangian. In particular, since $\frac{\partial K}{\partial \Omega _1}=0$ one might be able to obtain a conserved quantity and reduce one degree of freedom of the system. This might be obtained through the Routh reduction procedure for abelian Lie groups of symmetries (Bloch 2015; Marsden and Ratiu 1999). This has been done before in aerospace applications, e.g., the dumbbell spacecraft model used in Sanyal et al. (2005).

Denote by $C^{\infty }(Q,q_0,q_T)$ the space of smooth function from [0, T] to Q with fixed endpoints points, denoted by $q_0$ and $q_T$, respectively. Consider the action functional $\mathcal {A}:C^{\infty }(Q,q_0,q_T)\rightarrow \mathbb {R}$ given by

$$\begin{aligned} \mathcal {A}(c(t))=\int _{0}^{T} L(c(t),\dot{c}(t))\, \mathrm{d}t + \sum _{j=1}^{2} \int _{0}^{T} \left( ||f_jR_je_3||_{\mathbb {R}^{3}}^{2} + ||\hat{M}_j||^2_{\mathfrak {so}(3)} - c \dot{l}_j\right) \,\, \mathrm{d}t = 0, \end{aligned}$$

(1)

where $||\hat{M}_j||_{\mathfrak {so}(3)}:=\langle \hat{M}_j,\hat{M}_j\rangle ^{1/2}=\sqrt{\hbox {Tr}(\hat{M}_j^{T}\hat{M}_j)}$, with $c(t):=(q_\mathrm{r}(t),x_\mathrm{r}(t),q_j(t),l_j(t),R_j(t)))\in C^{\infty }(Q,q_0,q_T)$. In order to use the aforementioned Lagrange d’Alembert Variational Principle, we must describe the variations of our state variables. These variations must be tangent vectors in the tangent spaces of the submanifolds of the configuration space in which the state variables live. In addition, they must vanish at the end points, because tangent vectors on the tangent bundle of $C^{\infty }(Q,q_0,q_T)$ must satisfy such a condition (see for instance Holm et al. 2009; Marsden and Ratiu 1999).

In particular, we choose $\delta x_\mathrm{r} \in \mathbb {R}^3$ and $\delta l_j \in \mathbb {R}$ arbitrary, $\delta q_j = \frac{\mathrm{d}}{\mathrm{d}\epsilon }\mid _{\epsilon =0}\exp (\epsilon \hat{\xi }_j)q_j=\xi _j \times q_j \in T_{q_j} S^2$, $\delta q_\mathrm{r}=\frac{\mathrm{d}}{\mathrm{d}\epsilon }\mid _{\epsilon =0}\exp (\epsilon \hat{\xi }_\mathrm{r})q_\mathrm{r}= \xi _\mathrm{r} \times q_\mathrm{r}\in T_{q_\mathrm{r}} S^2$, satisfying $\xi _j\cdot q_j=0$ and $\xi _\mathrm{r}\cdot q_\mathrm{r}=0$, for arbitrary vectors $\xi _j, \ \xi _\mathrm{r} \in \mathbb {R}^3$ and $j = 1,2$. In addition by defining the curve on the Lie algebra $\mathfrak {so}(3)$ given by $\hat{\eta }_j = R_j^T \delta R_j \in \mathfrak {so}(3)$, it can be shown that (see, for instance, (Marsden and Ratiu 1999) Chapter 13) $\widehat{\delta \Omega }_j = \hat{\Omega }_j \hat{\eta }_j + \dot{\hat{\eta }}_j$ with $\hat{\eta }_j$ satisfying $\hat{\eta }_j(0)= \hat{\eta }_j(T)=0$ (since $\delta R_j(0)=\delta R_j(T)=0)$. Moreover, we have the following relations

$$\begin{aligned} \delta x_{Q_j}&= \delta x_\mathrm{r} + (-1)^jL_\mathrm{r} \delta q_\mathrm{r} - (\delta l_j) q_j - l_j (\delta q_j), \\ \delta \dot{x}_{Q_j}&= \delta \dot{x}_\mathrm{r} + (-1)^j L_\mathrm{r} \delta \dot{q}_\mathrm{r} - (\delta \dot{l}_j) q_j - (\delta l_j) \dot{q}_j - \dot{l}_j (\delta q_j) - l_j (\delta \dot{q}_j). \end{aligned}$$

Proposition 1

Critical points of the action functional $\mathcal {A}$ for variations with fixed endpoints corresponds with solutions of the controlled Euler–Lagrange equations

$$\begin{aligned} \dot{x}_\mathrm{r}&= v_\mathrm{r}, \end{aligned}$$

(2)

$$\begin{aligned} m_{\text {eff}} ( \dot{v}_\mathrm{r} + ge_3)&= u_1 + u_2 + m_\mathrm{Q} (\ddot{\zeta }_1 + \ddot{\zeta }_2 ), \end{aligned}$$

(3)

$$\begin{aligned} \dot{q}_\mathrm{r}&= \omega _\mathrm{r} \times q_\mathrm{r}, \end{aligned}$$

(4)

$$\begin{aligned} I_{\text {eff}} \dot{\omega }_\mathrm{r}&= q_\mathrm{r} \times \left[ u_2 - u_1 + m_\mathrm{Q}( \ddot{\zeta }_{2} - \ddot{\zeta }_1) \right] , \end{aligned}$$

(5)

$$\begin{aligned} m_\mathrm{Q} q_j^T \ddot{\zeta }_j&= m_\mathrm{Q} q_j^T \left( \dot{v}_\mathrm{r} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r} + ge_3 - \frac{1}{m_\mathrm{Q}}u_j\right) - c \dot{l}_j + k(L_\mathrm{c} - l_j), \end{aligned}$$

(6)

$$\begin{aligned} q_j \times \ddot{\zeta }_j&= q_j \times \left( \dot{v}_\mathrm{r} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r} + ge_3 - \frac{1}{m_\mathrm{Q}} u_j\right) , \end{aligned}$$

(7)

$$\begin{aligned} \dot{R}_j&= R_j \hat{\Omega }_j, \end{aligned}$$

(8)

$$\begin{aligned} J_\mathrm{Q} \dot{\Omega }_j&= J_\mathrm{Q} \Omega _j \times \Omega _j + M_j, \quad \text {for}\, j = 1,2, \end{aligned}$$

(9)

where $m_{\text {eff}} := 2m_\mathrm{Q} + m_\mathrm{r}, \ I_{\text {eff}} := (2m_\mathrm{Q} + \frac{2}{3} m_\mathrm{r})L_\mathrm{r}$, and $\zeta _{j} := l_j q_j$.

Remark 2

Equations (2)–(3) describe the kinematics and dynamics of the rod’s position, respectively. Similarly, Eqs. (4)–(5) describe the kinematics and dynamics of the rod’s attitude, and Eqs. (8)–(9) correspond with the kinematics and dynamics of the attitudes of each quadrotor, respectively.

Equation (6), indexed for $j = 1,2$, describes the dynamics of the lengths of the elastic cables. This can be understood by observing that the projection of $\ddot{\zeta }_j$ onto $q_j$ preserves the acceleration of the length (which is inherently oriented along the cable), while removing the acceleration of the attitude from consideration with the identity $q_j^T \ddot{q}_j = -||\dot{q}_j||^2$. Conversely, Eq. (7), indexed for $j = 1,2$, describes the dynamics of the attitudes of the elastic cables, as the cross-product with $q_j$ preserves the acceleration of the cable attitude while annihilating the acceleration of the cable length.

Proof of Proposition 2.1

We wish to apply Lagrange–d’Alembert Variational Principle. Therefore, our system dynamics must satisfy

$$\begin{aligned} \delta \int _{0}^{T} L(c(t),\dot{c}(t))\, \mathrm{d}t + \sum _{j=1}^{2} \int _{0}^{T} \left( \delta x_{Q_j}^T u_j + \left<R_j^T \delta R_j, \hat{M}_j\right> - c \dot{l}_j\delta l_j\right) \mathrm{d}t = 0, \end{aligned}$$

(10)

where the integral on the right represents the virtual work done by the thrust controls $u_j$, the moment controls $M_j \in \mathbb {R}^3$, and the spring damping, respectively.

Expanding the variations within (10), substituting the corresponding infinitesimal variations, and grouping like terms, we obtain

$$\begin{aligned} 0&= \int _0^{T} \left[ \delta \dot{x}_\mathrm{r}^T ( m_{\text {eff}} \dot{x}_\mathrm{r} - m_\mathrm{Q}(\dot{\zeta }_1 + \dot{\zeta }_2)) + \delta x_\mathrm{r}^T (-m_{\text {eff}} ge_3 + u_1 + u_2 ) \right] \mathrm{d}t \\&\quad + \ L_\mathrm{r} \int _0^{T} \left[ \dot{\xi }_\mathrm{r}^T ( q_\mathrm{r} \times (I_{\text {eff}} \dot{q}_\mathrm{r} + m_\mathrm{Q}(\dot{\zeta }_2 - \dot{\zeta }_1 )) + \xi _\mathrm{r}^T (\dot{q}_\mathrm{r} \times m_\mathrm{Q}(\dot{\zeta }_2 - \dot{\zeta }_1) + q_\mathrm{r} \times (u_2 - u_1) \right] \mathrm{d}t \\&\quad - \sum _{j=1}^{2}\int _0^{T} \left[ m_\mathrm{Q}(\delta \dot{l}_j) q_j^T \dot{x}_{Q_j} + \delta l_j ( m_\mathrm{Q} \dot{q}_j^T \dot{x}_{Q_j} - m_\mathrm{Q} ge_3^T q_j - k(L_\mathrm{c} - l_j) + c \dot{l}_j + q_j^T u_j ) \right] \mathrm{d}t \\&\quad - \sum _{j=1}^{2}\int _0^{T} \left[ \xi _j^T \left( q_j \times (m_\mathrm{Q} \dot{l}_j \dot{x}_{Q_j} - m_\mathrm{Q} g l_j e_3 + l_j u_j) + \dot{q}_j \times m_\mathrm{Q} l_j \dot{x}_{Q_j} \right) + \dot{\xi }_j^T (q_j \times m_\mathrm{Q} l_j \dot{x}_{Q_j}) \right] \mathrm{d}t \\&\quad +\sum _{j=1}^{2} \int _0^{T} \left[ \dot{\eta }_j^T J_\mathrm{Q} \Omega _j + \eta _j^T \left( J_\mathrm{Q} \Omega _j \times \Omega _j + M_j \right) \right] \mathrm{d}t, \end{aligned}$$

where $\zeta _j := l_j q_j$, $m_{\text {eff}} := 2m_\mathrm{Q} + m_\mathrm{r}$, and $I_{\text {eff}} := (2m_\mathrm{Q} + \frac{2}{3} m_\mathrm{r})L_\mathrm{r}$. Integrating by parts and applying the equality of mixed partial derivatives and the fact that variations vanish on the endpoints, we obtain

$$\begin{aligned} 0=&\int _{0}^{T} \delta x_\mathrm{r} \left[ m_{\text {eff}} (\ddot{x}_\mathrm{r} + ge_3) - m_\mathrm{Q}(\ddot{\zeta }_1 + \ddot{\zeta }_2) - (u_1 + u_2 )) \right] \mathrm{d}t\\&+ \sum _{j=1}^{2}\int _0^{T} \eta _j^T \left[ J_\mathrm{Q} \dot{\Omega }_j - J_\mathrm{Q} \Omega _j \times \Omega _j - M_j \right] \mathrm{d}t \\&+ \ L_\mathrm{r} \int _0^T \xi _\mathrm{r}^T \left[ I_{\text {eff}}(q_\mathrm{r} \times \ddot{q}_\mathrm{r}) - q_\mathrm{r} \times \left( u_2 - u_1 + m_\mathrm{Q}( \ddot{\zeta }_{2} - \ddot{\zeta }_1) \right) \right] \mathrm{d}t \\&- \sum _{j=1}^{2}\int _0^{T} \delta l_j \left[ m_\mathrm{Q} q_j^T( \ddot{x}_\mathrm{r} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r} - \ddot{\zeta }_j+ ge_3) - c \dot{l}_j + k(L_\mathrm{c} - l_j) - q_j^T u_j \right] \mathrm{d}t \\&- l_j \sum _{j=1}^{2}\int _0^{T} \xi _j^T \left[ m_\mathrm{Q} q_j \times ( \ddot{x}_\mathrm{r} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r} - \ddot{\zeta }_j + ge_3) - q_j \times u_j \right] \mathrm{d}t. \end{aligned}$$

Each of these integrals can be treated independently, as their respective variations are independent. That is, for the above equation to be satisfied, we necessarily have that each integral vanish identically. Applying the Fundamental Lemma of the Calculus of Variations (Gelfand and Fomin 1963) to each integral yields the dynamical system:

$$\begin{aligned} m_{\text {eff}} ( \ddot{x}_\mathrm{r} + ge_3)&= u_1 + u_2 + m_\mathrm{Q} (\ddot{\zeta }_1 + \ddot{\zeta }_2 ),\\ I_{\text {eff}}(q_\mathrm{r} \times \ddot{q}_\mathrm{r})&= q_\mathrm{r} \times \left[ u_2 - u_1 + m_\mathrm{Q}( \ddot{\zeta }_{2} - \ddot{\zeta }_1) \right] ,\\ m_\mathrm{Q} q_j^T( \ddot{x}_\mathrm{r} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r} - \ddot{\zeta }_j+ ge_3)&= c \dot{l}_j - k(L_\mathrm{c} - l_j) + q_j^T u_j, \\ m_\mathrm{Q} q_j \times ( \ddot{x}_\mathrm{r} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r} - \ddot{\zeta }_j + ge_3)&= q_j \times u_j, \\ \dot{R}_j&=R_j \hat{\Omega }_j,\\ J_\mathrm{Q} \dot{\Omega }_j&= J_\mathrm{Q} \Omega _j \times \Omega _j + M_j, \qquad \text {for }\,j = 1,2. \end{aligned}$$

where we have made the assumption that $l_j \ne 0$. After implicitly defining the translational and angular velocities of the load with the kinematic equations $\dot{v}_\mathrm{r} = x_\mathrm{r}$ and $\dot{q}_\mathrm{r} = \omega _\mathrm{r} \times q_\mathrm{r}$, and rearranging terms, we have the desired dynamical control system. $\square$

3 Reduced Model

While the use of elastic cables provides the benefit of reducing impulsive forces on the bar, large or rapid oscillations of the bar can produce undesired aggressive movements, compromising the safety of the cooperative task. Therefore, the strategy is to use elastic cables with high stiffness and damping to guarantee the safety for the bar in the transportation task. To this end, we will employ techniques from singular perturbation theory (Holmes 2012) to study such a situation.

In particular, we will consider the case that $\displaystyle {k = \frac{\bar{k}}{\epsilon ^2}}$ and $\displaystyle {c = \frac{\bar{c}}{\epsilon }}$ with $\bar{k}, \bar{c} > 0$ and $\epsilon > 0$ sufficiently small, and we will show that the dynamics approach that of the same model with inelastic cables (that is, with $l \equiv L_\mathrm{c}$) as $\epsilon \rightarrow 0$. We further consider a change of variables of the form $l_j = \epsilon ^2 y_j + L_\mathrm{c}$ and $\dot{l}_j = \epsilon z_j$, which is motivated by observing that $k( L_\mathrm{c} - l_j) = -\bar{k}y_j$ and $c \dot{l}_j = \bar{c} z_j$. From this, we can see that $\zeta _j = (\epsilon ^2 y_j + L_\mathrm{c})q_j$. Therefore, $\ddot{\zeta }_j = L_\mathrm{c}\ddot{q}_j + \epsilon (\dot{z}_j q_j + z_j \dot{q}_j) + \epsilon ^2 y_j \ddot{q}_j$. Making these substitutions into the dynamics described in Proposition 1, in addition to defining the angular velocity of the cables $\omega _j$ by $\dot{q}_j = \omega _j \times q_j$ and $\omega _j^T q_j = 0$, we obtain

$$\begin{aligned} \dot{x}_\mathrm{r}&= v_\mathrm{r}, \\ m_{\text {eff}} ( \dot{v}_\mathrm{r} + ge_3)&= u_1 + u_2 + m_\mathrm{Q} L_\mathrm{c} (\ddot{q}_1 + \ddot{q}_2) + m_\mathrm{Q} \epsilon \left( \dot{z}_1 q_1 + \dot{z}_2 q_2 + z_1 \dot{q}_1 + z_2 \dot{q}_2 \right) \\ {}&\quad + m_\mathrm{Q} \epsilon ^2 ( y_1 \ddot{q}_1 + y_2 \ddot{q}_2),\\ \dot{q}_\mathrm{r}&= \omega _\mathrm{r} \times q_\mathrm{r}, \\ I_{\text {eff}}\dot{\omega }_\mathrm{r}&= q_\mathrm{r} \times \left[ u_2 - u_1 + m_\mathrm{Q} L_\mathrm{c} (\ddot{q}_2 - \ddot{q}_1)\right. \\&\quad \left. + m_\mathrm{Q} \epsilon \left( \dot{z}_2 q_2 - \dot{z}_1 q_1 + z_2 \dot{q}_2 - z_1 \dot{q}_1 \right) + m_\mathrm{Q} \epsilon ^2 ( y_2 \ddot{q}_2 - y_1 \ddot{q}_1) \right] , \\ \epsilon \dot{y}_j&= z_j, \\ \epsilon \dot{z}_j&= \frac{1}{m_\mathrm{Q}}q_j^T \left[ -\bar{c}z_j q_j - \bar{k} y_j q_j - u_j + m_\mathrm{Q} (L_\mathrm{c} + \epsilon ^2 y_j)\ddot{q}_j\right. \\&\quad \left. + m_\mathrm{Q} ( \dot{v}_\mathrm{r} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r}+ ge_3) \right] , \\ \dot{q}_j&= \omega _j \times q_j, \\ \dot{\omega }_j&= \frac{1}{L_\mathrm{c}} q_j \times \left[ \dot{v}_\mathrm{r} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r} + ge_3 - \frac{1}{m_\mathrm{Q}} u_j - \epsilon ( \dot{z}_j q_j + z_j \omega _j) - \epsilon ^2 y_j \ddot{q}_j \right] , \\ \dot{R}_j&= R_j \hat{\Omega }_j, \\ J_\mathrm{Q} \dot{\Omega }_j&= J_\mathrm{Q} \Omega _j \times \Omega _j + M_j, \quad \text {for}\, j = 1,2. \end{aligned}$$

The previous system of differential equations can be written as

$$\begin{aligned} \dot{x}&= f(t, x, z; \epsilon ), \end{aligned}$$

(11)

$$\begin{aligned} \epsilon \dot{z}&= g(t, x, z; \epsilon ), \end{aligned}$$

(12)

where f and g are smooth functions, x is the vector representing $(x_\mathrm{r}, v_\mathrm{r}, q_\mathrm{r}, \omega _\mathrm{r}, q_j, \omega _j, R_j, \Omega _j)$, and z is the vector representing $(y_j, z_j)$, for $j = 1,2$. The above dynamical system is known as a singular perturbation model (Holmes 2012; Khalil 2002), with (11) describing the slow dynamics and (12) describing the fast dynamics.

Evaluating at $\epsilon = 0$, the fast dynamics provide us with algebraic equations that can be solved to obtain $z = h(t, x)$. In particular,

$$\begin{aligned} y_j&= \frac{1}{\bar{k}} q_j^T \left[ -u_j + m_\mathrm{Q} L_\mathrm{c}\ddot{q}_j + m_\mathrm{Q} ( \dot{v}_\mathrm{r} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r}+ ge_3) \right] , \end{aligned}$$

(13)

$$\begin{aligned} z_j&= 0. \end{aligned}$$

(14)

Substituting these equations back into the slow dynamics, we obtain the reduced (slow) model of the control system describing the cooperative task, given by $\dot{x} = f(t, x, h(t, x), 0)$. That is,

$$\begin{aligned} \dot{x}_\mathrm{r}&= v_\mathrm{r}, \end{aligned}$$

(15)

$$\begin{aligned} m_{\text {eff}} ( \dot{v}_\mathrm{r} + ge_3)&= u_1 + u_2 + m_\mathrm{Q}L_\mathrm{c} (\ddot{q}_1 + \ddot{q}_2 ), \end{aligned}$$

(16)

$$\begin{aligned} \dot{q}_\mathrm{r}&= \omega _\mathrm{r} \times q_\mathrm{r}, \end{aligned}$$

(17)

$$\begin{aligned} I_{\text {eff}} \omega _\mathrm{r}&= q_\mathrm{r} \times \left[ u_2 - u_1 + m_\mathrm{Q} L_\mathrm{r} ( \ddot{q}_{2} - \ddot{q}_1) \right] , \end{aligned}$$

(18)

$$\begin{aligned} \dot{q}_j&= \omega _j \times q_j, \end{aligned}$$

(19)

$$\begin{aligned} m_\mathrm{Q} L_\mathrm{c} \dot{\omega }_j&= m_\mathrm{Q} q_j \times ( \dot{v}_\mathrm{r} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r}+ ge_3) - q_j \times u_j, \end{aligned}$$

(20)

$$\begin{aligned} \dot{R}_j&= R_j \hat{\Omega }_j, \end{aligned}$$

(21)

$$\begin{aligned} J_\mathrm{Q} \dot{\Omega }_j&= J_\mathrm{Q} \Omega _j \times \Omega _j + M_j, \quad \text {for j = 1,2} . \end{aligned}$$

(22)

Note that the previous dynamical control system is equivalent to the model with inelastic cables (that is, where $l \equiv L$). Achieving exponentially stable tracking of the reduced model on some set of initial conditions will guarantee exponentially stable tracking in some subset of those initial conditions—whose relative size depends on $\epsilon$. This claim will be formalized in the subsequent section, and will make direct use of Theorem 11.2 in Khalil (2002). We will work within this reduced model to design geometric controllers toward the end of tracking the position and attitude of the rod.

Remark 3

As discussed in Kotaru et al. (2017), Sreenath et al. (2013), it is more physically realistic to model our system by a hybrid dynamical system which transitions between the cases of a taut cable (with positive tension magnitude) and a cable with zero tension. However, such a consideration will not play a role in the control design and subsequent analysis, so we will omit such a development.

Observe that the reduced model (15)–(22) preserves the original 8 inputs given by $f_1, f_2, M_1, M_2$, but two degrees of freedom (namely the cable lengths) have been removed from the configuration space. Hence, the reduced model has 7 degrees of under-actuation. We now show that it is in fact differentially flat (Mellinger and Kumar 2011). In other words, its states and inputs can be written as algebraic functions of 8 flat outputs and their derivatives. Such a notion dramatically reduces the difficulty involved in generating dynamically feasible trajectories for under-actuated systems.

The differential flatness of the under-actuated system comprised of one quadrotor carrying a cable-suspended point-mass load is discussed, for instance, in Sreenath et al. (2013). In that case, the 4 flat outputs are given by $(x_L, \psi ) \in \mathbb {R}^3 \times \mathbb {R}$, where $x_L$ is the load position and $\psi$ is the yaw angle of the quadrotor. The strategy for the rod is similar, as summarized in the following lemma.

Lemma 1

$\mathcal {Y} = (x_{L_1}, x_{L_2}, \psi _1, \psi _2) \in (\mathbb {R}^3)^2 \times (\mathbb {R})^2$ is a set of flat outputs for the reduced model (15)–(22), where $\psi _j \in \mathbb {R}$ denotes the yaw angle of the $j^{\text {th}}$ quadrotor.

Proof

We may follow the same analysis as in Sreenath et al. (2013) to show that the state variables and inputs $q_j, R_j, \Omega _j, u_j, M_j$ may be recovered from the outputs $(x_{L_j}, \psi _j) \in \mathbb {R}^3 \times \mathbb {R}$ for $j=1,2.$ It remains to be seen that the load position $x_\mathrm{r}$ and load attitude $q_\mathrm{r}$ can additionally be recovered. This follows immediately from the fact that $x_{L_j} = x_\mathrm{r} + (-1)^j L_\mathrm{r} q_\mathrm{r}$ for $j = 1,2$, as we obtain $\frac{1}{2} (x_{L_1} + x_{L_2}) = x_\mathrm{r}$ and $\frac{1}{2L_\mathrm{r}}(x_{L_2} - x_{L_1}) = q_\mathrm{r}$. $\square$

4 Control Design for Position and Attitude Trajectory Tracking of the Rigid Bar

In this section, we will design a thrust controller $u_j\in \mathbb {R}^{3}$ such that the position and attitude of the rigid rod reach a desired position $\tilde{x}_\mathrm{r}\in \mathbb {R}^{3}$ and attitude $\tilde{q}_\mathrm{r}\in S^{2}$. The strategy is to split $u_j$ into its components which are parallel and perpendicular to the cable attitudes $q_j$. This is motivated by the fact that these components appear independently from one another within the system, and as such can be considered as decoupled controllers.

Notice that Eqs. (21)–(22) describing the quadrotor attitude are independent from the rest of the dynamical system, and the moment controllers $M_j$ appear exclusively within them. Moreover, these equations are identical to those that appear in Lee et al. (2010), Lee (2015), for which $M_j$ was designed to attain almost-global exponential stability. We use the same controller for the attitude of the quadrotors, and disregard the equations for the remainder of this paper.

We will also introduce configuration error functions for each state variable, from which we may derive our error dynamics. The controls will be selected such that the origin is an exponentially stable equilibrium point of the error dynamics. In particular, the controls will take the form of a geometric PD controller with some additional feedback terms.

4.1 Error Dynamics

We begin by further simplifying the dynamical system (15)–(20). In particular, we find an equation for $\ddot{q}_j$ that we will substitute into Eqs. (16) and (20). By differentiating (19) and expanding it with the vector triple product identity, it can be shown that $\ddot{q}_j = \dot{\omega }_j \times q_j - ||\omega _j ||^2 q_j$. Now we may substitute (20) in for $\dot{\omega }_j$ to find that

$$\begin{aligned} m_\mathrm{Q} L_\mathrm{c} \ddot{q}_j&= -q_j \times (m_\mathrm{Q} L_\mathrm{c}\dot{\omega }_j) - m_\mathrm{Q} L_\mathrm{c}||\omega _j||^2 q_j \\&= -q_j \times \left[ m_\mathrm{Q} q_j \times ( \dot{v}_\mathrm{r} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r} + ge_3) - q_j \times u_j \right] - m_\mathrm{Q} L_\mathrm{c} ||\omega _j||^2 q_j\\&= -m_\mathrm{Q} \hat{q}_j^2 \left[ \dot{v}_\mathrm{r} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r} + ge_3\right] + \hat{q}_j^2 u_j - m_\mathrm{Q} L_\mathrm{c} ||\omega _j||^2 q_j \\&= m_\mathrm{Q} (\dot{v}_\mathrm{r}^{\perp _j} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r}^{\perp _j} + ge_3^{\perp _j}) - u_j^{\perp _j} - m_\mathrm{Q} L_\mathrm{c} ||\omega _j||^2 q_j, \end{aligned}$$

where “$\perp _j$” stands for the component of the vector that is perpendicular to the cable attitude $q_j\in S^{2}$. Similarly, for every vector $v \in \mathbb {R}^3$, we define the component $v^{\parallel _j}$ parallel to $q_j$ such that $v = v^{\parallel _j} + v^{\perp _j}$. Notice that $v^{\parallel _j} = (v^T q_j)q_j$ and $v^{\perp _j} = -\hat{q}_j^2 v$. Substituting the above equation for $m_\mathrm{Q} L_\mathrm{c} \ddot{q}_j$ into (16) and making use of the fact that $m_{\text {eff}} = 2m_\mathrm{Q} + m_\mathrm{r}$, we obtain

$$\begin{aligned} m_{r} ( \dot{v}_\mathrm{r} + ge_3)&= \left[ u_1 - m_\mathrm{Q}( \dot{v}_\mathrm{r} + ge_3) + m_\mathrm{Q} L_\mathrm{c} \ddot{q}_1 \right] + \left[ u_2 - m_\mathrm{Q}(\dot{v}_\mathrm{r} + ge_3)+ m_\mathrm{Q}L_\mathrm{c}\ddot{q}_2 \right] ,\\&= \left[ u_1^{\parallel _1} - m_\mathrm{Q} (\dot{v}_\mathrm{r}^{\parallel _1} + ge_3^{\parallel _1} + L_\mathrm{c} ||\omega _1||^2 q_1 - L_\mathrm{r} \ddot{q}_\mathrm{r}^{\perp _1}) \right] \\ {}&\quad + \left[ u_2^{\parallel _2} - m_\mathrm{Q} (\dot{v}_\mathrm{r}^{\parallel _2} + ge_3^{\parallel _2} + L_\mathrm{c} ||\omega _2||^2 q_2 + L_\mathrm{r} \ddot{q}_\mathrm{r}^{\perp _2}) \right] . \end{aligned}$$

Define the parallel component of the thrust controllers as

$$\begin{aligned} u_j^{\parallel _j} := \mu _j + m_\mathrm{Q} (\ddot{x}_\mathrm{r}^{\parallel _j} + ge_3^{\parallel _j} + L_\mathrm{c} ||\omega _j||^2 q_j + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r}^{\parallel _j}), \end{aligned}$$

(23)

where $\mu _j$ is an additional control to be designed later—and which is constrained to be parallel to $q_j$. Repeating this procedure with (18) yields

$$\begin{aligned} I_{\text {eff}} \omega _\mathrm{r}&= q_\mathrm{r} \times \left[ u_2 + m_\mathrm{Q} L_\mathrm{c} \ddot{q}_2 \right] - q_\mathrm{r} \times \left[ u_1 + m_\mathrm{Q} L_\mathrm{c} \ddot{q}_1 \right] , \\&= q_\mathrm{r} \times \left[ u_2^{\parallel _2} + m_\mathrm{Q} (\dot{v}_\mathrm{r}^{\perp _2} + ge_3^{\perp _2} - L_\mathrm{c} ||\omega _2||^2 q_2 + L_\mathrm{r} \ddot{q}_\mathrm{r}^{\perp _2}) \right] \\&\quad - q_\mathrm{r} \times \left[ u_1^{\parallel _1} + m_\mathrm{Q} (\dot{v}_\mathrm{r}^{\perp _1} + ge_3^{\perp _1} - L_\mathrm{c} ||\omega _1||^2 q_1 - L_\mathrm{r} \ddot{q}_\mathrm{r}^{\perp _1}) \right] \\&= q_\mathrm{r} \times \left[ \mu _2 - \mu _1 + 2m_\mathrm{Q} L_\mathrm{r} \ddot{q}_\mathrm{r} \right] . \end{aligned}$$

Further making use of the fact that $I_{\text {eff}} = 2m_\mathrm{Q}L_\mathrm{r} + \frac{2}{3} m_\mathrm{r} L_\mathrm{r}$, we obtain the following dynamical system

$$\begin{aligned} \dot{x}_\mathrm{r}&= v_\mathrm{r}, \end{aligned}$$

(24)

$$\begin{aligned} m_\mathrm{r} ( \dot{v}_\mathrm{r} + ge_3)&= \mu _1 + \mu _2, \end{aligned}$$

(25)

$$\begin{aligned} \dot{q}_\mathrm{r}&= \omega _\mathrm{r} \times q_\mathrm{r}, \end{aligned}$$

(26)

$$\begin{aligned} \frac{2}{3} m_\mathrm{r} L_\mathrm{r} \dot{\omega }_\mathrm{r}&= q_\mathrm{r} \times ( \mu _2 - \mu _1 ), \end{aligned}$$

(27)

$$\begin{aligned} \dot{q}_j&= \omega _j \times q_j, \end{aligned}$$

(28)

$$\begin{aligned} m_\mathrm{Q} L_\mathrm{c} \dot{\omega }_j&= m_\mathrm{Q} q_j \times ( \ddot{x}_\mathrm{r} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r} + ge_3) - q_j \times u_j. \end{aligned}$$

(29)

Equations (24), (26), and (28) are the kinematic equations for the load position, load attitude, and cable attitude, respectively, while Eqs. (25), (27), and (29) describe the dynamics. Notice also that the cross-product $q_j \times u_j$ in Eq. (29) will annihilate $u_j^{\parallel _j}$, so that we may view $\mu _1, \mu _2,$ and $q_j \times u_j$ as completely independent. We now introduce the tracking errors for the position and velocity of the rod as $e_{x_\mathrm{r}} := x_{r} - \tilde{x}_{r}$ and $e_{v_\mathrm{r}} := v_\mathrm{r} - \tilde{v}_\mathrm{r} = \dot{e}_x$, respectively. These clearly have the desirable property that $e_{x_\mathrm{r}} = e_{v_\mathrm{r}} = 0$ implies $x_\mathrm{r} = \tilde{x}_\mathrm{r} \text { and } v_\mathrm{r} = \tilde{v}_\mathrm{r}$.

We define the tracking error for the attitude of the rod as $e_{q_\mathrm{r}}:= \tilde{q}_\mathrm{r} \times q_\mathrm{r}$, which is a tangent vector in $T_{q_\mathrm{r}} S^2$ with the property that if $e_{q_\mathrm{r}} = 0$ then $q_\mathrm{r} = \tilde{q}_\mathrm{r} \text { or } q_\mathrm{r} = -\tilde{q}_\mathrm{r}$. Note that $\omega _{r}$ and $\tilde{\omega }_\mathrm{r}$ will in general belong to different tangent spaces, and so to compare them, we must first translate $\tilde{\omega }_\mathrm{r}$ to $T_{q_\mathrm{r}}S^2$. After which, they are vectors belonging to the same vector space and can be compared with their difference just as we did with $e_{x_\mathrm{r}}$ and $e_{v_\mathrm{r}}$. That is, we can define the tracking error for the angular velocity of the rod as $e_{\omega _\mathrm{r}} = \omega _\mathrm{r} + \hat{q}_\mathrm{r}^2 \tilde{\omega }_\mathrm{r}.$ This analysis is not specific to $q_\mathrm{r}$ or $\omega _\mathrm{r}$, but instead relies only on the manifold structure of $S^2$. Hence, we may use the same configuration errors to compare $q_j, \omega _j$ with their respective desired trajectories for $j = 1,2$.

Similarly, we define the configuration error function on $S^2$ for $q_j$ as $\Psi _{j} = 1 - \tilde{q}_{j}^T q_j$, for $j = 1,2,r$, which clearly satisfies $0 \le \Psi _{j} \le 2$, with $\Psi _j = 0$ if and only if $q_j = \tilde{q}_j$. Observe that for some $\theta \in [0, 2 \pi )$, we may write $\Psi _{j} = 1 - \cos (\theta )$ and $||e_{q_\mathrm{r}}||^2 = \sin ^2(\theta )$. With this representation, is it easy to see that whenever $\Psi _{j} \le \psi _{j} < 1$, we have $\frac{1}{2} ||e_{q_j}||^2 \le \Psi _{j} \le \frac{1}{2 - \psi _{j}} ||e_{q_j}||^2$.

Note that, from (25), the error dynamics for the load position are given by $m_\mathrm{r}(\dot{e}_{v_\mathrm{r}} + \dot{\tilde{v}}_\mathrm{r} + ge_3) = \mu _1 + \mu _2$.

while the error dynamics for the load attitude are described by

$$\begin{aligned} \frac{2}{3} m_\mathrm{r} L_\mathrm{r}\dot{e}_{\omega _\mathrm{r}}&= \frac{2}{3} m_\mathrm{r} L_\mathrm{r} \left[ \dot{\omega }_\mathrm{r} + \dot{q}_\mathrm{r} \times (q_\mathrm{r} \times \tilde{\omega }_\mathrm{r}) + q_\mathrm{r} \times (\dot{q}_\mathrm{r} \times \tilde{\omega }_\mathrm{r}) + \hat{q}_\mathrm{r}^2 \dot{\tilde{\omega }}_\mathrm{r} \right] \\&= \frac{2}{3} m_\mathrm{r} L_\mathrm{r} \left[ \dot{\omega }_\mathrm{r} + \hat{q}_\mathrm{r}^2 \dot{\tilde{\omega }}_\mathrm{r} + (\dot{q}_\mathrm{r}^T \tilde{\omega }_\mathrm{r})q_\mathrm{r} + (q_\mathrm{r}^T \tilde{\omega }_\mathrm{r})\dot{q}_\mathrm{r}\right] \\&= \hat{q}_\mathrm{r} \left[ \mu _2 - \mu _1 + \frac{2}{3} m_\mathrm{r} L_\mathrm{r} \hat{q}_\mathrm{r} \dot{\tilde{\omega }}_\mathrm{r} - \frac{2}{3} m_\mathrm{r} L_\mathrm{r}(q_\mathrm{r}^T \tilde{\omega }_\mathrm{r}) (e_{\omega _\mathrm{r}} - \hat{q}_\mathrm{r}^2 \tilde{\omega }_\mathrm{r}) \right] + \frac{2}{3} m_\mathrm{r} L_\mathrm{r} (\dot{q}_\mathrm{r}^T \tilde{\omega }_\mathrm{r})q_\mathrm{r}. \end{aligned}$$

This motivates us to choose our "desired" controls $\tilde{\mu }_1, \tilde{\mu }_2$ such that their sum is a feedback linearization plus a PD controller for the above error dynamics. That is

$$\begin{aligned} \tilde{\mu }_1 + \tilde{\mu }_2&= m_\mathrm{r}(\dot{\tilde{v}}_\mathrm{r} + ge_3 - k_{v_\mathrm{r}} e_{v_\mathrm{r}} - k_{x_\mathrm{r}} e_{x_\mathrm{r}}), \end{aligned}$$

(30)

$$\begin{aligned} \tilde{\mu }_2 - \tilde{\mu }_1&= \frac{2}{3} m_\mathrm{r} L_\mathrm{r} \left[ -\hat{q}_\mathrm{r} \dot{\tilde{\omega }}_\mathrm{r} + (q_\mathrm{r}^T \tilde{\omega }_\mathrm{r}) \hat{q}_\mathrm{r}^2 \tilde{\omega }_\mathrm{r} - (q_\mathrm{r}^T \tilde{\omega }_\mathrm{r})e_{\omega _\mathrm{r}} + k_{\omega _\mathrm{r}} \hat{q}_\mathrm{r} e_{\omega _\mathrm{r}} + k_{q_\mathrm{r}}\hat{q}_\mathrm{r} e_{q_\mathrm{r}} \right] . \end{aligned}$$

(31)

Note, however, that we cannot simply take $\mu _j = \tilde{\mu }_j$, as $\tilde{\mu }_j$ is not guaranteed to satisfy the constraint of parallelism to $q_j$. Therefore, we take $\mu _j$ as the projection of $\tilde{\mu }_j$ onto the corresponding cable attitude, given explicitly by $\mu _j = (I + \hat{q}_j^2)\tilde{\mu }_j$. We further select our desired cable attitudes with the goal that $q_j \rightarrow \tilde{q}_j$ as $\tilde{\mu }_j \rightarrow \mu _j$. In particular, we define $\displaystyle {\tilde{q}_j = -\frac{\tilde{\mu }_j}{||\tilde{\mu }_j||}}$, so that $\tilde{q}_j$ is parallel to $\tilde{\mu }_j$. With such a choice, the error dynamics of the translational and angular velocities of the rod become

$$\begin{aligned} \dot{e}_{v_\mathrm{r}}&= -k_{v_\mathrm{r}} e_{v_\mathrm{r}} - k_{x_\mathrm{r}} e_{x_\mathrm{r}} + \frac{1}{m_\mathrm{r}} ||\tilde{\mu }_1||\hat{q}_1 e_{q_1} + \frac{1}{m_\mathrm{r}} ||\tilde{\mu }_2|| \hat{q}_2 e_{q_2}, \\ \dot{e}_{\omega _\mathrm{r}}&= (\dot{q}_\mathrm{r}^T \tilde{\omega }_\mathrm{r})q_\mathrm{r} - k_{\omega _\mathrm{r}} e_{\omega _\mathrm{r}} - k_{q_\mathrm{r}} e_{q_\mathrm{r}} + \frac{3}{2 m_\mathrm{r} L_\mathrm{r}}\hat{q}_\mathrm{r} (||\tilde{\mu }_2|| \hat{q}_2 e_{q_2} - ||\tilde{\mu }_1|| \hat{q}_1 e_{q_1}). \end{aligned}$$

Next, we design the perpendicular component $u_j^{\perp }$ of the thrust controller in such a way $q_j$ approaches $\tilde{q}_j$ asymptotically. Recall that the dynamics for the cables are

$$\begin{aligned} \dot{q}_j&= \omega _j \times q_j, \\ m_\mathrm{Q} L_\mathrm{c} \dot{\omega }_j&= m_\mathrm{Q} q_j \times ( \ddot{x}_\mathrm{r} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r} + ge_3) - q_j \times u_j. \end{aligned}$$

Repeating the procedure that we used to find $e_{\omega _\mathrm{r}}$, we find that the error dynamics for the angular velocities of the cables as

$$\begin{aligned} m_\mathrm{Q} L_\mathrm{c} \dot{e}_{\omega _j}&= m_\mathrm{Q} L_\mathrm{c} \dot{\omega }_j + m_\mathrm{Q} L_\mathrm{c} \left[ \dot{q}_j \times (q_j \times \tilde{\omega }_j) + q_j \times (\dot{q}_j \times \tilde{\omega }_j) + \hat{q}_j^2 \dot{\tilde{\omega }}_j) \right] \\&= m_\mathrm{Q} \hat{q}_j ( \ddot{x}_\mathrm{r} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r} + ge_3) + m_\mathrm{Q} L_\mathrm{c} \left[ \hat{q}_j^2 \dot{\tilde{\omega }}_j\right. \\&\quad \left. - (q_j^T \tilde{\omega }_j)\hat{q}_j \omega _j + (\dot{q}_j^T \tilde{\omega }_j)q_j\right] - \hat{q}_j u_j \\&=m_\mathrm{Q} \hat{q}_j \left[ \ddot{x}_\mathrm{r} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r} + ge_3\right. \\&\quad \left. + L_\mathrm{c} \hat{q}_j \dot{\tilde{\omega }}_j - L_\mathrm{c}(q_j^T \tilde{\omega }_j) \omega _j \right] + m_\mathrm{Q} L_\mathrm{c}(\dot{q}_j^T \tilde{\omega }_j)q_j - \hat{q}_j u_j. \end{aligned}$$

Since $\hat{q}_j u_j = \hat{q}_j u_j^{\perp _j}$, we can choose $u_j^{\perp _j}$ such that

$$\begin{aligned} \hat{q}_j u_j^{\perp _j}&= m_\mathrm{Q} \hat{q}_j \left[ \ddot{x}_\mathrm{r} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r} + ge_3 + L_\mathrm{c} \hat{q}_j \dot{\tilde{\omega }}_j - L_\mathrm{c}(q_j^T \tilde{\omega }_j) \omega _j \right] + m_\mathrm{Q} L_\mathrm{c} \left[ k_{q_j} e_{q_j} + k_{\omega _j} e_{\omega _j}\right] \nonumber \\ u_j^{\perp _j}&= -m_\mathrm{Q} \hat{q}_j^2\left[ \ddot{x}_\mathrm{r} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r} + ge_3 + L_\mathrm{c} \hat{q}_j \dot{\tilde{\omega }}_j - L_\mathrm{c}(q_j^T \tilde{\omega }_j) \omega _j \right] - m_\mathrm{Q} L_\mathrm{c} \hat{q}_j \left[ k_{q_j} e_{q_j} + k_{\omega _j} e_{\omega _j} \right] , \end{aligned}$$

(32)

which clearly satisfies the orthogonality constraints and leads to the following error dynamics for $\omega _j$

$$\begin{aligned} \dot{e}_{\omega _j} = (\dot{q}_j^T \tilde{\omega }_j)q_j - k_{q_j} e_{q_j} - k_{\omega _j} e_{\omega _j}. \end{aligned}$$

4.2 Control Design for the Reduced Model

We now show that an appropriate choice of gains will cause the origin of the error dynamics for the reduced model to be exponentially stable, where the control inputs are defined as above. In particular, we use a Lyapunov candidate to find sufficient conditions under which the origin of the error dynamics is exponentially stable. These conditions are written in terms of the gains and some arbitrary Lyapunov parameters. Then, we show that these conditions can be satisfied, provided that the initial errors in the cable attitudes are sufficiently small.

Consider the indexing set $\mathcal {I} = {1, 2, r}$, the domain

$$\begin{aligned} \mathcal {D}&= \left\{ (e_{x_\mathrm{r}}, e_{v_\mathrm{r}}, e_{q_\mathrm{r}}, e_{\omega _\mathrm{r}}, e_{q_1}, e_{\omega _1}, e_{q_2}, e_{\omega _2}) | \ ||e_{x_\mathrm{r}}||\right. \\&\left. \le \bar{e}_{x_\mathrm{r}}, ||e_{v_\mathrm{r}}|| \le \bar{e}_{v_\mathrm{r}}, \ {||}e_{\omega _j}|| \le \bar{e}_{\omega _j}, \ \Psi _{j} \le \psi _j \ \text { for } \ j \in \mathcal {I}\right\} , \end{aligned}$$

and define a Lyapunov candidate function on $\mathcal {D}$ given by

$$\begin{aligned} V = \frac{1}{2} ||e_{v_\mathrm{r}}||^2 + \frac{1}{2} k_{x_\mathrm{r}} ||e_{x_\mathrm{r}}||^2 + c_{x_\mathrm{r}} e_{x_\mathrm{r}}^T e_{v_\mathrm{r}} + \sum _{j\in \mathcal {I}} \left[ \frac{1}{2} ||e_{\omega _j}||^2 + k_{q_j} \Psi _{j} + c_{q_j} e_{q_j}^T e_{\omega _j} \right] , \end{aligned}$$

where $c_{x_\mathrm{r}}$ and $c_{q_j}$ are positive real numbers for $j \in \mathcal {I}$. Observe that $V_x$ defined as $V_{x} := \frac{1}{2} ||e_{v_{r}}||^2 + c_{x_\mathrm{r}} e_{x_\mathrm{r}}^T e_{v_\mathrm{r}}+ \frac{1}{2} k_{x_{r}} ||e_{x_\mathrm{r}}||^2$ can be bounded from above and below as $\frac{1}{2} z_{x}^T {P}_{x} z_{x} \le \ V_{x} \le \frac{1}{2} z_{x}^T \bar{P}_{x} z_{x}$ where ${P}_x = \begin{bmatrix} k_{x_\mathrm{r}} &{} -c_{x_\mathrm{r}} \\ -c_{x_\mathrm{r}} &{} 1 \end{bmatrix}, \bar{P}_x = \begin{bmatrix} k_{x_\mathrm{r}} &{} c_{x_\mathrm{r}} \\ c_{x_\mathrm{r}} &{} 1 \end{bmatrix}$, and $z_x = \begin{bmatrix} ||e_{x_\mathrm{r}}||&||e_{v_\mathrm{r}}|| \end{bmatrix}^T.$ Further note that both ${P}_x$ and $\bar{P}_x$ are positive definite, provided that $c_{x_\mathrm{r}} < \sqrt{k_{x_\mathrm{r}}}$.

Similarly, for $j\in \mathcal {I}$, we define $V_{q_j} := \frac{1}{2} ||e_{\omega _j}||^2 + c_{q_j} e_{q_j}^T e_{\omega _j} + k_{q_j} \Psi _{q_j}$, which is bounded as $\frac{1}{2} z_{q_j}^T {P}_{q_j} z_{q_j} \le V_{q_j} \le \frac{1}{2} z_{q_j}^T \bar{P}_{q_j} z_{q_j},$ where ${P}_{q_j} = \begin{bmatrix} k_{q_j} &{} -c_{q_j} \\ -c_{q_j} &{} 1\end{bmatrix}, \bar{P}_{q_j} = \begin{bmatrix} \frac{2k_{q_j}}{2 - \psi _{q_j}} &{} c_{q_j} \\ c_{q_j} &{} 1\end{bmatrix},$ and $z_{q_j} = \begin{bmatrix} ||e_{q_j}||&||e_{\omega _j}|| \end{bmatrix}^T$. As before, ${P}_{q_j}$ and $\bar{P}_{q_j}$ are positive definite when $c_{q_j} < \sqrt{k_{q_j}}.$

Observing that $V = V_x + \sum _{j \in \mathcal {I}} V_{q_j}$, we then have that our Lyapunov candidate is bounded as $\frac{1}{2} z^T {P} z \le V \le \frac{1}{2} z^T \bar{P} z,$ where $z {=} \begin{bmatrix} ||e_{x_\mathrm{r}}||&||e_{v_\mathrm{r}}||&||e_{q_\mathrm{r}}||&||e_{\omega _\mathrm{r}}||&||e_{q_1}||&||e_{\omega _1}||&||e_{q_2}||&||e_{\omega _2}|| \end{bmatrix}^T,$

$$\begin{aligned} {P}&= \begin{bmatrix} {P}_x &{} 0 &{} 0 &{} 0 \\ 0 &{} {P}_{q_\mathrm{r}} &{} 0 &{} 0 \\ 0 &{} 0 &{} {P}_{q_1} &{} 0 \\ 0 &{} 0 &{} 0 &{} {P}_{q_2} \end{bmatrix}, \quad \text { and } \quad \bar{P} = \begin{bmatrix} \bar{P}_x &{} 0 &{} 0 &{} 0 \\ 0 &{} \bar{P}_{q_\mathrm{r}} &{} 0 &{} 0 \\ 0 &{} 0 &{} \bar{P}_{q_1} &{} 0 \\ 0 &{} 0 &{} 0 &{} \bar{P}_{q_2} \end{bmatrix}. \end{aligned}$$

where ${P}, \bar{P}$ are positive definite for $c_{x_\mathrm{r}} < \sqrt{k_{x_\mathrm{r}}}$ and $c_{q_j} < \sqrt{k_{q_j}}$. Next, note that by the invariance of circular shifts of the scalar triple product and the fact that $q_j^T e_{q_j} = 0$, we have:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\Psi _{q_j}&= -\tilde{q}^T_j \dot{q}_j - q_j^T \dot{\tilde{q}}_j = -\tilde{q}_j^T (\omega _j \times q_j) - q_j^T (\tilde{\omega }_j \times \tilde{q}_j)\\&= \omega _j^T (\tilde{q}_j \times q_j) - \tilde{\omega }_j^T (\tilde{q}_j \times q_j) \\&= (\omega _j - \tilde{\omega }_j)^T e_{q_j} = (\omega _j + (q_j^T \tilde{\omega }) q_j - \tilde{\omega }_j)^T e_{q_j} = e_{\omega _j}^T e_{q_j}. \end{aligned}$$

Additionally, from the vector triple product, we see

$$\begin{aligned} \dot{e}_{q_j}&= (\dot{\tilde{q}}_j \times q_j) + (\tilde{q}_j \times \dot{q}_j) = (\tilde{\omega }_j \times \tilde{q}_j) \times q_j - (\omega _j \times q_j) \times \tilde{q}_j \\&= \tilde{\omega }_j \times (\tilde{q}_j \times q_j) - \tilde{q}_j \times (\tilde{\omega }_j \times q_j) - \omega _j \times (q_j \times \tilde{q}_j) + q_j \times (\omega _j \times \tilde{q}_j) \\&= (\omega _j + \tilde{\omega }_j) \times e_{q_j} + (\tilde{q}_j^T q_j)e_{\omega _j} - (\tilde{q}_j^T q_j) (q_j^T \tilde{\omega }_j)q_j \\&= e_{\omega _j} \times e_{q_j} + (\tilde{q}_j^T q_j)e_{\omega _j} + 2\tilde{\omega }_j \times e_{q_j} - (\tilde{q}_j^T q_j) (q_j^T \tilde{\omega }_j)q_j, \end{aligned}$$

so that

$$\begin{aligned} \dot{e}_{q_j}^T e_{\omega _j}&= (\tilde{q}_j^T q_j)||e_{\omega _j}||^2 + 2(\tilde{\omega }_j \times e_{q_j})^T e_{\omega _j} \le ||e_{\omega _j}||^2 + C_{q_j} ||e_{q_j}|| ||e_{\omega _j}||, \end{aligned}$$

where $C_{q_j} \le 2\sup ||\tilde{\omega }_j||$ is a nonnegative constant depending on $\bar{e}_{x_\mathrm{r}}, \ \bar{e}_{v_\mathrm{r}}, \ \bar{e}_{\omega _j}$, and $\psi _j$ for $j \in \mathcal {I}$, as well as the desired trajectories $\tilde{x}_\mathrm{r}$ and $\tilde{q}_\mathrm{r}$. Therefore, the time derivative of the proposed Lyapunov function is bounded as

$$\begin{aligned} \dot{V} \le&-(k_{v_\mathrm{r}} - c_{x_\mathrm{r}}) ||e_{v_\mathrm{r}}||^2 + c_{x_\mathrm{r}} k_{v_\mathrm{r}} ||e_{v_\mathrm{r}}|| ||e_{x_\mathrm{r}}|| - c_{x_\mathrm{r}}k_{x_\mathrm{r}}||e_{x_\mathrm{r}}||^2 \\&+ \frac{1}{m_\mathrm{r}}(||e_{v_\mathrm{r}}|| + c_{x_\mathrm{r}} ||e_{x_\mathrm{r}}||) ||Y|| -(k_{\omega _\mathrm{r}} - c_{q_\mathrm{r}})||e_{\omega _\mathrm{r}}||^2\\ {}&+ c_{q_\mathrm{r}}(k_{\omega _\mathrm{r}} + C_{q_\mathrm{r}})||e_{\omega _\mathrm{r}}||||e_{q_\mathrm{r}}|| - c_{q_\mathrm{r}} k_{q_\mathrm{r}} ||e_{q_\mathrm{r}}||^2 - c_{q_j} k_{q_j} ||e_{q_j}||^2\\&+ \frac{2}{3 m_\mathrm{r} L_\mathrm{r}} (||e_{\omega _\mathrm{r}}|| + c_{q_\mathrm{r}} ||e_{q_\mathrm{r}}||) ||Y|| -(k_{\omega _j} - c_{q_j}) ||e_{\omega _j}||^2 \\&+ c_{q_j} (k_{\omega _j} + C_{q_j} ) ||e_{q_j}|| ||e_{\omega _j}||, \end{aligned}$$

where Y satisfies the inequality

$$\begin{aligned} ||Y||&\le \left[ m_\mathrm{r} (k_{v_\mathrm{r}} ||e_{v_\mathrm{r}}|| + k_{x_\mathrm{r}} ||e_{x_\mathrm{r}}||) + \frac{2}{3} m_\mathrm{r} L_\mathrm{r} ((C^2_{q_\mathrm{r}}\right. \\&\quad \left. + k_{\omega _\mathrm{r}}) ||e_{\omega _\mathrm{r}}|| + k_{q_\mathrm{r}}||e_{q_\mathrm{r}}||) + C\right] (||e_{q_1}|| + ||e_{q_2}||) \end{aligned}$$

for a nonnegative constant $C \le m_\mathrm{r} \sup ||\dot{\tilde{v}}_\mathrm{r}|| + \frac{2}{3} m_\mathrm{r} L_\mathrm{r} \sup ||\dot{\tilde{\omega }}_\mathrm{r}||$. Furthermore, within $\mathcal {D}$, we have $||e_{q_j}|| \le \sqrt{\psi _{q_j} (2 - \psi _{q_j})} := \alpha _j$. With $\alpha = 2\max \{ \alpha _1, \alpha _2 \}$ and $I_\mathrm{r} = \frac{2}{3} m_\mathrm{r} L_\mathrm{r}$, we have

$$\begin{aligned} \frac{1}{m_\mathrm{r}}(||e_{v_\mathrm{r}}|| + c_{x_\mathrm{r}} ||e_{x_\mathrm{r}}||) ||Y|| \le&\alpha (k_{v_\mathrm{r}}||e_{v_\mathrm{r}}||^2 + c_{x_\mathrm{r}}k_{v_\mathrm{r}}||e_{x_\mathrm{r}}||||e_{v_\mathrm{r}}|| + c_{x_\mathrm{r}} ||e_{x_\mathrm{r}}||^2 ) \\&+ \frac{I_\mathrm{r}}{m_\mathrm{r}} \alpha (||e_{v_\mathrm{r}}|| + c_{x_\mathrm{r}} ||e_{x_\mathrm{r}}||)((C_{q_\mathrm{r}}^2 + k_{\omega _\mathrm{r}})||e_{\omega _\mathrm{r}}|| + k_{q_\mathrm{r}}||e_{q_\mathrm{r}}||) \\&+ \frac{1}{m_\mathrm{r}}((C + m_\mathrm{r} k_{x_\mathrm{r}} \bar{e}_{x_\mathrm{r}})||e_{v_\mathrm{r}}|| + c_{x_\mathrm{r}} C ||e_{x_\mathrm{r}}||) (||e_{q_1}|| + ||e_{q_2}||), \end{aligned}$$

and,

$$\begin{aligned} (||e_{\omega _\mathrm{r}}|| + c_{q_\mathrm{r}} ||e_{q_\mathrm{r}}||) ||Y|| \le&I_\mathrm{r}\alpha ((C_{q_\mathrm{r}}^2 + k_{\omega _\mathrm{r}})||e_{\omega _\mathrm{r}}||^2\\ {}&+ c_{q_\mathrm{r}}(C_{q_\mathrm{r}}^2 + k_{\omega _\mathrm{r}})||e_{q_\mathrm{r}}||||e_{\omega _\mathrm{r}}|| + c_{q_\mathrm{r}} k_{q_\mathrm{r}}||e_{q_\mathrm{r}}||^2) \\&+ m_\mathrm{r} \alpha ( ||e_{\omega _\mathrm{r}}|| + c_{q_\mathrm{r}} ||e_{q_\mathrm{r}}|| )(k_{v_\mathrm{r}} ||e_{v_\mathrm{r}}|| + k_{x_\mathrm{r}} ||e_{x_\mathrm{r}}||) \\&+ ((C + I_\mathrm{r} k_{q_\mathrm{r}} \alpha _\mathrm{r}) ||e_{\omega _\mathrm{r}}|| + c_{q_\mathrm{r}}C ||e_{q_\mathrm{r}}|| )(||e_{q_1}|| + ||e_{q_2}||). \end{aligned}$$

Applying this inequality directly to the above bound for $\dot{V}$, we find that $\dot{V} \le -z^T \mathcal {W} z$, where $\mathcal {W}$ is the $8\times 8$ matrix defined as

$$\mathcal {W}_j = \begin{bmatrix} 2W_{x_\mathrm{r}} &{} - W_{x_\mathrm{r}, q_\mathrm{r}} &{} -\frac{1}{2} W_{x_\mathrm{r}, q_1} &{} -\frac{1}{2} W_{x_\mathrm{r}, q_2} \\ -W_{x_\mathrm{r}, q_\mathrm{r}} &{} 2W_{q_\mathrm{r}} &{} -\frac{1}{2} W_{q_\mathrm{r}, q_1} &{} -\frac{1}{2} W_{q_\mathrm{r}, q_1} \\ -\frac{1}{2} W_{x_\mathrm{r}, q_1} &{} -\frac{1}{2} W_{q_\mathrm{r}, q_1} &{} W_{q_1} &{} 0\\ -\frac{1}{2} W_{x_\mathrm{r}, q_2} &{} -\frac{1}{2} W_{q_\mathrm{r}, q_2} &{} 0 &{} W_{q_2}\\ \end{bmatrix}$$

for $2\times 2$ sub-matrices given by

$$\begin{aligned} W_{x_\mathrm{r}}&= \frac{1}{2} \begin{bmatrix} (1 - \alpha )c_{x_\mathrm{r}} k_{x_\mathrm{r}} &{} -\frac{1}{2} (1 + \alpha ) c_{x_\mathrm{r}} k_{v_\mathrm{r}} \\ -\frac{1}{2} (1 + \alpha ) c_{x_\mathrm{r}} k_{v_\mathrm{r}} &{} (1 - \alpha ) k_{v_\mathrm{r}} - c_{x_\mathrm{r}} \end{bmatrix}, \\ W_{q_j}&= \begin{bmatrix} c_{q_j} k_{q_j} &{} -\frac{1}{2} c_{q_j}(k_{\omega _j} + C_{q_j}) \\ -\frac{1}{2} c_{q_j}(k_{\omega _j} + C_{q_j}) &{} k_{\omega _j} - c_{q_j} \end{bmatrix}, \\ W_{q_\mathrm{r}}&= \frac{1}{2} \begin{bmatrix} (1 - \alpha )c_{q_\mathrm{r}} k_{q_\mathrm{r}} &{} - \frac{1}{2} c_{q_\mathrm{r}}((1 + \alpha )k_{\omega _\mathrm{r}} + C_{q_\mathrm{r}} + \alpha C_{q_\mathrm{r}}^2) \\ - \frac{1}{2} c_{q_\mathrm{r}}((1 + \alpha )k_{\omega _\mathrm{r}} + C_{q_\mathrm{r}} + \alpha C_{q_\mathrm{r}}^2) &{} (1 - \alpha )k_{\omega _\mathrm{r}} - c_{q_\mathrm{r}} - \alpha C_{q_\mathrm{r}}^2 \end{bmatrix}\\ W_{x_\mathrm{r}, q_\mathrm{r}}&= \alpha \begin{bmatrix} \frac{I_\mathrm{r}}{m_\mathrm{r}}c_{x_\mathrm{r}}k_{q_\mathrm{r}} + \frac{m_\mathrm{r}}{I_\mathrm{r}} c_{q_\mathrm{r}} k_{x_\mathrm{r}} &{} \frac{I_\mathrm{r}}{m_\mathrm{r}}c_{x_\mathrm{r}}(C_{q_\mathrm{r}}^2 + k_{\omega _\mathrm{r}}) + \frac{m_\mathrm{r}}{I_\mathrm{r}} k_{x_\mathrm{r}} \\ \frac{I_\mathrm{r}}{m_\mathrm{r}} k_{q_\mathrm{r}} + \frac{m_\mathrm{r}}{I_\mathrm{r}} c_{q_\mathrm{r}} k_{v_\mathrm{r}} &{} \frac{I_\mathrm{r}}{m_\mathrm{r}}(C_{q_\mathrm{r}}^2 + k_{\omega _\mathrm{r}}) + \frac{m_\mathrm{r}}{I_\mathrm{r}} k_{v_\mathrm{r}} \end{bmatrix}, \\ W_{x_\mathrm{r}, q_j}&= \frac{1}{m_\mathrm{r}} \begin{bmatrix} c_{x_\mathrm{r}} C &{} 0 \\ C + m_\mathrm{r} k_{x_\mathrm{r}} \bar{e}_{x_\mathrm{r}} &{} 0 \end{bmatrix}, \,\, W_{q_\mathrm{r}, q_j} = \frac{1}{I_\mathrm{r}} \begin{bmatrix} c_{q_\mathrm{r}} C &{} 0 \\ C + I_\mathrm{r} k_{q_\mathrm{r}} \alpha _\mathrm{r} &{} 0 \end{bmatrix}. \end{aligned}$$

Note that $\mathcal {W}$ is not necessarily symmetric, so the quadratic form defined by $z^T \mathcal {W} z$ is positive definite if and only if the symmetric part of $\mathcal {W}$—that is $\frac{1}{2} (\mathcal {W} + \mathcal {W}^T)$—is a positive definite matrix. The following Theorem states, in essence, that the gains and Lyapunov constants can be chosen such that ${P}, \bar{P},$ and $\frac{1}{2} (\mathcal {W} + \mathcal {W}^T)$ are simultaneously positive definite—thus ensuring that the origin is exponentially stable, provided that the initial errors in the cable attitudes are sufficiently small. We now state the main result of this work:

Theorem 1

Consider the control system defined by Eqs. 24–29 with control inputs 30, 31, and 32. For sufficiently small $\alpha$, there exists control gains $k_{x_\mathrm{r}}$, $k_{v_\mathrm{r}}$, $k_{q_\mathrm{r}}$, $k_{\omega _\mathrm{r}}$, $k_{q_1}$, $k_{\omega _1}$, $k_{q_2}$, and $k_{\omega _2}$ such that the zero equilibrium of the tracking errors $e_{x_\mathrm{r}}$, $e_{v_\mathrm{r}}$, $e_{q_\mathrm{r}}$, $e_{\omega _\mathrm{r}}$, $e_{q_1}$, $e_{\omega _1}$, $e_{q_2}$ and $e_{\omega _2}$ is exponentially stable.

Before proving this theorem, we state some general facts about positive-definite matrices that will be used multiple times in the proof.

Lemma 2

(Facts about positive-definite matrices) Let $A \succ 0$ and $B \succeq 0$ with $\lambda _{\min }(A) > \lambda _{\max }(B)$, and M arbitrary, be $n\times n$ matrices. Then, the following characterizations hold

• 1. $||x||||y|| \lambda _{\min }(A) \le x^T A y \le ||x||||y|| \lambda _{\max }(A)$,

• 2. $M^T A M \succeq 0$,

• 3. $A - B \succ 0$ with $\lambda _{\min }(A-B) \ge \lambda _{\min }(A) - \lambda _{\max }(B)$ and $\lambda _{\max }(A-B) \le \lambda _{\max }(A)$.

• 4. $A + B \succ 0$ with $\lambda _{\min }(A+B) \ge \lambda _{\min }(A) + \lambda _{\min }(B)$.

4.3 Proof of Theorem 1

Observe that the condition $\dot{V} \le z^T \mathcal {W} z$ is equivalent to $\dot{V} \le \sum _{j=1,2} z_j^T \mathcal {W}_j z_j$, where

$\small {z = \begin{bmatrix} ||e_{x_\mathrm{r}}||&||e_{v_\mathrm{r}}||&||e_{q_\mathrm{r}}||&||e_{\omega _\mathrm{r}}||&||e_{q_j}||&||e_{\omega _j}|| \end{bmatrix}^T}$ and $\small {\mathcal {W}_j = \begin{bmatrix} W_{x_\mathrm{r}} &{} -\frac{1}{2} W_{x_\mathrm{r}, q_\mathrm{r}} &{} -\frac{1}{2} W_{x_\mathrm{r}, q_j} \\ -\frac{1}{2} W_{x_\mathrm{r}, q_\mathrm{r}} &{} W_{q_\mathrm{r}} &{} -\frac{1}{2} W_{q_\mathrm{r}, q_j} \\ -\frac{1}{2} W_{x_\mathrm{r}, q_j} &{} -\frac{1}{2} W_{q_\mathrm{r}, q_j} &{} W_{q_j} \\ \end{bmatrix}}$. By Lemma 2, it suffices to show that each $\mathcal {W}_j$ is positive definite. Denote the symmetric part of $\mathcal {W}_{j}$ by $\bar{\mathcal {W}}_{j} = \frac{1}{2} (\mathcal {W}_{j} + \mathcal {W}_{j}^T)$ and similarly define the symmetric parts of the submatrices by $\bar{W}_{x_\mathrm{r}, q_\mathrm{r}}, \bar{W}_{x_\mathrm{r}, q_j},$ and $\bar{W}_{q_\mathrm{r}. q_j}$. It is clear that $\bar{\mathcal {W}}_{j}$ can be expressed in the form $\bar{\mathcal {W}}_{j} = \begin{bmatrix} P &{} S \\ S^T &{} Q \end{bmatrix}$, where $P = \begin{bmatrix} W_{x_\mathrm{r}} &{} -\frac{1}{2} \bar{W}_{x_\mathrm{r}, q_\mathrm{r}} \\ -\frac{1}{2} \bar{W}_{x_\mathrm{r}, q_\mathrm{r}} &{} {W}_{q_\mathrm{r}} \end{bmatrix}$, $S = -\frac{1}{2} \begin{bmatrix} \bar{W}_{x_\mathrm{r}, q_j}&\bar{W}_{q_\mathrm{r}, q_j} \end{bmatrix}^T$, and $Q = {W}_{q_j}$.

Now, observe that $\mathcal {W}$ can be decomposed as:

$$\begin{aligned} \begin{bmatrix} P &{} S \\ S^T &{} Q \end{bmatrix} = \begin{bmatrix} I &{} SQ^{-1} \\ 0 &{} I \end{bmatrix} \begin{bmatrix} P - SQ^{-1}S^T &{} 0 \\ 0 &{} Q \end{bmatrix} \begin{bmatrix} I &{} SQ^{-1} \\ 0 &{} I \end{bmatrix}^T \end{aligned}$$

(33)

where $P - SQ^{-1}S^T$ is often referred to as the Schur complement of Q. From Lemma 2, it then follows that $\mathcal {\bar{W}}_{j} \succ 0$ if and only if $P - SQ^{-1} S^T \succ 0$ and $Q \succ 0.$ Note that $P - SQ^{-1}S^T$ can itself be expressed in form of a $4\times 4$ block matrix given by

$$\begin{aligned} P - SQ^{-1}S^T = \begin{bmatrix} {W}_{x_\mathrm{r}} - \frac{1}{4} \bar{W}_{x_\mathrm{r}, q_j} {W}_{q_j}^{-1} \bar{W}_{x_\mathrm{r}, q_j} &{} -\frac{1}{2} \bar{W}_{x_\mathrm{r},q_\mathrm{r}} - \frac{1}{4} \bar{W}_{q_\mathrm{r},q_j}{W}_{q_j}^{-1}\bar{W}_{x_\mathrm{r},q_j} \\ -\frac{1}{2} \bar{W}_{x_\mathrm{r},q_\mathrm{r}} - \frac{1}{4} \bar{W}_{q_\mathrm{r},q_j}{W}_{q_j}^{-1}\bar{W}_{x_\mathrm{r},q_j} &{} {W}_{q_\mathrm{r}} -\frac{1}{4} \bar{W}_{q_\mathrm{r},q_j}{W}_{q_j}^{-1}\bar{W}_{q_\mathrm{r},q_j} \end{bmatrix}. \end{aligned}$$

Repeating the previous analysis, but now on $P - SQ^{-1}S^T$, we find that $\bar{\mathcal {W}}_{j} \succ 0$ if and only if the following three conditions hold:

• (1) $W_{q_j} \succ 0$,    (2) $W_{q_\mathrm{r}} - \frac{1}{4} \bar{W}_{q_\mathrm{r}, q_j} W_{q_j}^{-1} \bar{W}_{q_\mathrm{r}, q_j} \succ 0$,

• (3)
  $$\begin{aligned} 0\prec&W_{x_\mathrm{r}} - \frac{1}{4} \bar{W}_{x_\mathrm{r}, q_j} W_{q_j}^{-1} \bar{W}_{x_\mathrm{r}, q_j} - \frac{1}{4} \bar{W}_{x_\mathrm{r}, q_\mathrm{r}} (W_{q_\mathrm{r}} - \frac{1}{4} \bar{W}_{q_\mathrm{r}, q_j} W_{q_j}^{-1} \bar{W}_{q_\mathrm{r},q_j})^{-1} \bar{W}_{x_\mathrm{r}, q_\mathrm{r}} \\&- \frac{1}{8} \bar{W}_{x_\mathrm{r}, q_\mathrm{r}} (W_{q_\mathrm{r}} - \frac{1}{4} \bar{W}_{q_\mathrm{r}, q_j} W_{q_j}^{-1} \bar{W}_{q_\mathrm{r},q_j})^{-1} \bar{W}_{q_\mathrm{r},q_j}W_{q_j}^{-1}\bar{W}_{x_\mathrm{r}, q_j} \\&- \frac{1}{8} \bar{W}_{x_\mathrm{r},q_j} W_{q_j}^{-1} \bar{W}_{q_\mathrm{r},q_j} (W_{q_\mathrm{r}} - \frac{1}{4} \bar{W}_{q_\mathrm{r}, q_j} W_{q_j}^{-1} \bar{W}_{q_\mathrm{r},q_j})^{-1} \bar{W}_{x_\mathrm{r}, q_\mathrm{r}} \\&- \frac{1}{16} \bar{W}_{x_\mathrm{r},q_j} W_{q_j}^{-1} \bar{W}_{q_\mathrm{r},q_j} (W_{q_\mathrm{r}} - \frac{1}{4} \bar{W}_{q_\mathrm{r}, q_j} W_{q_j}^{-1} \bar{W}_{q_\mathrm{r},q_j})^{-1} \bar{W}_{q_\mathrm{r},q_j}W_{q_j}^{-1}\bar{W}_{x_\mathrm{r}, q_j}. \end{aligned}$$

Moreover, the minimum (maximum) eigenvalue of $\mathcal {W}_{j}$ is exactly the smallest (largest) of the minimum (maximum) eigenvalues of the three matrices in the above conditions. We now seek to verify that appropriate choices in the gains and constants can be made to satisfy the above conditions. First, by looking at the characteristic equation of $W_{q_j}$, it can be seen that

$$\begin{aligned} 2\lambda _{\min }(W_{q_j}) = (k_{\omega _j} - c_{q_j} + c_{q_j}k_{q_j}) - \sqrt{(k_{\omega _j} - c_{q_j} - c_{q_j}k_{q_j}) + c_{q_j}^2(k_{\omega _j} + C_{q_j})^2 }. \end{aligned}$$

By taking $c_{q_j}$ sufficiently small, $k_{\omega _j}$ sufficiently large, and $k_{q_j} = \frac{k_{\omega _j}}{c_{q_j}} - 1$, $\lambda _{\min }(W_{q_j})$ can be made arbitrarily large. Consequently, $\lambda _{\max }(W_{q_j}^{-1}) = \lambda _{\min }(W_{q_j})^{-1}$ can be made arbitrarily small (and positive). From Lemma 2, we have that $\frac{1}{4} \bar{W}_{q_\mathrm{r}, q_j} W_{q_j}^{-1} \bar{W}_{q_\mathrm{r}, q_j} \succeq 0$ and, since $\bar{W}_{q_\mathrm{r}, q_j}$ and $W_{q_j}$ are independent, we can shrink the maximum eigenvalue of $\bar{W}_{q_\mathrm{r}, q_j} W_{q_j}^{-1} \bar{W}_{q_\mathrm{r}, q_j}$ arbitrarily by shrinking the maximum eigenvalue of $W_{q_j}^{-1}$.

Similarly, from the characteristic equation of $W_{q_\mathrm{r}}$, we see that the eigenvalues satisfy

$$\begin{aligned} 2 \lambda _{\pm }&= ((1 - \alpha )c_{q_\mathrm{r}}k_{q_\mathrm{r}} + (1 - \alpha )k_{\omega _\mathrm{r}} - c_{q_\mathrm{r}} - \alpha C_{q_\mathrm{r}}^2)\\ {}&\pm \sqrt{((1 - \alpha )c_{q_\mathrm{r}}k_{q_\mathrm{r}} - (1 - \alpha )k_{\omega _\mathrm{r}} + c_{q_\mathrm{r}} + \alpha C_{q_\mathrm{r}}^2)^2 + c_{q_\mathrm{r}}^2((1 + \alpha )k_{\omega _\mathrm{r}} + C_{q_\mathrm{r}} + \alpha C_{q_\mathrm{r}}^2)^2}. \end{aligned}$$

Now choose $k_{\omega _\mathrm{r}} = \frac{\alpha }{1 - \alpha }C_{q_\mathrm{r}}^2 + c_{q_\mathrm{r}}k_{q_\mathrm{r}} + \frac{1}{1-\alpha }c_{q_\mathrm{r}} > 0$ and define $\bar{k}_{q_\mathrm{r}} = c_{q_\mathrm{r}} k_{q_\mathrm{r}}$. Then,

$$\begin{aligned} 2 \lambda _{\min }(W_{q_\mathrm{r}}) = 2(1 - \alpha )\bar{k}_{q_\mathrm{r}} - c_{q_\mathrm{r}}\left( \frac{2\alpha }{1-\alpha }C_{q_\mathrm{r}}^2 + C_{q_\mathrm{r}} + (1+\alpha )\bar{k}_{q_\mathrm{r}} + \frac{1+\alpha }{1-\alpha }c_{q_\mathrm{r}} \right) , \end{aligned}$$

from which it is clear that $\lambda _{\min }(W_{q_\mathrm{r}})$ can be made arbitrarily large (and positive) by choosing $c_{q_\mathrm{r}}$ and $\bar{k}_{q_\mathrm{r}}$ appropriately. Another application of Lemma 2 then shows that $W_{q_\mathrm{r}} - \frac{1}{4} \bar{W}_{q_\mathrm{r}, q_j} W_{q_j}^{-1} \bar{W}_{q_\mathrm{r}, q_j} \succ 0$, and its minimum eigenvalue can be made arbitrarily large with appropriate choices of $k_{q_j}, k_{\omega _j}, c_{q_j}$ for $j \in \mathcal {I}$.

Now we look at condition 3. First, choose $k_{x_\mathrm{r}}, k_{v_\mathrm{r}}, c_{x_\mathrm{r}}$ such that $W_{x_\mathrm{r}} \succ 0$ (this can always be done by, for instance, choosing $c_{x_\mathrm{r}}$ sufficiently small). We now wish to show that the remaining subtractive terms can be shrunk arbitrarily. Observe that $\bar{W}_{x_\mathrm{r}, q_j}$ and $W_{q_j}^{-1}$ are independent, so that we may force the maximum eigenvalue of $\bar{W}_{x_\mathrm{r}, q_j} W_{q_j}^{-1} \bar{W}_{x_\mathrm{r}, q_j} \succeq 0$ to be arbitrarily small after (potentially) further shrinking the maximum eigenvalue of $W_{q_j}^{-1}$. Observe that we may write the third term, $\frac{1}{4} \bar{W}_{x_\mathrm{r}, q_\mathrm{r}} (W_{q_\mathrm{r}} - \frac{1}{4} \bar{W}_{q_\mathrm{r}, q_j} W_{q_j}^{-1} \bar{W}_{q_\mathrm{r}, q_j})^{-1} \bar{W}_{x_\mathrm{r}, q_\mathrm{r}}$, in the form $\alpha ^2 M^T A M$, where M is independent of $\alpha$ and the terms of A are at most of $O(\frac{1}{\alpha })$. Hence, we may shrink this term arbitrarily by shrinking $\alpha .$ The fourth and fifth terms are transposes of each other and therefore may be handled simultaneously. Note that find that the maximum eigenvalue is bounded above by

$$\begin{aligned}&\lambda _{\max }((\bar{W}_{q_\mathrm{r}} - \frac{1}{4} \bar{W}_{q_\mathrm{r}, q_j} \bar{W}_{q_j}^{-1}\bar{W}_{q_\mathrm{r}, q_j})^{-1})||\bar{W}_{q_\mathrm{r}, q_j} \bar{W}_{q_j}^{-1} \bar{W}_{x_\mathrm{r}, q_j}|| \ ||\bar{W}_{x_\mathrm{r}, q_\mathrm{r}}|| \\&\quad \le \sqrt{\lambda _{\max }(\bar{W}_{q_j}^{-1})} \lambda _{\max }((\bar{W}_{q_\mathrm{r}} - \frac{1}{4} \bar{W}_{q_\mathrm{r}, q_j} \bar{W}_{q_j}^{-1}\bar{W}_{q_\mathrm{r}, q_j})^{-1}) ||\bar{W}_{q_\mathrm{r}, q_j}|| \ || \bar{W}_{x_\mathrm{r}, q_j}|| \ ||\bar{W}_{x_\mathrm{r}, q_\mathrm{r}}||. \end{aligned}$$

This term therefore can be arbitrarily shrunk by shrinking the maximum eigenvalue of $\bar{W}_{q_j}$. Moreover, the presence of the norm $||W_{x_\mathrm{r}, q_\mathrm{r}}||$ also gives us control of the size of the term via $\alpha .$ The final term is handled similarly—we find that the maximum eigenvalue is bounded by

$$\begin{aligned}&\lambda _{\max }((\bar{W}_{q_\mathrm{r}} - \frac{1}{4} \bar{W}_{q_\mathrm{r}, q_j} \bar{W}_{q_j}^{-1}\bar{W}_{q_\mathrm{r}, q_j})^{-1})||\bar{W}_{q_\mathrm{r}, q_j} \bar{W}_{q_j}^{-1} \bar{W}_{x_\mathrm{r}, q_j}||^2 \\&\quad \le \lambda _{\max }(\bar{W}_{q_j}^{-1}) \lambda _{\max }((\bar{W}_{q_\mathrm{r}} - \frac{1}{4} \bar{W}_{q_\mathrm{r}, q_j} \bar{W}_{q_j}^{-1}\bar{W}_{q_\mathrm{r}, q_j})^{-1}) ||\bar{W}_{q_\mathrm{r}, q_j}||^2 \ || \bar{W}_{x_\mathrm{r}, q_j}||^2, \end{aligned}$$

which again may be shrunk arbitrarily by shrinking the maximum eigenvalue of $\bar{W}_{q_j}^{-1}$. In summation, for sufficiently small $\alpha$ and $\lambda _{\max }(W_{q_j})$ sufficiently large, condition 3 is satisfied and $\mathcal {\bar{W}}_{j} \succ 0.$

Now, letting $x \in S^6$ such that $x = (x_1, x_2) \in \mathbb {R}^4 \times \mathbb {R}^2$, we get that

$\lambda _{\min }(\bar{\mathcal {W}}_{j}) \ge \min \{ \lambda _{\min }(Q), \ \lambda _{\min }(P - SQ^{-1}S^T)\} ||x + SQ^{-1}x_2||^2$. Note that $||SQ^{-1}x_2||$ can be made arbitrarily small by increasing the maximum eigenvalue of Q, so that $||x + SQ^{-1}x_2||$ can be made arbitrarily close to 1. Further decomposing $P - SQ^{-1}S^T$, we find that the minimum eigenvalue of $\bar{\mathcal {W}}_{j}$ is bounded below by a quantity that can be made arbitrarily close to the minimum of the minimum eigenvalue of the matrices in conditions (1), (2), and (3) above—all of which can be made arbitrarily large. Hence, the minimum eigenvalue of $\bar{\mathcal {W}}_{j}$ can be made arbitrarily large. Hence, the minimum eigenvalue of $\bar{\mathcal {W}}$ can also be made arbitrarily large. $\square$

Remark 4

Observe that, in the proof of Theorem 1, it is not important that the minimum eigenvalue can be made arbitrarily large-we need only have that it is positive. However, in Theorem 2 of Sect. 5, we will introduce unstructured bounded disturbances to the problem. In such a case, this fact will be crucial.

Moreover, while we have no exact estimates on the gains needed to guarantee exponential tracking, the proof does provide us with a strategy which may be used to decrease the complexity in numerically calculating/verifying gains. In particular, for any gains $k_{x_\mathrm{r}} > 0$ and $k_{v_\mathrm{r}} > 0$, we have that $W_{x_\mathrm{r}}, W_{q_\mathrm{r}}, W_{q_j}, {P}_{x_\mathrm{r}}, {P}_{q_\mathrm{r}}, {P}_{q_j} \succ 0$ if the following 7 conditions are satisfied:

• (I) $c_{x_\mathrm{r}} < \min \left\{ \frac{(1-\alpha )^2 k_{x_\mathrm{r}} k_{v_\mathrm{r}}}{(1 - \alpha )k_{x_\mathrm{r}} + \frac{1}{4} (1 + \alpha )^2 k_{v_\mathrm{r}}^2}, \ \sqrt{k_{x_\mathrm{r}}}\right\} ,$

• (II) $k_{q_\mathrm{r}} > \frac{\alpha }{(1-\alpha )^2} C_{q_\mathrm{r}}^2 + \frac{1}{2(1 - \alpha )} C_{q_\mathrm{r}}$,

• (III) $c_{q_\mathrm{r}} < \min \left\{ \frac{2(1 - \alpha ) k_{q_\mathrm{r}} - \frac{2 \alpha }{1 - \alpha } C_{q_\mathrm{r}}^2 - C_{q_\mathrm{r}}}{(1 + \alpha )k_{q_\mathrm{r}} + \frac{1 + \alpha }{1-\alpha }}, \ \sqrt{k_{q_\mathrm{r}}}\right\}$,

• (IV) $k_{\omega _\mathrm{r}} = \frac{\alpha }{1 - \alpha }C_{q_\mathrm{r}}^2 + c_{q_\mathrm{r}}k_{q_\mathrm{r}} + \frac{1}{1-\alpha }c_{q_\mathrm{r}}$,

• (V) $k_{\omega _j} > C_{q_j} + 2$,

• (VI) $1< c_{q_j} < \frac{2 k_{\omega _j}}{k_{\omega _j} + C_{q_j} + 2}$,

• (VII) $k_{q_j} = \frac{k_{\omega _j}}{c_{q_j}} + 1$.

It is easily verified that these conditions are consistent. The proof of Theorem 1 tells us exactly that exponential tracking is guaranteed so long as $\alpha$ is sufficiently small and $\lambda _{\min }(W_{q_j})$ is sufficiently large. The latter of which can always be satisfied, for instance, by fixing $c_{q_j} = 1+\epsilon$ for some arbitrary small $0< \epsilon < 1$ and taking $k_{\omega _j}$ sufficiently large. In particular, this reduces the 9 degrees of freedom involved in satisfying $\mathcal {W}_j \succ 0$ to a single degree of freedom—namely $k_{\omega _j}$—while simultaneously guaranteeing that ${P}_{x_\mathrm{r}}, {P}_{q_\mathrm{r}}, {P}_{q_j} \succ 0$. Finding an appropriate $k_{\omega _j}$ can then be solved numerically, provided that $\alpha$ is sufficiently small to guarantee a solution.

Remark 5

Due to the constraint $x_{Q_j} = x_\mathrm{r} + (-1)^j L_\mathrm{r} q_\mathrm{r} - L_\mathrm{c} q_j$, and the fact that the desired cable attitudes are pre-selected as $\tilde{q}_j = \tilde{\mu }_j / ||\tilde{\mu }_j||$, we are not able to choose the desired trajectories of the quadrotors while also choosing the desired trajectories for the load position and attitude. In particular, such choices will force the "desired" quadrotor positions $\tilde{x}_{Q_j}$ to similarly obey $\tilde{x}_{Q_j} = \tilde{x}_\mathrm{r} + (-1)^j L_\mathrm{r} \tilde{q}_\mathrm{r} - L_\mathrm{c} \tilde{\mu }_j / ||\tilde{\mu }_j||$. This leads to the concern that the quadrotors may stretch apart and play "tug of war" with the rod, or in the case that $2L_\mathrm{c} > L_\mathrm{r}$, may even collide with one another.

To find conditions under which this behavior is avoided, note that

$$\begin{aligned} \tilde{x}_{Q_2} - \tilde{x}_{Q_1}&= L_\mathrm{c} \left( \tilde{\mu }_1 / ||\tilde{\mu }_1|| - \tilde{\mu }_2 / ||\tilde{\mu }_2||\right) - 2L_\mathrm{r} \tilde{q}_\mathrm{r}.\\ \tilde{\mu }_j&= \frac{1}{2} m_\mathrm{r} \left( \dot{\tilde{v}}_\mathrm{r} + ge_3 \right) + (-1)^j \frac{1}{3} m_\mathrm{r} L_\mathrm{r} \left( -\hat{q}_\mathrm{r} \dot{\tilde{\omega }}_\mathrm{r}\right. \\&\quad \left. + (q_\mathrm{r}^T \tilde{\omega }_\mathrm{r})\hat{q}_\mathrm{r}^2 \tilde{\omega }_\mathrm{r} \right) + O(e_{x_\mathrm{r}}, e_{v_\mathrm{r}}, e_{q_\mathrm{r}}, e_{\omega _\mathrm{r}}). \end{aligned}$$

Suppose now that $||\frac{1}{3} m_\mathrm{r} L_\mathrm{r} \left( -\hat{q}_\mathrm{r} \dot{\tilde{\omega }}_\mathrm{r} + (q_\mathrm{r}^T \tilde{\omega }_\mathrm{r})\hat{q}_\mathrm{r}^2 \tilde{\omega }_\mathrm{r} \right) ||$ is small compared to $||\frac{1}{2} m_\mathrm{r} \left( \dot{\tilde{v}}_\mathrm{r} + ge_3 \right) ||$. This can be accomplished, for instance, by choosing $\tilde{q}_\mathrm{r}$ such that $||\tilde{\omega }_\mathrm{r}||$ and $||\dot{\tilde{\omega }}_\mathrm{r}||$ are sufficiently small (that is, that the desired angular velocity and angular acceleration of the rod’s orientation are sufficiently small). Further suppose that the initial errors $e_{x_\mathrm{r}}(0), e_{v_\mathrm{r}}(0), e_{q_\mathrm{r}}(0),$ and $e_{\omega _\mathrm{r}}(0)$ are small, and that the gains are chosen so that the origin of the error dynamics is an exponentially stable equilibrium point (in accordance with Theorem 1). It follows that both $\tilde{\mu }_1$ and $\tilde{\mu }_2$ will remain close to the vector $\frac{1}{2} m_\mathrm{r} \left( \dot{\tilde{v}}_\mathrm{r} + ge_3 \right)$, so that $\tilde{x}_{Q_2} - \tilde{x}_{Q_1}$ will remain close to $2L_\mathrm{r} \tilde{q}_\mathrm{r}$. In particular, this implies that $||\tilde{x}_{Q_2} - \tilde{x}_{Q_1}||$ remains close to $2L_\mathrm{r}$. Moreover, since the gains have been chosen to guarantee exponential tracking, we further have that $||x_{Q_2} - x_{Q_1}||$ will remain within some small neighborhood of $2L_\mathrm{r}$, from which it is clear that the quadrotors will neither converge to nor diverge from one another to an undesirable degree.

4.4 Control Design for the Original Model

Note that for the design of the geometric controllers $u_j$ we assumed that each quadrotor can generates a thrust along any direction. However, the dynamics of each quadrotor is underactuated since the direction of the total thrust is always parallel to its third body-fixed axis, despite the magnitude of the total thrust can be arbitrarily changed (recall that the total thrust is given by $u_j = f_j R_j e_3$, being $f_j$ the total thrust magnitude and $R_ie_3$ the direction of the third body-fixed axis). The attitude of each quadrotor is controlled such that the third body-fixed axis becomes parallel to the direction of the control force $u_j$ designed by (23) and (32).

The desired direction of the third body-fixed axis for each quadrotor, denoted by $b^{3}_j\in S^2$ is given by $b_{j}^{3} = \frac{u_j}{\Vert u_j\Vert }.$ Usually, such expression is considered as a constraint on the desired attitude of each quadrotor. Therefore to solve the dimensionality problem arising after introduce the constraint, and to be able to solve the system, the desired direction of the first body-fixed axis $b^{1}_j(t)\in S^2$ is introduced as a smooth function of time. Since the first body-fixed axis is normal to the third body-fixed axis, one cannot reach the arbitrary body axis $b^{1}_{j}$ exactly. The usual strategy in this situation is to project into the plane normal to $b^{3}_j$, and the desired direction of the second body-fixed axis is chosen to obtain an orthonormal frame. That is, the desired attitude for each quadrotor is given by $\displaystyle { R_{j,d} = \begin{bmatrix}\frac{(\hat{b}^{3}_j)^2 b^{1}_j}{\Vert (\hat{b}^{3}_j)^2 b^{1}_j\Vert },&-\frac{\hat{b}^{3}_jb^{1}_j}{\Vert \hat{b}^{3}_jb^{1}_j\Vert },&-b^{3}_j\end{bmatrix}}\in SO(3)$.

Using (21), the desired angular velocity for each quadrotor is $\Omega _{j,d} = (R_{j,d}^T\dot{R}_{j,d})^\vee \in \mathbb {R}^3$, where ${(\cdot )}^\vee :\mathfrak {so}(3)\rightarrow \mathbb {R}^3$ denotes the inverse of the hat map. Define the tracking error vectors for the attitude of each quadrotors $e_{R_j} = \frac{1}{2}(R_{j,d}^T R_j -R_j^T R_{j,d})^\vee$ and the tracking error vectors for the angular velocity of each quadrotor as $e_{\Omega _j} = \Omega _j - R_j^T R_{j,d}\Omega _{j,d}$. The thrust magnitude is chosen as the length of $u_j$, projected on to $R_je_3$, and the control moment is chosen as a tracking controller on SO(3), that is,

$$\begin{aligned} f_j&= u_j\cdot R_j e_3,\end{aligned}$$

(34)

$$\begin{aligned} M_j&= -\frac{k_R}{\epsilon ^2} e_{R_j} -\frac{k_\Omega }{\epsilon } e_{\Omega _j} + \Omega _j\times J_j\Omega _j- J_j (\hat{\Omega }_j R_j^T R_{j,d}\Omega _{j,d}-R_j^T R_{j,d}\dot{\Omega }_{j,d}),\qquad j=1,2, \end{aligned}$$

(35)

where $\epsilon ,k_R,k_\Omega$ are positive constants.

Stability of the corresponding controlled systems for the unreduced model can be studied by using singular perturbation theory for the attitude dynamics of quadrotors as in Sreenath et al. (2013), Lee et al. (2013). In particular, as a direct application of Lee (2014, 2018), in the context of Theorem 1 for our particular cooperative transportation task lead to the following result.

Corollary 1

Consider the control system defined by (15)–(22) and the control inputs designed by (34) and (35). Then, there exists $\delta > 0$, such that for all $\epsilon < \delta$, the zero equilibrium of the tracking errors

$(e_{x_\mathrm{r}}, e_{v_\mathrm{r}}, e_{q_\mathrm{r}}, e_{\omega _\mathrm{r}}, e_{q_1}, e_{\omega _1}, e_{q_2}, e_{\omega _2}, e_{R_1},e_{\Omega _1},e_{R_2},e_{\Omega _2})$ is exponentially stable.

Now that we have established the exponential tracking of the full reduced model, we wish to connect this back to our original model with elastic cables. This can be done by showing that our system is under the conditions of Theorem 11.2 in Khalil (2002). The first condition is a regularity condition for f, g, h (as defined by (11)–(12) and (13)–(14)), and the continuity and boundedness of their partial derivatives. Both the original and reduced model have smooth dynamics, and h is clearly smooth as well, so that the regularity follows. Moreover, we consider our control system as evolving on the bounded domain $\mathcal {D}$, so that boundedness follows immediately. The second condition requires that the reduced model has an exponentially stable equilibrium point at the origin (note that we must consider the error dynamics instead of the dynamical model (15)–(22) for this to make sense, but the result follows all the same since the configuration errors are smooth functions of the state variables). This follows immediately by Theorem 1. The third condition in Theorem 11.2 in Khalil (2002) is that the boundary layer system for (11)–(12) have an exponentially stable equilibrium point at the origin—which we define now.

Definition 1

The boundary layer system for the singular perturbation problem given by (11)–(12) is defined as:

$$\begin{aligned} \frac{\partial r}{\partial \tau } = g(t,x,r+h(t,x), 0), \end{aligned}$$

where $r := z - h(t,x)$ with h(t, x) as defined by (13)–(14) and $\tau := \frac{t - t_0}{\epsilon }$ for $t_0$ the value of time from which we obtain our initial data.

Corollary 2

The boundary layer system for (11)–(12) with control inputs $u_j$ and $M_j$ as defined above has an exponentially stable equilibrium point at the origin.

Proof

The analysis follows almost immediately from the case of a single quadrotor transporting a point mass load with an elastic cable (see Lemma 2 in Kotaru et al. (2017)). $\square$

With all conditions of Theorem 11.2 in Khalil (2002) satisfied, we obtain the following proposition relating the dynamics of the original model to the dynamics of the reduced model.

Proposition 2

Let the control inputs $u_j$ and $M_j$ be defined as above. Denote by x(t) a trajectory of the reduced model (15)–(22) which converges exponentially to the desired trajectory. Denote by r(t) a trajectory of the boundary layer system which converges exponentially to the origin. Then, there exists a positive constant $\epsilon ^*$ such that for all $t \ge t_0$ and $0< \epsilon < \epsilon ^*$, there exists a unique solution $x(t, \epsilon )$, $z(t, \epsilon )$ of the singular perturbation problem (11)–(12) on $[t_0, \infty )$ satisfying

$$\begin{aligned} x(t, \epsilon ) - x(t)&= \mathcal {O}(\epsilon ),\\ z(t, \epsilon ) - h(t, x(t)) - r\left( \frac{t - t_0}{\epsilon }\right)&= \mathcal {O}(\epsilon ), \end{aligned}$$

uniformly on $t \in [t_0, \infty )$. Moreover, for $t_1 > t_0$, we have

$$\begin{aligned} z(t,\epsilon ) - h(t,x(t)) = O(\epsilon ),\end{aligned}$$

uniformly on $(t_1, \infty )$ for $\epsilon< \epsilon ^{**} < \epsilon ^*$.

4.5 Simulation Results

We now test the results of Theorem 1 with numerical simulations. Simulations of the dynamics for the reduced model were conducted using the proposed controller.

We implement a Euler method for the numerical integration of Eqs. (24)–(29) with time step $h = 0.002$ and $T=20$ seconds. The system parameters were chosen as $m_\mathrm{Q} = 0.755, \ m_\mathrm{r} = 0.5, \ L_\mathrm{c} = L_\mathrm{r} = 1.0,$ and $J_\mathrm{Q} = \begin{bmatrix} 0.082 &{} 0 &{} 0 \\ 0 &{} 0.0845 &{} 0 \\ 0 &{} 0 &{} 0.1377 \end{bmatrix}$. The gains we consider are $k_{x_\mathrm{r}} = 9, \ k_{v_\mathrm{r}} = 6, \ k_{q_\mathrm{r}} = 2, \ k_{w_\mathrm{r}} = 2 \sqrt{2}, \ k_{q_1} = 36, \ k_{w_1} = 12, \ k_{q_2} = 36, \ k_{w_2} = 12$. It should be noted that both smaller and larger gain sets were found that yielded convergence. This particular set was chosen because it offered an appropriate balance between performance and feasibility, in particular with regards to the convergence of the load position, which was chosen as the Lissajous curve described by $\tilde{x}(t)= (1.2 \sin (0.4 \pi t), \ 4.2 \cos (0.2 \pi t), \ -0.5)$, together with a constant desired load attitude $\tilde{q}_\mathrm{r}(t) = (0, 1, 0)$ (in accordance with Remark 5 to guarantee that the quadrotors do not collide nor stretch apart). The initial conditions were chosen as $x_\mathrm{r}(0) = (1, 4.9, -1), \ v_\mathrm{r}(0) = (1.2, 0.55, 0.15), \ q_\mathrm{r}(0) = (0.24, 0.97, -0.1), \ \omega _\mathrm{r}(0) = (0.1, -0.1, 0), \ q_1 = (0.53, 0.63, -0.56), \ \omega _1(0) = (0, 0, 0), \ q_2(0) = (0.48, 0.67, -0.56),$

$\omega _2(0) = (0, 0, 0).$

Figure 2 shows the magnitude of the error functions versus times. In each case, the blue curve represents the error in the position/attitude, and red curve represents the error in the velocity/angular velocity. Additionally, we plot the magnitude of the controllers $||u_1||$ and $||u_2||$ versus time. For illustrative purposes, we also include Fig. 3, which plots the load position (blue curve), the desired trajectory for the load (red curve), and the positions of the quadrotors (green and yellow curves) in 3D space. The highlighted points along the yellow and green curves mark the final positions of the two quadrotors.

Fig. 2

Configuration errors versus time and control magnitude versus time

Note that, as expected, the error asymptotically converges to zero (or a small neighborhood of zero) in all cases, while the controls approach steady state solutions.

Fig. 3

Position curves for the load (blue) and two quadrotors (green and yellow), together with the desired trajectory of the load (red) (Color figure online)

5 Extension to the Control Design in the Presence of (Unstructured) Disturbances

While the control scheme developed in Sect. 4 is theoretically sound, in practice there may be practical constraints such as disturbances and measurement errors which cause its failure. This in part is handled by the well-known fact that exponential stability is robust to small disturbances (Khalil 2015). However, it would additionally be beneficial to understand how the proposed controller behaves when it is subject to larger disturbances. Toward that end, we introduce bounded unstructured disturbances to the reduced dynamical model (24)–(29). That is, for some real numbers $\delta x_\mathrm{r}, \delta q_j$ for $j \in \mathcal {I}$, we consider the dynamical system

$$\begin{aligned} \dot{x}_\mathrm{r}&= v_\mathrm{r}, \end{aligned}$$

(36)

$$\begin{aligned} m_\mathrm{r} ( \dot{v}_\mathrm{r} + ge_3)&= \mu _1 + \mu _2 + \Delta x_\mathrm{r}, \end{aligned}$$

(37)

$$\begin{aligned} \dot{q}_\mathrm{r}&= \omega _\mathrm{r} \times q_\mathrm{r}, \end{aligned}$$

(38)

$$\begin{aligned} \frac{2}{3} m_\mathrm{r} L_\mathrm{r} \dot{\omega }_\mathrm{r}&= q_\mathrm{r} \times ( \mu _2 - \mu _1 ) + \Delta q_\mathrm{r}, \end{aligned}$$

(39)

$$\begin{aligned} \dot{q}_j&= \omega _j \times q_j, \end{aligned}$$

(40)

$$\begin{aligned} m_\mathrm{Q} L_\mathrm{c} \dot{\omega }_j&= m_\mathrm{Q} q_j \times ( \ddot{x}_\mathrm{r} + (-1)^j L_\mathrm{r} \ddot{q}_\mathrm{r} + ge_3) - q_j \times u_j + \Delta q_j, \end{aligned}$$

(41)

where for $j \in \mathcal {I}$, $\Delta x_\mathrm{r}, \Delta q_\mathrm{r}, \Delta q_j$ are unstructured disturbances satisfying $||\Delta x_\mathrm{r}|| \le \delta x_\mathrm{r}$ and $||\Delta q_j|| \le \delta q_j$. Defining the controllers, configuration errors, and Lyapunov candidate V as in Sect. 4, the bounds on the Lyapunov function remain the same. That is, we have $\frac{1}{2} z_{q_j}^T {P}_{q_j} z_{q_j} \le V_{q_j} \le \frac{1}{2} z_{q_j}^T \bar{P}_{q_j} z_{q_j}.$ However, some additional terms appear in its derivative (last three terms in the following inequality):

$$\begin{aligned} \dot{V} \le&-(k_{v_\mathrm{r}} - c_{x_\mathrm{r}}) ||e_{v_\mathrm{r}}||^2 + c_{x_\mathrm{r}} k_{v_\mathrm{r}} ||e_{v_\mathrm{r}}|| ||e_{x_\mathrm{r}}|| - c_{x_\mathrm{r}}k_{x_\mathrm{r}}||e_{x_\mathrm{r}}||^2 + \frac{1}{m_\mathrm{r}}(||e_{v_\mathrm{r}}|| + c_{x_\mathrm{r}} ||e_{x_\mathrm{r}}||) ||Y|| \\&-(k_{\omega _\mathrm{r}} - c_{q_\mathrm{r}})||e_{\omega _\mathrm{r}}||^2 + c_{q_\mathrm{r}}(k_{\omega _\mathrm{r}} + C_{q_\mathrm{r}})||e_{\omega _\mathrm{r}}||||e_{q_\mathrm{r}}|| - c_{q_\mathrm{r}} k_{q_\mathrm{r}} ||e_{q_\mathrm{r}}||^2 - c_{q_j} k_{q_j} ||e_{q_j}||^2\\&+ \frac{2}{3 m_\mathrm{r} L_\mathrm{r}} (||e_{\omega _\mathrm{r}}|| + c_{q_\mathrm{r}} ||e_{q_\mathrm{r}}||) ||Y|| -(k_{\omega _j} - c_{q_j}) ||e_{\omega _j}||^2 + c_{q_j} (k_{\omega _j} + C_{q_j} ) ||e_{q_j}|| ||e_{\omega _j}|| \\&+ E_{x_\mathrm{r}}^T (e_{v_\mathrm{r}} + c_{x_\mathrm{r}} e_{x_\mathrm{r}}) + E_{q_\mathrm{r}}^T (e_{\omega _\mathrm{r}} + c_{q_\mathrm{r}} e_{q_\mathrm{r}}) + E_{q_j}^T (e_{\omega _j} + c_{q_j} e_{q_j}), \end{aligned}$$

where $E_{x_\mathrm{r}}, E_{q_\mathrm{r}},$ and $E_{q_j}$ are defined as $E_{x_\mathrm{r}} = \frac{\Delta x_\mathrm{r}}{m_\mathrm{r}}, E_{q_\mathrm{r}} = \frac{3 \Delta q_\mathrm{r}}{2m_\mathrm{r} L_\mathrm{r}}, E_{q_j} = \frac{\Delta q_j}{m_\mathrm{Q} L_\mathrm{c}}$. We may then write this is the form $\dot{V} \le -z^T \mathcal {W} z + E^T z,$ where $E := \begin{bmatrix} \frac{c_{x_\mathrm{r}}\delta x_\mathrm{r}}{m_\mathrm{r}}, \frac{\delta x_\mathrm{r}}{m_\mathrm{r}}, \frac{c_{q_\mathrm{r}}3\delta q_\mathrm{r}}{2m_\mathrm{r} L_\mathrm{r}}, \frac{3\delta q_\mathrm{r}}{2m_\mathrm{r} L_\mathrm{r}}, \frac{c_{q_1}\delta q_1}{m_\mathrm{Q} L_\mathrm{c}}, \frac{\delta q_1}{m_\mathrm{Q} L_\mathrm{c}}, \frac{c_{q_2}\delta q_2}{m_\mathrm{Q} L_\mathrm{c}}, \frac{\delta q_2}{m_\mathrm{Q} L_\mathrm{c}} \end{bmatrix}$ and $\mathcal {W}$ is as in Sect. 4. From Young’s Inequality, we have $E^T z \le \frac{||E||^2}{4 \epsilon } + \epsilon ||z||^2$ for any $\epsilon > 0$. Hence,

$$\begin{aligned} \dot{V} \le -z^T (\mathcal {W} - \epsilon I) z + \frac{||E||^2}{4 \epsilon }. \end{aligned}$$

Fix $\epsilon > 0.$ Analogous to before, we replace the matrix $\mathcal {W} - \epsilon I$ with its symmetric part $\bar{\mathcal {W}}^*:= \frac{1}{2}(\mathcal {W} + \mathcal {W}^T) - \epsilon I$. Observe that:

$$\begin{aligned} \lambda _{\min }(\mathcal {\bar{W}}^*)&= \min _{x \in S^6} \{ x^T (\mathcal {\bar{W}} - \epsilon I) x \} = \min _{x \in S^6} \{ x^T \mathcal {\bar{W}} x - \epsilon ||x||^2 \} = \min _{x \in S^6} \{ x^T \mathcal {\bar{W}} x \} - \epsilon \\&= \lambda _{\min }(\mathcal {\bar{W}}) - \epsilon \end{aligned}$$

From the proof of Theorem 1, $\lambda _{\min }(\mathcal {\bar{W}})$ can be made arbitrarily large by choosing gains appropriately. Hence, we can choose them so that $\bar{\mathcal {W}}^*\succ 0$, with an arbitrarily large minimum eigenvalue. We then have the following inequalities:

$$\begin{aligned} \lambda _{\min }( {P})||z||^2&\le V \le \lambda _{\max }(\bar{P})||z||^2, \\ \dot{V}&\le -\lambda _{\min }(\bar{\mathcal {W}}^*)||z||^2 + \frac{||E||^2}{4\epsilon }. \end{aligned}$$

This implies that $\dot{V} \le -\frac{\lambda _{\min }(\bar{\mathcal {W}}^*)}{\lambda _{\max }(\bar{P})}V + \frac{||E||^2}{4\epsilon }$, so that $\dot{V} < 0$ when $V> \frac{\lambda _{\max }(\bar{P})}{\lambda _{\min }(\bar{\mathcal {W}}^*)}\frac{||E||^2}{4\epsilon }:= d_1 > 0.$ Clearly, $d_1$ can be arbitrarily small by making $\lambda _{\min }(\bar{\mathcal {W}}^*)$ sufficiently large. If we now define the set $S_{r} := \{z \in \mathcal {D} : V(z) < r \}$, where r is some real number, then any trajectory starting in the open set $\mathcal {D} \setminus \bar{S}_{d_1}$ will converge exponentially to the region $\bar{S}_{d_1}$, where $\bar{S}_{d_1}$ denotes the topological closure of $S_{d_1}$. Since V is continuous and positive, $\bar{S}_{d_1}$ is some closed neighborhood of the origin that can be made arbitrarily small (by shrinking $d_1$). We formalize this result with the following theorem:

Theorem 2

Consider the control system with disturbances defined by Eqs. 36–41 with control inputs 30, 31, and 32. For sufficiently small $\alpha$, there exists control gains $k_{x_\mathrm{r}}$, $k_{v_\mathrm{r}}$, $k_{q_\mathrm{r}}$, $k_{\omega _\mathrm{r}}$, $k_{q_1}$, $k_{\omega _1}$, $k_{q_2}$, and $k_{\omega _2}$ such that the zero equilibrium of the tracking errors $e_{x_\mathrm{r}}$, $e_{v_\mathrm{r}}$, $e_{q_\mathrm{r}}$, $e_{\omega _\mathrm{r}}$, $e_{q_1}$, $e_{\omega _1}$, $e_{q_2}$, and $e_{\omega _2}$ are uniformly ultimately bounded with an arbitrarily small ultimate bound.

Remark 6

We will not extend this result to include the quadrotor attitude kinematics and dynamics here, nor relate it back to the original elastic model. Such a task follows by essentially the same strategy as employed in Sect. 4, just replacing exponential stability with uniform ultimate boundedness where appropriate.

6 Conclusion and Future Work

In this paper, we propose a model and geometric trajectory tracking controller for the cooperative task of two quadrotor UAVs transporting a rigid bar via inflexible elastic cables. This is handled in three stages: (i) Reduction of the model to that of a similar model with inelastic cables. We accomplish this by assuming sufficient stiffness and damping of the cables (a realistic condition in applications) and utilizing the results of singular perturbation theory. (ii) Design of a geometric tracking controller in the reduced model. Lyapunov analysis is used to find sufficient conditions for stability, and Theorem 1 proves the existence of gains satisfying these conditions for sufficiently small initial errors in the cable attitudes. (ii) We show that—under the same control law—trajectories of the original (elastic) model converge uniformly to the trajectories of the reduced model as the stiffness and damping of the cables approach infinity. We also extended the proposed approach to design a control law for the case when the system under study is subject to unstructured bounded disturbances.

We are currently working to add uncertainties in order to further explore the robustness of the proposed controller. We also plan to study the construction of force variational integrators in optimal control problems, in a similar fashion to Colombo et al. (2016) and Colombo et al. (2015), dynamic interpolation problems (Bloch 2019), and obstacle avoidance problems (Bloch et al. 2017) for the cooperative mission. Finally, note also that in our model, cables are attached to the center of each quadrotor. It would be interesting to shift those attachment points and see how to deal with the resulting coupled systems—instead of a decoupled system as it is in this paper—as well as heterogeneous agents.