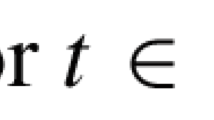Non-autonomous Differential Systems with Delays: A Global Attraction Analysis

Abstract

In this paper, we derive criteria of global attractivity of a (possibly constant) positive periodic solution in non-autonomous systems of delay differential equations. Our approach can be viewed as the extension for non-autonomous systems of the folkloric connection between discrete dynamics and scalar delay differential equations. It is worth mentioning that we provide delay-dependent criteria of global attraction that cover the best delay independent conditions. We apply our results to non-autonomous variants of several classical models such that Nicholson’s blowfly equation, Goodwin’s model oscillator, the Mackey–Glass equation and systems with patch structure.

1 Introduction

The seasonal fluctuations of the environmental conditions play a central role in the regulation of populations, the structuring of ecological communities and the functioning of ecosystems (Lou and Zhao 2017; Lou et al. 2019). In epidemiology, the transmission of most infectious diseases also depends on several temporal variables (Barrientos et al. 2017; Li et al. 2020). For example, seasonal influenza generally recurs with a large epidemic in winter and a negligible presence in summer. Given the importance of the seasonal fluctuations, non-autonomous equations are certainly useful in any life-system. On the other hand, time delays are rather common in applied sciences to model, for instance, age-structure, maturation periods or hatching times (Lou et al. 2019; Ruiz-Herrera 2019). Taking together both frameworks, we arrive at non-autonomous delay differential systems. These models have attracted much attention in the last decades, see Berezansky et al. (2010), Faria (2021, 2017), Faria et al. (2018), Li et al. (2020), Lou and Zhao (2017) and Lou et al. (2019) and the references therein. The main reason for this interest is that the interplay between time-delays and seasonality brings great challenges to the mathematical analysis.

When one faces with a particular model, the natural question is to study the existence of a globally attracting solution. There are mainly two approaches for this problem: the construction of Lyapunov functions (McCluskey 2015) and the theory of monotone systems (Smith 2011). In the context of autonomous scalar delay differential equations, Ivanov and Sharkovsky (1992) and Mallet-Paret and Nussbaum (1986) proposed an alternative methodology. Specifically, they proved that ${\bar{x}}$ is a globally attracting solution in

$$\begin{aligned} x'(t)=-d x(t)+ \beta h(x(t-\tau )) \end{aligned}$$

(1)

provided ${\bar{x}}$ is a globally attracting fixed point for the difference equation

$$\begin{aligned} x_{n+1}=f(x_{n}) \end{aligned}$$

where $f(x)=\frac{\beta }{d} h(x)$ is the function that determines the equilibria in (1). The connection between discrete and continuous equations was a considerable step in the understanding of delay differential equations. The obvious advantage is that we can handle an equation where the initial conditions belong to an infinite dimensional space via an equation with initial conditions in an one-dimensional space. Moreover, the connection typically leads to the best delay independent condition of global attraction. It is worth mentioning that the direct extension for systems is not possible. In general, it is necessary to add extra conditions, see Example 3 in Ruiz-Herrera (2020).

In this paper, we propose a connection between non-autonomous delay differential systems and discrete equations similar to that in Ivanov and Sharkovsky (1992), Mallet-Paret and Nussbaum (1986). Our methodology is new and follows the next steps: First, we prove the existence of a (possibly constant) positive periodic solution $x_{*}(t)$. Then, we employ a change of variable and identify a class of “amenable” nonlinearities. Finally, we construct an adequate function depending on the upper and lower bounds of the possible positive periodic solutions of the system. A strength of our results is that we recover the best delay independent conditions of global attraction and some classical delay dependent criteria (see Gyori and Trofimchuk 1999) when we study autonomous equations. We stress that the function that “codes” the dynamical behavior in

$$\begin{aligned} x'(t)=-d(t) x(t)+\beta (t) f(x(t-\tau )), \end{aligned}$$

is not clear. This first difficulty could explain why the analysis in Ivanov and Sharkovsky (1992) or Mallet-Paret and Nussbaum (1986) has not been extended to non-autonomous systems yet.

Another motivation of the paper is to examine critical issues such as the influence of the seasonal fluctuations of the environment and time-delays on the creation/suppression of oscillations or the density of population, i.e., whether or not a population is adversely affected by a periodic environment. Apart from these issues, we derive sufficient conditions for the existence of a globally attracting periodic solution in the Mackey–Glass equation and Nicholson’s blowfly model with periodic coefficients. Despite the variety of methods and tools that have been proposed in the literature for these models, we obtain sharper criteria than the existing ones, see Faria (2017) and the references therein. We also analyze the Goodwin oscillator model (Ruoff and Rensing 1996; El-Morshedy and Ruiz-Herrera 2020) and some classical metapopulation models subject to seasonal fluctuations of the environment (El-Morshedy and Ruiz-Herrera 2017, 2020; Faria 2014).

The structure of the paper is as follows. In Sect. 2, we give some useful lemmas on discrete dynamics. In Sect. 3, we derive criteria of global attractivity of a (possibly constant) positive periodic solution in scalar delay differential equations. In Sect. 4, we extend the results to systems. We finish the paper with a discussion on our findings. A critical tool in this paper will be the fluctuation lemma. We recall its statement for the reader’s convenience.

Lemma 1.1

(Lemma A.1 page 154 in Smith 2011) Let $\varphi :[a,+\infty )\longrightarrow {\mathbb {R}}$ be a bounded function of class ${\mathcal {C}}^{1}$. Then, there exist two sequences $\{t_{n}\}$ and $\{s_{n}\}$ tending to $+\infty$ with the following properties:

• $\lim _{n\rightarrow +\infty } \varphi (t_{n})= \limsup _{x\rightarrow +\infty } \varphi (x)$ and $\lim _{n\rightarrow +\infty } \varphi '(t_{n})= 0$.

• $\lim _{n\rightarrow +\infty } \varphi (s_{n})= \liminf _{x\rightarrow +\infty } \varphi (x)$ and $\lim _{n\rightarrow +\infty } \varphi '(s_{n})= 0$.

To conclude this section, we introduce some notation. Given a subset $A\subset {\mathbb {R}}^{N}$ and two positive constants $\tau ,T>0$ with $\tau \ge T$, we define

$$\begin{aligned} {\mathcal {C}}([-\tau ,0], A)=\{\phi :[-\tau ,0]\longrightarrow A\;\;\mathrm{continuous}\}. \end{aligned}$$

For $\phi \in {\mathcal {C}}([-\tau ,0], A)$ such that $\phi (t+T)=\phi (t)$ for all $t,t+T\in [-\tau ,0]$, we write ${\widetilde{\phi }}$ for the T-periodic function defined in ${\mathbb {R}}$ which coincides with $\phi$ on $[-\tau ,0]$. We denote by ${\mathcal {C}}_{T}(A)$ the set of T-periodic continuous functions $\phi :{\mathbb {R}}\longrightarrow A$, which can be identified as a subset of ${\mathcal {C}}([-\tau ,0], A)$ respectively, with the same topology. Given $v=(v_{1},\ldots ,v_{N})\in {\mathbb {R}}^{N}$, we write $v\gg 0$ when $v_{i}>0$ for all $i=1,\ldots ,N$.

2 Mathematical Framework and Some Useful Results

Given a function $h:[0,+\infty )\longrightarrow [0,+\infty )$ of class ${\mathcal {C}}^{1}$ with $h((0,+\infty ))\subset (0,+\infty )$, we define $H:(0,+\infty )^2\longrightarrow (0,+\infty )$ as

$$\begin{aligned} H(t,x)=\frac{h(tx)}{h(t)}. \end{aligned}$$

The next conditions play a crucial role in our analysis:

(A):

h is bounded.

(B):

$\frac{\partial H }{\partial t}(t,x)\ge 0$ for all $(t,x)\in (0,+\infty )\times (0,1)$.

(C):

$\frac{\partial H }{\partial t}(t,x)\le 0$ for all $(t,x)\in (0,+\infty )\times (1,+\infty )$.

Lemma 2.1

Fix $\theta _{0}\in (0,+\infty )$ and consider $g(x)=H(\theta _{0},x)$. Assume (A), (B) and (C) together with the condition:

(Q):

$g(x)>x$ if $x\in (0,1)$ and $g(x)<x$ if $x\in (1,+\infty )$.

If $H(\theta ,a)\ge a$ (resp. $H(\theta ,a)\le a$) for some $(\theta ,a)\in [\theta _{0},+\infty )\times (0,+\infty )$, then $a\le 1$ (resp. $a\ge 1$). In particular, if $H(\theta ,a)=a$ for some $(\theta ,a)\in [\theta _{0},+\infty )\times (0,+\infty )$, then $a=1$.

Proof

Take $(\theta ,a)\in [\theta _{0},+\infty )\times (0,+\infty )$ with $H(\theta ,a)\ge a$. Assume, by contradiction, that $a>1$. Then, by (C),

$$\begin{aligned} a\le H(\theta ,a)\le g(a). \end{aligned}$$

(2)

On the other hand, since $a>1$, condition (Q) implies that $g(a)<a$, a contradiction with (2). The property regarding $H(\theta ,a)\le a$ is analogous (using condition (B)) and we omit the details. Finally, if $H(\theta ,a)=a$, we have that $H(\theta ,a)\ge a$ and $H(\theta ,a)\le a$. Using the first statement of the lemma, we conclude that $a=1$. $\square$

Lemma 2.2

Fix $\theta _{0},\theta _{1}\in (0,+\infty )$ with $\theta _{0}\le \theta _{1}$ and consider $g(x)=H(\theta _{0},x)$ and $f(x)=H(\theta _{1},x)$. Assume (A), (B), (C) and (Q). Suppose that there are six positive constants $L_{1},S_{1}, {\widetilde{L}}, {\widetilde{S}}, L,S$ with the following properties:

• $L_{1},S_{1}\in [\theta _{0},\theta _{1}]$.

• $L<S$.

• ${\widetilde{L}},{\widetilde{S}}\in [L,S]$.

• $H(L_{1},{\widetilde{L}})\le L$ and $H(S_{1},{\widetilde{S}})\ge S$.

Then, ${\widetilde{S}}<1<{\widetilde{L}}$, $f({\widetilde{L}})\le L$ and $f({\widetilde{S}})\ge S$.

Proof

Notice that $H(L_{1},{\widetilde{L}})\le L\le {\widetilde{L}}$ and $H(S_{1},{\widetilde{S}})\ge S\ge {\widetilde{S}}$. Thus, we automatically have by the previous lemma that ${\widetilde{S}}\le 1$ and ${\widetilde{L}}\ge 1$. Let us prove that ${\widetilde{S}}<1$. Assume, by contradiction, that ${\widetilde{S}}=1$. Then,

$$\begin{aligned} 1=H(S_{1},1)=H(S_{1},{\widetilde{S}})\ge S. \end{aligned}$$

Using that $1={\widetilde{S}}\le S$, we obtain that $S=1$. Since ${\widetilde{L}}\le S=1$ and ${\widetilde{L}}\ge 1$, we conclude that ${\widetilde{L}}=1$. Finally, $1=H(L_{1},{\widetilde{L}})=H(L_{1},1)\le L$ together with $L\le {\widetilde{L}}=1$ imply that $L=1$. Collecting the above information, we arrive at $L=S=1$. This is a contradiction with $L<S$. Arguing in a similar manner, we can deduce that ${\widetilde{L}}>1$. At this moment, we know that ${\widetilde{S}}<1<{\widetilde{L}}$. By conditions (B) and (C), we easily deduce that $f({\widetilde{L}})\le H(L_{1},{\widetilde{L}})\le L$ and $f({\widetilde{S}})\ge H(S_{1},{\widetilde{S}})\ge S$. $\square$

The main results of this paper are based on the global attraction of a scalar discrete equation of the form:

$$\begin{aligned} x_{n+1}=\varphi (x_{n}) \end{aligned}$$

(3)

with $\varphi :[0,+\infty )\longrightarrow [0,+\infty )$ a function of class ${\mathcal {C}}^{1}$ satisfying that $\varphi ((0,+\infty ))\subset (0,+\infty )$. To facilitate understanding, we recall two basic results on discrete dynamics that we will use in a recurrent manner.

Proposition 2.1

(Lemma 2.5 in El-Morshedy and Lopez 2008) Assume that ${\bar{x}}\in (0,+\infty )$ with $\varphi ({\bar{x}})={\bar{x}}$ is a global attractor of (3) in $(0,+\infty )$, that is, for all $x_{0}\in (0,+\infty )$,

$$\begin{aligned} \lim _{n\longrightarrow +\infty }\varphi ^{n}(x_{0})={\bar{x}}. \end{aligned}$$

Then, there is no interval $[L,S]\subset (0,+\infty )$ with $L<S$ so that $[L,S]\subset \varphi ([L,S])$.

Proposition 2.2

Assume that $\varphi$ is a decreasing or unimodal function of class ${\mathcal {C}}^{3}$ with negative Schwarzian derivative, that is,

$$\begin{aligned} (S\varphi )(x)=\frac{\varphi '''(x)}{\varphi '(x)}-\frac{3}{2}\left( \frac{\varphi ''(x)}{\varphi '(x)}\right) ^{2}<0,\quad for\;all\; x>0\; \end{aligned}$$

provided $\varphi '(x)\not =0$. If (3) has a unique positive equilibrium ${\bar{x}}>0$ and $|\varphi '({\bar{x}})|\le 1$, then ${\bar{x}}$ is a global attractor of (3) in $(0,+\infty )$.

The previous result can be found in Corollary 2.10 of El-Morshedy and Lopez (2008) for unimodal functions. For decreasing maps, we can deduce the result by a simple adaptation of the arguments in Singer (1978). It is worth mentioning that $\varphi (x)=x e^{\rho (1-x)}$ with $\rho >0$ and $\varphi (x)=\frac{1+\rho ^{\gamma }}{1+(\rho x)^\gamma } x$ with $\rho >0$ and $\gamma >1$ are unimodal functions with negative Schwarzian derivative.

3 Scalar Equations with Periodic Coefficients

In this section, we derive criteria of global attractivity of a positive T-periodic solution in

$$\begin{aligned} x'(t)=-d(t) x(t)+\beta (t) h(x(t-\tau )) \end{aligned}$$

(4)

where $d,\beta :{\mathbb {R}}\longrightarrow (0,+\infty )$ are continuous and T-periodic; $\tau >0$ and $h:[0,+\infty )\longrightarrow [0,+\infty )$ is a function of class ${\mathcal {C}}^{1}$ with $h((0,+\infty ))\subset (0,+\infty )$. We stress that the term T-periodic function in this paper encompasses the constant functions. Additionally, we impose that h satisfies conditions (A), (B) and (C).

Our approach has two important ingredients:

• The connection of (4) with a suitable discrete equation.

• An a-priori estimate of upper and lower bounds for the possible positive T-periodic solutions of (4).

In Sect. 3.3, we will apply our results to the classical Nicholson’s blowfly equation with periodic coefficients. The reader can consult (Liz and Ruiz-Herrera 2013; Yi and Zou 2008, 2010) for different approaches relating discrete dynamics and continuous equations. We stress that the positive periodic solutions in (4) are generally non-constant. In Sect. 3.4, we illustrate how to apply our tools when the positive periodic solution in (4) is a constant function, i.e., $d(t)=k\beta (t)$ for some constant $k>0$.

3.1 Theoretical Results

For any initial function $\phi \in {\mathcal {C}}([-\tau ,0], [0,+\infty ))$, there is a unique (local) solution $x(t,\phi )$ of (4) with $x(t,\phi )=\phi (t)$ for all $t\in [-\tau ,0]$. Based on the variation of the constant formula, Eq. (4) can be written as:

$$\begin{aligned} x(t)=x(0)e^{-\int _{0}^{t}d(s){\mathrm{d}}s}+ e^{-\int _{0}^{t}d(s){\mathrm{d}}s}\int _{0}^{t}e^{\int _{0}^{s} d(r){\mathrm{d}}r}\beta (s) h(x(s-\tau )){\mathrm{d}}s. \end{aligned}$$

This expression implies that $x(t,\phi )\ge 0$ for all $t\ge 0$ on its interval of definition. Actually, if $\phi \in {\mathcal {C}}([-\tau ,0], (0,+\infty ))$, we can guarantee that $x(t,\phi )>0$ because $h((0,+\infty ))\subset (0,+\infty )$. Next, we prove that the solutions of (4) cannot blow up. Take $\Omega _{2}$ a constant so that

$$\begin{aligned} \Omega _{2}>\max \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} M \end{aligned}$$

(5)

with M an upper bound of h, (see (A)). If a solution x(t) of (4) satisfies that $x(t_{0})\ge \Omega _{2}$ for some $t_{0}>0$, then x(t) is strictly decreasing in a neighborhood of $t_{0}$. Notice that

$$\begin{aligned} \frac{x'(t_{0})}{d(t_{0})}=-x(t_{0})+\frac{\beta (t_{0})}{d(t_{0})} h(x(t_{0}-\tau ))< -x(t_{0})+\Omega _{2}. \end{aligned}$$

(6)

Thus, the solutions of (4) with initial function in ${\mathcal {C}}([-\tau ,0], [0,+\infty ))$ are defined for all $t\ge 0$.

In the rest of the section, we always work with solutions with initial function in ${\mathcal {C}}([-\tau ,0], (0,+\infty ))$. We refer to them as positive solutions.

Our next goal is to prove that the positive solutions of (4) are uniformly bounded.

Proposition 3.1

Assume (A). Then,

$$\begin{aligned} \limsup _{t\longrightarrow +\infty } x(t)\le \Omega _{2} \end{aligned}$$

for any positive solution x(t) of (4) with $\Omega _{2}$ the constant given in (5).

Proof

Take x(t) a positive solution of (4). As mentioned above, if $x(t_{0})\ge \Omega _{2}$ for some $t_{0}>0$, then x(t) is strictly decreasing in a neighborhood of $t_{0}$. We can also deduce that if $x(t_{1})\le \Omega _{2}$ for some $t_{1}> 0$, then $x(t)\le \Omega _{2}$ for all $t\ge t_{1}$. Next we prove that there is a time $t_{2}>0$ so that $x(t_{2})\le \Omega _{2}$. Assume, by contradiction, that $x(t)>\Omega _{2}$ for all $t>0$. In such a case, $x'(t)<0$ for all $t> 0$ by (6). Hence, there exists $\xi \ge \Omega _{2}$ so that $\lim _{t\longrightarrow +\infty } x(t)=\xi$. Moreover, we can take a sequence $t_{n}\longrightarrow +\infty$ so that $\lim _{n\longrightarrow +\infty } x'(t_{n})=0$. Evaluating (4) at $t_{n}$, we obtain that

$$\begin{aligned} \frac{x'(t_{n})}{d(t_{n})}=-x(t_{n})+\frac{\beta (t_{n})}{d(t_{n})} h(x(t_{n}-\tau ))\le -x(t_{n})+ \max \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} M. \end{aligned}$$

Making $n\longrightarrow +\infty$ and using that d(t) is T-periodic and positive, we conclude that

$$\begin{aligned} 0\le -\xi +\max \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} M. \end{aligned}$$

This implies that $\xi <\Omega _{2}$, a contradiction. $\square$

To guarantee the uniform boundedness away from zero for the positive solutions, we impose the following condition:

(P):

There are two constants $c>0$ and $\eta >1$ so that

$$\begin{aligned} \frac{\beta (t)}{d(t)} h(x)>\eta x \end{aligned}$$

for all $x\in (0,c)$ and $t\in [0,T]$.

We stress that if $h(0)>0$, then (P) automatically holds. On the other hand, if $h(x)=x q(x)$ with $q(x)>0$ for all $x\in (0,+\infty )$ and $\frac{\beta (t)}{d(t)}q(0)>1$ for all $t\in [0,T]$, then (P) is satisfied as well.

The next result shows that any constant $\Omega _{1}>0$ satisfying

$$\begin{aligned} \min \left\{ \frac{\beta (t)}{d(t)}h(x):x\in [c,\Omega _{2}], t\in [0,T]\right\} >\Omega _{1} \end{aligned}$$

(7)

with $\Omega _{2}$ and c the upper bound given in (5) and the constant in property (P), respectively, is an uniform lower bound for the positive solutions of Eq. (4).

Proposition 3.2

Assume (A) and (P). Then,

$$\begin{aligned} 0<\Omega _{1}\le \liminf _{t\longrightarrow +\infty } x(t) \end{aligned}$$

for any positive solution x(t) of (4).

Proof

We fix x(t) a positive solution of (4). We split the proof into two steps:

Step 1 $\liminf _{t\longrightarrow +\infty } x(t)>0$.

Assume, by contradiction, that $\liminf _{t\longrightarrow +\infty } x(t)=0$. In this case, we can take a sequence $\{s_{n}\}\longrightarrow +\infty$ with the following properties:

(S1):

$x'(s_{n})\le 0$ for all $n\in {\mathbb {N}}$.

(S2):

$x(s_{n})=\min \{x(t):t\in [0,s_{n}]\}$ for all $n\in {\mathbb {N}}$.

(S3):

$\lim _{n\rightarrow +\infty } x(s_{n})=0$.

The construction of this sequence is as follows: For $m=\min \{x(t):t\in [-\tau ,0]\}$, define

$$\begin{aligned} s_{n}=\min \left\{ t\in [0,+\infty ):x(t)=\frac{m}{2 n}\right\} \end{aligned}$$

for all $n\in {\mathbb {N}}$.

By (S1) and the expression of Eq. (4), we have that

$$\begin{aligned} d(s_{n})x(s_{n})\ge \beta (s_{n}) h(x(s_{n}-\tau )) \end{aligned}$$

for all $n\in {\mathbb {N}}$, or equivalently,

$$\begin{aligned} x(s_{n})\ge \frac{\beta (s_{n})}{d(s_{n})} h(x(s_{n}-\tau )) \end{aligned}$$

(8)

for all $n\in {\mathbb {N}}$.

If $x(s_{n}-\tau )\not \rightarrow 0$ as $n\rightarrow +\infty$, then there are $\xi _{1}>0$ and a subsequence $x(s_{\sigma (n)}-\tau )$ so that $x(s_{\sigma (n)}-\tau )\rightarrow \xi _{1}$ as $n\rightarrow +\infty$, (recall that x(t) is bounded). In light of (8), $x(s_{\sigma (n)})$ cannot tend to 0 as $n\rightarrow +\infty$. This is a contradiction with (S3). If $x(s_{n}-\tau )\rightarrow 0$ as $n\rightarrow +\infty$, then $x(s_{n}-\tau )\in (0,c)$ for n large enough where (0, c) is the interval given in (P). Now by (P), (S2) and (8), we obtain that

$$\begin{aligned} x(s_{n})\ge \eta x(s_{n}-\tau )\ge \eta x(s_{n}) \end{aligned}$$

with $\eta >1$. This contradiction completes the proof of the first step.

Step 2 $\liminf _{t\longrightarrow +\infty } x(t)>\Omega _{1}$.

By the previous step, $\liminf _{t\longrightarrow +\infty } x(t)=L>0$ for a suitable constant L. By Lemma 1.1, there is a sequence $\{s_{n}\}$ tending to $+\infty$ so that $x(s_{n})\longrightarrow L$ and $x'(s_{n})\longrightarrow 0$. By the expression of Eq. (4), we have that

$$\begin{aligned} \frac{x'(s_{n})}{d(s_{n})}=- x(s_{n})+\frac{\beta (s_{n})}{d(s_{n})} h(x(s_{n}-\tau )). \end{aligned}$$

(9)

It is not restrictive to assume that $x(s_{n}-\tau )\rightarrow {\widetilde{L}}$ with ${\widetilde{L}}\in [L,\Omega _{2}]$; $\frac{\beta (s_{n})}{d(s_{n})}\rightarrow \theta$ with $\theta \ge \min \{\frac{\beta (t)}{d(t)}:t\in [0,T]\}>0$. Making $n\longrightarrow +\infty$ in (9) and using that d(t) is strictly positive and T-periodic, we conclude that

$$\begin{aligned} 0=-L+\theta h({\widetilde{L}}) \end{aligned}$$

or equivalently,

$$\begin{aligned} L=\theta h({\widetilde{L}}). \end{aligned}$$

If ${\widetilde{L}}\in (0,c)$, we have that

$$\begin{aligned} L>\eta {\widetilde{L}} \end{aligned}$$

with $\eta >1$, (see condition (P)). This is a contradiction with $L\le {\widetilde{L}}$. Thus, ${\widetilde{L}}\in [c,\Omega _{2}]$. As a consequence of (7), we conclude that $L> \Omega _{1}$. $\square$

Next we recall a result on the existence of positive T-periodic solutions for Eq. (4).

Theorem 3.1

(Corollary 3.1 in Faria 2017) Assume conditions (A) and (P). Then, there exists a T-periodic solution $x_{*}(t)$ of (4) so that $x_{*}(t)>0$ for all $t>0$.

In Faria (2017), the author considered functions satisfying $h(0)=0$, $h'(0)=1$ and $\frac{\beta (t)}{d(t)}>1$ for all $t\in [0,T]$. However, Corollary 3.1 in Faria (2017) also holds under (A) and (P). Notice that in Theorem 3.1 in Faria (2017), she really used condition (P), [see second step (page 519 in Faria 2017) and lines above (3.8) in page 521 in Faria (2017)].

As a direct consequence of Propositions 3.1 and 3.2, the positive T-periodic solutions of (4) are bounded and bounded away from zero in an uniform manner. In the rest of this subsection, we take $\theta _{\min }>0$ and $\theta _{\max }>0$ so that

$$\begin{aligned} \theta _{\min }\le \min \{x_{*}(t):t\in [0,T]\}\le \max \{x_{*}(t):t\in [0,T]\} \le \theta _{\max } \end{aligned}$$

for any positive T-periodic solution $x_{*}(t)$ of (4). We also define

$$\begin{aligned} g(x)=H(\theta _{\min },x)=\frac{h(\theta _{\min }x)}{h(\theta _{\min })} \end{aligned}$$

and

$$\begin{aligned} f(x)=H(\theta _{\max },x)=\frac{h(\theta _{\max }x)}{h(\theta _{\max })}. \end{aligned}$$

(10)

Next, we introduce an extra condition regarding the function g:

(Q):

$g(x)>x$ for all $x\in (0,1)$ and $g(x)<x$ for all $x\in (1,+\infty )$.

As we will see, this last condition is satisfied in most classical models.

Fix $x_{*}(t)$ a positive T-solution of (4). The critical step in our arguments is to employ the change of variable $y(t)=\frac{x(t)}{x_{*}(t)}$. After some straightforward computations, we arrive at

$$\begin{aligned} y'(t)=\frac{\beta (t)}{x_{*}(t)}\Big ( h(x_{*}(t-\tau ) y(t-\tau ))-y(t) h(x_{*}(t-\tau ))\Big ). \end{aligned}$$

(11)

Our aim now is to prove that Eq. (11) admits an unique positive equilibrium.

Lemma 3.1

Assume conditions (A), (B), (C), (P) and (Q). Then, $y=1$ is the unique positive constant solution of (11).

Proof

Let $y=a>0$ be an equilibrium of (11). Then,

$$\begin{aligned} h(x_{*}(t-\tau ) a)-a h(x_{*}(t-\tau ))=0 \end{aligned}$$

for all $t\in {\mathbb {R}}$, or equivalently,

$$\begin{aligned} H(x_{*}(t-\tau ),a)=\frac{h(x_{*}(t-\tau ) a)}{h(x_{*}(t-\tau ))}=a \end{aligned}$$

for all $t>0$. By Lemma 2.1 with $\theta _{0}=\theta _{\min }$, we conclude that $a=1$. $\square$

Proposition 3.3

Assume conditions (A), (B), (C), (P) and (Q). Fix $x_{*}(t)>0$ a T-periodic solution of (4). Suppose that there exists a positive solution x(t) of (4) so that $x(t)-x_{*}(t)$ does not converge to 0 as $t\rightarrow +\infty$. Then, there are four positive constants L, S, ${\widetilde{L}}$ and ${\widetilde{S}}$ with the following properties:

(i):

$0<L<S$.

(ii):

${\widetilde{S}}<1<{\widetilde{L}}$.

(iii):

${\widetilde{S}},{\widetilde{L}}\in [L,S].$

(iv):

$f({\widetilde{L}})\le L$ and $f({\widetilde{S}})\ge S$ (the function given in (10)).

Proof

Define

$$\begin{aligned} y(t)=\frac{x(t)}{x_{*}(t)}. \end{aligned}$$

Since $x(t)-x_{*}(t)$ does not converge to 0 as $t\longrightarrow +\infty$, we deduce that y(t) does not converge to 1 as $t\longrightarrow +\infty$. Note that $x(t)-x_{*}(t)=x_{*}(t)(y(t)-1)$ and $x_{*}(t)$, x(t) are bounded and positive. On the other hand, as a direct consequence of Propositions 3.1 and 3.2, we have that y(t) is bounded and $\liminf _{t\longrightarrow +\infty } y(t)>0$. Hence, using that 1 is the unique positive equilibrium of (11) by Lemma 3.1 and y(t) does not converge to 1 as $t\rightarrow +\infty$, we conclude that

$$\begin{aligned} 0<\liminf _{t\longrightarrow +\infty } y(t)<\limsup _{t\longrightarrow +\infty } y(t)<+\infty . \end{aligned}$$

Set $L=\liminf _{t\longrightarrow +\infty } y(t)$ and $S=\limsup _{t\longrightarrow +\infty } y(t)$. By Lemma 1.1, we can take a sequence $\{t_{n}\}\longrightarrow +\infty$ satisfying:

• $\lim _{n\longrightarrow +\infty }y'(t_{n})=0$.

• $\lim _{n\longrightarrow +\infty } y(t_{n})=S$.

It is not restrictive to assume, after taking sub-sequences if necessary, that

$$\begin{aligned} \lim _{n\longrightarrow +\infty }x_{*}(t_{n}-\tau )= S_{1}\in [\theta _{\min },\theta _{\max }] \end{aligned}$$

and

$$\begin{aligned} \lim _{n\longrightarrow +\infty }y(t_{n}-\tau )= {\widetilde{S}}\in [L,S]. \end{aligned}$$

Now we evaluate Eq. (11) at $t_{n}$, that is,

$$\begin{aligned} y'(t_{n})=\frac{\beta (t_{n})}{x_{*}(t_{n})}\Big ( h(x_{*}(t_{n}-\tau ) y(t_{n}-\tau ))-y(t_{n}) h(x_{*}(t_{n}-\tau ))\Big ). \end{aligned}$$

Making $n\longrightarrow +\infty$ and using that

$$\begin{aligned} \nu _{1}\ge \frac{\beta (t_{n})}{x_{*}(t_{n})}\ge \nu _{2}>0 \end{aligned}$$

for all $n\in {\mathbb {N}}$ with $\nu _{1},\nu _{2}>0$ suitable constants, we obtain that

$$\begin{aligned} h({\widetilde{S}} S_{1})=S h(S_{1}) \end{aligned}$$

or equivalently

$$\begin{aligned} H(S_{1},{\widetilde{S}})=S. \end{aligned}$$

Arguing in an analogous manner with $0<L=\liminf _{t\longrightarrow +\infty } y(t)$, we can find two constants ${\widetilde{L}}\in [L,S]$ and $L_{1}\in [\theta _{\min },\theta _{\max }]$ so that

$$\begin{aligned} H(L_{1},{\widetilde{L}})=L. \end{aligned}$$

The constants L, S, ${\widetilde{L}}$ and ${\widetilde{S}}$ satisfy (i) and (iii).

Finally, we apply Lemma 2.2 with $\theta _{0}=\theta _{\min }$ and $\theta _{1}=\theta _{\max }$ to deduce (ii) and (iv). $\square$

Now we are ready to give the main delay independent criterion of global attraction for Eq. (4).

Theorem 3.2

Assume conditions (A), (B), (C), (P) and (Q). If 1 is a global attractor in $(0,+\infty )$ for the difference equations

$$\begin{aligned} x_{n+1}=f(x_{n}), \end{aligned}$$

then there exists a positive T-periodic solution $x_{*}(t)$ of (4) which is globally attracting, that is, for all x(t) positive solution of (4),

$$\begin{aligned} \lim _{t\longrightarrow +\infty }(x(t)-x_{*}(t))=0. \end{aligned}$$

Proof

By Theorem 3.1, we can take $x_{*}(t)$ a positive T-periodic solution of (4). Assume, by contradiction, that there exists a positive solution x(t) of (4) so that $x_{*}(t)-x(t)$ does not converge to 0 as $t\longrightarrow +\infty$. Then, by Proposition 3.3, there are four positive constants ${\widetilde{S}},{\widetilde{L}}, L$ and S with the following properties:

• $0<L<S$.

• ${\widetilde{S}},{\widetilde{L}}\in [L,S].$

• $f({\widetilde{L}})\le L$ and $f({\widetilde{S}})\ge S$.

Therefore, $[L,S]\subset f([L,S])$. The existence of this interval contradicts Proposition 2.1. $\square$

Let us refine Proposition 3.3 in order to obtain a delay-dependent criterion of global attraction. First, we fix a positive constant $\omega$ so that

$$\begin{aligned} \omega \ge \max \left\{ \frac{\beta (t)}{x_{*}(t)}:t\in [0,T]\right\} M \end{aligned}$$

(12)

with $x_{*}(t)$ the positive T-periodic solution of (4) fixed previously and M an upper bound of h (see (A)). Then, we define

$$\begin{aligned} {\widetilde{f}}(x)=e^{-\omega \tau }+ (1-e^{-\omega \tau }) f(x) \end{aligned}$$

where $\tau >0$ is the delay of Eq. (4) and f is given in (10).

Proposition 3.4

Assume (A), (B), (C), (P) and (Q). Fix $x_{*}(t)>0$ a T-periodic solution of (4). Suppose that there exists a positive solution x(t) of (4) so that $x(t)-x_{*}(t)$ does not converge to 0 as $t\longrightarrow +\infty$. Then, there are four positive constants L, S, $\rho _{1}$ and $\rho _{2}$ with the following properties:

(i):

$0<L<S$.

(ii):

$\rho _{1},\rho _{2}\in [L,S].$

(iii):

${\widetilde{f}}(\rho _{1})> S$ and ${\widetilde{f}}(\rho _{2})< L$.

Proof

Arguing in the same manner as in the proof of Proposition 3.3, we have that $y(t)=\frac{x(t)}{x_{*}(t)}$ does not converge to 1 as $t\rightarrow +\infty$. As mentioned there,

$$\begin{aligned} y'(t)=\frac{\beta (t)}{x_{*}(t)}(h(x_{*}(t-\tau ) y(t-\tau ))-y(t) h(x_{*}(t-\tau ))). \end{aligned}$$

(13)

Let

$$\begin{aligned} a(t)=\frac{\beta (t)}{x_{*}(t)}. \end{aligned}$$

With this notation, Eq. (13) now writes as:

$$\begin{aligned} y'(t)=a(t)h(x_{*}(t-\tau )y(t-\tau ))-a(t)h(x_{*}(t-\tau )) y(t). \end{aligned}$$

Using the variation of the constants formula, we know that

$$\begin{aligned}&y(t)=y(t-\tau ) e^{-\int _{t-\tau }^{t} a(s) h(x_{*}(s-\tau )){\mathrm{d}}s}\nonumber \\&+e^{-\int _{0}^{t} a(s) h(x_{*}(s-\tau )){\mathrm{d}}s}\int _{t-\tau }^{t} e^{\int _{0}^{s} a(r) h(x_{*}(r-\tau )){\mathrm{d}}r}a(s) h(x_{*}(s-\tau )y(s-\tau )){\mathrm{d}}s.\nonumber \\ \end{aligned}$$

(14)

On the other hand, since 1 is the unique equilibrium of (13), (see Lemma 3.1), we observe that

$$\begin{aligned} 0<L<S \end{aligned}$$

with $L=\liminf _{t\rightarrow +\infty } y(t)$ and $S=\limsup _{t\rightarrow +\infty } y(t)$. Again, as mentioned in the proof of Proposition 3.3, there exists a sequence $\{t_{n}\}\rightarrow +\infty$ satisfying the following conditions:

(C1):

$\lim _{n\rightarrow +\infty }x_{*}(t_{n}-\tau )=S_{1}\in [\theta _{\min },\theta _{\max }]$.

(C2):

$\lim _{n\rightarrow +\infty }y(t_{n}-\tau )={\widetilde{S}}\in [L,S]$ with ${\widetilde{S}}<1$.

(C3):

$\lim _{n\rightarrow +\infty }y(t_{n})=S$.

We evaluate Eq. (14) at $t_{n}$, that is,

$$\begin{aligned}&y(t_{n})=y(t_{n}-\tau )e^{-\int _{t_{n}-\tau }^{t_{n}}a(s)h(x_{*}(s-\tau )){\mathrm{d}}s}\\&+\,e^{-\int _{0}^{t_{n}}a(s)h(x_{*}(s-\tau )){\mathrm{d}}s}\int _{t_{n}-\tau }^{t_{n}}e^{\int _{0}^{t_{n}}a(r)h(x_{*}(r-\tau )){\mathrm{d}}r} a(s) h(x_{*}(s-\tau )y(s-\tau )){\mathrm{d}}s \end{aligned}$$

for all $n\in {\mathbb {N}}$. Dividing and multiplying by $h(x_{*}(s-\tau ))$ in the last integral term, we arrive at

$$\begin{aligned}&y(t_{n})=y(t_{n}-\tau )e^{-\int _{t_{n}-\tau }^{t_{n}}a(s)h(x_{*}(s-\tau )){\mathrm{d}}s} +\,e^{-\int _{0}^{t_{n}}a(s)h(x_{*}(s-\tau )){\mathrm{d}}s}\\&\quad \int _{t_{n}-\tau }^{t_{n}}e^{\int _{0}^{t_{n}}a(r)h(x_{*}(r-\tau )){\mathrm{d}}r} a(s)h(x_{*}(s-\tau )) \frac{h(x_{*}(s-\tau )y(s-\tau ))}{h(x_{*}(s-\tau ))}{\mathrm{d}}s \end{aligned}$$

for all $n\in {\mathbb {N}}$. Thus,

$$\begin{aligned}&y(t_{n})\le y(t_{n}-\tau )e^{-\int _{t_{n}-\tau }^{t_{n}}a(s)h(x_{*}(s-\tau )){\mathrm{d}}s}\\&\quad +e^{-\int _{0}^{t_{n}}a(s)h(x_{*}(s-\tau )){\mathrm{d}}s}\int _{t_{n}-\tau }^{t_{n}}\frac{{\mathrm{d}}}{{\mathrm{d}}s}\left( e^{\int _{0}^{t_{n}}a(r)h(x_{*}(r-\tau )){\mathrm{d}}r}\right) M_{n} {\mathrm{d}}s \end{aligned}$$

for all $n\in {\mathbb {N}}$ with

$$\begin{aligned} M_{n}=\max \left\{ \frac{h(x_{*}(s-\tau )y(s-\tau ))}{h(x_{*}(s-\tau ))}:s\in [t_{n}-\tau ,t_{n}]\right\} \end{aligned}$$

for all $n\in {\mathbb {N}}$. After simple computations, we obtain that

$$\begin{aligned} y(t_{n})\le y(t_{n}-\tau ) e^{-\int _{t_{n}-\tau }^{t_{n}}a(s)h(x_{*}(s-\tau )){\mathrm{d}}s}+\left( 1-e^{-\int _{t_{n}-\tau }^{t_{n}}a(s)h(x_{*}(s-\tau )){\mathrm{d}}s}\right) M_{n}.\nonumber \\ \end{aligned}$$

(15)

Let $\xi _{n}\in [t_{n}-\tau ,t_{n}]$ be a sequence of points so that

$$\begin{aligned} \frac{ h(x_{*}(\xi _{n}-\tau )y(\xi _{n}-\tau ))}{h(x_{*}(\xi _{n}-\tau ))}=M_{n} \end{aligned}$$

for all $n\in {\mathbb {N}}$. We can assume, after passing to sub-sequences if necessary, the following properties:

• $\lim _{n\rightarrow +\infty }x_{*}(\xi _{n}-\tau )=\widetilde{\theta _{1}}\in [\theta _{\min },\theta _{\max }]$.

• $\lim _{n\rightarrow +\infty }y(\xi _{n}-\tau )=\rho _{1}\in [L,S]$.

• $\lim _{n\rightarrow +\infty }\int _{t_{n}-\tau }^{t_{n}}a(s)h(x_{*}(s-\tau )){\mathrm{d}}s={\widetilde{\omega }}\in (0,+\infty )$.

Notice that the function $a(s)h(x_{*}(s-\tau ))$ is periodic, positive and continuous. It is worth noting that

$$\begin{aligned} {\widetilde{\omega }}\le \omega \tau , \end{aligned}$$

(16)

(see definition of $\omega$ in (12)). Making $n\longrightarrow +\infty$ in Eq. (15), we deduce that

$$\begin{aligned} S\le {\widetilde{S}} e^{-{\widetilde{\omega }}}+(1-e^{-{\widetilde{\omega }}}) \frac{ h(\widetilde{\theta _{1}}\rho _{1})}{h(\widetilde{\theta _{1}})}. \end{aligned}$$

(17)

Using that ${\widetilde{S}}<1<S$, we obtain that

$$\begin{aligned} H({\widetilde{\theta }}_{1},\rho _{1})= \frac{ h(\widetilde{\theta _{1}}\rho _{1})}{h(\widetilde{\theta _{1}})}>1. \end{aligned}$$

(18)

It is also clear that

$$\begin{aligned} S< H({\widetilde{\theta }}_{1},\rho _{1}). \end{aligned}$$

Since $\rho _{1}\in [L,S]$, we have that $\rho _{1}\le H({\widetilde{\theta }}_{1},\rho _{1}).$ By Lemma 2.1, we deduce that $\rho _{1}\le 1$. Obviously, $\rho _{1}\not =1$ by (18). Now, after a simple computation of $G'(x)$, $G(x)=e^{-x}+(1-e^{-x})H({\widetilde{\theta }}_{1},\rho _{1})$ is strictly increasing in $(0,+\infty )$ because $H({\widetilde{\theta }}_{1},\rho _{1})>1$. Hence, using (16), (17) and ${\widetilde{S}}<1$, we conclude that

$$\begin{aligned} S\le e^{-\omega \tau }+(1-e^{-\omega \tau })\frac{h({\widetilde{\theta }}_{1}\rho _{1})}{h({\widetilde{\theta }}_{1})}. \end{aligned}$$

(19)

On the other hand, by (B) together with ${\widetilde{\theta }}_{1}\in [\theta _{\min },\theta _{\max }]$ and $\rho _{1}<1$, we have that

$$\begin{aligned} H({\widetilde{\theta }}_{1},\rho _{1})=\frac{h({\widetilde{\theta }}_{1}\rho _{1})}{h({\widetilde{\theta }}_{1})}\le H(\theta _{\max },\rho _{1})= f (\rho _{1}). \end{aligned}$$

Inserting this inequality in (19), we arrive at

$$\begin{aligned} S\le e^{-\omega \tau }+(1-e^{-\omega \tau })f(\rho _{1}). \end{aligned}$$

Arguing in a similar manner with $\liminf _{t\longrightarrow +\infty } y(t)$, we can find $\rho _{2}>1$ with $\rho _{2}\in [L,S]$ so that

$$\begin{aligned} L\ge e^{-\omega \tau }+(1-e^{-\omega \tau })f(\rho _{2}). \end{aligned}$$

$\square$

Theorem 3.3

Assume conditions (A), (B), (C), (P) and (Q). If 1 is a global attractor in $(0,+\infty )$ for the difference equations

$$\begin{aligned} x_{n+1}={\widetilde{f}}(x_{n}), \end{aligned}$$

then there exists a positive T-periodic solution $x_{*}(t)$ of (4) which is globally attracting, that is, for all x(t) positive solution of (4),

$$\begin{aligned} \lim _{t\rightarrow +\infty }[x(t)-x_{*}(t)]=0. \end{aligned}$$

Proof

The proof of this result is exactly the same as that in Theorem 3.2 using Proposition 3.4 instead of Proposition 3.3. $\square$

3.2 Estimating Upper and Lower Bounds for the Positive T-Periodic Solutions of Eq. (4)

The main results of the previous subsection are expressed in terms of the global attraction of a suitable discrete equation. In turn, this equation depends on $\theta _{\max }$ and $\theta _{\min }$, upper and lower bounds (non-necessarily optimal) of the positive T-periodic solutions of (4). In this subsection, we provide an estimate of these bounds when h is strictly decreasing or of the form $h(x)=x q(x)$ with $q:[0,+\infty )\longrightarrow (0,+\infty )$ strictly decreasing. Recall that we always assume that h is of class ${\mathcal {C}}^1$. We focus on the second class of functions. The first class can be treated analogously and we omit the details.

We introduce some notation to simplify the statement of the results:

$$\begin{aligned}&\Delta _{1}=q^{-1}\left( \min \left\{ \frac{d(t)}{\beta (t)}:t\in [0,T]\right\} \right) , \\&\Delta _{2}=q^{-1}\left( \max \left\{ \frac{d(t)}{\beta (t)}:t\in [0,T]\right\} \right) , \\&{\widetilde{\Delta }}_{1}=\max \left\{ \frac{\beta (t)}{d(t)} x q(x):x\in [0,\Delta _{1}], t\in [0,T]\right\} \end{aligned}$$

and

$$\begin{aligned} {\widetilde{\Delta }}_{2}=\min \left\{ \frac{\beta (t)}{d(t)} x q(x):x\in [\Delta _{2},{\widetilde{\Delta }}_{1}], t\in [0,T]\right\} . \end{aligned}$$

Proposition 3.5

Assume (A) and (P). Moreover, suppose that $h(x)=x q(x)$ with $q:[0,+\infty )\longrightarrow (0,+\infty )$ strictly decreasing, $\lim _{x\longrightarrow +\infty }q(x)=0$ and $q(0)>\max \{\frac{d(t)}{\beta (t)}:t\in [0,T]\}$. Let $x_{*}(t)$ be a T-periodic solution of (4) with $x_{*}(t)>0$ for all $t\in [0,T]$.

(i):

If $\tau =k T$ with $k\in {\mathbb {N}}$, then $\Delta _{2}\le x_{*}(t)\le \Delta _{1}$ for all $t\in [0,T]$.

(ii):

If $\tau \not =k T$ with $k\in {\mathbb {N}}$, then ${\widetilde{\Delta }}_{2}\le x_{*}(t)\le {\widetilde{\Delta }}_{1}$ for all $t\in [0,T]$.

Proof

Take $t_{0}\in [0,T]$ so that $x_{*}'(t_{0})=0$ and

$$\begin{aligned} x_{*}(t_{0})=\max \{x_{*}(t):t\in [0,T]\}. \end{aligned}$$

By the expression of (4),

$$\begin{aligned} d(t_{0}) x_{*}(t_{0})=\beta (t_{0}) x_{*}(t_{0}-\tau ) q(x_{*}(t_{0}-\tau )). \end{aligned}$$

(20)

If $\tau =k T$ with $k\in {\mathbb {N}}$, then $x_{*}(t_{0})=x_{*}(t_{0}-\tau )$. Thus,

$$\begin{aligned} \frac{d(t_{0})}{\beta (t_{0})}=q(x_{*}(t_{0})) \end{aligned}$$

or equivalently,

$$\begin{aligned} x_{*}(t_{0})=q^{-1}\left( \frac{d(t_{0})}{\beta (t_{0})}\right) . \end{aligned}$$

Now it is clear that $x_{*}(t)\le \Delta _{1}$ for all $t\in [0,T]$ provided $\tau =k T$. In an analogous manner, we can prove that $\Delta _{2}\le x_{*}(t)$ for all $t\in [0,T]$. To prove (ii), we observe that by (20),

$$\begin{aligned} \frac{d(t_{0})}{\beta (t_{0})} x_{*}(t_{0})=x_{*}(t_{0}-\tau ) q(x_{*}(t_{0}-\tau )). \end{aligned}$$

Using that $x_{*}(t_{0}-\tau )\le x_{*}(t_{0})$, we conclude that

$$\begin{aligned} \frac{d(t_{0})}{\beta (t_{0})}\le q(x_{*}(t_{0}-\tau )). \end{aligned}$$

Hence,

$$\begin{aligned} x_{*}(t_{0}-\tau )\le \Delta _{1}. \end{aligned}$$

Using (20) and the previous inequality, it is clear that

$$\begin{aligned} x_{*}(t_{0})\le {\widetilde{\Delta }}_{1} \end{aligned}$$

for all $t\in [0,T].$ Arguing as above, we can deduce that

$$\begin{aligned} {\widetilde{\Delta }}_{2}\le x_{*}(t) \end{aligned}$$

for all $t\in [0,T]$. $\square$

Remark 3.1

By the previous proposition, we can take $\theta _{\max }=\Delta _{1}$, $\theta _{\min }=\Delta _{2}$ if $\tau =k T$ with $k\in {\mathbb {N}}$ and $\theta _{\max }={\widetilde{\Delta }}_{1}$, $\theta _{\min }={\widetilde{\Delta }}_{2}$ otherwise.

For the case $h:[0,+\infty )\longrightarrow (0,+\infty )$ strictly decreasing, we take $\varphi (x)=\frac{x}{h(x)}$. Notice that $\varphi$ is strictly increasing. Set

$$\begin{aligned}&\delta _{1}=\varphi ^{-1}\left( \max \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} \right) , \\&\delta _{2}=\varphi ^{-1}\left( \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} \right) , \\&{\widetilde{\delta }}_{1}=\max \left\{ \frac{\beta (t)}{d(t)} h(0): t\in [0,T]\right\} \end{aligned}$$

and

$$\begin{aligned} {\widetilde{\delta }}_{2}=\min \left\{ \frac{\beta (t)}{d(t)} h({\widetilde{\delta }}_{1}): t\in [0,T]\right\} . \end{aligned}$$

Proposition 3.6

Suppose (A). Moreover, assume that $h:[0,+\infty )\longrightarrow (0,+\infty )$ is strictly decreasing with $\lim _{x\longrightarrow +\infty }\varphi (x)>\max \{\frac{\beta (t)}{d(t)}:t\in [0,T]\}$. Let $x_{*}(t)$ be a T-periodic solution of (4) with $x_{*}(t)>0$ for all $t\in [0,T]$.

(i):

If $\tau =k T$ with $k\in {\mathbb {N}}$, then $\delta _{2}\le x_{*}(t)\le \delta _{1}$ for all $t\in [0,T]$.

(ii):

If $\tau \not =k T$ with $k\in {\mathbb {N}}$, then ${\widetilde{\delta }}_{2}\le x_{*}(t)\le {\widetilde{\delta }}_{1}$ for all $t\in [0,T]$.

Remark 3.2

As mentioned in Sect. 3.1, if $h:[0,+\infty )\longrightarrow [0,+\infty )$ satisfies that $h((0,+\infty ))\subset (0,+\infty )$ and $h(0)>0$, then (P) automatically holds.

3.3 Example: Nicholson’s Blowfly Equation with Periodic Coefficients

In this subsection, we apply the previous theoretical results to

$$\begin{aligned} x'(t)=-d(t) x(t)+\beta (t) x(t-\tau ) e^{-x(t-\tau )} \end{aligned}$$

(21)

where $d,\beta :[0,+\infty )\longrightarrow (0,+\infty )$ are continuous and T-periodic and $\tau >0$. We assume that

$$\begin{aligned} d(t)<\beta (t) \end{aligned}$$

(22)

for all $t\in [0,T]$. In this framework, it is straightforward to check conditions (A), (B), (C) and (P). Notice that $h(x)=x e^{-x}$ and

$$\begin{aligned} H(t,x)=\frac{h(tx)}{h(t)}=xe^{t(1-x)}. \end{aligned}$$

As a consequence of Theorem 3.1, Eq. (21) admits, at least, a T-periodic solution $x_{*}(t)$ with $x_{*}(t)>0$ for all $t\in [0,T]$. Moreover, the positive T-periodic solutions are uniformly bounded and bounded apart from zero by Propositions 3.1 and 3.2. Let $\theta _{\min }$ and $\theta _{\max }$ be positive lower and upper bounds for the positive T-periodic solutions of (21). Since $g(x)=x e^{\theta _{\min }(1-x)}$ and $f(x)=x e^{\theta _{\max }(1-x)}$, (Q) clearly holds. Given a positive constant $\omega$ with

$$\begin{aligned} \omega \ge \frac{\max \{\beta (t):t\in [0,T]\}}{\theta _{\min }} e^{-1}, \end{aligned}$$

(23)

$$\begin{aligned} {\widetilde{f}}(x)=e^{-\omega \tau }+(1-e^{-\omega \tau }) f(x) \end{aligned}$$

is an unimodal function with negative Schwarzian derivative. As a direct consequence of Proposition 2.2, 1 is a global attractor in $(0,+\infty )$ for the difference equation

$$\begin{aligned} x_{n+1}={\widetilde{f}}(x_{n}) \end{aligned}$$

(24)

if $|{\widetilde{f}}'(1)|\le 1$. This last condition is equivalent to

$$\begin{aligned} \theta _{\max }\le \frac{2-e^{-\omega \tau }}{1-e^{-\omega \tau }}. \end{aligned}$$

By this discussion and using Theorem 3.3 (see (23) for the definition of $\omega$) and Proposition 3.5, we have the following result:

Theorem 3.4

Assume conditions (22), $\tau =k T$ with $k\in {\mathbb {N}}$ and

$$\begin{aligned} -\ln \left( \min \left\{ \frac{d(t)}{\beta (t)}:t\in [0,T]\right\} \right) \le \frac{2-e^{-\omega k T}}{1-e^{-\omega k T}} \end{aligned}$$

with

$$\begin{aligned} \omega =\frac{\max \{\beta (t):t\in [0,T]\}}{-\ln (\max \{\frac{d(t)}{\beta (t)}:t\in [0,T]\})}e^{-1}. \end{aligned}$$

Then, there exists a T-periodic solution $x_{*}(t)$ of (21) with $x_{*}(t)>0$ for all $t\in [0,T]$ which is globally attracting, that is, for any positive solution x(t) of (21),

$$\begin{aligned} \lim _{t\longrightarrow +\infty }[x(t)-x_{*}(t)]=0. \end{aligned}$$

Notice that 1 is a global attractor in $(0,+\infty )$ for the difference Eq. (24) if $\theta _{\max }\le 2$. Using this fact, we can obtain the following delay independent criterion of global attraction.

Corollary 3.1

Assume conditions (22), $\tau =k T$ with $k\in {\mathbb {N}}$ and

$$\begin{aligned} \max \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} \le e^2. \end{aligned}$$

Then, there exists a T-periodic solution $x_{*}(t)$ of (21) with $x_{*}(t)>0$ for all $t\in [0,T]$ which is globally attracting, that is, for any positive solution x(t) of (21),

$$\begin{aligned} \lim _{t\longrightarrow +\infty }[x(t)-x_{*}(t)]=0. \end{aligned}$$

To assess the potential of our approach, we recall that the best delay independent conditions for global attractivity of the positive equilibrium in the autonomous Nicholson’s blowfly equation

$$\begin{aligned} x'(t)=-d x(t)+\beta x(t-\tau ) e^{-x(t-\tau )} \end{aligned}$$

are

$$\begin{aligned} 1<\frac{\beta }{d}\le e^{2}. \end{aligned}$$

Informally speaking, Theorem 3.4 can be viewed as the extension of the results developed in Gyori and Trofimchuk (1999) for (21). To the best of our knowledge, there are no results in the literature regarding delay-dependent criteria of global attraction that cover the best delay independent conditions, see the different comparisons in Faria (2017).

Next we derive criteria of global attraction when the delay is not a multiple of T.

Theorem 3.5

Assume conditions (22) and

$$\begin{aligned} \max \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} e^{-1}\le \frac{2-e^{-\omega \tau }}{1-e^{-\omega \tau }} \end{aligned}$$

with

$$\begin{aligned} \omega =\frac{\max \{\beta (t):t\in [0,T]\}\max \{\frac{d(t)}{\beta (t)}:t\in [0,T]\}}{(-\ln (\max \{\frac{d(t)}{\beta (t)}:t\in [0,T]\}))}e^{\max \{\frac{\beta (t)}{d(t)}:t\in [0,T]\} e^{-1}} e^{-1}. \end{aligned}$$

Then, there exists a T-periodic solution $x_{*}(t)$ of (21) with $x_{*}(t)>0$ for all $t\in [0,T]$ which is globally attracting, that is, for any positive solution x(t) of (21),

$$\begin{aligned} \lim _{t\longrightarrow +\infty }[x(t)-x_{*}(t)]=0. \end{aligned}$$

Proof

Observe that the constants of Proposition 3.5(ii) satisfy

$$\begin{aligned}&\Delta _{1}=\ln \left( \max \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} \right) \\&\Delta _{2}=\ln \left( \min \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} \right) \\&\widetilde{\Delta _{1}}\le \max \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} e^{-1} \\&\widetilde{\Delta _{2}}\ge \min \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} \left( -\ln \left( \max \left\{ \frac{d(t)}{\beta (t)}:t\in [0,T]\right\} \right) \right) e^{-\max \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} e^{-1}}. \end{aligned}$$

$\square$

As above, we can obtain the following delay independent criterion of global attraction.

Corollary 3.2

Assume condition (22) and

$$\begin{aligned} \max \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} \le 2e. \end{aligned}$$

Then, there exists a T-periodic solution $x_{*}(t)$ of (21) with $x_{*}(t)>0$ for all $t\in [0,T]$ which is globally attracting, that is, for any positive solution x(t) of (21),

$$\begin{aligned} \lim _{t\longrightarrow +\infty }[x(t)-x_{*}(t)]=0. \end{aligned}$$

3.4 Nicholson’s Blowfly Equation with Periodic Coefficients and a Positive Constant Solution

In the previous subsections, we always stress that the positive T-periodic solution of (4) can be in fact a constant function. This happens when the equation is autonomous, or more generally, when $\beta (t)=r d(t)$ for some positive constant r. In this subsection, we show that Theorem 3.4 can be strengthened for this particular case because we can work with better estimates of the upper and lower bounds of the positive T-periodic solutions. Generally speaking, better (a-priori) bounds of the positive T-periodic solutions lead to sharper results.

Consider

$$\begin{aligned} x'(t)=-d(t)x(t)+ r d(t) x(t-\tau )e^{-x(t-\tau )} \end{aligned}$$

(25)

where $d:[0,+\infty )\rightarrow (0,+\infty )$ is continuous and T-periodic, $r>1$ and $\tau =k T$ with $k\in {\mathbb {N}}$. We first observe that $x_{*}(t)=\ln r$ is the unique positive T-periodic solution of (25). Indeed, fix $x_{*}(t)$ a T-periodic solution of (25) and take $t_{0},t_{1}\in [0,T]$ so that

$$\begin{aligned} x_{*}(t_{0})=\max \{x_{*}(t):t\in [0,T]\} \end{aligned}$$

and

$$\begin{aligned} x_{*}(t_{1})=\min \{x_{*}(t):t\in [0,T]\}. \end{aligned}$$

By Eq. (25) and using that $x_{*}(t-\tau )=x_{*}(t)$ for all t, we conclude that

$$\begin{aligned} x_{*}(t_{0})=x_{*}(t_{1})=\ln (r). \end{aligned}$$

After this remark, we can take $\theta _{\max }=\theta _{\min }=\ln r$ and

$$\begin{aligned} \omega =\max \{d(t):t\in [0,T]\}\frac{r e^{-1}}{\ln r}. \end{aligned}$$

Repeating the argument made in Theorem 3.4, we obtain the following result:

Theorem 3.6

Assume $r>1$, $\tau =k T$ with $k\in {\mathbb {N}}$ and

$$\begin{aligned} \ln r\le \frac{2-e^{-\omega k T}}{1-e^{-\omega k T}} \end{aligned}$$

with

$$\begin{aligned} \omega =\max \{d(t):t\in [0,T]\}\frac{r e^{-1}}{\ln r}. \end{aligned}$$

Then, for any positive solution x(t) of (25),

$$\begin{aligned} \lim _{t\longrightarrow +\infty }x(t)=\ln r. \end{aligned}$$

4 Systems of Delay Differential Equations with Periodic Coefficients

Many ideas developed in the previous section also work in systems of delay differential equations. We illustrate this fact with two classical examples: Goodwin’s model oscillator (Ruoff and Rensing 1996) and systems with patch structure (El-Morshedy and Ruiz-Herrera 2017; Faria 2017). We analyze models with nonlinearities different from $h(x)=x e^{-x}$ to show the versatility of our results. Throughout this section, we say that a vector $v=(v_{1},\ldots ,v_{N})$ is positive is $v_{i}>0$ for all $i=1,\ldots ,N$. As mentioned above, the constant functions are trivially T-periodic.

4.1 Goodwin’s Model Oscillator

Consider

$$\begin{aligned} \left\{ \begin{array}{lll}x'(t)= a(t) y(t-\sigma _{1})-b(t) x(t)\\ y'(t)=\beta (t) h(x(t-\sigma _{2})) -d(t) y(t) \end{array}\right. \end{aligned}$$

(26)

where $\sigma _{1},\sigma _{2}> 0$ and $a,b,\beta ,d:{\mathbb {R}}\longrightarrow (0,+\infty )$ are continuous and T-periodic. The function $h:[0,+\infty )\longrightarrow [0,+\infty )$ is of class ${\mathcal {C}}^{1}$ with $h((0,+\infty ))\subset (0,+\infty )$ and satisfies (A), (B), (C). We additionally assume the following conditions:

(G1):

$\frac{a(t)}{b(t)}\ge 1$ for all $t\in [0,T].$

(G2):

There are $c>0$ and $\eta >1$ so that

$$\begin{aligned} \frac{\beta (t)}{d(t)}h(x)>\eta x \end{aligned}$$

for all $t\in [0,T]$ and $x\in (0,c)$.

For any initial function $(\phi _{1},\phi _{2})\in {\mathcal {C}}([-\sigma ,0], [0,+\infty )^2)$ with $\sigma =\max \{\sigma _{1},\sigma _{2}\}$, there is a unique (local) solution $(x(t,(\phi _{1},\phi _{2}),y(t,(\phi _{1},\phi _{2}))$ of (26) with $x(t,(\phi _{1},\phi _{2}))=\phi _{1}(t)$ and $y(t,(\phi _{1},\phi _{2}))=\phi _{2}(t)$ for all $t\in [-\sigma ,0]$. The variation of the constant formula allows us to write system (26) as:

$$\begin{aligned} x(t)= & {} x(0)e^{-\int _{0}^{t}b(s){\mathrm{d}}s}+e^{-\int _{0}^{t}b(s){\mathrm{d}}s}\int _{0}^{t}e^{\int _{0}^{s}b(r){\mathrm{d}}r}a(s)y(s-\sigma _{1}){\mathrm{d}}s \\ y(t)= & {} y(0)e^{-\int _{0}^{t}d(s){\mathrm{d}}s}+e^{-\int _{0}^{t}d(s){\mathrm{d}}s}\int _{0}^{t}e^{\int _{0}^{s}d(r){\mathrm{d}}r}\beta (s)h(x(s-\sigma _{2})){\mathrm{d}}s. \end{aligned}$$

This expression implies that $x(t,(\phi _{1},\phi _{2}))\ge 0$ and $y(t,(\phi _{1},\phi _{2}))\ge 0$ for all $t\ge 0$ on its interval of definition. In fact, if $(\phi _{1},\phi _{2})\in {\mathcal {C}}([-\sigma ,0], (0,+\infty )^2)$, we can guarantee that $x(t,(\phi _{1},\phi _{2}))> 0$ and $y(t,(\phi _{1},\phi _{2}))> 0$ because $h((0,+\infty ))\subset (0,+\infty )$. Next, we prove that the solutions of (26) cannot blow up. Take ${\widetilde{\Upsilon }}_{2}$ a constant so that

$$\begin{aligned} {\widetilde{\Upsilon }}_{2}>\max \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} M \end{aligned}$$

(27)

with M an upper bound of h, (see (A)). If (x(t), y(t)) is a solution of (26) with initial function in ${\mathcal {C}}([-\sigma ,0], [0,+\infty )^2)$, then $y'(t)<0$ provided that $y(t)\ge {\widetilde{\Upsilon }}_{2}$ and $t>0$. Notice that, by the second equation of (26), we have that

$$\begin{aligned} \frac{y'(t)}{d(t)}=-y(t)+\frac{\beta (t)}{d(t)} h(x(t-\sigma _{2}))< -y(t)+{\widetilde{\Upsilon }}_{2}. \end{aligned}$$

Thus, y(t) cannot blow up. It is clear that x(t) cannot blow up either because we can see the first equation of (26) as an ordinary linear differential equation with bounded coefficients. Collecting the above information, we conclude that the solutions of (26) with initial function in ${\mathcal {C}}([-\sigma ,0], [0,+\infty )^2)$ are defined for all $t\ge 0$.

In the rest of the subsection, we always work with solutions with initial function in ${\mathcal {C}}([-\sigma ,0], (0,+\infty )^2)$. We refer to them as positive solutions.

Our next goal is to prove that the positive solutions of (26) are uniformly bounded.

Proposition 4.1

Assume (A) and (G1). Take a constant $\Upsilon _{2}$ so that

$$\begin{aligned} \Upsilon _{2}>\max \left\{ \frac{a(t)}{b(t)}:t\in [0,T]\right\} {\widetilde{\Upsilon }}_{2} \end{aligned}$$

(28)

with ${\widetilde{\Upsilon }}_{2}$ defined in (27). Then,

$$\begin{aligned} \max \left\{ \limsup _{t\longrightarrow +\infty } x(t),\limsup _{t\longrightarrow +\infty } y(t)\right\} < \Upsilon _{2} \end{aligned}$$

for any positive solution (x(t), y(t)) of (26).

Proof

Take (x(t), y(t)) a positive solution of (26). As mentioned above, if $y(t_{0})>{\widetilde{\Upsilon }}_{2}$ for some $t_{0}>0$, then y(t) is strictly decreasing in a neighborhood of $t_{0}$. This implies that if $y(t_{1})\le {\widetilde{\Upsilon }}_{2}$, then $y(t)\le {\widetilde{\Upsilon }}_{2}$ for all $t\ge t_{1}$. Arguing as in the proof of Proposition 3.1, we deduce that there is ${\widetilde{t}}>0$ so that $y(t)<{\widetilde{\Upsilon }}_{2}$ for all $t\ge {\widetilde{t}}$. Now, by the first equation of (26), we have that

$$\begin{aligned} x'(t)< a(t){\widetilde{\Upsilon }}_{2}-b(t)x(t) \end{aligned}$$

for all $t\ge {\widetilde{t}}+\sigma _{1}$. Repeating the argument of the proof of Proposition 3.1, we can find $t_{*}>{\widetilde{t}}$ so that

$$\begin{aligned} x(t)\le \max \left\{ \frac{a(t)}{b(t)}:t\in [0,T]\right\} {\widetilde{\Upsilon }}_{2} \end{aligned}$$

for all $t>t_{*}$. By (G1), ${\widetilde{\Upsilon }}_{2}\le \Upsilon _{2}$. $\square$

Next we prove that these solutions are bounded away from 0 in an uniform manner.

Proposition 4.2

Assume (A), (G1) and (G2). Take a positive constant $\Upsilon _{1}$ so that

$$\begin{aligned} \min \left\{ \frac{\beta (t)}{d(t)} h(x):t\in [0,T], x\in [c,\Upsilon _{2}] \right\} >\Upsilon _{1} \end{aligned}$$

(29)

with $\Upsilon _{2}$ and c the constants given in (28) and (G2), respectively. Then,

$$\begin{aligned} \min \left\{ \liminf _{t\longrightarrow +\infty } x(t),\liminf _{t\longrightarrow +\infty } y(t)\right\} \ge \Upsilon _{1} \end{aligned}$$

for any positive solution (x(t), y(t)) of (26).

Proof

We divide the proof into two steps.

Step 1 $\min \{\liminf _{t\longrightarrow +\infty } x(t),\liminf _{t\longrightarrow +\infty } y(t)\}> 0$ for all (x(t), y(t)) positive solution of (26).

Assume, by contradiction, that there exists a positive solution (x(t), y(t)) so that

$$\begin{aligned} \min \left\{ \liminf _{t\longrightarrow +\infty } x(t),\liminf _{t\longrightarrow +\infty } y(t)\right\} = 0. \end{aligned}$$

Then, we can take $\{t_{n}\}\longrightarrow +\infty$ so that one of the following sets of conditions is satisfied:

(X1):

$x'(t_{n})\le 0$ for all $n\in {\mathbb {N}}$,

(X2):

$x(t_{n})=\min \{x(t),y(t):t\in [0,t_{n}]\}$ for all $n\in {\mathbb {N}}$,

(X3):

$\lim _{n\longrightarrow +\infty } x(t_{n})=0$,

or

(Y1):

$y'(t_{n})\le 0$ for all $n\in {\mathbb {N}}$,

(Y2):

$y(t_{n})=\min \{x(t),y(t):t\in [0,t_{n}]\}$ for all $n\in {\mathbb {N}}$,

(Y3):

$\lim _{n\longrightarrow +\infty } y(t_{n})=0$.

We refer to the proof of Proposition 3.1 for the construction of the previous sequence $\{t_{n}\}$.

Assume that the first block of conditions (i.e., (X1)–(X3)) holds. By the first equation of (26) and (G1), we deduce that

$$\begin{aligned} x(t_{n})\ge \frac{a(t_{n})}{b(t_{n})} y(t_{n}-\sigma _{1})\ge y(t_{n}-\sigma _{1}) \end{aligned}$$

for all $n\in {\mathbb {N}}$. Thus, it is not restrictive to assume that the second block (i.e., (Y1)–(Y3)) holds. Notice that by Proposition 4.1, we can take $t_{0}>0$ large enough so that

$$\begin{aligned} \max \{x(t),y(t)\}\le \Upsilon _{2} \end{aligned}$$

for all $t\ge t_{0}$. This implies that there exists $n_{0}\in {\mathbb {N}}$ so that $x(t_{n}-\sigma _{2})\le \Upsilon _{2}$ and $y(t_{n})\le \Upsilon _{2}$ for all $n\ge n_{0}$. By the second equation of (26) and (Y1), we have that

$$\begin{aligned} y(t_{n})\ge \frac{\beta (t_{n})}{d(t_{n})} h(x(t_{n}-\sigma _{2})) \end{aligned}$$

(30)

for all $n\in {\mathbb {N}}$. If $x(t_{n}-\sigma _{2})\ge c$ for all $n\ge n_{0}$, we deduce by (30) that

$$\begin{aligned} y(t_{n})\ge \Upsilon _{1} \end{aligned}$$

for all $n\ge n_{0}$. This is a contradiction with (Y3). If there exists n with $n\ge n_{0}$ so that $x(t_{n}-\sigma _{2})<c$, we also have a contradiction. Indeed, notice that using (G2) in (30), we have that

$$\begin{aligned} y(t_{n})\ge \eta x(t_{n}-\sigma _{2}) \end{aligned}$$

with $\eta >1$. Thus, $y(t_{n})> x(t_{n}-\sigma _{2})$. On the other hand, we know by (Y2) that $x(t_{n}-\sigma _{2})\ge y(t_{n})$.

Step 2: Conclusion.

Take (x(t), y(t)) a positive solution of (26). Let

$$\begin{aligned} 0<L=\min \left\{ \liminf _{t\rightarrow +\infty } x(t),\liminf _{t\longrightarrow +\infty } y(t)\right\} . \end{aligned}$$

Assume that $L=\liminf _{t\rightarrow +\infty } y(t)$. By the fluctuation lemma (see Lemma 1.1), we can take a sequence $\{t_{n}\}\rightarrow +\infty$ so that

$$\begin{aligned} \lim _{n\rightarrow +\infty }y'(t_{n})=0 \end{aligned}$$

and $\lim _{n\rightarrow +\infty } y(t_{n})=\liminf _{t\rightarrow +\infty } y(t).$ Evaluating the second equation of (26) at $t_{n}$, we obtain that

$$\begin{aligned} \frac{y'(t_{n})}{d(t_{n})}=-y(t_{n})+\frac{\beta (t_{n})}{d(t_{n})} h(x(t_{n}-\sigma _{2})). \end{aligned}$$

It is not restrictive, after passing to subsequences if necessary, to assume that

$$\begin{aligned} \lim _{n\longrightarrow +\infty } \frac{\beta (t_{n})}{d(t_{n})}=\theta \end{aligned}$$

with $\theta \ge \min \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\}$ and

$$\begin{aligned} \lim _{n\longrightarrow +\infty } x(t_{n}-\sigma _{2})= {\widetilde{L}}\in [L,\Upsilon _{2}], \end{aligned}$$

with $\Upsilon _{2}$ the constant given in (28). Making $n\longrightarrow +\infty$ and using that d(t) is positive and T-periodic, we conclude that

$$\begin{aligned} L=\theta h({\widetilde{L}}). \end{aligned}$$

(31)

If ${\widetilde{L}}\in (0,c)$, we deduce by (G2) that

$$\begin{aligned} L\ge \eta {\widetilde{L}} \end{aligned}$$

with $\eta >1$, a contradiction with the fact ${\widetilde{L}}\in [L,\Upsilon _{2}]$. Therefore, ${\widetilde{L}}\in [c, \Upsilon _{2}]$. In this case, $L\ge \Upsilon _{1}$ as a direct consequence of (31) and (29). If $L=\liminf _{t\rightarrow +\infty } x(t)$, then, by the fluctuation lemma (see Lemma 1.1), we can take a sequence $\{t_{n}\}\rightarrow +\infty$ so that

$$\begin{aligned} \lim _{n\rightarrow +\infty }x'(t_{n})= 0 \end{aligned}$$

and $\lim _{n\rightarrow +\infty } x(t_{n})=\liminf _{t\rightarrow +\infty } x(t).$ Then, evaluating the first equation of (26) at $t_{n}$, we obtain that

$$\begin{aligned} \frac{x'(t_{n})}{b(t_{n})}=\frac{a(t_{n})}{b(t_{n})} y(t_{n}-\sigma _{1})-x(t_{n}). \end{aligned}$$

Using (G1), we have that

$$\begin{aligned} \frac{a(t_{n})}{b(t_{n})} y(t_{n}-\sigma _{1})-x(t_{n})\ge y(t_{n}-\sigma _{1})-x(t_{n}). \end{aligned}$$

In this case, the limit of a subsequence of $y(t_{n}-\sigma _{1})$ is less or equal than L. Thus, it is not restrictive to assume that $L=\liminf _{t\rightarrow +\infty } y(t)$. $\square$

The next result guarantees the existence of a positive T-periodic solution for (26). The method of proof is basically the adaptation of the ideas developed in Theorem 3.1 in Faria (2017).

Theorem 4.1

Assume (A), (G1) and (G2). Then, system (26) admits a T-periodic solution $(x_{*}(t),y_{*}(t))$ with $x_{*}(t)>0$ and $y_{*}(t)>0$ for all $t\in [0,T].$

Proof

It is not restrictive to assume that $\sigma =\max \{\sigma _{1},\sigma _{2}\}\ge T$ (otherwise we choose some ${\bar{\sigma }}>\sigma$ and insert ${\mathcal {C}}^{+}:={\mathcal {C}}([-\sigma ,0],(0,+\infty )^2)$ into ${\mathcal {C}}([-{\bar{\sigma }},0],(0,+\infty )^2)$). By the variation of the constant formula, we have that the solutions of (26) with initial condition $(x(t),y(t))\in {\mathcal {C}}^{+}$ are given by

$$\begin{aligned} \left\{ \begin{array}{lll} x(t)=x(t_{0})e^{-\int _{t_{0}}^{t}b(s){\mathrm{d}}s}+e^{-\int _{0}^{t}b(s){\mathrm{d}}s}\int _{t_{0}}^{t}e^{\int _{0}^{s}b(r){\mathrm{d}}r}a(s)y(s-\sigma _{1}){\mathrm{d}}s\\ y(t)=y(t_{0})e^{-\int _{t_{0}}^{t}d(s){\mathrm{d}}s}+e^{-\int _{0}^{t}d(s){\mathrm{d}}s}\int _{t_{0}}^{t}e^{\int _{0}^{s}d(r){\mathrm{d}}r}\beta (s)h(x(s-\sigma _{2})){\mathrm{d}}s \end{array}\right. \end{aligned}$$

(32)

with $t_{0}\in [0,+\infty )$ and $t\ge 0$. It is clear that we have a T-periodic solution of system (26) if $x(t+T)=x(t)$ and $y(t+T)=y(t)$ for all $t\in [-\sigma , 0].$ We deduce by (32) that if

$$\begin{aligned} \left\{ \begin{array}{lll} x(t)=x(t)e^{-\int _{t}^{t+T}b(s){\mathrm{d}}s}+e^{-\int _{0}^{t+T}b(s){\mathrm{d}}s}\int _{t}^{t+T}e^{\int _{0}^{s}b(r){\mathrm{d}}r}a(s)y(s-\sigma _{1}){\mathrm{d}}s\\ y(t)=y(t)e^{-\int _{t}^{t+T}d(s){\mathrm{d}}s}+e^{-\int _{0}^{t+T}d(s){\mathrm{d}}s}\int _{t}^{t+T}e^{\int _{0}^{s}d(r){\mathrm{d}}r}\beta (s)h(x(s-\sigma _{2})){\mathrm{d}}s \end{array}\right. \nonumber \\ \end{aligned}$$

(33)

for all $t\in [-\sigma ,0]$, (recall that $\sigma \ge T$), then (x(t), y(t)) is a T-periodic solution. Let

$$\begin{aligned} \zeta _{1}=(1-e^{-\int _{t}^{t+T}b(s){\mathrm{d}}s})^{-1}\;\;\;\mathrm{and}\;\;\;\zeta _{2}=(1-e^{-\int _{t}^{t+T}d(s){\mathrm{d}}s})^{-1}. \end{aligned}$$

In light of (33), the fixed points of the operator

$$\begin{aligned} P:{\mathcal {C}}_{T}((0,+\infty )^2)\longrightarrow {\mathcal {C}}^{+} \end{aligned}$$

given by

$$\begin{aligned}&P(x,y)(t)=(P_{1}(x,y)(t),P_{2}(x,y)(t)) \\&P_{1}(x,y)(t)=\zeta _{1}e^{-\int _{0}^{t+T}b(s){\mathrm{d}}s}\int _{t}^{t+T}e^{\int _{0}^{s}b(r){\mathrm{d}}r}a(s)y(s-\sigma _{1}){\mathrm{d}}s \\&P_{2}(x,y)(t)=\zeta _{2}e^{-\int _{0}^{t+T}d(s){\mathrm{d}}s}\int _{t}^{t+T}e^{\int _{0}^{s}d(r){\mathrm{d}}r}\beta (s)h(x(s-\sigma _{2})){\mathrm{d}}s \end{aligned}$$

are T-periodic solutions of (26). After several steps, we will prove that the operator P satisfies the assumptions of the classical Schauder’s theorem.

Step 1 P(x, y)(t) is a T-periodic function provided (x(t), y(t)) is a T-periodic function.

Notice that

$$\begin{aligned} P_{1}(x,y)(t+T)&=\zeta _{1}e^{-\int _{0}^{t+2T}b(s){\mathrm{d}}s}\int _{t+T}^{t+2T}e^{\int _{0}^{s}b(r){\mathrm{d}}r}a(s)y(s-\sigma _{1}){\mathrm{d}}s \\&=\zeta _{1}\int _{t+T}^{t+2T}e^{\int _{t+2T}^{s}b(r){\mathrm{d}}r}a(s)y(s-\sigma _{1}){\mathrm{d}}s\\&=\zeta _{1}\int _{t}^{t+T}e^{\int _{t+2T}^{{\widetilde{s}}+T}b(r){\mathrm{d}}r}a({\widetilde{s}}+T)y({\widetilde{s}}+T-\sigma _{1}){\mathrm{d}}{\widetilde{s}}. \end{aligned}$$

In the last equality, we have employed the change of variable $s={\widetilde{s}}+T$. Using that a, y, and b are T-periodic, we conclude that

$$\begin{aligned} \zeta _{1}\int _{t}^{t+T}e^{\int _{t+2T}^{s+T}b(r){\mathrm{d}}r}a(s+T)y(s+T-\sigma _{1}){\mathrm{d}}s&=\zeta _{1}\int _{t}^{t+T}e^{\int _{t+T}^{s}b(r){\mathrm{d}}r}a(s)y(s-\sigma _{1}){\mathrm{d}}s \\&=P_{1}(x,y)(t). \end{aligned}$$

We can reason in an analogous manner with $P_{2}(x,y)(t)$. Thus,

$$\begin{aligned} P:{\mathcal {C}}_{T}((0,+\infty )^2)\longrightarrow {\mathcal {C}}_{T}((0,+\infty )^2). \end{aligned}$$

Step 2 Define

$$\begin{aligned} {\mathcal {B}}=\{(x,y)\in {\mathcal {C}}_{T}((0,+\infty )^2): x(t)\le Q_{1}, y(t)\le Q_{2}\} \end{aligned}$$

where

$$\begin{aligned} Q_{1}= & {} \max \left\{ \frac{a(t)}{b(t)}:t\in [0,T]\right\} \max \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} \cdot M \\ Q_{2}= & {} \max \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} \cdot M \end{aligned}$$

with M an upper bound of h, (see (A)). Note that by (G1), $Q_{1}\ge Q_{2}$. We prove that $P({\mathcal {B}})\subset {\mathcal {B}}$.

If $(x(t),y(t))\in {\mathcal {B}}$,

$$\begin{aligned} P_{1}(x,y)(t)&=\zeta _{1}e^{-\int _{0}^{t+T}b(s){\mathrm{d}}s}\int _{t}^{t+T}e^{\int _{0}^{s}b(r){\mathrm{d}}r}a(s)y(s-\sigma _{1}){\mathrm{d}}s \\&=\zeta _{1}e^{-\int _{0}^{t+T}b(s){\mathrm{d}}s}\int _{t}^{t+T}e^{\int _{0}^{s}b(r){\mathrm{d}}r} b(s)\frac{a(s)}{b(s)}y(s-\sigma _{1}){\mathrm{d}}s \\&\le \zeta _{1}e^{-\int _{0}^{t+T}b(s){\mathrm{d}}s}\int _{t}^{t+T}\frac{{\mathrm{d}}}{{\mathrm{d}}s}e^{\int _{0}^{s}b(r){\mathrm{d}}r} \max \left\{ \frac{a(t)}{b(t)}:t\in [0,T]\right\} Q_{2}{\mathrm{d}}s \\&=\zeta _{1}e^{-\int _{0}^{t+T}b(s){\mathrm{d}}s}\int _{t}^{t+T}\frac{{\mathrm{d}}}{{\mathrm{d}}s}e^{\int _{0}^{s}b(r){\mathrm{d}}r} Q_{1} {\mathrm{d}}s. \end{aligned}$$

Observe that

$$\begin{aligned} \zeta _{1}e^{-\int _{0}^{t+T}b(s){\mathrm{d}}s}\int _{t}^{t+T}\frac{{\mathrm{d}}}{{\mathrm{d}}s}e^{\int _{0}^{s}b(r){\mathrm{d}}r}{\mathrm{d}}s=1. \end{aligned}$$

Analogously we can prove that $P_{2}(x,y)(t)\le Q_{2}$. The proof of this step is completed.

Using (G2), we can take $\gamma >0$ so that

$$\begin{aligned} \min \left\{ \frac{\beta (t)}{d(t)} h(x):t\in [0,T], x\in [\gamma ,Q_{1}]\right\} >\gamma . \end{aligned}$$

We define

$$\begin{aligned} {\mathcal {B}}_{\gamma }=\{(x,y)\in {\mathcal {C}}_{T}((0,+\infty )^2):\gamma \le x(t)\le Q_{1}, \gamma \le y(t)\le Q_{2}\}. \end{aligned}$$

Step 3 $P({\mathcal {B}}_{\gamma })\subset {\mathcal {B}}_{\gamma }$.

Take $(x(t),y(t))\in {\mathcal {B}}_{\gamma }$. Then,

$$\begin{aligned} P_{1}(x,y)(t)&=\zeta _{1}e^{-\int _{0}^{t+T}b(s){\mathrm{d}}s}\int _{t}^{t+T}e^{\int _{0}^{s}b(r){\mathrm{d}}r}a(s) y(s-\sigma _{1}){\mathrm{d}}s \\&=\zeta _{1}e^{-\int _{0}^{t+T}b(s){\mathrm{d}}s}\int _{t}^{t+T}e^{\int _{0}^{s}b(r){\mathrm{d}}r}b(s)\frac{a(s)}{b(s)} y(s-\sigma _{1}){\mathrm{d}}s \\&\ge \zeta _{1}e^{-\int _{0}^{t+T}b(s){\mathrm{d}}s}\int _{t}^{t+T}\frac{{\mathrm{d}}}{{\mathrm{d}}s}e^{\int _{0}^{s}b(r){\mathrm{d}}r}\nu \gamma {\mathrm{d}}s=\nu \gamma \end{aligned}$$

with $\nu =\min \{\frac{a(s)}{b(s)}:s\in [0,T]\}\ge 1.$ For the second component of P(x, y)(t),

$$\begin{aligned} P_{2}(x,y)(t)&=\zeta _{2}e^{-\int _{0}^{t+T}d(s){\mathrm{d}}s}\int _{t}^{t+T}e^{\int _{0}^{s}d(r){\mathrm{d}}r}\beta (s)h( x(s-\sigma _{2})){\mathrm{d}}s \\&=\zeta _{2}e^{-\int _{0}^{t+T}d(s){\mathrm{d}}s}\int _{t}^{t+T}e^{\int _{0}^{s}d(r){\mathrm{d}}r}d(s)\frac{\beta (s)}{d(s)} h(x(s-\sigma _{2})){\mathrm{d}}s \\&\ge \zeta _{2}e^{-\int _{0}^{t+T}d(s){\mathrm{d}}s}\int _{t}^{t+T}\frac{{\mathrm{d}}}{{\mathrm{d}}s}e^{\int _{0}^{s}d(r){\mathrm{d}}r} \gamma {\mathrm{d}}s=\gamma . \end{aligned}$$

Step 4 P is equicontinuous in ${\mathcal {B}}_{\gamma }$.

Take $t_{1},t_{2}\in [-\sigma ,0]$ and $(x,y)\in {\mathcal {B}}_{\gamma }$. We analyze the first component of P (the analysis of the second component is analogous).

$$\begin{aligned}&|P_{1}(x,y)(t_{1})-P_{1}(x,y)(t_{2})| \\&\quad =|\zeta _{1}e^{-\int _{0}^{t_{1}+T}b(s){\mathrm{d}}s}\int _{t_{1}}^{t_{1}+T}e^{\int _{0}^{s}b(r){\mathrm{d}}r}a(s) y(s-\sigma _{1}){\mathrm{d}}s\\&\qquad -\zeta _{1}e^{-\int _{0}^{t_{2}+T}b(s){\mathrm{d}}s}\int _{t_{2}}^{t_{2}+T}e^{\int _{0}^{s}b(r){\mathrm{d}}r}a(s) y(s-\sigma _{1}){\mathrm{d}}s| \\&\quad \le \zeta _{1}\left| e^{-\int _{0}^{t_{1}+T}b(s){\mathrm{d}}s}-e^{-\int _{0}^{t_{2}+T}b(s){\mathrm{d}}s}\right| \int _{t_{1}}^{t_{1}+T}e^{\int _{0}^{s}b(r){\mathrm{d}}r}a(s) y(s-\sigma _{1}){\mathrm{d}}s \\&\qquad +\zeta _{1} e^{-\int _{0}^{t_{2}+T}b(s){\mathrm{d}}s}\left| \int _{t_{1}}^{t_{1}+T}e^{\int _{0}^{s}b(r){\mathrm{d}}r}a(s) y(s-\sigma _{1}){\mathrm{d}}s\right. \\&\qquad \left. -\int _{t_{2}}^{t_{2}+T}e^{\int _{0}^{s}b(r){\mathrm{d}}r}a(s) y(s-\sigma _{1}){\mathrm{d}}s\right| . \end{aligned}$$

Notice that the last integral term is smaller than

$$\begin{aligned} \zeta _{1} e^{-\int _{0}^{t_{2}+T}b(s){\mathrm{d}}s}\left( \left| \int _{t_{1}}^{t_{2}}e^{\int _{0}^{s}b(r){\mathrm{d}}r}a(s) y(s-\sigma _{1}){\mathrm{d}}s\right| +\left| \int _{t_{1}+T}^{t_{2}+T}e^{\int _{0}^{s}b(r){\mathrm{d}}r}a(s) y(s-\sigma _{1}){\mathrm{d}}s\right| \right) . \end{aligned}$$

In light of this type of estimates, we can deduce that P is equicontinuous.

The conclusion follows from the classical Schauder’s theorem. We stress that ${\mathcal {B}}_{\gamma }$ is a convex set. $\square$

The positive T-periodic solutions of (26) are bounded and bounded away from zero in an uniform manner (see Propositions 4.1 and 4.2). As in the scalar case, we take positive constants $\theta _{\min }$ and $\theta _{\max }$ so that

$$\begin{aligned} 0<\theta _{\min }\le \min \{x_{*}(t),y_{*}(t):t\in [0,T]\} \end{aligned}$$

and

$$\begin{aligned} \theta _{\max }\ge \max \{x_{*}(t),y_{*}(t):t\in [0,T]\} \end{aligned}$$

for all positive T-periodic solution $(x_{*}(t),y_{*}(t))$ of (26). We define

$$\begin{aligned} g(x)=\frac{h(\theta _{\min }x)}{h(\theta _{\min })} \end{aligned}$$

and

$$\begin{aligned} f(x)=\frac{h(\theta _{\max }x)}{h(\theta _{\max })}. \end{aligned}$$

We assume that $g:[0,+\infty )\longrightarrow [0,+\infty )$ satisfies condition (Q) introduced in Sect. 3. Next we fix a positive T-periodic solution $(x_{*}(t),y_{*}(t))$ of (26) and employ the change of variable

$$\begin{aligned} z_{1}(t)=\frac{x(t)}{x_{*}(t)}\;\;\mathrm{and}\;\;z_{2}(t)=\frac{y(t)}{y_{*}(t)}. \end{aligned}$$

After simple manipulations, system (26) is transformed into

$$\begin{aligned} \left\{ \begin{array}{lll} z_{1}'(t)=\frac{a(t)y_{*}(t-\sigma _{1})}{x_{*}(t)}(z_{2}(t-\sigma _{1})-z_{1}(t))\\ z_{2}'(t)=\frac{\beta (t)}{y_{*}(t)}( h(x_{*}(t-\sigma _{2})z_{1}(t-\sigma _{2}))-z_{2}(t) h(x_{*}(t-\sigma _{2}))). \end{array}\right. \end{aligned}$$

(34)

Lemma 4.1

Assume (A), (B), (C), (G1), (G2) and (Q). If $(a,b)\in (0,+\infty )^2$ is a constant solution of (34), then $a=b=1$.

Proof

By the expression of the first equation of (34), $a=b$. Using the second equation of the system, we have that

$$\begin{aligned} h(x_{*}(t-\sigma _{2})a)=a h(x_{*}(t-\sigma _{2})) \end{aligned}$$

for all $t>0$ or, equivalently,

$$\begin{aligned} H(x_{*}(t-\sigma _{2}),a)=a \end{aligned}$$

for all $t>0$. We conclude that $a=1$ by Lemma 2.1 with $\theta _{0}=\theta _{\min }$. $\square$

Next we give the variant of Proposition 3.3 for system (26).

Proposition 4.3

Assume conditions (A), (B), (C), (G1), (G2) and (Q). Fix $(x_{*}(t),y_{*}(t))$ a positive T-periodic solution of (26). Suppose that there exists a positive solution (x(t), y(t)) of (26) so that $(x(t),y(t))-(x_{*}(t),y_{*}(t))$ does not converge to (0, 0) as $t\longrightarrow +\infty$. Then, there are four positive constants L, S, ${\widetilde{L}}$ and ${\widetilde{S}}$ with the following properties:

(i):

$0<L<S$.

(ii):

${\widetilde{S}}<1<{\widetilde{L}}$.

(iii):

${\widetilde{S}},{\widetilde{L}}\in [L,S].$

(iv):

$f({\widetilde{L}})\le L$ and $f({\widetilde{S}})\ge S$.

Proof

First, we employ the change of variable $z_{1}(t)=\frac{x(t)}{x_{*}(t)}$ and $z_{2}(t)=\frac{y(t)}{y_{*}(t)}$. Let

$$\begin{aligned} L=\min \left\{ \liminf _{t\rightarrow +\infty } z_{1}(t),\liminf _{t\rightarrow +\infty } z_{2}(t)\right\} \end{aligned}$$

and

$$\begin{aligned} S=\max \left\{ \limsup _{t\rightarrow +\infty } z_{1}(t),\limsup _{t\rightarrow +\infty } z_{2}(t)\right\} . \end{aligned}$$

It is not restrictive to assume that

$$\begin{aligned} L=\liminf _{t\rightarrow +\infty } z_{2}(t)\;\;\mathrm{and}\;\; S=\limsup _{t\rightarrow +\infty } z_{2}(t). \end{aligned}$$

Notice that if, for example, $L=\liminf _{t\rightarrow +\infty } z_{1}(t)$, then by the fluctuation lemma (see Lemma 1.1), there would exist a sequence $\{t_{n}\}$ tending to $+\infty$ satisfying that $\lim _{n\longrightarrow +\infty }z_{1}'(t_{n})=0$ and $\lim _{n\longrightarrow +\infty }z_{1}(t_{n})=L$. Evaluating the first equation of (34) at $t_{n}$, we obtain that

$$\begin{aligned} z_{1}'(t_{n})=\frac{a(t_{n})y_{*}(t_{n}-\sigma _{1})}{x_{*}(t_{n})}(z_{2}(t_{n}-\sigma _{1})-z_{1}(t_{n})). \end{aligned}$$

Since $a(t), y_{*}(t)$ and $x_{*}(t)$ are positive and T-periodic functions, we have that $\lim _{n\longrightarrow +\infty }z_{2}(t_{n}-\sigma _{1})=\lim _{n\longrightarrow +\infty }z_{1}(t_{n})=L$. On the other hand, if $(x(t),y(t))-(x_{*}(t),y_{*}(t))$ does not converge to (0, 0) as $t\longrightarrow +\infty$, then $(z_{1}(t),z_{2}(t))$ does not converge to (1, 1) as $t\longrightarrow +\infty$. Note that

$$\begin{aligned} x_{*}(t)(z_{1}(t)-1)=x(t)-x_{*(t)}\;\;\mathrm{and}\;\;y_{*}(t)(z_{2}(t)-1)=y(t)-y_{*(t)}. \end{aligned}$$

Observe that if $L=S$, then $\lim _{t\rightarrow +\infty } z_{2}(t)=L=S=\lim _{t\rightarrow +\infty } z_{1}(t)$. This is a contradiction because (1, 1) is the unique positive equilibrium of (34). Hence, $L<S$. Moreover, the solutions of (34) are bounded and bounded away from zero by Propositions 4.1 and 4.2. Hence, $L>0$ and $S<+\infty$. The rest of the proof is exactly the same as that in Proposition 3.3. Specifically, we take a sequence $\{t_{n}\}$ tending to $+\infty$ so that $z_{2}'(t_{n})\longrightarrow 0$ and $z_{2}(t_{n})\longrightarrow S$. Then, we arrive at

$$\begin{aligned} S=H(S_{1}, {\widetilde{S}}) \end{aligned}$$

with $S_{1}\in [\theta _{\min },\theta _{\max }]$ and ${\widetilde{S}}\in [L,S]$. Repeating the argument with L, we obtain that

$$\begin{aligned} L=H(L_{1}, {\widetilde{L}}) \end{aligned}$$

with $L_{1}\in [\theta _{\min },\theta _{\max }]$ and ${\widetilde{L}}\in [L,S]$. The proof follows from Lemma 2.2. $\square$

Repeating the argument of the proof of Theorem 3.2, we obtain the following result.

Theorem 4.2

Assume (A), (B), (C), (G1), (G2) and (Q). If 1 is a global attractor in $(0,+\infty )$ for the difference equation

$$\begin{aligned} x_{n+1}=f(x_{n}), \end{aligned}$$

then there exists a positive T-periodic solution $(x_{*}(t),y_{*}(t))$ of (26) which is globally attracting, that is, for any (x(t), y(t)) positive solution of (26),

$$\begin{aligned} \lim _{t\longrightarrow +\infty }[(x(t),y(t))-(x_{*}(t),y_{*}(t))]=0. \end{aligned}$$

To complete this section, we apply the previous theorem when h is decreasing.

Theorem 4.3

Assume that $h:[0,+\infty )\longrightarrow (0,+\infty )$ is of class ${\mathcal {C}}^{3}$ with $S(h)(x)<0$ (the Schwarzian derivative) and $h'(x)<0$ for all $x\in (0,+\infty )$. In addition, we assume that (B), (C) and (G1) hold. If

$$\begin{aligned} \frac{h'(\theta _{\max })\theta _{\max }}{h(\theta _{\max })}\ge -1 \end{aligned}$$

with

$$\begin{aligned} \theta _{\max }=\max \left\{ \frac{a(t)}{b(t)}:t\in [0,T]\right\} \cdot \max \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} h(0), \end{aligned}$$

then there is a T-periodic solution $(x_{*}(t),y_{*}(t))$ of (26) with $x_{*}(t)>0$ and $y_{*}(t)>0$ for all $t\in [0,T]$ that is a global attractor for all positive solutions of (26).

Proof

We notice that (A) and (G2) are automatically satisfied. Then, by Theorem 4.1, there exists a T-periodic solution $(x_{*}(t),y_{*}(t))$ of (26) with $x_{*}(t)>0$ and $y_{*}(t)>0$ for all $t\in [0,T]$. We also realize that $h'(x)<0$ for all $x\in (0,+\infty )$ implies that (Q) holds for any $\theta _{\min }>0$. Next, we prove that

$$\begin{aligned} \theta _{\max }=\max \left\{ \frac{a(t)}{b(t)}:t\in [0,T]\right\} \cdot \max \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} h(0) \end{aligned}$$

is an (uniform) upper bound for the positive T-periodic solutions of (26). Let $(x_{*}(t),y_{*}(t))$ be a positive T-periodic solution of (26). Take $t_{0}\in [0,T]$ so that $y_{*}(t_{0})=\max \{y_{*}(t):t\in [0,T]\}$. Then, $y_{*}'(t_{0})=0$. By the second equation of (26), we deduce that

$$\begin{aligned} y(t_{0})\le \max \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} h(0). \end{aligned}$$

Analogously, take $s_{0}\in [0,T]$ so that $x_{*}(s_{0})=\max \{x_{*}(t):t\in [0,T]\}$. Then, $x_{*}'(s_{0})=0$. By the first equation of (26), we obtain that

$$\begin{aligned} x_{*}(s_{0})\le \max \left\{ \frac{a(t)}{b(t)}:t\in [0,T]\right\} \cdot \max \{y(t):t\in [0,T]\}. \end{aligned}$$

The conclusion follows from Theorem 4.2 and Proposition 2.2. Notice that

$$\begin{aligned} f'(1)=\frac{h'(\theta _{\max })\theta _{\max }}{h(\theta _{\max })}. \end{aligned}$$

$\square$

Examples of functions satisfying the conditions of the previous theorem are $h(x)= e^{-x}$ or $h(x)=\frac{1}{1+x}$. Specifically, consider

$$\begin{aligned} \left\{ \begin{array}{lll}x'(t)= a(t) y(t-\sigma _{1})-b(t) x(t)\\ y'(t)=\beta (t) e^{-x(t-\sigma _{2})} -d(t) y(t), \end{array}\right. \end{aligned}$$

(35)

with $\sigma _{1},\sigma _{2}>0$ and $a,b,\beta ,d:{\mathbb {R}}\longrightarrow (0,+\infty )$ continuous and T-periodic functions. In this case, $H(t,x)=e^{t(1-x)}$,

$$\begin{aligned} \theta _{\max }=\max \left\{ \frac{a(t)}{b(t)}:t\in [0,T]\right\} \cdot \max \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} , \end{aligned}$$

and

$$\begin{aligned} \frac{h'(\theta _{\max })\theta _{\max }}{h(\theta _{\max })}=-\theta _{\max }. \end{aligned}$$

Therefore, if $a(t)\ge b(t)$ for all $t\in [0,T]$ and

$$\begin{aligned} \max \left\{ \frac{a(t)}{b(t)}:t\in [0,T]\right\} \cdot \max \left\{ \frac{\beta (t)}{d(t)}:t\in [0,T]\right\} \le 1, \end{aligned}$$

then the assumptions of Theorem 4.3 are satisfied in system (35). On the other hand, for system

$$\begin{aligned} \left\{ \begin{array}{lll}x'(t)= a(t) y(t-\sigma _{1})-b(t) x(t)\\ y'(t)=\frac{\beta (t)}{1+x(t-\sigma _{2})} -d(t) y(t), \end{array}\right. \end{aligned}$$

$H(t,x)=\frac{1+t}{1+tx}$. It is clear that the assumptions of Theorem 4.3 are satisfied if $a(t)\ge b(t)$ for all $t\in [0,T]$. Notice that for $h(x)=\frac{1}{1+x}$, $\frac{h'(\theta _{\max })\theta _{\max }}{h(\theta _{\max })}\ge -1$ always holds.

4.2 Models for Populations with Patch Structure

Consider the system

$$\begin{aligned} x_{i}'(t)=-d_{i}(t) x_{i}(t)+\sum _{j=1,j\not =i}^{N}a_{ij}(t)x_{j}(t)+\sum _{k=1}^{m}\beta _{i k}(t) h(x_{i}(t-\tau _{i k})) \end{aligned}$$

(36)

for $i=1,\ldots ,N$ where $d_{i},a_{ij},\beta _{ik}:{\mathbb {R}}\longrightarrow [0,+\infty )$ are continuous and T-periodic, $\tau _{ik}\ge 0$ and $h:[0,+\infty )\longrightarrow [0,+\infty )$ is a function of class ${\mathcal {C}}^{1}$ with $h((0,+\infty ))\subset (0,+\infty )$. As in the previous section, we assume that h is bounded, (condition (A) according to the notation of the previous sections). We additionally suppose the following conditions:

(P1):

$d_{i}(t)>0$ for all $t\in {\mathbb {R}}$ and $i=1,\ldots ,N$.

(P2):

There exists a vector $u=(u_{1},\ldots ,u_{N})\gg 0$ such that

$$\begin{aligned} d_{i}(t)u_{i}\ge \sum _{j=1, j\not =i}^{N}a_{ij}(t) u_{j} \end{aligned}$$

for $t\in {\mathbb {R}}$ with

$$\begin{aligned} d_{i}(t_{0})u_{i}>\sum _{j=1, j\not =i}^{N}a_{ij}(t_{0})u_{j} \end{aligned}$$

$i=1,\ldots ,N$ for some $t_{0}\in {\mathbb {R}}$.

(P3):

$\beta _{i}(t)=\sum _{k=1}^{m}\beta _{ik}(t)>0$ for all $t\in {\mathbb {R}}$, $i=1,\ldots ,N$.

(P4):

$h(0)=0$ and $h'(0)=1$.

We define by A(t), B(t), D(t), M(t) the T-periodic square matrices of order N given by

$$\begin{aligned} D(t)= & {} {\mathrm{diag}}(d_{1}(t),\ldots ,d_{N}(t)), \\ A(t)= & {} (a_{ij}(t)), \\ B(t)= & {} {\mathrm{diag}}(\beta _{1}(t),\ldots ,\beta _{N}(t)), \\ M(t)= & {} B(t)+A(t)-D(t), \end{aligned}$$

where $a_{ii}(t)=0$ for $1\le i\le N$. We also need the following condition:

(P5):

There exists $v=(v_{1},\ldots ,v_{N})\gg 0$ such that $M(t)v\gg 0$ for all $t\in [0,T]$.

The previous assumptions guarantee the existence and uniqueness of solutions for (36) with initial condition in ${\mathcal {C}}([-\sigma ,0], [0,+\infty )^{N})$ with $\sigma =\max \{\tau _{ik}:i=1,\ldots ,N, k=1,\ldots ,m\}.$ Motivated by its biological meaning, we focus on initial conditions taken in ${\mathcal {C}}([-\sigma ,0], (0,+\infty )^{N})$. We refer to them as positive solutions.

The following two results are taken directly from Faria (2017). It is worth noting that under (A) and (P1)–(P5), conditions (H0)–(H5) in Faria (2017) are satisfied. To check (H4) in Faria (2017), we simply take $h_{i}^{-}(x)=h(x)$ for all $i=1,\ldots ,m$. Actually, (H0)–(H5) are much more general than our conditions.

Theorem 4.4

(Theorem 2.1 in Faria 2017) Assume conditions (A) and (P1)–(P5). Then, there are two positive constants $\kappa _{1}$, $\kappa _{2}$ such that given any initial condition $\phi \in {\mathcal {C}}([-\sigma ,0], (0,+\infty )^{N})$, there exists $t_{0}$ (depending on $\phi$) for which the solution $x(t)=(x_{1}(t),\ldots ,x_{N}(t))$ which initial condition $\phi$ satisfies that

$$\begin{aligned} \kappa _{1}\le x_{i}(t)\le \kappa _{2} \end{aligned}$$

for all $t\ge t_{0}$ and $i=1,\ldots ,N$.

Theorem 4.5

(Theorem 3.1 in Faria 2017) Assume conditions (A) and (P1)–(P5). Then, system (36) has a T-periodic solution $x_{*}(t)=(p_{1}(t),\ldots ,p_{N}(t))$ with $p_{i}(t)>0$ for all $t\in [0,T]$ and $i=1,\ldots ,N$.

Our aim is to prove the existence of a globally attracting positive T-periodic solution for system (36). As in previous sections, we assume that h also satisfies (B) and (C).

Fix $x_{*}(t)=(p_{1}(t),\ldots ,p_{N}(t))$ a positive T-periodic solution of (36). The change of variable

$$\begin{aligned} y_{i}(t)=\frac{x_{i}(t)}{p_{i}(t)} \end{aligned}$$

for $i=1,\ldots ,N$ transforms system (36) into

$$\begin{aligned} y'_{i}(t)= & {} \sum _{j=1, j\not =i}^{N} a_{ij}(t)\frac{p_{j}(t)}{p_{i}(t)}(y_{j}(t)-y_{i}(t))\nonumber \\&+\sum _{k=1}^{m}\frac{\beta _{ik}(t) }{p_{i}(t)}\left( h(p_{i}(t-\tau _{ik}) y_{i}(t-\tau _{ik}))-y_{i}(t) h(p_{i}(t-\tau _{ik}))\right) \end{aligned}$$

(37)

for $i=1,\ldots ,N$. Since the positive T-periodic solutions of (36) are bounded and bounded away from zero in an uniform manner, we can take two positive constants $\theta _{\min }$ and $\theta _{\max }$ so that

$$\begin{aligned} \theta _{\max }\ge & {} \max \{p_{i}(t):t\in [0,T], i=1,\ldots ,N\} \\ \theta _{\min }\le & {} \min \{p_{i}(t):t\in [0,T], i=1,\ldots ,N\} \end{aligned}$$

for any $x_{*}(t)=(p_{1}(t),\ldots ,p_{N}(t))$ positive T-periodic solution of system (36). We also define

$$\begin{aligned} f(x)=H(\theta _{\max },x)\;\;\;\mathrm{and}\;\;\; g(x)=H(\theta _{\min },x). \end{aligned}$$

As in previous sections, we impose condition (Q), that is,

(Q):

$g(x)>x$ for all $x\in (0,1)$ and $g(x)<x$ for all $x\in (1,+\infty )$.

Our first aim is to prove that (37) has a unique positive equilibrium.

Lemma 4.2

Assume conditions (A), (B), (C), (P1)–(P5) and (Q). If $\zeta =(\zeta _{1},\ldots ,\zeta _{N})\gg 0$ is an equilibrium of (37) then $\zeta _{i}=1$ for all $i=1,\ldots ,N$.

Proof

First we prove that if $\zeta =(a,\ldots ,a)$ is an equilibrium of (37) with $a>0$, then $a=1$. Observe that

$$\begin{aligned} \sum _{k=1}^{m}\frac{\beta _{ik}(t) }{p_{i}(t)}\left( h(p_{i}(t-\tau _{ik}) a)-a h(p_{i}(t-\tau _{ik}))\right) =0 \end{aligned}$$

for all $i=1,\ldots ,N$ and for all $t\in [0,T]$. Since $\frac{\beta _{ik}(t)}{p_{i}(t)}>0$ for all $t\in [0,T]$, we can find two times $t_{0},t_{1}$ and two indices i, k so that

$$\begin{aligned} h(p_{i}(t_{0}-\tau _{ik}) a)-a h(p_{i}(t_{0}-\tau _{ik}))\le 0 \end{aligned}$$

and

$$\begin{aligned} h(p_{i}(t_{1}-\tau _{ik}) a)-a h(p_{i}(t_{1}-\tau _{ik}))\ge 0. \end{aligned}$$

As a consequence of Lemma 2.1, we conclude that $a=1$.

Next we take $\zeta =(\zeta _{1},\ldots ,\zeta _{N})\gg 0$ an arbitrary equilibrium of (37). Let $u=\min \{\zeta _{i}:i=1,\ldots ,N\}>0$ and $U=\max \{\zeta _{i}:i=1,\ldots ,N\}$. We prove that $u=U$. Assume, by contradiction, that $u<U$. Take an index $i_{0}$ so that $u=\zeta _{i_{0}}$. We focus on the $i_{0}$-th equation of (37). Observe that

$$\begin{aligned} \sum _{j=1, j\not =i_{0}}^{N} a_{i_{0}j}(t)\frac{p_{j}(t)}{p_{i_{0}}(t)}(\zeta _{j}-\zeta _{i_{0}})>0 \end{aligned}$$

for all $t\in [0,T]$. Thus,

$$\begin{aligned} \sum _{k=1}^{m}\frac{\beta _{i_{0}k}(t) }{p_{i_{0}}(t)}\left( h(p_{i_{0}}(t-\tau _{i_{0}k}) \zeta _{i_{0}})-\zeta _{i_{0}} h(p_{i_{0}}(t-\tau _{i_{0}k}))\right) <0 \end{aligned}$$

for all $t\in [0,T]$. In particular, there are $k\in \{1,\ldots ,m\}$ and $t_{0}$ so that

$$\begin{aligned} h(p_{i_{0}}(t_{0}-\tau _{i_{0}k}) \zeta _{i_{0}})-\zeta _{i_{0}} h(p_{i_{0}}(t_{0}-\tau _{i_{0}k}))<0 \end{aligned}$$

or equivalently,

$$\begin{aligned} H(p_{i_{0}}(t_{0}-\tau _{i_{0}k}), \zeta _{i_{0}})<\zeta _{i_{0}}. \end{aligned}$$

By Lemma 2.1, we deduce that $u=\zeta _{i_{0}}\ge 1$. Arguing in a similar manner with U, we conclude that $U\le 1$. This is a contradiction because $u<U$.

Next we develop a delay independent criterion of global attraction for system (36).

Proposition 4.4

Assume conditions (A), (B), (C), (P1)–(P5) and (Q). Fix $x_{*}(t)=(p_{1}(t),\ldots ,p_{N}(t))$ a positive T-periodic solution of (36). Suppose that there exists a positive solution $x(t)=(x_{1}(t),\ldots ,x_{N}(t))$ of (36) so that $x(t)-x_{*}(t)$ does not converge to 0 as $t\longrightarrow +\infty$. Then, there are four positive constants L, S, ${\widetilde{L}}$ and ${\widetilde{S}}$ with the following properties:

(i):

$0<L<S$.

(ii):

${\widetilde{S}}<1<{\widetilde{L}}$.

(iii):

${\widetilde{S}},{\widetilde{L}}\in [L,S].$

(iv):

$f({\widetilde{L}})\le L$ and $f({\widetilde{S}})\ge S$.

Proof

We employ the change of variable

$$\begin{aligned} y_{i}(t)=\frac{x_{i}(t)}{p_{i}(t)} \end{aligned}$$

for $i=1,\ldots ,N$. Let

$$\begin{aligned} S= & {} \max \left\{ \limsup _{t\rightarrow +\infty } y_{i}(t):i=1,\ldots ,N\right\} \\ L= & {} \min \left\{ \liminf _{t\rightarrow +\infty } y_{i}(t):i=1,\ldots ,N\right\} . \end{aligned}$$

By Theorem 4.4, $0<L$ and $S\in {\mathbb {R}}$. We know that

$$\begin{aligned} x_{i}(t)-p_{i}(t)=p_{i}(t)(y_{i}(t)-1) \end{aligned}$$

for $i=1,\ldots ,N$. Using that $x(t)-x_{*}(t)$ does not converge to 0 as $t\longrightarrow +\infty$, we deduce that $(y_{1}(t),\ldots ,y_{N}(t))$ does not converge to $(1,\ldots ,1)$. Notice that $L<S$. To see this claim, we observe that if $L=S$, then $\lim _{t\rightarrow +\infty }y_{i}(t)=L=S$ for all $i=1,\ldots ,N$. However, this is not possible because $(1,\ldots ,1)$ is the unique non-trivial equilibrium of (37) by Lemma 4.2 and we know that $(y_{1}(t),\ldots ,y_{N}(t))$ does not converge to (1, .., 1).

Take $i_{0}\in \{1,\ldots ,N\}$ so that

$$\begin{aligned} S=\limsup _{t\rightarrow +\infty } y_{i_{0}}(t). \end{aligned}$$

By Lemma 1.1, we can take $\{t_{n}\}$ a sequence tending to $+\infty$ so that $\lim _{n\rightarrow +\infty }y_{i_{0}}'(t_{n})= 0$ and $\lim _{n\rightarrow +\infty }y_{i_{0}}(t_{n})= S$. It is not restrictive to assume that there exists $n_{0}\in {\mathbb {N}}$ large enough so that

$$\begin{aligned} y_{j}(t_{n})-y_{i_{0}}(t_{n})\le 0 \end{aligned}$$

for all $n\ge n_{0}$ and $j\in \{1,\ldots ,N\}$. We can also suppose that $p_{i_{0}}(t_{n})$, $\beta _{i_{0}k}(t_{n})$, $p_{i_{0}}(t_{n}-\tau _{i_{0}k})$, $y_{i_{0}}(t_{n}-\tau _{i_{0}k})$ are convergent as $n\longrightarrow +\infty$ with

$$\begin{aligned}&y_{i_{0}}(t_{n}-\tau _{i_{0}k})\longrightarrow {\widetilde{S}}_{k}\in [L,S] \\&p_{i_{0}}(t_{n}-\tau _{i_{0}k})\longrightarrow S_{k}\in [\theta _{\min },\theta _{\max }] \end{aligned}$$

for all $k\in \{1,\ldots ,m\}$. Evaluating the $i_{0}$-th equation of (37) at $t_{n}$, we obtain that

$$\begin{aligned} y'_{i_{0}}(t_{n})&=\sum _{j=1, j\not =i_{0}}^{N} a_{i_{0}j}(t_{n})\frac{p_{j}(t_{n})}{p_{i_{0}}(t_{n})}(y_{j}(t_{n})-y_{i_{0}}(t_{n}))\\&\quad +\sum _{k=1}^{m}\frac{\beta _{i_{0}k}(t_{n}) }{p_{i_{0}}(t_{n})}\left( h(p_{i_{0}}(t_{n}-\tau _{i_{0}k}) y_{i_{0}}(t_{n}-\tau _{i_{0}k}))-y_{i_{0}}(t_{n}) h(p_{i_{0}}(t_{n}-\tau _{i_{0}k}))\right) . \end{aligned}$$

Using that $y_{j}(t_{n})-y_{i_{0}}(t_{n})\le 0$ and $a_{i_{0}j}(t_{n})>0$ for all $n\ge n_{0}$ and $j\in \{1,\ldots ,N\}$, we conclude that

$$\begin{aligned} \sum _{k=1}^{m}\frac{\beta _{i_{0}k}(t_{n}) }{p_{i_{0}}(t_{n})}\left( h(p_{i_{0}}(t_{n}-\tau _{i_{0}k}) y_{i_{0}}(t_{n}-\tau _{i_{0}k}))-y_{i_{0}}(t_{n}) h(p_{i_{0}}(t_{n}-\tau _{i_{0}k}))\right) \ge 0. \end{aligned}$$

Making $n\rightarrow +\infty$ in the previous expressions and using (P3), we conclude that there exists $k_{0}\in \{1,\ldots ,m\}$ so that

$$\begin{aligned} h(S_{k_{0}}{\widetilde{S}}_{k_{0}})-S h(S_{k_{0}})\ge 0. \end{aligned}$$

That is, $S\le H(S_{k_{0}},{\widetilde{S}}_{k_{0}})$. Repeating the analogous argument with L, we deduce the existence of an index $j_{0}\in \{1,\ldots ,m\}$, and two constants ${\widetilde{L}}_{j_{0}}\in [L,S]$ and $L_{j_{0}}\in [\theta _{\min }, \theta _{\max }]$ so that $L\ge H(L_{j_{0}},{\widetilde{L}}_{j_{0}})$. The conclusion follows from Lemma 2.2. $\square$

Theorem 4.6

Assume conditions (A), (B), (C), (P1)-(P5) and (Q). If 1 is a global attractor in $(0,+\infty )$ for the difference equations

$$\begin{aligned} x_{n+1}=f(x_{n}), \end{aligned}$$

then there exists a positive T-periodic solution $x_{*}(t)=(p_{1}(t),\ldots ,p_{N}(t))$ of (36) which is globally attracting, that is, for any $x(t)=(x_{1}(t),\ldots ,x_{N}(t))$ positive solution of (36)

$$\begin{aligned} \lim _{t\longrightarrow +\infty }(x(t)-x_{*}(t))=0. \end{aligned}$$

4.3 Estimating an Upper Bound for the Positive T-Periodic Solutions of (36) and Applications

In this subsection, we translate the abstract criterion developed in Theorem 4.6 into a more applied one. We suppose that h(x) is a bounded function of class ${\mathcal {C}}^{1}$. We also impose that $d_{i},a_{ij},\beta _{ik}:{\mathbb {R}}\longrightarrow [0,+\infty )$ are continuous and T-periodic and $\tau _{ik}\ge 0$. For simplicity, in this subsection we work with functions of the form $h(x)=x q(x)$ where $q:[0,+\infty )\longrightarrow (0,+\infty )$ is strictly decreasing and $q(0)=1$. Since h is bounded, it is clear that $\lim _{x\longrightarrow +\infty } q(x)=0$. In this framework, (P4) holds and the rest of conditions, when $u=v=(1,\ldots ,1)$, can be re-written in the following manner:

(A1):

$d_{i}(t)>0$ for all $t\in {\mathbb {R}}$ and $i\in \{1,\ldots ,N\}$.

(A2):

$d_{i}(t)-\sum _{j=1, j\not =i}^{N}a_{ij}(t)>0$ for all $t\in {\mathbb {R}}$ and $i\in \{1,\ldots ,N\}$.

(A3):

$\beta _{i}(t)=\sum _{k=1}^{m}\beta _{ik}(t)>0$ for all $t\in {\mathbb {R}}$ and $i\in \{1,\ldots ,N\}$.

(A4):

$\beta _{i}(t)-d_{i}(t)+\sum _{j=1, j\not =i}^{N}a_{ij}(t)>0$ for all $t\in {\mathbb {R}}$ and $i\in \{1,\ldots ,N\}$.

As discussed in Faria (2017), it is easy to manage the general case from the choice $u=v=(1,\ldots ,1)$.

Next, we take

$$\begin{aligned} \Delta _{1}=\min \left\{ \frac{d_{i}(t)-\sum _{j=1, j\not =i}^{N}a_{ij}(t)}{\beta _{i}(t)}:i=1,\ldots ,N, t\in [0,T]\right\} . \end{aligned}$$

and M an upper bound of h(x).

First, we estimate an uniform upper bound for the positive T-periodic solutions of (36).

Proposition 4.5

Assume that $h(x)=x q(x)$ is a bounded map of class ${\mathcal {C}}^1$ with $q:[0,+\infty )\longrightarrow (0,+\infty )$ is strictly decreasing and $q(0)=1$. In addition, suppose that (A1)–(A4) hold. We have the following:

(i):

If $\tau _{ik}=n_{ik}T$ with $n_{ik}\in {\mathbb {N}}$ for $i=1,\ldots ,N$ and $k=1,\ldots ,m$, then, for all positive T-periodic solution $(p_{1}(t),\ldots ,p_{N}(t))$ of (36), $(p_{1}(t),\ldots ,p_{N}(t))$ $p_{i}(t)\le q^{-1}(\Delta _{1})$ for $i=1,\ldots ,N$ and $t\in [0,T]$.

(ii):

If $\tau _{ik}\not =n_{ik}T$ with $n_{ik}\in {\mathbb {N}}$ for some $i=1,\ldots ,N$, $k=1,\ldots ,m$, then, for all positive T-periodic solution $(p_{1}(t),\ldots ,p_{N}(t))$ of (36), $p_{i}(t)\le \frac{M}{\Delta _{1}}$ for $i=1,\ldots ,N$ and $t\in [0,T]$.

Proof

(i) Take $t_{0}\in [0,T]$ and $i_{0}\in \{1,\ldots ,N\}$ with

$$\begin{aligned} p_{i_{0}}(t_{0})=\max \{p_{i}(t):t\in [0,T],i\in \{1,\ldots ,N\}\} \end{aligned}$$

(38)

and $p_{i_{0}}'(t_{0})=0$. Notice that $p_{i_{0}}(t_{0}-\tau _{i_{0}k})= p_{i_{0}}(t_{0})$ because $p_{i_{0}}(t)$ is T-periodic and $\tau _{i_{0}k}= n_{i_{0}k} T$ for all $k=1,\ldots ,m$. Using the expression of the $i_{0}$-th equation of (36) and (38), we have that

$$\begin{aligned} d_{i_{0}}(t_{0}) p_{i_{0}}(t_{0})\le p_{i_{0}}(t_{0})\left( \sum _{j=1,j\not =i_{0}}^{N}a_{i_{0}j}(t_{0}))+\beta _{i_{0} }(t_{0}) p_{i_{0}}(t_{0}) q(p_{i_{0}}(t_{0})\right) . \end{aligned}$$

Thus,

$$\begin{aligned} q (p_{i_{0}}(t_{0}))\ge \frac{d_{i_{0}}(t_{0})-\sum _{j=1,j\not =i_{0}}^{N}a_{i_{0}j}(t_{0})}{\beta _{i_{0}}(t_{0})}. \end{aligned}$$

Now, the conclusion of (i) is clear. To prove (ii), we take $t_{0}$ and $i_{0}$ as above. We observe that

$$\begin{aligned} 0\le -d_{i_{0}}(t_{0}) p_{i_{0}}(t_{0})+\sum _{j=1,j\not =i_{0}}^{N}a_{i_{0}j}(t_{0})p_{i_{0}}(t_{0})+\sum _{k=1}^{m}\beta _{i_{0} k}(t_{0}) M, \end{aligned}$$

or equivalently,

$$\begin{aligned} p_{i_{0}}(t_{0})\le \frac{M}{\Delta _{1}}. \end{aligned}$$

$\square$

Remark 4.1

Informally speaking, Proposition 4.5 says that we can take $\theta _{\max }=q^{-1}(\Delta _{1})$ in (i) and $\theta _{\max }=\frac{M}{\Delta _{1}}$ in (ii).

To conclude this section, we apply Theorem 4.6 in system (36) with $h(x)=\frac{x}{1+x^2}$. In this case,

$$\begin{aligned} H(t,x)=\frac{1+t^2}{1+(tx)^2}x. \end{aligned}$$

It is clear that (A), (B) and (C) hold. Moreover, condition (Q) is satisfied for any $\theta >0$. On the other hand, for each $t>0$, we have that

$$\begin{aligned} \left| \frac{\partial }{\partial x} H(t,1)\right| < 1. \end{aligned}$$

Thus, for each $\theta _{\max }>0$, $f(x)= H(\theta _{\max },x)$ is a function with negative Schwarzian derivative and $|f'(1)|< 1$. By Proposition 2.2, we conclude that 1 is a global attractor in $(0,+\infty )$ for the difference equation

$$\begin{aligned} x_{n+1}=f(x_{n}). \end{aligned}$$

In conclusion, if we consider system (36) with $h(x)=\frac{x}{1+x^2}$ and (A1)–(A4) are satisfied, then there is a positive T-periodic solution that is globally attracting for all positive solutions of (36).

In general, for $h(x)=\frac{x}{1+x^{\gamma }}$ with $\gamma \ge 2$, the global attraction of a T- periodic solution in system (36) is guaranteed if

$$\begin{aligned} 2\ge (\gamma -2)\theta _{\max }^\gamma \end{aligned}$$

with $\theta _{\max }$ the upper bound given in Remark 4.1.

In Section 4 in Faria (2017), Faria analyzed the existence of a global attracting positive T-periodic solution in (36) when $h(x)=xe^{-x}$ and all delays are multiple of the period. Following our strategy with this nonlinearity, we recover exactly the same results as those in Faria (2017). Our contribution in comparison with Faria (2017) is that our approach is not restricted to $h(x)=xe^{-x}$. We stress that the main result in Faria (2017) on the existence of a positive T-periodic solution, the key contribution of that paper, is not restricted to Nicholson’s system.

5 Discussion

A major challenge in theoretical biology is to understand the influence of the seasonal fluctuations of the environment on the evolution of the species (Lou and Zhao 2017; Lou et al. 2019). To approach this problem, we offer new criteria of global attractivity of a positive periodic solution in non-autonomous systems of delay differential equations. Generally speaking, our approach can be viewed as the extension for non-autonomous systems of the popular connection between scalar delay differential equations and discrete equations developed in Ivanov and Sharkovsky (1992) and Mallet-Paret and Nussbaum (1986). As particular examples, we have studied non-autonomous variants of some classical models that include Nicholson’s blowfly equation or Mackey–Glass model (Berezansky et al. 2010), the Goodwin oscillator for chemical reactions (Ruoff and Rensing 1996) and models with patch structure (Faria 2017). The main advantages of our results in comparison with those in Faria (2021), Faria et al. (2018), Li et al. (2020), Lou and Zhao (2017) are:

(1):

We cover the common nonlinearities employed in mathematical biology.

(2):

We provide delay-dependent criteria of global attraction that include the best delay independent results.

(3):

We can apply our results in non-monotone models.

To apply our results, it is critical to determine an (uniform) upper bound for the positive T-periodic solutions of the model. Moreover, a better estimate leads to a sharper result. In light of some numerical simulations (see Fig. 1), it seems that the estimates given in Proposition 3.5 when the delays are not multiple of the period can be improved. We will study this issue in future works.

Fig. 1

Representation of two different solutions of Eq. (21) with parameters $d(t)=1$, $\beta (t)=5+ (e^{2}-5) \cos ^{2}(t)$ and $\tau =8$. Notice that Theorem 3.5 cannot be applied in this situation but there exists a globally attracting periodic solution

A controversial result in ecology deduced from equation

$$\begin{aligned} x'(t)=r x(t)\left( 1-\frac{x(t)}{K(t)}\right) \end{aligned}$$

is that seasonality has a deleterious influence on the overall population size (Henson and Cushing 1997). That is, the average of the population size is always less than the average of the carrying capacity. When we analyze a similar question with Nicholson’s blowfly equation, we have observed that the delay can promote or reverse that deleterious influence, see Fig. 2. Particularly, time delays in (21) can stimulate a more efficient use of the resources.

Fig. 2

Representation of $\int _{200-2\pi }^{200} x(t) {\mathrm{d}}(t)$ with x(t) a positive solution of $x'(t)=-x(t)+(1.4+h \sin (t)) x(t-\tau )e^{-x(t-\tau )}$. We measure the intensity of the seasonality by h. Observe that $\int _{0}^{2\pi }1.4+h \sin (t) dt=1.4$ for all h. That is, the average of the resource of the medium is the same for all values of h; (lower curve) $\tau =2.$ (upper curve) $\tau =6$