Equilibria of Plane Convex Bodies

Abstract

We obtain a formula for the number of horizontal equilibria of a planar convex body K with respect to a center of mass O in terms of the winding number of the evolute of $\partial K$ with respect to O. The formula extends to the case where O lies on the evolute of $\partial K$ and a suitably modified version holds true for non-horizontal equilibria.

1 Introduction

We study the number of static equilibria of a planar convex body K supported by a horizontal line subject to a uniform vertical gravity field. It is well-known that the number of static equilibria with respect to the centroid of a homogeneous body K is $\ge 4$ [see Domokos et al. (1994) and Proposition 3.4 below]. It was pointed out in Varkonyi and Domokos (2006) that this result is equivalent to the four-vertex theorem. For an arbitrary center of mass, one can find planar convex bodies with only one stable and one unstable equilibrium—the 3-dimensional counterparts of such objects are known as roly-poly toys. In Varkonyi and Domokos (2006) it is shown that there exists a homogeneous convex roly-poly toy with exactly one stable and one unstable equilibrium, the so-called gömböc—thus answering a long-standing conjecture by Arnol’d in the affirmative.

In this article, we provide a geometric characterization of the number n of static equilibria of a planar convex body K in terms of the winding number of the evolute of $\partial K$ with respect to a given center of mass O of K: If $\partial K$ is parametrized by a positively oriented curve $\gamma$ and O is not a point of the evolute of $\partial K$, then the winding number of the evolute of $\partial K$ is an integer $m\le 0$ and the formula

$$\begin{aligned} n=2-2m \end{aligned}$$

(1.1)

holds true.

On an intuitive level, this might be explained as follows: The number of equilibria of K with respect to O equals the number of normals to $\gamma$ that can be dropped from O. Since the envelope of the family of normals to $\gamma$ is the evolute of $\gamma$, each equilibrium gives rise to a tangent line from O to the evolute. The number of normals through a given point is a locally constant function on the complement of the evolute: It changes by 2 if one crosses the evolute at a smooth point since locally, two tangents to the evolute are added or removed, where the sign of the change depends on whether it happens from the concave to the convex side of the evolute or the other way round (note that the evolute of a convex curve does not have any inflection points: see the beautiful book Fuchs and Tabachnikov 2007, Lecture 10). Furthermore, for points O very far from K, exactly 2 normals can be dropped onto $\gamma$ which explains the additional term 2 in the formula.

There are a few caveats concerning the heuristics above: If a portion of the evolute of $\gamma$ is traversed more than once, multiplicity has to be taken into account. Furthermore, tangents are added or removed locally if one crosses a smooth point of the evolute, but other tangents might appear or disappear since we are looking at a global problem. So, it turned out to be difficult to convert the above geometric arguments into a formal proof. We have therefore decided to give an analytic proof which also covers the cases where O is a point on the evolute, possibly even a cusp. In this case, m may be half-integer valued, but the result still admits a nice geometric interpretation (see Fig. 6). Our main theorem is the following:

Theorem 1.1

Let K be a strongly convex compact set with $C^3$-boundary $\partial K$ such that the curvature of $\partial K$ has only finitely many stationary points, and let O be a point in the plane. Then the number n of horizontal equilibria of K with respect to O is given by

$$\begin{aligned} n=2-2m, \end{aligned}$$

where $0\ge m \in \frac{1}{2}{\mathbb {Z}}$ is the winding number of the evolute of $\partial K$ with respect to O.

The strategy of the proof is to identify the horizontal equilibria as zeros of the first derivative of a support function that parametrizes $\partial K$ and using the zero-counting integral developed in Hungerbühler and Wasem (2018) in order to count its zeros. The resulting integral can then be related to the generalized winding number (see Hungerbühler and Wasem 2019) of the evolute of $\partial K$.

In Sect. 4 we replace the horizontal supporting line of the body K by an inclined line with inclination angle $\alpha \in (-\frac{\pi }{2},\frac{\pi }{2})$. It is interesting that for any angle $\alpha \ne 0$, there exist homogeneous bodies K such that the inequality $n\ge 4$ fails. In fact, for every $\alpha \ne 0$, there are such bodies with exactly one metastable equilibrium and also bodies with exactly one stable and one unstable equilibrium with respect to the centroid (see Proposition 4.1 below). Moreover, we construct a homogeneous convex body for which the function $\alpha \mapsto n_\alpha$, which assigns to a given angle $0\le \alpha < \tfrac{\pi }{2}$ the number of oblique equilibria with respect to $\alpha$ is not monotonically decreasing.

Finally, a formula like (1.1) holds true for $\alpha \ne 0$, where m is the winding number of the evolute of a suitable modification of $\partial K$.

We end the introduction by fixing some notations and conventions. For $x,y\in {\mathbb {R}}^2$, let $(x,y) = \left\{ tx + (1-t)y, t\in (0,1)\right\}$ denote the line segment between the points x and y. A set $K\subset {\mathbb {R}}^2$ is called convex if for any $x,y\in K$ it holds that $(x,y)\cap K=(x,y)$. The set K is called strictly convex if $(x,y)\cap \mathring{K}=(x,y)$ for any $x,y\in K$. A bounded convex set $K\subset {\mathbb {R}}^2$ with $C^n$-boundary, $n\ge 2$ is called strongly convex if $\partial K$ can be parametrized by a curve $\gamma :S^1\rightarrow \partial K$ such that $\Vert \dot{\gamma }\Vert =1$ and $\ddot{\gamma }$ does not vanish. We will use the identification $S^1\cong {\mathbb {R}}/2\pi {\mathbb {Z}}$ and the notation $u(\varphi )=(\cos (\varphi ),\sin (\varphi ))^\top$ throughout this article.

2 Support Functions

In this section, we are going to collect several facts about support functions and convex sets. Some of the material here is classical, but to our best knowledge, Lemma 2.1 is new and so is Corollary 2.2 for curves of class $C^2$.

The boundary $\partial K$ of a strictly convex compact set K admits a parametrization by support functions p and q, i.e., there exists a parametrization $z:S^1\rightarrow \partial K$ such that $z(\varphi ) = p(\varphi )u(\varphi )+q(\varphi )u'(\varphi )$ (see Euler 1778), as indicated in Fig. 1: Here S is a reference point and $\ell$ a ray emanating in S from which we measure angles.

Fig. 1

The support functions p and q of a strictly convex compact set K

In fact, for fixed $\varphi$, the orthogonal projection of K to the line $g=\{\lambda u(\varphi )\mid \lambda \in {\mathbb {R}}\}$ is a compact interval (see Fig. 2), and for its endpoint P we have

$$\begin{aligned} P=pu(\varphi )\text { with }p=\max \{ \langle X,u(\varphi )\rangle \mid X\in K \}. \end{aligned}$$

Since K is strictly convex, $p=\langle Z,u(\varphi )\rangle$ for a unique $Z\in K$. Hence, by choosing $p(\varphi )=p$, and $q(\varphi )$ as the oriented distance of Z and P we have indeed

$$\begin{aligned} Z=z(\varphi )=p(\varphi )u(\varphi )+q(\varphi )u'(\varphi ). \end{aligned}$$

Fig. 2

Existence and uniqueness of the support functions

The connection between the regularity of the boundary curve $\partial K$ and the support functions is described in the following lemma. Note that here we need that K is strongly convex.

Lemma 2.1

Let K be a strongly convex compact set with $C^n$ boundary $\partial K$, $n\ge 2$. Then $\partial K$ can be parametrized by $\varphi \mapsto z(\varphi )=p(\varphi )u(\varphi )+p'(\varphi )u'(\varphi )$, where $p\in C^n(S^1,{\mathbb {R}}^2)$.

This result is remarkable in that p as a function of arc length s along $\partial K$ instead of $\varphi$ is only in $C^{n-1}$ in general.

Proof

Let $\gamma$ be a $C^n$ arc length parametrization of $\partial K$ and let $J=\left( {\begin{matrix}0&{}-1\\ 1&{}0\end{matrix}}\right)$. Observe that $\{-J\dot{\gamma }(s),\dot{\gamma }(s)\}$ forms an orthonormal basis of ${\mathbb {R}}^2$ for every s, where the dot indicates the derivative with respect to arc length. Hence we may write

$$\begin{aligned} \gamma (s)=-{p(s)}J\dot{\gamma }(s)+{q(s)}\dot{\gamma }(s), \end{aligned}$$

(2.1)

where

$$\begin{aligned} {p(s)}= & {} -\langle \gamma (s),J\dot{\gamma }(s)\rangle \in C^{n-1}\nonumber \\ {q(s)}= & {} \,\, \langle \gamma (s),\dot{\gamma }(s)\rangle \in C^{n-1}. \end{aligned}$$

See Fig. 3. It holds that $\varphi (s) = \arg \dot{\gamma }(s) - \frac{\pi }{2}=-\arctan \left( \frac{\dot{\gamma }_1(s)}{\dot{\gamma }_2(s)}\right)$ is of class $C^{n-1}$. Hence $\varphi \mapsto q(s(\varphi ))$ is of class $C^{n-1}$ and

$$\begin{aligned} \frac{\mathrm d\varphi }{\mathrm ds} = - \frac{1}{1+\left( \frac{\dot{\gamma }_1}{\dot{\gamma }_2}\right) ^2} \cdot \frac{\ddot{\gamma }_1\dot{\gamma }_2-\dot{\gamma }_1\ddot{\gamma }_2}{\dot{\gamma }_2^2} = -\frac{\ddot{\gamma }_1\dot{\gamma }_2-\dot{\gamma }_1\ddot{\gamma }_2}{\dot{\gamma }_1^2+\dot{\gamma }_2^2} = -\langle \dot{\gamma },J\ddot{\gamma }\rangle . \end{aligned}$$

(2.2)

We now show that the derivative $(p\circ s)'(\varphi ) = (q\circ s)(\varphi )$ which implies that $\varphi \mapsto p(s(\varphi ))$ is of class $C^n$: Indeed we have

$$\begin{aligned} (p\circ s)'(\varphi )= & {} -\frac{\mathrm d}{\mathrm d\varphi }\Big \langle \gamma (s(\varphi )),J\dot{\gamma }(s(\varphi ))\Big \rangle \\= & {} -\Big \langle \dot{\gamma }(s(\varphi )),J\dot{\gamma }(s(\varphi ))\Big \rangle \frac{\mathrm ds}{\mathrm d\varphi } - \Big \langle \gamma (s(\varphi )),J\ddot{\gamma }(s(\varphi ))\Big \rangle \frac{\mathrm ds}{\mathrm d\varphi }\\&{\mathop {=}\limits ^{(2.2)}}&\frac{\langle \gamma (s(\varphi )),J\ddot{\gamma }(s(\varphi ))\rangle }{\langle \dot{\gamma }(s(\varphi )),J\ddot{\gamma }(s(\varphi ))\rangle } \\= & {} \Big \langle \gamma (s(\varphi )),\dot{\gamma }(s(\varphi ))\Big \rangle = (q\circ s)(\varphi ), \end{aligned}$$

where we have used $J\ddot{\gamma }\parallel \dot{\gamma }$ in the last line. $\square$

Fig. 3

Parametrization by arc length

Corollary 2.2

Let K be a strongly convex compact set with $C^n$ boundary $\partial K$, $n\ge 2$. If $\partial K$ is parametrized by $z(\varphi ) = p(\varphi )u(\varphi ) + p'(\varphi )u'(\varphi )$, then $z'(\varphi )=u'(\varphi )\rho (\varphi )$, where $\rho (\varphi ) = p(\varphi ) + p''(\varphi )$ is the radius of curvature of $\partial K$ in $z(\varphi )$.

Proof

It follows from Lemma 2.1 that p is of class $C^n$. First, by direct calculation, we see that $z'=(p+p'')u'$, because $u''=-u$. If $n\ge 3$, we compute $z'' = (p + p'')u'' + (p'+p''')u'$. Since the radius of curvature $\rho$ is the projection of $z''$ onto $u''$ we obtain the desired result. If $n=2$ we consider again a parametrization $\gamma$ of $\partial K$ by arc length and use $\rho \ddot{\gamma }= J\dot{\gamma }$ and $J^2=-{\text {id}}$ to compute by (2.1)

$$\begin{aligned} \dot{\gamma }= & {} -pJ\ddot{\gamma }- \dot{p}J\dot{\gamma }+ q\ddot{\gamma }+ \dot{q}\dot{\gamma }\\= & {} \frac{p}{\rho }\dot{\gamma }- \dot{p}J\dot{\gamma }+ \frac{q}{\rho }J\dot{\gamma }+ \dot{q}\dot{\gamma }\\= & {} \left( \frac{p}{\rho }+\dot{q}\right) \dot{\gamma }+ \left( \frac{q}{\rho }-\dot{p}\right) J\dot{\gamma }. \end{aligned}$$

Hence we have $\frac{p}{\rho }+\dot{q}\equiv 1$ and $\frac{q}{\rho }-\dot{p}\equiv 0$. Using $\dot{q} = 1 - \frac{p}{\rho }$ we find

$$\begin{aligned} \begin{aligned} p + p''&= p + q' = p + \dot{q} \cdot \frac{\mathrm ds}{\mathrm d\varphi } = p+\frac{1-\frac{p}{\rho }}{-\langle \dot{\gamma },J\ddot{\gamma }\rangle } = p+\frac{1-\frac{p}{\rho }}{\frac{1}{\rho }\langle \dot{\gamma },\dot{\gamma }\rangle } = \rho . \end{aligned} \end{aligned}$$

$\square$

We will now collect a few expressions for relevant geometric quantities in terms of the parametrization for $\partial K$ from Lemma 2.1: First of all the arc length $s(\varphi )$ of $z|_{[0,\varphi ]}$ is given by

$$\begin{aligned} s(\varphi ) = \int _0^\varphi |z'|\,\mathrm d\phi = \int _0^\varphi (p+p'')\,\mathrm d\phi = \int _0^\varphi p\,\mathrm d\phi + p'(\varphi )-p'(0) \end{aligned}$$

(2.3)

and hence the perimeter of K is

$$\begin{aligned} s(2\pi ) = \int _0^{2\pi } p\,\mathrm d\varphi =:L. \end{aligned}$$

The center of mass of the curve $\partial K$ is given by

$$\begin{aligned} \frac{1}{L}\int _0^{2\pi } z |z'|\,\mathrm d\varphi = \frac{1}{L}\int _0^{2\pi }(pu+p'u')(p+p'')\,\mathrm d\varphi = \frac{1}{L}\int _0^{2\pi }\left( p^2-\frac{p'^2}{2}\right) u\,\mathrm d\varphi , \end{aligned}$$

where we have integrated by parts. Similarly, the area A and the centroid O of K are given by

$$\begin{aligned} A=\frac{1}{2}\int _0^{2\pi }(p^2-p'^2)\,\mathrm d\varphi ,\quad \text {and}\quad O=\frac{1}{3A}\int _0^{2\pi }(pu+p'u')p(p+p'')\,\mathrm d\varphi . \end{aligned}$$

3 The Evolute of $\varvec{\partial K}$

Let K be a strongly convex set of class $C^2$. Then, the evolute of $\partial K$ is given by

$$\begin{aligned} e(\varphi )= & {} z(\varphi )-\rho (\varphi )u(\varphi )\nonumber \\= & {} z(\varphi ) + (p(\varphi )+p''(\varphi ))u''(\varphi )\nonumber \\= & {} p(\varphi )u(\varphi ) + p'(\varphi )u'(\varphi )-(p(\varphi )+p''(\varphi ))u(\varphi ) \nonumber \\= & {} p'(\varphi )u'(\varphi )-p''(\varphi )u(\varphi ). \end{aligned}$$

(3.1)

Thus, the evolute is obtained from the original curve $\partial K$ by replacing its support function p by $p'$ and a rotation about $90^\circ$. Formula (3.1) shows that all parallel curves of $\partial K$, which have support function $p + \text {constant}$, have the same evolute as K.

3.1 Curves of Constant Width

Suppose that K is a strongly convex set with $C^2$-boundary $\partial K$ and assume in addition that $\partial K$ is a curve of constant width $d>0$. Then $\partial K$ can be parametrized by a support function p that satisfies $p(\varphi )+p(\varphi + \pi )\equiv d$. This equation implies that $p^{(k)}(\varphi )=-p^{(k)}(\varphi +\pi )$ for $k=1,2$, and it follows for the evolute e of $\partial K$

$$\begin{aligned} \begin{aligned} e(\varphi +\pi )&= p'(\varphi +\pi )\overbrace{u'(\varphi +\pi )}^{=-u'(\varphi )}-p''(\varphi +\pi )\overbrace{u(\varphi +\pi )}^{=-u(\varphi )}\\&= p'(\varphi )u'(\varphi )-p''(\varphi )u(\varphi )\\&= e(\varphi ). \end{aligned} \end{aligned}$$

Hence $e:S^1\rightarrow {\mathbb {R}}^2$ is $\pi$-periodic. This means that the evolute of a curve of constant width is traversed twice.

3.2 Cusps of the Evolute

Even if $\partial K$ is a smooth regular curve, its evolute has necessarily at least four singular points (cusps). The situation is described in the following lemma:

Lemma 3.1

Let K be strongly convex and compact with $\partial K$ of class $C^3$ parametrized by $\varphi \mapsto z(\varphi )=p(\varphi )u(\varphi )+p'(\varphi )u'(\varphi )$. We assume that the curvature of $\partial K$ has only finitely many stationary points. Then, the evolute of $\partial K$, given by $\varphi \mapsto e(\varphi )=p'(\varphi )u'(\varphi )-p''(\varphi )u(\varphi )$, is regular and of class $C^2$ except for points where the radius of curvature $\rho$ of $\partial K$ is stationary. More precisely:

• If $\rho$ has a local minimum in $\varphi _0$, then e has a cusp in $\varphi _0$ pointing toward the point $z(\varphi _0)$ (see Fig. 4).

• If $\rho$ has a local maximum in $\varphi _0$, then e has a cusp in $\varphi _0$ pointing away from the point $z(\varphi _0)$ (see Fig. 4).

• If $\rho$ has a saddle point in $\varphi _0$, then e is $C^1$ in $\varphi _0$.

Remarks

• By the four-vertex theorem (see Mukhopadhyaya 1909, Kneser 1912 or Osserman 1985), it follows that the evolute of $\partial K$ has at least four cusps. Since maxima and minima alternate, the number of cusps is always even.

• Note that the $C^2$-regularity of e is not evident, since the parametrization of e with respect to $\varphi$ is obviously only $C^1$ in general.

• The connection between the cusps of the evolute and strict local extrema of the base curve has first been observed by Light (1919).

Proof

First of all, note that

$$\begin{aligned} z' = \rho u' \text {\quad and\quad } e'= -\rho 'u \end{aligned}$$

which shows that $\langle z',e'\rangle = 0$. Suppose now, that $\rho '(\varphi _0)=0$.

• 1. case: $\rho$ has a local minimum in $\varphi _0$. Then

  $$\begin{aligned} \lim _{\varphi \nearrow \varphi _0}\frac{e'(\varphi )}{\Vert e'(\varphi )\Vert }=u(\varphi _0) \text {\quad and\quad } \lim _{\varphi \searrow \varphi _0}\frac{e'(\varphi )}{\Vert e'(\varphi )\Vert }=-u(\varphi _0). \end{aligned}$$

• 2. case: $\rho$ has a local maximum in $\varphi _0$. Then

  $$\begin{aligned} \lim _{\varphi \nearrow \varphi _0}\frac{e'(\varphi )}{\Vert e'(\varphi )\Vert }=-u(\varphi _0) \text {\quad and\quad } \lim _{\varphi \searrow \varphi _0}\frac{e'(\varphi )}{\Vert e'(\varphi )\Vert }=u(\varphi _0). \end{aligned}$$

• 3. case: $\rho$ has a saddle point in $\varphi _0$, i.e., $\rho '$ does not change sign in $\varphi _0$. Then $\lim _{\varphi \rightarrow \varphi _0}\frac{e'(\varphi )}{\Vert e'(\varphi )\Vert }$ exists, and e is $C^1$ in $\varphi _0$.

To check the regularity of the evolute, we interpret the curve locally as a graph of a function $x_2(x_1)$ or $x_1(x_2)$. Then, by the chain rule, we have for $x_1(x_2)$

$$\begin{aligned} \frac{\mathrm dx_2}{\mathrm dx_1}(\varphi )=\frac{\frac{\mathrm dz_2(\varphi )}{\mathrm d\varphi }}{\frac{\mathrm dz_1(\varphi )}{\mathrm d\varphi }}=\tan (\varphi ) \end{aligned}$$

and

$$\begin{aligned} \frac{\mathrm d^2x_2}{\mathrm dx_1^2}(\varphi )=\frac{\frac{\mathrm d\tan (\varphi )}{\mathrm d\varphi }}{\frac{\mathrm dz_1(\varphi )}{\mathrm d\varphi }}=-\frac{1}{\rho '(\varphi )\cos ^3(\varphi )}. \end{aligned}$$

The case $x_1(x_2)$ is similar. Since $\rho '$ is $C^0$, we conclude that locally, in points $\varphi$ where $\rho '(\varphi )\ne 0$, the curve e is $C^2$. $\square$

Corollary 3.2

If we count the arc length of the evolute e between two cusps alternating positive and negative, the resulting sum vanishes (see Fig. 4).

Proof

The factor $\rho '$ in $e'= -\rho 'u$ changes its sign in every cusp. The length of e is

$$\begin{aligned} \int _0^{2\pi }\Vert e'\Vert \, \mathrm d\varphi = \int _0^{2\pi }|\rho '|\, \mathrm d\varphi \end{aligned}$$

and hence the alternating sum of the lengths between cusps equals

$$\begin{aligned} \int _0^{2\pi }\rho '\, \mathrm d\varphi =0. \end{aligned}$$

$\square$

Fig. 4

The blue squares are maxima of the curvature of z, and the round magenta points are minima. The sum of the lengths of the red arcs of the evolute e equals the sum of lengths of the green arcs. We also refer the reader to (Fuchs and Tabachnikov 2007, Lecture 10) which gives a very nice geometrical view on the topic of evolutes

3.3 Equilibria

We now choose a measure $\mu$ with support in the compact convex set $K\subset {\mathbb {R}}^2$ which models the density of a distribution of mass. The center of mass of $\mu$ is a point $O\in K$. Vice versa, given a point $O\in K$, there is a measure supported in K with center of mass O (e.g., a Dirac mass in O). In a physical model, this scenario can be realized by fixing a heavy lead ball in the point O on a thin, lightweight plate which has shape K. If the density in K is constant the center of mass is usually called the centroid. If we allow signed measures, the center of mass can be any point O in ${\mathbb {R}}^2$, and vice versa, given an arbitrary point $O\in {\mathbb {R}}^2$, there is a signed measure supported in K with center of mass in O. A physical model can be manufactured be glueing a long, thin batten to K joining K to a point $O\notin K$ and to fix a heavy lead ball at its far end in O.

We are interested in the following question: Suppose K is equipped with a center of mass O, as discussed above, and is rolling along a horizontal straight line $\ell$. Horizontal means that $\ell$ is perpendicular to the direction of the gravitational force g. What can we say about the number of equilibria with respect to O in terms of the geometry of $\partial K$? In particular, how many equilibrium positions are there?

Physically, an equilibrium position is characterized by the fact that the vector v from the center of mass O of K to the contact point of $\partial K$ with the supporting straight line $\ell$ is parallel to the gravitational force. This follows from Varignon’s theorem of the resulting torque and the principle of angular momentum. In case of a horizontal supporting line $\ell$, this means that v is orthogonal to $\ell$. The equilibrium is stable, if the potential energy of K (i.e., of its center of mass) has a strict local minimum with respect to the direction $-g$, and it is unstable, if the potential energy has a strict local maximum. This translates into the following definition:

Definition 3.3

Let K be strongly convex and compact with $\partial K$ of class $C^3$ parametrized by $\varphi \mapsto z(\varphi )=p(\varphi )u(\varphi )+p'(\varphi )u'(\varphi )$, where the origin is chosen in the center of mass O of K. Then, a horizontal equilibrium position with respect to O is a point $z(\varphi _0)\in \partial K$ such that $p'(\varphi _0)=0$. The equilibrium is stable if p has a strict local minimum in $\varphi _0$, and unstable if p has a strict local maximum in $\varphi _0$.

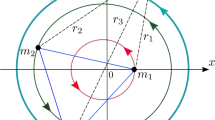
A horizontal equilibrium $z\in \partial K$ is therefore a point where the tangent at z and the line joining z and the center of mass are perpendicular. Figure 5 shows a shape K which has one stable and one unstable horizontal equilibrium with respect to the center of mass O. We start by investigating the number of equilibria for the special case of the centroid O of a homogeneous body.

Fig. 5

K rolling along the horizontal line $\ell$. The dashed line is the trace of the red center of mass O. The dotted red line emanating from O corresponds to the angle $\varphi =0$. Stable equilibrium on the left (p has a strict local minimum), non-equilibrium in the middle ($p'(\varphi )\ne 0$), unstable equilibrium on the right (p has a strict local maximum).

Proposition 3.4

Let K be a convex and compact set with $C^1$ boundary. Then K has at least four horizontal equilibria with respect to its centroid.

Proof

Suppose the boundary $\partial K$ is given in polar coordinates as $r:S^1\rightarrow (0,\infty ), \varphi \mapsto r(\varphi )$, such that the origin is the centroid of K. The tangent in a point $z(\varphi )=r(\varphi )(\cos (\varphi ),\sin (\varphi ))^\top \in \partial K$ is perpendicular to the line joining $z(\varphi )$ with the origin if and only if $r'(\varphi )=0$. So we have to show that $r'$ has at least four zeros on $[0,2\pi )$. The condition that the centroid is at the origin leads upon integrating by parts to

$$\begin{aligned} \int _0^{2\pi }r^2(\varphi )r'(\varphi )\begin{pmatrix}\sin (\varphi )\\ -\cos (\varphi )\end{pmatrix}\,\mathrm d\varphi = 0. \end{aligned}$$

(3.2)

This implies that (3.2) remains valid if $g(\varphi ) = r^2(\varphi )r'(\varphi )$ is replaced by any translation $\varphi \mapsto g(\varphi -c)$, where $c\in {\mathbb {R}}$. We will now assume that there is no interval on which r is constant; otherwise, there is nothing to show. If $r'$ has only two zeros, then $r'>0$ on an interval of length $l\in (0,\frac{\pi }{2}]$, or $r'<0$ on an interval of length $l\in (0,\frac{\pi }{2}]$. We only discuss the first case (the second case is analogue). By a suitable translation we may assume that $r'>0$ on $(a,\pi -a)$, where $0\le a <\pi /2$. By periodicity of $r^3$, we find

$$\begin{aligned} \int _0^{2\pi }g(\varphi )\,\mathrm d\varphi = 0, \end{aligned}$$

and therefore

$$\begin{aligned} \int _{0}^{\pi }g(\varphi )\,\mathrm d\varphi > 0. \end{aligned}$$

It follows that

$$\begin{aligned} \begin{aligned} \int _0^{\pi }g(\varphi )\sin (\varphi )\,\mathrm d\varphi >\sin (a)\int _{0}^{\pi }g(\varphi )\,\mathrm d\varphi \ge 0. \end{aligned}\end{aligned}$$

(3.3)

On the other hand

$$\begin{aligned} \int _{\pi }^{2\pi }g(\varphi )\sin (\varphi )\,\mathrm d\varphi >0, \end{aligned}$$

(3.4)

and (3.3) and (3.4) contradict (3.2). Observe that the argument goes through if $r'$ has a third zero either in $(a,\pi -a)$ or in $[0,2\pi )\setminus (a,\pi -a)$ and hence we conclude that $r'$ must have at least 4 zeros as claimed. $\square$

The previous proposition already appears in Domokos et al. (1994) and could also be obtained using the Sturm–Hurwitz theorem (Theorem 5.16 in Tabachnikov (2005)).

The next theorem reveals a connection between the number of equilibrium points of K with respect to an arbitrary point O which is not a point of the evolute of $\partial K$ and the winding number of the evolute of $\partial K$ around O.

Theorem 3.5

Let K be a strongly convex compact set with $C^3$-boundary $\partial K$ and O a point in the plane. Suppose that O is not a point of the evolute of $\partial K$. Then the number n of horizontal equilibria of K with respect to O is given by

$$\begin{aligned} n=2-2m, \end{aligned}$$

where $0\ge m\in {\mathbb {Z}}$ is the winding number of the evolute of $\partial K$ with respect to O.

Proof

We consider the parametrization $z(\varphi ) = p(\varphi )u(\varphi ) + p'(\varphi )u'(\varphi )$ of $\partial K$ with origin O. The function p is of class $C^3$ by Lemma 2.1, and hence, $p'$ is of class $C^2$. The evolute e of $\partial K$ is then given by $e(\varphi )=p'(\varphi )u'(\varphi )-p''(\varphi )u(\varphi )$. In particular, since O is not a point on e, $p'$ can only have simple zeros, and by periodicity of p, the number n of zeros of $p'$ is at least 2. Then according to Lemma 1.1 in Hungerbühler and Wasem (2018), n and hence the number of horizontal equilibria of K is given by

$$\begin{aligned} n = \frac{1}{\pi }\int _0^{2\pi }\frac{p''(\varphi )^2-p'(\varphi )p'''(\varphi )}{p'(\varphi )^2+p''(\varphi )^2}\,\mathrm d\varphi . \end{aligned}$$

(3.5)

Hence n equals twice the winding number of the curve $\varphi \mapsto (p''(\varphi ),p'(\varphi ))$ with respect to O. The evolute can be rewritten as follows:

$$\begin{aligned} e(\varphi ) = \underbrace{\begin{pmatrix}\cos (\varphi ) &{} -\sin (\varphi ) \\ \sin (\varphi ) &{} \cos (\varphi )\end{pmatrix}}_{=:R(\varphi )}\begin{pmatrix}-p''(\varphi )\\ p'(\varphi )\end{pmatrix}. \end{aligned}$$

Since $R(\varphi )$ causes one counterclockwise rotation around the origin and since the winding number of $\varphi \mapsto (-p''(\varphi ),p'(\varphi ))$ equals $-\frac{n}{2}$, the winding number m of the evolute is given by $m=1-\frac{n}{2}$. The claim follows immediately. $\square$

Remark

According to Sect. 3.1 the number of equilibria of a curve of constant width with respect to a point not on the evolute is 2 modulo 4.

The foregoing proof can be obtained by a direct computation which remains valid in a more general setting: Since e is a piecewise $C^2$ immersion under the assumptions of Lemma 3.1, the winding number of e with respect to O is given (see Proposition 2.3 in Hungerbühler and Wasem (2019)) by

$$\begin{aligned} \begin{aligned} m = \frac{1}{2\pi }\int _0^{2\pi }\frac{\langle Je,e'\rangle }{\Vert e\Vert ^2}\,\mathrm d\varphi = \frac{1}{2\pi }\int _0^{2\pi }\frac{p'(p'+p''')}{p'^2+p''^2}\,\mathrm d\varphi \end{aligned} \end{aligned}$$

(3.6)

and the corresponding integrand is bounded. In the case of simple zeros of $p'$ as discussed in Theorem 3.5, the integrand is even continuous. Then it holds that

$$\begin{aligned} \begin{aligned} -2m+2&{\mathop {=}\limits ^{(3.6)}} \frac{1}{\pi }\int _0^{2\pi }\frac{-p'(p'+p''')}{p'^2+p''^2}\,\mathrm d\varphi + \frac{1}{\pi }\int _0^{2\pi }\frac{p'^2+p''^2}{p'^2+p''^2}\,\mathrm d\varphi \\&= \frac{1}{\pi }\int _0^{2\pi }\frac{p''^2-p'p'''}{p'^2+p''^2}\,\mathrm d\varphi {\mathop {=}\limits ^{(3.5)}} n. \end{aligned}\end{aligned}$$

(3.7)

The last equality of this computation also holds true by Theorem 2.4 in Hungerbühler and Wasem (2018) in a more general setting: In particular, the computation remains valid if $p'$ has zeros of order at most 2 and the relevant integrands are continuous by the following lemma:

Lemma 3.6

If $p\in C^k$, $k\ge 3$ and $p'$ only has zeros of order at most $k-1$, then the integrands in (3.7) are continuous.

Proof

It suffices to show the continuity of the integrands in 0 provided $\varphi = 0$ is a zero of $p'$ of multiplicity $k-1$. Using Proposition 2.5 in Hungerbühler and Wasem (2018) we find by Taylor expansion

$$\begin{aligned} p'(\varphi )&= \left( \frac{p^{(k)}(0)}{(k-1)!}+r_0(\varphi )\right) \varphi ^{k-1},\\ p''(\varphi )&= \left( \frac{p^{(k)}(0)}{(k-2)!}+r_1(\varphi )\right) \varphi ^{k-2},\\ p'''(\varphi )&= \left( \frac{p^{(k)}(0)}{(k-3)!}+r_2(\varphi )\right) \varphi ^{k-3},\\ \end{aligned}$$

where $r_i$ are continuous functions with $\lim _{\varphi \rightarrow 0}r_i(\varphi ) = 0$. Then

$$\begin{aligned} \lim _{\varphi \rightarrow 0}\frac{p''(\varphi )^2-p'(\varphi )p'''(\varphi )}{p'(\varphi )^2+p''(\varphi )^2} = \frac{1}{k-1} \end{aligned}$$

and

$$\begin{aligned} \lim _{\varphi \rightarrow 0}\frac{p'(\varphi )(p'(\varphi )+p'''(\varphi ))}{p'(\varphi )^2+p''(\varphi )^2} = \frac{k-2}{k-1}. \end{aligned}$$

$\square$

In order to prove Theorem 1.1 it remains to discuss the cases where the center of mass O of K is possibly a point of the evolute. We continue to assume, as in Lemma 3.1, that the radius of curvature of $\partial K$ has only finitely many stationary points and $\partial K$ is of class $C^3$. We will distinguish two cases:

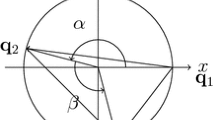
• 1. If O is a regular point of the evolute of $\partial K$, then whenever $e(\varphi _0)=0$, it holds that $e'(\varphi _0)\ne 0$. This corresponds to the two black points in Fig. 6 which are labeled by 3 and 4. Since $e'=-\rho 'u$ this means that $\varphi _0$ is not a stationary point of $\rho$ and hence $p'''(\varphi )\ne 0$. Therefore the set $e^{-1}(0)$ consists of zeros of $p'$ of multiplicity 2, and we conclude that $p'$ has zeros of order at most 2. In this case, computation (3.7) remains valid by Proposition 2.3 in Hungerbühler and Wasem (2019) and Theorem 2.4 in Hungerbühler and Wasem (2018) and the integrands are continuous according to Lemma 3.6. Proposition 2.2 in Hungerbühler and Wasem (2019) tells us (since the angles in O are equal to $\pi$) that $2m\in {\mathbb {Z}}$ and we conclude that $n=2-2m$, but m might be half-integer valued.

• 2. If O is a singular point of the evolute of $\partial K$, there exist values $\varphi _0$ such that $e(\varphi _0)=e'(\varphi _0)=0$. See, e.g., the black point in Fig. 6 which is labeled by 2. In this case, $\varphi _0$ is a stationary point of $\rho$ which is either a saddle point or a cusp of e according to Lemma 3.1. Since $e=p'u'-p''u$ and $e'=-(p'+p''')u$ we conclude that such points are zeros of $p'$ of order at least 3. Computation (3.7) remains valid in this case if we can show that $p'$ is an admissible function in the sense of Definition 2.4 in Hungerbühler and Wasem (2018). More precisely, the first equality is then justified by Proposition 2.3 in Hungerbühler and Wasem (2019) and the last one by Theorem 2.4 in Hungerbühler and Wasem (2018). According to Proposition 2.2 in Hungerbühler and Wasem (2019) (since the angles in O are 0, $\pi$ or $2\pi$) we find again $2m\in {\mathbb {Z}}$. Since $p'\in C^2$, it suffices to show that the zeros of $p'$ are admissible in the sense of Definition 2.1 in Hungerbühler and Wasem (2018), i.e., we have to show that whenever $p'(\varphi _0)=0$, then

  $$\begin{aligned} \lim _{\varphi \nearrow \varphi _0}\frac{p''(\varphi )}{p'(\varphi )}=-\infty \text { and }\lim _{\varphi \searrow \varphi _0}\frac{p''(\varphi )}{p'(\varphi )}=+\infty . \end{aligned}$$

  Let $\varphi _0=0$ be a zero of $p'$. If this zero is of multiplicity one or two, then the admissibility follows immediately from the 5th point in the remark after Definition 2.1 in Hungerbühler and Wasem (2018). In the present case we assume that $p'(0)=p''(0)=p'''(0)=0$. In this case, $\rho (0)=p(0)$ and $\rho '(0)=0$ and we can solve the ODE $\rho =p+p''$ with initial value $p'(0)=0$ in order to obtain

  $$\begin{aligned} p(\varphi )= & {} \int _0^\varphi \sin (\varphi -t)\rho (t)\,\mathrm dt+p(0)\cos (\varphi )\\= & {} \int _0^\varphi \sin (\varphi -t)(\rho (t)-\rho (0))\,\mathrm dt+\rho (0). \end{aligned}$$

  Upon integrating by parts (since $\rho$ is of class $C^1$) we get the formulas

  $$\begin{aligned} \begin{aligned} p(\varphi )&= \rho (\varphi ) - \int _0^{\varphi }\cos (\varphi -t)\rho '(t)\,\mathrm dt,\\ p'(\varphi )&= \int _0^{\varphi }\sin (\varphi -t)\rho '(t)\,\mathrm dt,\\ p''(\varphi )&= \int _0^{\varphi }\cos (\varphi -t)\rho '(t)\,\mathrm dt. \end{aligned} \end{aligned}$$

  Since the number of zeros of $\rho '$ is finite, we can consider the case where, e.g., $\rho ' > 0$ on $(0,\varphi )$ provided $\varphi >0$ is small enough. Then

  $$\begin{aligned} p''(\varphi ) \ge \int _0^\varphi (1-(\varphi -t)^2)\rho '(t)\,\mathrm dt\ge (1-\varphi ^2)\int _0^{\varphi }\rho '(t)\,\mathrm dt \end{aligned}$$

  and

  $$\begin{aligned} p'(\varphi ) \le \varphi \int _0^{\varphi }\rho '(t)\,\mathrm dt. \end{aligned}$$

  We conclude that

  $$\begin{aligned} \frac{p''(\varphi )}{p'(\varphi )}\ge \frac{1-\varphi ^2}{\varphi }{\mathop {\rightarrow }\limits ^{\varphi \searrow 0}}+\infty . \end{aligned}$$

  The remaining cases are similar, and we find

  $$\begin{aligned} \lim _{\varphi \nearrow 0}\frac{p''(\varphi )}{p'(\varphi )}=-\infty \text { and }\lim _{\varphi \searrow 0}\frac{p''(\varphi )}{p'(\varphi )}=+\infty \end{aligned}$$

  and therefore, the zeros of $p'$ are admissible.

This concludes the proof of Theorem 1.1.

Remarks

• 1. According to Sect. 3.1 the number of equilibria of a curve of constant width with respect to a point on the evolute is even.

• 2. It follows from the conclusion of Theorem 1.1 that the number of zeros of $p'$ is finite. This also follows a priori from the fact that the number of extrema of $\rho$ is finite. Indeed, if $p'(\varphi _0)=0$, then the tangent of z in $\varphi _0$ is perpendicular to $z(\varphi _0)$ and $z(\varphi _0)$ is parallel to $e'(\varphi _0)$. Since every arc of the evolute e is convex, there are at most 2 tangents to such an arc through $z(\varphi _0)$. Since the curvature of $\partial K$ has only finitely many stationary points, e is made of only finitely many arcs and there are only twice as many zeros of $p'$ as there are extrema of $\rho$.

• 3. For points on the evolute, one can formulate the result alternatively as follows: If the center of mass O lies on the evolute, then the number of equilibrium positions with respect to O is the average of the number of equilibrium positions in the neighboring areas defined by the evolute, where each neighboring area is weighted by its angle in O. For example, the number of equilibrium positions in the black points in Fig. 6 can be obtained in this way: $\underline{3}$ is the average of 2 and 4, $\underline{4}$ is the average of 4 and 4 (with equal weight) and 2 and 6 (with equal weight), and $\underline{2}$ is the average of 2 (with full weight) and 4 (with weight zero).

Fig. 6

The number of equilibria with respect to a given center of mass is 2 minus twice the winding number of the evolute. The number of equilibria is indicated in the figure for areas bounded by the evolute in red and for selected black points on the evolute by underlined numbers.

4 Oblique Equilibria

Here we investigate the equilibrium positons of K with respect to a center of mass O on an oblique line $\ell$ with angle of inclination $\alpha \ne 0$. The situation is shown in Fig. 7. We can immediately read off the condition for an equilibrium position in terms of the support function p: An equilibrium point is characterized by the condition

$$\begin{aligned} p'(\varphi ) = \tan (\alpha )p(\varphi ), \end{aligned}$$

(4.1)

or, if $p(\varphi )\ne 0$, equivalently by

$$\begin{aligned} \tan (\alpha )=\frac{p'(\varphi )}{p(\varphi )}=(\ln |p(\varphi )|)'. \end{aligned}$$

In particular, the number $n_\alpha$ of solutions of (4.1) on $[0,2\pi )$ corresponds to the number of equilibrium points. This number varies with $\alpha$: See Fig. 8. From a physical point of view it seems reasonable to conjecture that the number $n_\alpha$ of equilibria decreases monotonically with $\alpha \in [0,\pi /2)$: Indeed you destroy more and more equilibria as you increase the angle $\alpha$. However, this is surprisingly not always the case: In general $n_\alpha$ is not monotonically decreasing with $\alpha$ (see point 5 in Proposition 4.1).

Fig. 7

Equilibrium position on an oblique line $\ell$

If we denote by $v=\begin{pmatrix}\cos (\alpha )\\ sin(\alpha )\end{pmatrix}$ the vector in the downhill direction of $\ell$ and by $s(\varphi )$ the arclength on $\partial K$ corresponding to the parameter interval $[0,\varphi ]$ we can express the position of O in coordinates with respect to fixed horizontal and vertical axis as

$$\begin{aligned} O(\varphi )=\begin{pmatrix}O_1(\varphi )\\ O_2(\varphi )\end{pmatrix}=(s(\varphi )-p'(\varphi ))v+ p(\varphi )v^\bot , \end{aligned}$$

where $v^\bot =\begin{pmatrix}\sin (\alpha )\\ \cos (\alpha )\end{pmatrix}$. An equilibrium corresponds to a point with stationary potential energy, i.e., $O_2'(\varphi )=0$. A sufficient condition for an equilibrium to be stable is $O_2''(\varphi )>0$, corresponding to a strict local minimum of the potential energy. Similarly, $O_2''(\varphi )<0$ implies that an equilibrium is unstable. According to (2.3) we have

$$\begin{aligned}&O_2'(\varphi )=p'(\varphi )\cos (\alpha )-p(\varphi )\sin (\alpha ),\text { and }\\&O_2''(\varphi )=p''(\varphi )\cos (\alpha )-p'(\varphi )\sin (\alpha ). \end{aligned}$$

Thus, for an equilibrium $O_2'(\varphi )=0$, we obtain

• if $p''(\varphi )>p(\varphi )\tan ^2(\alpha )$, then $\varphi$ is a stable equilibrium,

• if $p''(\varphi )<p(\varphi )\tan ^2(\alpha )$, $\varphi$ is an unstable equilibrium.

In particular a center of mass O on $\partial K$ is always a stable equilibrium.

Fig. 8

Number of equilibrium points with respect to $\alpha$. The value $\tan (\alpha )$ is drawn for several values of $\alpha$

Interesting observations are

Proposition 4.1

• 1. There are shapes K which have oblique equilibrium points with respect to the centroid for angle of inclination $\alpha$, but no equilibrium for angle $-\alpha$.

• 2. For all $\alpha \in (-\pi /2,\pi /2)$ there exist shapes K which have stable equilibrium positions with respect to $\alpha$ for the centroid.

• 3. For all small $\alpha > 0$ there exist shapes K which have only one metastable equilibrium, and no other equilibrium, with respect to $\alpha$ for the centroid.

• 4. For all small $\alpha > 0$ there exist shapes K which have only one stable and one unstable equilibrium with respect to $\alpha$ for the centroid.

• 5. There exist shapes K for which the number $n_\alpha$ of equilibrium positions is not monotonically decreasing for $\alpha \in [0,\pi /2)$.

Remark

Properties 3. and 4. are in sharp contrast to Proposition 3.4 for $\alpha =0$.

Proof

Consider the support function

$$\begin{aligned} p(\varphi )=3 -\tfrac{279}{8570} \sin (\varphi ) + \tfrac{36}{857} \cos (\varphi )+ \tfrac{3}{10} \bigl (\sin (2 \varphi ) + \cos (2 \varphi )\bigr ) + \tfrac{1}{5}\cos (3 \varphi ) . \end{aligned}$$

One can check that $p(\varphi )+p''(\varphi )>0$ and that $\max (\ln p)'+\min (\ln p)'>0$. Moreover, the centroid is at the origin. So, for $\alpha$ such that $-\min (\ln p)'<\tan (\alpha )<\max (\ln p)'$ the shape with this support function p has the property mentioned in the first part of the proposition.

For the second part, observe that the ellipse with half axis $a>1$ and $b=1$ has two stable and two unstable equilibria with respect to its center for every angle $\alpha <\arctan (\frac{a^2-1}{2a})$.

For part 3. and 4. let

$$\begin{aligned} p_c(\varphi ) = 3 + 3c (\cos (2 \varphi ) +\sin (2 \varphi )) + 2c\cos (3 \varphi )\\ + \tfrac{36 c^2}{9 - 43 c^2} \cos (\varphi ) - \tfrac{9 (4 - 9 c) c^2}{9 - 43 c^2} \sin (\varphi ). \end{aligned}$$

Let $c>0$ be sufficiently small, so that $z=p_cu+p_c'u'$ parametrizes the boundary of a convex body K. By construction, the centroid of K lies at the origin. One can check that the function $p_c'(\varphi )/p_c(\varphi )$ has a unique maximum for each such c. Choose $\alpha _c$ in such a way that $\tan (\alpha _c) = \max p'_c/p_c$. Then K has exactly one equilibrium for $\alpha _c$ and for a slightly smaller angle one stable and one unstable equilibrium. Since $\frac{p'_c}{p_c}$ converges uniformly to 0 for $c\searrow 0$ the claim follows.

For the last part, consider the support function

$$\begin{aligned} p(\varphi )=3+ \tfrac{15}{2602}\cos (\varphi ) -\tfrac{1}{5}\cos (3\varphi ) -\tfrac{60}{1301}\sin (\varphi )-\tfrac{1}{3}\sin (2\varphi ). \end{aligned}$$

This example is constructed in such a way, that the centroid is at the origin, $p(\varphi )+p''(\varphi )>0$, and $p'(\varphi )/p(\varphi )$ has a positive local minimum: Indeed, for $\alpha \in [0,\frac{1}{100}]$ there are 4 equilibrium positions, but for $\alpha \in [\frac{3}{100},\frac{1}{10}]$ there are 6 equilibrium positions. $\square$

In view of Theorem 1.1 it is natural to ask, if the number $n_\alpha$ of oblique equilibria with respect to angle $\alpha >0$ can be obtained as $n_{\alpha }=2-2m_{\alpha }$, where $m_\alpha$ is the winding number of the evolute of a suitable modification of $\partial K$. Consider therefore again a strongly convex and compact set K with $C^3$ boundary and such that the radius of curvature of $\partial K$ has only finitely many stationary points. Let $z=pu+p'u'$ be the usual $C^2$ parametrization of $\partial K$, and let $e=p'u'-p''u$ be the evolute of $\partial K$. Define $e_{\alpha }=e - \tan (\alpha )Jz$ and $p'_\alpha = p'-\tan (\alpha )p$. Let $p_\alpha$ be a primitive of $p'_\alpha$ with constant of integration large enough such that $p_\alpha + p''_\alpha =:\rho _\alpha >0$. In this case, $p_\alpha$ is again the support function of a curve $C_\alpha$ and the evolute of $C_\alpha$ is precisely $e_\alpha$. Note that in general, $p_\alpha$ will not be periodic and therefore $C_\alpha$ will not be closed.

Proposition 4.2

If the curvature of $C_\alpha$ admits only finitely many stationary points, then the number $n_\alpha$ of oblique equilibria of $\partial K$ with respect to $O\in {\mathbb {R}}^2$ and angle of inclination $\alpha$ is given by $n_\alpha = 2 - 2m_\alpha$, where $m_\alpha \in \frac{1}{2}{\mathbb {Z}}$ is the winding number of the evolute of $C_\alpha$ with respect to O.

Proof

Observe that $e_\alpha$ is a piecewise $C^2$ immersion, since e is piecewise $C^2$, z is of class $C^2$, and the number of zeros of $e_\alpha '$ is finite. In this case, the winding number $m_\alpha$ of $e_\alpha$ is given by

$$\begin{aligned} m_\alpha = \frac{1}{2\pi }\int _0^{2\pi }\frac{\langle Je_\alpha ,e_\alpha '\rangle }{\Vert e_\alpha \Vert ^2}\,\mathrm d\varphi \end{aligned}$$

and using $p'_{\alpha }=p'-\tan (\alpha )p$ we obtain

$$\begin{aligned} -2m_\alpha + 2 = \frac{1}{\pi }\int _0^{2\pi }\frac{{p''_{\alpha }}^2-{p'_{\alpha }} p'''_{\alpha }}{{p'_{\alpha }}^2+{p''_{\alpha }}^2}\,\mathrm d\varphi =n_\alpha , \end{aligned}$$

in analogous manner to the case where $\alpha =0$.$\square$

Remark

It is clear by definition that $e_\alpha$ diverges as $\alpha \rightarrow \pm \frac{\pi }{2}$; however, the renormalized perturbed evolute $e_\alpha /\tan (\alpha )$ converges to $-Jz$ as $\alpha \rightarrow \pm \frac{\pi }{2}$. Moreover $m_\alpha \rightarrow 1$ as $\alpha \rightarrow \pm \frac{\pi }{2}$ so that $n_{\pm \frac{\pi }{2}}=0$, as expected.