Semi-Analytical Estimates for the Orbital Stability of Earth’s Satellites

Abstract

Normal form stability estimates are a basic tool of Celestial Mechanics for characterizing the long-term stability of the orbits of natural and artificial bodies. Using high-order normal form constructions, we provide three different estimates for the orbital stability of point-mass satellites orbiting around the Earth. (i) We demonstrate the long-term stability of the semimajor axis within the framework of the $J_2$ problem, by a normal form construction eliminating the fast angle in the corresponding Hamiltonian and obtaining ${\mathcal {H}}_{J_2}$. (ii) We demonstrate the stability of the eccentricity and inclination in a secular Hamiltonian model including lunisolar perturbations (the ‘geolunisolar’ Hamiltonian ${\mathcal {H}}_\mathrm{gls}$), after a suitable reduction of the Hamiltonian to the Laplace plane. (iii) We numerically examine the convexity and steepness properties of the integrable part of the secular Hamiltonian in both the ${\mathcal {H}}_{J_2}$ and ${\mathcal {H}}_\mathrm{gls}$ models, which reflect necessary conditions for the holding of Nekhoroshev’s theorem on the exponential stability of the orbits. We find that the ${\mathcal {H}}_{J_2}$ model is non-convex, but satisfies a ‘three-jet’ condition, while the ${\mathcal {H}}_\mathrm{gls}$ model restores quasi-convexity by adding lunisolar terms in the Hamiltonian’s integrable part.

1 Introduction

One of the major goals of Celestial Mechanics is the analysis of the stability of the dynamics of celestial bodies. Knowing the behavior in time of the orbital elements of an object allows one to predict its future, in particular whether it will cross the orbit of other celestial bodies and eventually undergo collisions. When applied to artificial spacecraft and space debris orbiting around the Earth, the question of the stability becomes of crucial importance, especially in view of the problem of estimating the orbital survival times of operating satellites or space debris. It is therefore crucial to devise methods that allow to study the orbital stability of objects moving around our planet.

In this work we will not consider the complex dynamics of an artificial spacecraft, which should include the analysis of its shape, composition as well its rotational motion. We will rather consider a point-mass body around the Earth that we can identify with one of the several millions of space debris orbiting our planet. In fact, the proliferation of artificial satellites in the last decades has led to the generation of an enormous amount of space debris with different sizes, from meters down to microns, and at different altitudes. Space debris is remnants of non-operational satellites or the result of break-up events, either collisions or explosions. Since the altitude determines the contribution of the different forces acting on the object (the gravitational attraction of the Earth, its geopotential perturbation, the influence of Sun and Moon, the Solar radiation pressure, etc.), it is convenient to make a distinction in terms of the altitude. To this end, the space in the surrounding of the Earth is commonly split into three main regions: LEO (‘Low Earth Orbit’) denotes the region up to about 2000 km of altitude in which the Earth’s attraction, the geopotential and the atmospheric drag are the terms which greatly affect the dynamics of an Earth’s satellite; MEO (‘Medium Earth Orbit’) refers to the region between 2000 and 30 000 km in which the effects of Moon, Sun and Solar radiation pressure become important; GEO (‘Geosynchronous Earth Orbit’) refers to a thin ($\sim 200$ km) zone around the geostationary orbits (at 42 164 km from Earth’s center), where the satellites are in synchronous resonance with the 24-hour rotation of the Earth around its spin axis.

The huge amount of objects (up to millions) in LEO, MEO, GEO needs a careful control of their orbits and the analysis of their dynamical stability (Celletti and Galeş 2014; Celletti et al. 2017; Celletti and Galeş 2018; Celletti et al. 2020; Gkolias and Colombo 2019; Schettino et al. 2019), also in view of devising appropriate mitigation measures (see, e.g., Jenkin et al. 2019; Park et al. 2018; Choi et al. 2015). For objects in LEO, it is of crucial importance to evaluate the orbital lifetime, which is strongly affected by the atmospheric drag which provokes a decay of the orbits (King-Hele and Walker 1988; Krag et al. 2013; Liu and Wang 2000; Shute and Chiville 1966; Westerman 1963). In this work we focus on objects in MEO, GEO and beyond, thus not taking into account the dissipative effect of the atmosphere. Instead of using a propagation of the orbits to predict the stability time of the orbital elements, we propose a procedure based on analytical perturbative methods (see also Gachet et al. 2017). More precisely, via a suitably defined sequence of canonical transformations, we construct a normal form of the Hamiltonian function, which enjoys the property that one or more of the Hamiltonian’s Delaunay actions define quasi-integrals of motion (namely, integrals of the integrable part of the new Hamiltonian). Once the transformed Hamiltonian is obtained, the size of its remainder (which gives a control on the goodness of the approximation) can then be used to provide bounds on the time variations and hence the stability time of the orbital elements (semimajor axis, eccentricity, inclination) as a function of the distance of the object from the Earth. We refer to this procedure as semi-analytical, which means that it uses an analytical method, precisely normal forms, whose coefficients are calculated numerically, namely with the aid of a computer.

We consider two different models to describe the motion of the debris around the Earth. The first model takes into account only the influence of the geopotential up to the term $J_2$ of its expansion in spherical harmonics; we refer to this problem as the $J_2$ model and denote the corresponding Hamiltonian as ${\mathcal {H}}_{J_2}$, which results from truncating to a suitable power of the coordinates around reference values, and normalizing up to a suitable order, as described in Sect. 4.1. The second model, referred to as the secular ‘geolunisolar’ model (Hamiltonian ${\mathcal {H}}_\mathrm{gls}$, truncated and normalized similarly to ${\mathcal {H}}_{J_2}$, see Sects. 2.2 and 5.1 ), includes also the effects of the Moon and the Sun, placing, for simplicity, the Moon strictly on the ecliptic; this last restriction means to omit from the Hamiltonian terms corresponding to lunisolar resonances other than the ‘inclination-dependent’ ones. The latter resonances, on the other hand, are those producing the most important effects as regards orbital stability (see Celletti et al. 2020, 2017 for a review). Furthermore, instead of formally eliminating the fast angle via canonical transformations (as we do in the pure $J_2$ problem), in ${\mathcal {H}}_\mathrm{gls}$ we just take the average of the Hamiltonian with respect to all fast angles, namely, the mean anomaly of the satellite as well as the fast angles of the Moon and Sun: this averaged model allows us to focus on the satellite’s long-term dynamics (i.e., the secular one). The averaging is done in closed form and leads to formulas equivalent to those described in Kaula (1966). Furthermore, we reduce this last Hamiltonian to action-angle variables around each forced equilibrium point, which corresponds to a nonzero inclination defining the so-called Laplace plane (see Sect. 2.2).

In summary, our stability estimates are obtained according to the procedure (i)–(iii) outlined below:

• (i) Within the $J_2$ model, we make a formal elimination in the Hamiltonian of the fast angle (mean longitude); as a consequence, we get the preservation of the conjugate action variable corresponding to the semimajor axis. This allows us to compute the stability time for the semimajor axis at different altitudes, yielding stability times that increase with the altitude.

• (ii) Using ${\mathcal {H}}_\mathrm{gls}$, instead, the semimajor axis becomes a parameter (with a priori constant value), while we proceed to analyze the behavior of eccentricity and inclination. The latter is obtained using a quasi-resonant normal form, which reflects the 1:1 near-resonance of the integrable part of ${\mathcal {H}}_\mathrm{gls}$ between the frequencies of the longitude of the ascending node and the sum of the argument of perigee and the longitude of the ascending node (see Sect. 2.2.1). This means that, close to the Laplace plane, the quasi-preserved secular quantities cannot be defined neither as the eccentricity e nor the inclination i alone, but rather by the Kozai–Lidov combination ${\mathcal {I}}=1-\sqrt{1-e^2}\cos i\approx (e^2+i^2)/2$ (for e, i small). We then explore the dependence of the stability time of ${\mathcal {I}}$ on the altitude of the orbit. Our results show that the $J_2$ and lunisolar terms have an opposite effect on the time of stability as the distance from the Earth increases. As a by-product of this analysis, we also compute the so-called forced inclination (that is, the inclination of the Laplace plane), which corresponds to the shift of the secular equilibrium from a strictly equatorial orbit to an orbit with small positive initial inclination, an effect caused by the fact that the perturbing bodies (Moon and Sun) are in orbits inclined with respect to the Earth’s equator.

• (iii) Finally, as a first step toward obtaining exponential stability estimates à la Nekhoroshev (Nekhoroshev 1977), we check whether some so-called steepness conditions are satisfied for the integrable part of both Hamiltonians ${\mathcal {H}}_{J_2}$ and ${\mathcal {H}}_\mathrm{gls}$, namely whether the integrable parts are convex, quasi-convex, or satisfy the three-jet condition (see Chierchia et al. 2018 and references therein). The results show that the $J_2$ model is three-jet non-convex, while the contribution of the lunisolar terms removes the intrinsic degeneracy of the $J_2$ part and allows us to conclude that the geolunisolar model is quasi-convex. A detailed application of the non-resonant form of Nekhoroshev’s theorem in the Hamiltonian ${\mathcal {H}}_\mathrm{gls}$ is the subject of an independent paper (see Celletti et al. 2021).

Summarizing, the previous strategy allows us to obtain three different stability results: one for the semimajor axis in the $J_2$ model, a second for the stability of the eccentricity and inclination in the geolunisolar model, and a third on the holding, altogether, of necessary conditions for Nekhoroshev-type stability of the satellite orbits. All three results point toward the same direction, i.e., that, at least far from exact resonances, orbital stability can be ensured at MEO, GEO and beyond for quite long times ($10^4 - 10^6$ orbital periods, $10^2 - 10^4$ years). Besides these general numbers, one may remark that the calculation of the size of the remainder of the normal form actually provides an estimate of the rate of drift of the orbits in element space, an information required in orbital diffusion studies for defunct satellites and space debris.

This work is organized as follows. In Sect. 2 we present the $J_2$ and geolunisolar models. Section 3 briefly presents the method of the composition of Lie series, used in the computation of all our normal forms, along with some general estimates on the convergence of the normalizing transformation and the size of the normal form’s remainder. Section 4 focuses on the stability estimates with the ${\mathcal {H}}_{J_2}$ model, while Sect. 5 deals with the stability in the framework of the ${\mathcal {H}}_\mathrm{gls}$ model. Finally, the analysis of the steepness conditions for the Hamiltonians ${\mathcal {H}}_{J_2}$ and ${\mathcal {H}}_\mathrm{gls}$ is presented in Sect. 6.

2 The $J_2$ and Geolunisolar Models

Bodies orbiting around the Earth are primarily affected by the Keplerian attraction with our planet. However, for an accurate description of the dynamics it is mandatory to assume that the Earth is non-spherical. Beside the Earth, the satellite dynamics is subject to the gravitational influence of Sun and Moon. Section 2.1 describes the Hamiltonian model ${\mathcal {H}}_{J_2kep}$, which includes the Earth’s Keplerian term and the first non-trivial term in the expansion of the geopotential. Section 2.2 presents the Hamiltonian model ${\mathcal {H}}_{\mathrm{gls, sec}}$, which includes $J_2$ and lunisolar terms, averaged over the fast angles.

2.1 The $J_2$ Model

We consider a model describing the motion of a point-mass body, say a satellite S, under the effect of the Earth’s gravitational attraction, including an approximation of the geopotential due to the oblateness of the Earth. Let ${\underline{r}}\equiv (x,y,z)$ be the position vector of S in a geocentric reference frame, with the plane (x, y) coinciding with the equatorial plane, and x pointing toward a fixed celestial point (e.g., the equinox). We consider the Hamiltonian describing the motion of S under the geopotential as the sum of two terms

$$\begin{aligned} {\mathcal {H}}_{J_2kep}={\mathcal {H}}_{kep}+{\mathcal {V}}_{J_2}\ , \end{aligned}$$

(1)

where

$$\begin{aligned} {\mathcal {H}}_{kep} = {p^2\over 2} - {\mu _E\over r} \end{aligned}$$

(2)

is the Keplerian part ($r=|{\underline{r}}|$), and

$$\begin{aligned} {\mathcal {V}}_{J_2}=-J_2\frac{\mu _ER_E^2}{r^3}\left( \frac{1}{2}-\frac{3z^2}{2r^2}\right) \, \end{aligned}$$

(3)

is the $J_2$ potential term, arising from expanding the geopotential in spherical harmonics and retaining only the largest coefficient (see, e.g., Kaula 1966). The constants are the Earth’s mass parameter $\mu _E = {\mathcal {G}}M_E$ (${\mathcal {G}} =$ Newton’s constant, $M_E =$ Earth’s mass), $R_E$ is the mean Earth’s radius, and $J_2$ is a dimensionless coefficient describing the oblate shape of the Earth. The numerical values are:

• $\mu _E=1.52984\times 10^9$ $R_E^3/yr^2$;

• $R_E=6378.14$ km;

• $J_2= -1082.6261\times 10^{-6}$.

Hamiltonian (1) is expressed in Cartesian coordinates. However, by a standard procedure, it can be transformed to an expression in the following set of modified Delaunay canonical action-angle variables

$$\begin{aligned} {\left\{ \begin{array}{ll} L=\sqrt{\mu _E a}\\ P=\sqrt{\mu _E a}(1-\sqrt{1-e^2})\\ Q=\sqrt{\mu _E a}\sqrt{1-e^2}(1-\cos {i})\\ \end{array}\right. } {\left\{ \begin{array}{ll} \lambda =M+\omega +\Omega \\ p=-\omega -\Omega \\ q=-\Omega \ ,\\ \end{array}\right. } \end{aligned}$$

(4)

where $(a,e,i,M,\omega ,\Omega )$ are the orbital elements of the satellite (semimajor axis, eccentricity, inclination, mean anomaly, argument of the perigee, longitude of the nodes). The passage is done by first expressing Hamiltonian (1) in elements via the relations (see e.g., Murray and Stanley 1999)

$$\begin{aligned} x= & {} {1\over 2}r(1+\cos i)\cos (f+\omega +\Omega ) +{1\over 2}r(1-\cos i)\cos (f+\omega -\Omega ) \nonumber \\ y= & {} {1\over 2}r(1+\cos i)\sin (f+\omega +\Omega ) -{1\over 2}r(1-\cos i)\sin (f+\omega -\Omega ) \nonumber \\ z= & {} r \sin i\sin (f+\omega ), \end{aligned}$$

(5)

where f is the true anomaly and r, $\cos f$, and $\sin f$ are given by the series

$$\begin{aligned} r= & {} a\left[ 1+{e^2\over 2} - 2e\sum _{\nu =1}^{\infty } {\left( J_{\nu -1}(\nu e)-J_{\nu +1}(\nu e)\right) \cos (\nu M)\over 2\nu } \right] \nonumber \\ \cos f= & {} {2(1-e^2)\over e}\sum _{\nu =1}^{\infty }J_\nu (\nu e)\cos (\nu M) - e \nonumber \\ \sin f= & {} 2\sqrt{1-e^2}\sum _{\nu =1}^{\infty }\frac{1}{2} \left( J_{\nu -1}(\nu e)-J_{\nu +1}(\nu e)\right) \sin (\nu M)~~~. \end{aligned}$$

(6)

In the actual calculations, all series are truncated to order $N = 15$ in the eccentricity e. Finally, we pass from the elements $(a,e,i,M,\omega ,\Omega )$ to the canonical variables $(L,P,Q,\lambda ,p,q)$ by inverting Eq. (4).

To perform the high-order normal form computations described in Sect. 4, using computer algebra, it is convenient that the dependence of the Hamiltonian on the action-angle variables can be expressed as a trigonometric polynomial. To this end, we first make a shift transformation $L\rightarrow \delta L$ around a reference value $a_*$, with

$$\begin{aligned} \delta L=L-L_*=\sqrt{\mu _E a}-\sqrt{\mu _E a_*}\ . \end{aligned}$$

(7)

This means that the Hamiltonian found after expanding in powers of the quantity $\delta L$ refers to the local dynamics of orbits with semimajor axis $a\approx a_*$. Every time when we change the reference value $a_*$ (i.e., the ‘altitude’ or ‘distance’ of the orbit from the Earth’s center), we then perform the Hamiltonian expansion anew around $L_*$ and obtain the stability estimates corresponding to that reference value. One may also note that $P={\mathcal {O}}(e^2/2)$ and $Q={\mathcal {O}}(i^2/2)$; thus, all three quantities $\delta L$, P, and Q are small quantities for orbits not very far from the equator and not very far from circular. We then expand ${\mathcal {H}}_{J_2kep}(\delta L,P,Q,\lambda ,p,q)$ in powers of $\sqrt{\delta L}$, $\sqrt{P}$, and $\sqrt{Q}$ up to the same order $N=15$ as the original expansion in the eccentricity (this ensures missing no term in P, Q in the Hamiltonian up to the order N). After this change, the truncated Hamiltonian takes the form (apart from a constant):

$$\begin{aligned} {\mathcal {H}}_{J_2kep}^{\le N}= & {} n_*\delta L + \omega _{1*} P +\omega _{2*} Q + \sum _{\begin{array}{c} s=1\\ s\ne 2 \end{array}}^{2N} {\mathcal {Z}}_{s}(\delta L,P,Q) \nonumber \\&+\sum _{s=1}^{2N}\sum _{\begin{array}{c} k_1,k_2,k_3\in {\mathbb {Z}}\\ 0<|k_1|+|k_2|+|k_3|\le s \end{array}} {\mathcal {P}}_{s,k_1,k_2,k_3}(\delta L,P,Q)\cos (k_1\lambda +k_2p+k_3q).\qquad \end{aligned}$$

(8)

The functions ${\mathcal {Z}}_{s}$ and ${\mathcal {P}}_{s,k_1,k_2,k_3}(\delta L,P,Q)$ are polynomials of degree s/2 in the action variables $(\delta L,P,Q)$. Finally, the frequencies $n_*$, $\omega _{1*}$, $\omega _{2*}$ are equal to:

$$\begin{aligned} n_* = \sqrt{{\mu _E\over a_*^3}}+J_2{3\mu _E^{1/2} R_E^2\over a_*^{7/2}}, ~~~~~~~~~~~ \omega _{1*} = -J_2 {3\mu _E^{1/2} R_E^2\over 2 a_*^{7/2}},~~~~~~ \omega _{2*} = J_2 {3\mu _E^{1/2} R_E^2\over 2 a_*^{7/2}}. \end{aligned}$$

(9)

Hamiltonian (8) is the point of departure for the stability estimates on the orbits’ semimajor axes; one notices that $\omega _{1*}= -\omega _{2*} = {\mathcal {O}}\left( J_2\right)$, a fact implying that both these frequencies are way smaller than $n_*\simeq (\mu _E/a_*^3)^{1/2}$ (third Kepler’s law). Accordingly, for all orbits the angle $\lambda$ circulates at a rate which is ${\mathcal {O}}(1/J_2)$ faster than the rate of circulation of the angles p, q. Hence, $\lambda$ constitutes the ‘fast angle’ of the Hamiltonian ${\mathcal {H}}_{J_2kep}^{\le N}$. Its elimination through a suitable sequence of canonical transformations leads to the approximate constancy of the value of the semimajor axis, as detailed in Sect. 4.

2.2 The Geolunisolar Hamiltonian

While stability estimates for the semimajor axis depend mostly on the Earth’s $J_2$ term, the question of the long-term stability as regards secular variations in eccentricity and inclination requires considering the effects of the Lunar and Solar gravitational tides. Let us consider a celestial body B (either Moon or Sun) with mass $M_b$ moving around the Earth and whose orbit is exterior to that of the satellite. Let ${\underline{r}}=(x,y,z)$ and ${\underline{r}}_b=(x_b,y_b,z_b)$ be the position vectors of S and B in a geocentric reference frame, with $r=|{\underline{r}}|$ and $r_b=|{\underline{r}}_b|$. The tidal disturbance caused by B on S is described by the potential

$$\begin{aligned} {\mathcal {V}}_b({\underline{r}},t)= & {} -\mu _b\left( \frac{1}{|{\underline{r}}-{\underline{r}}_b(t)|} -\frac{{\underline{r}}\cdot {\underline{r}}_b(t)}{r_b^3(t)}\right) =-\frac{\mu _b}{r_b(t)}+\frac{\mu _b}{2r_b^3(t)}r^2+\frac{3}{2}\frac{\mu _b({\underline{r}}\cdot {\underline{r}}_b(t))^2}{r_b^5(t)}\nonumber \\&+{\mathcal {O}}\left( \left( \frac{r}{r_b}\right) ^3\right) \ , \end{aligned}$$

(10)

where $\mu _b={\mathcal {G}}M_b$. The first term $-\mu _b/r_b$ in multipolar expansion (10) does not depend on the coordinates of S; therefore, it can be omitted from the Hamiltonian of motion of S. Thus, the tidal (or ‘third body’) perturbation terms in the Hamiltonian takes the form:

$$\begin{aligned} {\mathcal {H}}_{3B}= & {} \mu _m\left( {1\over 2}\frac{r^2}{r_m^3(t)} -{3\over 2}\frac{({\underline{r}}\cdot {\underline{r}}_m(t))^2}{r_m^5(t)}\right) \nonumber \\&+ \mu _s\left( {1\over 2}\frac{r^2}{r_s^3(t)} -{3\over 2}\frac{({\underline{r}}\cdot {\underline{r}}_s(t))^2}{r_s^5(t)}\right) +O_3={\mathcal {H}}_m+{\mathcal {H}}_s, \end{aligned}$$

(11)

where $\mu _m,{\underline{r}}_m$ and $\mu _s,{\underline{r}}_s$ are the mass and geocentric position vectors of the Moon and Sun, respectively, and $O_3$ denotes octupolar or higher-order terms in the expansion of the third body potentials. The exact form of the term ${\mathcal {H}}_{3B}$ depends now on the model adopted for the geocentric orbits of the Sun and Moon. In the framework of the present paper, we adopt the following models for Sun and Moon:

• (1) we suppose that the Sun’s geocentric orbit is an ellipse lying in the Earth’s ecliptic plane (i.e., with inclination $i_{s0}=23.43^\circ$ with respect to the equatorial plane), $\Omega _s=0^\circ$, $a_s=1.496\cdot 10^8$ km and $e_s=0.0167$;

• (2) we assume the Lunar orbit as elliptic and also lying on the ecliptic plane, with $a_m=384748$ km, $e_m=0.065$, and $i_{m0}=i_{s0}$. Note that this assumption ignores the precession of the Lunar node (with period $\simeq 18.6$ y) associated with the inclination of the Moon’s orbit with respect to the ecliptic (by $5^\circ 15'$). While the precession of the Lunar node is important near secular lunisolar resonances,¹ it only has a minimal effect far from these resonances, as substantiated by numerical studies (e.g., Gkolias et al. 2016; Rosengren et al. 2019). Thus, we ignore this effect in our present estimates (Sect. 6).

Under the above approximations, the satellite Hamiltonian ${\mathcal {H}}_{J_2ls}$ takes the form

$$\begin{aligned} {\mathcal {H}}_{J_2ls}={\mathcal {H}}_{J_2kep}+{\mathcal {H}}_{3B}.\ \end{aligned}$$

(12)

This is a Hamiltonian depending on three degrees of freedom (the coordinates and momenta of the satellite) as well as on time (through the vectors ${\underline{r}}_m(t)$ and ${\underline{r}}_s(t)$). However, contrary to the case of the Hamiltonian ${\mathcal {H}}_{J_2kep}$, in which we are interested in establishing the long-term stability of the semimajor axis over short-period oscillations, here we are interested in the question of the stability of the eccentricity and inclination of the satellite over secular timescales. Thus, as customary (see Kaula 1966; Celletti et al. 2017), we average ${\mathcal {H}}_{J_2ls}$ with respect to the mean anomalies of the satellite, Moon and Sun. The averaging can be done in closed form (see, for example, Kaula 1966) and leads to:

$$\begin{aligned} {\mathcal {H}}^{(av)}_{J_2}= & {} {1\over 2\pi }\int _0^{2\pi }{\mathcal {H}}_{J_2kep} dM = \int _0^{2\pi }{\mathcal {H}}_{J_2kep}{r^2\over a^2\sqrt{1-e^2}}df\\ {\mathcal {H}}^{(av)}_{m}= & {} {1\over 4\pi ^2}\int _0^{2\pi }\int _0^{2\pi }{\mathcal {V}}_{m} dM dM_m = \\&\int _0^{2\pi }\int _0^{2\pi } {\mathcal {V}}_{m}(1-e\cos E){r_m^2\over a_m^2\sqrt{1-e_m^2}}dEdf_m\\ {\mathcal {H}}^{(av)}_{s}= & {} {1\over 4\pi ^2}\int _0^{2\pi }\int _0^{2\pi }{\mathcal {V}}_{s} dM dM_s = \int _0^{2\pi }\int _0^{2\pi } {\mathcal {V}}_{s}(1-e\cos E){r_s^2\over a_s^2\sqrt{1-e_s^2}}dEdf_s. \end{aligned}$$

Here, f, E are the satellite’s true and eccentric anomaly, while $f_m,f_s$ are the Moon’s and Sun’s true anomaly along their geocentric orbits. The averaged $J_2$ term takes the form (apart from constant terms):

$$\begin{aligned} {\mathcal {H}}_{J_2}^{(av)}(e,i,\omega ,\Omega )=-J_2\frac{\mu _E R_E^2}{a^3(1-e^2)^{3/2}}\left( \frac{1}{2}-\frac{3}{4}\sin ^2{i}\right) . \end{aligned}$$

(13)

The terms ${\mathcal {H}}^{(av)}_{m}(e,i,\omega ,\Omega )$ and ${\mathcal {H}}^{(av)}_{s}(e,i,\omega ,\Omega )$, instead, turn out to be identical to those given in equations (3.6) and (3.7) of Celletti et al. (2017), setting $i_M=0$. Then, the Hamiltonian averaged over all short period terms, hereafter referred to as the secular geolunisolar Hamiltonian, takes the form

$$\begin{aligned} {\mathcal {H}}_{\mathrm{gls, sec}}(e,i,\omega ,\Omega )={\mathcal {H}}_{J_2}^{(av)} +{\mathcal {H}}_{s}^{(av)}+{\mathcal {H}}_{m}^{(av)}\ , \end{aligned}$$

(14)

which, in terms of the Delaunay modified variables, has two degrees of freedom.

2.2.1 Expansion Around the Forced Inclination

As it was done in the case of the $J_2$ model [Eq. (8)], normal form computations for Hamiltonian (14), expressed in Delaunay action-angle variables, require a polynomial expansion in the action variables around some preselected values. In the case of secular geolunisolar Hamiltonian (14), a natural choice of the origin for such expansions is the forced element values: writing ${\mathcal {H}}_{\mathrm{gls, sec}}$ as a function of the Delaunay variables, say, ${\mathcal {H}}_{\mathrm{gls, sec}}(P,Q,p,q;a)$ (where the semimajor axis a is now a priori constant and, hence, can be considered as a parameter), a forced equilibrium is defined as an equilibrium point of the secular Hamiltonian, i.e., a point $(Q^{(eq)},P^{(eq)},q^{(eq)},p^{(eq)})$ for which the following relations hold:

$$\begin{aligned} \left( {\partial {\mathcal {H}}_{\mathrm{gls, sec}}\over \partial P}\right) _{eq} = \left( {\partial {\mathcal {H}}_{\mathrm{gls, sec}}\over \partial Q}\right) _{eq} = \left( {\partial {\mathcal {H}}_{\mathrm{gls, sec}}\over \partial p}\right) _{eq} = \left( {\partial {\mathcal {H}}_{\mathrm{gls, sec}}\over \partial q}\right) _{eq} =0, \end{aligned}$$

(15)

where the subscript ‘eq’ denotes the condition $Q=Q^{(eq)},P=P^{(eq)},q=q^{(eq)},p=p^{(eq)}$. In the case of Hamiltonian (14), a forced equilibrium solution can be computed by writing first ${\mathcal {H}}_{\mathrm{gls, sec}}$ in terms of the Poincaré variables as

$$\begin{aligned} {\left\{ \begin{array}{ll} X_1=\sqrt{2Q}\sin {q}\ , \quad &{}X_2=\sqrt{2P}\sin {p}\ ,\\ Y_1=\sqrt{2Q}\cos {q}\ , \quad &{}Y_2=\sqrt{2P}\cos {p}\ . \end{array}\right. } \end{aligned}$$

(16)

Expanding up to quadratic terms in the Poincaré variables, the truncated secular Hamiltonian has the form

$$\begin{aligned} \widetilde{{\mathcal {H}}}(Y_1,Y_2,X_1,X_2)=A_1Y_1+B_1(X_1^2+Y_1^2)+B_2(X_2^2+Y_2^2), \end{aligned}$$

(17)

where the coefficients $A_1$, $B_1$ are given by:

$$\begin{aligned} \begin{aligned}&A_1=-\frac{3R_E^2a^{7/4}\sin {(2i_{s0})}}{8({\mathcal {G}}M_E)^{1/4}} \left( \frac{{\mathcal {G}}M_m}{a_m^3}+\frac{{\mathcal {G}}M_s}{a_s^3}\right) ,\\&B_1=\frac{3}{4}\frac{\sqrt{{\mathcal {G}}M_E}R_E^2J_2}{a^{7/2}} +\frac{3{\mathcal {G}}M_m(2-3\sin ^2{i_{s0}})}{16\sqrt{\frac{{\mathcal {G}}M_E}{a^3}}a_m^3} +\frac{3{\mathcal {G}}M_s(2-3\sin ^2{i_{s0}})}{16\sqrt{\frac{{\mathcal {G}}M_E}{a^3}}a_s^3}. \end{aligned} \end{aligned}$$

(18)

Hamiltonian (17) corresponds to two decoupled harmonic oscillators in the variables $(X_1, Y_1)$ and $(X_2, Y_2)$. The second harmonic oscillator (corresponding to the action-angle pair (P, p), hence, to the orbit’s eccentricity vector) has an equilibrium point at $\left( X_2^{(eq)},Y_2^{(eq)}\right) =(0,0)$, implying $P^{(eq)}=0$ and any value $0\le p^{(eq)}<2\pi$. This implies that the sub-manifold of circular orbits $e=0$ (corresponding to $P=0$) is invariant under the flow of the secular geolunisolar Hamiltonian. On the other hand, as regards the pair $(X_1,Y_1)$, Hamilton’s equations for Hamiltonian (17) yield:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{X_1}=A_1+2B_1Y_1 \\ \dot{Y_1}=-2B_1X_1. \end{array}\right. } \end{aligned}$$

(19)

For $i_{s0}\ne 0$, the equilibrium point of (19) is given by

$$\begin{aligned} X_1^{(eq)}=0\ , \quad Y_1^{(eq)}=-\frac{A_1}{2B_1}\ne 0. \end{aligned}$$

Setting $Q^{(eq)} = \left( \left( X_1^{(eq)}\right) ^2+\left( Y_1^{(eq)}\right) ^2\right) /2$, $i_{eq} \simeq (2Q^{(eq)}/\sqrt{\mu _E a})^{1/2}$ (for $Q^{(eq)}$ small), we arrive at

$$\begin{aligned} i^{(eq)}\simeq -\frac{A_1}{2B_1}\frac{1}{(\mu _E a)^{1/4}}, ~~~q^{(eq)}=-\Omega ^{(eq)} = 0. \end{aligned}$$

(20)

More accurate expressions for the forced inclination $i^{(eq)}$ can be obtained by introducing (20) along with the remaining equilibrium values in the derivatives of full secular Hamiltonian (14) and finding the roots of Hamilton’s equations. One can readily verify that $q^{(eq)}=0$ at all orders, while $i^{(eq)}$ is subject to small corrections with respect to expression (20). In physical terms, the forced inclination $i^{(eq)}$ defines the inclination of the Laplace plane: since the perturbing bodies (Moon and Sun) are in orbits inclined with respect to the equator, a satellite orbit can maintain its inclination constant when the latter has the value $i^{(eq)}$. Inspecting the form of coefficients (18), we find that $i^{(eq)}\rightarrow 0$ as $a\rightarrow 0$, while it can be shown that $i^{(eq)}\rightarrow i_{s0}$ for values of a greater than the GEO one (see for example Rosengren et al. 2014), reflecting the fact that the Laplace plane tends to coincide with the equator for satellite orbits close to the Earth (as imposed by the oblateness of the Earth), while it tends to coincide with the ecliptic at large distances from the Earth (where the Lunar and Solar tides dominate).

Returning to the expansion of the secular geolunisolar Hamiltonian, making the shift transformation $\delta Y_1=Y_1-Y_1^{(eq)}$ allows us to express the Hamiltonian as a polynomial in the variables $(X_1,\delta Y_1)$ and $(X_2,Y_2)$. The Hamiltonian ${\mathcal {H}}_{\mathrm{gls, sec}}$ starts now with terms of second degree which we regroup in ${\mathcal {H}}_2$:

$$\begin{aligned} {\mathcal {H}}_2= {b_1+\epsilon _1\over 2} X_1^2 + {b_1+\epsilon _2\over 2} \delta Y_1^2 + {b_1+\epsilon _3\over 2} X_2^2 +{b_1+\epsilon _4\over 2} Y_2^2, \end{aligned}$$

(21)

where $b_1 = 2B_1$ and $\epsilon _1$, $\epsilon _2$, $\epsilon _3$, $\epsilon _4$ are corrections of order ${\mathcal {O}}(\mu _b a^{3/2}/(\mu _E^{1/2}a_b^3))$, with the index b referring to the Moon or Sun. All these corrections turn to be rather small, with relative size $\sim 10^{-3} B_{10}$ at semimajor axis $a\sim 10^4$ km, where

$$\begin{aligned} B_{10} = \frac{3}{4}\frac{\sqrt{{\mathcal {G}}M_E}R_E^2J_2}{a^{7/2}}. \end{aligned}$$

Thus, after a canonical rescaling $X_1 = c_{12} {\tilde{X}}_1$, $\delta Y_1={\tilde{Y}}_1/c_{12}$, $X_2 = c_{34} {\tilde{X}}_2$, $Y_2={\tilde{Y}}_2/c_{34}$, with $(c_{12})^4 = (b_1+\epsilon _2)/(b_1+\epsilon _1) = 1 + {\mathcal {O}}(\mu _b a^{3/2}/(B_{10}\mu _E^{1/2}a_b^3)$ and $(c_{34})^4 = (b_1+\epsilon _4)/(b_1+\epsilon _3) = 1 + {\mathcal {O}}(\mu _b a^{3/2}/(B_{10}\mu _E^{1/2}a_b^3)$, the secular lunisolar Hamiltonian resumes the form:

$$\begin{aligned} {\mathcal {H}}_{\mathrm{gls, sec}}= & {} {\nu _1\over 2}\left( {\tilde{X}}_1^2+{\tilde{Y}}_1^2\right) + {\nu _2\over 2}\left( {\tilde{X}}_2^2+{\tilde{Y}}_2^2\right) \nonumber \\&+ \sum _{s=3}^\infty \sum _{\begin{array}{c} k_1,k_2,l_1,l_2\in {\mathbb {N}}\\ k_1+k_2+l_1+l_2=s \end{array}} h_{k_1,k_2,l_1,l_2}{\tilde{X}}_1^{k_1}{\tilde{X}}_2^{k_2}{\tilde{Y}}_1^{l_1}{\tilde{Y}}_2^{l_2}. \end{aligned}$$

(22)

This is the typical form of a secular Hamiltonian, consisting of linear oscillators (with frequencies $\nu _1$, $\nu _2$) coupled with nonlinear terms. However, we have $\nu _1=\nu _2 + {\mathcal {O}}(\mu _b a^{3/2}/\mu _E^{1/2}a_b^3)$, implying that the two frequencies are nearly equal

$$\begin{aligned} \nu _1\simeq \nu _2 \simeq \frac{3}{2}\frac{\sqrt{{\mathcal {G}}M_E}R_E^2J_2}{a^{7/2}}~~. \end{aligned}$$

This is a consequence of the axisymmetry of the $J_2$ model, implying that the secular frequencies ${\dot{q}}=-{\dot{\Omega }}$ and ${\dot{p}}=-{\dot{\omega }}-{\dot{\Omega }}$ are equal for nearly equatorial orbits in this model. As we will see in Sect. 5, this near-equality implies that with the present normal form estimates one cannot establish independently the long-term stability of the eccentricity and the inclination, but only the long-term stability of the Kozai–Lidov integral ${\mathcal {I}} = {\tilde{X}}_1^2+{\tilde{Y}}_1^2 + {\tilde{X}}_2^2 + {\tilde{Y}}_2^2$, which couples oscillations between the eccentricity and the proper inclination of the satellite.

Finally, Hamiltonian (22) can be written in action-angle variables ${\tilde{X}}_1 = \sqrt{2I_1}\sin \phi _1$, ${\tilde{Y}}_1 = \sqrt{2I_1}\cos \phi _1$, ${\tilde{X}}_2 = \sqrt{2I_2}\sin \phi _2$, ${\tilde{Y}}_2 = \sqrt{2I_2}\cos \phi _2$ as

$$\begin{aligned}&{\mathcal {H}}_{\mathrm{gls, sec}} = \nu _1 I_1 + \nu _2 I_2 \nonumber \\&\quad + \sum _{s=3}^\infty \sum _{\begin{array}{c} s_1,s_2\in {\mathbb {N}}\\ s_1+s_2=s \end{array}} \sum _{\begin{array}{c} k_1,k_2\in {\mathbb {Z}}\\ |k_1|+|k_2|\le s\\ (|k|_1+|k|_2)\equiv s (\text {mod }2) \end{array}} {\tilde{h}}_{s_1,s_2,k_1,k_2} I_1^{s_1/2}I_2^{s_2/2}\cos (k_1\phi _1+k_2\phi _2). \end{aligned}$$

(23)

Hamiltonian (23) is the starting point for all normal form calculations in Sect. 5. For computational reasons, the expansion in (23) is truncated up to a maximal order $N=15$, leading to the truncated form

$$\begin{aligned}&{\mathcal {H}}_{\mathrm{gls, sec}}^{\le N}(I_1,I_2,\phi _1,\phi _2) =\nu _1 I_1 + \nu _2 I_2 \nonumber \\&\quad + \sum _{s=3}^N \sum _{\begin{array}{c} s_1,s_2\in {\mathbb {N}}\\ s_1+s_2=s \end{array}} \sum _{\begin{array}{c} k_1,k_2\in {\mathbb {Z}}\\ |k_1|+|k_2|\le s\\ (|k|_1+|k|_2)\equiv s (\text {mod }2) \end{array}} {\tilde{h}}_{s_1,s_2,k_1,k_2} I_1^{s_1/2}I_2^{s_2/2}\cos (k_1\phi _1+k_2\phi _2). \end{aligned}$$

(24)

3 Hamiltonian Normalization

In this section we briefly recall some basic definitions related to normal form theory and its use in obtaining stability estimates based on the size of the normal form’s remainder. In Sects. 4 and 5 we will discuss the particular normalizations implemented on Hamiltonians (8) and (24), respectively.

3.1 Normal Form and Remainder

Consider a Hamiltonian function of the form

$$\begin{aligned} {\mathcal {H}}({\underline{A}},{\underline{\varphi }}) = Z_0({\underline{A}}) + {\mathcal {H}}_1({\underline{A}},{\underline{\varphi }}) ={\underline{\omega }}\cdot {\underline{A}} + {\mathcal {H}}_1({\underline{A}},{\underline{\varphi }}), \end{aligned}$$

(25)

where $\omega _j$ are real constants, and $({\underline{A}},{\underline{\varphi }})\in {{\mathbb {R}}}^n\times {{\mathbb {T}}}^n$ are action-angle variables. We assume that ${\mathcal {H}}_1$ is analytic in the complex domain $({\underline{A}},{\underline{\varphi }})\in$ $D_{\rho ,\sigma }(U)=B_\rho U\times S_\sigma$ (or simply $D_{\rho ,\sigma }$), where U is an open domain of ${{\mathbb {R}}}^n$, $B_\rho U$ is a complex neighborhood of U of size $\rho$:

$$\begin{aligned} B_\rho U=\{{\underline{A}}\in {\mathbb {C}}^n:\ dist({\underline{A}},U)<\rho \}\ , \end{aligned}$$

(26)

$S_\sigma$ is the complex strip

$$\begin{aligned} S_\sigma =\{{\underline{\varphi }}\in {\mathbb {C}}^n:\ Re(\varphi _j)\in {\mathbb {T}},\ \vert Im(\varphi _j)\vert <\sigma , \quad j=1,\dots ,n\} \end{aligned}$$

(27)

for $\rho ,\sigma >0$. On $D_{\rho ,\sigma }(U)$ we define the norm of a function $f=f({\underline{A}},{\underline{\varphi }})$ as

$$\begin{aligned} \Vert f\Vert _{\rho ,\sigma }=\sup _{({\underline{A}},{\underline{\varphi }})\in D_{\rho ,\sigma }}|f({\underline{A}},{\underline{\varphi }})|\ . \end{aligned}$$

(28)

The aim of normalization theory is to introduce a near to identity canonical transformation $\Phi :~ ({\underline{A}},{\underline{\varphi }})\rightarrow ({\underline{A}}',{\underline{\varphi }}')$, so that in the new variables $({\underline{A}}',{\underline{\varphi }}')$ Hamiltonian (25) takes the form

$$\begin{aligned} {\mathcal {H}}\left( {\underline{A}}({\underline{A}}',{\underline{\varphi }}'), {\underline{\varphi }}({\underline{A}}',{\underline{\varphi }}')\right) = Z({\underline{A}}',{\underline{\varphi }}')+R({\underline{A}}',{\underline{\varphi }}') \end{aligned}$$

(29)

with the following properties:

• i) the transformation $\Phi$ is analytic in a domain $D_{\rho ',\sigma '}(U)$ with $0<\rho '<\rho$, $0<\sigma '<\sigma$,

• ii) the dynamics under $Z({\underline{A}}',{\underline{\varphi }}')$, called the normal form, has some desired properties (see below), and

• iii) under norm definition (28) one has $\Vert R\Vert _{\rho ',\sigma '}\ll \Vert Z\Vert _{\rho ',\sigma '}$ implying that the function $R({\underline{A}}',{\underline{\varphi }}')$, called the remainder, introduces only a small correction with respect to the flow under the normal form term $Z({\underline{A}}',{\underline{\varphi }}')$.

Regarding point ii) above, see, e.g., Efthymiopoulos (2011) for a definition of the properties of the normal form term in various contexts of perturbation theory (e.g., in the Kolmogorov-Arnold-Moser or Nekhoroshev theories). Here we mention three cases of particular interest, pertinent to our present work:

Case 1: Birkhoff normal form. The function Z is independent of the angles ${\underline{\varphi }}'$. This kind of normalization allows us to prove the near-constancy of the action variables ${\underline{A}}$.

Case 2: elimination of short-period terms. The real constants $\omega _j$ in (25), called the unperturbed frequencies, are divided in two groups, ‘fast’ $\{\omega _1,\ldots ,\omega _{K_f}\}$, $1\le K_f<n$, and ‘slow’ $\{\omega _{K_f+1},\ldots ,\omega _{n}\}$, such that $\min \{|\omega _1|,\ldots ,|\omega _{K_f}|\}\gg \max \{|\omega _{K_f+1}|,\ldots ,|\omega _{n}|\}$. In this case, it turns convenient to introduce a normalizing transformation $\Phi$ such that the normal form Z becomes independent of the ‘fast angles’ $\{\varphi _1',\ldots ,\varphi _{K_f}'\}$. Such is the case of the normal form encountered in Sect. 4, leading to estimates on the stability of the semimajor axis in the $J_2$ problem. The corresponding Hamiltonian is of form (25), with $n=3$, $A_1=\delta L$, $A_2 = P$, $A_3=Q$, $\varphi _1=\lambda$, $\varphi _2=p$, $\varphi _3=q$.

Case 3: resonant normal form. The frequencies $\omega _j$ satisfy one or more quasi-commensurability relations of the form ${\underline{m}}\cdot {\underline{\omega }} \simeq 0$, with ${\underline{m}}\in {\mathbb {Z}}^n,|{\underline{m}}|\ne 0$. The maximum number of linearly independent and irreducible integer vectors ${\underline{m}}_l$, $1\le l\le l_{max}$, yielding exact commensurabilities for a given set of frequencies $\omega _j$, satisfies $0\le l_{max}\le n$. Since ${\mathcal {H}}_1$ is analytic in $D_{\rho ,\sigma }(U)$ and periodic in ${\underline{\varphi }}$, ${\mathcal {H}}_1$ admits the Fourier decomposition

$$\begin{aligned} {\mathcal {H}}_1({\underline{A}},{\underline{\varphi }}) = \sum _{{\underline{k}}\in {\mathbb {Z}}^n} h_{1,{\underline{k}}}({\underline{A}}) e^{i{\underline{k}}\cdot {\underline{\varphi }}}, \end{aligned}$$

(30)

where, according to Fourier theorem, the coefficients $|h_{1,{\underline{k}}}({\underline{A}})|$ are bounded by exponentially decaying quantities ${\mathcal {O}}(e^{-|{\underline{k}}|\sigma })$. Then, it turns out that the appropriate normal form Z has the resonant form:

$$\begin{aligned} Z({\underline{A}}',{\underline{\varphi }}') = \sum _{{\underline{k}}\in {\mathcal {M}}} \zeta _{{\underline{k}}}(\underline{A'}) e^{i{\underline{k}}\cdot {\underline{\varphi }}'}, \end{aligned}$$

(31)

for some Fourier coefficients $\zeta _{{\underline{k}}}({\underline{A}}')$ and where

$$\begin{aligned} {\mathcal {M}}:=\{{\underline{k}}\in {\mathbb {Z}}^n: {\underline{k}}\cdot {\underline{m}}_l=0 \text{ for } \text{ all } l=1,\ldots ,l_{max}\} \end{aligned}$$

is the ‘resonant module.’ A normal form of form (31) implies the existence of $n-l_{max}$ quasi-integrals of the form $I_i = {\underline{K}}_i\cdot {\underline{A}}$, $i=1,\ldots ,n-l_{max}$, where the vectors ${\underline{K}}_i$ satisfy the equations ${\underline{K}}_i\cdot {\underline{m}}_l=0$ for all l with $1\le l\le l_{max}$. The quantities $I_i$ are called the resonant integrals of Hamiltonian (31).

As an example, whenever $\nu _1=\nu _2$ secular geolunisolar Hamiltonian (24) admits a resonant normal form. We have $n=2$, $l_{max}=1$, ${\underline{m}}_1 = (1,-1)$, $A_1=I_1$, $A_2=I_2$, $\varphi _1=\phi _1$, $\varphi _2 = \phi _2$. Therefore, the normal form contains terms independent of the angles or depending on the angles through trigonometric terms of the form $\cos (k(\phi _1'-\phi _2'))$, $k=1,2,\ldots$. The associated resonant integral corresponds to the ‘Kozai–Lidov’ integral ${\mathcal {I}}=I_1+I_2$ (see Lidov 1962).

Definition 1

A r-th step Hamiltonian normalization process is a composition of near-identity transformations

$$\begin{aligned} \Phi ^{(r)} = \Phi _r\circ \Phi _{r-1}\circ \ldots \circ \Phi _1 \end{aligned}$$

(32)

mapping the initial action-angle variables to the r-th step normalized action-angle variables via the successive transformations $({\underline{A}}^{(s)},{\underline{\phi }}^{(s)})=\Phi ^{(s)}({\underline{A}}^{(s-1)},{\underline{\phi }}^{(s-1)})$, $s=1,2,,\ldots ,r$, $({\underline{A}}^{(0)}, {\underline{\varphi }}^{(0)})\equiv ({\underline{A}},{\underline{\varphi }})$, defined so that the compositions

$$\begin{aligned} \Phi ^{(s)} = \Phi _s\circ \Phi _{s-1}\circ \ldots \circ \Phi _1 \end{aligned}$$

for all $s=1,\ldots ,r$ are analytic and with inverse analytic within non-null domains $D_{\rho ^{(s)},\sigma ^{(s)}} \ne \emptyset$, and the rth-step Hamiltonian takes the form:

$$\begin{aligned} {\mathcal {H}}^{(r)}\left( {\underline{A}}({\underline{A}}^{(r)},{\underline{\varphi }}^{(r)}), {\underline{\varphi }}({\underline{A}}^{(r)},{\underline{\varphi }}^{(r)})\right) = Z^{(r)}({\underline{A}}^{(r)},{\underline{\varphi }}^{(r)})+R^{(r)}({\underline{A}}^{(r)} ,{\underline{\varphi }}^{(r)}) \end{aligned}$$

(33)

with $\Vert R^{(r)}\Vert _{\rho ^{(r)},\sigma ^{(r)}}\ll \Vert Z^{(r)}\Vert _{\rho ^{(r)},\sigma ^{(r)}}$.

The semi-analytical estimates of stability that we will develop in the next sections are based on defining a suitable r-step sequence of canonical transformations $\Phi _1,\Phi _2,\ldots ,\Phi _r$ reducing the size of the remainder $\Vert R^{(r)}\Vert _{\rho ^{(r)},\sigma ^{(r)}}$ as much as possible given the initial Hamiltonian model considered. The appropriate sequence is found using the method of Lie series (see Sect. 4). The obtained times of stability are of order $\Vert R^{(r_{opt})}\Vert _{\rho ^{(ropt)},\sigma ^{(ropt)}}^{-1}$, where $r_{opt}$ is the normalization order yielding the smallest possible remainder norm. The value of $r_{opt}$ can be obtained via theoretical estimates (see Efthymiopoulos et al. 2004), but in practice, it is also limited by the maximum order in which our computer-algebra normal form calculations can proceed. Theoretical estimates imply that the size of the remainder norm is exponentially small in the inverse of the size of the perturbation $\Vert {\mathcal {H}}_1\Vert _{\rho ,\sigma }$ in Eq. (25). For example, in the simplest case of the Birkhoff normal form, we have the following theorem (see Fassò and Benettin 1989 for full details).

Theorem 2

Consider the Hamiltonian expressed in action-angle variables ${\mathcal {H}}({\underline{A}},{\underline{\varphi }})= {\underline{\omega }}\cdot {\underline{A}}+f({\underline{A}},{\underline{\varphi }})$, where ${\underline{\omega }}\in {\mathbb {R}}^n$ satisfies the following Diophantine condition: there exist $\tau ,\gamma >0$ such that

$$\begin{aligned} |{\underline{k}}\cdot {\underline{\omega }}|\ge \frac{\gamma }{|{\underline{k}}|^\tau }\ \qquad \forall {\underline{k}}\in {\mathbb {Z}}^n\backslash {\{{\underline{0}}\}}\ \end{aligned}$$

(34)

and f is real analytic on $D_{\rho ,\sigma }$ for some $\rho ,\sigma >0$. Consider two positive parameters $\delta <\rho /2$ and $\xi <\sigma /2$, and for $r\ge 1$, let

$$\begin{aligned} \epsilon _1^*=\frac{\gamma \delta \xi ^{\tau +1}}{2^{n-\tau +4}\sqrt{(2\tau +2)!}\ \Vert f\Vert _{\rho ,\sigma }}\ ,\qquad \epsilon _r^*=\frac{\epsilon _1^*}{r^{\tau +2}}\ . \end{aligned}$$

(35)

Then, for any

$$\begin{aligned} r<\left( \frac{\gamma \delta \xi ^{\tau +1}}{2^{n-\tau +4} \sqrt{(2\tau +2)!}}\right) ^{1/\tau +2}\frac{1}{\Vert f\Vert _{\rho ,\sigma }^{1/\tau +2}}\ , \end{aligned}$$

(36)

there exists a real analytic canonical transformation $\Phi :D_{\rho -2\delta , \sigma -2\xi }\mapsto D_{\rho ,\sigma }$ such that the transformed Hamiltonian has the form

$$\begin{aligned} {\mathcal {H}}\circ \Phi =h({\underline{A}})+ \sum _{s=1}^rZ_s({\underline{A}}) +R^{(r+1)}({\underline{A}},{\underline{\varphi }})\ , \end{aligned}$$

(37)

where the remainder $R^{(r+1)}$ can be bounded as

$$\begin{aligned} \Vert R^{(r+1)}\Vert _{\rho -2\delta , \sigma -2\xi }\le \frac{\Vert f\Vert _{\rho ,\sigma }}{4r^{\tau +2}} \left( \frac{1}{\epsilon _r^*}\right) ^r\frac{\epsilon _r^*}{\epsilon _r^*-1}\ . \end{aligned}$$

(38)

Casting together (35) and (38), one readily sees that the remainder grows more rapidly than any power of r, namely as $(r^{\tau +2})^{r-1}$. Consequently, this procedure does not converge for $r\rightarrow \infty$. In any case, we remark that, as the threshold value for the normalization order r is proportional to the inverse of $\Vert f\Vert _{\rho ,\sigma }^{1/(\tau +2)}$, if we manage to reduce the size of the initial remainder function, then we can increase the maximum value of r for which Theorem 2 is satisfied.

Similar estimates hold in the case of the resonant normal form constructions (see Efthymiopoulos et al. 2004). The behavior of the size of the remainder as a function of the normalization order r will be examined in detail in our semi-analytical computations in Sects. 4 and 5.

3.2 Book-keeping and Construction of the Normal Form

Both Hamiltonians (8) and (24) are of form (25); therefore, the above results on Hamiltonian normalization apply. In order to compute the composition of canonical transformations required in Eq. (32), we implement the method of composition of Lie series, after introducing a suitable book-keeping (see Efthymiopoulos 2011) to separate terms in the Hamiltonian according to estimates of their order of smallness.

Definition 3

Consider a ‘book-keeping symbol’ $\epsilon$, with numerical value $\epsilon =1$. A book-keeping rule is a splitting of the initial Hamiltonian ${\mathcal {H}}({\underline{A}}, {\underline{\varphi }})$ in the form

$$\begin{aligned} {\mathcal {H}}({\underline{A}},{\underline{\varphi }}) = {\underline{\omega }}\cdot {\underline{A}} + \sum _{s=1}^\infty \epsilon ^s {\mathcal {H}}_s({\underline{A}},{\underline{\varphi }}). \end{aligned}$$

(39)

Remark 4

The splitting can in principle be arbitrary. However, the sequence of remainders $\Vert R^{(r)}\Vert _{\rho ^{(r)},\sigma ^{(r)}}$ found by Hamiltonian normalization behaves well, i.e., $\Vert R^{(s)}\Vert _{\rho ^{(s)},\sigma ^{(s)}}<\Vert R^{(s-1)}\Vert _{\rho ^{(s-1)}, \sigma ^{(s-1)}}$ for $s=1,\ldots ,r_{opt}$ when splitting (39) is done so as to reflect the order of smallness of different terms in the Hamiltonian. Roughly speaking, one must have $\Vert {\mathcal {H}}_s\Vert _{\rho ,\sigma } = {\mathcal {O}}\left( \Vert {\mathcal {H}}_1\Vert _{\rho ,\sigma }^s\right)$ (see Efthymiopoulos 2011).

Proposition 5

Lie series: Let $\chi ({\underline{A}},{\underline{\varphi }})$, called the Lie generating function, be a function analytic in the domain $D_{\rho ,\sigma }(U)$, and ${\mathcal {L}}_\chi$ denote the Poisson bracket operator ${\mathcal {L}}_\chi \cdot = \{\cdot ,\chi \}$. Given positive numbers $\delta <\rho$ and $\xi <\sigma$, assume that

$$\begin{aligned} \min \left( \delta \Vert {\partial \chi \over \partial q}\Vert _{\rho -\delta ,\sigma -\xi }^{-1}, \xi \Vert {\partial \chi \over \partial p}\Vert _{\rho -\delta ,\sigma -\xi }^{-1}\right) >1.~~ \end{aligned}$$

Then, the mapping

$$\begin{aligned} ({\underline{A}}',{\underline{\varphi }}') = \exp ({\mathcal {L}}_\chi )({\underline{A}},{\underline{\varphi }}) = \sum _{j=0}^\infty {1\over j!}{\mathcal {L}}_\chi ^j({\underline{A}},{\underline{\varphi }}) \end{aligned}$$

(40)

is an analytic canonical transformation of the domain $D_{\rho -\delta ,\sigma -\xi }(U)$ onto itself.

The proof consists in implementing Proposition 1 of Fassò and Benettin (1989) with $r=1$.

Proposition 6

Exchange theorem: Let f be a real analytic function $f: U\times {{\mathbb {T}}}^n \rightarrow {{\mathbb {R}}}$ extended to the domain $D_{\rho ,\sigma }(U)$. The equality

$$\begin{aligned} f({\underline{A}}',{\underline{\varphi }}') = \left( \exp ({\mathcal {L}}_\chi )f({\underline{A}},{\underline{\varphi }})\right) _{{\underline{A}}={\underline{A}}',{\underline{\varphi }}={\underline{\varphi }}'} \end{aligned}$$

(41)

holds, where $({\underline{A}}',{\underline{\varphi }}')$ are given by transformation (40) and $({\underline{A}}',{\underline{\varphi }}')\in D_{\rho -\delta ,\sigma -\xi }(U)$.

See Giorgilli (2002) for the proof. In simple words, the exchange theorem implies that the result of a Lie series canonical transformation onto a function depending on $({\underline{A}},{\underline{\varphi }})$ can be found by implementing the sequence of Poisson brackets of the exponential operator $\exp ({\mathcal {L}}_\chi )$ directly on the function f, and substituting, after this operation, the arguments $({\underline{A}},{\underline{\varphi }})$ with $({\underline{A}}',{\underline{\varphi }}')$.

Normal form algorithm: The above definitions allow us to establish an algorithm for the calculation of the sequence of canonical transformations (32) using Lie series. The algorithm is obtained recursively by defining the r-th step as follows. Assume the Hamiltonian after $r-1$ normalization steps, denoted by ${\mathcal {H}}^{(r-1)}$, is in normal form up to the book-keeping order $r-1$:

$$\begin{aligned} {\mathcal {H}}^{(r-1)}=Z_0+\epsilon Z_1+\ldots +\epsilon ^{r-1}Z_{r-1} + \epsilon ^{r} R^{(r-1)}_{r}+\epsilon ^{r+1} R^{(r-1)}_{r+1} +\epsilon ^{r+2} R^{(r-1)}_{r+2}+\ldots \end{aligned}$$

(42)

Then, the r-th step Lie generating function $\chi _r$ and Hamiltonian ${\mathcal {H}}^{(r)}$ are computed as follows:

• (i) split $R^{(r-1)}_{r}$ as $R^{(r-1)}_r = Z^{(r-1)}_r+h^{(r-1)}_r$, where $Z^{(r-1)}_r$ denotes the part of $R^{(r-1)}_{r}$ being in normal form;

• (ii) compute $\chi _r$ as the solution of the homological equation

  $$\begin{aligned} \{{\underline{\omega }}\cdot {\underline{A}},\chi _r\} + \epsilon ^r h^{(r-1)}_r=0 ; \end{aligned}$$

  (43)

• (iii) compute the r-th step normalized Hamiltonian as ${\mathcal {H}}^{(r)} = \exp ({\mathcal {L}}_{\chi _r}){\mathcal {H}}^{(r-1)}$. This yields the Hamiltonian

  $$\begin{aligned} {\mathcal {H}}^{(r)}=Z_0+\epsilon Z_1+\ldots +\epsilon ^{r-1}Z_{r-1} + \epsilon ^{r}Z_{r}+ \epsilon ^{r+1} R^{(r)}_{r+1}+\epsilon ^{r+2} R^{(r)}_{r+2}+\ldots \end{aligned}$$

  (44)

  where $Z_r = Z^{(r-1)}_r$.

Remark 7

In the above algorithm, the notation $f^{(r)}$ implies a function depending on the canonical variables $({\underline{A}}^{(r)},{\underline{\varphi }}^{(r)})$, which are connected to the original variables $({\underline{A}},{\underline{\varphi }})$ via the composition of Lie series transformations

$$\begin{aligned} ({\underline{A}},{\underline{\varphi }}) = \exp ({\mathcal {L}}_{\chi _r})\circ \exp ({\mathcal {L}}_{\chi _{r-1}})\circ \ldots \circ \exp ({\mathcal {L}}_{\chi _1})({\underline{A}}^{(r)},{\underline{\varphi }}^{(r)}). \end{aligned}$$

(45)

For simplicity of notation, unless explicitly required in the sequel we do not write the superscripts in the canonical variables defined in every step, but only in the functions in which these variables are arguments of.

Remark 8

In the computer-algebraic implementation of the normalization algorithm, all functions are truncated up to a maximum book-keeping order, specified by computational restrictions.

Remark 9

The solution of homological Eq. (43) is trivial when the functions $h^{(r-1)}_r$ are written in the Fourier representation

$$\begin{aligned} h^{(r-1)}_r = \sum _{{\underline{k}}\in {\mathbb {Z}}^n} {\tilde{h}}^{(r-1)}_{r,{\underline{k}}}({\underline{A}}) \exp (i{\underline{k}}\cdot {\underline{\varphi }}), \end{aligned}$$

which gives

$$\begin{aligned} \chi _r = \epsilon ^r \sum _{{\underline{k}}\in {\mathbb {Z}}^n} {i{\tilde{h}}^{(r-1)}_{r,{\underline{k}}}({\underline{A}})\over {\underline{k}}\cdot {\underline{\omega }}}\exp (i{\underline{k}}\cdot {\underline{\varphi }}). \end{aligned}$$

4 Stability of the Semimajor Axis in the $J_2$ Model

We will now implement the Hamiltonian normalization discussed in Sect. 3 to eliminate the short period terms (depending on the mean longitude $\lambda$) in Hamiltonian (8), leading to estimates on the long-term stability of the orbits’ semimajor axis.

4.1 Normal Form

We express the Hamiltonian function in form (39), choosing the book-keeping power equal to $s-2$, where s is the index in Hamiltonian expansion (8), that is, collecting together at book-keeping order s all polynomials ${\mathcal {Z}}_{s-2}$ and ${\mathcal {P}}_{s-2,k_1,k_2,k_3}$. Then

$$\begin{aligned} \begin{aligned}&{\mathcal {H}}_{J_2}^{(0)}(\delta L, P, Q, \lambda ,p,q)=\\&\quad ={\mathcal {H}}_0(\delta L,P,Q)+\epsilon {\mathcal {H}}_1(\delta L, P, Q, \lambda ,p,q)+\dots +\epsilon ^N {\mathcal {H}}_N(\delta L, P, Q, \lambda ,p,q)\ \end{aligned} \end{aligned}$$

(46)

with ${\mathcal {H}}_0 = n_*\delta L+\omega _{1*}P+\omega _{2*}Q$. The truncation order (in eccentricity and inclination) is $N=15$.

With reference to the algorithm of Sect. 3.2, normal form terms are specified as those non-depending on the mean longitude $\lambda$. That is, the Fourier harmonics $\cos (k_1\lambda +k_2p+k_3q)$ to survive in normal form are selected by the choice of resonant module (see Sect. 3.1) defined by the relation $l_{max}=1$, $m_1=(1,0,0)$. Following the choice of book-keeping as described above, the normal form and remainder computations where done using a program written by the authors in the symbolic package Mathematica$^{\copyright }$. The symbolic program performs $M=12$ normalization steps, implementing steps (i) to (iii) of the normalization algorithm discussed at the end of Sect. 3. The operation $H^{(r)} = \exp ({\mathcal {L}}_{\chi _r})H^{(r-1)}$ is truncated in book-keeping up to the order $N=15$. The symbolic program performs this truncation automatically, since every term in both the Hamiltonians $H^{(r-1)}$ and the generating functions $\chi _r$, $r=1,\ldots ,M$ carries the book-keeping symbol $\epsilon$ raised to some power. Mild memory requirements (of the order of 100 Mb) are required for the whole process. We also note that for given book-keeping rule, this process takes automatically care of the minimum and maximum powers in the action variables, as well as the minimum and maximum Fourier harmonics associated with every book-keeping order (see Efthymiopoulos (2011) for a detailed description of this process).

After M normalization steps, the Hamiltonian takes the form

$$\begin{aligned} {\mathcal {H}}_{J_2}&\equiv {\mathcal {H}}_{J_2}^{(M)}(\delta L, P, Q, \lambda ,p,q)\nonumber \\&={\mathcal {H}}_{J_2,sec}^{(M)}(\delta L,P,Q,p,q) +{\mathcal {R}}_{J_2}^{(M)}(\delta L,P,Q,\lambda , p,q)\ , \end{aligned}$$

(47)

where (setting the book-keeping $\epsilon =1$)

$$\begin{aligned} \begin{aligned} {\mathcal {H}}_{J_2,sec}^{(M)}&= Z_0+\ldots +Z_M,\\ {\mathcal {R}}_{J_2}^{(M)}&= R^{(M)}_{M+1}+\ldots +R^{(M)}_{N} \end{aligned} \end{aligned}$$

with $Z_0={\mathcal {H}}_0$.

The term ${\mathcal {H}}_{J_2,sec}^{(M)}$ will be referred to as the ‘secular Hamiltonian’ (not depending on the fast angle $\lambda$). On the other hand, the remainder ${{\mathcal {R}}}_{J_2}^{(M)}$ quantifies the difference between the true evolution of all canonical variables and the one induced by ${\mathcal {H}}_{J_2,sec}^{(M)}$. Since in (47) we can only compute a truncated remainder, we probe numerically that the finite sum of the leading terms in the remainder (up to order N) yields a remainder norm close to the limiting one (which corresponds to the limit $N\rightarrow \infty$). To this end, we take as maximum normalization order $M=N-3$, ensuring that at least the three first leading terms are included in the remainder (see Steichen and Giorgilli 1997). Also, in estimating the size of the remainder through a suitable definition of the norm, we compute the sup norm on a closed and bounded domain ${\mathcal {D}}\subset {{\mathbb {R}}}^2$:

$$\begin{aligned} \Vert f\Vert _{\infty , {\mathcal {D}}}= \sup _{\begin{array}{c} (e,i)\in {\mathcal {D}}\\ (\lambda ,p,q)\in {\mathbb {T}}^3 \end{array}} |f(e,i,\lambda ,p,q)|\ . \end{aligned}$$

(48)

The calculation of the sup norm in a fixed domain $(e,i)\in {\mathcal {D}}$, $(\lambda ,p,q)\in {\mathbb {T}}^3$ can only be done approximately, by taking a grid of values for all variables involved in this domain, and computing the maximum of the absolute value of the function involved on this grid. Since this process can lead to quite strong fluctuations in the norm estimate, for practical purposes we substitute the sup norm calculation with one based on majorization: consider a function of the form

$$\begin{aligned} f(e,i,\lambda ,p,q) = \sum _{k_1,k_2,k_3} f_{k_1,k_2,k_3}(e,i)\cos (k_1\lambda +k_2p + k_3 q), \end{aligned}$$

(49)

where the sum is over an arbitrary (finite) number of harmonics $(k_1,k_2,k_3)\in {\mathbb {Z}}^3$ with $|k_1|+|k_2|+|k_3|\ne 0$, and the functions $f_{k_1,k_2,k_3}(e,i)$ are sums of polynomials

$$\begin{aligned} f_{k_1,k_2,k_3}(e,i)= \sum _{s_1}\sum _{s_2} g_{k_1,k_2,k_3,s_1,s_2}P^{s_1/2}(e)Q^{s_2/2}(i) \end{aligned}$$

(50)

over a finite set of integer pairs $s_1,s_2$. Define the domain ${\mathcal {D}}_*(e_*,i_*)$ in the action space (P, Q) via the relation: ${\mathcal {D}}_*(e_*,i_*) = \{0\le P\le P(e_*), 0\le Q\le Q(e_*, i_*)\}$. Then, one has:

$$\begin{aligned}&\sup _{\begin{array}{c} (e,i)\in {\mathcal {D}}_*\\ (\lambda ,p,q)\in {\mathbb {T}}^3 \end{array}} |f(e,i,\lambda ,p,q)| \le ||f||_{\infty ,{\mathcal {D}}_*} \nonumber \\&\quad = \sum _{k_1,k_2,k_3}\sum _{s_1,s_2} |g_{k_1,k_2,k_3,s_1,s_2}|P^{s_1/2}(e_*)Q^{s_2/2}(e_*,i_*). \end{aligned}$$

(51)

We can then use norm (51) as an estimate substituting the sup norm in all actual calculations.

4.2 Numerical Results: Stability of the Semimajor Axis

Having fixed the procedure for the normal form and remainder computations, we proceed in deriving stability estimates based on the time variations of the value of the semimajor axis in the $J_2$ problem. Fixing a reference value $a_*$ of the semimajor axis, we assume that, at the time $t=0$, we have $L=L_*=\sqrt{\mu a_*}$, i.e., $\delta L=0$. Our aim is to estimate the fluctuations of L as functions of the orbital parameters e and i.

The first question to settle is that, for every value of the reference parameter $a_*$ we have to specify the range of values of the variables (e, i) for which the remainder ${\mathcal {R}}_{J_2}^{(M)}$ is small enough to represent only a perturbation with respect to the dynamics determined by the secular part. In applications, we compute the value of $\Vert {\mathcal {R}}_{J_2}^{(M)}\Vert _{\infty ,{{\mathcal {D}}_*}}$ in the domain $(e,i)\in {\mathcal {D}}=[0,0.15]\times [0,\pi /2]$, so that the inclination can take all possible values; the eccentricity is instead taken in a reasonable interval, where we can find almost all main Earth’s satellites.

With reference to Hamiltonian (47), if we consider the dynamics induced only by the secular part, we obtain that

$$\begin{aligned} \frac{d}{dt}\delta L=-\frac{\partial {\mathcal {H}}_{J_2,sec}^{(M)}}{\partial \lambda }=0\ , \end{aligned}$$

which implies that $\delta L$ (hence L) is a constant of motion. We remind that $\delta L$ is not the original Delaunay variable, but rather the one obtained after M normalization steps. If we denote by $\delta L^{(0)}$ the original variable, then we have

$$\begin{aligned} \delta L=\exp (-{\mathcal {L}}_{\chi ^{(1)}}(\dots (\exp (-{\mathcal {L}}_{\chi ^{(M)}}(\delta L^{(0)})))))\ . \end{aligned}$$

(52)

To obtain $\delta L^{(0)}$ as a function of the new variable $\delta L$, we need to invert transformation (52); we observe that

$$\begin{aligned} \left( \exp ({\mathcal {L}}_{\chi })\right) ^{-1}=\exp (-{\mathcal {L}}_{\chi })\ , \end{aligned}$$

implying

$$\begin{aligned} \delta L^{(0)}=\exp ({\mathcal {L}}_{\chi ^{(M)}} (\dots (\exp ({\mathcal {L}}_{\chi ^{(1)}}(\delta L)))))\ . \end{aligned}$$

Since we are dealing with near-identity canonical transformations, we realize that $\delta L^{(0)}$ is the sum of $\delta L$ and short period (small) variations which do not affect its stability.

If we consider the full Hamiltonian in (47), then L is not constant anymore because of the dependence of ${{\mathcal {R}}}_{J_2}^{(M)}$ on $\lambda$. Using again Hamilton’s equations, we see that

$$\begin{aligned} \frac{d}{dt}L=\frac{d}{dt}(\delta L+L_*)=\frac{d}{dt}\delta L =-\frac{\partial {\mathcal {H}}_{J_2}}{\partial \lambda } =-\frac{\partial {{\mathcal {R}}}_{J_2}^{(M)}}{\partial \lambda }\ . \end{aligned}$$

Then, for every set of values, say $(e^*,i^*,\lambda ^*,p^*,q^*)\in {\mathcal {D}}\times {\mathbb {T}}^3$, we obtain

$$\begin{aligned} \bigg |\frac{d}{dt}L(e^*,i^*,\lambda ^*,p^*,q^*) \bigg |\le \sup _{\begin{array}{c} (e,i)\in {\mathcal {D}}\\ (\lambda ,p,q)\in {\mathbb {T}}^3 \end{array}}\bigg | \frac{d}{dt}L(e,i,\lambda ,p,q)\bigg |\le \bigg |\bigg |\frac{\partial {{\mathcal {R}}}_{J_2}^{(M)}}{\partial \lambda }\bigg |\bigg |_{\infty , {{\mathcal {D}}_*}}\ . \end{aligned}$$

Let $L(e,i,\lambda ,p,q;T)$ be the value at time $t=T$. To estimate its distance from the equilibrium point $L_*$, we can use the mean value theorem which gives

$$\begin{aligned} \vert L(e,i,\lambda ,p,q;T)-L_*\vert \le \Vert L(e,i,\lambda ,p,q;T)-L_*\Vert _{\infty ,{{\mathcal {D}}_*}} \le \bigg |\bigg |\frac{dL}{dt}\bigg |\bigg |_{\infty ,{{\mathcal {D}}_*}}T\ . \end{aligned}$$

(53)

Requiring that the right-hand side of (53) is of order of unity, then the stability time T becomes order of $O\left( 1/\Vert dL/dt\Vert _{\infty ,{{\mathcal {D}}_*}}\right)$. Let us fix a constant value $\Delta L$ and suppose that we want to estimate the minimal time $T_1$ up to which the variation of $L(e,i,\lambda ,p,q;T)$ stays bounded by $\Delta L$:

$$\begin{aligned} \Vert L(e,i,\lambda ,p,q;T)-L_*\Vert _{\infty ,{{\mathcal {D}}_*}}\le \Delta L\ . \end{aligned}$$

Using (53) we obtain that $T_1$ is given by

$$\begin{aligned} T_1\ge \frac{\Delta L}{\Vert dL/dt\Vert _{\infty ,{{\mathcal {D}}_*}}}\ . \end{aligned}$$

(54)

Equation (54) can be used to derive the stability time of the semimajor axis a: recalling that, in general, $L=\sqrt{\mu a}$, one has that $\Delta L=\Delta a/2\sqrt{\mu / a}$, which allows to obtain a lower bound for the stability time of a given by

$$\begin{aligned} T_2=\frac{1}{2}\sqrt{\frac{\mu }{a_*}}\frac{\Delta a}{\Vert dL/dt\Vert _{\infty ,{{\mathcal {D}}_*}}}. \end{aligned}$$

(55)

This estimate will be used in Sect. 5.3 to obtain results on the stability time at different altitudes; in particular, $\Delta a$ is set to be equal to 0.1 $R_E$.

To check that the norm $\Vert {{\mathcal {R}}}_{J_2}^{(M)}\Vert _{\infty ,{{\mathcal {D}}_*}}$ is small in the domain ${\mathcal {D}}=[0,0.15]\times [0,\pi /2]$, we compute its value by taking a set of samples for the reference value of the semimajor axis $a_*$ that correspond to different distances from the Earth’s center (the radius of the Earth is $R_E=6378.14$ km). Precisely, we consider the following semimajor axes:

• $a_*^{(1)}=(42164$ $km)/R_E$: the reference value for GEO satellites;

• $a_*^{(2)}=(26560$ $km)/R_E$: the reference value for GPS satellites;

• $a_*^{(3)}=(8524.75$ $km)/R_E$: an intermediate value in terms of the altitude;

• $a_*^{(4)}=(7258.69$ $km)/R_E$: very close to the Earth’s surface. We remark that in this case the results obtained are not very relevant from a practical point of view, because the effect of the atmosphere becomes important.

Table 1 Estimates of $\Vert {{\mathcal {R}}}_{J_2}^{(M)}\Vert _{\infty ,{{\mathcal {D}}_*}}$ for different values of $a_*$ in the $J_2$ model

Table 1 shows the values of $\Vert {{\mathcal {R}}}_{J_2}^{(M)}\Vert _{\infty ,{{\mathcal {D}}_*}}$ computed for the above values of $a_*$ and for $J_2=1.084\cdot 10^{-3}$, namely the real value of the coefficient for the Earth. As we can see, $\Vert {{\mathcal {R}}}_{J_2}^{(M)}\Vert _{\infty ,{{\mathcal {D}}_*}}$ is typically very small for all values of $a_*$: this confirms that for the $J_2$ problem it is reasonable to take the domain in eccentricity and inclination as ${\mathcal {D}}=[0,0.15]\times [0,\pi /2]$.

Table 2 Estimates of $\Vert dL/dt\Vert _{\infty ,{{\mathcal {D}}_*}}$ for different values of $a_*$ in the $J_2$ model

Table 2 provides the results for the estimate of $\Vert dL/dt\Vert _{\infty ,{{\mathcal {D}}_*}}$, which show that, using (54) with $\Delta L$ equal for all the considered distances $a_*$, the stability time for L increases with the altitude.

Fig. 1

Plots of $\Vert {{\mathcal {R}}}_{J_2}^{(M)}\Vert _{\infty ,{{\mathcal {D}}_*}}$ for $(e,i)\in {\mathcal {D}}$: $a_*=a_*^{(1)}$ (left) and $a_*=a_*^{(4)}$ (right) in the $J_2$ model

Fig. 2

Stability estimates for the GEO case (with $a=a_*^{(1)}$) in the $J_2$ model. Left: plot of $||dL/dt||_{\infty ,{{\mathcal {D}}_*}}$ as a function of e for fixed values of i. Right: plot of $||dL/dt||_{\infty ,{{\mathcal {D}}_*}}$ as a function of i for fixed values of e

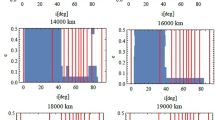
Figure 1 shows the logarithmic plot of $\Vert {{\mathcal {R}}}_{J_2}^{(M)}\Vert _{\infty ,{{\mathcal {D}}_*}}$ in the limit cases $a_*=a_*^{(1)}$ and $a_*=a_*^{(4)}$. The plots show that the remainder decreases as one gets farther from the Earth and it becomes larger when increasing the eccentricity and inclination.

Fig. 3

Stability estimates for the near-Earth case (with $a=a_*^{(4)}$) in the $J_2$ model. Left: plot of $||dL/dt||_{\infty ,{{\mathcal {D}}_*}}$ as a function of e for fixed values of i. Right: plot of $||dL/dt||_{\infty ,{{\mathcal {D}}_*}}$ as a function of i for fixed values of e

Figures 2 and 3 refer, respectively, to $a=a_*^{(1)}$ and $a=a_*^{(4)}$; the left plots provide the graph of $||dL/dt||_{\infty ,{{\mathcal {D}}_*}}$ as a function of the eccentricity for fixed values of the inclination, while the right plots give the norm as a function of the inclination for fixed values of the eccentricity. We notice that the norms tend to decrease when the eccentricity and the inclination are smaller, although the effect is more evident in the GEO region than closer to the Earth.

We now examine how the stability time changes as a function of the semimajor axis $a_*$: in this case, we consider 1000 values for $a_*$ uniformly distributed from $a_{in}=1.15679$ (corresponding to an altitude of 1000 km, which we take as the first reference value, although in this region weak dissipative effects are possibly affecting the dynamics) to $a_f=16.6786$ (corresponding to an altitude of $10^5$ km), using Eq. (55) with $\Delta a=0.1$ $R_E$. Figure 4 confirms that the stability time increases with the altitude also in the case of the semimajor axis. Indeed, while for $a_*=a_{in}$ we can ensure the stability of the semimajor axis for a period of the order of one year, in the case $a_*=a_{f}$ we have a stability time of the order of $10^{{3}}$ years. From an analytical point of view, this behavior of the stability time can be explained by the fact that, for higher distances, our model can be approximated by Kepler’s problem in which the semimajor axis is constant.

Fig. 4

Stability time in the $J_2$ model for $a\in [a_{in},a_{f}]$ (see the text for the definition of $a_{in}$, $a_{f}$) allowing a variation of 0.1 $R_E$

5 Secular Stability in the Geolunisolar Model

Using the $J_2$ model, we have demonstrated how the stability of the semimajor axis can be established against short-period perturbations (depending on the satellite’s mean anomaly). In this section, we focus, instead, on the long-term variations in the eccentricity and inclination of the satellite’s orbit, for orbits close to circular ($e<0.1$ rad) and with small inclination $(|i|<0.1)$. One can easily verify that, within the geolunisolar problem (Hamiltonian ${\mathcal {H}}_{\mathrm{gls, sec}}^{\le N}$, see Eq. (24)), the phase-space manifold $e=0$, corresponding to $I_2=0$, constitutes an invariant manifold of the flow, implying that circular orbits remain so for infinitely long times independently of their variations in inclination and longitude of the node. On the other hand, for e small, but nonzero, long-term variations of both the eccentricity and inclination can occur on timescales given by the inverse of the frequencies $\nu _1$ and $\nu _2$ [Eq. (22)]. Since $\nu _1\simeq \nu _2 \simeq \frac{3}{2}\frac{\sqrt{{\mathcal {G}}M_E}R_E^2J_2}{a^{7/2}}$, the secular timescale is of order of $T_\mathrm{sec}={\mathcal {O}}\left( (a/R_E)^2J_2^{-1}\right) T_{\mathrm{short}}$, where $T_{\mathrm{short}}$ is the characteristic time of the frequency associated to the fast angle. Since $J_2\approx 10^{-3}$, the short and long periods are separated by three orders of magnitudes, a fact which justifies altogether the simple averaging over mean anomalies which leads to the model of departure ${\mathcal {H}}_{\mathrm{gls, sec}}^{\le N}$ for the analysis of the secular stability. On the other hand, the fact that $\nu _1\simeq \nu _2$ implies that, near the equator (or, more precisely, for orbits near the Laplace plane, see Sect. 2.2.1), the eccentricity and inclination have coupled variations (the so-called Kozai–Lidov mechanism). This fact implies that, close to the Laplace plane, the term ‘secular stability’ cannot mean the long-term preservation of the eccentricity and inclination one independently of the other, but only the approximate preservation of the combination ${\mathcal {I}}\approx e^2+i^2$ (see below for exact expressions) known as the Kozai–Lidov integral. The normal form construction and remainder estimates in the present section reflect these basic properties of the dynamics.

5.1 Normal Form

Starting with the model ${\mathcal {H}}_{\mathrm{gls, sec}}^{\le N}$ given in Eq. (24), the construction of the normal form proceeds with the algorithm described in Sect. 3 and the following settings:

• i) The book-keeping rule (exponent s in Eq. (39)) is set as $s=s_1+s_2-2$, where $s_1$ and $s_2$ are the exponents appearing in Eq. (24).

• ii) The resonant module [Eq. (31], case 3 of Subsection 3.1) is set as:

  $$\begin{aligned} {\mathcal {M}}:=\{(k_1,k_2)\in {\mathbb {Z}}^2: k_1+k_2=0\} \end{aligned}$$

  where $k_1,k_2$ are the integers specifying each Fourier harmonic in Eq. (24).

• iii) The maximum truncation order is set to $N=15$, while the maximum normalization order is set to $M=12$.

Here, as well, we use a symbolic program to perform all normalizations, which works in essentially the same way as described in Sect. 4.1 for the case of the normal form of the $J_2$ problem.

With the following settings, the Hamiltonian after r normalization steps, where r can take the values $r=1,2,...M$, resumes the form:

$$\begin{aligned} {\mathcal {H}}_{\mathrm{gls, sec}}^{(r)}(I_1,I_2, \phi _1, \phi _2)&={\mathcal {Z}}_{\mathrm{gls, sec}}^{(r)}(I_1, I_2) +{\mathcal {Z}}_{gls, res}^{(r)}(I_1, I_2, \phi _1-\phi _2)\nonumber \\&\quad +{{\mathcal {R}}}_\mathrm{gls}^{(r)}(I_1,I_2,\phi _1,\phi _2)~~. \end{aligned}$$

(56)

The term ${\mathcal {Z}}_{\mathrm{gls, sec}}^{(r)}(I_1, I_2)$, hereafter called the secular part, contains all terms independent of the angles (corresponding to the choice $k_1=k_2=0$ in the resonant module). The dynamics of this term implies separate preservation of the eccentricity and inclination (the latter around the Laplace plane). Instead, ${\mathcal {Z}}_{gls, res}^{(r)}(I_1,I_2, \phi _1-\phi _2)$, called the resonant part of the normal form, collects all normal form terms depending on the resonant angle $\phi _1-\phi _2$. Finally, ${{\mathcal {R}}}_\mathrm{gls}^{(r)}(I_1,I_2, \phi _1,\phi _2)$ is the remainder term, which contains non-normalized terms of book-keeping orders $s=r+1,\ldots ,N$. After M normalization steps, we obtain the final geolunisolar Hamiltonian ${\mathcal {H}}_\mathrm{gls}\equiv {\mathcal {H}}_{\mathrm{gls, sec}}^{(M)}$.

We now look at the dynamics induced by the sum of secular and resonant parts:

$$\begin{aligned} {\mathcal {H}}_{norm}(I_1,I_2,\phi _1,\phi _2)={\mathcal {Z}}_{\mathrm{gls, sec}}^{(M)}(I_1,I_2)+{\mathcal {Z}}_{gls, res}^{(M)}(I_1,I_2,\phi _1-\phi _2), \end{aligned}$$

called, altogether, the resonant normal form ${\mathcal {H}}_{norm}$ (for simplicity, we drop the dependence on the normalization order r from the notation). The quantity $I_1+I_2$ is a first integral for the dynamics induced by ${\mathcal {H}}_{norm}$, which implies that the vertical component of the angular momentum, which coincides with $\Theta$, is preserved.² Given that L is constant, say $L=L_*=\sqrt{\mu _E a_*}$, the quantity

$$\begin{aligned} I_1+I_2=L_*-L_*\sqrt{1-e^2}(1-\cos {i}) \end{aligned}$$

(57)

is a first integral and, as a consequence, the quantity

$$\begin{aligned} {\mathcal {I}}(e,i)=1-\sqrt{1-e^2}(1-\cos {i}) \end{aligned}$$

(58)

is constant for the dynamics induced by the normal form. This means that e and i can change only in such a way that the value of ${\mathcal {I}}(e,i)$ remains constant.

The fact that the presence of resonant first integrals determines a locking in the values of e and i is at the basis of the so-called Kozai–Lidov effect (Lidov 1962; Kozai 1962), which is common, in a wide range of resonant combinations, in many models of Celestial Mechanics.

5.2 Remainder and Stability Estimates

As already mentioned in Sect. 4.2, we need to guarantee that the remainder is small with respect to the normal part; we denote again by ${\mathcal {D}}$ the domain over which the norm $\Vert {{\mathcal {R}}}_\mathrm{gls}^{(M)}\Vert _{\infty ,{{\mathcal {D}}_*}}$ is computed. For a function $f=f(e,i,\phi _1,\phi _2)$ of the form:

$$\begin{aligned} f(e,i,\phi _1,\phi _2)=\sum _{k_1,k_2}\sum _{s_1,s_2} f_{k_1,k_2,s_1,s_2} I_1(e,i)^{s_1/2}I_2(e,i)^{s_2/2}, \end{aligned}$$

(59)

where the sums are over a finite number of terms, we have

$$\begin{aligned} \sup _{(e,i)\in {\mathcal {D}},(\phi _1,\phi _2)\in {{\mathbb {T}}}^2} |f(e,i,\phi _1,\phi _2) \le \Vert f\Vert _{\infty ,{{\mathcal {D}}_*}}, \ \end{aligned}$$

where, recalling the definition in (51), the norm of f is defined as

$$\begin{aligned} \Vert f\Vert _{\infty ,{{\mathcal {D}}_*}}=\sum _{k_1,k_2}\sum _{s_1,s_2} |f_{k_1,k_2,s_1,s_2}| I_1(e_*,i_*)^{s_1/2}I_2(e_*,i_*)^{s_2/2}. \end{aligned}$$

(60)

There exists an optimal value of M that minimizes the estimate of the remainder’s norm, as shown in Sect. 5.3 for GEO orbits.

Since $I_1+I_2$ is a first integral for ${\mathcal {H}}_{norm}$, we have that

$$\begin{aligned} \{I_1+I_2, {\mathcal {H}}_{norm}\}=0. \end{aligned}$$

To evaluate the stability of ${\mathcal {I}}(e,i)$, we use the relation:

$$\begin{aligned} \frac{d}{dt}(I_1+I_2)=\{I_1+I_2, {\mathcal {H}}_\mathrm{gls}\}=\{I_1+I_2, {{\mathcal {R}}}_\mathrm{gls}^{(M)}\}; \end{aligned}$$

then, for every $(e^*,i^*,\phi _1^*,\phi _2^*)\in {\mathcal {D}}\times {\mathbb {T}}^2$, we have the following estimate:

$$\begin{aligned} \bigg \vert \frac{d}{dt}(I_1+I_2)(e^*,i^*,\phi _1^*,\phi _2^*)\bigg \vert\le & {} \sup _{\begin{array}{c} (e,i)\in {\mathcal {D}}\\ (\phi _1,\phi _2)\in {\mathbb {T}}^2 \end{array}}\bigg \vert \frac{d}{dt}(I_1+I_2)(e,i,\phi _1,\phi _2)\bigg \vert \\\le & {} \Vert \{I_1+I_2,{{\mathcal {R}}}_\mathrm{gls}^{(M)}\}\Vert _{\infty , {{\mathcal {D}}_*}}\ . \end{aligned}$$

Let us now consider an orbit with initial point $(I_{1,0}, I_{2,0})$ such that the corresponding eccentricity and inclination belong to ${\mathcal {D}}$; consider its evolution up to $t=T$. Using the mean value theorem, we have that

$$\begin{aligned} \Vert (I_1(T)+I_2(T))-(I_{1,0}+I_{2,0})\Vert \le \Vert \{I_1+I_2,{{\mathcal {R}}}_\mathrm{gls}^{(M)}\}\Vert _{\infty , {{\mathcal {D}}_*}}\ T. \end{aligned}$$

(61)

Setting $\Gamma$ to be the maximum value for the variation of $I_1+I_2$ in time, let us denote by ${\widetilde{T}}$ the minimum time such that for every $T\le {\tilde{T}}$

$$\begin{aligned} \Vert (I_1(T)+I_2(T))-(I_{1,0}+I_{2,0})\Vert \le \Gamma \ . \end{aligned}$$

From (61), we have

$$\begin{aligned} {\widetilde{T}}\ge \frac{\Gamma }{\Vert \{I_1+I_2, {{\mathcal {R}}}_\mathrm{gls}^{(M)}\}\Vert _{\infty , {{\mathcal {D}}_*}}}; \end{aligned}$$

then we can use the value of T as $T=\Gamma /\Vert \{I_1+I_2,{{\mathcal {R}}}_\mathrm{gls}^{(M)}\}\Vert _{\infty , {{\mathcal {D}}_*}}$, which gives an estimate for the stability time of $I_1+I_2$ and, consequently, of ${\mathcal {I}}(e,i)$. The stability results for the quantity ${\mathcal {I}}$ can be translated in terms of the orbital elements (e, i) as follows: in view of (58), for small values of e and i we find

$$\begin{aligned} {\mathcal {I}}\simeq L_*\frac{e^2+i^2}{2}, \end{aligned}$$

(62)

hence, if we consider the variations of ${\mathcal {I}}$, e and i, they are connected by the relation

$$\begin{aligned} \frac{\Delta {\mathcal {I}}}{{\mathcal {I}}}\simeq 2\frac{e\Delta e+i\Delta i}{e^2+i^2}. \end{aligned}$$

(63)

For the limit case of e or i fixed and small, one finds

$$\begin{aligned} \frac{\Delta {\mathcal {I}}}{{\mathcal {I}}}\simeq 2\frac{\Delta e}{e}\simeq 2\frac{\Delta i}{i}; \end{aligned}$$

(64)

then the relative variation of ${\mathcal {I}}$ (and, as a consequence, of $I_1+I_2$) is proportional to the relative variations of the orbital elements by a factor 2.

To make the stability results for the geolunisolar model consistent with the ones obtained in Sect. 4.2 for the $J_2$ model, in Sect. 5.3 we set

$$\begin{aligned} \Gamma =0.05\sqrt{\frac{\mu }{a_*}}, \end{aligned}$$

(65)

namely, recalling that $\Delta L=\Delta a/2\sqrt{\mu /a}$ and $\Delta a=0.1$, the maximal variation of $I_1+I_2$ in the geolunisolar model is equal to the maximal variation allowed for the action L in the $J_2$ model.

5.3 Numerical Results for the Geolunisolar Model

For the geolunisolar model, we take the domain $(e,i)\in {\mathcal {D}}=[0,0.1]\times [0,0.1]$ around the forced eccentricity (which is always zero) and the forced inclination (which depends on the chosen altitude).

Since the stability results strongly depend on the distance from the Earth, we select five different altitudes that correspond to cases of interest for the satellite’s problem:

• $h^{(1)}=3000$ km, above the atmosphere;

• $h^{(2)}=20000$ km, that is in MEO region;

• $h^{(3)}=35786$ km, the altitude of GEO orbits;

• $h^{(4)}=50000$ km, corresponding to far objects;

• $h^{(5)}=100000$ km, that corresponds to objects which are very far from the Earth’s surface.

The value of the remainder’s norm depends on the altitude of the orbit: in particular, we can state that the stability time decreases as the altitude increases.

Table 3 Estimate of $\Vert {{\mathcal {R}}}_\mathrm{gls}^{(M)}\Vert _{\infty , {{\mathcal {D}}_*}}$, with $M=12$, in the geolunisolar model with ${\mathcal {D}}=[0,0.1]\times [0,0.1]$ for different altitudes

Fig. 5

Remainder’s norm for the geolunisolar model in the domain ${\mathcal {D}}'=[0,0.1]\times [0,\pi /2]$ for $h^{(i)}$, $i=1,\dots , 5$ (see the text for the definition of $h^{(i)}$)

Table 3 provides the value of $\Vert {{\mathcal {R}}}_\mathrm{gls}^{(M)}\Vert _{\infty ,{{\mathcal {D}}_*}}$ as a function of the altitude, showing a significant worsening for altitudes after the GEO region.

Figure 5 shows the behavior of the remainder’s norm as a function of (e, i) in the bigger domain ${\mathcal {D}}'=[0,0.1]\times [0,\pi /2]$: as we can see, in all cases the domain ${\mathcal {D}}'$ is too large to ensure the smallness of $\Vert {{\mathcal {R}}}_\mathrm{gls}^{(M)}\Vert _{\infty ,{{\mathcal {D}}'_*}}$. Moreover, the magnitude of $\Vert {{\mathcal {R}}}_\mathrm{gls}^{(M)}\Vert _{\infty ,{{\mathcal {D}}'_*}}$ increases significantly with the altitude. We can easily notice that the value of $\Vert {{\mathcal {R}}}_\mathrm{gls}^{(M)}\Vert _{\infty ,{{\mathcal {D}}'_*}}$ is strongly dependent on the inclination: using this fact, we can detect a value of i, denoted by $i_{crit}$, which is the minimum value of the inclination for which $\Vert {{\mathcal {R}}}_\mathrm{gls}^{(M)}\Vert _{\infty ,{{\mathcal {D}}'_*}}$ is of the order of unity. Table 4 shows the computed values of $i_{crit}$ (converted in degrees) for the considered altitudes: we can notice that the smallness domain shrinks substantially between 50000 km and 100000 km; in any case, we can see that for every value of the considered altitudes the domain ${\mathcal {D}}=[0,0.1]\times [0,0.1]$ is contained in the smallness domain of ${{\mathcal {R}}}_\mathrm{gls}^{(M)}$.

Table 4 Value of $i_{crit}$ as a function of different values of the altitude for the geolunisolar model

As mentioned in Sect. 5, the remainder’s norm depends on the normalization order M. Although the norm does not converge to zero if M tends to infinity, there is a value of M, called the optimal normalization order, say $M_{opt}$, for which the norm of the remainder is minimal. Typically, this optimal value is greater than the order of the Taylor expansions of the numerically computed functions, and the estimates for the remainder are so good that there is no reason to push further the order of the expansion; for example, this is the case for the normalized Hamiltonian function which describes the geolunisolar problem computed for the GEO altitude.

Fig. 6

Estimate of $\Vert {{\mathcal {R}}}_\mathrm{gls}^{(M)}\Vert _{\infty , {{\mathcal {D}}_*}}$ as a function of the normalization order M for $h=h^{(3)}$ (GEO distance) in the domain ${\mathcal {D}}=[0,0.1]\times [0,0.1]$ for the geolunisolar model

As we can see from Fig. 6, the optimal normalization order is greater than or equal to 12, that is the order at which we make our estimates.

Once obtained the smallness of $\Vert {{\mathcal {R}}}_\mathrm{gls}^{(M)}\Vert _{\infty ,{{\mathcal {D}}_*}}$ in ${\mathcal {D}}$, we proceed to compute the stability time for the quantity ${\mathcal {I}}(e,i)=1-\sqrt{1-e^2}(1-\cos {i})$.

Table 5 Stability times in years for different altitudes in the domain $(e,i)\in {\mathcal {D}}=[0,0.1]\times [0,0.1]$ for the geolunisolar model

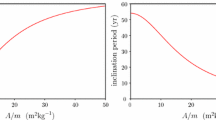
As we can see from Table 5, the stability times are extremely long: this fact depends on the model we considered, with the Lunar orbit in the ecliptic plane without precession effects. However, we can notice a relevant decrease in the stability time for distances greater than GEO. This behavior is opposite to that of the $J_2$ model where the stability time was increasing with the altitude (see Fig. 4). In fact, at low altitudes the $J_2$ model is strongly affected by the Keplerian part and the geopotential, while the geolunisolar model takes into account both the inner effect due to the Earth and the outer effect due to Moon and Sun.

As a final remark, to show the importance of taking the right domain in eccentricity and inclination, let us assume $h=h^{(5)}$ and consider the domain $(e,i)\in B=[0,0.1]\times [0,0.5]$, which is larger than the convergence domain $[0,0.1]\times [0,i_{crit}]$ (see Table 4). If we compute the stability time in the enlarged domain B, we obtain just the value $T=0.00085$ years.

6 Non-degeneracy Conditions

In the previous sections, we examined the question of the long-term stability of the elements (a, e, i) in the case of the Earth’s satellite orbits using a semi-analytical computation based on the size of the remainder of the Birkhoff normal form, computed as described in Sects. 4 and 5. While providing stability times quite long with respect to any application of practical interests, such estimates cannot probe the question of the dependence of the optimal remainder on the small parameters of the problem (the value of $J_2$, as well as the values of (e, i) for non-resonant satellite orbits). Also, it was stressed before that we have no guarantee of the optimality of the estimates themselves with respect to the normalization order, which, in theory, should scale as a power of the inverse of the small parameters of the problem (see Efthymiopoulos 2011 for a tutorial introduction).

All such scalings can be examined, instead, in the framework of the outstanding theorem developed by Nekhoroshev (1977). Under suitable assumptions, the theorem gives a confinement of the action variables for exponentially long times. In particular, the Hamiltonian must satisfy a non-degeneracy condition which, in the original formulation, is called steepness condition. The definition of the steepness condition is quite technical and typically not trivial to verify for a specific Hamiltonian system. However, there are some sufficient conditions which imply steepness, whose verification requires the resolution of algebraic equalities and inequalities. This motivates the introduction of the following definition (see Knezevic and Pavlovic 2008; Pöschel 1993).

Definition 10

Consider the Hamiltonian $h=h({\underline{J}})$ for ${\underline{J}}\in B$ where $B\subset {{\mathbb {R}}}^n$ is an open connected set. Denote by ${\underline{\omega }}({\underline{J}})$ the gradient of h and by ${\mathcal {Q}}({\underline{J}})$ its Hessian matrix. Then:

• (1) $h({\underline{J}})$ is convex in ${\underline{J}}\in B$ if

  $$\begin{aligned} \forall {\underline{u}}\in {\mathbb {R}}^n \quad {\mathcal {Q}}({\underline{J}}){\underline{u}}\cdot {\underline{u}}=0\Leftrightarrow {\underline{u}}={\underline{0}}; \end{aligned}$$

• (2) $h({\underline{J}})$ is quasi-convex in ${\underline{J}}\in B$ if ${\underline{\omega }}({\underline{J}})\ne 0$ and

  $$\begin{aligned} \forall {\underline{u}}\in {\mathbb {R}}^n\qquad {\left\{ \begin{array}{ll} {\underline{\omega }}({\underline{J}})\cdot {\underline{u}}=0 \\ {\mathcal {Q}}({\underline{J}}){\underline{u}}\cdot {\underline{u}}=0 \end{array}\right. } \Leftrightarrow {\underline{u}}={\underline{0}}; \end{aligned}$$

• (3) $h({\underline{J}})$ is three-jet non-degenerate in ${\underline{J}}\in B$ if ${\underline{\omega }}({\underline{J}})\ne 0$ and

  $$\begin{aligned} \forall {\underline{u}}\in {\mathbb {R}}^n\qquad {\left\{ \begin{array}{ll} {\underline{\omega }}({\underline{J}})\cdot {\underline{u}}=0 \\ {\mathcal {Q}}({\underline{J}}){\underline{u}}\cdot {\underline{u}}=0 \\ \sum _{i,j,k=1}^n\frac{\partial ^3 h}{\partial J_i\partial J_j \partial J_k}({\underline{J}})u_iu_ju_k=0 \end{array}\right. } \Leftrightarrow {\underline{u}}={\underline{0}}. \end{aligned}$$

We remark that the convexity condition is equivalent to require that the Hessian matrix ${\mathcal {Q}}({\underline{J}})$ is positive (or negative) definite in ${\underline{J}}$. We add also the following definition of isoenergetically non-degenerate which, for Hamiltonian systems with 2 degrees of freedom, implies quasi-convexity.

Definition 11

The Hamiltonian $h=h({\underline{J}})$ is called isoenergetically non-degenerate in ${\underline{J}}\in B$ with $B\subset {{\mathbb {R}}}^n$ open, if

$$\begin{aligned} \det \begin{pmatrix} \frac{\partial ^2h}{\partial {\underline{J}}^2}({\underline{J}}) &{} \frac{\partial h({\underline{J}})}{\partial {\underline{J}}} \\ \left( \frac{\partial h({\underline{J}})}{\partial {\underline{J}}}\right) ^T &{} {\underline{0}} \end{pmatrix} \ne 0. \end{aligned}$$

One can prove (see Bambusi and Fusé 2017) that, for every Hamiltonian system with n degrees of freedom, quasi-convexity implies isoenergetically non-degeneracy: as a consequence, for two-dimensional Hamiltonian systems, the two conditions are equivalent.

6.1 Numerical Verification of the Non-degeneracy Conditions

We now apply the above definitions to the Hamiltonian functions introduced in Sect. 2. We consider the following cases:

• the Hamiltonian function related to the $J_2$ problem ${\mathcal {H}}_{J_2}$, in form of Taylor expansion up to order 15 in eccentricity and inclination, normalized up to order 12 with respect to the fast angle $\lambda$; we denote the resulting Hamiltonian including the normalized part ${\mathcal {H}}_{J_2,sec}^{(M)}$ and the remainder ${{\mathcal {R}}}_{J_2}^{(M)}$ [see Eq. (47)], as

  $$\begin{aligned} {\mathcal {H}}_{J_2}(\delta L, P, Q, \lambda , p, q)={\mathcal {H}}_{J_2, sec}^{(M)}(\delta L, P, Q, p, q)+{{\mathcal {R}}}^{(M)}_{J_2}(\delta L, P, Q, \lambda , p, q)\ . \end{aligned}$$

  Given the practical stability of the semimajor axis established in Sect. 4.2, in our computations we set $L=L_*$, i.e., $\delta L=0$;

• the Hamiltonian function related to the geolunisolar problem ${\mathcal {H}}_{\mathrm{gls, sec}}$ in (14), expanded around the forced values of inclination and eccentricity (see Sect. 2.2.1) up to order 15 in eccentricity and inclination, see (24). The Hamiltonian ${\mathcal {H}}_{\mathrm{gls, sec}}$ is averaged over the fast angle $\lambda$ and put in resonant normal form with respect to the angles $\phi _1$ and $\phi _2$ up to order 12 in eccentricity and inclination. As a consequence, the resulting Hamiltonian ${\mathcal {H}}_\mathrm{gls}={\mathcal {H}}_{\mathrm{gls, sec}}^{(M)}$, including the normalized part ${\mathcal {Z}}_{\mathrm{gls, sec}}^{(M)}$, the resonant part ${\mathcal {Z}}_{gls,res}^{(M)}$ and the remainder ${{\mathcal {R}}}_\mathrm{gls}^{(M)}$ [see Eq. (56)], has two degrees of freedom and it is the sum of three terms:

  $$\begin{aligned} {\mathcal {H}}_\mathrm{gls}(I_1,I_2, \phi _1,\phi _2)= & {} {\mathcal {H}}_{\mathrm{gls, sec}}(I_1,I_2)+{\mathcal {H}}_{gls,res}(I_1,I_2,\phi _1,\phi _2)\\&+{{\mathcal {R}}}_\mathrm{gls}(I_1,I_2, \phi _1,\phi _2), \end{aligned}$$

  where ${\mathcal {H}}_{gls, res}$ depends only on the quasi-resonant combination $\phi _1-\phi _2$.

To analyze the non-degeneracy conditions, we write the Hamiltonian as the sum of two terms, namely an integrable Hamiltonian h and a perturbing function f. For the $J_2$-Hamiltonian, we set h(P, Q) to contain all the terms of ${\mathcal {H}}_{J_2}$ that are independent on all angles, while the perturbing function f contains all other terms. For the geolunisolar case, we choose $h(I_1,I_2)$ to be the angle-independent part of the truncation up to order 2 of ${\mathcal {H}}_\mathrm{gls}$: in this way, the Hessian matrix of h is independent of the actions, and the computations are easier.³

Since the Hamiltonian functions depend on the parameter $L_*=\sqrt{\mu a_*}$, we select four reference values for the altitudes that correspond to distances of interest in satellite dynamics:

• 3000 km, for near-Earth objects;

• 20000 km, for distance of the order of MEO;

• 35790 km, for GEO orbits;

• 50000 km, for far objects.

For each of these values, we check the non-degeneracy conditions of convexity, quasi-convexity and three-jet, for both the case of the $J_2$-problem and the geolunisolar models in the domain⁴$(e,i)\in {\mathcal {D}}=[0,0.1]\times [0,0.1]$, which corresponds to a domain in the actions ${\mathcal {D}}''=[0,P_{max}]\times [0,Q_{max}]\subset {\mathbb {R}}^2$, where $P_{max}$, $Q_{max}$ correspond to $e=0.1$, $i=0.1$ and can be computed numerically.

Remark 12

We notice that a Hamiltonian $h=h(P,Q)$ (or, equivalently, $h(I_1,I_2)$ in the geolunisolar case) is convex in ${\mathcal {D}}''\in {\mathbb {R}}^2$, if the product of the eigenvalues of the Hessian matrix of h is greater than zero for every $(P,Q)\in {\mathcal {D}}''$. Moreover, h(P, Q) is quasi-convex in ${\mathcal {D}}''\in {\mathbb {R}}^2$, if for every $(P,Q)\in {\mathcal {D}}''$ the determinant of the matrix

$$\begin{aligned} A= \begin{pmatrix} h_{11}(P,Q) &{} h_{12}(P,Q) &{} h_1(P,Q) \\ h_{21}(P,Q) &{} h_{22}(P,Q) &{} h_2(P,Q) \\ h_1(P,Q) &{} h_2(P,Q) &{} 0 \end{pmatrix} \end{aligned}$$

(66)

is nonzero.

If the convexity and quasi-convexity tests fail, one can control the three-jet non-degeneracy condition, that we compute, again, numerically, checking that the system

$$\begin{aligned} {\left\{ \begin{array}{ll} {\underline{\omega }}(P,Q)\cdot {\underline{u}}=0 \\ (\partial ^2 h(P,Q){\underline{u}})\cdot {\underline{u}}=0 \\ ((\partial ^3 h(P,Q){\underline{u}}){\underline{u}})\cdot {\underline{u}}=0 \end{array}\right. } \end{aligned}$$

(67)

evaluated on a grid of values $(P,Q)\in {\mathcal {D}}''$ admits only the trivial solution ${\underline{u}}=(0,0,0)$. Since convexity implies quasi-convexity and quasi-convexity implies three-jet non-degeneracy, to identify which of the conditions is satisfied, we proceed in the following way:

• we begin with the convexity test on the product of the eigenvalues: if the product is positive for every value of $(P,Q)\in {\mathcal {D}}''$, then h(P, Q) is convex;

• if the convexity test fails, we pass to the quasi-convexity condition, checking the criteria given in Definition 10 and Remark 12;

• if the quasi-convexity test fails, we check the three-jet non-degeneracy through the numerical test based on Definition 10.

6.2 Non-degeneracy of the $J_2$ Hamiltonian

We start from the convexity test; we denote by $\lambda _1$, $\lambda _2$ the eigenvalues of the Hessian matrix of h.

Table 6 Values of $\lambda _1\, \lambda _2$ for the $J_2$ model for different altitudes and $(P,Q)\in {\mathcal {D}}''$

Table 6 gives the numerical values of $\lambda _1\lambda _2$ for different altitudes and (P, Q) in the domain ${\mathcal {D}}''$ (we recall that, since the values in the Hessian matrix depend on P and Q, we have an interval for $\lambda _1\lambda _2$ instead of a single value). As one can see, the product of the eigenvalues is always negative or zero within numerical precision level, leading to the conclusion that the Hamiltonian ${\mathcal {H}}_{J_2}$ is not convex in ${\mathcal {D}}''$ for the considered altitudes.

Table 7 Values of $\det {A}$, with A as in (66) for the $J_2$ model for different altitudes and $(P,Q)\in {\mathcal {D}}''$

We can then pass to the quasi-convexity test. We consider the determinant of the matrix A defined in (66) for $(P,Q)\in {\mathcal {D}}''$. As we can see from Table 7, for every considered altitude the values of $\det {A}$ are equal to zero within the numerical precision level, leading to the conclusion that the $J_2$ Hamiltonian is not quasi-convex in ${\mathcal {D}}''$.

The failure of the quasi-convexity for the $J_2$ problem is a relevant fact: as we will see in Sect. 6.3, the effects of the lunisolar attraction will eliminate such degeneracy, making the total Hamiltonian quasi-convex.

We conclude with the test on the three-jet non-degeneracy condition. To make the computations quantitative, we solved system (67) for values $(P_i,Q_j)$ on a mesh of 10000 points in ${\mathcal {D}}''$. For every pair of values $(P_i,Q_j)$ the only solution of the system is the trivial one ${\underline{u}}=(0,0)$, leading to conclude that the Hamiltonian of the $J_2$ model is three-jet non-degenerate in ${\mathcal {D}}''$. This fact is not unexpected as for systems up to 3 degrees of freedom the three-jet condition is generically satisfied (see Schirinzi and Guzzo 2015).

6.3 Quasi-convexity of the Geolunisolar Hamiltonian

As for the $J_2$ model, we start from the convexity test. In this case, the unperturbed Hamiltonian is a polynomial of degree 2 in the actions; then, the Hessian matrix of $h(I_1,I_2)$ does not depend on the values of $I_1$ and $I_2$, and the same holds for its eigenvalues. This makes the test on the convexity of the Hamiltonian easier.

Table 8 Values of $\lambda _1$ and $\lambda _2$ for different altitudes in the geolunisolar model

Table 8 shows the values of $\lambda _1$ and $\lambda _2$ for different altitudes. As we can see, in every case the eigenvalues of the Hessian have opposite sign, showing that the geolunisolar unperturbed Hamiltonian is not convex in ${\mathbb {R}}^2$, and hence in ${\mathcal {D}}''$.

As for the quasi-convexity, we check whether the matrix A defined in (66) is non-degenerate for every value $(I_1,I_2)\in {\mathcal {D}}''$.

Table 9 Values of $\det {A}$, with A in (66) in the geolunisolar case for different altitudes and $(I_1,I_2)\in {\mathcal {D}}''$

From Table 9 we can see that the determinant of A is strictly positive for every value of the selected altitudes and every $(I_1,I_2)\in {\mathcal {D}}''$. Hence, we conclude that the Hamiltonian for the geolunisolar case is quasi-convex. As observed at the end of Sect. 6.2, this fact is highly non-trivial, since it means that the lunisolar perturbation of the $J_2$ model removes the degeneracy.