The Height Invariant of a Four-Parameter Semitoric System with Two Focus–Focus Singularities

Abstract

Semitoric systems are a special class of completely integrable systems with two degrees of freedom that have been symplectically classified by Pelayo and Vũ Ngọc about a decade ago in terms of five symplectic invariants. If a semitoric system has several focus–focus singularities, then some of these invariants have multiple components, one for each focus–focus singularity. Their computation is not at all evident, especially in multi-parameter families. In this paper, we consider a four-parameter family of semitoric systems with two focus–focus singularities. In particular, apart from the polygon invariant, we compute the so-called height invariant. Moreover, we show that the two components of this invariant encode the symmetries of the system in an intricate way.

1 Introduction

In the last decades, various efforts have been made towards the construction of classifications within the theory of completely integrable dynamical systems. These classifications are based on invariants that capture various aspects of a system with respect to different notions of equivalence. They are useful for two main reasons: they give an overview of all possible systems within a certain class and allow us to distinguish between non-equivalent systems. If we restrict ourselves to classifications of symplectic type, important accomplishments are the classification of toric systems, due to Delzant (1988), Atiyah (1982) and Guillemin and Sternberg (1982) and the classification of semitoric systems, due to Pelayo and Vũ Ngọc (2009, 2011) and recently extended by Palmer et al. (2019). Another significant result in this line is the symplectic classification of completely integrable systems using characteristic classes, introduced by Zung (2003).

Semitoric systems are a class of dynamical systems defined on connected four-dimensional symplectic manifolds, introduced by Vũ Ngọc (2007). They are integrable systems, so they have two conserved quantities, one of which is a proper map that induces an effective circle action. Moreover, all singularities are required to be non-degenerate and must not have hyperbolic components. From a topological point of view, these systems can be described using the theory of singular Lagrangian fibrations, cf. Byrd and Friedman (1954). The original definition by Vũ Ngọc (2007) allowed for a diffeomorphism on the base, but it was later adapted by Pelayo and Vũ Ngọc (2009) for classification purposes, removing this diffeomorphism.

From the symplectic point of view, one of the motivations to study semitoric systems comes from the analysis of systems with monodromy in the quantum physics and chemistry literature, see, for example, Child et al. (1999), Sadovskii and Zhilinskii (1999) for a theoretical approach and Assémat et al. (2010), Fitch et al. (2009), Winnewisser et al. (2005) for experimental studies.

In this setting, one has the joint spectrum of a set of unknown quantum operators and wants to recover information about the system. An overview of the possible candidate systems can be obtained by means of a classification. Since classical systems are generally easier to understand, one can make use of Bohr’s correspondence principle or Zauberstab and focus on constructing a classification for classical systems. However, in order for the results to be valid after quantisation, it is important that this classification preserves the symplectic structure, cf. Pelayo (2021) for more details on this approach.

Two foundational examples of the semitoric systems theory are the coupled spin-oscillator and the coupled angular momenta. The first one is a particular case of the Jaynes and Cummings (1963) model from quantum optics and it consists of the coupling of a classical spin on the two-sphere $\mathbb {S}^2$ with a harmonic oscillator on the plane $\mathbb {R}^2$, cf. Pelayo and Vũ Ngọc (2012). The second one is the classical version of the addition of two quantum angular momenta, defined on the product of two copies of $\mathbb {S}^2$. It models, for example, the reduced Hamiltonian of a hydrogen-like atom in the presence of parallel electric and magnetic fields, cf. Sadovskii et al. (1996). In the last years, several other examples of semitoric systems have been discovered: Hohloch and Palmer (2018) introduced a family with two focus–focus points, Le Floch and Palmer (2018) proved the existence of examples in all Hirzebruch surfaces and De Meulenaere and Hohloch (2021) proposed a system with four focus–focus points that has double pinched focus–focus fibres for a certain value of the parameter.

The classification of semitoric systems is based on five symplectic invariants: the number of focus–focus points, the polygon invariant, the height invariant, the Taylor series invariant and the twisting index invariant.

The survey article by Alonso and Hohloch (2019) gives an overview of the state of the art concerning examples and computations of invariants reached in 2019. Note that the computation of these invariants is far from trivial, especially if the aim is to make a general calculation of the invariants for a whole family of systems depending on several parameters, instead of for only one explicitly given, concrete system.

So far, the full list of invariants has only been computed for the two foundational examples. The computation of the invariants in these two cases is based on the use of the properties of elliptic integrals, cf. Alonso (2019). In the case of the coupled spin-oscillator, it was initiated by Pelayo and Vũ Ngọc (2012) and completed by Alonso et al. (2019). In this case, two parameters are taken into account, but the dependence is quite simple. For the coupled angular momenta, it was initiated by Le Floch and Pelayo (2018) and completed by Alonso et al. (2020). In this case, the dependence is of three parameters and significantly more involved.

Expressing the invariants as a function of the parameters of the system is important because, besides the quantitative results, it also allows for qualitative considerations. For instance, one can compare the roles played by geometric parameters, i.e. those related to the symplectic manifold, and by coupling parameters, i.e. those only appearing in the momentum map. In case some parameters also affect the type of singularities, for example making focus–focus singularities appear and disappear, one can also see what happens to the invariants as the critical values of the parameters are approached.

In both foundational examples, the invariants display the symmetries of the systems. Moreover, for the coupled angular momenta, the terms of the Taylor series invariant go to infinity as the coupling parameter approaches the critical values, cf. Alonso et al. (2020). However, a limitation of these examples is that the number of focus–focus points is at most one. Semitoric systems with more than one focus–focus point are interesting because, in this case, the symplectic invariants have multiple components, one for each focus–focus point. So the different components can (and should) be compared with each other. In particular, it is interesting to see how the different components depend on the parameters of the system and how they reflect the possible symmetries of the system.

Note that the presence of multiple focus–focus points increases the complexity of the computations significantly. So far, the only results in this direction are the computation of the polygon invariant and the height invariant of two families of systems with a relatively simple dependence on two parameters, cf. Le Floch and Palmer (2018). There is, in general, a certain trade-off between, on the one hand, the qualitative richness of having the invariants expressed as functions of several parameters and, on the other hand, the feasibility of their computations.

In the present paper, we choose the former option, i.e. focusing on dependence on multiple parameters. We managed to compute the number of focus–focus points invariant, the polygon invariant, and the height invariant. However, due to the number of parameters and the complexity of the computations, the Taylor series invariant and the twisting index invariant are beyond current computational methods and resources, cf. Alonso (2019).

Let $(M,\omega )$ be the symplectic manifold $M=\mathbb {S}^2 \times \mathbb {S}^2$ with symplectic form $\omega = - (R_1\, \omega _{\mathbb {S}^2} \oplus R_2\, \omega _{\mathbb {S}^2})$, where $\omega _{\mathbb {S}^2}$ is the standard symplectic form of the unit sphere and $0<R_1 <R_2$ or $0< R_2< R_1$. Given $(x_1,y_1,z_1, x_2,y_2,z_2)$ Cartesian coordinates in M and $s_1, s_2 \in [0,1]$, we consider the integrable system $(M,\omega ,F)$, where $F:=(L,H)$ is defined by

(1)

It is a family of semitoric systems that can have up to two focus–focus singularities and depends on four parameters in total, two geometric parameters $R_1,R_2>0,$ $R_1 \ne R_2$ and two coupling parameters $s_1,s_2 \in [0,1]$.

Our first result is the computation of the number ${n_{\text {FF}}}$ of focus–focus singularities, which is the first symplectic invariant of a semitoric system:

Theorem 1

The number of focus–focus points invariant of system (1) is ${n_{\text {FF}}}=0$ if $E>0$ and ${n_{\text {FF}}}=2$ if $E<0$, where

$$\begin{aligned} \begin{aligned} E&= {R_2}^2 (1 - 2 {s_1})^2 (-1 + {s_2})^2 + {R_1}^2 (1 - 2 {s_1})^2 {s_2}^2 - 2 {R_1} {R_2} (8 (-1 + {s_1})^2 {s_1}^2 \\ {}&\quad + {s_2} - 12 (-1 + {s_1}) {s_1} {s_2} + (7 + 12 (-1 + {s_1}) {s_1}) {s_2}^2 - 16 {s_2}^3 + 8 {s_2}^4). \end{aligned} \end{aligned}$$

If $E=0$, the system fails to be semitoric.

Theorem 1 is a reformulation of Theorem 15 and Corollary 16 stated later in the paper. The number of focus–focus points invariant is illustrated in Fig. 6. The image of the momentum map of system (1) is plotted in Fig. 5 which is the starting point for the computation of the polygon invariant. The polygon invariant is the result of a straightening procedure of the image of the momentum map, introduced in Vũ Ngọc (2007), as a generalisation of Delzant’s polygon invariant for toric systems, cf. Delzant (1988).

Fig. 1

Representation of the height invariant for $R_1=1$, $R_2=4$

Theorem 2

The polygon invariant of the system (4) is determined by the following cases:

• If ${n_{\text {FF}}}=2$, the polygon invariant is the $((\mathbb {Z}_2)^2\times \mathbb {Z})$-orbit generated by any of the polygons represented in Fig. 7.

• If ${n_{\text {FF}}}=0$ and $(s_1,s_2)$ lies in the same connected component as the point (0, 0) or (1, 1), then the polygon invariant is the $\mathbb {Z}$-orbit generated by the polygon in Fig. 7b.

• If ${n_{\text {FF}}}=0$ and $(s_1,s_2)$ lies in the same connected component as the point (1, 0) or (0, 1), then the polygon invariant is the $\mathbb {Z}$-orbit generated by the polygon in Fig. 7c.

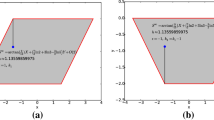
Whenever ${n_{\text {FF}}}=2$, the height invariant is defined and has two components. This invariant describes the position of the focus–focus values in the polygon after the straightening procedure. Their explicit computation is our main result:

Theorem 3

For the values of $(s_1,s_2)$ for which the system (1) has two focus–focus singularities, the height invariant $h :=(h_1,h_2)$ is given by

$$\begin{aligned} h_1&= -\dfrac{1}{2\pi } \mathcal {F}(s_1,s_2,R_1,R_2) + 2 u\left( (s_1-\tfrac{1}{2} )(s_2 - \tfrac{R_2}{R_2+R_1}) \right) , \\ h_2&= \, \dfrac{1}{2\pi } \mathcal {F}(s_1,s_2,R_1,R_2) +2 u\left( -(s_1-\tfrac{1}{2} )(s_2 - \tfrac{R_2}{R_2+R_1}) \right) = 2-h_1 \end{aligned}$$

where u is the Heaviside step function and

$$\begin{aligned}&\mathcal {F}(s_1,s_2,R_1,R_2) := 2 R_2 \arctan \left( \frac{\gamma _C}{\sqrt{\gamma _A} (2 {s_1}-1) (R_2 ({s_2}-1)+R_1{s_2})}\right) \\&\quad + 2 R_1 \arctan \left( \frac{\gamma _D}{\sqrt{\gamma _A} (2 {s_1}-1) (R_2 ({s_2}-1)+R_1{s_2})}\right) \\&\quad + \frac{(2 {s_1}-1) (R_2 ({s_2}-1)+R_1{s_2}) }{2 \left( {s_1}^2-{s_1}+{s_2}^2-{s_2}\right) }\log \left( \frac{-\sqrt{\gamma _B}}{2 (R_2+R_1) \left( {s_1}^2-{s_1}+{s_2}^2-{s_2}\right) +\sqrt{\gamma _A}}\right) . \end{aligned}$$

The height invariant is plotted in Fig. 1 and the coefficients $\gamma _A$ $\gamma _B$, $\gamma _C$ and $\gamma _D$ are explicitly stated in Proposition 4.

The coefficients encode the dependence of the height invariant on the various parameters. This dependence is polynomial, except for some radicals.

Proposition 4

The coefficients $\gamma _A$ $\gamma _B$, $\gamma _C$ and $\gamma _D$ of Theorem 3 are given by

$$\begin{aligned} \gamma _A&:= -{R_2}^2 (1-2 {s_1})^2 ({s_2}-1)^2+2 R_2 R_1 \left( 8 {s_1}^4-16 {s_1}^3+4 {s_1}^2 \left( 3 {s_2}^2-3 {s_2}+2\right) \right. \\&\quad \left. -12 {s_1} ({s_2}-1) {s_2}+{s_2} \left( 8 {s_2}^3-16 {s_2}^2+7 {s_2}+1\right) \right) -{R_1}^2(1-2 {s_1})^2 {s_2}^2 \\ \gamma _B&:= {R_2}^2 \left( 4 {s_1}^4-8 {s_1}^3+4 {s_1}^2 \left( 3 {s_2}^2-4 {s_2}+2\right) -4 {s_1} \left( 3 {s_2}^2-4 {s_2}+1\right) \right. \\&\quad \left. +({s_2}-1)^2 \left( 4 {s_2}^2+1\right) \right) -2 R_2 R_1 \left( 4 {s_1}^4-8 {s_1}^3+4 {s_1}^2 \left( {s_2}^2-{s_2}+1\right) \right. \\&\quad \left. -4 {s_1} ({s_2}-1) {s_2}+{s_2} \left( 4 {s_2}^3-8 {s_2}^2+3 {s_2}+1\right) \right) + {R_1}^2 \left( 4 {s_1}^4-8 {s_1}^3 \right. \\&\quad \left. +4 {s_1}^2 \left( 3 {s_2}^2-2 {s_2}+1\right) +4 {s_1} {s_2} (2-3 {s_2})+{s_2}^2 \left( 4 {s_2}^2-8 {s_2}+5\right) \right) \\ \gamma _C&:= -4 {R_2}^2 {s_1}^2 {s_2}^2+8 {R_2}^2 {s_1}^2 {s_2}-4 {R_2}^2 {s_1}^2+4 {R_2}^2 {s_1} {s_2}^2-8 {R_2}^2 {s_1} {s_2}+4 {R_2}^2 {s_1}\\&\quad -{R_2}^2 {s_2}^2+2 {R_2}^2 {s_2}-{R_2}^2+8 {R_2 R_1} {s_1}^4-16 {R_2 R_1} {s_1}^3\\&\quad +8 {R_2 R_1} {s_1}^2 {s_2}^2-8 {R_2 R_1} {s_1}^2 {s_2}\\&\quad +8 {R_2 R_1} {s_1}^2-8 {R_2 R_1} {s_1} {s_2}^2+8 {R_2 R_1} {s_1} {s_2}+8 {R_2 R_1} {s_2}^4\\&\quad -16 {R_2 R_1} {s_2}^3+6 {R_2 R_1} {s_2}^2\\&\quad +2 {R_2 R_1} {s_2}+4R_1 \sqrt{{\gamma _B}} \left( -{s_1}^2+{s_1}-{s_2}^2+{s_2}\right) -8{R_1}^2 {s_1}^4\\&\quad +16{R_1}^2 {s_1}^3-20{R_1}^2 {s_1}^2 {s_2}^2\\&\quad +16 {R_1}^2{s_1}^2 {s_2}-8{R_1}^2 {s_1}^2+20{R_1}^2 {s_1} {s_2}^2-16{R_1}^2 {s_1} {s_2}-8{R_1}^2 {s_2}^4\\&\quad +16{R_1}^2 {s_2}^3-9{R_1}^2 {s_2}^2 \\ \gamma _D&:= -8 {R_2}^2 {s_1}^4+16 {R_2}^2 {s_1}^3-20 {R_2}^2 {s_1}^2 {s_2}^2+24 {R_2}^2 {s_1}^2 {s_2}\\&\quad -12 {R_2}^2 {s_1}^2+20 {R_2}^2 {s_1} {s_2}^2\\&\quad -24 {R_2}^2 {s_1} {s_2}+4 {R_2}^2 {s_1}-8 {R_2}^2 {s_2}^4+16 {R_2}^2 {s_2}^3-9 {R_2}^2 {s_2}^2+2 {R_2}^2 {s_2}-{R_2}^2\\&\quad +4 R_2 \sqrt{{\gamma _B}} \left( -{s_1}^2+{s_1}-{s_2}^2+{s_2}\right) +8 {R_2 R_1} {s_1}^4\\&\quad -16 {R_2 R_1} {s_1}^3+8 {R_2 R_1} {s_1}^2 {s_2}^2\\&\quad -8 {R_2 R_1} {s_1}^2 {s_2}+8 {R_2 R_1} {s_1}^2-8 {R_2 R_1} {s_1} {s_2}^2+8 {R_2 R_1} {s_1} {s_2}\\&\quad +8 {R_2 R_1} {s_2}^4-16 {R_2 R_1} {s_2}^3\\&\quad +6 {R_2 R_1} {s_2}^2+2 {R_2 R_1} {s_2}-4{R_1}^2 {s_1}^2 {s_2}^2+4{R_1}^2 {s_1} {s_2}^2-{R_1}^2{s_2}^2. \end{aligned}$$

Theorem 3 implies the following relation between the height invariant and the parameters of system (1):

Remark 5

The two components $(h_1, h_2)$ of the height invariant have an intricate dependence on the four parameters $s_1, s_2, R_1, R_2$ of the system but a very simple relation between each other, namely $h_2=2-h_1$.

Theorem 3 and Proposition 4 are restated and proven as Theorem 22 later in the paper. Remark 5 reappears as Remark 23 at the very end of the paper.

All computations in this paper were verified with Mathematica.

Structure of the paper

This paper is structured as follows. In Sect. 2, we briefly summarise the definition of simple semitoric systems and the classification in terms of symplectic invariants. In Sect. 3, we introduce our family of semitoric systems and compute the number of focus–focus points and the polygon invariant. Section 4 is devoted to the computation of the height invariant associated with both focus–focus singularities.

Figures

All figures have been made with Mathematica. Figure 2 has also been edited with Inkscape.

2 The symplectic invariants of semitoric systems

In this section, we briefly summarise the symplectic classification of simple semitoric systems. More details can be found in the original papers by Pelayo and Vũ Ngọc (2009, 2011).

Let $(M,\omega )$ denote a connected four-dimensional symplectic manifold. The triplet $(M,\omega ,F)$ is said to be a completely integrable system if $F:=(L,H):M \rightarrow \mathbb {R}^2$ is a smooth map such that dF has maximal rank almost everywhere and the components L, H Poisson-commute, i.e. $\{L,H\}:= \omega (\mathcal {X}_L,\mathcal {X}_H)=0$, where $\mathcal {X}_f$ is the Hamiltonian vector field associated with a smooth map $f:M \rightarrow \mathbb {R}$ via $\omega (\mathcal {X}_f,\cdot ) = -\mathrm {d}f$. This definition of integrability is sometimes referred to as Liouville integrability in the literature. The singularities of $(M,\omega ,F)$ are the points where the differentials DL, DH fail to be linearly independent, so the rank of DF is not maximal. Non-degenerate singularities (see Byrd and Friedman (1954) or Vey (1978) for a precise definition) can be locally characterised using normal forms, cf. Eliasson (1984, 1990), Miranda and Zung (2006), Miranda and Vũ Ngọc (2005), Vũ Ngọc and Wacheux (2013), and others. In particular, they can be decomposed into regular, elliptic, hyperbolic and focus–focus components.

Definition 6

A semitoric system is a completely integrable system $(M,\omega ,F)$ with two degrees of freedom, where $F:=(L,H): M \rightarrow \mathbb {R}^2$ is smooth and the following conditions are satisfied:

• (1) All singularities are non-degenerate and have no hyperbolic components.

• (2) The map L induces an effective $\mathbb {S}^1$-action on M with a $2\pi$-periodic flow.

• (3) L is proper, i.e. the preimage of a compact set by L is compact again.

Moreover, if the following condition is satisfied, the semitoric system is said to be simple:

• (4) In each level set of L there is at most one singularity of focus–focus type.

In the present work, we will only consider simple semitoric systems. Note, also, that if M is compact, then condition (3) is automatically satisfied. In the context of semitoric systems, we have two degrees of freedom and we exclude hyperbolic components, so the rank of DF can only be 0 or 1. Singularities of rank 0 can either be of focus–focus type or of elliptic–elliptic type, i.e. having two elliptic components. Singularities of rank 1 must necessarily have a regular and an elliptic component, so they are called elliptic-regular singularities.

Fig. 2

Example fibration of a semitoric system, corresponding to the coupled angular momenta for $t=1/2$ and $R_2>R_1$. The fibration has three elliptic–elliptic fibres, one focus–focus fibre and three 1-parameter families of elliptic-regular fibres. On $B_\text {reg}$, the fibres are regular 2-tori

2.1 The singular Lagrangian fibration

The momentum map $F:=(L,H)$ of a semitoric system induces a two-dimensional singular Lagrangian fibration on M. The base of this fibration is the image $B:=F(M)$, which is a contractible subset of $\mathbb {R}^2$. Since L is proper, we know that all fibres of F are compact. The case of a proper momentum map F but not proper L has been studied in Pelayo et al. (2017). Vũ Ngọc (2007) showed that the fibres of semitoric systems are connected and he also characterised the structure of the fibration over B. The boundary $\partial B \subset B$ consists of all elliptic–elliptic and elliptic-regular critical values. The former are located in the vertices, while the latter always come in one-parameter families and form the edges. The set $B_{FF}$ of focus–focus critical values is finite and lies in the interior of B. The regular fibres are thus mapped to $B_{\text {reg}} := \mathring{B} \backslash B_{FF}$.

Singular fibres are those containing a singularity. Elliptic–elliptic singularities constitute always their own fibres. Elliptic-regular fibres are homeomorphic to a circle. Fibres containing a focus–focus singularity are homeomorphic to a pinched torus, see Fig. 2. If simplicity is not assumed (cf. Definition 6), then fibres containing more than one focus–focus singularity, homeomorphic to a multi-pinched torus, are also possible. This situation has been studied by Pelayo and Tang (2018) and Palmer et al. (2019).

Regular fibres are those containing no singularities. According to the action-angle theorem by Arnold (1963), regular fibres are homeomorphic to the two-torus $\mathbb {T}^2$. More precisely, for each regular value $c \in B_\text {reg}$ we can find a neighbourhood U of c and $V \subset \mathbb {R}^2$ of the origin such that $F^{-1}(U) \subset M$ is symplectically equivalent to $V \times \mathbb {T}^2 \subset T^* \mathbb {T}^2$. This defines an integral-affine structure on $B_\text {reg}$. Let $\Lambda _c = F^{-1}(c) \simeq \mathbb {T}^2$ be the fibre corresponding to the value c and let $\{\gamma _1(c), \gamma _2(c)\}$ be a basis of $H_1(\Lambda _c)$, varying smoothly with c. Then, the action coordinates $(I_1,I_2)$ on V are given by the expression

$$\begin{aligned} I_j(c):=\dfrac{1}{2\pi } \oint _{\gamma _j(c)} \varpi ,\qquad j=1,2, \end{aligned}$$

(2)

where $\varpi$ is defined on a semiglobal neighbourhood of $\Lambda _c$ and is a primitive of the symplectic form, i.e. $\mathrm {d}\varpi = \omega$ on $\Lambda _c$.

Since the Hamiltonian flow of L induces a global circular action on M, we can take $\gamma _1(c)$ to be the orbit of L. This way, we will have $I_1(c) = L(c)$. Different choices of $\gamma _2(c)$ belonging to different homology classes will result in different values of $I_2(c)$, so there is an integer degree of freedom in the definition of this action coordinate.

2.2 The polygon and height invariants

Vũ Ngọc (2007) used the action coordinates to define the so-called cartographic homeomorphism as follows. Let ${n_{\text {FF}}}\in \mathbb {Z}$ be the number of focus–focus points and $c_1,\ldots ,c_{n_{\text {FF}}}\in B$ their critical values. For each $r =1,\ldots ,{n_{\text {FF}}}$, pick a sign choice $\epsilon _r \in \{-1,1\} \simeq \mathbb {Z}_2$ and consider the segment $b_r^{\epsilon _r} \subset B$ that starts in $c_r$ and extends upwards if $\epsilon _r = +1$ and downwards if $\epsilon _r = -1$. Let $b^\epsilon = \cup _r b_r^{\epsilon _r}$. Then, for any set of choices $\epsilon = (\epsilon _1,\ldots ,\epsilon _{n_{\text {FF}}})$ there exists a map $f:=f^{\epsilon }:B \rightarrow \mathbb {R}^2$ that is a homeomorphism onto its image $\Delta := f(M)$, it preserves the first coordinate, i.e. $f(l,h) = (l,f^{(2)}(l,h))$ and $f|_{B\backslash b^\epsilon }$ is a diffeomorphism onto its image. This process is illustrated in Fig. 3.

Fig. 3

The cartographic homeomorphism f brings the image of the momentum map $F(M)=:B$ to a polygon $f(B)=:\Delta$. It preserves the first coordinate and adds corners at the focus–focus values following the cutting directions $\epsilon = (\epsilon _1, \epsilon _2)$. In this case, we have $\epsilon = (1,-1)$

The map f is constructed by extending the coordinates $(L,I_2)$ defined by equation (2). The non-smoothness along the segments $b^\epsilon _r$ is a consequence of the monodromy induced by the presence of focus–focus singularities, an obstruction to globally defined action-angle coordinates studied, among others, by Nekhoroshev (1972) and Duistermaat (1980).

The image $\Delta \subset \mathbb {R}^2$ of the cartographic homeomorphism is a convex rational polygon, which is compact if and only if M is compact, cf. Pelayo and Vũ Ngọc (2011). Since the definition of the action $I_2$ is not unique, neither is $\Delta$. There is a $\mathbb {Z}$-action that relates all possible choices of $I_2$. Besides that, there is a $(\mathbb {Z}_2)^{n_{\text {FF}}}$-action of sign choices $\epsilon$ that also acts on f.

Definition 7

The polygon invariant associated with the simple semitoric system $(M,\omega ,F)$ is the equivalence class $[\Delta ]$ of the polygon $\Delta = f(B)$ by the $(\mathbb {Z}_2)^{n_{\text {FF}}}\times \mathbb {Z}$-action that relates all possible choices of f.

The image of the focus–focus critical values under the cartographic homeomorphism is the intuition for next invariant: for each focus–focus critical value $c_r$, $r=1,\ldots ,{n_{\text {FF}}}$, we can compute the vertical distance between the image of the critical value under f and the edge of the polygon $\Delta$,

$$\begin{aligned} h_r := f^{(2)}(c_r) - \min _{c \in \Delta \cap b^{-1}_r} \pi _2(c), \end{aligned}$$

(3)

where $\pi _2:\mathbb {R}^2 \rightarrow \mathbb {R}$ is the canonical projection onto the second coordinate. This quantity is independent of the choice of map f, cf. Pelayo and Vũ Ngọc (2009). The height $h_r$ can also be interpreted as the symplectic volume of the submanifold $Y_r^- := \{ p \in M$ | $L(p) = L(m_r)$ and $H(p) < H(m_r)\}$, that is, the real volume of $Y_r^-$ divided by $2\pi$, where $m_r \in M$ is the focus–focus singularity corresponding to $c_r$.

Definition 8

The height invariant associated with the simple semitoric system $(M,\omega ,F)$ is the ${n_{\text {FF}}}$-tuple $h = (h_1,\ldots ,h_{n_{\text {FF}}})$. It is independent of the choice of cartographic homeomorphism f.

The polygon and height invariants are, respectively, invariants (iii) and (iv) in Pelayo and Vũ Ngọc (2009).

2.3 The other invariants and the symplectic classification

The remaining two invariants are related to the structure of the action $I_2$ as we approach focus–focus singularities. In this paper, we do not work with these two invariants, but for sake of completeness, we review them quickly. More details can be found in Pelayo and Vũ Ngọc (2009, 2011). Let us pick one of the focus–focus singularities, i.e. we fix $r \in \{1,\ldots ,{n_{\text {FF}}}\}$. In a neighbourhood of the singular fibre containing $m_r$, Vũ Ngọc (2003) proved that the action $I_2$ can be written as

$$\begin{aligned} 2\pi I_2(w) = 2\pi I_2(0) - \text {Im}(w\log w -w) + S_r(w), \end{aligned}$$

where $w:= l + ij$, i is the imaginary unit, l is the value of $L-L(m_r)$, and j is the value of the second Eliasson function around $m_r$. The function $S_r(w)$ is a smooth function that can be understood as a desingularised action. Different choices of $I_2$ change $S_r$ by a multiple of $2\pi l$, so we can fix a choice $I_{2,r}$ of $I_2$ in this neighbourhood by imposing $0 \le \partial _l S_r(0) < 2\pi$. If we denote its Taylor series by $S_r^\infty$, then the ${n_{\text {FF}}}$-tuple $S^\infty = (S_1^\infty , \ldots , S_{n_{\text {FF}}}^\infty )$ is the Taylor series invariant. In Sect. 4.3, we show that $h_r$ can also be related to $I_{2,r}(0)$.

Fix now a polygon $\Delta$ and its corresponding homeomorphism f. Then, for each $r=1,\ldots ,{n_{\text {FF}}}$, the values of $f^{(2)}$ around $c_r$ will differ from those of $I_{2,r}$ by a multiple $\kappa _r \in \mathbb {Z}$ of $2\pi l$. The ${n_{\text {FF}}}$-tuple $\kappa = (\kappa _1,\ldots ,\kappa _{n_{\text {FF}}})$ depends on the choice of f. The equivalence class of $\kappa$ under the $(\mathbb {Z}_2)^{n_{\text {FF}}}\times \mathbb {Z}$-action that acts on f determines the twisting index invariant. The Taylor series and twisting index invariants are, respectively, invariants (ii) and (v) in Pelayo and Vũ Ngọc (2009).

Consider now the following definition of isomorphism between semitoric systems:

Definition 9

Two semitoric systems $(M_1,\omega _1,F_1)$ and $(M_2,\omega _2,F_2)$ are said to be isomorphic if there exists a pair $(\varphi , \varrho )$, such that $\varphi :(M_1,\omega _1) \rightarrow (M_2, \omega _2)$ is a symplectomorphism and $\varrho : B_1 \rightarrow B_2$ is a diffeomorphism between $B_1 := F_1(M_1)$ and $B_2 := F_2(M_2)$ that satisfies $\varrho \circ F_1 = F_2 \circ \varphi$ and is of the form

$$\begin{aligned} \varrho (l,h) = (l,\varrho ^{(2)}(l,h)),\quad \dfrac{\partial \varrho ^{(2)}}{\partial h} >0. \end{aligned}$$

The pair $(\varphi , \varrho )$ is called semitoric isomorphism.

Pelayo and Vũ Ngọc (2009, 2011) give a classification of simple semitoric systems up to isomorphism using the number of focus–focus points ${n_{\text {FF}}}$ and the other four invariants introduced in this section.

Theorem 10

(Pelayo and Vũ Ngọc 2009, 2011) There exists a symplectic classifications of simple semitoric systems in the following sense:

• (1) To each simple semitoric system, we can associate the following five symplectic invariants, namely the number of focus–focus points ${n_{\text {FF}}}$, the polygon invariant $[\Delta ]$, the height invariant h, the Taylor series invariant $S^\infty$, and the twisting index invariant $[\kappa ]$.

• (2) Two semitoric systems are isomorphic if and only if their list of invariants coincide.

• (3) Given a list of admissible invariants, there exists a simple semitoric system $(M, \omega , F)$ that has that list as its list of invariants.

3 A symmetric family with two focus–focus points

Consider $M=\mathbb {S}^2 \times \mathbb {S}^2$, together with the symplectic form $\omega = - (R_1\, \omega _{\mathbb {S}^2} \oplus R_2\, \omega _{\mathbb {S}^2})$, where $\omega _{\mathbb {S}^2}$ is the standard symplectic form of the unit sphere $\mathbb {S}^2$ and $R_1,R_2$ are two positive real numbers. Consider Cartesian coordinates $(x_1,y_1,z_1, x_2,y_2,z_2)$ on M, where $(x_i,y_i,z_i),$ $i=1,2$, are Cartesian coordinates on the unit sphere $\mathbb {S}^2 \subset \mathbb {R}^3$. We define a 4-parameter family of integrable systems $(M,\omega ,(L,H))$, where $L,H:M \rightarrow \mathbb {R}$ are the smooth functions given by

(4)

The parameters $R_1,R_2$ are called geometric parameters, because they are related to the symplectic manifold. The parameters $s_1,s_2 \in [0,1]$ are the coupling parameters of the system. For now, we will assume that $R_2 > R_1$. The function L represents the sum of the height functions on both spheres, and its Hamiltonian vector field corresponds to a simultaneous rotation of both spheres around the vertical axis. The function H corresponds to an interpolation of the height function on the first sphere, on the second sphere, and the relative polar angle between the two position vectors, see Fig. 4.

Fig. 4

Representation of the system (4). The phase space is $M=\mathbb {S}^2 \times \mathbb {S}^2$, with position vectors $(x_1,y_1,z_1)$ in blue and $(x_2,y_2,z_2)$ in red. These vectors determine the value of the functions L, H

Remark 11

The system (4) is a particular case of the general family of systems

$$\begin{aligned} {\left\{ \begin{array}{ll} L(x_1,y_1,z_1,x_2,y_2,z_2)\;:=R_1 z_1 + R_2 z_2, \\ H(x_1,y_1,z_1,x_2,y_2,z_2):=t_1 z_1 + t_2 z_2 + t_3 (x_1x_2 + y_1y_2) + t_4 z_1 z_2 \end{array}\right. } \end{aligned}$$

defined in Hohloch and Palmer (2018) obtained by setting

Proposition 12

The system $(M,\omega ,(L,H))$ defined by equation (4) is completely integrable for all choices of radii $0<R_1<R_2$ and coupling parameters $s_1,s_2 \in [0,1]$.

Proof

Remark 11 allows us to use (Hohloch and Palmer 2018, Theorem 3.1), which states that the system is completely integrable if $t_3 \ne 0$. We have that $t_3 = 2(s_1+s_2-{s_1}^2 - {s_2}^2)>0$ for all values $s_1,s_2 \in [0,1]$ except for the points $(s_1,s_2) \in \{0,1\}^2$. We investigate these four particular cases separately:

Since $\{z_i,z_j\}=0$ for $i,j=1,2$, the functions L and H Poisson-commute: $\{L,H\}=0$. Moreover, since $R_1,R_2>0$, DL is linearly independent of $\pm D z_i$ for $i=1,2$, so these four systems are also completely integrable. $\square$

The four extreme cases considered in the proof of Proposition 12 are actually of toric type, that is, toric up to a diffeomorphism on the base, cf. Vũ Ngọc (2007, Definition 2.1). In particular, all their flows are periodic. This is because the flow of $H = \pm z_i$, $i=1,2$ corresponds to rotations around the vertical axis in the i-th sphere.

In Fig. 5, we can see the evolution of the image of the momentum map (L, H) as we move the coupling parameters $s_1,s_2$. The extreme cases correspond to the images on the four corners.

Fig. 5

Image of the momentum map $F=(L,H)$ with $R_1=1$, $R_2=2$ for different values of $s_1,s_2 \in [0,1]^2$. The parameter $s_1$ varies horizontally from 0 (left) to 1 (right) and $s_2$ varies vertically, from 0 (top) to 1 (bottom)

3.1 The number of focus–focus points

The first symplectic invariant that we compute is the number of focus–focus points, which corresponds to invariant (i) in Pelayo and Vũ Ngọc (2009).

Proposition 13

The rank 0 fixed points of the system (4) are the four products of poles: $N \times N, N \times S, S \times N$ and $S \times S$. The points $N\times N$ and $S \times S$ are always of elliptic–elliptic type. The points $N\times S$ and $S \times N$ are of elliptic–elliptic type if $E>0$ and of focus–focus type if $E<0$, where

$$\begin{aligned} \begin{aligned} E&= {R_2}^2 (1 - 2 {s_1})^2 (-1 + {s_2})^2 + {R_1}^2 (1 - 2 {s_1})^2 {s_2}^2 - 2 {R_1} {R_2} (8 (-1 + {s_1})^2 {s_1}^2 \\&\quad + {s_2} - 12 (-1 + {s_1}) {s_1} {s_2} + (7 + 12 (-1 + {s_1}) {s_1}) {s_2}^2 - 16 {s_2}^3 + 8 {s_2}^4). \end{aligned} \end{aligned}$$

(5)

The number of focus–focus singularities as a function of the system parameters $s_1,s_2$ is illustrated in Fig. 6.

Fig. 6

Representation of the number of focus–focus points for $R_1=1$, $R_2=2$ as a function of the coupling parameters $s_1,s_2$. In the green area, we have ${n_{\text {FF}}}=2$ and, in the white one, we have ${n_{\text {FF}}}=0$

Proof

From (Hohloch and Palmer 2018, Lemma 3.4), we know that the product of poles, $N \times N$, $S \times S$, $N \times S$ and $S \times N$, are precisely the rank 0 singularities of the system. From (Hohloch and Palmer 2018, Corollary 3.6) we know that, if m is the product of poles $(z_1,z_2)=(\pm 1, \pm 1)$ and $\Omega :=\omega _m$ is the symplectic form on $T_mM$, then the characteristic polynomial of $A_H = \Omega ^{-1} D^2H$ is

$$\begin{aligned} \chi (X)&= X^4 + \dfrac{1}{{R_1}^2 {R_2}^2} \left( {R_1}^2 ({t_2} + {z_1} {t_4})^2 + 2 {z_1} {z_2} {R_1} {R_2} {t_3}^2 + {R_2}^2 ({t_1} + {z_2} {t_4})^2 \right) X^2 \\&\quad + \dfrac{1}{{R_1}^2 {R_2}^2} \left( ({t_2} + {z_1} {t_4})^2 ({t_1} + {z_2} {t_4})^2 - 2 {z_1} {z_2} ({t_2} + {z_1} {t_4}) ({t_1} + {z_2} {t_4}) {t_3}^2 + {t_3}^4 \right) \end{aligned}$$

which is a quadratic polynomial in $Y := X^2$ with discriminant

$$\begin{aligned} D&= \dfrac{1}{{R_1}^2 {R_2}^2} \left( {R_1}^2 ({t_2} - {z_1} {t_4})^2 + 2 {z_1} {z_2} {R_1} {R_2} {t_3}^2 + {R_2}^2 ({t_1} + {z_2} {t_4})^2)\right) ^2 \\&- \dfrac{4}{{R_1}^2 {R_2}^2} \left( ({t_2} + {z_1} {t_4})^2 ({t_1} + {z_2} {t_4})^2 - 2 {z_1} {z_2} ({t_2} - {z_1} {t_4}) ({t_1} + {z_2} {t_4}) {t_3}^2 + {t_3}^4 \right) . \end{aligned}$$

The rank 0 criterion (Hohloch and Palmer 2018, Proposition 3.7) tells us that a rank 0 singularity is non-degenerate of focus–focus type if $D<0$ and non-degenerate of elliptic–elliptic type if $D>0$. We consider four different cases:

• $\underline{{Case\ }N \times N\hbox { and }S \times S\hbox { for }s_1 \ne \tfrac{1}{2}:}$

  In this case, the discriminant becomes

  $$\begin{aligned} D&= \dfrac{1}{{R_1}^4 {R_2}^4}(1 - 2 {s_1})^2 ({R_2} + {R_1} {s_2} - {R_2} {s_2})^2 \\&\quad \times \left( {R_2}^2 (1 - 2 {s_1})^2 (-1 + {s_2})^2 + {R_1}^2 (1 - 2 {s_1})^2 {s_2}^2 \right. \\&\quad + \left. 2 {R_1} {R_2} (-16 {s_1}^3 + 8 {s_1}^4 - 20 {s_1} (-1 + {s_2}) {s_2} + 4 {s_1}^2 (2 + 5 (-1 + {s_2}) {s_2}) \right. \\&\quad \left. + (-1 + {s_2}) {s_2} (1 + 8 (-1 + {s_2}) {s_2}))\right) . \end{aligned}$$

  The first three factors are always strictly positive. We divide the fourth factor by ${R_1}^2$ and express it as a function of $s_1, s_2$ and $R := \tfrac{R_2}{R_1}$:

  $$\begin{aligned} \bar{D}&= R^2 (1-2s_1)^2 (1-s_2)^2 + (1-2s_1)^2{s_2}^2 + 2R (-16 {s_1}^3 + 8 {s_1}^4 \\&\quad - 20 {s_1} (-1 + {s_2}) {s_2} + 4 {s_1}^2 (2 + 5 (-1 + {s_2}) {s_2}) \\&\quad + (-1 + {s_2}) {s_2} (1 + 8 (-1 + {s_2}) {s_2})). \end{aligned}$$

  Our goal is to show that this smooth factor is positive in the region defined by $0 \le s_1,s_2 \le 1$ and $R>1$. The value of $\bar{D}$ at the vertices $R=1$, $(s_1,s_2) \in \{0,1\}^2$ is 1. Now we look at the eight edges of the region:

  • $\underline{R=1,\,s_1=0,1}$: There are three critical points: a maximum at $s_2=\tfrac{1}{2}$ with value 1 and two minima at $s_2=\tfrac{1}{4}(2 \pm \sqrt{2})$ with value $\tfrac{3}{4}$.

  • $\underline{R=1,\,s_2=0,1}$: Same as above, but in $s_1=\tfrac{1}{2}$ and $s_1=\tfrac{1}{4}(2 \pm \sqrt{2})$.

  • $\underline{s_1=0,1,\, s_2=0,1}$: No critical points.

  Now we consider the five faces of the region:

  • $\underline{R=1}$: There are five critical points: a maximum at $(s_1,s_2)=(\tfrac{1}{2},\tfrac{1}{2})$ with value 4 and four saddle points at $(s_1,s_2) = (\tfrac{1}{10}(5 \pm 2 \sqrt{5}), \tfrac{1}{10}(5 \pm 2 \sqrt{5}))$ with value $\tfrac{4}{5}$.

  • $\underline{s_1=0,1}$: There is only one critical point at $(s_2,R) = (\tfrac{1}{12}(7 + \sqrt{13}), \tfrac{1}{9}(5 + 2\sqrt{13}))$, which is a saddle with value $\tfrac{587 + 143\sqrt{13}}{1458} >0$.

  • $\underline{s_2=0,1}$: There are no critical points.

  Finally, there are no local extrema in the interior of the region, $\bar{D}$ just grows indefinitely as $R \rightarrow \infty$. We conclude thus that $\bar{D}$ is positive in all the region. This means that the discriminant D is positive, too, and therefore the singularities are non-degenerate and of elliptic–elliptic type.

• $\underline{{\ Case\ }N \times N{\ and\ }S \times S{\ for\ }s_1 = \tfrac{1}{2}:}$

  In this case, the discriminant D vanishes, so we may compute instead the characteristic polynomial of $A_L+A_H = \Omega ^{-1} (D^2L + D^2H)$, which is

  $$\begin{aligned} \chi (X)=\dfrac{(1 + 4 {s_2} - 4 {s_2}^2)^4 + 8 {R_1} {R_2} (1 + 4 {s_2} - 4 {s_2}^2)^2 (-1 + X^2) + 16 {R_1}^2 {R_2}^2 (1 + X^2)^2}{16 {R_1}^2 {R_2}^2}. \end{aligned}$$

  It is also quadratic in $Y=X^2$ and has discriminant

  $$\begin{aligned} \dfrac{4 (1 + 8 {s_2} + 8 {s_2}^2 - 32 {s_2}^3 + 16 {s_2}^4)}{{R_1} {R_2}}>0. \end{aligned}$$

  Therefore, the singularities are non-degenerate and of elliptic–elliptic type.

• $\underline{Case\ N \times S\ and\ S \times N\ for\ s_1\ne \tfrac{1}{2}:}$ In this case, the discriminant becomes:

  $$\begin{aligned} \begin{aligned} D&=\dfrac{1}{{R_1}^4 {R_2}^4} (1 - 2 {s_1})^2 ({R_2} + {R_1} {s_2} - {R_2} {s_2})^2\, E \end{aligned} \end{aligned}$$

  (6)

  where

  $$\begin{aligned} E&:= {R_2}^2 (1 - 2 {s_1})^2 (-1 + {s_2})^2 + {R_1}^2 (1 - 2 {s_1})^2 {s_2}^2 \\&\qquad - 2 {R_1} {R_2} (8 (-1 + {s_1})^2 {s_1}^2 + {s_2}\\&\qquad - 12 (-1 + {s_1}) {s_1} {s_2} + (7 + 12 (-1 + {s_1}) {s_1}) {s_2}^2 - 16 {s_2}^3 + 8 {s_2}^4). \end{aligned}$$

  Since $s_1 \ne \tfrac{1}{2}$, the factors in front of E in (6) are always positive. The equation $E=0$ determines a closed curve $\gamma$, which is the border of the region depicted in Fig. 6. This curve is simple as a consequence of the implicit function theorem since the derivatives $\tfrac{\partial E}{\partial s_1}$ and $\tfrac{\partial E}{\partial s_2}$ do not vanish simultaneously within $0\le s_1\le 1$, $0 \le s_2 \le 1$. Outside the curve, the discriminant is positive and therefore the singularities are of elliptic–elliptic type. Inside the curve, the discriminant is negative and therefore the singularities $N \times S$ and $S \times N$ are of focus–focus type.

• $\underline{Case\ N \times S\ and\ S \times N\ for\ s_1= \tfrac{1}{2}:}$

  In this case, the discriminant D vanishes, so we can compute instead the characteristic polynomial of $A_L+A_H = \Omega ^{-1} (D^2L + D^2H)$, which is

  $$\begin{aligned} \dfrac{(1 + 4 {s_2} - 4 {s_2}^2)^4 - 8 {R_1} {R_2} (1 + 4 {s_2} - 4 {s_2}^2)^2 (-1 + X^2) + 16 {R_1}^2 {R_2}^2 (1 + X^2)^2}{16 {R_1}^2 {R_2}^2}, \end{aligned}$$

  which is also quadratic in $Y=X^2$ and has discriminant

  $$\begin{aligned} -\dfrac{4 (1 + 8 {s_2} + 8 {s_2}^2 - 32 {s_2}^3 + 16 {s_2}^4)}{{R_1} {R_2}}<0. \end{aligned}$$

  Therefore, the singularities are non-degenerate and of focus–focus type. $\square$

We now look at the singularities of rank 1.

Proposition 14

The system (4) has only singularities of rank 1 that are non-degenerate and of elliptic-regular type, for any choice $(s_1,s_2) \in [0,1]^2$.

Proof

We make use of (Hohloch and Palmer 2018, Proposition 3.14) that provides a criterion for the singularities of rank 1. More specifically, let l be the fixed value of the function L, i.e. $l:=R_1 z_1 + R_2 z_2$ and set $\vartheta := \theta _1-\theta _2$, where $\theta _1,\theta _2$ are the polar angles on $\mathbb {S}^2 \times \mathbb {S}^2$. We consider the symplectic reduction of the system (4) on the level $L^{-1}(l)$. Note that from (Hohloch and Palmer 2018, Lemma 3.10), rank 1 singularities always satisfy $z_1,z_2 \ne \pm 1$. Define

$$\begin{aligned} \mathcal {B}(z_1) := (1-{z_1}^2) \left( 1-\left( \dfrac{l-R_1 z_1}{R_2} \right) ^2 \right) = (1-{z_1}^2)(1-{z_2}^2), \end{aligned}$$

which is the content of the square root after the transformation of H in the reduced coordinates $(\vartheta ,z_1)$, cf. Eq. (8) in the next section. Let $t_3,t_4$ be as in Remark 11. Then, the fixed points of rank 1 are non-degenerate and of elliptic-regular type if

$$\begin{aligned} \dfrac{2t_4 R_1}{t_3 R_2} \cos (\vartheta ) > \dfrac{2 \mathcal {B}''(z_1) \mathcal {B}(z_1) - (\mathcal {B}'(z_1))^2}{4(\mathcal {B}(z_1))^{\frac{3}{2}}}. \end{aligned}$$

(7)

In our case, $t_4=0$, so the left hand side vanishes. The right hand side is

$$\begin{aligned} - \dfrac{{R_1}^2(1-{z_1}^2)^2 + 2z_1 z_2 R_1 R_2 (1-{z_1}^2)(1-{z_2}^2) + {R_2}^2(1-{z_2}^2)^2}{{R_2}^2 (1-{z_1}^2)^{\frac{3}{2}}(1-{z_2}^2)^{\frac{3}{2}} }. \end{aligned}$$

The numerator lies always between $-(\alpha + \beta )^2$ and $-(\alpha - \beta )^2$, where $\alpha := R_1 (1-{z_1}^2)$ and $\beta := R_2 (1-{z_2}^2)$, because $-1< z_1 z_2 < 1$, so it is always negative and the denominator is always positive. Thus, the right hand side of (7) is always negative and the criterion (Hohloch and Palmer 2018, Proposition 3.14) can be applied. We conclude that all singularities of rank 1 are non-degenerate. $\square$

Theorem 15

The system (4) is semitoric for almost any choice of coupling parameters $(s_1,s_2) \in [0,1]^2$. It only fails to be semitoric in the piecewise smooth curve defined by $E=0$, where E is defined in equation (5). At this curve, the singularities $N \times S$ and $S \times N$ become degenerate.

Proof

Immediate from Propositions 12, 13 and 14. The curve $E=0$ is the border of the coloured region in Fig. 6. $\square$

Corollary 16

The number of focus–focus points invariant is determined by Proposition 13 as $n_{FF}=2$ or $n_{FF}=0$ and displayed in Fig. 6.

Figures 5 and 6 suggest that system (4) has several symmetries. This will have an effect on the symplectic invariants.

Proposition 17

We define the following transformations, acting on the manifold $(M,\omega )$ and the system parameters $(R_1,R_2,s_1,s_2)$:

$$\begin{aligned}&\Psi _1: (x_1,y_1,z_1,x_2,y_2,z_2;R_1,R_2,s_1,s_2) \mapsto (-x_1,-y_1,z_1,-x_2,-y_2,z_2;R_1,R_2,s_1,s_2) \\&\Psi _2: (x_1,y_1,z_1,x_2,y_2,z_2;R_1,R_2,s_1,s_2) \mapsto (x_1,-y_1,-z_1,x_2,-y_2,-z_2;R_1,R_2,1-s_1,s_2) \\&\Psi _3: (x_1,y_1,z_1,x_2,y_2,z_2;R_1,R_2,s_1,s_2) \mapsto (x_2,y_2,z_2,x_1,y_1,z_1;R_2,R_1,s_1,1-s_2) \\&\Psi _4: (x_1,y_1,z_1,x_2,y_2,z_2;R_1,R_2,s_1,s_2) \mapsto (-x_1,-y_1,z_1,x_2,y_2,z_2;R_1,R_2,1-s_1,s_2) \\&\Psi _5: (x_1,y_1,z_1,x_2,y_2,z_2;R_1,R_2,\tfrac{1}{2},s_2)\; \mapsto (x_1,y_1,z_1,x_2,y_2,z_2;R_1,R_2,\tfrac{1}{2},1-s_2) \end{aligned}$$

They preserve the symplectic form, $\Psi _i^*\omega = \omega$, and act on the system (4) as

$$\begin{aligned}&{\Psi _i}^*(L,H) = (L,H)&\text { for } i=1,3,5 \\&{\Psi _i}^*(L,H) = (-L,H)&\text { for } i=2 \\&{\Psi _i}^*(L,H) = (L,-H)&\text { for } i=4. \end{aligned}$$

Proof

Simple substitution in Eq. (4). $\square$

Corollary 18

The transformations $\Psi _i$ with $i=1,3,5$ induce semitoric isomorphisms. The systems related by one of these transformations have the same symplectic invariants.

Proof

Consequence of Theorem 10. $\square$

Remark 19

The transformation $\Psi _2$ induces an isomorphism that reverses the sign of L, which resembles the isomorphism that relates the standard and reverse cases of the coupled angular momenta studied in Alonso et al. (2020). Similarly, the transformation $\Psi _4$ induces an isomorphism that reverses the sign of H, which resembles the discrete symmetry of the coupled spin oscillator studied in Alonso et al. (2019).

3.2 The polygon invariant

The polygon invariant of the system (4) can be obtained from the isotropic weights of the function L by making use of the following theorem that relates the slopes of the polygon to the derivative of the Duistermaat–Heckman function $\rho _L(l)$, that is, the symplectic volume of the reduced space $L^{-1}(l)/\mathbb {S}^{1}$.

Theorem 20

(Vũ Ngọc 2007) Let $\Delta = f(M)$ be a representative of the polygon invariant. Denote by $\alpha ^+(l)$ the slope of the top boundary of $\Delta$ and $\alpha ^-(l)$ the bottom boundary. Then, the derivative of $\rho _L$ is given by

$$\begin{aligned} \rho _L'(l) = \alpha ^+(l) - \alpha ^-(l) \end{aligned}$$

and it is locally constant on $L(M) \backslash$Crit(L), where Crit(L) is the set of critical points of L. If $\lambda \in \!$ Crit(L),

$$\begin{aligned} \rho _L'(\lambda + 0) - \rho _L'(\lambda -0) = -c -e^+ - e^-, \end{aligned}$$

where $c=1$ if there is a focus–focus point on $L^{-1}(\lambda )$ and $c=0$ otherwise. The number $e^+$ ($e^-$ resp.) vanishes if there is no elliptic–elliptic point on the top (bottom resp.) border of $L^{-1}(\lambda )$ and otherwise is given by

$$\begin{aligned} e^\pm := -\dfrac{1}{a^\pm b^\pm } \ge 0, \end{aligned}$$

where a, b are the corresponding isotropic weights.

Since the phase space $(M,\omega )$ and the function L coincide with that of the coupled angular momenta, we can use the isotropic weights computed by Le Floch and Pelayo (2018). We obtain the following result:

Theorem 21

The polygon invariant of the system (4) is determined by the following cases:

• If ${n_{\text {FF}}}=2$, the polygon invariant is the $((\mathbb {Z}_2)^2\times \mathbb {Z})$-orbit generated by any of the polygons represented in Fig. 7.

• If ${n_{\text {FF}}}=0$ and $(s_1,s_2)$ lies in the same connected component as the point (0, 0) or (1, 1), then the polygon invariant is the $\mathbb {Z}$-orbit generated by the polygon in Fig. 7b.

• If ${n_{\text {FF}}}=0$ and $(s_1,s_2)$ lies in the same connected component as the point (1, 0) or (0, 1), then the polygon invariant is the $\mathbb {Z}$-orbit generated by the polygon in Fig. 7c.

Proof

We distinguish between two situations:

• $\underline{Case\ {n_{\text {FF}}}=2:}$ The polygon invariant consists of the quotient of a $((\mathbb {Z}_2)^2\times \mathbb {Z})$-orbit of a polygon by the $((\mathbb {Z}_2)^2\times \mathbb {Z})$-action, where the action of $(\mathbb {Z}_2)^2$ comes from the choice of signs $\epsilon =(\epsilon _1,\epsilon _2)$, one per focus–focus singularity, and the action of $\mathbb {Z}$ comes from the choice of a cartographic homeomorphism f.

  In this case, the polygons coincide, in principle, with those of the coupled angular momenta, namely Figs. 7b, d but, since we have an additional focus–focus singularity, we also have an additional sign choice, corresponding to the cutting direction on the second singularity. This means that we have to add two more polygons, that is, the ones that coincide with 7b, d on the left of the image of the second focus–focus singularity and change the slope by one on its right, cf. Fig. 7a, c.

• $\underline{Case\ {n_{\text {FF}}}=0:}$ In this case, we do not have any sign choice, so the polygon invariant is the quotient of a $\mathbb {Z}$-orbit by the $\mathbb {Z}$-action. If ${n_{\text {FF}}}=0$ and $(s_1,s_2)$ lies in the same connected component as the point (0, 0) or (1, 1), by looking at Fig. 5 and comparing it with Fig. 7, we identify that the right polygon is Fig. 7b.

  If ${n_{\text {FF}}}=0$ and $(s_1,s_2)$ lies in the same connected component as the point (1, 0) or (0, 1), then the comparison gives the polygon in Fig. 7c. $\square$

Fig. 7

Some representatives of the polygon invariant of the system (4) for different choices of signs $\epsilon =(\epsilon _1,\epsilon _2)$ with the corresponding cutting directions indicated. The horizontal values of the singularities are $L = \pm R_1 \pm R_2$

4 The height invariant

We compute now the height invariant of the system (4) for the values of $s_1,s_2$ for which there are two focus–focus singularities. We start by rewriting the system in a more convenient form. Take cylindrical coordinates $(\theta _1,z_1,\theta _2,z_2)$ on M, so that the system (4) becomes

(8)

with the symplectic form $\omega = -(R_1\, \mathrm {d}\theta _1 \wedge \mathrm {d}z_1 + R_2\, \mathrm {d}\theta _2 \wedge \mathrm {d}z_2).$ We now perform the following affine transformation,

$$\begin{aligned} \begin{array}{lll} {\widetilde{q}}_1 := -\theta _1 &{}&{} {\widetilde{q}}_2 := \theta _1-\theta _2 \\ {\tilde{p}}_1 := R_1 z_1 + R_2 z_2 &{}&{} {\tilde{p}}_2 := R_2 (z_2+1), \end{array} \end{aligned}$$

which leads to $L({\widetilde{q}}_1,{\tilde{p}}_1,{\widetilde{q}}_2,{\tilde{p}}_2) = {\tilde{p}}_1$ and

$$\begin{aligned}&H({\widetilde{q}}_1,{\tilde{p}}_1,{\widetilde{q}}_2,{\tilde{p}}_2)= \dfrac{1-2s_1}{R_1 R_2} \left( R_2 ({\tilde{p}}_1-{\tilde{p}}_2+R_2)(1-s_2) + s_2 R_1({\tilde{p}}_2-R_2) \right) \\&\quad +\dfrac{2(s_1+s_2-{s_1}^2 - {s_2}^2)}{R_1 R_2} \\&\quad \times \sqrt{{\tilde{p}}_2 ({\tilde{p}}_2-2R_2)({\tilde{p}}_2-{\tilde{p}}_1-R_1-R_2)({\tilde{p}}_2-{\tilde{p}}_1+R_1-R_2)} \cos ({\widetilde{q}}_2), \end{aligned}$$

with symplectic form $\omega = \mathrm {d}{\widetilde{q}}_1 \wedge \mathrm {d}{\tilde{p}}_1 + \mathrm {d}{\widetilde{q}}_2 \wedge \mathrm {d}{\tilde{p}}_2$. In these coordinates, we see that the function H is independent of ${\widetilde{q}}_1$. We simplify now our notation by scaling some of the variables and functions by a factor of $R_1$. We use caligraphic letters to refer to scaled functions and standard letters for unscaled functions:

$$\begin{aligned} \begin{array}{lllll} q_1 := {\widetilde{q}}_1 &{}&{} q_2 := {\widetilde{q}}_2 &{}&{} \mathcal {L}:= \frac{1}{R_1}L\\ p_1 :=\frac{1}{R_1} {\tilde{p}}_1 &{}&{} p_2 :=\frac{1}{R_1} {\tilde{p}}_2 &{}&{} \mathcal {H}:= H. \end{array} \end{aligned}$$

(9)

This way we can express our problem entirely in terms of $R:= \frac{R_2}{R_1}$. At the end of our computations (proof of Theorem 22) we will undo the change of variables (9) in order to obtain the result in the original unscaled coordinates. We will do now singular symplectic reduction by the $\mathbb {S}^1$-action generated by L. We will use two different sets of notations, one adapted to the singularity $N \times S$ and the other to the singularity $S \times N$.

4.1 Reduced system for the singularity $N \times S$

We start by doing symplectic reduction on the level $\mathcal {L}=l+(1-R)$, which is singular in $l=0$, since the focus–focus point $N \times S$ lies on the level set $l=0$. Expressed in coordinates $(q_2,p_2)$, we obtain the reduced Hamiltonian

$$\begin{aligned} \begin{aligned}&\mathcal {H}^{NS}_l(q_2,p_2) \\&\quad := \dfrac{1}{R} (1-2s_1)(R(1+l-2s_2-l s_2)+p_2(s_2-R+R s_2)) \\&\qquad + \dfrac{2(s_1+s_2-{s_1}^2 - {s_2}^2)}{R} \sqrt{p_2(p_2-l)(p_2-2R)(p_2-l-2)}\cos ( q_2). \end{aligned} \end{aligned}$$

From this equation, we see that the physical region, i.e. the domain of definition of l and $p_2$ is given by $l \in [-2,2R]$ and $p_2$ satisfying the inequalities $p_2\ge 0$, $p_2 \ge l$, $p_2 \le 2R$ and $p_2 \le l + 2$. The region is depicted in Fig. 8. For simplicity, we write

$$\begin{aligned} \mathcal {H}^{NS}_l(q_2,p_2) = \mathcal {A}^{NS}_l(p_2) + \sqrt{\mathcal {B}^{NS}_l(p_2)} \cos (q_2), \end{aligned}$$

where

$$\begin{aligned} \mathcal {A}^{NS}_l(p_2)&:= \dfrac{1}{R} (1-2s_1)(R(1+l-2s_2-l s_2)+p_2(s_2-R+R s_2)) \\ \mathcal {B}^{NS}_l(p_2)&:= \dfrac{4(s_1+s_2-{s_1}^2 - {s_2}^2)^2}{R^2} p_2(p_2-l)(p_2-2R)(p_2-l-2). \end{aligned}$$

Fig. 8

Physical region in the plane $(l,p_2)$ for the reduced model for $N \times S$, corresponding to the values for which $\mathcal {B}_l^{NS}(p_2)\ge 0$

We now define the polynomial

$$\begin{aligned} \mathcal {P}_l^{NS}(p_2)&:= \mathcal {B}_l^{NS}(p_2) -\left( h + (1-2s_1)(1-2s_2)-\mathcal {A}_l^{NS} (p_2)\right) ^2 \\&= \dfrac{1}{R^2} \left( 4 (-1 + (1 + l - {p_2})^2) {p_2} ({p_2} - 2 R) ((-1 + {s_1}) {s_1} + (-1 + {s_2}) {s_2})^2 \right. \\&\quad \left. - (h R - (-1 + 2 {s_1}) (l R (-1 + {s_2}) + {p_2} (R - (1 + R) {s_2})))^2\right) \end{aligned}$$

which is defined in such a way that the singularity $N \times S$ lies precisely on $(l,h)=(0,0)$. The polynomial is of degree 4 in $p_2$.

4.2 Reduced system for the singularity $S \times N$

We focus now on the singularity $S \times N$, so we do symplectic reduction on the level $\mathcal {L}=l+(1-R)$, which is singular in $l =0$ since the focus–focus point $S \times N$ lies on the level set $l=0$. We also change the coordinates $(q_2,p_2)$ to

$$\begin{aligned} q_2 \mapsto -q_2,\qquad p_2 \mapsto 2R-p_2 \end{aligned}$$

in order to create a similar notation to the one of Sect. 4.1 while preserving the symplectic form. In these new coordinates, the reduced Hamiltonian becomes

$$\begin{aligned} \begin{aligned}&\mathcal {H}^{SN}_l(q_2,p_2) \\&:= \dfrac{1}{R} (1-2s_1)(R(-1+l+2s_2-l s_2)+p_2(s_2-R+R s_2)) \\&\qquad + \dfrac{2(s_1+s_2-{s_1}^2 - {s_2}^2)}{R} \sqrt{p_2(p_2+l)(p_2-2R)(p_2+l-2)}\cos ( q_2). \end{aligned} \end{aligned}$$

Fig. 9

Physical region in the plane $(l,p_2)$ for the reduced model for $S \times N$, corresponding to the values for which $\mathcal {B}_l^{SN}(p_2) \ge 0$. Compared to the one corresponding to the reduced model of $N \times S$ in Fig. 8, it is reflected on the vertical axis through the focus–focus value

The physical region in this case will be given by $l \in [-2R,2]$ and $p_2$ satisfying the inequalities $p_2\ge 0$, $p_2 \ge -l$, $p_2 \le 2R$ and $p_2 \le -l + 2$. The region is depicted in Fig. 9. We write

$$\begin{aligned} \mathcal {H}^{SN}_l(q_2,p_2) = \mathcal {A}^{SN}_l(p_2) + \sqrt{\mathcal {B}^{SN}_l(p_2)} \cos (q_2), \end{aligned}$$

where

$$\begin{aligned} \mathcal {A}^{SN}_l(p_2)&:= \dfrac{1}{R} (1-2s_1)(R(-1+l+2s_2-l s_2)+p_2(s_2-R+R s_2)) \\ \mathcal {B}^{SN}_l(p_2)&:= \dfrac{4(s_1+s_2-{s_1}^2 - {s_2}^2)^2}{R^2} p_2(p_2+l)(p_2-2R)(p_2+l-2). \end{aligned}$$

We now define the polynomial

$$\begin{aligned}&\mathcal {P}_l^{SN}(p_2) \\&\quad := \mathcal {B}_l^{SN}(p_2) -\left( h - (1-2s_1)(1-2s_2)-\mathcal {A}_l^{SN} (p_2)\right) ^2 \\&\quad = \dfrac{1}{R^2} \left( 4 {p_2} (-2 + l + {p_2}) (l + {p_2}) ({p_2} - 2 R) ((-1 + {s_1}) {s_1} + (-1 + {s_2}) {s_2})^2 \right. \\&\qquad \left. - (h R + (-1 + 2 {s_1}) ((l + {p_2}) R - ({p_2} + (l + {p_2}) R) {s_2}))^2\right) , \end{aligned}$$

in such a way that the singularity $S \times N$ lies precisely on $(l,h)=(0,0)$. The polynomial is also of degree 4 in $p_2$.

4.3 Computation of the height invariant

Now that we have the two reduced models, the next step is to compute the height invariant $h=(h_1,h_2)$ of the system (4). We recall from Sect. 2 that the height $h_r$ associated with the focus–focus singularity $m_r \in M$ is the symplectic volume of

$$\begin{aligned} Y_{r}^- := \{ p \in M\; |\; L(p)=L(m_{r}) \text { and } H(p)< H(m_{r})\},\quad r=1,2. \end{aligned}$$

As suggested by Proposition 17, we are dealing with a very symmetric situation. In particular, the transformation $s_1 \mapsto 1-s_1$ brings the situation of the singularity $N \times S$ to the situation of the singularity $S \times N$ and vice versa. In Fig. 11, we can see a plot of this volume for the singularity $N\times S$, so $r=1$ and, in Fig. 12, we can see the same for the case $r=2$.

Theorem 22

The height invariant $h :=(h_1,h_2)$ associated with the system (4) for the values of $(s_1,s_2)$ in which it has two focus–focus singularities is given by

$$\begin{aligned} h_1&= -\dfrac{1}{2\pi } \mathcal {F}(s_1,s_2,R_1,R_2) + 2 u\left( (s_1-\tfrac{1}{2} )(s_2 - \tfrac{R_2}{R_2+R_1}) \right) , \\ h_2&= \, \dfrac{1}{2\pi } \mathcal {F}(s_1,s_2,R_1,R_2) +2 u\left( -(s_1-\tfrac{1}{2} )(s_2 - \tfrac{R_2}{R_2+R_1}) \right) = 2-h_1 \end{aligned}$$

where u is the Heaviside step function and

$$\begin{aligned} \mathcal {F}(s_1,s_2,R_1,R_2)&:= 2 R_2 \arctan \left( \frac{\gamma _C}{\sqrt{\gamma _A} (2 {s_1}-1) (R_2 ({s_2}-1)+R_1{s_2})}\right) \\&\quad + 2 R_1 \arctan \left( \frac{\gamma _D}{\sqrt{\gamma _A} (2 {s_1}-1) (R_2 ({s_2}-1)+R_1{s_2})}\right) \\&\quad + \frac{(2 {s_1}-1) (R_2 ({s_2}-1)+R_1{s_2}) }{2 \left( {s_1}^2-{s_1}+{s_2}^2-{s_2}\right) }\\&\qquad \log \left( \frac{-\sqrt{\gamma _B}}{2 (R_2+R_1) \left( {s_1}^2-{s_1}+{s_2}^2-{s_2}\right) +\sqrt{\gamma _A}}\right) . \end{aligned}$$

The invariant is represented in Fig. 10.

Fig. 10

Representation of the height invariant for $R_1=1$, $R_2=2$

The coefficients $\gamma _A$, $\gamma _B$, $\gamma _C$ and $\gamma _D$ are given by

$$\begin{aligned} \gamma _A&:= -{R_2}^2 (1-2 {s_1})^2 ({s_2}-1)^2+2 R_2 R_1 \left( 8 {s_1}^4-16 {s_1}^3+4 {s_1}^2 \left( 3 {s_2}^2-3 {s_2}+2\right) \right. \\&\quad \left. -12 {s_1} ({s_2}-1) {s_2}+{s_2} \left( 8 {s_2}^3-16 {s_2}^2+7 {s_2}+1\right) \right) -{R_1}^2(1-2 {s_1})^2 {s_2}^2 \\ \gamma _B&:= {R_2}^2 \left( 4 {s_1}^4-8 {s_1}^3+4 {s_1}^2 \left( 3 {s_2}^2-4 {s_2}+2\right) -4 {s_1} \left( 3 {s_2}^2-4 {s_2}+1\right) \right. \\&\quad \left. +({s_2}-1)^2 \left( 4 {s_2}^2+1\right) \right) -2 R_2 R_1 \left( 4 {s_1}^4-8 {s_1}^3+4 {s_1}^2 \left( {s_2}^2-{s_2}+1\right) \right. \\&\quad \left. -4 {s_1} ({s_2}-1) {s_2}+{s_2} \left( 4 {s_2}^3-8 {s_2}^2+3 {s_2}+1\right) \right) + {R_1}^2 \left( 4 {s_1}^4-8 {s_1}^3 \right. \\&\quad \left. +4 {s_1}^2 \left( 3 {s_2}^2-2 {s_2}+1\right) +4 {s_1} {s_2} (2-3 {s_2})+{s_2}^2 \left( 4 {s_2}^2-8 {s_2}+5\right) \right) \\ \gamma _C&:= -4 {R_2}^2 {s_1}^2 {s_2}^2+8 {R_2}^2 {s_1}^2 {s_2}-4 {R_2}^2 {s_1}^2+4 {R_2}^2 {s_1} {s_2}^2-8 {R_2}^2 {s_1} {s_2}+4 {R_2}^2 {s_1}\\&\quad -{R_2}^2 {s_2}^2+2 {R_2}^2 {s_2}-{R_2}^2+8 {R_2 R_1} {s_1}^4-16 {R_2 R_1} {s_1}^3\\&\quad +8 {R_2 R_1} {s_1}^2 {s_2}^2-8 {R_2 R_1} {s_1}^2 {s_2}\\&\quad +8 {R_2 R_1} {s_1}^2-8 {R_2 R_1} {s_1} {s_2}^2+8 {R_2 R_1} {s_1} {s_2}+8 {R_2 R_1} {s_2}^4\\&\quad -16 {R_2 R_1} {s_2}^3+6 {R_2 R_1} {s_2}^2\\&\quad +2 {R_2 R_1} {s_2}+4R_1 \sqrt{{\gamma _B}} \left( -{s_1}^2+{s_1}-{s_2}^2+{s_2}\right) -8{R_1}^2 {s_1}^4\\&\quad +16{R_1}^2 {s_1}^3-20{R_1}^2 {s_1}^2 {s_2}^2\\&\quad +16 {R_1}^2{s_1}^2 {s_2}-8{R_1}^2 {s_1}^2+20{R_1}^2 {s_1} {s_2}^2-16{R_1}^2 {s_1} {s_2}-8{R_1}^2 {s_2}^4\\&\quad +16{R_1}^2 {s_2}^3-9{R_1}^2 {s_2}^2 \\ \gamma _D&:= -8 {R_2}^2 {s_1}^4+16 {R_2}^2 {s_1}^3-20 {R_2}^2 {s_1}^2 {s_2}^2+24 {R_2}^2 {s_1}^2 {s_2}\\&\quad -12 {R_2}^2 {s_1}^2+20 {R_2}^2 {s_1} {s_2}^2\\&\quad -24 {R_2}^2 {s_1} {s_2}+4 {R_2}^2 {s_1}-8 {R_2}^2 {s_2}^4+16 {R_2}^2 {s_2}^3-9 {R_2}^2 {s_2}^2+2 {R_2}^2 {s_2}-{R_2}^2\\&\quad +4 R_2 \sqrt{{\gamma _B}} \left( -{s_1}^2+{s_1}-{s_2}^2+{s_2}\right) +8 {R_2 R_1} {s_1}^4-16 {R_2 R_1} {s_1}^3+8 {R_2 R_1} {s_1}^2 {s_2}^2\\&\quad -8 {R_2 R_1} {s_1}^2 {s_2}+8 {R_2 R_1} {s_1}^2-8 {R_2 R_1} {s_1} {s_2}^2+8 {R_2 R_1} {s_1} {s_2}\\&\quad +8 {R_2 R_1} {s_2}^4-16 {R_2 R_1} {s_2}^3\\&\quad +6 {R_2 R_1} {s_2}^2+2 {R_2 R_1} {s_2}-4{R_1}^2 {s_1}^2 {s_2}^2+4{R_1}^2 {s_1} {s_2}^2-{R_1}^2{s_2}^2. \end{aligned}$$

Proof

Let $(\bar{h}_1,\bar{h}_2)$ be the height invariant after the rescaling of coordinates (9). We first compute $(\bar{h}_1,\bar{h}_2)$ and undo the rescaling at the end to obtain $(h_1,h_2)$. We start by focussing first on the singularity $N \times S$, i.e. $r=1$. We know that $(L,H)(m_1) = (1-R,(1-2s_1)(1-2s_2))$ and we want to compute the symplectic volume of

$$\begin{aligned} Y_{1}^- := \{ p \in M\; |\; L(p)=1-R \text { and } H(p)< (1-2s_1)(1-2s_2)\}, \end{aligned}$$

which is the area represented in Fig. 11, divided by $2\pi$. In the notation of Sect. 4.1, the singularity lies at $(l,h)=(0,0)$. This means that

$$\begin{aligned} \mathcal {H}^{NS}_0(q_2,p_2) = \mathcal {A}^{NS}_0(p_2) + \sqrt{\mathcal {B}^{NS}_0(p_2)} \cos (q_2), \end{aligned}$$

where in this case

$$\begin{aligned} \mathcal {A}^{NS}_0(p_2)&:= \dfrac{1}{R} (1-2s_1)(R(1-2s_2)+p_2(s_2-R+R s_2)) \\ \mathcal {B}^{NS}_0(p_2)&:= \dfrac{4(s_1+s_2-{s_1}^2 - {s_2}^2)^2}{R^2} {p_2}^2(p_2-2R)(p_2-2) \end{aligned}$$

and $\mathcal {P}_0^{NS}(p_2) := \mathcal {B}_0^{NS}(p_2) -\left( (1-2s_1)(1-2s_2)-\mathcal {A}_0^{NS}(p_2) \right) ^2$. The phase space is given by $-\pi \le q_2\le \pi$ and $0 \le p_2 \le 2$. The roots of $\mathcal {P}_0^{NS}(p_2)$ are

$$\begin{aligned} \zeta _1&= \zeta _2=0 \\ \zeta _3&= 1+R - \frac{\sqrt{\gamma _B}}{2({s_1}-{s_1}^2 + s_2 - {s_2}^2)}\\ \zeta _4&= 1+R + \frac{\sqrt{\gamma _B}}{2({s_1}-{s_1}^2 + s_2 - {s_2}^2)}, \end{aligned}$$

and the physical region lies between $\zeta _2$ and $\zeta _3$. There are two trivial cases, $s_1= \tfrac{1}{2}$ and $s_2 = \tfrac{R}{R+1}$. In both cases, $\mathcal {P}_0^{NS}(p_2) := \mathcal {B}^{NS}_0(p_2)$ and therefore the roots are $\zeta _1=\zeta _2=0$, $\zeta _3=2$ and $\zeta _4=2R$. These trivial cases form the border between two different behaviours, i.e. we distinguish the following situations:

• Case I: $s_1<\tfrac{1}{2}$ and $s_2 < \tfrac{R}{R+1}$

• Case II: $s_1=\tfrac{1}{2}$ or $s_2 = \tfrac{R}{R+1}$

• Case III: $s_1>\tfrac{1}{2}$ and $s_2 < \tfrac{R}{R+1}$

• Case IV: $s_1<\tfrac{1}{2}$ and $s_2 > \tfrac{R}{R+1}$

• Case V: $s_1>\tfrac{1}{2}$ and $s_2 > \tfrac{R}{R+1}$

Fig. 11

Area corresponding to the height invariant of the singularity $N \times S$ for $R=2$

If we look at Fig. 11, we see that cases I and V, top-left and bottom-right, respectively, are connected from above. Case II, in the centre, corresponds to the trivial transition situation. Cases III and IV, top-right and bottom-left, respectively, are not connected from above. Therefore, for cases I and V we write

$$\begin{aligned} \bar{h}_1&= \dfrac{1}{2\pi } \left( 4\pi - \oint _{h=0} \arccos \dfrac{ (1-2s_1)(1-2s_2)-\mathcal {A}^{NS}_0(p_2)}{\sqrt{\mathcal {B}^{NS}_0(p_2)}} \mathrm {d}p_2 \right) \\&= \dfrac{1}{2\pi } \left( 4\pi -2 \int _{\zeta _2}^{\zeta _3} \arccos \dfrac{ (1-2s_1)(1-2s_2)-\mathcal {A}^{NS}_0(p_2)}{\sqrt{\mathcal {B}^{NS}_0(p_2)}} \mathrm {d}p_2 \right) \end{aligned}$$

and for the cases III and IV we write

$$\begin{aligned} \bar{h}_1&= \dfrac{1}{2\pi } \left( 4\pi - \oint _{h=0} \arccos \dfrac{ (1-2s_1)(1-2s_2)-\mathcal {A}^{NS}_0(p_2)}{\sqrt{\mathcal {B}^{NS}_0(p_2)}} \mathrm {d}p_2 -2\pi (2-\zeta _3) \right) \\&= \dfrac{1}{2\pi } \left( 4\pi -2 \int _{\zeta _2}^{\zeta _3} \arccos \dfrac{ (1-2s_1)(1-2s_2)-\mathcal {A}^{NS}_0(p_2)}{\sqrt{\mathcal {B}^{NS}_0(p_2)}} \mathrm {d}p_2 -2\pi (2-\zeta _3) \right) . \end{aligned}$$

For the trivial case II, we have

$$\begin{aligned} h_1 = \dfrac{1}{2\pi } \left( \dfrac{1}{2} 4\pi \right) = 1. \end{aligned}$$

As we did in for the general action integral in Sect. 4.1, we integrate by parts to compute this integral. For the cases I and V, we obtain

$$\begin{aligned} h_1 = \dfrac{1}{2\pi } \left( 4\pi - \bar{\mathcal {F}}(s_1,s_2,R) \right) \end{aligned}$$

and for the cases III and IV,

$$\begin{aligned} h_1 = \dfrac{1}{2\pi } \left( -\bar{\mathcal {F}}(s_1,s_2,R) \right) , \end{aligned}$$

where

$$\begin{aligned} \bar{\mathcal {F}}(s_1,s_2,R) := \dfrac{2}{2\pi } \int _{\zeta _2}^{\zeta _3} \dfrac{V(p_2)}{\sqrt{Q(p_2)}} \mathrm {d}p_2. \end{aligned}$$

(10)

The rational function $V(p_2)$ and the polynomial $Q(p_2)$ are given by

$$\begin{aligned} V(p_2)&=-(2 {s_1}-1) (R {s_2}-R+{s_2}) +\frac{-2 R {s_1} {s_2}+2 R {s_1}+R {s_2}-R-2 {s_1} {s_2}+{s_2}}{{p_2}-2} \\&\quad + \frac{-2 R^2 {s_1} {s_2}+2 R^2 {s_1}+R^2 {s_2}-R^2-2 R {s_1} {s_2}+R {s_2}}{{p_2}-2 R}\\ Q(p_2)&=4 ({p_2}-2) ({p_2}-2 R) (({s_1}-1) {s_1}+({s_2}-1) {s_2})^2\\&\quad -(1-2 {s_1})^2 (R ({s_2}-1)+{s_2})^2. \end{aligned}$$

Fig. 12

Area corresponding to the height invariant of the singularity $S \times N$ for $R=2$

Here, it is important to observe that the polynomial $Q(p_2)$ is of degree 2 in $p_2$, so the integral (10) is not elliptic but can be solved explicitly in terms of elementary functions. We will need the following definite integrals

$$\begin{aligned} \mathcal {N}_A(\alpha ,\beta ,\gamma ):=\int _0^{\tfrac{-\beta -\sqrt{\beta ^2-4 \alpha \gamma }}{2\alpha }} \dfrac{\mathrm {d}x}{\sqrt{\alpha x^2 + \beta x + \gamma }} = \dfrac{1}{\sqrt{\alpha }} \log \left( \dfrac{- \sqrt{\beta ^2 - 4 \alpha \gamma }}{\beta + 2\sqrt{\alpha \gamma }} \right) \end{aligned}$$

and

$$\begin{aligned} \mathcal {N}_B(\alpha ,\beta ,\gamma ,\delta )&:=\int _0^{\tfrac{-\beta -\sqrt{\beta ^2-4 \alpha \gamma }}{2\alpha }} \dfrac{\mathrm {d}x}{(\delta -x)\sqrt{\alpha x^2 + \beta x + \gamma }} \\ {}&= \dfrac{1}{\sqrt{\gamma + \delta (\beta + \alpha \delta )}} \log \left( \dfrac{-2\gamma - \beta \delta + 2 \sqrt{\gamma ^2 + \gamma \delta (\beta + \alpha \delta )}}{\delta \sqrt{\beta ^2-4 \alpha \gamma }} \right) \\&= \dfrac{2}{\sqrt{-\gamma - \delta (\beta + \alpha \delta )}} \arctan \left( \dfrac{2 \gamma + \delta \left( \beta + \sqrt{\beta ^2-4\alpha \gamma } \right) }{2 \sqrt{-\gamma (\gamma + \delta (\beta + \alpha \delta ))}} \right) . \end{aligned}$$

In the last step, we have used the identity $\arctan (z) = \tfrac{i}{2} \left( \log (1-iz) - \log (1+iz) \right)$ with

$$\begin{aligned} z = -\dfrac{i\left( 2 \gamma + \delta \left( \beta + \sqrt{\beta ^2-4\alpha \gamma } \right) \right) }{2 \sqrt{-\gamma (\gamma + \delta (\beta + \alpha \delta ))}}. \end{aligned}$$

We rewrite now the integral (10) as

$$\begin{aligned} \bar{\mathcal {F}}(s_1,s_2,R)&= \dfrac{1}{\pi } \int _0^{\tfrac{-\beta -\sqrt{\beta ^2-4 \alpha \gamma }}{2\alpha }} \left( V_1 + \dfrac{V_2}{2-p_2} + \dfrac{V_3}{2R-p_2}\right) \dfrac{\mathrm {d}p_2}{\sqrt{\alpha {p_2}^2 + \beta p_2 + \gamma }}\\&= \dfrac{1}{\pi } \left( V_1 \mathcal {N}_A(\alpha ,\beta ,\gamma ) + V_2 \mathcal {N}_B(\alpha ,\beta ,\gamma ,2) + V_3 \mathcal {N}_B(\alpha ,\beta ,\gamma ,2R) \right) , \end{aligned}$$

where

$$\begin{aligned} V_1&:= -(2 {s_1}-1) (R {s_2}-R+{s_2}) \\ V_2&:= -(-2 R {s_1} {s_2}+2 R {s_1}+R {s_2}-R-2 {s_1} {s_2}+{s_2}) \\ V_3&:= -(-2 R^2 {s_1} {s_2}+2 R^2 {s_1}+R^2 {s_2}-R^2-2 R {s_1} {s_2}+R {s_2})\\ \alpha&:= \, 4 \left( {s_1}^2-{s_1}+({s_2}-1) {s_2}\right) ^2 \\ \beta&:= -8 (1 + R) (-{s_1} + {s_1}^2 + (-1 + {s_2}) {s_2})^2 \\ \gamma&:= -R^2 (1-2 {s_1})^2 ({s_2}-1)^2+2 R \left( 8 {s_1}^4-16 {s_1}^3+4 {s_1}^2 \left( 3 {s_2}^2-3 {s_2}+2\right) \right. \\&\quad \left. -12 {s_1} ({s_2}-1) {s_2}+{s_2} \left( 8 {s_2}^3-16 {s_2}^2+7 {s_2}+1\right) \right) -(1-2 {s_1})^2 {s_2}^2. \end{aligned}$$

By substituting $\mathcal {N}_A(\alpha ,\beta ,\gamma )$ and $\mathcal {N}_B(\alpha ,\beta ,\gamma ,\delta )$ we obtain,

$$\begin{aligned}&\bar{\mathcal {F}}(s_1,s_2,R) := 2 R \arctan \left( \frac{\bar{\gamma }_C}{\sqrt{\bar{\gamma }_A} (2 {s_1}-1) (R ({s_2}-1)+{s_2})}\right) \\&\quad + 2 \arctan \left( \frac{\bar{\gamma }_D}{\sqrt{\bar{\gamma }_A} (2 {s_1}-1) (R ({s_2}-1)+{s_2})}\right) \\&\quad + \frac{(2 {s_1}-1) (R ({s_2}-1)+{s_2}) }{2 \left( {s_1}^2-{s_1}+{s_2}^2-{s_2}\right) }\log \left( \frac{-\sqrt{\bar{\gamma }_B}}{2 (R+1) \left( {s_1}^2-{s_1}+{s_2}^2-{s_2}\right) +\sqrt{\bar{\gamma }_A}}\right) , \end{aligned}$$

where

$$\begin{aligned} \bar{\gamma }_A&:= -R^2 (1-2 {s_1})^2 ({s_2}-1)^2+2 R \left( 8 {s_1}^4-16 {s_1}^3+4 {s_1}^2 \left( 3 {s_2}^2-3 {s_2}+2\right) \right. \\&\quad \left. -12 {s_1} ({s_2}-1) {s_2}+{s_2} \left( 8 {s_2}^3-16 {s_2}^2+7 {s_2}+1\right) \right) -(1-2 {s_1})^2 {s_2}^2 \\ \bar{\gamma }_B&:= R^2 \left( 4 {s_1}^4-8 {s_1}^3+4 {s_1}^2 \left( 3 {s_2}^2-4 {s_2}+2\right) -4 {s_1} \left( 3 {s_2}^2-4 {s_2}+1\right) \right. \\&\quad \left. +({s_2}-1)^2 \left( 4 {s_2}^2+1\right) \right) -2 R \left( 4 {s_1}^4-8 {s_1}^3+4 {s_1}^2 \left( {s_2}^2-{s_2}+1\right) \right. \\&\quad \left. -4 {s_1} ({s_2}-1) {s_2}+{s_2} \left( 4 {s_2}^3-8 {s_2}^2+3 {s_2}+1\right) \right) +4 {s_1}^4-8 {s_1}^3\\&\quad +4 {s_1}^2 \left( 3 {s_2}^2-2 {s_2}+1\right) +4 {s_1} {s_2} (2-3 {s_2})+{s_2}^2 \left( 4 {s_2}^2-8 {s_2}+5\right) \\ \bar{\gamma }_C&:= -4 R^2 {s_1}^2 {s_2}^2+8 R^2 {s_1}^2 {s_2}-4 R^2 {s_1}^2+4 R^2 {s_1} {s_2}^2-8 R^2 {s_1} {s_2}+4 R^2 {s_1}\\&\quad -R^2 {s_2}^2+2 R^2 {s_2}-R^2+8 R {s_1}^4-16 R {s_1}^3+8 R {s_1}^2 {s_2}^2-8 R {s_1}^2 {s_2}\\ {}&\quad +8 R {s_1}^2-8 R {s_1} {s_2}^2+8 R {s_1} {s_2}+8 R {s_2}^4-16 R {s_2}^3+6 R {s_2}^2+2 R {s_2}\\&\quad +4 \sqrt{{\bar{\gamma }_B}} \left( -{s_1}^2+{s_1}-{s_2}^2+{s_2}\right) -8 {s_1}^4+16 {s_1}^3-20 {s_1}^2 {s_2}^2+16 {s_1}^2 {s_2}\\&\quad -8 {s_1}^2+20 {s_1} {s_2}^2-16 {s_1} {s_2}-8 {s_2}^4+16 {s_2}^3-9 {s_2}^2 \\ \bar{\gamma }_D&:= -8 R^2 {s_1}^4+16 R^2 {s_1}^3-20 R^2 {s_1}^2 {s_2}^2+24 R^2 {s_1}^2 {s_2}-12 R^2 {s_1}^2+20 R^2 {s_1} {s_2}^2\\&\quad -24 R^2 {s_1} {s_2}+4 R^2 {s_1}-8 R^2 {s_2}^4+16 R^2 {s_2}^3-9 R^2 {s_2}^2+2 R^2 {s_2}-R^2\\&\quad +4 R \sqrt{{\bar{\gamma }_B}} \left( -{s_1}^2+{s_1}-{s_2}^2+{s_2}\right) +8 R {s_1}^4-16 R {s_1}^3+8 R {s_1}^2 {s_2}^2-8 R {s_1}^2 {s_2}\\&\quad +8 R {s_1}^2-8 R {s_1} {s_2}^2+8 R {s_1} {s_2}+8 R {s_2}^4-16 R {s_2}^3+6 R {s_2}^2+2 R {s_2}-4 {s_1}^2 {s_2}^2\\&\quad +4 {s_1} {s_2}^2-{s_2}^2.\\ \end{aligned}$$

The proof for the singularity $S \times N$ is completely analogous but taking into account that the cases II and V should be exchanged and the same for the cases I and IV. The last step is to undo the rescaling (9) by defining $\mathcal {F}(s_1,s_2,R_1,R_2) := R_1 \bar{\mathcal {F}}(s_1,s_2,\tfrac{R_2}{R_1})$, $\gamma _A := {R_1}^2\, \bar{\gamma }_A$, $\gamma _B := {R_1}^2\, \bar{\gamma }_B$, $\gamma _C := {R_1}^2\, \bar{\gamma }_C$, $\gamma _D := {R_1}^2\, \bar{\gamma }_D$. We obtain thus the desired result. $\square$

Remark 23

The two components $(h_1, h_2)$ of the height invariant have an intricate dependence on the four parameters $s_1, s_1, R_1, R_2$ of the system but a very simple relation between each other, namely $h_2=2-h_1$.

We can finally extend our results to the case $R_1>R_2$:

Corollary 24

The transformation $\Psi _3$ from Proposition 17 extends Theorem 15, Corollary 16, Theorems 21 and 22 to the case $R_1 > R_2$.

Note that the condition $R_1 = R_2$ results in a non-simple semitoric system, which lies outside the scope of the present work.