Inflection, Canards and Folded Singularities in Excitable Systems: Application to a 3D FitzHugh–Nagumo Model

Abstract

Specific kinds of physical and biological systems exhibit complex Mixed-Mode Oscillations mediated by folded-singularity canards in the context of slow-fast models. The present manuscript revisits these systems, specifically by analysing the dynamics near a folded singularity from the viewpoint of inflection sets of the flow. Originally, the inflection set method was developed for planar systems [Brøns and Bar-Eli in Proc R Soc A 445(1924):305–322, 1994; Okuda in Prog Theor Phys 68(6):1827–1840, 1982; Peng et al. in Philos Trans R Soc A 337(1646):275–289, 1991] and then extended to N-dimensional systems [Ginoux et al. in Int J Bifurc Chaos 18(11):3409–3430, 2008], although not tailored to specific dynamics (e.g. folded singularities). In our previous study, we identified components of the inflection sets that classify several canard-type behaviours in 2D systems [Desroches et al. in J Math Biol 67(4):989–1017, 2013]. Herein, we first survey the planar approach and show how to adapt it for 3D systems with an isolated folded singularity by considering a suitable reduction of such 3D systems to planar non-autonomous slow-fast systems. This leads us to the computation of parametrized families of inflection sets of one component of that planar (non-autonomous) system, in the vicinity of a folded node or of a folded saddle. We then show that a novel component of the inflection set emerges, which approximates and follows the axis of rotation of canards associated to folded-node and folded-saddle singularities. Finally, we show that a similar inflection-set component occurs in the vicinity of a delayed Hopf bifurcation, a scenario that can arise at the transition between folded node and folded saddle. These results are obtained in the context of a canonical model for folded-singularity canards and subsequently we show it is also applicable to complex slow-fast models. Specifically, we focus the application towards the self-coupled 3D FitzHugh–Nagumo model, but the method is generically applicable to higher-dimensional models with isolated folded singularities, for instance in conductance-based models and other physical-chemical systems.

Appendix: Singularity Theory Approach

We build upon our previous studies that established that inflection sets and their topological shape changes (parameterised by a distinguished parameter expressed in the context of bifurcation singularity theory by Golubitsky and Schaeffer) can characterise and classify specific classes of canard mediated transitions. We extend our studies and show that a wider class of canards, namely canards mediated by folded-singularities can also be studied by the same framework. To unveil more information about the relationship between inflection sets and the dynamics near a folded singularity (saddle or node), it is useful to evaluate the inflection equation close to the folded singularity and along time instants t. To this end, we conveniently write Eq. (18) by completing the square yielding

$$\begin{aligned} \bar{h}^2-\frac{1}{4}\left[ \varepsilon \mu -2x(\mu t+z_0+x)\right] ^2+\varepsilon (\mu t+z_0+x)^2 = 0, \end{aligned}$$

(36)

with

$$\begin{aligned} \bar{h}=h+\frac{1}{2}\left( \varepsilon \mu -2x(\mu t+z_0+x)\right) , \end{aligned}$$

(37)

which is equivalently rewritten as follows

$$\begin{aligned} \bar{h}^2-\left( \sqrt{\frac{\varepsilon \mu }{2}}\right) ^4 +(\mu t+z_0+x)^2(\varepsilon -x^2)+ \left( \sqrt{\frac{\varepsilon \mu }{2}}\right) ^2 2x(\mu t+z_0+x) = 0. \end{aligned}$$

(38)

Following from our previous studies, we recast Eq. (38) as a bifurcation problem with a distinguished parameter, which leads to the case $8^-$ (of the singularity theory) on page 208 of Golubitsky and Schaeffer (1985) as follows

$$\begin{aligned} X^2-\lambda ^4+\alpha +\beta \lambda +\gamma \lambda ^2, \end{aligned}$$

(39)

Fig. 9

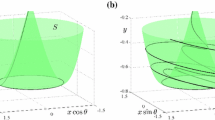
A replica of the bifurcation surface of a bifurcation problem case from Golubitsky and Schaeffer (1985) (case 8$^-$, page 208) showing the possibility for a bubble to emerge [panel (b)]; compare with Figs. 3c and 4c. The associated bifurcation equation with distinguished parameters is: $x^2-\lambda ^4+\alpha +\beta \lambda +\gamma \lambda ^2=0$ where $\lambda$ is the distinguished parameter and $(\alpha ,\beta ,\gamma )$ are three unfolding parameters. Taking different values for the triple of unfolding parameters give the three dots labelled (a), (b) and (c) on the left panel, which give topologically different transversal intersections separated by bifurcations (Color figure online)

with

$$\begin{aligned} X&= \bar{h},\nonumber \\ \lambda&= \sqrt{\frac{\varepsilon \mu }{2}},\nonumber \\ \alpha&= (\mu t+z_0+x)^2(\varepsilon -x^2),\nonumber \\ \beta&= 0,\nonumber \\ \gamma&= 2x(\mu t+z_0+x). \end{aligned}$$

(40)

The topological shape of the solution to Eq. (39) is shown on Fig. 9. The figure also shows the topological changes as a bifurcation parameter is varied. In particular, it shows that when $\mu >0$ (i.e. in the folded node case) an additional closed component of the inflection curve emerges, which corresponds to the inflection bubble that we have studied in the present work and it is in contrast to the planar case where only a single point of this bubble exists, namely the equilibrium point.