1 Introduction

One of the fundamental achievements of evolution is the ability of various animals to move efficiently throughout the natural terrain. Something as mundane as a running human or dog is itself a complex interplay of motor, neural, and muscular systems (Dickinson et al. 2000; Gordon et al. 2017). Therefore, the research on movement is intense and spans many disciplines such as biomechanics, sports medicine, applied mathematics, and robotics (Biewener and Patek 2018; Daniels et al. 1978; Tibshirani 2005; Collins et al. 2005). Building a complete model of running can be prohibitively difficult and, thus, to proceed one may just focus on some particular features or simplify matters with a use of low-dimensional conceptual models (Dickinson et al. 2000). There are many approaches to that problem. For example, in sports one usually is concerned about finishing the race in a shortest time. Hence, a particular model can focus only on several relevant parameters such as runner’s power, air drag, or race strategy. This was a basis for a conceptual model of Keller proposed in the second half of the twentieth century (Keller 1973) (which, in turn, stemmed from fundamental ideas of Hill forwarded about fifty years earlier Hill 1925). An interested reader can find some more modern accounts of competitive running models in Woodside (1991), Pritchard (1993), Aftalion (2017), Aftalion and Martinon (2019).

In this paper, we are mainly concerned not in race performance but rather the very mechanism of running. In particular, we analyse the classical spring–mass model that has been highly successful in describing the motion and dynamics of legged locomotion. The model has been firstly analysed in seminal papers (Blickhan 1989; McMahon and Cheng 1990) where authors compared theoretical predictions with real data. This model is based on an inverted elastic pendulum which acts in two phases: grounded (stance) and aerial. As was noted in Blickhan and Full (1993), despite of tremendous diversity of various locomotion modes, anatomical differences, and sizes of particular animals, the spring–mass model describes the fundamental mechanical principles of bouncing gaits very accurately. Therefore, this simple model is very robust and has been investigated in many studies from different vantage points: experimental (Farley et al. 1991, 1993; Dickinson et al. 2000) and biomechanical modelling (He et al. 1991; Geyer et al. 2005). Further, the spring–mass model was a starting point of many projects in robotics (where it is usually called the Spring Loaded Inverted-Pendulum (SLIP) model). From the first SLIP-based hopper (Raibert 1986) to more advanced modern robots (Rummel and Seyfarth 2008; Akinfiev et al. 2003; Armour et al. 2007), this seemingly simple dynamical system inspired the design of many fast legged robots. A very readable survey about locomotion in robotics can be found in Aguilar et al. (2016). Apart from that, the basic spring–mass model has been generalized and extended in many different directions. For example: multiple leg hoppers (Gan and Remy 2014; Geyer et al. 2006), dynamic swing leg motion when the attack angle is not constant (Gan et al. 2018), damping (Saranlı et al. 2010), and various control problems (Ghigliazza et al. 2005; Sato and Buehler 2004; Takahashi et al. 2017; Shahbazi et al. 2016). On the other hand, from the mathematical point of view, the spring–mass model possesses interesting dynamical properties such as complex bifurcation diagrams (Merker et al. 2015) or periodic gait stability issues (Geyer et al. 2005; Seipel and Holmes 2007; Hamzaçebi and Morgül 2017). A detailed numerical analysis of the dynamics has recently been conducted in Zaytsev et al. (2019). Moreover, in certain situations one aims to find approximate solutions of the considered model since they can be used in studying global dynamics under certain assumptions. This programme has been conducted for example in Geyer et al. (2005), Schwind and Koditschek (2000), Ghigliazza et al. (2005), Saranlı et al. (2010) and also in the prequel of our present investigations Płociniczak and Wróblewska (2020) which we conduct in a similar spirit. An interested reader will find a very thorough account of running models formulated as dynamical systems in Holmes et al. (2006).

The spring stiffness present in the model has to be adjusted accordingly in order to smoothly move from the grounded phase into the aerial. This gives rise to an interesting nonlinear boundary value problem. In our previous work (Płociniczak and Wróblewska 2020), we have proved that it has a unique solution for sufficiently small angles of attack (realistic assumption). We have also provided several asymptotic expansion of the solution for small angles. As a by-product, we have obtained a useful approximation of the important parameter being the leg stiffness. This work expands and completes several ideas born therein. While in Płociniczak and Wróblewska (2020), we were concerned mostly about various properties of solutions, here we are mainly concerned about the leg stiffness, its asymptotic form, and dependence on several other physical parameters. Since it is impossible to find an exact form of the stiffness, we have to use other methods to infer about its behaviour. In particular, we prove a rigorous result that gives a two-term asymptotic expansion of the stiffness for small angles. In the leading order, it coincides with our previous heuristics. Moreover, we consider the mathematically interesting singular case of large velocity in which we have to use a two-parameter perturbation. These results give very simple expressions that reveal some biomechanical properties of the running or hoping leg. Furthermore, numerical analysis shows that they are accurate and, hence, may be used in practical work. To sum up, this paper extends, formalizes, and improves the estimate on leg stiffness found in Płociniczak and Wróblewska (2020) along with additional material concerning large velocity asymptotics.

In the next section, we introduce the model and devise the main boundary value problem. The subsequent section deals with perturbation methods and asymptotic solution. There, we state our main results. Throughout the paper, we include some numerical examples that illustrate the theory.

2 Model and Problem Statement

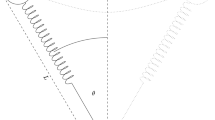
The schematic of the model setting is depicted in Fig. 1. One leg is modelled as an inverted elastic pendulum with an axis on the ground. By equating forces in the Cartesian coordinates, we can write (for details, see Blickhan 1989; McMahon and Cheng 1990; Płociniczak and Wróblewska 2020)

$$\begin{aligned} \left\{ \begin{array}{l} m\dfrac{\mathrm{d}^2 x}{\mathrm{d}t^2} = k \left( l_0-\sqrt{x^2+y^2}\right) \sin \theta , \\ m\dfrac{\mathrm{d}^2 y}{\mathrm{d}t^2} = k \left( l_0-\sqrt{x^2+y^2}\right) \cos \theta - m g, \end{array} \right. \end{aligned}$$
(1)

where \(l_0\) is the equilibrium length of the spring and k is its stiffness. We supplement the above system with initial conditions

$$\begin{aligned} x(0) = -l_0 \sin \alpha , \quad \frac{\mathrm{d}x}{\mathrm{d}t}(0) = u, \quad y(0) = l_0 \cos \alpha , \quad \frac{\mathrm{d}y}{\mathrm{d}t}(0) = v, \end{aligned}$$
(2)

where u and v are, respectively, horizontal and vertical velocities, and \(\alpha \) is the angle of attack. As we noted in Płociniczak and Wróblewska (2020), it is much more convenient to analyse (1) in polar coordinates. Transforming and rescaling leads us to

$$\begin{aligned} \left\{ \begin{array}{l} L\dfrac{\mathrm{d}^2 \theta }{\mathrm{d}t^2} + 2 \dfrac{\mathrm{d}L}{\mathrm{d}t} \dfrac{\mathrm{d}\theta }{\mathrm{d}t} = \sin \theta , \\ \dfrac{\mathrm{d}^2 L}{\mathrm{d}t^2} - \left( \dfrac{\mathrm{d}\theta }{\mathrm{d}t}\right) ^2 L = K \left( 1-L\right) -\cos \theta , \end{array} \right. \end{aligned}$$
(3)

where \(L = \sqrt{x^2+y^2}/l_0\), and the nondimensional stiffness is given by

$$\begin{aligned} K = \frac{k l_0}{m g}. \end{aligned}$$
(4)

The initial conditions now have the form

$$\begin{aligned} \theta (0) = -\alpha , \quad \frac{\mathrm{d}\theta }{\mathrm{d}t}(0) = U \cos \alpha -V \sin \alpha , \quad L(0) = 1, \quad \frac{\mathrm{d}L}{\mathrm{d}t}(0) = - U \sin \alpha - V \cos \alpha , \end{aligned}$$
(5)

with the horizontal and vertical Froude numbers

$$\begin{aligned} U = \frac{u}{\sqrt{g l_0}}, \quad V = \frac{v}{\sqrt{g l_0}}. \end{aligned}$$
(6)

Data from McMahon and Cheng (1990), Farley et al. (1993) indicate that for a wide variety of animals we have

$$\begin{aligned} \alpha \approx 0.2-0.5, \quad U \approx 0.8-2.6, \quad V \approx 0.05-0.5, \end{aligned}$$
(7)

therefore \(\alpha \) and V can be considered small, while U is of order of unity.

Fig. 1
figure 1

A schematic of the main model (taken from Płociniczak and Wróblewska 2020)

Full size image

In the above biomechanical setting, a certain boundary value problem naturally arises. It is to find the stiffness \(K^*\) and the smallest time \(t^*\) for which we have

$$\begin{aligned} L(t^*,K^*) = 1, \quad \theta (t^*,K^*) = \alpha . \end{aligned}$$
(8)

That is to say, we have to determine the stiffness for which the leg has travelled an angle \(2\alpha \) precisely at the time of returning to its original length (see Fig. 1). In Płociniczak and Wróblewska (2020), we have shown that this problem has a unique solution at least for small \(\alpha \) and provided some approximations to \(K^*\) and \(t^*\). Specifically, we have found that for U of order of unity we formally have

$$\begin{aligned} K^* \approx \left( \frac{\pi (U \cos \alpha -V \sin \alpha )}{2\alpha }\right) ^2, \quad t^* \approx \frac{\pi }{\sqrt{K^*}}. \end{aligned}$$
(9)

In what follows, we show that the above approximations are indeed the leading order expansions as \(\alpha \rightarrow 0\), more precisely we prove that

$$\begin{aligned} \begin{array}{l} K^* = \left( \dfrac{\pi U}{2 \alpha }\right) ^2 + \left( \dfrac{\pi ^2 V}{2}+ \dfrac{2}{V}\left( 1-U^2+2 V^2\right) \right) \dfrac{U}{\alpha } + O(\alpha ^0), \\ t^* = \dfrac{2\alpha }{U} - \dfrac{2\left( \pi ^2+8\right) }{\pi ^2 U^2}\alpha ^2 + O(\alpha ^3), \end{array} \quad \text { as } \alpha \rightarrow 0^+, \end{aligned}$$
(10)

Moreover, we also consider an interesting case of large U for which

$$\begin{aligned} \begin{array}{l} K^* = \dfrac{3 U V}{\alpha ^3} + O(U\alpha ^{-1}) + O(U^0), \\ t^* = \dfrac{2\alpha }{U} + \dfrac{4V \alpha ^3}{5U^2}+ O(U^{-2}\alpha ^5)+ O(U^{-3}), \end{array} \quad \text { as } U\rightarrow \infty \text { and } \alpha \rightarrow 0^+. \end{aligned}$$
(11)

In this way, we prove that \(K^*\) depends linearly on U for large velocities what has been observed before with numerical means only. Notice that above formulas are asymptotic also for small \(\alpha \). However, led by our analytical results we also show that \(K^*\) can be very accurately approximated with the following quasi-empirical formula for all meaningful angles

$$\begin{aligned} K^* \approx \frac{3 U V}{\alpha ^3}\left( 1+\frac{1}{2}\alpha ^2\right) , \quad U\rightarrow \infty . \end{aligned}$$
(12)

The above extrapolates the small-angle leading order asymptotic behaviour of \(K^*\) into the larger interval \(\alpha \in [0,1]\).

3 Asymptotic Solution

We begin by noticing that the main equation (3) for L can be written as

$$\begin{aligned} \frac{\mathrm{d}^2 L}{\mathrm{d}t^2} +\left[ K-\left( \frac{\mathrm{d}\theta }{\mathrm{d}t}\right) ^2\right] L = K - \cos \theta . \end{aligned}$$
(13)

It follows that the nature of the solution depends on the relative sizes of K and \(d\theta /dt\). The latter, in turn, has a magnitude of order of U. Loosely speaking, the solutions are either of trigonometric or hyperbolic nature. This makes a profound difference for the solution of the problem (8). Below, we explore these two regimes perturbatively.

Because of a large number of different quantities, the scope of below two subsections is local. This means that all introduced variable names are valid only within the respective subsection. Specifically, x and y are different in each of them.

3.1 Small Angle

The solution of the boundary value problem (8) requires that \(K=K(\alpha )\). We start our analysis with an observation that \(K(\alpha )\alpha ^2\) is bounded when \(\alpha \rightarrow 0^+\). This makes the subsequent perturbation theory possible. Moreover, this result has important implications since previously the angular dependence of \(K^*\) has been known only numerically.

Lemma 1

Let \((K^*(\alpha ),t^*(\alpha ))\) be the solution of the boundary value problem (8). Then,

$$\begin{aligned} \lim \limits _{\alpha \rightarrow 0^+} \alpha ^2 K^*(\alpha ) = \frac{\pi ^2 U^2}{4}. \end{aligned}$$
(14)

Proof

Start by using a new time scale

$$\begin{aligned} {\widehat{\tau }} = \sqrt{K} t. \end{aligned}$$
(15)

Then, the \(\theta \)-equation in (3) can be transformed into the integral form by multiplying it by L and integrating twice. We have

$$\begin{aligned} \theta ({\widehat{\tau }}) = -\alpha + \frac{U\cos \alpha -V\sin \alpha }{\sqrt{K}} \int _0^{{\widehat{\tau }}} L(s)^{-2} \mathrm{d}s + \frac{1}{K} \int _0^{{\widehat{\tau }}} G({\widehat{\tau }}-s)\sin \theta (s)\mathrm{d}s, \end{aligned}$$
(16)

where G is the kernel whose explicit form can be found. Setting \(\theta ({\widehat{\tau }}) = \alpha \), we obtain an implicit equation for \(K^*\)

$$\begin{aligned} 2\alpha = \frac{U\cos \alpha -V\sin \alpha }{\sqrt{K^*}} \int _0^{{\widehat{\tau }}^*} L(s)^{-2} \mathrm{d}s + \frac{1}{K^*} \int _0^{{\widehat{\tau }}^*} G({\widehat{\tau }}-s)\sin \theta (s)\mathrm{d}s. \end{aligned}$$
(17)

Now, in Płociniczak and Wróblewska (2020) we have shown that there exists a monotone relation \(K^*=K^*(\alpha )\) for sufficiently small \(\alpha \). Moreover, \(K^*(\alpha ) \rightarrow \infty \) and \({\widehat{\tau }}^*(\alpha ) \rightarrow \pi \) as \(\alpha \rightarrow 0^+\). If we take the same limit in the equation above the second term on the right vanishes since, as can be checked with an elementary calculation, G is uniformly bounded for each \(\alpha \). Our previous results (Płociniczak and Wróblewska 2020) also indicate that in this limit \(L \rightarrow 1\) and hence, for the both sides to be equal to each other we should have \(K(\alpha ) \sim \pi ^2 U^2 \alpha ^{-2} / 4\) as \(\alpha \rightarrow 0^+\). This finishes the proof. \(\square \)

Since we are interested in solving the boundary value problem (8), we will rescale the relevant variables in a natural way to simplify matters. First, set

$$\begin{aligned} L_d(\alpha ) = U \sin \alpha +V\cos \alpha , \quad \theta _d(\alpha ) = U\cos \alpha -V \sin \alpha , \end{aligned}$$
(18)

which are initial conditions for L and \(\theta \) as in (5). Then, we put

$$\begin{aligned} L = 1 - \frac{L_d(\alpha )}{\sqrt{K(\alpha )}} \, x, \quad \theta = \alpha (1-2 y), \end{aligned}$$
(19)

for new dependent variables x and y. As we can see x measures the spring departure from initial length while y is normalized angle. The magnitude of \(1-L\) is chosen according to the asymptotic analysis done in our previous work (Płociniczak and Wróblewska 2020) (but see also Geyer et al. 2005). As for the time scale, we choose the one balancing \(L''\) with L in (3)

$$\begin{aligned} t = \frac{\sqrt{K(\alpha )}}{\omega (\alpha )} \tau , \quad \omega (\alpha ) = 1 + \omega _1 \alpha + \omega _2 \alpha ^2, \end{aligned}$$
(20)

where \(\tau \) is the strained fast time variable introduced because of the frequency modulation. Notice that \(\omega \) is terminated after the second-order term. We will not conduct the higher-order expansion. In these new variables, Eq. (3) has the form

$$\begin{aligned} \left\{ \begin{array}{l} \omega (\alpha )^2 x'' + (1-4\alpha ^2 \omega (\alpha )^2 y'^2)x = -\dfrac{4 \alpha ^2 \omega (\alpha )^2 \sqrt{K(\alpha )}}{L_d(\alpha )}y'^2\\ \quad +\dfrac{1}{L_d(\alpha )\sqrt{K(\alpha )}}\cos (\alpha (1-2y)), \\ -\left( 1-\dfrac{L_d(\alpha )}{\sqrt{K(\alpha )}}x\right) y''+\dfrac{2L_d(\alpha )}{\sqrt{K(\alpha )}}x' y' = \dfrac{\omega (\alpha )^{-1}}{2\alpha K(\alpha )}\sin (\alpha (1-2y)), \end{array} \right. \end{aligned}$$
(21)

with initial conditions

$$\begin{aligned} x(0) = 0, \quad x'(0) = 1, \quad y(0) = 1, \quad y'(0) = - \frac{\theta _d(\alpha )}{2\alpha \, \omega (\alpha ) \sqrt{K(\alpha )}}. \end{aligned}$$
(22)

Here, prime denotes the derivative with respect to the fast time \(\tau \). We can see that due to Lemma 1 the derivative \(y'(0)\) is bounded as \(\alpha \rightarrow 0^+\).

Now, we make the following perturbation expansions for the solutions of ODEs

$$\begin{aligned} x(\tau ) = x_0(\tau ) + x_1(\tau ) \alpha + x_2(\tau ) \alpha ^2 + \cdots , \quad y(\tau ) = y_0(\tau ) + y_1(\tau ) \alpha + y_2(\tau ) \alpha ^2 + \cdots , \end{aligned}$$
(23)

and the unknown stiffness

$$\begin{aligned} \sqrt{K(\alpha )} = \frac{k_{-1}}{\alpha } + k_0 + k_1 \alpha + \cdots , \end{aligned}$$
(24)

where we notice that it is more feasible to expand the square root of K. Plugging these into (21), collecting respective powers of \(\alpha \), and using initial conditions (22) yields the following systems

$$\begin{aligned} \begin{array}{ll} \alpha ^0: &{} \left\{ \begin{array}{lll} x_0'' + x_0 = 0, &{} x_0(0) = 0, &{} x_0'(0) = 1, \\ y_0'' = 0, &{} y_0(0) = 1, &{} y_0'(0) = - \dfrac{U}{2 k_{-1}}, \end{array} \right. \\ \alpha ^1: &{} \left\{ \begin{array}{lll} x_1'' + x_1 = \dfrac{1}{V k_{-1}} - \dfrac{4 k_{-1}}{V} y_0'^2 - 2 \omega _1 x_0'', &{} x_1(0) = 0, &{} x_1'(0) = -\omega _1, \\ y_1'' = \dfrac{V}{k_{-1}}\left( 2x_0' y_0'+x_0 y_0''\right) , &{} y_1(0) = 0, &{}\\ \quad y_0'(0) = - \dfrac{1}{2 k_{-1}^2}\left( -V k_{-1}+ U k_0 + U k_{-1} \omega _1\right) . \end{array} \right. \end{array} \end{aligned}$$
(25)

The \(\alpha ^0\) equation can immediately be solved

$$\begin{aligned} x_0(\tau ) = \sin \tau , \quad y_0(\tau ) = 1 - \frac{U}{2 k_{-1}}\tau . \end{aligned}$$
(26)

Now, since \(x_0''(\tau ) = -\sin \tau \) we can remove the secular terms from the \(\alpha ^1\) equation only by taking \(\omega _1 = 0\). The corresponding solution will then have the form

$$\begin{aligned} x_1(\tau )= & {} \frac{1}{V k_{-1}} (1-U^2) (1-\cos \tau ), \nonumber \\ y_1(\tau )= & {} -\frac{UV}{k_{-1}^2}(1-\cos \tau ) + \frac{1}{2 k_{-1}^2}\left( U k_0-V k_{-1} \right) \tau . \end{aligned}$$
(27)

Further, the second-order correction to the frequency \(\omega _2\) can be determined from the \(\alpha ^2\) equation

$$\begin{aligned} \alpha ^2: x_2''+x_2 = \left( 2\omega _2 + \dfrac{5 U^2}{k_{-1}^2}\right) \sin \tau - \dfrac{U}{V^2 k_{-1}}\left( 1-U^2+2V^2\right) + \dfrac{U^2-1}{V k_{-1}^2} k_0. \end{aligned}$$
(28)

Therefore, by removing the secular terms we have

$$\begin{aligned} \omega _2 = - \frac{5}{2} \frac{U^2}{k_{-1}^2}. \end{aligned}$$
(29)

The process can be continued in a standard way however, as can be seen, equations become very cluttered. Nevertheless, we have all the expansions needed to determine \(k_{-1}\) and \(k_0\). Our systematic expansions can be compared with more heuristic approach in Geyer et al. (2006) where Authors find some accurate approximations, couple them with the aerial phase, and investigate the stability of such model.

We require that \(K(\alpha ) \sim K^*(\alpha )\) as \(\alpha \rightarrow 0^+\) that is to say, coefficients \(k_i\) have to be chosen to asymptotically solve the boundary value problem (8). To this end, we make the further expansion for the time \(t^*\)

$$\begin{aligned} \tau ^*(\alpha ) = \tau _0 + \tau _1 \alpha + \tau _2 \alpha ^2 + \cdots . \end{aligned}$$
(30)

Now, \(t_i\) and \(k_i\) can be found by perturbatively solving

$$\begin{aligned} 0= & {} x(\tau ^*(\alpha )) = x_0(\tau ^*(\alpha )) + x_1(\tau ^*(\alpha )) \alpha +\cdots , \nonumber \\ 0= & {} y(\tau ^*(\alpha )) = y_0(\tau ^*(\alpha )) + y_1(\tau ^*(\alpha )) \alpha + \cdots \end{aligned}$$
(31)

Using (26), (27), and collecting respective powers of \(\alpha \), we obtain a series of linear systems

$$\begin{aligned} \begin{array}{ll} \alpha ^0: &{} \left\{ \begin{array}{l} \sin \tau _0 = 0, \\ 1-\dfrac{U \tau _0}{2 k_{-1}} = 0, \end{array} \right. \\ \alpha ^1: &{} \left\{ \begin{array}{l} \left( \cos \tau _0\right) t_1 + \dfrac{\left( 1-U^2\right) \left( 1-\cos \tau _0\right) }{V k_{-1}} =0 , \\ U k_0 t_0 - U k_{-1} t_1 - V k_{-1} \tau _0 + 2 UV\left( 1-\cos \tau _0\right) = 0. \end{array} \right. \\ \ldots \end{array} \end{aligned}$$
(32)

Solving the above leads us to

$$\begin{aligned} t_0 = \pi , \quad t_1 = \frac{4 (1-U^2)}{U V}, \quad k_{-1} = \frac{\pi U}{2}, \quad k_0 = \frac{4(1-U^2)+(8+\pi ^2)V^2}{2\pi V}. \end{aligned}$$
(33)

It is now only a matter of returning to the original time scale t and squaring \(\sqrt{K(\alpha )}\). Therefore, we have proved the following result.

Theorem 1

Let \((K^*(\alpha ), t^*(\alpha ))\) be the solution of the problem (8). Then, the expansion (10) holds.

The numerical example of the above expansion is depicted in Fig. 2. We have plotted the relative error of the asymptotic approximation \(K^*_i\) of the numerical solution \(K^*\) of (8). Here, \(i\in \{-1,0,1\}\) denotes the largest order of \(\alpha \) taken in the expansion. Clearly, all errors converge to 0 for small angles and what could have been anticipated, \(K^*_1\) looses accuracy for larger values of \(\alpha \) (say, \(\alpha >0.3\)). We can see that \(K^*_0\) provides a reasonable approximation even for larger angles.

Fig. 2
figure 2

Relative error of the asymptotic approximation \(K^*_i\) of the solution \(K^*\) to the problem (8). Here \(i=-1,0,1\) denotes the largest order of \(\alpha \) taken in the expansion. The plot below is the magnification of the above for \(\alpha \in [0,0.1]\)

Full size image

3.2 Large Velocity

Similarly as in the previous section, we begin by finding the leading order of the expansion \(K=K(U)\) when \(U\rightarrow \infty \). Here however, we determine only how fast K(U) approaches infinity as U increases.

Lemma 2

Let \((K^*(U), t^*(U))\) be the solution of the boundary value problem (8). Then \(K(U)U^{-1}\) is bounded when \(U\rightarrow \infty \).

Proof

Similarly as in the proof of Lemma 1, we start by introducing a faster time scale

$$\begin{aligned} {\widehat{\tau }} = K t. \end{aligned}$$
(34)

Now, we have \(K=K(U)\) and the initial derivatives have the form

$$\begin{aligned} \frac{\mathrm{d}\theta }{\mathrm{d}{\widehat{\tau }}}(0) = \frac{U\cos \alpha -V\sin \alpha }{K(U)}, \quad \frac{\mathrm{d}L}{\mathrm{d}{\widehat{\tau }}}(0) = -\frac{U\sin \alpha +V\cos \alpha }{K(U)}. \end{aligned}$$
(35)

Since, by assumption (8) has a solution for \(U\rightarrow \infty \) the derivatives has to stay bounded in the limit. We have then two possibilities: either \(U/K(U)\rightarrow 0\) or \(U/K(U)\rightarrow C > 0\) what means that \(K(U)\rightarrow \infty \). Moreover, in the former case (3) becomes

$$\begin{aligned} \frac{\mathrm{d}^2L}{\mathrm{d}{\widehat{\tau }}^2} - 2 L \left( \frac{\mathrm{d}\theta }{\mathrm{d}{\widehat{\tau }}}\right) ^2 = 0, \quad L \frac{\mathrm{d}^2\theta }{\mathrm{d}{\widehat{\tau }}^2} + 2 \frac{\mathrm{d}L}{\mathrm{d}{\widehat{\tau }}} \frac{\mathrm{d}\theta }{\mathrm{d}{\widehat{\tau }}} = 0. \end{aligned}$$
(36)

with initial conditions

$$\begin{aligned} \theta (0) = -\alpha , \quad \frac{\mathrm{d}\theta }{\mathrm{d}{\widehat{\tau }}}(0) = 0, \quad L(0) = 1, \quad \frac{\mathrm{d}L}{\mathrm{d}{\widehat{\tau }}}(0) = 0. \end{aligned}$$
(37)

Notice that the equation for \(\theta \) can be rewritten as a conservation of angular momentum

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}{\widehat{\tau }}} \left( L^2 \frac{\mathrm{d}\theta }{\mathrm{d}{\widehat{\tau }}}\right) = 0, \end{aligned}$$
(38)

which, using the initial conditions, yields \(\theta ({\widehat{\tau }}) = -\alpha \) for all \({\widehat{\tau }}\) which is a contradiction since it is impossible to have \(\theta = \alpha \). Therefore, we are left with \(U/K(U) > 0\) for \(U\rightarrow \infty \) what concludes the proof. \(\square \)

Thanks to the above result we know that \(K(U) \propto U\) for large U. This observation has been made before in McMahon and Cheng (1990) but only on the basis of numerical calculations. In what follows we will find the proportionality constant in this dependence. It appears that this problem is more difficult than the one considered before since the first-order perturbation equation does not posses an analytical solution. However, we will see that further expanding in the small \(\alpha \) can help to obtain useful results.

We start by introducing appropriate scaling. Let

$$\begin{aligned} L = x, \quad \theta = \alpha \left( 1-2 y\right) , \quad t = \frac{2\alpha }{U}\tau . \end{aligned}$$
(39)

We have thus rescaled the angle according to its range in the considered problem. The time scale has been chosen based on the linear approximation to \(\theta \) for which \(\theta (t) \approx -\alpha + (U\cos \alpha - V \sin \alpha )t\). Then, \(\theta (t) \approx \alpha \) when \(t \approx 2\alpha (U\cos \alpha - V \sin \alpha )^{-1}\) which gives the above chosen time scale for large U and small \(\alpha \).

Now, Eq. (3) transforms into

$$\begin{aligned} \left\{ \begin{array}{l} x'' - 4\alpha ^2 x y'^2 = \epsilon ^2 \left( K(\epsilon )(1-x)-\cos \left( \alpha (1-2y)\right) \right) , \\ x y'' + 2 x' y' = \epsilon ^2 \dfrac{\sin \left( \alpha (1-2y)\right) }{\alpha }, \end{array} \right. \end{aligned}$$
(40)

where we have denoted the small parameter

$$\begin{aligned} \epsilon := \frac{2\alpha }{U} \ll 1, \end{aligned}$$
(41)

and the prime denotes a derivative with respect to \(\tau \). The initial conditions (5) have the form

$$\begin{aligned} x(0) = 1, \quad x'(0) = -2\alpha \sin \alpha -\epsilon V \cos \alpha , \quad y(0) = 1, \quad y'(0) = -\cos \alpha + \epsilon \frac{V}{2\alpha }\sin \alpha . \end{aligned}$$
(42)

Therefore, we can see that both dependent variables and their derivatives are now of order of unity.

We are ready to make the perturbation expansion

$$\begin{aligned} x(\tau )= & {} x_0(\tau ) + x_1(\tau )\epsilon + O(\epsilon ^2), \quad y(\tau ) = y_0(\tau ) + y_1(\tau )\epsilon + O(\epsilon ^2), \nonumber \\ K(\epsilon )= & {} K_1 \epsilon + O(\epsilon ^2) \quad \text { as } \quad \epsilon \rightarrow 0^+, \end{aligned}$$
(43)

for which (40) becomes an array of equations

$$\begin{aligned} \begin{array}{ll} \epsilon ^0: &{} \left\{ \begin{array}{lll} x_0'' - 4\alpha ^2 x_0 y_0'^2 = 0, &{} x_0(0) = 1, &{} x_0'(0) = -2\alpha \sin \alpha , \\ x_0 y''_0 + 2 x'_0 y'_0 = 0, &{} y_0(0) = 1, &{} y_0'(0) = -\cos \alpha , \end{array} \right. \\ \epsilon ^1: &{} \left\{ \begin{array}{lll} x_1'' -4 \alpha ^2 \left( x_1 y_0'^2+2 x_0 y'_0 y'_1 \right) = K_1 (1-x_0), &{} x_1(0) = 0, &{} x_1'(0) = -V \cos \alpha , \\ x_0 y_1''+x_1 y_0'' + 2\left( x_0' y_1'+ x_1' y_0'\right) = 0, &{} y_1(0) = 0, &{} y_1'(0) = \dfrac{V}{2\alpha } \sin \alpha . \end{array} \right. \end{array} \end{aligned}$$
(44)

Notice that the above equations are nonlinear in all orders. However, the \(\epsilon ^0\) system can be exactly integrated in a closed form. To see this notice that from the second equation we have the conservation of angular momentum

$$\begin{aligned} \left( x_0^2 y_0'\right) ' = 0. \end{aligned}$$
(45)

From which it follows that

$$\begin{aligned} y_0' = -\frac{\cos \alpha }{x_0^2}. \end{aligned}$$
(46)

Plugging it to the first equation, we obtain a single nonlinear ODE

$$\begin{aligned} x_0^3 x_0'' = 4\alpha ^2 \cos ^2\alpha . \end{aligned}$$
(47)

This equation has an analytical solution which can be obtained by reduction in order

$$\begin{aligned} x_0(\tau ) = \sqrt{1-4 \tau \alpha \sin \alpha + 4\alpha ^2 t^2}. \end{aligned}$$
(48)

After returning to \(y_0\) and integrating, we have

$$\begin{aligned} y_0(\tau ) = 1 + \frac{1}{2\alpha }\arctan \left( \frac{2\tau \alpha \cos \alpha }{1-2\tau \alpha \sin \alpha }\right) . \end{aligned}$$
(49)

Notice that this equation is degenerate in the sense that it does not contain the \(K_1\) coefficient but, nevertheless, automatically solves (8). To wit, note that the leading order time of the solution is

$$\begin{aligned} \tau _0^* = \frac{\sin \alpha }{\alpha }, \end{aligned}$$
(50)

for which we have both \(x_0(\tau ^*) = 1\) and \(y_0(\tau ^*) = 0\).

In order to gain some insight how does the solution of (40) behave for small positive \(\epsilon \) we have to analyze the \(\epsilon ^1\) equation in (44). Unfortunately, we cannot obtain its closed-form solution. However, since \(\alpha \) is small, we can at least try to find the subsequent perturbation approximation. To this end, put

$$\begin{aligned} x_1(\tau ) = x_{10}(\tau ) + x_{12}(\tau ) \alpha ^2 + O(\alpha ^4), \quad y_1(\tau ) = y_{10}(\tau ) + y_{12}(\tau ) \alpha ^2 + O(\alpha ^4) \quad \text {as} \quad \alpha \rightarrow 0. \end{aligned}$$
(51)

Notice that we expand only in the even powers of \(\alpha \) since both \(\epsilon ^1\) equation and the initial conditions (44) have even \(\alpha \)-expansion. Plugging the above expansion into (44) and using the found leading order solution (48)–(49), we obtain the following equations

$$\begin{aligned} \begin{array}{ll} \alpha ^0: &{} \left\{ \begin{array}{lll} x_{10}'' = 0, &{} x_{10}(0) = 0, &{} x_{10}'(0) = -V, \\ y_{10}' - 2 x_{10}' = 0, &{} y_{10}(0) = 0, &{} y_{10}'(0) = \dfrac{V}{2}, \end{array} \right. \\ \alpha ^2: &{} \left\{ \begin{array}{lll} x_{12}'' = 4\left( x_{10}-2 y_{10}' + \dfrac{1}{2}K_1 \tau (\tau -1)\right) , &{} x_{12}(0) = 0, &{} x_{12}'(0) = \dfrac{V}{2}, \\ \begin{aligned} y_{12}'' = &{}-\left( 8 t^2-8 t+1\right) x_{10}'-2 t (t+1) y_{10}''+2 x_{12}' \\ &{}-4(2 t-1)\left( x_{10}+y_{10}'\right) \end{aligned}, &{} y_{12}(0) = 0, &{} y_{12}'(0) = -\dfrac{V}{12}. \end{array} \right. \end{array}\nonumber \\ \end{aligned}$$
(52)

This system is easy to be solved explicitly yielding

$$\begin{aligned} \begin{array}{ll} x_{10}(\tau ) = - \tau V, &{} x_{12}(\tau ) = \dfrac{\tau }{6} \left( 3 (1-2 \tau )^2 V-K_1 (\tau -2) \tau ^2\right) , \\ y_{10}(\tau ) = \dfrac{V \tau }{2} \left( 1-2 \tau \right) , &{} y_{12}(\tau ) = \dfrac{\tau }{60}\left( 2 K_1 (5-2 \tau ) \tau ^3+5 V (24\tau (\tau -1) (2 \tau -1)-1) \right) . \end{array}\nonumber \\ \end{aligned}$$
(53)

Having these expansions in hand, we can proceed to the solution (8). To this end, we set

$$\begin{aligned} \tau ^*(\epsilon ) = \tau ^*_0 + \epsilon \tau ^*_1 + O(\epsilon ) \quad \text {as} \quad \epsilon \rightarrow 0^+, \end{aligned}$$
(54)

and then require that

$$\begin{aligned} \begin{aligned} 1&= x_0(\tau ^*(\epsilon )) + \epsilon \left( x_{10}(\tau ^*(\epsilon ))+x_{12}(\tau ^*(\epsilon ))\alpha ^2 + O(\alpha ^4)\right) + O(\epsilon ^2), \\ 0&= y_0(\tau ^*(\epsilon )) + \epsilon \left( y_{10}(\tau ^*(\epsilon ))+y_{12}(\tau ^*(\epsilon ))\alpha ^2+ O(\alpha ^4)\right) + O(\epsilon ^2), \end{aligned} \end{aligned}$$
(55)

as \(\epsilon \rightarrow 0^+\) and \(\alpha \rightarrow 0^+\). The asymptotic solution of the above algebraic system is \(\tau ^*_0\) given by (50) and

$$\begin{aligned} \tau ^*_1 = \frac{V\alpha }{5} + O(\alpha ^3), \quad K_1 = \frac{6 V}{\alpha ^2} + O(\alpha ^0) \quad \text {as} \quad \alpha \rightarrow 0^+, \end{aligned}$$
(56)

which coincides with (11) after returning to the original time scale. Therefore, we have proved the following result.

Theorem 2

Let \((K^*(\alpha ), t^*(\alpha ))\) be the solution of the problem (8). Then, the expansion (11) holds.

Notice that according to (56), we have \(K_1 \propto V \alpha ^{-2}\) for small angles. Since our approximation is only the asymptotic leading order for angles and not the exact solution, it is interesting to extend this result numerically and find the empirical proportionality constant valid for a larger set of \(\alpha \). Let

$$\begin{aligned} {\widetilde{K}}_{1} = \frac{6 V}{\alpha ^2}, \end{aligned}$$
(57)

The ratio of \({\widetilde{K}}_1\) to the numerical value of \(K_1\) found by solving the boundary value problem (8) corresponding to Eq. (40) is plotted in Fig. 3. As we can see, the analysed quantity is almost independent of V. Whence, it is motivated to stipulate that

$$\begin{aligned} K_1 \approx {\widetilde{K}}_p := \frac{6 V}{\alpha ^2} \, G(\alpha ), \end{aligned}$$
(58)

for some G with \(G(0) = 1\). Numerical calculations plotting \(K_1 / {\widetilde{K}}_{1}\) are shown in Fig. 4. We can see that the sought form of \(G(\alpha )\) is approximately quadratic and the least squares best fit is given by

$$\begin{aligned} G(\alpha ) = 1 + 0.51 \alpha ^2 \approx 1 + \frac{1}{2}\alpha ^2, \end{aligned}$$
(59)

with the determination coefficient \(R^2 = 0.999\). The accuracy is thus very good for \(\alpha \in [0,1]\).

Fig. 3
figure 3

A ratio of \(K_1\) found from the numerical solution of the boundary value problem (8) for Eq. (40) and its approximation \({\widetilde{K}}_{1}\) defined in (57). Here, \(\epsilon = 10^{-4}\)

Full size image
Fig. 4
figure 4

A ratio of \(K_1\) found from the numerical solution of the boundary value problem (8) for Eq. (40) and its approximation \({\widetilde{K}}_{1}\) defined in (57). Points represent numerical calculations while solid line is \(G(\alpha )\) as in (59). Here, \(\epsilon = 10^{-4}\) and \(V=0.1\)

Full size image

On Fig. 5, we plot the relative error of the approximation (11) to the solution of the problem (8) for the original Eq. (3). Notice that the approximations achieve an accuracy of several percent for \(U = O(10^2)\). Also, the corrected coefficient \({\widetilde{K}}_p\) as in (58) performs very well even for large angles while the leading order term \({\widetilde{K}}_1\) does not converge to 0 for such.

Fig. 5
figure 5

Log–log plot of the relative error of the approximation \({\widetilde{K}}_{1,p}\) to the boundary value problem (8). Here, \(V=0.1\)

Full size image

4 Conclusion

The perturbation analysis conducted above helped us to determine the asymptotic form of the solution of (8). As was shown, the physically important case of small angles, in principle could have been resolved for any required order. However, the complexity of expressions forced us to stop at two meaningful terms. Nevertheless, the rest can be obtained in a standard way with a use of some symbolic manipulation environment such as Wolfram Mathematica as was in our case. Moreover, found analytic formulas proved to be very accurate in their region of validity and explained how does the leg stiffness depends on the attack angle and velocities.

The case of large (horizontal) velocity also proved to be attackable with the perturbation theory. However, the leading order equations were nonlinear forcing higher orders not to be resolvable analytically. Despite this difficulty, we have been able to use the additional expansion in small angles and find leading order behaviour in two parameters. This let us to determine the form of dependence of the leg stiffness to other physical parameters and, thanks to that knowledge, to empirically extend the approximation for all meaningful angles.

Asymptotic analysis was only possible due to the fact that we firstly have found the leading order behaviours of \(K^*(\alpha )\) and \(K^*(U)\) in the respective limits. Moreover, the key step was to perturbatively look for expansions of the stiffness \(K^*\) and the time \(t^*\). Of course, this programme can be carried over to higher orders with a symbolic manipulation software. However, our findings are sufficient to understand the fundamental relations between stiffness and various physical parameters. We hope that this research will contribute to the understanding of various gaits in locomotion and robotics.