The Quasiconvex Envelope of Conformally Invariant Planar Energy Functions in Isotropic Hyperelasticity

Abstract

We consider conformally invariant energies W on the group ${{\,\mathrm{GL}\,}}^{\!+}(2)$ of $2\times 2$-matrices with positive determinant, i.e., $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} W(A\, F\, B) = W(F) \quad \text {for all }\; A,B\in \{a\, R\in {{\,\mathrm{GL}\,}}^{\!+}(2) \,|\,a\in (0,\infty ),\; R\in {{\,\mathrm{SO}\,}}(2)\}, \end{aligned}$$

where ${{\,\mathrm{SO}\,}}(2)$ denotes the special orthogonal group and provides an explicit formula for the (notoriously difficult to compute) quasiconvex envelope of these functions. Our results, which are based on the representation $W(F)=h\bigl (\frac{\lambda _1}{\lambda _2}\bigr )$ of W in terms of the singular values $\lambda _1,\lambda _2$ of F, are applied to a number of example energies in order to demonstrate the convenience of the singular-value-based expression compared to the more common representation in terms of the distortion ${\mathbb {K}}:=\frac{1}{2}\frac{\Vert F \Vert ^2}{\det F}$. Applying our results, we answer a conjecture by Adamowicz (in: Atti della Accademia Nazionale dei Lincei. Classe di Scienze Fisiche, Matematiche e Naturali. Rendiconti Lincei. Serie IX. Matematica e Applicazioni, vol 18(2), pp 163, 2007) and discuss a connection between polyconvexity and the Grötzsch free boundary value problem. Special cases of our results can also be obtained from earlier works by Astala et al. (Elliptic partial differential equations and quasiconformal mappings in the plane, Princeton University Press, Princeton, 2008) and Yan (Trans Am Math Soc 355(12):4755–4765, 2003). Since the restricted domain of the energy functions in question poses additional difficulties with respect to the notion of quasiconvexity compared to the case of globally defined real-valued functions, we also discuss more general properties related to the $W^{1,p}$-quasiconvex envelope on the domain ${{\,\mathrm{GL}\,}}^{\!+}(n)$ which, in particular, ensure that a stricter version of Dacorogna’s formula is applicable to conformally invariant energies on ${{\,\mathrm{GL}\,}}^{\!+}(2)$.

1 Introduction

A recent contribution (Martin et al. 2017) introduced a number of criteria for generalized convexity properties (including quasiconvexity) of so-called conformally invariant functions (or energies) on the group ${{\,\mathrm{GL}\,}}^{\!+}(2)$ of $2\times 2$-matrices with positive determinant, i.e., functions $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow {\mathbb {R}}$ with

$$\begin{aligned} W(Z_1\, F\, Z_2) = W(F) \quad \text {for all }\; Z_1,Z_2\in {{\,\mathrm{CSO}\,}}(2), \end{aligned}$$

(1.1)

where

$$\begin{aligned} {{\,\mathrm{CSO}\,}}(2):={\mathbb {R}}^+\cdot {{\,\mathrm{SO}\,}}(2)=\{a\, R\in {{\,\mathrm{GL}\,}}^{\!+}(2) \,|\,a\in (0,\infty ),\; R\in {{\,\mathrm{SO}\,}}(2)\} \end{aligned}$$

denotes the conformal special orthogonal group.¹ This requirement can equivalently be expressed as

$$\begin{aligned} W(R_1F)=W(F)=W(FR_2),\quad W(aF)=W(F) \quad \text {for all }\;&R_1,R_2\in {{\,\mathrm{SO}\,}}(2),\nonumber \\&a\in (0,\infty ), \end{aligned}$$

(1.2)

i.e., left- and right-invariance under the special orthogonal group ${{\,\mathrm{SO}\,}}(2)$ and invariance under scaling. In nonlinear elasticity theory, where $F=\nabla \varphi$ represents the so-called deformation gradient of a deformation $\varphi$, the former two invariances correspond to the objectivity and isotropy of W, respectively. In this context, an energy W satisfying $W(aF)=W(F)$ is more commonly known as isochoric and is often additively coupled (Richter 1949; Charrier et al. 1988) with a volumetric energy term of the form $f(\det F)$ for some convex function $f:(0,\infty )\rightarrow {\mathbb {R}}$.

In this contribution, we consider the quasiconvex envelopes of conformally invariant energies on ${{\,\mathrm{GL}\,}}^{\!+}(2)$. Based on our previous results, we provide an explicit formula that allows for a direct computation of the quasiconvex (as well as the rank-one convex and polyconvex) envelope for this class of functions. We also discuss different ways of expressing conformally invariant energies, including representations based on the singular values of F, i.e., the eigenvalues of $\sqrt{F^TF}$, in order to highlight the difficulties which arise from focusing on the seemingly more simple representation in terms of the distortion ${\mathbb {K}}=\frac{1}{2}\frac{\Vert F \Vert ^2}{\det F}$.

Our main result (Theorem 3.1) has been tested against a numerical algorithm for computing the polyconvex envelope (Bartels 2005) for a range of parameters, yielding agreement up to computational precision. In two special cases, we show that our results completely match previous developments of Astala et al. (2008) and Yan (2001, (2003). We also present direct finite element simulations of the microstructure using a trust-region–multigrid method (Conn et al. 2000; Sander 2012) which shows consistent results. In Sect. 5, we answer two questions by Adamowicz (2007) and discuss a related relaxation result by Dacorogna and Koshigoe (1993).

1.1 Conformal and Quasiconformal Mappings

Energy functions of the form (1.1) are intrinsically linked to conformal geometry and geometric function theory (Astala et al. 2008). A mapping $\varphi :\Omega \rightarrow {\mathbb {R}}^2$ is called conformal if and only if $\nabla \varphi (x)\in {{\,\mathrm{CSO}\,}}(2)$ on $\Omega$ or, equivalently,

$$\begin{aligned} \nabla \varphi ^\mathrm{T}\nabla \varphi = (\det \nabla \varphi )\cdot {\mathbb {1}}, \end{aligned}$$

where ${\mathbb {1}}\in {{\,\mathrm{GL}\,}}^{\!+}(2)$ denotes the identity matrix. If ${\mathbb {R}}^2$ is identified with the complex plane ${\mathbb {C}}$, then $\varphi$ is conformal if and only if $\varphi :\Omega \subset {\mathbb {C}}\rightarrow {\mathbb {C}}$ is holomorphic and the derivative is non-zero everywhere. Although the Riemann mapping theorem states that any non-empty, simply connected open planar domain can be mapped conformally to the unit disc, conformal mappings exhibit aspects of rigidity (Faraco and Zhong 2005) that make them too restrictive for many interesting applications. In particular, since the Riemann mapping is uniquely determined by prescribing the function value for three points, conformal mappings are not able to satisfy arbitrary boundary conditions.

A significantly larger and more flexible class is given by the so-called quasiconformal mappings, i.e., functions $\varphi :\Omega \rightarrow {\mathbb {R}}^2$ that satisfy the uniform bound

$$\begin{aligned} \Vert {\mathbb {K}} \Vert _\infty :=\mathop {\mathrm{ess\, sup }}\limits _{x\in \Omega }{\mathbb {K}}(\nabla \varphi (x))\le L \quad \text {for some }\;L\ge 1, \end{aligned}$$

(1.3)

where ${\mathbb {K}}$ denotes the distortion function (Iwaniec and Onninen 2009; Astala et al. 2010) or outer distortion (Iwaniec and Onninen 2011)

$$\begin{aligned} {\mathbb {K}}:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow {\mathbb {R}},\quad {\mathbb {K}}(F) :=\frac{1}{2}\, \frac{\Vert F \Vert ^2}{\det F} = \frac{\sum _{i,j=1}^2 F_{ij}^2}{2\, \det F}. \end{aligned}$$

(1.4)

Due to Hadamard’s inequality, ${\mathbb {K}}(F)\ge 1$ for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$. In particular, if (1.3) is satisfied with $L=1$, then ${\mathbb {K}}(\nabla \varphi )\equiv 1$, which implies that $\varphi$ is conformal.

The classical Grötzsch free boundary value problem (Grötzsch 1928) (cf. Sect. 5) is to find and characterize quasiconformal mappings of rectangles into rectangles that minimize the maximal distortion $\Vert {\mathbb {K}} \Vert _\infty$ and map faces to corresponding faces, i.e., to solve the minimization problem

$$\begin{aligned} \Vert {\mathbb {K}}(\nabla \varphi ) \Vert _\infty \rightarrow \min ,\quad&\varphi :[0,a_1]\times [0,1]\rightarrow [0,a_2]\times {[0,1],}\nonumber \\&\varphi ([0,a_1]\times \{0\})=[0,a_2]\times \{0\}, \quad \varphi ([0,a_1]\times \{1\})=[0,a_2]\times \{1\},\nonumber \\&\varphi (\{0\}\times [0,1])=\{0\}\times [0,1], \quad \,\,\,\,\,\varphi (\{a_1\}\times [0,1]) =\{a_2\}\times [0,1]. \nonumber \\ \end{aligned}$$

(1.5)

A much more involved problem has been solved by Teichmüller (1944) and Alberge (2015). The classical Teichmüller problem is to find and characterize quasiconformal solutions to

$$\begin{aligned} \Vert {\mathbb {K}}(\nabla \varphi ) \Vert _\infty \rightarrow \min ,\quad \varphi \in W^{1,2}(B_1(0);{\mathbb {R}}^2),\quad \varphi (x)|_{\partial B_1(0)}=x,\quad \varphi (0)=(0,-b)^T \end{aligned}$$

(1.6)

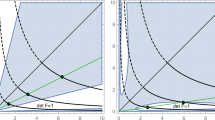
for $0<b<1$ on the unit ball $B_1(0)\subset {\mathbb {R}}^2$. According to Strebel’s Theorem (Strebel 1978) (cf. Lui et al. 2015, Theorem 2.7), any solution $\varphi$ to (1.6) is a so-called Teichmüller map, i.e., ${\mathbb {K}}(\varphi )$ is constant on $B_1(0)\setminus \{(0,-b)^T\}$. An approximate solution to (1.6) for $b=0.8$ is presented in Fig. 1, showing that while the determinant varies throughout the unit disc, the distortion ${\mathbb {K}}$ remains almost constant excluding a small area around the shifted center point.

Fig. 1

Finite element approximation of a minimizer $\varphi$ of $\int _\Omega |{\mathbb {K}}(\nabla \varphi ) |^{100}{\mathrm {d}x}$, subjected to a forced downward displacement of the circle center by $b=0.8$. The coloring shows the values of $\det (\nabla \varphi )$ (left) and the distortion ${\mathbb {K}}(\nabla \varphi )$ (right) in the deformed configuration, i.e., with the grid points displaced by $\varphi$. The result approximates a Teichmüller map, with ${\mathbb {K}}$ almost constant outside a small neighborhood around the center

Computational approaches for calculating extremal quasiconformal mappings (with direct applications in engineering) are discussed, e.g., in Weber et al. (2012). However, the analytical difficulties posed by this problem also motivate the study of integral generalizations of (1.6), i.e.,

$$\begin{aligned}&\int _{B_1(0)}\Psi ({\mathbb {K}}(\nabla \varphi ))\,{\mathrm {d}x}\rightarrow \min ,\quad \varphi \in W^{1,2}(B_1(0);{\mathbb {R}}^2),\\&\quad \varphi (x)|_{\partial B_1(0)}=x,\quad \varphi (0)=(0,-b)^T, \end{aligned}$$

where $\Psi :[1,\infty )\rightarrow [0,\infty )$ is assumed to be strictly increasing. Further generalizing the domain, boundary condition and additional constraints, we obtain a more classical problem in the calculus of variations: the existence and uniqueness of mappings between planar domains with prescribed boundary values that minimize certain integral functions of ${\mathbb {K}}$, i.e., the minimization problem

$$\begin{aligned} \int _\Omega \Psi ({\mathbb {K}}(\nabla \varphi ))\,{\mathrm {d}x}\;\rightarrow \min ,\quad \varphi \in W^{1,2}(\Omega ;{\mathbb {R}}^2),\quad \varphi \big |_{\partial \Omega } = \varphi _0\big |_{\partial \Omega } \end{aligned}$$

(1.7)

for given $\Psi :[1,\infty )\rightarrow {\mathbb {R}}$ and $\varphi _0:\Omega \rightarrow {\mathbb {R}}^2$. Since ${\mathbb {K}}(a\, R\, \nabla \varphi )={\mathbb {K}}(\nabla \varphi \, a R)={\mathbb {K}}(\nabla \varphi )$ for all $a>0$ and all $R\in {{\,\mathrm{SO}\,}}(2)$, the distortion function ${\mathbb {K}}$ is conformally invariant, and indeed every conformally invariant energy W on ${{\,\mathrm{GL}\,}}^{\!+}(2)$ can be expressed in the form $W(F)=\Psi ({\mathbb {K}}(F))$, see Martin et al. (2017).

However, the mapping $F\mapsto {\mathbb {K}}(F)$ is non-convex. Without additional restrictions on $\Psi$, it is therefore difficult to establish results regarding the existence or regularity of minimizers. It is generally believed (Astala et al. 2008, Conjecture 21.2.1, p. 599) that for “well-behaved” functions $\Psi$, e.g., if $\Psi$ is smooth, strictly increasing and convex, any solution to the minimization problem (1.7) is a $C^{1,\alpha }$-diffeomorphism; this would contrast typical regularity results for more general problems in the calculus of variations (including nonlinear elasticity), where only partial regularity (e.g., $C^{1,\alpha }$ up to a set of measure zero) can be expected. Note that the existence of minimizers follows from the polyconvexity (Dacorogna 2008; Charrier et al. 1988; Ball 1976) of the mapping $F\rightarrow \Psi ({\mathbb {K}}(F))$.

In this contribution, we are interested in cases where $\Psi$ is not well behaved in the above sense; more specifically, we allow for some lack of convexity and monotonicity of $\Psi$. Our results demonstrate that the common representation $W(F)=\Psi ({\mathbb {K}}(F))$ of an arbitrary conformally invariant function W on ${{\,\mathrm{GL}\,}}^{\!+}(2)$ is neither ideal nor “natural” as far as convexity properties of W are concerned. Instead, by introducing the linear distortion (or (large) dilatationWeber et al. 2012)

$$\begin{aligned} K(F)= & {} \frac{{{{{\varvec{|}}}}}F{{{{\varvec{|}}}}}^2}{\det F}=\frac{\lambda _{\mathrm{max}}(\sqrt{F^TF})}{\lambda _{\mathrm{min}}(\sqrt{F^TF})}={\mathbb {K}}(F) +\sqrt{{\mathbb {K}}(F)^2-1}=\mathrm{e}^{{{\,\mathrm{arcosh}\,}}{\mathbb {K}}(F)},\\&\quad \text {i.e.}\quad {\mathbb {K}}=\frac{1}{2}\Bigl (K+\frac{1}{K}\Bigr ), \end{aligned}$$

where ${{{{\varvec{|}}}}}F{{{{\varvec{|}}}}}=\sup _{\Vert \xi \Vert =1}\Vert F\, \xi \Vert _{{\mathbb {R}}^2}$ denotes the operator norm (i.e., the largest singular value) of F, we can equivalently express any conformally invariant energy W as $W(F)=h(K(F))$ for some $h:[1,\infty )\rightarrow {\mathbb {R}}$. Although the representation in terms of the distortion function ${\mathbb {K}}$ is preferable for numerical approaches to relaxation of conformally invariant energies (since ${\mathbb {K}}$ is differentiable on all of ${{\,\mathrm{GL}\,}}^{\!+}(2)$), the representation in terms of K turns out to be much more convenient and suitable with respect to convexity properties of W.

In particular, our results (cf. Remark 3.3) will allow us to easily generalize a consequence of a theorem by Astala et al. (2008, Theorem 21.1.3, p. 591), stating that for $F_0\in {{\,\mathrm{GL}\,}}^{\!+}(2)$ and $\Omega =B_1(0)$ and any strictly increasing $\Psi :[1,\infty )\rightarrow [0,\infty )$ with sublinear growth,

$$\begin{aligned} \inf \left\{ \int _{B_1(0)} \Psi ({\mathbb {K}}(\nabla \varphi ))\,{\mathrm {d}x},\; \varphi \in W^{1,2}(B_1(0);{\mathbb {R}}^2),\; \varphi \big |_{\partial B_1(0)}(x)=F_0\, x \right\} \;=\; \pi \cdot \Psi (1). \end{aligned}$$

(1.8)

Note that the corresponding minimization problem has no solution unless $F_0\in {{\,\mathrm{CSO}\,}}(2)$, cf. Corollary 4.4.

Equality (1.8) represents a specific relaxation result. The need for relaxation methods arises from the analysis of non-quasiconvex problems for which energy minimizers might not exist even under affine linear boundary conditions. In such cases, the corresponding infimization problem is directly related to the quasiconvex envelope QW of the energy W: If a Borel measurable function $W:{\mathbb {R}}^{n\times n}\rightarrow {\mathbb {R}}$ is locally bounded and bounded below, then (Dacorogna 2008; Šilhavý 2001; Pedregal 2000; Šilhavý 1997)

$$\begin{aligned} QW(F_0) = \inf \left\{ \frac{1}{|\Omega |}\int _\Omega W(\nabla \varphi )\,{\mathrm {d}x},\; \varphi \in W^{1,\infty }(\Omega ;{\mathbb {R}}^2),\; \varphi \big |_{\partial \Omega }(x)=F_0\, x \right\} \end{aligned}$$

(1.9)

for any domain $\Omega \subset {\mathbb {R}}^2$ with Lebesgue measure $|\Omega |$ such that $|\partial \Omega |=0$. In particular, if $QW(F_0)<W(F_0)$ for some $F_0\in {{\,\mathrm{GL}\,}}^{\!+}(2)$, then the equilibrium state of the homogeneous deformation $\varphi (x)=F_0\, x$ is unstable; in this case, it is possible that there are infimizing sequences with highly oscillating gradients which converge weakly (presuming appropriate coercivity conditions), but whose weak limit is not a minimizer.

In continuum mechanics, this phenomenon is further related to the occurrence of microstructure in a body: If W represents an elastic energy potential, then the modeled material shows an energetic preference to develop finer and finer spatially modulated deformations at fixed averaged deformation $F_0\, x$. In engineering applications, these are typically shear bands or laminate structures which are encountered, for example, in shape-memory alloys.

Note that Eq. (1.9), known as Dacorogna’s formula (Dacorogna 2008), is not immediately applicable to conformally invariant energy functions due to the determinant constraint, i.e., the restriction of the energy W to the domain ${{\,\mathrm{GL}\,}}^{\!+}(2)$. Furthermore, the set of admissible functions for minimization problems of the form (1.7) is typically not contained in $W^{1,\infty }(\Omega ;{\mathbb {R}}^2)$. In order to establish our relaxation results for conformally invariant energy functions, we will therefore first consider some fundamental properties related to quasiconvexity and the more general notion of $W^{1,p}$-quasiconvexity for the special case of functions defined on the domain ${{\,\mathrm{GL}\,}}^{\!+}(n)$.

2 Generalized Convexity on the Domain ${{\,\mathrm{GL}\,}}^{\!+}(n)$

The notion of quasiconvexity was originally introduced by Morrey (1952) exclusively for real-valued functions on a matrix space ${\mathbb {R}}^{m\times n}$. In particular, Morrey did not state a corresponding definition for extended-real-valued functions (i.e., those attaining the value $+\infty$) or functions on restricted domains. Motivated by numerous applications (including nonlinear elasticity theory) which require certain constraints to be posed on the gradient of admissible mappings, such generalizations of quasiconvexity have often been considered in the past, leading to multiple definitions throughout the literature (Müller 1999; Conti 2008; Ball and Murat 1984; Ball 2002; Conti and Dolzmann 2015) which often differ in minor details, especially with respect to requirements of regularity and boundedness.

In order to precisely state our relaxation results, which concern real-valued functions on the domain ${{\,\mathrm{GL}\,}}^{\!+}(2)$, we will therefore first discuss a number of basic properties related to the quasiconvexity and the relaxation of a function $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}$. The exact notions of convexity used here and throughout are stated by the following definition; some well-known basic results related to these convexity properties are provided in “Appendix A”.

Definition 2.1

Let $n\in {\mathbb {N}}$ and $p\in [1,\infty ]$.

• 1) A function $W:{\mathbb {R}}^{n\times n}\rightarrow {\mathbb {R}}\cup \{+\infty \}$ is called

  • i) rank-one convex if for all $F_1,F_2\in {\mathbb {R}}^{m\times n}$ with ${{\,\mathrm{rank}\,}}(F_2-F_1)=1$,

    $$\begin{aligned} W((1-t)F_1+tF_2) \le (1-t)\, W(F_1) + t\, W(F_2) \quad \text {for all }\;t\in [0,1]\,; \end{aligned}$$

  • ii) polyconvex if there exists a convex function $P:{\mathbb {R}}^{\tau (n)}\rightarrow {\mathbb {R}}\cup \{+\infty \}$ such that

    $$\begin{aligned} W(F) = P({{\,\mathrm{adj}\,}}(F)) \quad \text {for all }\;F\in {\mathbb {R}}^{n\times n}\,; \end{aligned}$$

    here

    $$\begin{aligned} {{\,\mathrm{adj}\,}}:{\mathbb {R}}^{n\times n}\rightarrow {\mathbb {R}}^{\tau (n)},\quad&{{\,\mathrm{adj}\,}}(F) = (F,{{\,\mathrm{adj}\,}}_2(F),\dotsc ,{{\,\mathrm{adj}\,}}_n(F)) \\&\text {with }\; \smash { \tau (n) :=\sum _{i=1}^n \left( {\begin{array}{c}n\\ i\end{array}}\right) ^2 } , \end{aligned}$$

    where ${{\,\mathrm{adj}\,}}_k(F)$ denotes the matrix of all $(k\times k)$–minors of F;

  • iii) $W^{1,p}$-quasiconvex (Ball and Murat 1984) if for every bounded open set $\Omega \subset {\mathbb {R}}^n$ with $|\partial \Omega |=0$,

    $$\begin{aligned} \int _{\Omega } W(F+\nabla \vartheta (x)) \,{\mathrm {d}x}\ge |\Omega |\cdot W(F) \end{aligned}$$

    (2.1)

    for all $F\in {\mathbb {R}}^{n\times n}$ and all $\vartheta \in W^{1,p}_0(\Omega ;{\mathbb {R}}^n)$ for which the integral in (2.1) exists;

  • iv) quasiconvex if W is $W^{1,\infty }$-quasiconvex.

• 2) A function $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}$ is called rank-one convex [polyconvex/$W^{1,p}$-quasiconvex/quasiconvex] if the function

  $$\begin{aligned} {\widehat{W}}:{\mathbb {R}}^{n\times n}\rightarrow {\mathbb {R}}\cup \{+\infty \},\quad {\widehat{W}}(F)= {\left\{ \begin{array}{ll} W(F) &{}\;\text {if }\;F\in {{\,\mathrm{GL}\,}}^{\!+}(n),\\ +\infty &{}\;\text {if }\;F\notin {{\,\mathrm{GL}\,}}^{\!+}(n), \end{array}\right. } \end{aligned}$$

  is rank-one convex [polyconvex/$W^{1,p}$-quasiconvex/quasiconvex].

• 3) A function $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}$ is called convex if there exists a convex function ${\widehat{W}}:{\mathbb {R}}^{n\times n}\rightarrow {\mathbb {R}}$ such that ${\widehat{W}}(F)=W(F)$ for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(n)$.

Remark 2.2

It is well known (Müller 1999) that it is already sufficient for $W^{1,p}$-quasiconvexity of W that the required inequality (2.1) holds on a single bounded open set $\Omega \subset {\mathbb {R}}^n$ with $|\partial \Omega |=0$. Furthermore, it is easy to show that for $p\ge n$, inequality (2.1) only needs to hold for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(n)$ and all $\vartheta \in W^{1,p}_0(\Omega ;{\mathbb {R}}^n)$ such that $\det (F+\nabla \vartheta )>0$ a.e. for a function $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}$ to be $W^{1,p}$-quasiconvex. In a more general setting, this requirement (which incorporates the constraint on the determinant into the set of admissible variations) is also known as orientation-preserving $W^{1,p}$-quasiconvexity (Koumatos et al. 2015). In the following, we will use it as the main characterization of $W^{1,p}$-quasiconvexity.

Remark 2.3

The specific definition of convexity employed here takes into account that the domain ${{\,\mathrm{GL}\,}}^{\!+}(n)$ is not convex. It is common practice to define convexity of a function $W:D\rightarrow {\mathbb {R}}$ via the existence of a convex extension of the function to the convex hull ${{\,\mathrm{conv}\,}}(D)$ of the domain (Ball 1976; Rockafellar 1970); note that ${{\,\mathrm{conv}\,}}({{\,\mathrm{GL}\,}}^{\!+}(n))={\mathbb {R}}^{n\times n}$.

Differing generalized definitions of quasiconvexity include, for example, additional requirements of regularity or boundedness (Dacorogna and Marcellini 1997; Ball and Murat 1984; Wagner 2009; Koumatos et al. 2015) posed on W. Note that although we omit such further requirements in the definition, for some of our results (notably Theorem 3.1) we do assume W to be (locally) bounded.

Remark 2.4

Throughout the literature, the exact definition of polyconvexity for functions on the domain ${{\,\mathrm{GL}\,}}^{\!+}(n)$ differs slightly as well. In particular (Mielke 2005; Conti and Dolzmann 2015), a polyconvex function ${\widehat{W}}:{\mathbb {R}}^{n\times n}\rightarrow {\mathbb {R}}\cup \{+\infty \}$ is sometimes assumed to be lower semicontinuous on all of ${\mathbb {R}}^{n\times n}$, which corresponds to the additional growth condition $W(F)\rightarrow +\infty$ as $\det W\rightarrow 0$.

The relation between polyconvexity and quasiconvexity is well known even for extended-real-valued functions (Dacorogna 2008, Theorem 5.3), but will be stated explicitly in the following lemma in order to ensure compatibility with the precise definitions employed here.

Lemma 2.5

Let $p\in [n,\infty ]$. If $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}$ is polyconvex, then W is $W^{1,p}$-quasiconvex for any $p\in [n,\infty ]$.

Proof

If W is polyconvex, then there exists a convex function $P:{\mathbb {R}}^{\tau (n)}\rightarrow {\mathbb {R}}\cup \{+\infty \}$ such that $W(F)=P({{\,\mathrm{adj}\,}}(F))$ for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(n)$. Furthermore, P is finite-valued on the set (cf. Ball 1976)

$$\begin{aligned} M:={{\,\mathrm{conv}\,}}({{\,\mathrm{adj}\,}}({{\,\mathrm{GL}\,}}^{\!+}(n)))=\{X\in {\mathbb {R}}^{\tau (n)}\,|\,X_{\tau (n)}>0\}, \end{aligned}$$

and we can assume without loss of generality that $P(X)=+\infty$ for all $X\notin M$, i.e., that the effective domain ${{\,\mathrm{dom}\,}}P:=\{F\in {\mathbb {R}}^{\tau (n)}\,|\,W(F)<+\infty \}$ is given by ${{\,\mathrm{dom}\,}}P=M$ and thus convex and open. Thus for any $\vartheta \in W^{1,p}_0(\Omega ;{\mathbb {R}}^n)$, due to Jensen’s inequality (cf. Lemma A.2; note that ${{\,\mathrm{adj}\,}}(F+\vartheta )\in L^{\frac{p}{n}}(\Omega ;{\mathbb {R}}^n)\subset L^1(\Omega ;{\mathbb {R}}^n)$ for $p\ge n$) and Lemma A.3,

$$\begin{aligned} \frac{1}{|\Omega |}\int _\Omega W(F+\vartheta (x))\,{\mathrm {d}x}&= \frac{1}{|\Omega |}\int _\Omega P({{\,\mathrm{adj}\,}}(F+\vartheta (x)))\,{\mathrm {d}x}\\&\ge P\left( \frac{1}{|\Omega |}\int _\Omega {{\,\mathrm{adj}\,}}(F+\vartheta (x)) \right) = P({{\,\mathrm{adj}\,}}(F)) = W(F) . \end{aligned}$$

$\square$

While it is well known that quasiconvexity implies rank-one convexity for finite-valued functions (Morrey 1952; Ball 1976; Dacorogna 2008), this implication no longer holds in the generalized, extended-real-valued case (Ball and Murat 1984; Dacorogna 2008). It is, however, still valid for functions which are locally bounded above on the effective domain ${{\,\mathrm{GL}\,}}^{\!+}(n)$, i.e., bounded on every compact subset of ${{\,\mathrm{GL}\,}}^{\!+}(n)$.²

Again, while this result seems to be applied ubiquitously throughout the literature, we will state it here explicitly (following an analogous classical proof (Dacorogna 2008) for the real-valued case), accounting for the specific given definition of $W^{1,p}$-quasiconvexity.

Lemma 2.6

If $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}$ is quasiconvex and locally bounded above on ${{\,\mathrm{GL}\,}}^{\!+}(n)$, then W is rank-one convex.

Proof

Let W be quasiconvex and locally bounded above on ${{\,\mathrm{GL}\,}}^{\!+}(n)$, and assume that W is not rank-one convex. Then there exist $F_1,F_2\in {{\,\mathrm{GL}\,}}^{\!+}(n)$ and $t\in (0,1)$ such that ${{\,\mathrm{rank}\,}}(F_2-F_1)=1$ and $tW(F_1)+(1-t)W(F_2)<W(F)$ for $F=tF_1+(1-t)F_2$. Let $\Omega \subset {\mathbb {R}}^n$ be open and bounded with sufficiently smooth boundary. According to Lemma A.6, for any $\varepsilon >0$, there exist open sets $\Omega _1,\Omega _2\subset \Omega$ and a mapping $\varphi \in W^{1,\infty }(\Omega ;{\mathbb {R}}^n)$ such that

$$\begin{aligned} \left\{ \begin{aligned}&\bigl |\;|\Omega _1 |-t|\Omega |\; \bigr |\le \varepsilon ,\quad \bigl |\;|\Omega _2 |-(1-t)|\Omega |\; \bigr |\le \varepsilon ,\\&\varphi (x)=Fx \quad \text {on }\; \partial \Omega ,\\&{{\,\mathrm{dist}\,}}(\nabla \varphi (x),\,{{\,\mathrm{conv}\,}}(\{F_1,F_2\})) \le \varepsilon \;\;\text { a.e. in }\Omega ,\\&\nabla \varphi (x)= {\left\{ \begin{array}{ll} F_1 &{}\;\text {if }\;x\in \Omega _1,\\ F_2 &{}\;\text {if }\;x\in \Omega _2. \end{array}\right. } \end{aligned}\right. \end{aligned}$$

(2.2)

Due to the openness and rank-one convexity of ${{\,\mathrm{GL}\,}}^{\!+}(n)$, property (2.2)$_3$ ensures that $\nabla \varphi (x)\in {{\,\mathrm{GL}\,}}^{\!+}(n)$ for all sufficiently small $\varepsilon >0$.

Let $\vartheta (x)=\varphi (x)-Fx$. Then $\vartheta \in W^{1,\infty }_0(\Omega ;{\mathbb {R}}^n)$ and, due to (2.2)$_3$ and the assumption that W is locally bounded above, there exists $C>0$ such that $W(F+\nabla \vartheta (x))=W(\nabla \varphi (x))\le C$ a.e. on $\Omega$ for sufficiently small $\varepsilon >0$. We thus find

$$\begin{aligned} \int _\Omega W(F+\nabla \vartheta (x))\,{\mathrm {d}x}&= \int _{\Omega _1} W(F+\nabla \vartheta (x))\,{\mathrm {d}x}+ \int _{\Omega _2} W(F+\nabla \vartheta (x))\,{\mathrm {d}x}\\&\quad +\int _{\Omega \setminus (\Omega _1\cup \Omega _2)} W(F+\nabla \vartheta (x))\,{\mathrm {d}x}\\&\le |\Omega _1 |\cdot W(F_1) + |\Omega _2 |\cdot W(F_2) + |\Omega \setminus (\Omega _1\cup \Omega _2) |\cdot C\\&\le (t\, |\Omega |+\varepsilon )\cdot W(F_1) + ((1-t)\, |\Omega |+\varepsilon )\cdot W(F_2) + 2\, \varepsilon \, C\\&= |\Omega |\cdot (t\, W(F_1) + (1-t)\, W(F_2)) + \varepsilon \cdot (W(F_1)+W(F_2)+2\, C)\\&\le |\Omega |\cdot (t\, W(F_1) + (1-t)\, W(F_2)) + 4\, \varepsilon \, C \end{aligned}$$

and hence, letting $\varepsilon \rightarrow 0$,

$$\begin{aligned} \frac{1}{|\Omega |}\cdot \int _\Omega W(F+\nabla \vartheta (x))\,{\mathrm {d}x}\le t\, W(F_1) + (1-t)\, W(F_2) < W(F) \end{aligned}$$

in contradiction to the quasiconvexity of W. $\square$

Note that the proof of Lemma 2.6 relies solely on two properties of the set ${{\,\mathrm{GL}\,}}^{\!+}(n)$, namely its rank-one convexity and its openness. By a much more involved proof, Conti (Conti 2008) has shown that an analogous result holds on the (rank-one convex, but not open) domain ${{\,\mathrm{SL}\,}}(n)$. On the other hand, a classical example (Ball and Murat 1984, Example 3.5) of a quasiconvex but not rank-one convex function is given by

$$\begin{aligned} W(F)= {\left\{ \begin{array}{ll} 0 &{}\;\text {if }\;F=0\text { or }F=F_0,\\ +\infty &{}\;\text {otherwise,} \end{array}\right. } \end{aligned}$$

for some $F_0\in {\mathbb {R}}^{n\times n}$ with ${{\,\mathrm{rank}\,}}(F_0)=1$; note that the effective domain of W is clearly not rank-one convex.

Remark 2.7

Since convexity of $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}$ trivially implies that W is polyconvex, Lemmas 2.5 and 2.6 establish the chain of implications

$$\begin{aligned} \text {convexity }\implies \text { polyconvexity }\implies W^{1,p}\text {-quasiconvexity }\implies \text { rank-one convexity} \end{aligned}$$

(2.3)

for any $p\in [n,\infty ]$, provided that W is locally bounded above on ${{\,\mathrm{GL}\,}}^{\!+}(n)$. These implications are, of course, well known to hold for any finite-valued function on the domain ${\mathbb {R}}^{n\times n}$.

For dimension $n\ge 3$, it is also well known that the reverse holds for none of the implications in (2.3); in his now famous result, Šverák (1992) showed that rank-one convexity does not imply quasiconvexity with a counterexample consisting of a non-isotropic, non-objective polynomial of order four. In the two-dimensional case discussed here, however, the question whether rank-one convexity is equivalent to quasiconvexity, known as the remaining part of Morrey’s conjecture (Morrey 1952), is still unanswered (Morrey 1952; Astala et al. 2012) and is considered one of the major open problems in the calculus of variations (Ball 1987, 2002; Neff 2005).

2.1 Envelopes and Relaxation of Energy Functions

For each of the generalized notions of convexity given in Definition 2.1, we can define a corresponding envelope of a function on ${{\,\mathrm{GL}\,}}^{\!+}(n)$ which is bounded below.

Definition 2.8

For $n\in {\mathbb {N}}$ and $p\in [1,\infty ]$, let $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}$ be bounded below. Then the convex, polyconvex, $W^{1,p}$-quasiconvex, quasiconvex and rank-one convex envelope of W are given by

$$\begin{aligned} CW(F)&= \sup \{ w(F) \,|\,w:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}\,\text { convex },&w(X)&\le W(X) \,\text { for all }X\in {{\,\mathrm{GL}\,}}^{\!+}(n)\},\\ PW(F)&= \sup \{ w(F) \,|\,w:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}\,\text { polyconvex },&w(X)&\le W(X) \,\text { for all }X\in {{\,\mathrm{GL}\,}}^{\!+}(n)\},\\ Q_pW(F)&= \sup \{ w(F) \,|\,w:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}\, W^{1,p}\text {-quasiconvex }, \;&w(X)&\le W(X) \,\text { for all }X\in {{\,\mathrm{GL}\,}}^{\!+}(n)\},\\ QW(F)&= \sup \{ w(F) \,|\,w:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}\,\text { quasiconvex},&w(X)&\le W(X) \,\text { for all }X\in {{\,\mathrm{GL}\,}}^{\!+}(n)\},\\ RW(F)&= \sup \{ w(F) \,|\,w:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}\,\text { rank-one convex },&w(X)&\le W(X) \,\text { for all }X\in {{\,\mathrm{GL}\,}}^{\!+}(n)\}, \end{aligned}$$

respectively.

Among the most important properties of generalized convex envelopes is their relation to the relaxation of an energy.

Definition 2.9

Let $\Omega \subset {\mathbb {R}}^n$ be open and bounded with $|\partial \Omega |=0$. For $n\in {\mathbb {N}}$ and $p\in [1,\infty ]$, let $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}$ be bounded below. Then the quasiconvex relaxation and the $W^{1,p}$-quasiconvex relaxation of W are given by

$$\begin{aligned} Q^*W(F)&= \inf \left\{ \frac{1}{|\Omega |}\int _\Omega W(\nabla \varphi )\,{\mathrm {d}x},\; \varphi \in W^{1,\infty }(\Omega ;{\mathbb {R}}^n),\; \varphi \big |_{\partial \Omega }(x)=F\, x,\; \det \nabla \varphi>0\text { a.e.} \right\} ,\\ Q^*_pW(F)&= \inf \left\{ \frac{1}{|\Omega |}\int _\Omega W(\nabla \varphi )\,{\mathrm {d}x},\; \varphi \in W^{1,p}(\Omega ;{\mathbb {R}}^n),\; \varphi \big |_{\partial \Omega }(x)=F\, x,\; \det \nabla \varphi >0\text { a.e.} \right\} , \end{aligned}$$

respectively.

Remark 2.10

In the literature (Rindler 2018; Conti and Dolzmann 2015; Bartels et al. 2004), the term “quasiconvex envelope” is sometimes applied to $Q^*W$ instead of QW. The relaxation $Q^*_pW$ of an energy density $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}$ should also not be confused with the relaxation of the energy functional $\int _\Omega W(\nabla \varphi (x)\, {\mathrm {d}x}$, i.e., the “weakly lower semicountinuous envelope” given by (Rindler 2018)

$$\begin{aligned} I^*(\varphi ) = \sup \{ {\widehat{I}}(\varphi ) \,\,|\,\, {\widehat{I}}\,\text { weakly lower semicontinuous, }\; {\widehat{I}}\le I \}, \end{aligned}$$

where each ${\widehat{I}}$ is a functional on an appropriate space of admissible functions. Previous results (Conti and Dolzmann 2015) establishing the equalities

$$\begin{aligned} I^*(\varphi ) = \int _\Omega Q^*W(\nabla \varphi (x))\,{\mathrm {d}x}= \int _\Omega QW(\nabla \varphi (x))\,{\mathrm {d}x}\end{aligned}$$

require additional conditions to be posed on W.

Definition 2.9 is independent of the particular choice of $\Omega$. Moreover, by Definitions 2.8 and 2.9, $QW=Q_\infty W$ and $Q^*W=Q^*_\infty W$.

Furthermore, under suitable assumptions, the corresponding quasiconvex relaxation of a (finite-valued) function $W:{\mathbb {R}}^{n\times n}\rightarrow {\mathbb {R}}$ is equal to its quasiconvex envelope, i.e.,

$$\begin{aligned} QW(F)= & {} Q^*W(F) \nonumber \\= & {} \inf \left\{ \frac{1}{|\Omega |}\int _\Omega W(\nabla \varphi )\,{\mathrm {d}x}, \,\,|\,\, \varphi \in W^{1,\infty }(\Omega ;{\mathbb {R}}^n),\; \varphi \big |_{\partial \Omega }(x)=F\, x \right\} , \end{aligned}$$

(2.4)

an equality known as Dacorogna’s formula (Dacorogna 1982). If W attains the value $+\infty$, on the other hand, equality (2.4) has only been established for certain special cases (Dacorogna and Marcellini 1997; Conti and Dolzmann 2015). However, if the effective domain of W is given by ${{\,\mathrm{GL}\,}}^{\!+}(n)$, the generalized convex envelopes can still provide upper and lower estimates for the relaxation.

Proposition 2.11

For $n\in {\mathbb {N}}$, let $p\in [n,\infty ]$ and let $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}$ be bounded below and locally bounded above on ${{\,\mathrm{GL}\,}}^{\!+}(n)$. Then

$$\begin{aligned} CW(F) \le PW(F) \le Q_pW(F) \le Q^*_pW(F) \le RW(F) \end{aligned}$$

(2.5)

for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(n)$.

Proof

The inequalities $CW(F)\le PW(F)\le Q_pW(F)$ follow immediately from the implications in (2.3). Furthermore, for any $W^{1,p}$-quasiconvex function $w:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}$ with $w\le W$ on ${{\,\mathrm{GL}\,}}^{\!+}(n)$, we find

$$\begin{aligned} Q_p^* W(F)&= \inf \left\{ \frac{1}{|\Omega |}\int _\Omega W(\nabla \varphi )\,{\mathrm {d}x},\; \varphi \in W^{1,p}(\Omega ;{\mathbb {R}}^2),\; \varphi \big |_{\partial \Omega }(x)=F\, x,\; \det \nabla \varphi>0\text { a.e.} \right\} \\&\ge \inf \left\{ \frac{1}{|\Omega |}\int _\Omega w(\nabla \varphi )\,{\mathrm {d}x},\; \varphi \in W^{1,p}(\Omega ;{\mathbb {R}}^2),\; \varphi \big |_{\partial \Omega }(x)=F\, x,\; \det \nabla \varphi >0\text { a.e.} \right\} \\&= w(F), \end{aligned}$$

thus

$$\begin{aligned} Q_pW(F)&= \sup \{ w(F) \,|\,w:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}\text { is } W^{1,p}\text {-quasiconvex with } w\le W \} \\&\le Q^*_pW(F) \end{aligned}$$

for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(n)$.

It remains to show that $Q^*_pW(F)\le RW(F)$. Let $\varepsilon >0$. According to Lemma A.5, there exist $t_1,\dotsc ,t_m\in [0,1]$ and $F_1,\dotsc ,F_m\in {{\,\mathrm{GL}\,}}^{\!+}(n)$ with $\sum _{i=1}^m t_i=1$ and $\sum _{i=1}^m t_iF_i=F$ such that $(t_i,F_i)$ satisfy the $(H_{m})$-condition (see Definition A.4) and

$$\begin{aligned} \sum _{i=1}^m t_i W(F_i) \le RW(F) + \widetilde{\varepsilon }. \end{aligned}$$

Let $\Omega \subset {\mathbb {R}}^n$ be open and bounded with sufficiently smooth boundary. According to Corollary A.8, there exist $M\in {\mathbb {N}}$ and ${\overline{F}}_1,\dotsc ,{\overline{F}}_M\in {\mathbb {R}}^{n\times n}$ with

$$\begin{aligned} {{\,\mathrm{rank}\,}}({\overline{F}}_{j+1}-{\overline{F}}_j) = 1 \quad \text {for all }\;j\in \{1,\dotsc ,M-1\} \end{aligned}$$

such that for every $\varepsilon >0$, there exist a (piecewise affine) mapping $\varphi \in W^{1,\infty }(\Omega ;{\mathbb {R}}^n)$ and disjoint open sets $\Omega _1,\dotsc ,\Omega _m\subset \Omega$ such that

$$\begin{aligned} \left\{ \begin{aligned}&\bigl |\;|\Omega _i |-t_i|\Omega |\; \bigr |\le \varepsilon ,\\&\varphi (x)=Fx \quad \text {on }\; \partial \Omega ,\\&{{\,\mathrm{dist}\,}}\Bigl (\nabla \varphi (x),\,\bigcup \nolimits _{j=1}^{M-1} {{\,\mathrm{conv}\,}}(\{{\overline{F}}_j,{\overline{F}}_{j+1}\})\Bigr ) \le \varepsilon \;\;\text { a.e. in }\Omega ,\\&\nabla \varphi (x)=F_i \;\;\text { if }\;x\in \Omega _i \end{aligned}\right. \end{aligned}$$

(2.6)

for all $i\in \{1,\dotsc ,m\}$. Due to the openness and rank-one convexity of ${{\,\mathrm{GL}\,}}^{\!+}(n)$, property (2.6)$_3$ ensures that $\nabla \varphi (x)\in {{\,\mathrm{GL}\,}}^{\!+}(n)$ for all sufficiently small $\varepsilon >0$.

Let $\vartheta (x)=\varphi (x)-Fx$. Then $\vartheta \in W^{1,\infty }_0(\Omega ;{\mathbb {R}}^n)$ and, due to (2.6)$_3$ and the assumption that W is locally bounded above, there exists $C>0$ such that $W(F+\nabla \vartheta (x))=W(\nabla \varphi (x))\le C$ a.e. on $\Omega$ for sufficiently small $\varepsilon >0$. We thus find

$$\begin{aligned}&\int _\Omega W(F+\nabla \vartheta (x))\,{\mathrm {d}x}\\&\quad = \sum _{i=1}^m \int _{\Omega _i} Wz(F+\nabla \vartheta (x))\,{\mathrm {d}x}+ \int _{\Omega \setminus \left( \bigcup _{i=1}^m\Omega _i\right) } W(F+\nabla \vartheta (x))\,{\mathrm {d}x}\\&\quad \le \sum _{i=1}^m |\Omega _i |\cdot W(F_i) + |\Omega \setminus \left( \bigcup _{i=1}^m\Omega _i\right) |\cdot C\le \sum _{i=1}^m (|\Omega |\, t_i+\varepsilon )\, W(F_i) + m\, \varepsilon \, C\\&\quad = |\Omega |\cdot \sum _{i=1}^m t_i W(F_i) + \varepsilon \cdot \left( \sum _{i=1}^m W(F_i)+m\, C\right) \le |\Omega |\cdot \sum _{i=1}^m t_i W(F_i) + 2\, m\, \varepsilon \, C \end{aligned}$$

and hence, for $\varepsilon \rightarrow 0$,

$$\begin{aligned} Q^*_p(F)&= \inf \left\{ \frac{1}{|\Omega |}\int _\Omega W(\nabla \varphi )\,{\mathrm {d}x},\; \varphi \in W^{1,p}(\Omega ;{\mathbb {R}}^2),\; \varphi \big |_{\partial \Omega }(x)=F\, x,\; \det \nabla \varphi >0\text { a.e.} \right\} \\&\le \frac{1}{|\Omega |} \int _\Omega W(F+\nabla \vartheta (x))\,{\mathrm {d}x}\;\le \; \sum _{i=1}^m t_i W(F_i) \;\le \; RW(F) + \widetilde{\varepsilon }\end{aligned}$$

for any $\widetilde{\varepsilon }>0$, which establishes the remaining inequality $Q^*_p(F)\le RW(F)$. $\square$

In particular, the inequalities (2.5) provide upper and lower bounds³ on the quasiconvex envelope and the relaxed energy in terms of the polyconvex and the rank-one convex envelope, respectively. However, while a number of numerical methods are available to approximate RW (Dolzmann 2004; Bartels 2004; Oberman and Ruan 2017) as well as PW (Dolzmann 1999; Kruzık 1998; Bartels 2005; Aranda and Pedregal 2001), it is difficult to analytically compute either of the envelopes RW, PW or QW for a given energy W in general, although explicit representations have been found for a number of particular functions, including the St. Venant–Kirchhoff energy (Le Dret and Raoult 1995) and several challenging problems encountered in engineering applications (Cesana and DeSimone 2011; Albin et al. 2009). Further examples can be found in (Dacorogna 2008, Chapter 6).

More general methods for computing the quasiconvex envelope are often based on the observation that $RW=PW$ and thus $RW=QW$ for certain classes of energy functions W. In many such cases, even the equality $RW=CW$ holds (Dacorogna and Koshigoe 1993; Raoult 2010), i.e., the generalized convex envelopes are all identical to the classical convex envelope of W, cf. “Appendix C”.

Yan (1997) showed that non-constant rank-one convex conformal energy functions (cf. Footnote 1 for the distinction between conformally invariant and conformal energy functions) defined on all of ${\mathbb {R}}^{n\times n}$ for $n\ge 3$ must grow at least with power $\frac{n}{2}$, which implies that the quasiconvex envelope of a conformal energy W on ${\mathbb {R}}^{3\times 3}$ must be constant if W exhibits sublinear growth.⁴ The results given in the following show that an analogous property holds for conformally invariant energies on ${{\,\mathrm{GL}\,}}^{\!+}(2)$.

2.2 Convexity Properties of Conformally Invariant Functions

In order to state criteria for the convexity properties discussed above in the special case of conformally invariant functions on ${{\,\mathrm{GL}\,}}^{\!+}(2)$, we consider a number of different representations available to express such functions.

Lemma 2.12

(Martin et al. 2017, Lemma 3.1 and Lemma 4.4) Let $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow {\mathbb {R}}$ be conformally invariant. Then there exist uniquely determined functions $g:(0,\infty )\times (0,\infty )\rightarrow {\mathbb {R}}$, $h:(0,\infty )\rightarrow {\mathbb {R}}$ and $\Psi :[1,\infty )\rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} W(F) = g(\lambda _1,\lambda _2) = h\left( \frac{\lambda _1}{\lambda _2}\right) = h(K(F)) = \Psi ({\mathbb {K}}(F)) \end{aligned}$$

(2.7)

for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$ with (not necessarily ordered) singular values $\lambda _1,\lambda _2$, where $K(F)=\frac{\max \{\lambda _1,\lambda _2\}}{\min \{\lambda _1,\lambda _2\}}$, ${\mathbb {K}}(F):=\frac{1}{2}\, \frac{\Vert F \Vert ^2}{\det F}$ and $\Vert \,.\, \Vert$ denotes the Frobenius matrix norm with $\Vert F \Vert ^2=\sum _{i,j=1}^2 F_{ij}^2$. Furthermore,

$$\begin{aligned} h(x)=h\left( \frac{1}{x}\right) ,\quad g(x,y)=g(y,x) \quad \text { and }\quad g(ax,ay)=g(x,y) \end{aligned}$$

(2.8)

for all $a,x,y\in (0,\infty )$.

Conversely, if the requirements (2.8) are satisfied for otherwise arbitrary functions $g:(0,\infty )\times (0,\infty )\rightarrow {\mathbb {R}}$, $h:(0,\infty )\rightarrow {\mathbb {R}}$ or $\Psi :[1,\infty )\rightarrow {\mathbb {R}}$, then (2.7) defines a conformally invariant function W.

Note that h is already uniquely determined by its values on $[1,\infty )$ and recall that $K\ge 1$, with $K(\nabla \varphi )=1$ if and only if $\varphi$ is conformal.

The following proposition summarizes the main results from Martin et al. (2017) and completely characterizes the generalized convexity of conformally invariant functions on ${{\,\mathrm{GL}\,}}^{\!+}(2)$.

Proposition 2.13

(Martin et al. 2017, Theorem 3.3) Let $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow {\mathbb {R}}$ be conformally invariant, and let $g:(0,\infty )\times (0,\infty )\rightarrow {\mathbb {R}}$, $h:(0,\infty )\rightarrow {\mathbb {R}}$ and $\Psi :[1,\infty )\rightarrow {\mathbb {R}}$ denote the uniquely determined functions with

$$\begin{aligned} W(F) = g(\lambda _1,\lambda _2) = h\left( \frac{\lambda _1}{\lambda _2}\right) = \Psi ({\mathbb {K}}(F)) \end{aligned}$$

for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$ with singular values $\lambda _1,\lambda _2$, where ${\mathbb {K}}(F)=\frac{1}{2}\frac{\Vert F \Vert ^2}{\det F}$. Then the following are equivalent:

• i) W is polyconvex,

• ii) W is quasiconvex,

• iii) W is rank-one convex,

• iv) g is separately convex,

• v) h is convex on $(0,\infty )$,

• vi) h is convex and non-decreasing on $[1,\infty )$.

Furthermore, if h is twice continuously differentiable, then i)–vi) are equivalent to

• vii) $(x^2-1)\,(x+\sqrt{x^2-1})\,\Psi ^{\prime \prime }(x) + \Psi ^{\prime }(x)\ge 0$   for all $x\in (1,\infty )$. $\square$

In the following, we will mostly rely on the implications vi)$\implies$i) and iii)$\implies$vi) in Proposition 2.13. We briefly remark that the former follows directly from the polyconvexity (Ghiba et al. 2015) of the mapping $F\mapsto K(F)$ on ${{\,\mathrm{GL}\,}}^{\!+}(2)$, whereas the latter can be obtained by considering the mapping

$$\begin{aligned} t\mapsto h(t) = W({{\,\mathrm{diag}\,}}(t,1)) = W({\mathbb {1}}+(t-1){{\,\mathrm{diag}\,}}(1,0)), \end{aligned}$$

which is convex on $(0,\infty )$ if W is rank-one convex and thus, in particular, monotone on $[1,\infty )$ due to symmetry considerations (Martin et al. 2017).

Note that in terms of the representation function h, the convexity criteria can be expressed in a remarkably simple way, especially when compared to vii), i.e., the representation in terms of the classical distortion ${\mathbb {K}}$. In particular, while monotonicity and convexity of $\Psi$ are sufficient for the considered properties (recall that the mapping $F\mapsto {\mathbb {K}}(F)$ itself is polyconvex (Dacorogna 2008; Hartmann and Neff 2003) on ${{\,\mathrm{GL}\,}}^{\!+}(2)$), convexity of the energy with respect to ${\mathbb {K}}$ is not a necessary condition; for example, if $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow {\mathbb {R}}$ is given by

$$\begin{aligned} W(F)=K(F)=\frac{\max \{\lambda _1,\lambda _2\}}{\min \{\lambda _1,\lambda _2\}} = \frac{\lambda _{\mathrm{max}}}{\lambda _{\mathrm{min}}} = {\mathbb {K}}(F)+\sqrt{{\mathbb {K}}(F)^2-1} = \mathrm{e}^{{{\,\mathrm{arcosh}\,}}({\mathbb {K}}(F))} \end{aligned}$$

for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$ with singular values $\lambda _{\mathrm{max}}\ge \lambda _{\mathrm{min}}$, then W is polyconvex due to the convexity of $t\mapsto h(t)=\max \{t,\frac{1}{t}\}$ on $(0,\infty )$, whereas the representing function $\Psi :[1,\infty )\rightarrow {\mathbb {R}}$ with $\Psi (x)=x+\sqrt{x^2-1}$ is monotone increasing but not convex.

Example 2.14

Consider the isochoric, conformally invariant St. Venant–Kirchhoff-type energy function

$$\begin{aligned} W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow {\mathbb {R}},\quad W(F)=\Bigl \Vert \frac{F^TF}{\det F}-{\mathbb {1}} \Bigr \Vert ^2= & {} \left( \frac{\lambda _1}{\lambda _2}-1\right) ^2 + \left( \frac{\lambda _2}{\lambda _1}-1\right) ^2 \nonumber \\= & {} 4({\mathbb {K}}(F)^2-{\mathbb {K}}(F)), \end{aligned}$$

(2.9)

where ${\mathbb {1}}$ denotes the identity matrix. This energy W can be expressed in the form (2.7) with

$$\begin{aligned} g(x,y) = \left( \frac{x}{y}-1\right) ^2 + \left( \frac{y}{x}-1\right) ^2, \quad h(t) = (t-1)^2+\left( \frac{1}{t}-1\right) ^2, \quad \Psi (x) = 4(x^2-x). \end{aligned}$$

Since $h:(0,\infty )\rightarrow {\mathbb {R}}$ is convex, the planar isochoric St. Venant–Kirchhoff energy is quasiconvex according to Proposition 2.13, while, e.g., the non-conformally-invariant term $\Vert F^TF-{\mathbb {1}} \Vert ^2=(\lambda _1-1)^2+(\lambda _2-1)^2$ is not, cf. “Appendix C”.

In order to apply Proposition 2.13 to the computation of generalized convex envelopes, the following simple invariance property of the rank-one convex envelope will be required.

Lemma 2.15

If $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}$ is conformally invariant, then RW is conformally invariant.

Proof

It is well known that the left- and right-${{\,\mathrm{SO}\,}}(2)$-invariance is preserved by the rank-one convex envelope (Buttazzo et al. 1994; Dacorogna and Koshigoe 1993; Le Dret and Raoult 1994), so due to the characterization (1.2) of conformal invariance it remains to show that $RW(aF)=RW(F)$ for all $a>0$ and all $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$.

We use the characterization $RW(F)=\lim _{k\rightarrow \infty }R_kW(F)$ of the rank-one convex envelope (Dacorogna 2008, Theorem 6.10), where $R_0W(F)=W(F)$ and

$$\begin{aligned} R_{k+1}W(F) :=\inf \Big \{ t\, R_kW(F_1)+(1-t)\, R_kW(F_2) \,\,|\,\,&t\in [0,1],\, t\, F_1+(1-t)\, F_2=F,\,\\&{{\,\mathrm{rank}\,}}(F_1-F_2)=1 \Big \}, \end{aligned}$$

and show by induction that $R_kW(aF)=R_kW(F)$ for all $k\ge 0$. First, we find $R_0W(aF)=W(aF)=W(F)=R_0W(F)$, so assume that $R_kW(F) = R_kW(aF)$ for some $k\ge 1$. For any $\varepsilon >0$, choose $F_1,F_2\in {{\,\mathrm{GL}\,}}^{\!+}(2)$ and $t\in [0,1]$ with $tF_1+(1-t)F_2=F$ and ${{\,\mathrm{rank}\,}}(F_1-F_2)=1$ such that $tR_kW(F_1)+(1-t)R_kW(F_2)\le R_{k+1}W(F)+\varepsilon$. Then, since $t\, aF_1+(1-t)\, aF_2=aF$ and ${{\,\mathrm{rank}\,}}(aF_1-aF_2)=1$,

$$\begin{aligned} R_{k+1}W(aF)&\le t\, R_kW(aF_1)+(1-t)\, R_kW(aF_2) = t\, R_kW(F_1)+(1-t)\, R_kW(F_2) \\&\le R_{k+1}W(F)+\varepsilon , \end{aligned}$$

thus $R_{k+1}W(aF)\le R_{k+1}W(F)$. Analogously, we find $R_{k+1}W(F)\le R_{k+1}W(aF)$ and thereby $RW(aF)=\lim _{k\rightarrow \infty }R_kW(aF)=\lim _{k\rightarrow \infty }R_kW(F)=RW(F)$. $\square$

By direct computation, it is also easy to see that $Q^*_pW$ is conformally invariant if $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}$ is conformally invariant: The scaling invariance of $Q^*_pW$ follows directly from the equality

$$\begin{aligned} Q^*_pW(a\, F)&=\inf _{\vartheta \in W^{1,p}_0(\Omega ,{\mathbb {R}}^n)} \frac{1}{|\Omega |} \int _\Omega W(a\, F+\nabla \vartheta )\,{\mathrm {d}x}\\&=\inf _{\vartheta \in W^{1,p}_0(\Omega ,{\mathbb {R}}^n)} \frac{1}{|\Omega |} \int _\Omega W\left( a\left( F+\frac{1}{a}\, \nabla \vartheta \right) \right) \,{\mathrm {d}x}\\&= \inf _{\vartheta \in W^{1,p}_0(\Omega ,{\mathbb {R}}^n)} \frac{1}{|\Omega |} \int _\Omega W\left( F+\frac{1}{a}\, \nabla \vartheta \right) \,{\mathrm {d}x}\\&=\inf _{{\widetilde{\vartheta }}\in W^{1,p}_0(\Omega ,{\mathbb {R}}^n)} \frac{1}{|\Omega |} \int _\Omega W(F+\nabla {\widetilde{\vartheta }})\,{\mathrm {d}x}=Q^*_pW(F) \end{aligned}$$

holding for any $a>0$ and all $F\in {{\,\mathrm{GL}\,}}^{\!+}(n)$, and the left- and right-${{\,\mathrm{SO}\,}}(n)$-invariance of $Q^*_pW$ can be deduced in a similar way.

3 Main Result on the Quasiconvex Envelope

We can now state our main result.

Theorem 3.1

Let $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow {\mathbb {R}}$ be conformally invariant, bounded below and locally bounded on ${{\,\mathrm{GL}\,}}^{\!+}(2)$, and let $h:[1,\infty )\rightarrow {\mathbb {R}}$ denote the function uniquely determined by

$$\begin{aligned} W(F) = h(K(F)) = h\left( \frac{\lambda _{\mathrm{max}}}{\lambda _{\mathrm{min}}}\right) \end{aligned}$$

(3.1)

for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$ with ordered singular values $\lambda _{\mathrm{max}}\ge \lambda _{\mathrm{min}}$. Then for any $p\in [2,\infty ]$,

$$\begin{aligned} RW(F)=Q^*_pW(F)=Q_pW(F)=PW(F)=C_{\!M}h\left( \frac{\lambda _{\mathrm{max}}}{\lambda _{\mathrm{min}}}\right) \quad \text {for all }\;F\in {{\,\mathrm{GL}\,}}^{\!+}(2), \end{aligned}$$

(3.2)

where $C_{\!M}h:[1,\infty )\rightarrow {\mathbb {R}}$ denotes the monotone-convex envelope given by

$$\begin{aligned} C_{\!M}h(t) :=\sup \Big \{p(t) \,|\,p:[1,\infty )\rightarrow {\mathbb {R}}&\text { monotone increasing and convex}\\&\text {with } p(s)\le h(s)\;\forall \,s\in [1,\infty )\Big \} \end{aligned}$$

and

$$\begin{aligned}&Q^*_pW(F)\\&\quad = \inf \left\{ \frac{1}{|\Omega |}\int _\Omega W(\nabla \varphi )\,{\mathrm {d}x}\;\,|\,\; \varphi \in W^{1,p}(\Omega ;{\mathbb {R}}^2),\; \varphi \big |_{\partial \Omega }(x)=F\, x,\; \det \nabla \varphi >0\text { a.e.} \right\} . \end{aligned}$$

Proof

Let $w(F):=C_{\!M}h\bigl (\frac{\lambda _{\mathrm{max}}}{\lambda _{\mathrm{min}}}\bigr )$. Due to the convexity and monotonicity of $C_{\!M}h$ and the implication vi)$\implies$i) in Proposition 2.13, the mapping $w:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow {\mathbb {R}}$ is polyconvex. Therefore, since

$$\begin{aligned} w(F) = C_{\!M}h\left( \frac{\lambda _{\mathrm{max}}}{\lambda _{\mathrm{min}}}\right) \le h\left( \frac{\lambda _{\mathrm{max}}}{\lambda _{\mathrm{min}}}\right) = W(F), \end{aligned}$$

we find $w(F)\le PW(F)$ for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$. Since $PW(F)\le QW(F)\le Q^*_pW(F)\le RW(F)$, cf. Proposition 2.11, it only remains to show that $RW(F)\le w(F)$ in order to establish (3.2).

According to Lemma 2.15, RW is conformally invariant, thus according to Lemma 2.12 there exists a uniquely determined ${\widetilde{h}}:[1,\infty )\rightarrow {\mathbb {R}}$ such that $RW(F)={\widetilde{h}}\bigl (\frac{\lambda _{\mathrm{max}}}{\lambda _{\mathrm{min}}}\bigr )$ for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$ with singular values $\lambda _{\mathrm{max}}\ge \lambda _{\mathrm{min}}$. Due to the rank-one convexity of RW and the implication iii)$\implies$vi) in Proposition 2.13, the function ${\widetilde{h}}$ is convex and non-decreasing. Since

$$\begin{aligned} {\widetilde{h}}(t) = RW({{\,\mathrm{diag}\,}}(t,1)) \le W({{\,\mathrm{diag}\,}}(t,1)) = h(t) \end{aligned}$$

as well, we find ${\widetilde{h}}(t)\le C_{\!M}h(t)$ for all $t\in [1,\infty )$ and thus

$$\begin{aligned} RW(F) = {\widetilde{h}}\left( \frac{\lambda _{\mathrm{max}}}{\lambda _{\mathrm{min}}}\right) \le C_{\!M}h\left( \frac{\lambda _{\mathrm{max}}}{\lambda _{\mathrm{min}}}\right) =w(F) \end{aligned}$$

for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$. $\square$

Remark 3.2

If h is monotone increasing, then $C_{\!M}h=Ch$, i.e., the monotone-convex envelope (which is the largest convex non-decreasing function not exceeding h) is identical to the (classical) convex envelope Ch of h on $[1,\infty )$. More generally, it is easy to see that if h attains its minimum at some $t_0\in [1,\infty )$, then $C_{\!M}h(t)=h(t_0)$ for all $t\le t_0$ and $C_{\!M}h(t) = Ch(t)$ for all $t\ge t_0$. In particular, if h is continuous, then computing the monotone-convex envelope $C_{\!M}h$ can easily be reduced to the simple one-dimensional problem of finding the convex envelope $C{\widetilde{h}}$ of the function

$$\begin{aligned} {\widetilde{h}}:[1,\infty )\rightarrow {\mathbb {R}},\quad {\widetilde{h}}(t)= {\left\{ \begin{array}{ll} {\displaystyle \min _{s\in [1,\infty )}h(s)} &{}\;\text {if }\;t\le \min {{\,\mathrm{argmin}\,}}h,\\ \quad h(t) &{}\;\text {otherwise,} \end{array}\right. } \end{aligned}$$

where $\min {{\,\mathrm{argmin}\,}}h = \min \{s\in [1,\infty )\,|\,h(s)=\min h\}$, cf. Fig. 2.

Remark 3.3

If $\Psi :[1,\infty )\rightarrow {\mathbb {R}}$ is strictly monotone with sublinear growth, then both these properties hold for the function $h:[1,\infty )\rightarrow {\mathbb {R}}$ with $\Psi ({\mathbb {K}}(F))=h\bigl (\frac{\lambda _{\mathrm{max}}}{\lambda _{\mathrm{min}}}\bigr )=:W(F)$ as well, which implies

$$\begin{aligned} QW = C_{\!M}h = Ch \equiv h(1) = \Psi (1). \end{aligned}$$

For this special case, we directly recover the earlier result (1.8) originally due to Astala et al. (2008).

Remark 3.4

The monotone-convex envelope of $h:[1,\infty )\rightarrow {\mathbb {R}}$ can also be obtained by “reflecting” the graph of the function at $t=1$ and taking the classical convex envelope: if ${\widehat{h}}:{\mathbb {R}}\rightarrow {\mathbb {R}}$ denotes the extension of h to ${\mathbb {R}}$ defined by

$$\begin{aligned} {\widehat{h}}(t):={\left\{ \begin{array}{ll} h(t) &{}\;\text {if }\;t>1,\\ h(1-t) &{}\;\text {if }\;t\le 1, \end{array}\right. } \end{aligned}$$

then $C_{\!M}h = C {\widehat{h}}|_{{\mathbb {R}}_{[1,\infty )}}$, cf. Fig. 2 and “Appendix B”.

Fig. 2

Left: Example of a monotone-convex envelope. Right: The monotone-convex envelope $C_{\!M}h$ of $h:[1,\infty )\rightarrow {\mathbb {R}}$ can be obtained by restricting the convex envelope $C{\widehat{h}}$ of a suitably extension ${\widehat{h}}:{\mathbb {R}}\rightarrow {\mathbb {R}}$ of h back to $[1,\infty )$

4 Specific Relaxation Examples and Numerical Simulations

Theorem 3.1 can be used to explicitly compute the quasiconvex envelope for a substantial class of functions. In the following, a number of explicit relaxation examples will be considered and some of our analytical results will be compared to numerical simulations.

4.1 The Deviatoric Hencky Energy

First, consider the (planar) deviatoric Hencky strain energy (Hencky 1929; Neff et al. 2016) $W_{\mathrm {dH}}:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow {\mathbb {R}}$,

$$\begin{aligned} W_{\mathrm {dH}}(F)&= 2\, \Vert {{\,\mathrm{dev}\,}}_2\log U \Vert ^2 = 2\, \Vert {{\,\mathrm{dev}\,}}_2 \log \sqrt{F^TF} \Vert ^2 \\&= \left[ \log \left( \frac{\Vert F \Vert ^2}{2\, \det F}+\sqrt{\frac{\Vert F \Vert ^4}{4\, (\det F)^2}-1}\right) \right] ^2\\&=\left[ \log \left( {\mathbb {K}}(F)+\sqrt{{\mathbb {K}}(F)^2-1}\right) \right] ^2={{\,\mathrm{arcosh}\,}}^2({\mathbb {K}}(F)), \end{aligned}$$

where ${{\,\mathrm{dev}\,}}_n X :=X-\frac{1}{n}\,{{\,\mathrm{tr}\,}}(X)\cdot {\mathbb {1}}$ is the deviatoric (trace-free) part of $X\in {\mathbb {R}}^{n\times n}$ and $\log U$ denotes the principal matrix logarithm of the right stretch tensor $U:=\sqrt{F^T F}$. The energy $W_{\mathrm {dH}}$ can be expressed as

$$\begin{aligned} W_{\mathrm {dH}}(F) = \log ^2\left( \frac{\lambda _1}{\lambda _2}\right) = \log ^2(K(F)). \end{aligned}$$

Since the representing function $h:[1,\infty )\rightarrow {\mathbb {R}}$ with $h(t)=\log ^2(t)$ is monotone, we find $C_{\!M}h=Ch$ and thus

$$\begin{aligned} C_{\!M}h(t) = Ch(t) = 0 \quad \text {for all }\; t\in [1,\infty ) \end{aligned}$$

due to the sublinear growth of h. Therefore, according to Theorem 3.1,

$$\begin{aligned} RW_{\mathrm {dH}}= QW_{\mathrm {dH}}= PW_{\mathrm {dH}}\equiv 0. \end{aligned}$$

Remark 4.1

Interestingly, the deviatoric Hencky strain energy itself is directly related to the conformal group ${{\,\mathrm{CSO}\,}}(n)$: Let ${{\,\mathrm{dist}\,}}_{\mathrm {geod}}(\cdot ,\cdot )$ denote the geodesic distance on the Lie group ${{\,\mathrm{GL}\,}}^{\!+}(n)$ with respect to the canonical left-invariant Riemannian metric (Martin and Neff 2016; Mielke 2002). Then the distance of $F\in {{\,\mathrm{GL}\,}}^{\!+}(n)$ to the special orthogonal group ${{\,\mathrm{SO}\,}}(n)\subset {{\,\mathrm{GL}\,}}^{\!+}(n)$ is given by Neff et al. (2016, Theorem3.3)

$$\begin{aligned} {{\,\mathrm{dist}\,}}_{\mathrm {geod}}^2(F,{{\,\mathrm{SO}\,}}(n)) = \min _{{\widetilde{R}}\in {{\,\mathrm{SO}\,}}(n)}{{\,\mathrm{dist}\,}}_{\mathrm {geod}}^2(F,{\widetilde{R}}) = \Vert \log U \Vert ^2. \end{aligned}$$

(4.1)

The deviatoric Hencky strain energy can therefore be characterized by the equality

$$\begin{aligned} {{\,\mathrm{dist}\,}}_{\mathrm {geod}}^2(F,{{\,\mathrm{CSO}\,}}(n))&= \min _{A\in {{\,\mathrm{CSO}\,}}(n)}{{\,\mathrm{dist}\,}}_{\mathrm {geod}}^2(F,A)= \min _{\begin{array}{c} {\widetilde{R}}\in {{\,\mathrm{SO}\,}}(n)\\ a\in (0,\infty ) \end{array}}{{\,\mathrm{dist}\,}}_{\mathrm {geod}}^2(F,a\, {\widetilde{R}})\\&\overset{(*)}{=} \min _{a\in (0,\infty )} \, \min _{{\widetilde{R}}\in {{\,\mathrm{SO}\,}}(n)}{{\,\mathrm{dist}\,}}_{\mathrm {geod}}^2\left( \frac{F}{a},\,{\widetilde{R}}\right) \\&\overset{{(4.1)}}{=} \min _{a\in (0,\infty )} \, \Bigl \Vert \log \frac{U}{a} \Bigr \Vert ^2 \\&= \min _{a\in (0,\infty )} \, \Vert (\log U)- \log (a)\, {\mathbb {1}} \Vert ^2 = \Vert {{\,\mathrm{dev}\,}}_n\log U \Vert ^2, \end{aligned}$$

where $(*)$ holds due to the left-invariance of the metric.

4.2 The Squared Logarithm of ${\mathbb {K}}$

Similarly, consider

$$\begin{aligned} W_{\mathrm {log}}(F) = (\log {\mathbb {K}})^2 = \log ^2\left( \frac{1}{2}\left( \frac{\lambda _1}{\lambda _2} +\frac{\lambda _2}{\lambda _1}\right) \right) , \quad \text {i.e.}\quad h(t) = \log ^2\left( \frac{1}{2}\left( t+\frac{1}{t}\right) \right) . \end{aligned}$$

Since h is again monotone on $[1,\infty )$ with sublinear growth (cf. Fig. 3), we find

$$\begin{aligned} C_{\!M}h(t) = Ch(t) = 0 \quad \text {for all }\; t\in [1,\infty ) \end{aligned}$$

and thus

$$\begin{aligned} RW_{\mathrm {log}}= QW_{\mathrm {log}}= PW \equiv 0. \end{aligned}$$

Note that due to the sublinear growth of the representation ${\mathbb {K}}\mapsto (\log {\mathbb {K}})^2$, this result can also be obtained by Eq. (1.8), cf. Remark 3.3.

Fig. 3

Left: Visualization of $W_{\mathrm {dH}}(F) = \log ^2\bigl (\frac{\lambda _1}{\lambda _2}\bigr )$ with $h(t)=\log ^2(t)$. Right: Visualization of $W_{\mathrm {log}}(F)=(\log {\mathbb {K}})^2$ with $h(t)=\log ^2\bigl (\frac{1}{2}\left( t+\frac{1}{t}\right) \bigr )$

4.3 The Exponentiated Hencky Energy

Now, consider the exponentiated deviatoric Hencky energy (Neff et al. 2015a)

$$\begin{aligned} W_{\mathrm{eH}}:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow {\mathbb {R}},\quad W_{\mathrm{eH}}(F) = \mathrm{e}^{k\Vert {{\,\mathrm{dev}\,}}_2\log U \Vert ^2} \end{aligned}$$

for some parameter $k>0$. It has previously been shown (Neff et al. 2015b; Ghiba et al. 2015; Martin et al. 2018) that $W_{\mathrm{eH}}$ is polyconvex (and thus quasiconvex) for $k\ge \frac{1}{8}$. For any $0<k<\frac{1}{8}$, we can explicitly compute the quasiconvex envelope: since

$$\begin{aligned} W_{\mathrm{eH}}(F) = \mathrm{e}^{k\log ^2\bigl (\frac{\lambda _1}{\lambda _2}\bigr )}, \end{aligned}$$

and since the mapping $t\mapsto h(t)=\mathrm{e}^{k\log ^2(t)}$ is monotone increasing on $[1,\infty )$, we find

$$\begin{aligned} RW_{\mathrm{eH}}(F) = QW_{\mathrm{eH}}(F) = PW_{\mathrm{eH}}(F) = Ch\Bigl (\frac{\lambda _1}{\lambda _2}\Bigr ) \end{aligned}$$

for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$ with singular values $\lambda _1,\lambda _2$.

In order to further investigate the behavior of this quasiconvex relaxation with finite element simulations, we choose the particular value $k = 0.11 < \frac{1}{8}$ and consider the quasiconvex envelope QW(F) of

$$\begin{aligned} W(F)&=h\Bigl (\frac{\lambda _1}{\lambda _2}\Bigr )=\mathrm{e}^{0.11 \Bigl (\log \frac{\lambda _1}{\lambda _2}\Bigr )^2} =\mathrm{e}^{0.11\, [{{\,\mathrm{arcosh}\,}}{\mathbb {K}}(F)]^2}. \end{aligned}$$

Using Maxwell’s equal area rule (Šilhavý 1997, p. 319), we numerically compute the monotone-convex envelope of h up to five decimal digits:

$$\begin{aligned} C_{\!M}h(t)=Ch(t)\approx \left\{ \begin{array}{ll} h(t) &{} \quad \mathrm{if}\,\, {1}\le t\le 2.65363, \\ 0.872034+0.0898464\,t &{}\quad \mathrm{if}\,\, {2.65363}<t<35.4998,\\ h(t) &{}\quad \mathrm{if}\,\, 35.4998\le t . \end{array}\right. \end{aligned}$$

This explicit representation allows us to determine the set of all $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$ with $QW(F)<W(F)$, known as the binodal region (Grabovsky and Truskinovsky 2016, 2019). In particular, the microstructure energy gap (cf. Fig. 4) between h and Ch is maximal at $\frac{\lambda _1}{\lambda _2}\approx 12.0186=:t_0$ with a value of $\Delta \approx 0.0221558$. We therefore choose homogeneous Dirichlet boundary conditions given by

$$\begin{aligned} F_0=\begin{pmatrix} \sqrt{t_0} &{}\quad 0\\ 0 &{}\quad \frac{1}{\sqrt{t_0}} \end{pmatrix}=\begin{pmatrix} \sqrt{12.0186} &{} 0\\ 0 &{} \frac{1}{\sqrt{12.0186}} \end{pmatrix}, \end{aligned}$$

(4.2)

such that $K(F_0)=t_0$ and thus $\Delta =W(F_0)-Q^*W(F_0)$, for the finite element simulation. The energy level of the homogeneous solution is

$$\begin{aligned} I(\varphi _0)=\int _{B_1(0)} W(F_0)\,{\mathrm {d}x}=\pi \cdot W(F_0)\approx 6.20155, \end{aligned}$$

whereas the infimum of the energy levels of the microstructure solutions is

$$\begin{aligned}&\inf \left\{ \int _{B_1(0)} W(F_0+\nabla \vartheta )\,{\mathrm {d}x}\,\,|\,\, \vartheta \in W^{1,\infty }_0(B_1(0);{\mathbb {R}}^2) \right\} \\&\qquad = |B_1(0) |\cdot Q^*W(F_0) = \pi \, (W(F_0)-\Delta ) \approx 6.13194. \end{aligned}$$

Fig. 4

Visualization of the maximal microstructure energy gap $\Delta$ between h and $C_{\!M}h$ for an energy W which is not convex with respect to $K(F)=\frac{\lambda _1}{\lambda _2}$, similar to the case $W_{\mathrm{eH}}(F) = \mathrm{e}^{k\, \log ^2(\frac{\lambda _1}{\lambda _2})}$ for $k<\frac{1}{8}$

Figure 5 shows two numerical simulations of the microstructure on triangle grids with different resolutions. The illustration shows the reference configuration, colored according to the value of the determinant of the deformation gradient (plotting ${\mathbb {K}}$ instead results in similar images). The energy level of the configuration on the left is 6.17149 on a grid with 294,912 vertices. Repeating the computation on a grid with one additional step of uniform refinement leads to the configuration on the right, which has an energy level of 6.16216.

Note that the values obtained for the energy level still differ significantly from the expected value of 6.13194. It is unclear whether the discrepancy is solely due to insufficient mesh resolution; further numerical investigations on more performant hardware are planned for the future. The expected energy level was, however, obtained numerically using a modification of an algorithm by Bartels (2005) for computing the polyconvex envelope.

Fig. 5

Microstructure for the energy $W(F) = \mathrm{e}^{0.11\left[ {{\,\mathrm{arcosh}\,}}{\mathbb {K}}(F)\right] ^2}$ with boundary conditions $F_0$ given by (4.2) for two different mesh resolutions. Although the number of oscillations (laminates) is mesh-dependent, macroscopic quantities like volume ratios are mesh-independent; these macroscopic features are predicted by QW. Left: 294,912 grid vertices, energy level of 6.17149. Right: 1,179,648 vertices, energy level of 6.16216

4.4 An Energy Function Related to a Result by Yan

Lastly, we consider the energy function (cf. Fig. 6)

$$\begin{aligned} W(F)=\Psi _L({\mathbb {K}}(F))=\cosh ({\mathbb {K}}(F)-L)-1=\cosh \left( \frac{1}{2} \left( \frac{\lambda _1}{\lambda _2}+\frac{\lambda _2}{\lambda _1}\right) -L\right) -1, \end{aligned}$$

which penalizes the deviation of the distortion ${\mathbb {K}}$ from a prescribed value $L\ge 1$. According to Theorem 3.1, the quasiconvex envelope of W is given by

$$\begin{aligned} QW(F) = {\left\{ \begin{array}{ll} 0 &{}\quad \;\text {if }\;{1}\le {\mathbb {K}}(F) \le L, \\ W(F) &{}\quad \;\text {if }\;L\le {\mathbb {K}}(F). \end{array}\right. } \end{aligned}$$

(4.3)

Fig. 6

Visualization of $\Psi _L({\mathbb {K}})$, the corresponding representation $h_l(K)=\Psi _L\left( \frac{1}{2}\left( K+\frac{1}{K}\right) \right)$ and the monotone-convex envelope of the restriction of $h_l$ to $[1,\infty )$

Again, we want to further investigate the microstructure induced by W with numerical simulations on $\Omega =B_1(0)$. For our calculations, we consider the case $L=2$. At $x_0=\frac{\lambda _1}{\lambda _2}=1$, the microstructure energy gap between h and Ch is maximal with a value of $\Delta \approx 0.54308$, hence we use homogeneous Dirichlet boundary values with $F_0={\mathbb {1}}$. The energy value of the homogeneous solution is

$$\begin{aligned} I(\varphi _0)=\int _{B_1(0)} W(F_0)\,{\mathrm {d}x}=\pi \cdot W(F_0)\approx 1.70614, \end{aligned}$$

whereas the energy level of the microstructure solution should, in the limit, approach

$$\begin{aligned}&\inf \left\{ \int _{B_1(0)} W(F_0+\nabla \vartheta )\,{\mathrm {d}x}\,\,|\,\, \vartheta \in W^{1,\infty }_0(B_1(0);{\mathbb {R}}^2) \right\} \\&\quad = \pi \cdot Q^*W(F_0) = \pi \, (W(F_0)-\Delta ) = 0. \end{aligned}$$

We again compute the microstructure using finite element simulations. It is interesting to observe that the results of these simulations (cf. Figs. 7 and 8) significantly differ from those encountered in the previous example, showing a more complex structure than the simple laminate in Fig. 5; note, however, that these numerical results do not necessarily indicate that the energy infimum cannot be approximated by simple laminates as well.

As expected, we obtain deformations with ${\mathbb {K}}$ very close to the value 2 throughout the domain (Fig. 8). The energy levels obtained numerically are also very close to the expected value of 0. Specifically, for meshes with $294\,912$ and $1\,179\,648$ grid vertices, the obtained energy levels are $2.533\cdot 10^{-3}$ and $1.369\cdot 10^{-3}$, respectively.

Fig. 7

Microstructure for the energy $W(F) = \cosh ({\mathbb {K}}(F) -2) -1$ with boundary conditions $F_0 = {\mathbb {1}}$ on a grid with 294,912 vertices (deformed configuration). The coloring shows the distribution of $\det F$

Fig. 8

Microstructure for the energy $W(F) = \cosh ({\mathbb {K}}(F) -2) -1$ with boundary conditions $F_0 = {\mathbb {1}}$ on a grid with 1,179,648 vertices (deformed configuration). The coloring shows the distribution of ${\mathbb {K}}$, which is essentially constant except near the boundary

The quasiconvex envelope (4.3) and the observed microstructure are related to an earlier result by Yan who, in two remarkable contributions (Yan 2001, 2003), considered the Dirichlet problem

$$\begin{aligned} {{{{\varvec{|}}}}}\nabla \varphi {{{{\varvec{|}}}}}^n=l\, \det \nabla \varphi \quad \text {a.e. in }\;\Omega \subset {\mathbb {R}}^n \end{aligned}$$

for an arbitrary number $l\ge 1$ under affine boundary conditions and obtained the following existence result.

Theorem 4.2

(Yan 2003, Theorem 1.2) Let $l\ge 1$. Given any affine map $x \mapsto F_0\, x+b$, the Dirichlet problem

$$\begin{aligned} {{{{\varvec{|}}}}}\nabla \varphi {{{{\varvec{|}}}}}^n&=l\, \det \nabla \varphi \quad \text {a.e. in }\; \Omega ,\\ \varphi (x)&=F_0\, x+b \quad \text {on }\; \partial \Omega \end{aligned}$$

is solvable in $W^{1,n}(\Omega ;{\mathbb {R}}^n)$ if and only if ${{{{\varvec{|}}}}}F_0{{{{\varvec{|}}}}}^n\le l\det F_0$.

Since in the two-dimensional case $\frac{{{{{\varvec{|}}}}}\nabla \varphi {{{{\varvec{|}}}}}^2}{\det \nabla \varphi } =\frac{\lambda _{\mathrm{max}}}{\lambda _{\mathrm{min}}}=K(\nabla \varphi )$, Yan’s result can be stated in terms of the linear distortion K for $n=2$.

Corollary 4.3

In the planar case $n=2$, for any affine map $x \mapsto F_0\, x+b$, the Dirichlet problem

$$\begin{aligned} K(\nabla \varphi )&=l \quad \text {a.e. in }\; \Omega ,\\ \varphi (x)&= F_0\, x+b \quad \text {on }\; \partial \Omega \end{aligned}$$

is solvable in $W^{1,2}(\Omega ;{\mathbb {R}}^2)$ if and only if $K(F_0)\le l$.

Furthermore, recalling that ${\mathbb {K}}=\frac{1}{2}\left( K+\frac{1}{K}\right)$ and letting $L=\frac{1}{2}\left( l+\frac{1}{l}\right)$, Corollary 4.3 can equivalently be expressed in terms of the distortion ${\mathbb {K}}$.

Corollary 4.4

In the planar case $n=2$ for any affine map $x \mapsto F_0\, x+b$, the Dirichlet problem

$$\begin{aligned} \tfrac{\Vert \nabla \varphi \Vert ^2}{2\, \det \nabla \varphi } ={\mathbb {K}}(\nabla \varphi )&=L&\quad \text {a.e. in }\; \Omega ,\\ \varphi (x)&= F_0\, x+b \quad \text {on }\; \partial \Omega \end{aligned}$$

is solvable in $W^{1,2}(\Omega ;{\mathbb {R}}^2)$ if and only if $\frac{\Vert F_0 \Vert ^2}{2\, \det F_0}={\mathbb {K}}(F_0)\le L$.

Using Corollary 4.4, it is possible to obtain (4.3) for $p=2$ by directly computing the relaxation of $W(F)=\Psi _L({\mathbb {K}}(F))=\cosh ({\mathbb {K}}(F)-L)-1$, i.e.,

$$\begin{aligned} Q^*_2W(F) =\inf \left\{ \frac{1}{|\Omega |} \int _{B_1(0)} \!\!\! \Psi _L({\mathbb {K}}(\nabla \varphi ))\,{\mathrm {d}x}\,\,|\,\, \varphi \in W^{1,2}(B_1(0);{\mathbb {R}}^2),\; \varphi |_{\partial B_1(0)}=F\, x \right\} . \end{aligned}$$

For ${\mathbb {K}}(F)=L$, the infimum value zero is already realized by the homogeneous solution. For ${\mathbb {K}}(F)<L$, although there is no homogeneous equilibrium solution, there exist a deformation ${\widehat{\varphi }}\in W^{1,2}(\Omega ;{\mathbb {R}}^2)$ with ${\widehat{\varphi }}|_{\partial \Omega }=F\, x$ and ${\mathbb {K}}(\nabla {\widehat{\varphi }})=L$ due to Corollary 4.4. Then $\Psi _L({\mathbb {K}}(\nabla {\widehat{\varphi }}))=0$ and thus $Q^*_2W(F)=0$ for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$ with ${\mathbb {K}}(F)\le L$. Finally, since the mapping

$$\begin{aligned} F\mapsto {\widehat{W}}(F):={\left\{ \begin{array}{ll} \quad 0 &{}\;\text {if }\;{\mathbb {K}}(F)\le L, \\ W(F) &{}\;\text {if }\;{\mathbb {K}}(F)\ge L, \end{array}\right. } \end{aligned}$$

is convex and increasing with respect to ${\mathbb {K}}$ and thus polyconvex, it provides a lower bound for the polyconvex envelope of W, from which it easily follows that $PW=Q^*_2W={\widehat{W}}$.

5 Connections to the Grötzsch Problem

Proposition 2.13 also negatively answers a conjecture by Adamowicz (2007, Conjecture 1), which (in the two-dimensional case) states that if a conformally invariant energy $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow {\mathbb {R}}$ with $W(F)=\Psi ({\mathbb {K}}(F))$ is polyconvex, then $\Psi$ is non-decreasing and convex. A direct counterexample is given by $W(F)=\frac{\lambda _{\mathrm{max}}}{\lambda _{\mathrm{min}}}$, which is polyconvex due to criterion v) in Proposition 2.13 with $h(t)=t$ for $t\ge 1$, but the representation $W(F)=\Psi ({\mathbb {K}}(F))=\mathrm{e}^{{{\,\mathrm{arcosh}\,}}({\mathbb {K}}(F))}$ is not convex with respect to ${\mathbb {K}}(F)$.

Furthermore, criterion iv) in Proposition 2.13 reveals a direct connection between the so-called Gr${\ddot{o}}$tzsch property and quasiconvexity in the two-dimensional case.

Definition 5.1

(Adamowicz 2007) Let $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}$ be conformally invariant. Then W satisfies the Gr${\ddot{o}}$tzsch property if for every ${\mathbb {Q}}=[0,a_1]\times \cdots \times [0,a_n]\subset {\mathbb {R}}^n$ and every ${\mathbb {Q}}'=[0,a'_1]\times \cdots \times [0,a'_n]\subset {\mathbb {R}}^n$, the functional

$$\begin{aligned} I:{\mathcal {A}}\rightarrow {\mathbb {R}},\quad I(\varphi ) = \int _{{\mathbb {Q}}} W(\nabla \varphi )\,{\mathrm {d}x}\end{aligned}$$

attains its minimum at the affine mapping $\varphi :{\mathbb {Q}}\rightarrow {\mathbb {Q}}'$, $\varphi (x)=(\frac{a'_1}{a_1}x_1,\dotsc ,\frac{a'_n}{a_n}x_n)$; here, the set ${\mathcal {A}}$ of admissible functions consists of all $\varphi \in W^{1,p}_{\mathrm {loc}}({\mathbb {Q}};{\mathbb {Q}}'),\, p\ge n$ with $\det \nabla \varphi >0$ that satisfy the Gr${\ddot{o}}$tzsch boundary conditions, i.e., map each $(n-1)$–dimensional face of ${\mathbb {Q}}$ to the corresponding face of ${\mathbb {Q}}'$.

Note that the boundary condition imposed in Definition 5.1 does not require the admissible mappings to be affine at the boundary, since each of the faces can be mapped to the corresponding ones in an arbitrary (possibly nonlinear) manner.

In the two-dimensional case, the representation of the energy in terms of the singular values allows us to infer the quasiconvexity from the Grötzsch property in a particularly straightforward way.

Proposition 5.2

Let $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow {\mathbb {R}}$ be conformally invariant and satisfy the Grötzsch property for all ${\mathbb {Q}},{\mathbb {Q}}'$. Then W is polyconvex.

Proof

Assume that W is not polyconvex. Then $g:(0,\infty )^2\rightarrow {\mathbb {R}}$ with $W(F)=g(\lambda _1,\lambda _2)$ is not separately convex according to criterion iv) in Proposition 2.13. Therefore, there exist $\lambda _1,{\widehat{\lambda }}_1,\lambda _2\in (0,\infty )$ and $t\in (0,1)$ such that

$$\begin{aligned} tg(\lambda _1,\lambda _2)+(1-t)g({\widehat{\lambda }}_1,\lambda _2)<g(t\lambda _1+(1-t) {\widehat{\lambda }}_1,\lambda _2). \end{aligned}$$

Now, let ${\mathbb {Q}}=[0,1]^2$ and ${\mathbb {Q}}'=[0,t\lambda _1+(1-t){\widehat{\lambda }}_1]\times [0,\lambda _2]$, and define $\varphi :{\mathbb {Q}}\rightarrow {\mathbb {Q}}'$ by

$$\begin{aligned} \varphi (x) :={\left\{ \begin{array}{ll} \quad \begin{pmatrix} \lambda _1\, x_1\\ \lambda _2\, x_2 \end{pmatrix} &{}\;\text {if }\;x_1\le t,\\ \begin{pmatrix} {\widehat{\lambda }}_1\, x_1+t(\lambda _1-{\widehat{\lambda }}_1)\\ \lambda _2 x_2 \end{pmatrix}&\;\text {if }\;x_1>t. \end{array}\right. } \end{aligned}$$

Then $\varphi$ satisfies the Grötzsch boundary conditions, $\varphi \in W^{1,p}({\mathbb {Q}};{\mathbb {Q}}')$ for all $p\ge 1$ and

$$\begin{aligned} \int _{\mathbb {Q}}W(\nabla \varphi )\,{\mathrm {d}x}&= \int _{[0,t]\times [0,1]} W({{\,\mathrm{diag}\,}}(\lambda _1,\lambda _2))\,{\mathrm {d}x}+ \int _{[t,1]\times [0,1]} W({{\,\mathrm{diag}\,}}({\widehat{\lambda }}_1,\lambda _2))\,{\mathrm {d}x}\\&= \int _{[0,t]\times [0,1]} g(\lambda _1,\lambda _2)\,{\mathrm {d}x}+ \int _{[t,1]\times [0,1]} g({\widehat{\lambda }}_1,\lambda _2)\,{\mathrm {d}x}\\&=tg(\lambda _1,\lambda _2)+(1-t)g({\widehat{\lambda }}_1,\lambda _2)\\&<g(t\lambda _1+(1-t){\widehat{\lambda }}_1,\lambda _2) \;=\; W(F_0) = W(F_0)\cdot |{\mathbb {Q}} |, \end{aligned}$$

where $F_0={{\,\mathrm{diag}\,}}(t\lambda _1+(1-t){\widehat{\lambda }}_1,\lambda _2)$ is the boundary-compatible linear mapping from ${\mathbb {Q}}$ to ${\mathbb {Q}}'$. Therefore, W does not satisfy the Grötzsch condition. $\square$

Appendices

A Basic Results Related to Generalized Convexity

In order to avoid any ambiguities or lack of rigor arising from the consideration of extended-real-valued functions, we recall some basic properties related to different notions of convexity, stated in a form specifically applicable to the case of functions on the domain ${{\,\mathrm{GL}\,}}^{\!+}(n)$. First, we will require a version of Jensen’s inequality, an essential result for classically convex functions.

Lemma A.1

For $N\in {\mathbb {N}}$, let $P:{\mathbb {R}}^N\rightarrow {\mathbb {R}}\cup \{+\infty \}$ be convex such that the effective domain ${{\,\mathrm{dom}\,}}P :=\{y\in {\mathbb {R}}^N\,|\,P(y)<+\infty \}$ is open. Then for any $y_0\in {{\,\mathrm{dom}\,}}P$, there exists (a subgradient) $y_0^*\in {\mathbb {R}}^N$ such that

$$\begin{aligned} P(y) \ge P(y_0) + \langle y_0^*,y-y_0 \rangle \end{aligned}$$

for all $y\in {\mathbb {R}}^N$.

Proof

See (Rockafellar 1970, Theorem 23.4). $\square$

Lemma A.2

(Jensen’s inequality for extended-real-valued convex functions) Let $P:{\mathbb {R}}^N\rightarrow {\mathbb {R}}\cup \{+\infty \}$ be convex such that the effective domain ${{\,\mathrm{dom}\,}}P :=\{y\in {\mathbb {R}}^N\,|\,P(y)<+\infty \}$ is open. Let $\Omega \subset {\mathbb {R}}^n$ be open and bounded. Then for any $\Phi \in L^1(\Omega ;{\mathbb {R}}^N)$,

$$\begin{aligned} P \left( \frac{1}{|\Omega |}\,\int _\Omega \Phi (x)\,{\mathrm {d}x}\right) \le \frac{1}{|\Omega |}\,\int _\Omega P(\Phi (x))\,{\mathrm {d}x}\end{aligned}$$

(A.1)

whenever the right-hand side integral in (A.1) exists.

Proof

Let $y_0=\frac{1}{|\Omega |}\,\int _\Omega \Phi (x)\,{\mathrm {d}x}\in {\mathbb {R}}^N$, and assume without loss of generality that $y_0\in {{\,\mathrm{dom}\,}}P$. Then due to the convexity of P, according to Lemma A.1, there exists $y_0^*\in {\mathbb {R}}^N$ such that

$$\begin{aligned} P(y) \ge P(y_0) + \langle y_0^*,y-y_0 \rangle \end{aligned}$$

for all $y\in {\mathbb {R}}^N$. We therefore find

$$\begin{aligned} P(\Phi (x)) \ge P(y_0) + \langle y_0^*,\Phi (x)-y_0 \rangle \end{aligned}$$

for all $x\in \Omega$ and thus

$$\begin{aligned} \frac{1}{|\Omega |}\int _\Omega P(\Phi (x))\,{\mathrm {d}x}&\ge \frac{1}{|\Omega |}\int _\Omega P(y_0) + \langle y_0^*,\Phi (x)-y_0 \rangle \,{\mathrm {d}x}\\&= P(y_0) + \langle y_0^*, \frac{1}{|\Omega |}\int _\Omega \Phi (x)-y_0\,{\mathrm {d}x} \rangle \\&= P(y_0) + \langle y_0^*, \frac{1}{|\Omega |}\int _\Omega \Phi (x)\,{\mathrm {d}x}- y_0 \rangle \\&= P(y_0) + \langle y_0^*, \,y_0 - y_0 \rangle = P \left( \frac{1}{|\Omega |}\int _\Omega \Phi (x)\,{\mathrm {d}x}\right) . \qquad \square \end{aligned}$$

Many properties related to polyconvexity, of course, heavily rely on the fact that any minor of the Jacobian is a Null Lagrangian (Ball 1976), which is expressed by the following property of the adjoint mapping (cf. Definition 2.1).

Lemma A.3

Let $\Omega \subset {\mathbb {R}}^n$ be open and bounded, $F\in {\mathbb {R}}^{n\times n}$ and $\vartheta \in W^{1,p}_0(\Omega ;{\mathbb {R}}^n)$. Then

$$\begin{aligned} \frac{1}{|\Omega |}\,\int _\Omega {{\,\mathrm{adj}\,}}(F+\nabla \vartheta (x)) \,{\mathrm {d}x}= {{\,\mathrm{adj}\,}}(F) . \end{aligned}$$

Proof

See (Dacorogna 2008, Theorem 8.35 (ii)). $\square$

We will also require a number of fundamental results concerning the relation between rank-one convexity and quasiconvexity which are needed for establishing our main results. First, we consider a characterization of the rank-one convex envelope, originally due to Dacorogna (1987), Dacorogna (2008), in terms of the so-called $(H_{m})$-condition.

Definition A.4

(Dacorogna 2008, Definition 5.14) Let $m\in {\mathbb {N}}$, $F_1,\dotsc ,F_m\in {\mathbb {R}}^{n\times n}$ and $t_1,\dotsc ,t_m\in [0,1]$ such that $\sum _{i=1}^m t_i=1$. Then $(t_i,F_i)_{1\le i\le m}$ satisfy $(H_{m})$ if

• i) $m=2$ and ${{\,\mathrm{rank}\,}}(F_2-F_1)=1$,

• ii) $m>2$ and, up to a permutation, ${{\,\mathrm{rank}\,}}(F_2-F_1)=1$ and $({\widetilde{t}}_i,{\widetilde{F}}_i)_{1\le i\le m-1}$ satisfy $(H_{m-1})$, where

  $$\begin{aligned} {\widetilde{t}}_1 = t_1+t_2 ,\quad {\widetilde{F}}_1 = \frac{1}{t_1+t_2}\, (t_1F_1+t_2F_2) \quad&\text {and}\quad {\widetilde{t}}_i = t_{i+1} ,\quad {\widetilde{F}}_i =F_{i+1}\qquad \quad \\&\text {for }i\in \{2,\dotsc ,m-1\}. \nonumber \end{aligned}$$

  (A.2)

Lemma A.5

Let $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}$ be bounded below. Then

$$\begin{aligned} RW(F)&= \inf \left\{ \sum _{i=1}^m t_i W(F_i) \;\,\Big |\,\; t_1,\dotsc ,t_m\in [0,1],\; \sum _{i=1}^m t_i=1,\; \sum _{i=1}^m t_iF_i=F,\; \right. \nonumber \\&\quad ~ \left. (t_i,F_i)\text { satisfy }(H_{m}) \right\} \end{aligned}$$

(A.3)

for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(n)$.

Proof

See (Dacorogna (1987)) and Dacorogna (2008, Theorem 6.10). $\square$

In addition to its direct application toward characterizing the rank-one convex envelope of a function, the $(H_{m})$-condition also plays an important role for the construction of laminates in the theory of gradient Young measures (Roubıček 2011; Koumatos et al. 2016; Rindler 2018); here, we will apply it to a similar, but more straightforward approach (cf. Dacorogna and Marcellini 1997) involving only classical deformation mappings in an appropriate function space.

Lemma A.6

Let $\widehat{\Omega }\subset {\mathbb {R}}^n$ be open and bounded. Let ${\widehat{t}}\in [0,1]$ and ${\widehat{F}}_1,{\widehat{F}}_2\in {\mathbb {R}}^{n\times n}$ with ${{\,\mathrm{rank}\,}}({\widehat{F}}_2-{\widehat{F}}_1)=1$ and ${\widehat{F}}={\widehat{t}}{\widehat{F}}_1+(1-{\widehat{t}}){\widehat{F}}_2$. Then for every $\widehat{\varepsilon }>0$, there exist a (piecewise affine) mapping $\widehat{\varphi }\in W^{1,\infty }(\widehat{\Omega };{\mathbb {R}}^n)$ and disjoint open sets $\widehat{\Omega }_1,\widehat{\Omega }_2\subset \widehat{\Omega }$ such that

$$\begin{aligned} \left\{ \begin{aligned}&\bigl |\;|\widehat{\Omega }_1 |-{\widehat{t}}|\widehat{\Omega } |\; \bigr |\le \widehat{\varepsilon },\quad \bigl |\;|\widehat{\Omega }_2 |-(1-{\widehat{t}})|\widehat{\Omega } |\; \bigr |\le \widehat{\varepsilon },\\&\widehat{\varphi }(x)=Fx \quad \text {on }\; \partial \widehat{\Omega },\\&{{\,\mathrm{dist}\,}}(\nabla \widehat{\varphi }(x),\,{{\,\mathrm{conv}\,}}(\{{\widehat{F}}_1,{\widehat{F}}_2\})) \le \widehat{\varepsilon }\;\;\text { a.e. in }\widehat{\Omega },\\&\nabla \widehat{\varphi }(x)= {\left\{ \begin{array}{ll} {\widehat{F}}_1 &{}\;\text {if }\;x\in \widehat{\Omega }_1,\\ {\widehat{F}}_2 &{}\;\text {if }\;x\in \widehat{\Omega }_2, \end{array}\right. } \end{aligned}\right. \end{aligned}$$

(A.4)

where ${{\,\mathrm{conv}\,}}(\{{\widehat{F}}_1,{\widehat{F}}_2\})$ is the closed line segment connecting ${\widehat{F}}_1$ and ${\widehat{F}}_2$.

Proof

See Dacorogna (2008, Lemma 3.11). $\square$

Remark A.7

The inequality $|\;|\widehat{\Omega }_1 |-{\widehat{t}}|\widehat{\Omega } |\; |\le \widehat{\varepsilon }$ can equivalently be expressed as ${\widehat{t}}-\frac{\varepsilon }{\widehat{\Omega }}\le \frac{\widehat{\Omega }_1}{\widehat{\Omega }}\le {\widehat{t}}+\frac{\varepsilon }{\widehat{\Omega }}$.

Applying Lemma A.6 inductively, we obtain the following iterated generalization.

Corollary A.8

Let $\Omega \subset {\mathbb {R}}^n$ be open and bounded, let $t_1,\dotsc ,t_m\in [0,1]$ with $\sum _{i=1}^m t_i=1$ and $F_1,\dotsc ,F_m\in {\mathbb {R}}^{n\times n}$ such that $(t_i,F_i)_{1\le i\le m}$ satisfy $(H_{m})$, and let $F=\sum _{i=1}^m t_iF_i$. Then there exist $M\in {\mathbb {N}}$ and ${\overline{F}}_1,\dotsc ,{\overline{F}}_M\in {\mathbb {R}}^{n\times n}$ with

$$\begin{aligned} {{\,\mathrm{rank}\,}}({\overline{F}}_{j+1}-{\overline{F}}_j) = 1 \quad \text {for all }\;j\in \{1,\dotsc ,M-1\} \end{aligned}$$

such that for every $\varepsilon >0$, there exist a (piecewise affine) mapping $\varphi \in W^{1,\infty }(\Omega ;{\mathbb {R}}^n)$ and disjoint open sets $\Omega _1,\dotsc ,\Omega _m\subset \Omega$ such that

$$\begin{aligned} \left\{ \begin{aligned}&\bigl |\;|\Omega _i |-t_i|\Omega |\; \bigr |\le \varepsilon ,\\&\varphi (x)=Fx \quad \text {on }\; \partial \Omega ,\\&{{\,\mathrm{dist}\,}}\Bigl (\nabla \varphi (x),\,\bigcup \nolimits _{j=1}^{M-1} {{\,\mathrm{conv}\,}}(\{{\overline{F}}_j,{\overline{F}}_{j+1}\})\Bigr ) \le \varepsilon \;\;\text { a.e. in }\Omega ,\\&\nabla \varphi (x)=F_i \;\;\text { if }\;x\in \Omega _i \end{aligned}\right. \end{aligned}$$

(A.5)

for all $i\in \{1,\dotsc ,m\}$.

Proof

We will prove the corollary by induction. For $m=2$, the statement is identical to Lemma A.6 with $M=2$, ${\overline{F}}_1=F_1$ and ${\overline{F}}_2=F_2$.

Now let $m>2$. By assumption on $(t_i,F_i)_{1\le i\le m}$ and Definition A.4, $({\widetilde{t}}_1,{\widetilde{F}}_1),\dotsc ,({\widetilde{t}}_1,{\widetilde{F}}_{m-1})$ given by (A.2) satisfy $(H_{m-1})$ and ${{\,\mathrm{rank}\,}}(F_2-F_1)=1$ up to permutation. Applying the induction assumption to $({\widetilde{t}}_1,{\widetilde{F}}_1),\dotsc ,({\widetilde{t}}_1,{\widetilde{F}}_{m-1})$, we first choose suitable matrices $\widetilde{{\overline{F}}}_1,\dotsc ,\widetilde{{\overline{F}}}_{{\widetilde{M}}}$.

Now let $\varepsilon >0$ be given. Then for any $\widetilde{\varepsilon }<\varepsilon$, there exist $\widetilde{\Omega }_1,\dotsc ,\widetilde{\Omega }_{m-1}$ and a piecewise affine function $\widetilde{\varphi }\in W^{1,\infty }(\Omega ;{\mathbb {R}}^n)$ such that (A.5) is satisfied for all $i\in \{1,\dotsc ,m-1\}$. Applying Lemma A.6 to

$$\begin{aligned} \widehat{\Omega }=\widetilde{\Omega }_1 ,\quad \widehat{\varepsilon }=\widetilde{\varepsilon }\,\quad {\widehat{F}}_1=F_1 ,\quad {\widehat{F}}_2=F_2 \quad \text {and}\quad {\widehat{t}}=\frac{t_1}{t_1+t_2} , \end{aligned}$$

we obtain disjoint open sets $\widehat{\Omega }_1,\widehat{\Omega }_2\subset \widetilde{\Omega }_1\subset \Omega$ and a piecewise affine function $\widehat{\varphi }\in W^{1,\infty }(\Omega _1;{\mathbb {R}}^n)$ which satisfies (A.4). Let

$$\begin{aligned}&{\overline{F}}_1=F_1 ,\quad {\overline{F}}_2=F_2 ,\quad {\overline{F}}_3={\widetilde{F}}_1 ,\qquad&\Omega _1=\widehat{\Omega }_1 ,\quad \Omega _2=\widehat{\Omega }_2 ,\quad M={\widetilde{M}}+3 ,\\&{\overline{F}}_i=\widetilde{{\overline{F}}}_{i-3} \quad \text { for }\;i\in \{4,\dotsc ,M\} ,&\Omega _i=\widetilde{\Omega }_{i-1} \quad \text { for }\;i\in \{3,\dotsc ,m\} \end{aligned}$$

and

$$\begin{aligned} \varphi :\Omega \rightarrow {\mathbb {R}}^n ,\quad \varphi (x)= {\left\{ \begin{array}{ll} \widehat{\varphi }(x) &{}\;\text {if }\;x\in \Omega _1,\\ \widetilde{\varphi }(x) &{}\;\text {otherwise}. \end{array}\right. } \end{aligned}$$

Then $\varphi \in W^{1,\infty }(\Omega ,{\mathbb {R}}^n)$ is piecewise affine with $\varphi (x)=Fx$ on $\partial \Omega$ and $\nabla \varphi (x)= F_i$ on each $\Omega _i$. Furthermore, since

$$\begin{aligned} {{\,\mathrm{dist}\,}}(\nabla \varphi (x),\,{{\,\mathrm{conv}\,}}(\{{\overline{F}}_1,{\overline{F}}_2\})) = {{\,\mathrm{dist}\,}}(\nabla \widehat{\varphi }(x),\,{{\,\mathrm{conv}\,}}(\{{\widehat{F}}_1,{\widehat{F}}_2\})) \le \widehat{\varepsilon }< \varepsilon \;\;\text { a.e. in }\widetilde{\Omega }_1 \end{aligned}$$

by construction via Lemma A.6 and

$$\begin{aligned}&{{\,\mathrm{dist}\,}}\Bigl (\nabla \varphi (x),\,\bigcup \nolimits _{j=4}^{M-1} {{\,\mathrm{conv}\,}}(\{{\overline{F}}_j,{\overline{F}}_{j+1}\})\Bigr ) = {{\,\mathrm{dist}\,}}\Bigl (\nabla \widetilde{\varphi }(x),\,\bigcup \nolimits _{j=1}^{{\widetilde{M}}-1} {{\,\mathrm{conv}\,}}(\{\widetilde{{\overline{F}}}_j,\widetilde{{\overline{F}}}_{j+1}\})\Bigr )\\&\quad \le \widetilde{\varepsilon }< \varepsilon \;\;\text { a.e. in }\Omega \setminus \widetilde{\Omega }_1 \end{aligned}$$

by the induction assumption, we find the third condition in (A.5) satisfied as well; note that indeed ${{\,\mathrm{rank}\,}}({\overline{F}}_{j+1}-{\overline{F}}_j)=1$ for all $j\in \{1,\dotsc ,M-1\}$.

Finally, the induction assumption directly yields

$$\begin{aligned} \bigl |\;|\Omega _i |-t_i|\Omega |\; \bigr | = \bigl |\;|\widetilde{\Omega }_{i-1} |-{\widetilde{t}}_{i-1}|\Omega |\; \bigr | \le \widetilde{\varepsilon }< \varepsilon \end{aligned}$$

for $i\in \{3,\dotsc ,m\}$. For $i=1$, we find (cf. Remark A.7)

$$\begin{aligned} \frac{|\Omega _1 |}{|\Omega |} = \frac{|\Omega _1 |}{|\widehat{\Omega } |} \cdot \frac{|\widehat{\Omega } |}{|\Omega |}= & {} \frac{|\widehat{\Omega }_1 |}{|\widehat{\Omega } |} \cdot \frac{|\widetilde{\Omega }_1 |}{|\Omega |}\\\le & {} \left( {\widehat{t}}+\frac{\widehat{\varepsilon }}{|\widehat{\Omega } |}\right) \cdot \left( {\widetilde{t}}_1+\frac{\widetilde{\varepsilon }}{|\Omega |}\right) = \left( {\widehat{t}}+\frac{\widetilde{\varepsilon }}{|\widetilde{\Omega }_1 |}\right) \cdot \left( {\widetilde{t}}_1+\frac{\widetilde{\varepsilon }}{|\Omega |}\right) \end{aligned}$$

and thus, we choose $\widetilde{\varepsilon }>0$ sufficiently small

$$\begin{aligned} \left( {\widehat{t}}+\frac{|\Omega |}{|\widetilde{\Omega }_1 |}\, {\widetilde{t}}_1\right) \widetilde{\varepsilon }+\frac{\widetilde{\varepsilon }^2}{|\widetilde{\Omega }_1 |}\le \varepsilon , \end{aligned}$$

so that

$$\begin{aligned} \frac{|\Omega _1 |}{|\Omega |} \le {\widehat{t}}\cdot {\widetilde{t}}_1 + \frac{\varepsilon }{|\Omega |} = \frac{t_1}{t_1+t_2}\cdot (t_1+t_2) + \frac{\varepsilon }{|\Omega |}= t_1 + \frac{\varepsilon }{|\Omega |}. \end{aligned}$$

Similarly, $\frac{|\Omega _1 |}{|\Omega |}\ge t_1 - \frac{\varepsilon }{|\Omega |}$, which implies $||\Omega _1 |-t_1|\Omega | |\le \varepsilon$. The last remaining inequality for $i=2$ follows analogously.

B The Quasiconvex Envelope for a Class of Conformal Energies

The concept of monotone-convex envelopes is directly connected to an earlier result by Dacorogna and Koshigoe (1993), who obtained an explicit relaxation result for a subclass of conformal energy functions.

Lemma B.1

(Dacorogna and Koshigoe 1993, Proposition 5.1) Let $W:{\mathbb {R}}^{2\times 2}\rightarrow {\mathbb {R}}$ be of the form

$$\begin{aligned} W(F):=g(\sqrt{\Vert F \Vert ^2-2\, \det F}),\quad g:[0,\infty )\rightarrow {\mathbb {R}}. \end{aligned}$$

(B.1)

Define

$$\begin{aligned} {\widetilde{g}}:{\mathbb {R}}\rightarrow {\mathbb {R}},\qquad {\widetilde{g}}(x)= {\left\{ \begin{array}{ll} \quad g(x) &{}\;\text {if }\;x>0,\\ g(-x) &{}\;\text {if }\;x\le 0. \end{array}\right. } \end{aligned}$$

Then

$$\begin{aligned} CW(F)=PW(F)=QW(F)=RW(F)={\widetilde{g}}^{**}\bigl (\sqrt{\Vert F \Vert ^2-2\, \det F}\, \bigr ), \end{aligned}$$

where ${\widetilde{g}}^*$ is the Legendre-transformation of ${\widetilde{g}}$ and ${\widetilde{g}}^{**}=\left( {\widetilde{g}}^*\right) ^*$.

The same result can be found in (Šilhavý 2001, Prop. 4.1). Note that the convexity of the mapping $F\mapsto {\widetilde{g}}^{**}(\sqrt{\Vert F \Vert ^2-2\, \det F})={\widetilde{g}}^{**}(\sqrt{(\lambda _1-\lambda _2)^2})$ follows directly (Ball 1977) from the fact that ${\widetilde{g}}^{**}$ is convex and non-decreasing on $[0,\infty )$. Furthermore, if $g\ge 0$, then W of the form (B.1) is a conformal energy in the sense of Footnote 1.

If g is continuous and bounded below, then based on Dacorogna (2008, Theorem 2.43) it is easy to show that the monotone-convex envelope of g is exactly the restriction of $C{\widetilde{g}}$ to $[0,\infty )$:

$$\begin{aligned} C_{\!M}g = (C{\widetilde{g}})\big |_{[0,\infty )},\quad C\widetilde{g}={{\widetilde{g}}}^{**}. \end{aligned}$$

Similar to the geodesic distance considered in Sect. 4.1, the expression $\sqrt{\Vert F \Vert ^2-2\, \det F}$ can be characterized as a measure of distance to the conformal group:⁵ since the closure ${{\,\mathrm{CSO}\,}}(2)\cup \{0\}$ of ${{\,\mathrm{CSO}\,}}(2)$ is a linear subspace⁶ of ${\mathbb {R}}^{2\times 2}$ with an orthonormal basis given by

$$\begin{aligned} A_1 = \frac{\sqrt{2}}{2}\, \begin{pmatrix} 1&{}\quad 0\\ 0&{}\quad 1 \end{pmatrix},\quad A_2 = \frac{\sqrt{2}}{2}\, \begin{pmatrix} 0&{}\quad \quad 1\\ -1&{}\quad 0 \end{pmatrix}, \end{aligned}$$

thus

$$\begin{aligned} \mathrm {dist}_{\mathrm {euclid}}^2(F,{{\,\mathrm{CSO}\,}}(2))&:=\inf _{A\in {{\,\mathrm{CSO}\,}}(2)} \Vert F-A \Vert ^2\\&= \Vert F \Vert ^2 - (\langle F,A_1 \rangle ^2+\langle F,A_2 \rangle ^2) \\&= \Vert F \Vert ^2- \frac{1}{2}\, ((F_{11}+F_{22})^2 + (F_{12}-F_{21})^2)\\&= \Vert F \Vert ^2 - \frac{1}{2}\, (F_{11}^2+F_{22}^2+F_{12}^2+F_{21}^2 + 2\, (F_{11}\, F_{22}-F_{12}\, F_{21})) \\&= \frac{1}{2}\, (\Vert F \Vert ^2 - 2\, \det F), \end{aligned}$$

where $\langle \cdot ,\cdot \rangle$ denotes the canonical inner product on ${\mathbb {R}}^{2\times 2}$. Therefore, the energy functions considered in Lemma B.1 depend only on the Euclidean distance of F to ${{\,\mathrm{CSO}\,}}(2)$.

C The Convex Envelope of Conformally Invariant Planar Energies

The quasiconvex envelopes computed in Sect. 4 are, in general, not convex, i.e. $QW(F)>CW(F)$ for some $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$. In fact, the following explicit computation shows that the convex envelope of any conformally invariant energy is necessarily constant.

Recall that for a function $W:M\rightarrow {\mathbb {R}}$ which is defined on a non-convex domain $M\subset {\mathbb {R}}^{n\times n}$ (e.g. $M={{\,\mathrm{GL}\,}}^{\!+}(2)$) and bounded below, the convex envelope CW of W is given by the restriction $C{\widetilde{W}}|_M$ of the convex envelope $C{\widetilde{W}}$ of the function

$$\begin{aligned} {\widetilde{W}}:{{\,\mathrm{conv}\,}}(M)\rightarrow {\mathbb {R}}\cup \{+\infty \},\quad {\widetilde{W}}(F)= {\left\{ \begin{array}{ll} W(F) &{}\;\text {if }\;F\in M,\\ +\infty &{}\;\text {if }\;F\notin M, \end{array}\right. } \end{aligned}$$

to M, where ${{\,\mathrm{conv}\,}}(M)$ denotes the convex hull of the set M; cf. Remark 2.3. Note that $CW(F)<+\infty$ for all $F\in M$ and that ${\widetilde{W}}$ can be further extended to a convex function ${\widehat{W}}$ on ${\mathbb {R}}^{n\times n}$ by setting ${\widehat{W}}(F)=+\infty$ for all $F\notin {{\,\mathrm{conv}\,}}(M)$.

Proposition C.1

Let $W:{{\,\mathrm{GL}\,}}^{\!+}(2)\rightarrow {\mathbb {R}}$ be conformally invariant and bounded below. Then

$$\begin{aligned} CW(F)=\inf \left\{ W({\widetilde{F}})\;|\;{\widetilde{F}}\in {{\,\mathrm{GL}\,}}^{\!+}(2)\right\} \end{aligned}$$

for all $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$.

Proof

We only need to show that CW is constant on ${{\,\mathrm{GL}\,}}^{\!+}(2)$. First, observe that the convex envelope of W is conformally invariant (the proof of the bi-${{\,\mathrm{SO}\,}}(2)$-invariance of CW given by Buttazzo et al. (1994, Theorem 3.1) can easily be adapted to include the scaling invariance.). By the definition of convexity on ${{\,\mathrm{GL}\,}}^{\!+}(2)$ employed here, CW must be the restriction of a convex function ${\widetilde{W}}:{{\,\mathrm{conv}\,}}({{\,\mathrm{GL}\,}}^{\!+}(2))={\mathbb {R}}^{2\times 2}\rightarrow {\mathbb {R}}$ to ${{\,\mathrm{GL}\,}}^{\!+}(2)$. In particular, for any $F\in {\mathbb {R}}^{2\times 2}$, the mapping $p_{{\!}_F}:{\mathbb {R}}\rightarrow {\mathbb {R}}$ with $p_{{\!}_F}(t)={\widetilde{W}}(tF)$ is convex.

Let $b:={\widetilde{W}}(0)$. Then for any $F\in {{\,\mathrm{GL}\,}}^{\!+}(2)$ and $t\in {\mathbb {R}}$,

$$\begin{aligned} p_{{\!}_F}(t) = {\widetilde{W}}(tF) = {\left\{ \begin{array}{ll} CW(tF) &{}\;\text {if }\;t\ne 0\\ {\widetilde{W}}(0) &{}\;\text {if }\;t=0 \end{array}\right. } \;\;=\;\; {\left\{ \begin{array}{ll} CW(F) &{}\;\text {if }\;t\ne 0\\ b &{}\;\text {if }\;t=0 \end{array}\right. } \end{aligned}$$

due to the conformal invariance of CW on ${{\,\mathrm{GL}\,}}^{\!+}(2)$. Thus $p_{{\!}_F}$ is convex and constant on ${\mathbb {R}}\setminus \{0\}$, which implies that p is constant on ${\mathbb {R}}$; in particular, $CW(F)=p_{{\!}_F}(1)=p_{{\!}_F}(0)=b$.

Remark C.2

As indicated in Sect. 2.1, analytical methods for finding generalized convex envelopes have often been based on the observation that $RW=CW$ for certain classes of energy functions W and the subsequent computation of the classical convex envelope CW; for example, this method is applicable to the St. Venant–Kirchhoff energy function (Le Dret and Raoult 1995) $W_{\mathrm{SVK}}(F)=\frac{\mu }{4}\, \Vert F^TF-{\mathbb {1}} \Vert ^2+\frac{\lambda }{8} \left( {{\,\mathrm{tr}\,}}(F^TF-{\mathbb {1}})\right) ^2$.

One of the most frequently cited examples of an isotropic and objective energy function W with $RW=QW=PW\ne CW$ is the example of Kohn and Strang (1983, (1986), where, in the ${\mathbb {R}}^{2\times 2}$-case (Zhang 2002; Došl 1997),

$$\begin{aligned} W(F)= {\left\{ \begin{array}{ll} 1+\Vert F \Vert ^2 &{}\;\text {if }\;F \ne 0,\\ 0 &{}\;\text {if }\;F=0, \end{array}\right. } \quad \text {with}\quad CW(F)&= {\left\{ \begin{array}{ll} W(F) &{}\;\text {if }\;\Vert F \Vert \ge 1,\\ \quad 2\, \Vert F \Vert &{}\;\text {if }\;\Vert F \Vert< 1, \end{array}\right. }\\ \text {but}\quad QW(F)&= {\left\{ \begin{array}{ll} W(F) &{}\;\text {if }\;\Vert F \Vert +2\, \det F\ge 1,\\ 2\, \sqrt{\Vert F \Vert ^2+2\, \det F}-2\, \det F &{}\;\text {if }\;\Vert F \Vert +2\, \det F< 1. \end{array}\right. } \end{aligned}$$

Furthermore, if $W:{{\,\mathrm{GL}\,}}^{\!+}(n)\rightarrow {\mathbb {R}}$ is a volumetric energy function of the form $W(F)=f(\det F)$ with $f:(0,\infty )\rightarrow {\mathbb {R}}$, then $RW(F)=QW(F)=PW(F)=Cf(\det F)$ and, in general, $CW(F)<QW(F)$, see Dacorogna (2008, Theorem 6.24).