Abstract
A novel general framework for the study of \(\Gamma \)-convergence of functionals defined over pairs of measures and energy-measures is introduced. This theory allows us to identify the \(\Gamma \)-limit of these kind of functionals by knowing the \( \Gamma \)-limit of the underlying energies. In particular, the interaction between the functionals and the underlying energies results, in the case these latter converge to a non-continuous energy, in an additional effect in the relaxation process. This study was motivated by a question in the context of epitaxial growth evolution with adatoms. Interesting cases of application of the general theory are also presented.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Mathematical models for epitaxial crystal growth usually assume the interfaces to evolve via the so-called Einstein–Nernst relation (see, for instance, Fonseca et al. 2011, 2007a, 2012, 2015). For solid–vapor interfaces, it has been observed in Spencer and Tersoff (2010) that the usually neglected adatoms (atoms freely moving on the surface of the crystal) play an important role in the description of the evolution of the interface. For this reason, Fried and Gurtin (2004) introduced a model that includes the effect of adatoms, an additional variable whose evolution in time is coupled to the evolution in time of the interface of the crystal. In the simple case of a crystal growing on a general shape, i.e., not graph constrained, but without considering elastic effects or surface stress, the free energy of the system reads as:
Here \(E\subset {\mathbb {R}}^d\) is a set with finite perimeter representing the shape of the crystal, and \(u\in L^1(\partial ^*E;[0,+\,\infty ))\) is the density of the adatoms. The Borel function \(\psi {:}\,[0,+\,\infty )\rightarrow (0,+\,\infty )\) is assumed to be non-decreasing and satisfying \(\inf \psi >0\). From the physical point of view, this latter hypothesis is motivated by the fact that, energetically, even an interface without adatoms cannot be created for free.
The interest in considering model (1.1) lies in the intriguing and challenging mathematical questions that are connected to the related evolution equations. In order to perform numerical simulations of the evolution equations obtained formally as the gradient flow of (1.1), Rätz and Voigt (2006) (see also Burger 2006) considered, for \(\varepsilon >0\), the following phase field model inspired by the Modica–Mortola functional (Modica 1987; Modica and Mortola 1977)
Here \(\phi \in H^1({\mathbb {R}}^d)\) is the phase variable, \(W{:}\,{\mathbb {R}}\rightarrow [0,+\,\infty )\) is a continuous double well potential vanishing at 0 and 1, and \(u\in C^0({\mathbb {R}}^d;[0,+\,\infty ))\). The authors worked with the special case \(\psi (t):=1+\frac{t^2}{2}\). Since the Modica–Mortola functional approximates, in the sense of \(\Gamma \)-convergence, the perimeter functional, it is expected that the phase field model (1.2) approximates the sharp interface energy (1.1). The identification of the correct \(\Gamma \)-limit in the weakest topology ensuring compactness along sequences of uniformly bounded energy is currently missing in the literature. The main aim of this work consists in such an identification. The identification of the \(\Gamma \)-limit is an important ingredient for the study of the convergence of the solutions of the gradient flow of the phase field energy (1.2) to the solution of the gradient flow of the sharp interface energy (1.1). In Rätz and Voigt (2006), this convergence was justified by using formal matched asymptotic expansions. We would like to draw the attention to the fact that energies of type (1.1) are also used in model the evolution and equilibria configuration of surfactants in which a chemical additive is considered to be present on the interface of a bubble, driving the evolution (Acerbi and Bouchitté 2008; Alicandro et al. 2012; Baía et al. 2017; Fonseca et al. 2007b).
As observed in Caroccia et al. (2018), energy (1.1) is not lower semi-continuous with respect to the \(L^1\times w^*\) topology, where the density u is seen as the measure  . (Note that this topology allows for very general cracks in the crystal.) Therefore, the functional \({\mathcal {G}}\) cannot be the \(\Gamma \)-limit of the functionals \({\mathcal {G}}_\varepsilon \). Note that the \(L^1\) convergence for sets only implies the weak* convergence of the distributional derivative of the characteristic functions of the sets. Therefore, the relaxation of the functional \({\mathcal {G}}\) does not follow from the results of Buttazzo and Freddi (1991), for which the weak* convergence of the total variation of the distributional derivative of the characteristic functions of the sets would be required. In Caroccia et al. (2018), the authors identified the relaxed functional \(\overline{{\mathcal {G}}}\) of \({\mathcal {G}}\) with respect to the \(L^1\times w^*\) topology. The question is then the following: given that the Modica–Mortola functional
. (Note that this topology allows for very general cracks in the crystal.) Therefore, the functional \({\mathcal {G}}\) cannot be the \(\Gamma \)-limit of the functionals \({\mathcal {G}}_\varepsilon \). Note that the \(L^1\) convergence for sets only implies the weak* convergence of the distributional derivative of the characteristic functions of the sets. Therefore, the relaxation of the functional \({\mathcal {G}}\) does not follow from the results of Buttazzo and Freddi (1991), for which the weak* convergence of the total variation of the distributional derivative of the characteristic functions of the sets would be required. In Caroccia et al. (2018), the authors identified the relaxed functional \(\overline{{\mathcal {G}}}\) of \({\mathcal {G}}\) with respect to the \(L^1\times w^*\) topology. The question is then the following: given that the Modica–Mortola functional
is known to \(\Gamma \)-converge to the perimeter functional \({\mathcal {F}}\), is it true that the functionals \({\mathcal {G}}_\varepsilon \), which can be seen as adatom-density weighted versions of the functionals \({\mathcal {F}}_\varepsilon \), \(\Gamma \)-converge to \({\mathcal {G}}\), the adatom-density weighted versions of the functional \({\mathcal {F}}\)?
The above problem was the motivation to undertake the study of the Gamma convergence of such kind of functionals in a more general framework. The advantage in doing so is in getting a better insight on the technical reasons leading to the answer of the question, other than developing a theory comprehending a variety of other interesting situations. We now introduce this general framework. Let \(\Omega \subset {\mathbb {R}}^d\) be a bounded open set with Lipschitz boundary and denote by \({{\mathcal {A}}}(\Omega )\) the family of open subsets of \(\Omega \). For \(\varepsilon >0\), consider the functionals
where each \({{\mathcal {F}}}_\varepsilon \) is lower semi-continuous in the first variable on each open set \(A\in {{\mathcal {A}}}(\Omega )\). For every \(\phi \in L^1\), the maps
are assumed to be the restriction of Radon measures on \({{\mathcal {A}}}(\Omega )\). Suppose that for every open set \(A\in {{\mathcal {A}}}(\Omega )\) the family \(\{{{\mathcal {F}}}_\varepsilon (\cdot ; A)\}_{\varepsilon >0}\) is \(\Gamma \)-converging in the \(L^1\) topology to \({{\mathcal {F}}}(\cdot ;A)\). Let \(\psi {:}\,[0,+\,\infty )\rightarrow (0,+\,\infty )\) be a Borel function with \(\inf \psi >0\) and define the functionals
over couples \((\phi ,\mu )\), where \(\phi \in L^1(\Omega )\) and \(\mu \) is a finite nonnegative Radon measure on \(\Omega \) absolutely continuous with respect to the measure \({{\mathcal {F}}}_{\varepsilon }^{\phi }\). \({\mathcal {G}}^{{{\mathcal {F}}}_\varepsilon }\) is set to be \(+\,\infty \) otherwise. In the same spirit is defined
The question we want to investigate is the following: is the \(\Gamma \)-limit of the family \(\{{\mathcal {G}}^{{{\mathcal {F}}}_\varepsilon }\}_{\varepsilon >0}\) related to the relaxation of the functional \({\mathcal {G}}^{{\mathcal {F}}}\) in the \(L^1\times w^*\) topology?
This question is reminiscent of a classical problem studied by Buttazzo and Freddi (1991) (see also Buttazzo 1989) on the \(\Gamma \)-convergence of functionals defined over pairs of measures. Given a sequence of nonnegative Radon measures \(\nu _n\) on \(\Omega \), they studied the \(\Gamma \)-limit of functionals of the form
defined over vector-valued Radon measures \(\mu \) on \(\Omega \). Here \(f{:}\,\Omega \times {\mathbb {R}}^N\rightarrow [0,+\,\infty )\) is a continuous function, convex in the second variable. In Buttazzo and Freddi (1991), it is proved that, under suitable assumptions on f, if \(\nu _n{\rightharpoonup ^*}\,\nu \), then \({\mathcal {H}}_n{\mathop {\rightarrow }\limits ^{\Gamma }}{\mathcal {H}}\) with respect to the \(w^*\) convergence, where
where \(\mu =\frac{\,\mathrm {d}\mu }{\,\mathrm {d}\nu }\nu +\mu ^{\perp }\) is the Radon–Nikodym decomposition of \(\mu \) with respect to \(\nu \), and \(f^\infty \) is the recession function of f. Our framework includes their result for scalar-valued measures, and with f independent of \(x\in \Omega \) and sub-additive in the second variable. Indeed, it is possible to reduce the study of functionals (1.4) to our setting by taking \({{\mathcal {F}}}_\varepsilon \) and \({{\mathcal {F}}}\) constants.
The novelty of this paper is in the treatment of the problem in this general setting, where the convergence \(\nu _n{\rightharpoonup ^*}\,\nu \) is replaced by the \(\Gamma \)-convergence of the underlying functionals \({{\mathcal {F}}}_\varepsilon \) to \({{\mathcal {F}}}\). Since for each \(\phi \in L^1(\Omega )\) we will ask that there exists \(\{\phi _n\}\subset L^1(\Omega )\) with \(\phi _n\rightarrow \phi \) in \(L^1(\Omega )\) such that \({{\mathcal {F}}}_n^{\phi _n}{\rightharpoonup ^*}\,{{\mathcal {F}}}^\phi \), in a sense the result in Buttazzo and Freddi (1991) can be seen as a pointwise convergence in our setting. When \({{\mathcal {F}}}\) is not continuous in \(L^1\), the interaction between the underlying functionals \({{\mathcal {F}}}_\varepsilon \) and the function \(\psi \) gives rise, for a class of non-continuous functionals \({{\mathcal {F}}}\), to an additional relaxation effect for \({\mathcal {G}}^{{\mathcal {F}}}\). Because of the technical difficulties we have to deal with, the techniques we employ to prove our results, except for the liminf inequality, are independent from the ones present in Buttazzo and Freddi (1991).
1.1 Main Results and Idea of the Proofs
In the main result of this paper, Theorem 3.8 we are able to prove that the \(\Gamma \)-limit of the functionals \({\mathcal {G}}^{{{\mathcal {F}}}_\varepsilon }\) is \(\overline{{\mathcal {G}}}\): the relaxation of the functional \({\mathcal {G}}^{{\mathcal {F}}}\) in the \(L^1\times w^*\) topology. In particular, an application of Theorem 3.8 (Proposition 5.5) is used to prove the \(\Gamma \)-convergence of \({\mathcal {G}}_\varepsilon \) to \(\overline{{\mathcal {G}}}\).
We focus on a particular class of functionals for which continuity fails. Since we are assuming lower semi-continuity for the functional \({{\mathcal {F}}}\), continuity at some \(\phi \in L^1(\Omega )\) fails when
for some \(\{\phi _n\}_{n\in {\mathbb {N}}}\subset L^1(\Omega )\) with \(\phi _n\rightarrow \phi \) in \(L^1(\Omega )\). The class of functionals we consider are those for which the above loss of upper semi-continuity holds for all \(\phi \in L^1(\Omega )\) and locally in a quantitative way. Namely, we consider the family of functionals (Definition 3.1) for which for all \(\phi \in L^1(\Omega )\) and for all \(r\ge 1\) it is possible to find a sequence \(\{\phi _n\}_{n\in {\mathbb {N}}}\subset L^1(\Omega )\) such that \(\phi _n\rightarrow \phi \) in \(L^1(\Omega )\), and
for all Borel sets \(E\subset \Omega \) with \({{\mathcal {F}}}^\phi (\partial E)=0\). This class of functions contains some interesting cases, such as the perimeter functional and the total variation functional (Sects. 5.1, 5.2, respectively). In the former case, the validity of (1.5) was proved in Caroccia et al. (2018, Theorem 2) by using a wriggling construction: given a set of finite perimeter \(F\subset \Omega \), local oscillations of the boundary of \(\phi =\mathbb {1}_F\), whose intensity is determined by the factor r, were used in order to get (1.5). For this class of functionals (Theorem 3.8), the \(\Gamma \)-limit of the family \(\{{\mathcal {G}}^{{{\mathcal {F}}}_\varepsilon }\}_{\varepsilon >0}\) is
Here \(\psi ^{cs}\) is the convex sub-additive envelope of \(\psi \) (Definition 2.1) and
Note that \(\Theta ^{cs}<+\,\infty \), since \(\psi ^{cs}\) has at most linear growth at infinity (Lemma 2.5). Moreover, \(\psi ^{cs}\le \psi ^c\). Therefore, the quantitative loss of upper semi-continuity of the functional \({{\mathcal {F}}}\) results in having a lower energy density for the limiting functional.
We report here the ideas behind the proof of Theorem 3.8. The main technical difficulty of the paper is the fact that the underlying measures \({{\mathcal {F}}}^\phi \) we consider come from the energy \({{\mathcal {F}}}\). The assumptions we require do not seem to be too restrictive.
The liminf inequality (Proposition 4.1) follows easily from classical results on lower semi-continuity of functionals defined over pairs of measures originally proved in Buttazzo and Freddi (1991).
The construction of the recovery sequence is done by using several approximations. In particular, we pass from \(\psi \) to \(\psi ^{cs}\) in two steps: first from \(\psi \) to \(\psi ^c\) and then from \(\psi ^c\) to \(\psi ^{cs}\). This is possible because \((\psi ^{c})^{cs}=\psi ^{cs}\): the convex sub-additive envelope of the convex envelope corresponds to the convex sub-additive envelope of the function itself (Lemma 2.5).
Given \(\phi \in L^1(\Omega )\) and a nonnegative Radon measure \(\mu \) on \(\Omega \), we consider its decomposition with respect to \({{\mathcal {F}}}^\phi \). We first treat the singular part and we show that it can be energetically approximated by a finite sum of Dirac deltas whose, in turn, can be approximated by regular functions (Proposition 4.2). The main technical difficulty here is in having to deal with general Radon measures \({{\mathcal {F}}}^\phi \).
We then turn to the absolutely continuous part of the measure \(\mu \). After having showed that it is possible to assume the density u to be a piecewise constant function (Proposition 4.4), we prove that it suffices to approximate the energy with density \(\psi ^c\) (Proposition 4.5).
Finally, in Proposition 4.6, given a couple \((\phi ,u)\) we construct a sequence of pairs \(\{(\phi _n,u_n)\}_{n\in {\mathbb {N}}}\) such that
The technical construction is based on a measure-theoretical result, Lemma 6.1. This result allows to disintegrate \(\Omega \) in sub-domains containing, asymptotically, a certain percentage of \({{\mathcal {F}}}^\phi (\Omega )\), and such that \({{\mathcal {F}}}^\phi \) does not charge mass on their boundaries.
We also present applications of our general results to some interesting cases: the perimeter functional, a weighted total variation functional and the classical Dirichlet energy (Sects. 5.1–5.3, respectively). In the former case, the lack of lower semi-continuity was already provided in Caroccia et al. (2018, Theorem 2). Therefore, using the general theory we developed, we can answer the question raised by the application in Continuum Mechanics (Proposition 5.5).
In the second case, the family of approximating functionals we consider is the one introduced by Slepčev and García-Trillos in the context of point clouds (Trillos and Slepčev 2016), and that are of wide interest for the community (Bresson et al. 2013; Calatroni et al. 2017; Chambolle et al. 2010; Cristoferi and Thorpe 2018; García Trillos and Slepčev 2015, 2016; Szlam and Bresson 2010; Thorpe et al. 2017; Thorpe and Slepčev 2017; Thorpe and Theil 2017; van Gennip and Schönlieb 2017; Caroccia et al. 2020). The main technical result in studying this case is a wriggling result for the weighted total variation functional (Proposition 5.8), that allows us to use Theorem 3.8 to identify the \(\Gamma \)-limit in Proposition 5.14.
This paper is organized as follows: In Sect. 3, we state the main hypotheses and results of the paper. After introducing the main notation in Sect. 2, we devote Sect. 4 to the proofs of Theorem 3.8. Finally, the above-mentioned applications are treated in Sect. 5.
2 Notation and Preliminaries
In this section, we introduce the basic notation and recall the basic facts we need in the paper.
Convex and Convex Sub-Additive Envelope We collect here some properties of the convex sub-additive envelope of a function that we used in the paper. Since in this paper we always work with nonnegative functions, in the following all the definitions and statements are adapted to this particular case.
Definition 2.1
Let \(f{:}\,[0,+\,\infty )\rightarrow (0,+\,\infty )\) be a Borel function. We define \(f^c{:}\,[0,+\,\infty )\rightarrow (0,+\,\infty )\), the convex envelope of f, and \(f^{cs}{:}\,[0,+\,\infty )\rightarrow [0,+\,\infty )\), the convex sub-additive envelope of f, as
and
respectively. Moreover, we set
The first result is the key one that allows us to construct the recovery sequence in two steps.
Lemma 2.2
Let \(f{:}\,[0,+\,\infty )\rightarrow (0,+\,\infty )\) be a Borel function. Then \((f^{c})^{cs}=f^{cs}\).
Proof
It is immediate that, if \(g\le f\) is convex and sub-additive (since it is in particular convex), we have \(g\le f^c\). Henceforth \(f^{cs}\le f^c\), yielding
On the other hand, if \(g\le f^{c}\) is convex and sub-additive function, it holds in particular \(g\le f\). Hence, from \(g\le f^{cs}\) we get
yielding the desired equality. \(\square \)
Remark 2.3
Let us note that, in general, \((f^c)^s\ne f^{cs}\). Here, with \(f^s\), we denote the sub-additive envelope of a function f. Indeed, in general
As an example, let us consider the function \(f(t):=\max \{2|t|-1,1\}\). Since f is convex, we have \(f^c=f\) and thus \((f^c)^s=f^s\). It is possible to check that \(f^s\) is not convex. Therefore, it cannot coincide with the convex function \(f^{cs}\).
The following characterization of \(f^c\) is well known [see, for instance, Braides (2002, Remark 2.17 (c))].
Lemma 2.4
Let \(f{:}\,(0,+\,\infty )\rightarrow (0,+\,\infty )\) be a Borel function. Then
for all \(t\in (0,+\,\infty )\).
A useful geometrical characterization of the convex sub-additive envelope of a convex function has been proved in Caroccia et al. (2018, Proposition A.9 and Lemma A.11).
Lemma 2.5
Let \(f{:}\,[0,+\,\infty )\rightarrow (0,+\,\infty )\) be a convex function. Then there exist \(\{a_i\}_{i\in {\mathbb {N}}}\subset {\mathbb {R}}\), \(\{b_i\}_{i\in {\mathbb {N}}}\subset [0,+\,\infty )\) such that
Moreover, there exists \(t_0\in (0,+\,\infty ]\) such that \(f^{cs}=f\) on \([0,t_0)\), while \(f^{cs}\) is linear on \([t_0,+\,\infty )\).
Combining the results of Lemmas 2.2 and 2.5, we get the following.
Lemma 2.6
Let \(f{:}\,[0,+\,\infty )\rightarrow (0,+\,\infty )\) be a Borel function. Then there exists \(t_0\in (0,+\,\infty ]\) such that
In particular, if \(t_0<+\,\infty \), then
\(\Gamma \)-convergence We refer to Dal Maso (1993) for a comprehensive treatment of \(\Gamma \)-convergence. In this paper, we just need the sequential version of it for metric spaces.
Definition 2.7
Let (Y, d) be a metric space and let \(F{:}\,Y\rightarrow [0,+\,\infty ]\). We say that a sequence of functionals \(\{F_n\}_{n\in {\mathbb {N}}}\), where \(F_n{:}\,Y\rightarrow [0,+\,\infty ]\), \(\Gamma \)-converges to F with respect to the metric d, and we write \(F_n{\mathop {\longrightarrow }\limits ^{\Gamma -\,\mathrm {d}}}F\), if
- (i)
For every \(x \in Y\) and every \(\{x_n\}_{n\in {\mathbb {N}}}\subset Y\) such that \(x_n{\mathop {\rightarrow }\limits ^{\mathrm {d}}}x\),
$$\begin{aligned} F(x) \le \liminf _{n \rightarrow +\,\infty } F_n(x_n); \end{aligned}$$ - (ii)
For every \(x \in Y\) there exists \(\{x_n\}_{n\in {\mathbb {N}}}\subset Y\) such that \(x_n{\mathop {\rightarrow }\limits ^{\mathrm {d}}}x\) and
$$\begin{aligned} \limsup _{n \rightarrow +\,\infty } F_n(x_n)\le F(x). \end{aligned}$$
In the proof of Theorem 3.8, we will make use of the following.
Remark 2.8
Let \(x\in Y\). Assume that, for each \(\delta >0\), there exists a sequence \(\{x_n\}_{n\in {\mathbb {N}}}\subset Y\) such that \(x_n \rightarrow x\) and
Then, by using a diagonal procedure, it is possible to find a sequence \(\{y_n\}_{n\in {\mathbb {N}}}\subset Y\) with \(y_n \rightarrow x\) and
Radon Measures We collect here the main properties of Radon measures we will need in the paper. For a reference, see Ambrosio et al. (2000, Section 1.4), and Maggi (2012, Section 2).
Definition 2.9
We denote by \({\mathcal {M}}^+(\Omega )\) the space of finite nonnegative Radon measures on \(\Omega \). We say that a sequence \(\{\mu _n\}_{n\in {\mathbb {N}}} \subset {\mathcal {M}}^+(\Omega )\) is weakly* converging to \(\mu \in {\mathcal {M}}^+(\Omega )\), and we write \(\mu _n {\rightharpoonup ^*}\,\mu \), if
for every \(\varphi \in {{\mathcal {C}}}_0(\Omega )\).
The following characterization of weak* convergence will be widely used in the paper.
Lemma 2.10
Let \(\{\mu _n\}_{n\in {\mathbb {N}}} \subset {\mathcal {M}}^+(\Omega )\) such that \(\sup _{n\in {\mathbb {N}}}\mu _n(\Omega )<+\,\infty \). Then, \(\mu _n {\rightharpoonup ^*}\,\mu \), for some \(\mu \in {\mathcal {M}}^+(\Omega )\), if and only if
for all bounded Borel sets \(E \subset \subset \Omega \) such that \(\mu (\partial E) = 0\).
In order to use the metric definition of \(\Gamma \)-converge, we need a metric on the space \({\mathcal {M}}^+(\Omega )\) that induces the weak* topology. This is possible because \(C_0(\Omega )\) is separable. For a proof, see De Lellis (2008, Proposition 2.6).
Lemma 2.11
There exists a distance \(\,\mathrm {d}_{{\mathcal {M}}}\) on \({\mathcal {M}}^+(\Omega )\) such that
3 Main Results
In this section, we state the main result of the paper, along with a corollary. In the following, \(\Omega \subset {\mathbb {R}}^d\) will always denote a bounded open set.
Definition 3.1
Denote by \(\mathcal {A}(\Omega )\) the family of open subsets of \(\Omega \). Let \({{\mathcal {F}}}{:}\,L^1(\Omega ) \times \mathcal {A}(\Omega )\rightarrow [0,+\,\infty ]\) be a functional and set
We say that \({{\mathcal {F}}}\) is an admissible energy if it satisfies the following conditions:
- (Ad1)
For every open set \(A\subset \Omega \), the function \(\phi \mapsto {{\mathcal {F}}}(\phi ;A)\) is lower semi-continuous on \(L^1\);
- (Ad2)
For every \(\phi \in X\), the map \({{\mathcal {F}}}^\phi :={{\mathcal {F}}}(\phi ;\cdot ){:}\,\mathcal {A}(\Omega )\rightarrow [0,+\,\infty ]\) is the restriction of a Radon measure on \(\Omega \) to \(\mathcal {A}(\Omega )\);
- (Ad3)
For every \(\phi \in X\), and every open set \(A\in \mathcal {A}(\Omega )\) with \({{\mathcal {F}}}(\phi ;A)=0\), the following holds: for every \(U\in \mathcal {A}(\Omega )\) with \(U\subset \subset A\), and for every \(\varepsilon >0\), there exists \({\overline{\phi }}\in X\) with \({\overline{\phi }}=\phi \) on \(\Omega {\setminus } U\) such that
$$\begin{aligned} \Vert {\overline{\phi }}-\phi \Vert _{L^1}\le \varepsilon ,\quad {{\mathcal {F}}}^{{\overline{\phi }}}(\partial U)=0,\quad 0<{{\mathcal {F}}}^{{\overline{\phi }}}(A)={{\mathcal {F}}}^{{\overline{\phi }}}(U)<\varepsilon ; \end{aligned}$$ - (Ad4)
\({{\mathcal {F}}}^\phi \) is purely lower semi-continuous. Namely for all \(\phi \in X\) and for all \(f\in L^1(\Omega ,{{\mathcal {F}}}^{\phi })\), with \(f \ge 1\)\({{\mathcal {F}}}^\phi \)-a.e., there exists a sequence \(\{\phi _n\}_{n\in {\mathbb {N}}}\subset X\) such that
$$\begin{aligned} \phi _n\rightarrow \phi \,\, \text { in } L^1,\quad {{\mathcal {F}}}^{\phi _n}{\rightharpoonup ^*}\,f{{\mathcal {F}}}^\phi . \end{aligned}$$
We denote the class of admissible energies by \(\mathrm {Ad}\).
From now on, we will consider our functional \({{\mathcal {F}}}\) to be defined on X.
Remark 3.2
Note that if \({{\mathcal {F}}}\in \mathrm {Ad}\), then from (Ad1) it follows that
if \(\phi =\psi \) in A, for \(A\in \mathcal {A}(\Omega )\). Hypothesis (Ad3) is a non-degeneracy hypothesis needed to treat null sets for the measure \({{\mathcal {F}}}^\phi \).
Remark 3.3
Note that if \({{\mathcal {F}}}\) satisfies Definition 3.1, it is indeed lower semi-continuous and it has the property that any element \(\phi \in X\) can be approached in \(L^1\) with a sequence \(\{\phi _n\}_{n\in {\mathbb {N}}}\), which locally increases the energy of the prescribed amount \(f\ge 1\) (which acts as a Jacobian). Indeed, the convergence \({{\mathcal {F}}}^{\phi _n}{\rightharpoonup ^*}\,f{{\mathcal {F}}}^{\phi }\) implies
for all Borel sets \(E\subset \subset \Omega \) with \({{\mathcal {F}}}^\phi (\partial E)=0\). In particular, this also justifies in (Ad4) the name purely lower semi-continuous which encodes the fact that around any point \(\phi \in X\) a liminf-type inequality for \({{\mathcal {F}}}\) is the sharpest bound that can be expected.
We now introduce the class of approximating energies.
Definition 3.4
We say that a sequence \(\{{{\mathcal {F}}}_n\}_{n\in {\mathbb {N}}}\) of functionals \({{\mathcal {F}}}_n: L^1(\Omega ) \times \mathcal {A}(\Omega )\rightarrow [0,+\,\infty ]\) is a good approximating sequence for an energy \({{\mathcal {F}}}\in \mathrm {Ad}\) if
- (GA1)
For every open sets \(A\in \mathcal {A}(\Omega )\), and every \(\{\phi _n\}_{n\in {\mathbb {N}}}\subset L^1(\Omega )\) with \(\phi _n\rightarrow \phi \) in \(L^1(\Omega )\), we have
$$\begin{aligned} {{\mathcal {F}}}(\phi ;A)\le \liminf _{n\rightarrow +\,\infty } {{\mathcal {F}}}_n(\phi _n ;A); \end{aligned}$$ - (GA2)
For all \(n\in {\mathbb {N}}\), and \(\phi \in L^1(\Omega )\) with \({{\mathcal {F}}}_n(\phi ;\Omega )<+\,\infty \), the map \({{\mathcal {F}}}_n^\phi (\cdot ):={{\mathcal {F}}}_n(\phi ;\cdot )\) is the restriction of a Radon measure on \(\Omega \) to \(\mathcal {A}(\Omega )\);
- (GA3)
For every \(\phi \in X\), there exists a sequence \(\{\phi _n\}_{n\in {\mathbb {N}}}\subset X\) with \(\phi _n\rightarrow \phi \) in \(L^1(\Omega )\), such that \({{\mathcal {F}}}_n^{\phi _n}\) is non-atomic for all \(n\in {\mathbb {N}}\), and
$$\begin{aligned} {{\mathcal {F}}}^{\phi _n}_n{\rightharpoonup ^*}\,{{\mathcal {F}}}^{\phi }, \quad {{\mathcal {F}}}^{\phi _n}_n(\Omega )\rightarrow {{\mathcal {F}}}^\phi (\Omega ). \end{aligned}$$
The class of good approximating sequences for \({{\mathcal {F}}}\) will be denoted by \(\mathrm {GA}({{\mathcal {F}}})\).
Remark 3.5
It is immediate from the definition that if \(\{{{\mathcal {F}}}_n\}_{n\in {\mathbb {N}}}\) is a good approximating sequence for \({{\mathcal {F}}}\), then \({{\mathcal {F}}}_n{\mathop {\rightarrow }\limits ^{\Gamma }}{{\mathcal {F}}}\) with respect to the \(L^1\) topology. Hypothesis (GA3) is asking for the existence of a recovery sequence satisfying the additional requirement of recovering the energy also locally.
From (GA1), we deduce the following closeness property: if \(\{\phi _n\}_{n\in {\mathbb {N}}}\subset L^1(\Omega )\) with \(\phi _n\rightarrow \phi \) in \(L^1(\Omega )\) is such that
then \(\phi \in X\).
Remark 3.6
Notice that if \({{\mathcal {F}}}\in \mathrm {Ad}\) is non-atomic, i.e., \({{\mathcal {F}}}^{\phi }\) is a non-atomic Radon measure for all \(\phi \in X\), then the constant sequence \({{\mathcal {F}}}_n:={{\mathcal {F}}}\) is a good approximating sequence for \({{\mathcal {F}}}\).
We are now in the position to define the main objects of our study.
Definition 3.7
Let \(\psi {:}\,[0,+\,\infty )\rightarrow (0,+\,\infty )\) be a Borel function with \(\inf \psi >0\). For \({{\mathcal {F}}}{:}\,X\times {{\mathcal {A}}}(\Omega )\rightarrow [0,+\,\infty ]\), satisfying property (Ad2) of Definition 3.1, we define the \({{\mathcal {F}}}\)-relative energy \({\mathcal {G}}^{{{\mathcal {F}}}}{:}\,X \times {\mathcal {M}}^+(\Omega )\rightarrow [0,+\,\infty ]\) as
The main result of this paper concerns the behavior of sequences of \({{\mathcal {F}}}_{n}\)-relative energies for a good approximating sequence \(\{{{\mathcal {F}}}_n\}_n\in \mathrm {GA}({{\mathcal {F}}})\) of an admissible energy \({{\mathcal {F}}}\). The interaction between the underlying functional \({{\mathcal {F}}}\) and the functional \(\mathcal {G}^{{\mathcal {F}}}\) results in a lower limiting energy density, since \(\psi ^{cs}\le \psi ^c\).
Theorem 3.8
\((\Gamma \)-convergence for \({{\mathcal {F}}}\in \mathrm {Ad})\) Let \({{\mathcal {F}}}\in \mathrm {Ad}\), and \(\{{\mathcal {F}}_n\}_{n\in {\mathbb {N}}}\in \mathrm {GA}({{\mathcal {F}}})\). Then \({\mathcal {G}}^{{{\mathcal {F}}}_n}\)\(\Gamma \)-converges to \({\mathcal {G}}^{{\mathcal {F}}}_{\mathrm {lsc}}\) with respect to the \(L^1\times w^*\) topology, where the functional
is defined as
Here \(\mu =\frac{\,\mathrm {d}\mu }{\,\mathrm {d}{{\mathcal {F}}}^{\phi }}{{\mathcal {F}}}^{\phi }+\mu ^{\perp }\) is the Radon–Nikodym decomposition of \(\mu \) with respect to \({{\mathcal {F}}}^\phi \).
Remark 3.9
Note that \(\Theta ^{cs}<+\,\infty \), since \(\psi ^{cs}\) is at most linear at infinity (Lemma 2.6).
In particular, combining the above theorem with Remark 3.6, allows to identify, for certain energies in \(\mathrm {Ad}\), the relaxation of the \({{\mathcal {F}}}\)-relative energy \(\mathcal {G}^{{{\mathcal {F}}}}\) in the \(L^1\times w^*\) topology.
Corollary 3.10
Let \({{\mathcal {F}}}\in \mathrm {Ad}\) be non-atomic. Then, the relaxation of \({\mathcal {G}}^{{\mathcal {F}}}\) with respect to the \(L^1\times w^*\) topology is \({\mathcal {G}}^{{\mathcal {F}}}_{\mathrm {lsc}}\).
Remark 3.11
From the properties of \(\psi ^c\) and \(\psi ^{cs}\) and using Remark 3.5, it is possible to deduce the following compactness property. Assume that a good approximating sequence \(\{{{\mathcal {F}}}_n\}_{n\in {\mathbb {N}}}\) enjoys this compactness property: if \(\{\phi _n\}_{n\in {\mathbb {N}}}\subset L^1(\Omega )\) is such that
then \(\phi _n\rightarrow \phi \) in \(L^1(\Omega )\) for some \(\phi \in X\). Then, for every \(\{\phi _n\}_{n\in {\mathbb {N}}}\subset L^1(\Omega )\) and \(\{\mu _n\}_{n\in {\mathbb {N}}}\subset {\mathcal {M}}^+(\Omega )\) such that
it is possible to extract a subsequence (not relabeled) in such a way that \(\phi _n\rightarrow \phi \) in \(L^1\) and \(\mu _n{\rightharpoonup ^*}\,\mu \), for some \(\phi \in X\) and \(\mu \in {\mathcal {M}}^+(\Omega )\).
4 Proof of Main Theorems
Hereafter, \(\psi {:}\,[0,+\,\infty )\rightarrow (0,+\,\infty )\) will be a Borel function with \(\inf \psi >0\). We will denote by \(\,\mathrm {d}\) a metric on the space \(L^1(\Omega )\times {\mathcal {M}}^+(\Omega )\), which induces the \(L^1\times w^*\) topology on bounded sets (Lemma 2.11).
4.1 Liminf Inequality
The proof of the liminf inequality for the \(\Gamma \)-convergence result of Theorem 3.8 follows from the argument in Proposition (Ambrosio et al. 2000, Lemma 2.34). For the reader’s convenience, we report it here.
Proposition 4.1
Let \((\phi ,\mu )\in L^1(\Omega )\times {\mathcal {M}}^+(\Omega )\), and \(\{(\phi _n,\mu _n)\}_{n\in {\mathbb {N}}}\subset L^1(\Omega )\times {\mathcal {M}}^+(\Omega )\) be such that \((\phi _n,\mu _n)\rightarrow (\phi ,\mu )\). Fix \({{\mathcal {F}}}\in \mathrm {Ad}\) and consider a good approximating sequence \(\{{{\mathcal {F}}}_n\}_{n\in {\mathbb {N}}}\) for \({{\mathcal {F}}}\). Then
Proof
Assume, without loss of generality, that
Therefore, \(\mu _n=g_n {{\mathcal {F}}}_n^{\phi _n}\) for all \(n\in {\mathbb {N}}\). Since \(\inf \psi >0\), using Remark 3.5 we have that \(\phi \in X\). Note that \(\psi \ge \psi ^{cs}\), and that, by Lemma 2.5 there exist two sequences \(\{a_i\}_{i\in {\mathbb {N}}}\subset {\mathbb {R}}\), \(\{b_i\}_{i\in {\mathbb {N}}}\subset [0,+\,\infty )\), such that
Let \(\{A_j\}_{j=1}^M\) be a family of pairwise disjoint of open subset of \(\Omega \) and, for each \(j\in {\mathbb {N}}\), let \(v_j\in C^{\infty }_c(A_j)\), with \(v_j\in [0,1]\). We have that
By summing over \(j=1,\ldots ,M\), taking the limit as \(n\rightarrow +\,\infty \), exploiting the lower semi-continuity of \({{\mathcal {F}}}\), and using the fact that \(b_j>0\) together with \(\mu _n{\rightharpoonup ^*}\,\mu \), we get
Taking the supremum in (4.3) among all finite families \(\{A_j\}_{j\in J}\) of pairwise disjoint subsets of \(\Omega \), and \(v_j\in C_c^{\infty }(A_j)\) with \(v_j\in [0,1]\), we get
Here \(\psi ^+_j(x):=\max \{\psi _j(x),0\}\),
being N a set where \(\mu ^{\perp }\) is concentrated and \(\lambda ={{\mathcal {F}}}^{\phi }+\mu ^{\perp }\). Using Ambrosio et al. (2000, Lemma 2.35), we can infer
Hence, using (4.2), we get
This concludes the proof. \(\square \)
4.2 Limsup Inequality
The proof of the limsup inequality uses several approximations that we prove separately. We start by proving a density result that will allow us to construct the recovery sequence only for absolutely continuous couples, namely for pairs \((\phi , h{{\mathcal {F}}}^\phi )\) with \(h\in L^1(\Omega ;{{\mathcal {F}}}^\phi )\) (Fig. 1).
Proposition 4.2
Let \({{\mathcal {F}}}\in \mathrm {Ad}\), \(\zeta {:}\,[0,+\,\infty )\rightarrow (0,+\,\infty )\) a convex function such that
Then for any \((\phi ,\mu )\in X\times {\mathcal {M}}^+(\Omega )\), there exist \(\{\varphi _n\}_{n\in {\mathbb {N}}}\subset X\) and \(\{h_n \}_{n\in {\mathbb {N}}}\) with \(h_n\in L^1(\Omega ;{{\mathcal {F}}}^{\varphi _n})\) such that
and
Proof
Let \(n\in {\mathbb {N}}\) and consider a grid of open cubes \(\{Q_j^n\}_{j\in {\mathbb {N}}}\) of edge length 1/n. Without loss of generality, we can assume \({{\mathcal {F}}}^\phi (\partial Q_j^n\cap \Omega )=0\) for every \(j\in {\mathbb {N}}\). Write \(\mu =g{{\mathcal {F}}}^{\phi }+\mu ^{\perp }\), where \(g:=\frac{\,\mathrm {d}\mu }{\,\mathrm {d}{{\mathcal {F}}}^\phi }\). We divide the proof in four steps.
Step 1 We claim that there exists a sequence \(\{\lambda _n\}_{n\in {\mathbb {N}}}\subset {\mathcal {M}}^+ (\Omega )\) of the form
with \(x_j^n\in Q_j^n\cap {{\,\mathrm{spt}\,}}\mu ^{\perp }\), for all \(j=1,\ldots ,M_n\) such that
Define
For every \(j\in {\mathcal {J}}^n_{\mu ^{\perp }}\), choose \(x_j^n \in {{\,\mathrm{spt}\,}}\mu ^{\perp }\cap Q_j^n\) with
and define
Note that
Let \(E\subset \subset \Omega \) be a bounded Borel set with \(\mu ^{\perp }(\partial E)=0\). Set
Fix \(\eta >0\) and let \(U\supset \partial E\) be an open set such that \(\mu ^{\perp }(U)<\eta \). Take \(n_0\in {\mathbb {N}}\) large enough so that \(j\in {\mathcal {J}}^n_{\mu ^{\perp },\partial E}\) implies \(Q_j^n\subset \subset U\) for all \(n>n_0\). Note that
Therefore,
Since \(\eta >0\) is arbitrary, from (4.7) and (4.8) we get
This proves the claim.
Step 2 Let \(\{\lambda _n\}_{n\in {\mathbb {N}}}\subset {\mathcal {M}}^+(\Omega )\) be the sequence provided by Step 1. Then
for \(x^n_1,\ldots ,x^n_{M_n}\in {{\,\mathrm{spt}\,}}\mu ^{\perp }\). Note that, for every \(n\in {\mathbb {N}}\), the cubes \(\{Q^n_j\}_{j=1}^{M_n}\) are pairwise disjoint. The idea is to locally deform the function \(\phi \) around each point \(x_j^n\) and define a corresponding density \(h_j^n\) in a neighborhood of \(x_j^n\). Let
Fix \(n\in {\mathbb {N}}\). We show how to recursively define \(h^n_{j}\) and \(\phi ^n_{j}\). Set \(\phi ^n_0:=\phi \), and \(h^n_0:=g\). Assume \(\phi ^n_{j-1}\) and \(h^n_{j-1}\) are given and define \(\phi ^n_j\), and \(h^n_j\) as follows.
Case one\(j\in {\mathcal {I}}_a^n\). In this case, for any \(r>0\) we have \({{\mathcal {F}}}^{\phi }(B_r(x^n_j))>0\). Moreover using Ambrosio et al. (2000, Theorem 2.22), we get
In particular, we can find \(r_n\ll 1\) such that \(B_{r_n}(x^n_j)\subset Q_j^n\) and
for all \(j\in {\mathcal {I}}_a^n\). Then we define \(\phi ^n_j:=\phi ^n_{j-1}\), and
Case two\(x_j\in {\mathcal {I}}_b^n\). Therefore, there exists \(r_0>0\) such that for all \(r_0>r>0\) we have
Fix \(r_n<<1\) such that \(B_{2r_n}(x_j^n)\subset Q_j^n\), and invoke property (Ad3) of Definition 3.1 with \(A=B_{2r_n}(x_j^n)\), \(U=B_{r_n}(x_j^n)\), \(\varepsilon _n:= (M_n n)^{-1} \min _{j=1,\ldots ,M_n}\{\mu ^{\perp }(Q_j^n)\} \) to find \( \phi _j^n\in X\) such that \(\phi _j^n=\phi ^n_{j-1}\) on \(\Omega {\setminus } B_{r_n}(x_j)\), \({{\mathcal {F}}}^{\phi _j^n}(\partial B_{r_n}(x_j))=0\) and
for all \(j\in {\mathcal {I}}_b^n\). Define
Set \(\varphi _n:=\phi ^n_{M_n}\) and \(h_n:=h^n_{M_n}\). Note that \(\varphi _n=\phi \) that \(h_n=g\) outside \(\bigcup _{j=1}^{M_n} B_{r_n}(x_j^n)\), that
and that, by construction, \(\varphi _n\in X\). Moreover, \({{\mathcal {F}}}^{\varphi _n}(\partial B_{r_n}(x_j^n))=0\) and
Step 3 We claim that
Indeed, recalling Remark 3.2, we get
Fix \(\delta _0>0\). Using (4.11), it is possible to take n large enough so that
for all \(j=1,\ldots ,M_n\). In particular,
The arbitrariness of \(\delta _0>0\), together with (4.6), yields
Now, set
and note that from (4.9) and (4.10) we get that
as \(n\rightarrow +\,\infty \). Since \(g\in L^1(\Omega ;{{\mathcal {F}}}^{\phi })\), using (4.4), we get \(\zeta (g)\in L^1(\Omega ;{{\mathcal {F}}}^{\phi })\). Therefore, the Lebesgue-dominated convergence theorem yields
Using (4.12), (4.13) and (4.15), we get the claim.
Step 4 To complete the proof, it remains to show that \(h_n {{\mathcal {F}}}^{\varphi _n}{\rightharpoonup ^*}\,\mu \). Note that
Let \(E\subset \subset \Omega \) be a bounded Borel set such that \(\mu (\partial E)=0\). Fix \(\eta >0\) and take an open set \(U\subset \Omega \) with \(U\supset \partial E\) such that \(\mu (U)<\eta \). Set
and take \(n_0\in {\mathbb {N}}\) large enough so that \(j\in {\mathcal {J}}^n_{\partial E}\) implies \( Q_j^n\subset \subset U\) for all \(n>n_0\). Then
Recalling (4.5), we get
Therefore, using (4.14) and the arbitrariness of \(\eta >0\), we get
The claim follows at once by (4.5), (4.16) and the triangle inequality. \(\square \)
The next result will allow us to consider only a special class of absolutely continuous couples. Let us introduce the following notation for partition of \(\Omega \) into cubes. Let \(Q:=(-\frac{1}{2},\frac{1}{2})^d\). For \(p\in {\mathbb {R}}^d\) and \(\ell >0\), we define
and we write \(\partial G_{p,\ell } \) for
Definition 4.3
We say that \((\phi ,\mu )\in X\times {{\mathcal {M}}}^+(\Omega )\) is a regular absolutely continuous couple if \(\mu =g{{\mathcal {F}}}^{\phi }\) where \(g\in L^1(\Omega ,{{\mathcal {F}}}^{\phi })\) is of the form
where \(\alpha _1,\dots ,\alpha _M\in (0,+\,\infty )\), and \(\{\Omega _i\}_{i=1}^M=G_{p,\ell } \) for some \(p\in {\mathbb {R}}^d\) and \(\ell >0\), is such that
We denote by \( R(\Omega )\) the class of all regular absolutely continuous couples.
Proposition 4.4
Let \({{\mathcal {F}}}\in \mathrm {Ad}\), \(\zeta {:}\,[0,+\,\infty )\rightarrow (0,+\,\infty )\) be a convex function, and \((\phi ,g {{\mathcal {F}}}^{\phi })\in X\times {\mathcal {M}}^+(\Omega )\), with \(g\in L^1(\Omega ,{{\mathcal {F}}}^{\phi })\). Then there exists \(\{g_n\}_{n\in {\mathbb {N}}}\subset L^1(\Omega ,{{\mathcal {F}}}^{\phi })\) with \(\{ (\phi , g_n{{\mathcal {F}}}^{\phi })\}_{n\in {\mathbb {N}}} \subset R(\Omega )\), such that
and
Proof
For \(n\in {\mathbb {N}}\) let \(p_n\in {\mathbb {R}}^d\) be such that
Let \(\{Q_j^n\}_{j=1}^{M_n}\) be the cubes such that \(G_{p_n,1/n}=\{Q_j^n\cap \Omega \}_{j=1}^{M_n}\) and set
For \(j\in {\mathcal {J}}^n_{{{\mathcal {F}}}^{\phi }}\) set
and for \(j\notin {\mathcal {J}}^n_{{{\mathcal {F}}}^{\phi }}\) set
Define
We claim that \(g_n{{\mathcal {F}}}^{\phi }{\rightharpoonup ^*}\,g{{\mathcal {F}}}^{\phi }\). Note that
Let \(E\subset \subset \Omega \) be a bounded Borel set with \(g{{\mathcal {F}}}^{\phi }(\partial E)=0\). Fix \(\eta >0\), and let \(U\supset \partial E\) be an open set with \(g{{\mathcal {F}}}^{\phi }(U)\le \eta \). Let
and take \(n\in {\mathbb {N}}\) large enough so that \(j\in {\mathcal {J}}^n_{\partial E}\) implies \(Q_j^n\subset U\) for all \(n\ge n_0\). Then
Therefore,
Since \(\eta >0\) is arbitrary, we get the claim. To conclude the proof, we have to show that
Using the convexity of f, we have
Therefore,
On the other hand, using \(g_n{{\mathcal {F}}}^{\phi }{\rightharpoonup ^*}\,g{{\mathcal {F}}}^{\phi }\), the convexity of f, and Ambrosio et al. (2000, Theorem 2.34), we get
Using (4.18) and (4.19) we conclude. \(\square \)
Proposition 4.5
Let \({{\mathcal {F}}}\in \mathrm {Ad}\), and \((\phi ,g {{\mathcal {F}}}^{\phi })\in R(\Omega )\). Then there exists \(\{(\varphi _n, h_n {{\mathcal {F}}}^{\varphi _n})\}_{n\in {\mathbb {N}}}\subset R(\Omega )\) such that
and
Moreover, if we write \(h_n=\sum _{i=1}^M \kappa _i^n \mathbb {1}_{\Omega ^n_i}\), we can ensure that \(\kappa ^n_i\le t_0\) for all \(i=1,\ldots , M_n\), and \(n\in {\mathbb {N}}\), where \(t_0>0\) is given by Lemma 2.6.
Proof
If \(t_0=+\,\infty \), then there is nothing to prove, since this would mean that \(\psi ^{cs}=\psi ^c\). Thus, assume \(t_0\in (0,+\,\infty )\). Write \(g=\sum _{i=1}^M \alpha _i \mathbb {1}_{\Omega _i}\), where \(\alpha _i>0\), and let
Define the function
where
Let \(\{\phi _n\}_{n\in {\mathbb {N}}}\subset X\) be the sequence given by Definition 3.1 such that \(\phi _n\rightarrow \phi \) in X, and
In particular, for all \(i=1,\dots ,M\), it holds \({{\mathcal {F}}}^{\phi _n}(\partial \Omega _i)\rightarrow 0\). It is then possible, for all n sufficiently large, to choose \(\delta _n>0\) such that
for all \(i=1,\dots ,M\). Here \((\partial \Omega _i)_{\delta _n}:=\{ x\in {\mathbb {R}}^d \,\,|\,\, \mathrm {dist}(x,\partial \Omega _i)<\delta _n \}\). By definition of regular absolutely continuous couple, we have that \(\{\Omega _i\}_{i=1}^M = G_{p,\ell } \) for some \(p\in {\mathbb {R}}^d\), \(\ell >0\). Since \({{\mathcal {F}}}^{\phi _n}\) is a Radon measure, it is possible to slightly translate the underline grid of cubes of a small vector so that \(G_{p+v,\ell }\) do not charge energy \({{\mathcal {F}}}^{\phi _n}\) on \(\partial G_{p+v,\ell }(\Omega )\). More precisely, we can find a sequence \(\{v_n\}_{n\in {\mathbb {N}}}\subset {\mathbb {R}}^d\) with \(|v_n|<\delta _n\), such that
and
for all \(i=1,\dots ,M\) and \(n\in {\mathbb {N}}\). Define, for \(n\in {\mathbb {N}}\),
We claim that \(h_n{{\mathcal {F}}}^{\phi _n}{\rightharpoonup ^*}\,g{{\mathcal {F}}}^{\phi }\). Indeed,
and, for any bounded Borel set \(E\subset \subset \Omega \) with \({{\mathcal {F}}}^{\phi }(\partial E)=0\), we have that
where \(C:=\max \{t_0,\alpha _1,\dots ,\alpha _M\}\), and in the last step we used (4.22). We now observe that \({{\mathcal {F}}}^{\phi }(\partial (\Omega _i \cap E))=0\). Since \(f\ge 1\), this also implies \(f{{\mathcal {F}}}^{\phi }(\partial (\Omega _i \cap E))=0\). Using (4.21), we get
Therefore, from (4.23)–(4.25) we deduce that
To conclude the proof, (4.21) together with (4.22) yields
where in the third equality above we used Lemma 2.6. \(\square \)
Proposition 4.6
Let \({{\mathcal {F}}}\in \mathrm {Ad}\), and \(\{{{\mathcal {F}}}_n\}_{n\in {\mathbb {N}}}\in \mathrm {GA}({{\mathcal {F}}})\). Then, for every \((\phi ,g {{\mathcal {F}}}^{\phi })\in R(\Omega )\) there exists a sequence \(\{(\varphi _n,h_n {{\mathcal {F}}}_n^{\varphi _n})\}_{n\in {\mathbb {N}}}\subset X\times {\mathcal {M}}^+(\Omega )\) such that
and
Proof
Write \(g=\sum _{i=1}^M \alpha _i \mathbb {1}_{\Omega _i}\), where \(\alpha _i>0\). By exploiting property (GA3) of Definition 3.4, it is possible to find \(\{\varphi _n\}_{n\in {\mathbb {N}}}\subset X\) such that \({{\mathcal {F}}}_n^{\varphi _n}\) is non-atomic for each \(n\in {\mathbb {N}}\), \(\varphi _n\rightarrow \phi \) in \(L^1(\Omega )\), \({{\mathcal {F}}}_n^{\varphi _n}{\rightharpoonup ^*}\,{{\mathcal {F}}}^{\phi }\), and \({{\mathcal {F}}}_n^{\varphi _n}(\Omega )\rightarrow {{\mathcal {F}}}^{\phi }(\Omega )\). Using Lemma 2.4, for all \(i=1,\dots ,M\), and \(n\in {\mathbb {N}}\), it is possible to find \(\lambda ^i_n\in [0,1]\), and \(s^i_n,t^i_n\in [0,+\,\infty )\) with
such that
and
where \(\delta _n\rightarrow 0\) as \(n\rightarrow +\,\infty \). Up to a subsequence, not relabeled, we can assume \(\lambda ^i_n\rightarrow \lambda ^i\in [0,1]\), as \(n\rightarrow +\,\infty \).
By invoking Lemma 6.1, for all \(i=1,\ldots ,M\), there exists a sequence of Borel sets \(\{R^i_m\}_{m\in {\mathbb {N}}}\) with \(R^i_m\subset \Omega _i\) having the following properties:
- (a)
 as \(m\rightarrow +\,\infty \);
as \(m\rightarrow +\,\infty \); - (b)
 as \(m\rightarrow +\,\infty \);
as \(m\rightarrow +\,\infty \); - (c)
\({{\mathcal {F}}}_n^{\varphi _n}(\partial R^i_m)={{\mathcal {F}}}^\phi (\partial R^i_m)=0\) for all \(n\in {\mathbb {N}}\), \(m\in {\mathbb {N}}\), \(i=1,\ldots ,M\).
Using the fact that \({{\mathcal {F}}}^{\phi _n}_n{\rightharpoonup ^*}\,{{\mathcal {F}}}^\phi \) and that \({{\mathcal {F}}}^\phi (\partial \Omega _i)=0\) for all \(i=1,\dots ,M\), it is possible to select a subsequence \(\{m_n\}_{n\in {\mathbb {N}}}\) with \(m_n\rightarrow +\,\infty \) as \(n\rightarrow +\,\infty \) such that

and
as \(n\rightarrow +\,\infty \) for all \(i=1,\dots ,M\). Define
We claim that
Let \(E\subset \subset \Omega \) be a bounded Borel set with \(g{{\mathcal {F}}}^\phi (\partial E)=0\). Then, using (4.26) and property c, we get
Thanks to (4.28), (4.29) and the fact that \(\lambda ^i_n\rightarrow \lambda ^i\), we conclude that
Since
we obtain (4.31). Finally, we note that
Thus, taking the limit as \(n\rightarrow +\,\infty \) and using (4.28), (4.29) together with the fact that \(\lambda ^i_n\rightarrow \lambda ^i\), we get
This concludes the proof. \(\square \)
4.3 Proof of Theorem 3.8
The liminf inequality follows from Proposition 4.1. Let \((\phi ,\mu )\in X\times {\mathcal {M}}^+(\Omega )\), and write \(\mu =g{{\mathcal {F}}}^{\phi }+\mu ^{\perp }\). Fix \(\delta >0\). By Proposition 4.2, there exist \(\varphi _1 \in X\) and \(h_1\in L^1(\Omega ;{{\mathcal {F}}}^{\varphi _1})\) such that
Proposition 4.4 yields the existence of \(h_2\in L^1(\Omega ,{{\mathcal {F}}}^{\varphi _1})\) such that \((\varphi _1,h_2{{\mathcal {F}}}^{\varphi _1})\in R(\Omega )\) and
Thanks to Proposition 4.5, we can find \(\varphi _2\in X\), and \(h_3\in L^1(\Omega ,{{\mathcal {F}}}^{\varphi _2})\) such that \((\varphi _2,h_3{{\mathcal {F}}}^{\varphi _2})\in R(\Omega )\) and
Finally, let \((\varphi _{n_{\delta }},h_{n_{\delta }}{{\mathcal {F}}}_{n_{\delta }}^{\varphi _{n_{\delta }}})\in X\times {\mathcal {M}}^+(\Omega )\) be given by Proposition 4.6 such that
and
Therefore, from (4.34)–(4.38) we get
and
We conclude by using Remark 2.8. \(\square \)
5 Selected Applications
In this section, we assume the open set \(\Omega \subset {\mathbb {R}}^d\) to have Lipschitz boundary.
5.1 Perimeter Functional
As a first application of the general theory developed in the previous sections, we consider the perimeter functional. In the following, we will identify the space \(X:=BV(\Omega ;\{0,1\})\) with the space of sets with finite perimeter in \(\Omega \). We define the functional \({{\mathcal {F}}}{:}\,X\times {\mathcal {A}}(\Omega ) \rightarrow [0,+\,\infty )\) as
where \({\mathcal {P}}(\{\phi =1\};A)\) denotes the perimeter of the set \(\{\phi =1\}\) in A. The following result has been proved in Caroccia et al. (2018) (Caroccia et al. 2018, Theorem 2).
Theorem 5.1
Let \(E\subset {\mathbb {R}}^d\) be a set of finite perimeter, and \(f\in L^1(\partial ^* E;[1,+\,\infty ))\). Then there exists a sequence of smooth bounded sets \(\{E_n\}_{n\in {\mathbb {N}}}\subset {\mathbb {R}}^d\) with \(\mathbb {1}_{E_n}\rightarrow \mathbb {1}_{E}\) in \(L^1\), such that
for all Borel sets \(F\subset \subset {\mathbb {R}}^d\) with \({\mathcal {P}}(E;\partial F)=0\).
Using the above result, it is possible to obtain the following.
Proposition 5.2
The functional \({{\mathcal {F}}}\) is a purely lower semi-continuous admissible energy.
Proof
In order to show that the functional \({{\mathcal {F}}}\) is an admissible energy, we just need to prove property (Ad3), since the others are trivially satisfied. Let \(E\subset \Omega \) be a set of finite perimeter such that \(|D\mathbb {1}_E|(A)=0\) for some open set \(A\subset \Omega \). Then, \(\mathbb {1}_E\) is constant on A. Assume \(\phi :=\mathbb {1}_E=0\) on A. The other case can be treated similarly. Let \(U\subset \subset A\) be an open subset, and \(\varepsilon >0\). Pick \(B_R(x)\subset \subset U\) and for \(r\in (0,R)\) set \({\overline{\phi }}:= \mathbb {1}_E+\mathbb {1}_{B_r(x)}\). Then \({{\mathcal {F}}}({\overline{\phi }};\partial U)=0\), \(\Vert {\overline{\phi }}-\phi \Vert _{L^1}\le \omega _d r^d\), and
Taking
we get the desired result.
Finally, the fact that the energy \({{\mathcal {F}}}\) is purely lower semi-continuous follows by Theorem 5.1 localized in \(\Omega \). Indeed, the wriggling procedure used in the proof of Theorem 5.1 is a local construction. \(\square \)
5.1.1 The Modica–Mortola Approximation of the Perimeter
We now consider, for \(\varepsilon >0\), the Modica–Mortola functional \({{\mathcal {F}}}_\varepsilon {:}\,L^1(\Omega )\times \mathcal {A}(\Omega )\rightarrow [0,+\,\infty ]\) defined as
where \(W\in C^0({\mathbb {R}})\) is nonnegative potential with at least linear growth at infinity, and such that \(\{W=0\}=\{0,1\}\). We report here the classical result by Modica (Modica 1987; Modica and Mortola 1977).
Theorem 5.3
We have that \({{\mathcal {F}}}_\varepsilon {\mathop {\rightarrow }\limits ^{\Gamma -L^1}} \sigma _W{{\mathcal {F}}}\), where
Moreover, if \(\{\phi _n\}_{n\in {\mathbb {N}}}\subset L^1(\Omega )\) is such that
for some \(\varepsilon _n\rightarrow 0\), then, up to a subsequence (not relabeled), \(\phi _n\rightarrow \phi \) in \(L^1\), where \(\phi \in BV(\Omega ;\{0,1\})\)
A careful analysis of the proof of the above results yields the following.
Proposition 5.4
Let \(\{\varepsilon _n\}_{n\in {\mathbb {N}}}\) be such that \(\varepsilon _n\rightarrow 0\), and set \({{\mathcal {F}}}_n:={{\mathcal {F}}}_{\varepsilon _n}\) for \(n\in {\mathbb {N}}\). Then, the sequence \(\{{{\mathcal {F}}}_n\}_{n\in {\mathbb {N}}}\) is a good approximating sequence for \({{\mathcal {F}}}\).
Proof
We just have to prove property (GA3), being the others trivially satisfied. The statement of Theorem 5.3 holds for every open set \(U\subset \Omega \) with Lipschitz boundary, and such that \(|D\phi | (\partial U) =0\). Therefore, by using Lemma 6.2, we get (GA3). \(\square \)
Proposition 5.4 allows us to use the abstract results proved in the previous section. In particular, we obtain the following.
Proposition 5.5
Let \(\psi {:}\,[0,+\,\infty )\rightarrow (0,+\,\infty )\) be a Borel function with \(\inf \psi >0\). For \(\varepsilon >0\), consider the \({{\mathcal {F}}}_{\varepsilon }\)-relative energy
if \(\phi \in H^1(\Omega )\), \(\mu \in {\mathcal {M}}^+(\Omega )\) such that \(\mu = u ( \frac{1}{\varepsilon }W(\phi ) + \varepsilon |\nabla \phi |^2 ){{\mathcal {L}}}^d\), and \(+\,\infty \) otherwise in \(L^1(\Omega )\times {\mathcal {M}}^+(\Omega )\). Then, \({\mathcal {G}}_\varepsilon {\mathop {\rightarrow }\limits ^{\Gamma }}{\mathcal {G}}\) with respect to the \(L^1 \times w^*\) topology, where
is defined on any \(E\subset \Omega \) set of finite perimeter and for the Radon–Nikodym decomposition of  with respect to
with respect to  .
.
Remark 5.6
The functional \({\mathcal {G}}_\varepsilon \) has been used in Rätz and Voigt (2006) as a phase field diffuse approximation for a model describing the evolution of interfaces in the epitaxial growth with adatoms. The authors worked with the special case \(\psi (t):=1+\frac{t^2}{2}\). In the same paper, it has been claimed that the solutions of the gradient flow of the phase field model converge to the solution of the sharp interface one. This claim was supported by formal matching asymptotics. It is worth noticing that the evolution equations for the sharp model do not account for the recession part and neither for the convex sub-additive envelope of \(\psi \).
Proposition 5.5 answers the question posed in the introduction.
5.2 Total Variation Functional
In this section, we generalize the result of Sect. 5.1 by considering the total variation functional defined over the whole class of functions of bounded variation. Let \(\rho \in C^1(\Omega )\cap C^0({\overline{\Omega }})\) such that
and consider the energy \({{\mathcal {F}}}{:}\,BV(\Omega )\times \mathcal {A}(\Omega )\rightarrow [0,+\,\infty )\):
Proposition 5.7
\({{\mathcal {F}}}\in \mathrm {Ad}\).
We start by proving that the total variation is a purely lower semi-continuous functional.
Proposition 5.8
(A wriggling result for total variation) Let \(\phi \in BV(\Omega )\) and \(f\in L^1(\Omega ,|D\phi |)\) with \(f\ge 1\). Then there exists a sequence \(\{\phi _k\}_{k\in {\mathbb {N}}} \subset BV(\Omega )\) such that
for all Borel sets \(E\subset \subset \Omega \) with \(|D\phi |(\partial E)=0\).
The main technical step needed to get the above proposition is given by the following result.
Lemma 5.9
Fix \(p\ge 1\) and let \(Q_L\subset {\mathbb {R}}^d\) be a cube centered at the origin of edge length \(L>0\). Let \(\phi \in C^{\infty }(Q_L)\cap C^0({\overline{Q}}_L)\) and let \(r>1\). Then, there exists a sequence of piecewise \(C^1\) maps \(S_n{:}\,Q_L\rightarrow Q_L\) such that
and
- (1)
\(\lim _{n\rightarrow +\,\infty } \int _{Q_L} |\nabla (\phi \circ S_n)|^p \,\mathrm {d}x=r \int _{Q_L} |\nabla \phi |^p \,\mathrm {d}x\);
- (2)
\(\sup _{n\in {\mathbb {N}}} \Vert \nabla S_n\Vert _{L^\infty }<+\,\infty .\)
Proof
We divide the proof in several steps.
Step one\(\phi \)affine Write \(\phi (y)=y\cdot \nu +\phi _0\). First of all we note that it suffices to show that, given \(\beta >1\) and a cube \(Q'\subset Q_L\) with two of its faces orthogonal to \(\nu \), there exists a sequence of maps \(T_n: Q'\rightarrow Q'\) such that \(T_n=\mathrm{Id}\,\) on \(\partial Q'\), \(T_n\rightarrow \mathrm{Id}\,\) uniformly on \(\overline{Q'}\) and
Indeed, by simply extending the map \(T_n\) to the whole cube as the identity outside \(Q'\) we get
Since the map
is surjective on \([1,+\,\infty )\), given \(r>1\) it is possible to find \(\beta >1\) such that
Thus, using (5.1) we conclude.
Therefore, we can assume without loss of generality that \(\nu =\rho \mathrm {e}_d\), \(L=1, Q_L=Q\). For \(b>0\), let \(s_b{:}\,{\mathbb {R}}\rightarrow {\mathbb {R}}\) be the periodic extension of the function
for \(t\in [-\,1,1]\). For \(n\in {\mathbb {N}}\), define the function \(g_n{:}\,[-\,1,1]\rightarrow [0,+\,\infty )\) as
Moreover, let \(Q_n\subset Q\) be a cube of side length \(1-\frac{1}{n}\), and fix a smooth cutoff function \(\varphi _n{:}\,{\mathbb {R}}\rightarrow [0,1]\) with \(\varphi _n(t)=1\) for \(|t|\le 1-\frac{1}{n}\) and \(\varphi _n(t)=0\) for \(|t|\ge 1\), and such that
for some constant \(C>0\) independent of n. Define the function \(T_n{:}\,Q\rightarrow Q\) as
where \({\mathbb {P}}(x):=x-(x\cdot \mathrm {e}_d)\mathrm {e}_d\). We have
and
Note that \(T_n(Q)=Q\), \(T_n=\mathrm{Id}\,\) on \(\partial Q\) and that
where \(C_b>0\) depends only on b. Set \(L_n:=1-\frac{1}{n}\), \(Q_n:=(-L_n,L_n)^{d}\), \(Q^{d-1}_n:=(-L_n,L_n)^{d-1}\). Then
Hence,
On the other hand, using the definition of \(g_n\), of \(Q_n\), and (5.3), we get
Since the function
is surjective on \([1,+\,\infty )\), given \(r>1\), it is possible to find \(b>1\) such that, using (5.5) and (5.6), we get
The required convergence on \(T_n\rightarrow \mathrm{Id}\,\) follows at once.
Step two\(\phi \in C^{\infty }(Q_L)\). For \(n\in {\mathbb {N}}\) consider the grid \(\{Q_{i}^n\}_{i=1}^{n^d}\) of cubes of size \(\frac{1}{n}\), with centers \(x_{i}^n\) partition Q. Fix \(\delta >0\) and observe that there exists \(n_0\in {\mathbb {N}}\) such that for all \(n\ge n_0\) it holds
Set \(\nu _i^n:=\nabla \phi (x_i^n)\) and define
For every \(i=1,\ldots n^d\), thanks to the previous step, it is possible to find a map \(T_i^n{:}\,\overline{Q_i^n}\rightarrow \overline{Q_i^n}\) with \(T_i^n=\mathrm{Id}\,\) on \(\partial Q_i^n\) such that
Define \(T_n{:}\,Q\rightarrow Q\) as
where the constant \(C>0\) depends only on L and r. Therefore, from (5.8), (5.9), and (5.10), we get
where in the last step we used the inequality \(|a^p-b^p|\le |a-b|\,(|a|^{p-1}+|b|^{p-1})\). Since \(\delta >0\) is arbitrary, we conclude. \(\square \)
It is now useful to introduce the following notation. For a given Radon measure \(\mu \), we define the class of regular multipliers\({\mathfrak {m}}(\Omega ,\mu )\) as the family of \(f\in L^1(\Omega ,\mu )\) of the form
where
- (i)
\(r_i\ge 1\);
- (ii)
\(\{A_i\}_{i=1}^{N}\) is a finite family of pairwise disjoint open subset of \(\Omega \) with Lipschitz boundary;
- (iii)
\(\mu (\partial A_i)=0\) for all \(i=1,\ldots ,N\).
By standard arguments of measure theory, it is possible to prove the following density result.
Lemma 5.10
Let \(\mu \in {\mathcal {M}}^+(\Omega )\) be a Radon measure and pick \(f\in L^1(\Omega ,\mu )\) with \(f\ge 1\)\(\mu \)-a.e. on \(\Omega \). Then there exists a sequence \(\{f_k\}_{k\in {\mathbb {N}}}\subset {\mathfrak {m}}(\Omega ,\mu )\) such that \(f_k\mu {\rightharpoonup ^*}\,f\mu \).
Therefore, we just need to provide the wriggling construction for functions \(f\in {\mathfrak {m}}(\Omega ,|D\phi |)\). This will be done in the next result.
Lemma 5.11
Let \(\phi \in BV(\Omega )\) and let \(f\in {\mathfrak {m}}(\Omega ,|D\phi |)\). Then there exists a sequence of maps \(\{\phi _n\}_{n\in {\mathbb {N}}} \subset W^{1,1}(\Omega )\) such that \(\phi _n\rightarrow \phi \) in \(L^1\) and \(|D\phi _n|{\rightharpoonup ^*}\,f |D\phi |\).
Proof
We divide the proof in three steps.
Step one Fix an open set \(A\subset \Omega \), \(\varphi \in C^{\infty }(\Omega )\cap C^0(\overline{\Omega })\) and \(r\ge 1\). The goal of this step is to construct a sequence \(\{\varphi _k\}_{k\in {\mathbb {N}}}\subset W^{1,1}(\Omega )\) such that \(\varphi _k=\varphi \) on \(\Omega {\setminus } A\) and

For each \(k\in {\mathbb {N}}\), consider a grid of cubes \(\{Q_j^k\}_{j\in {\mathbb {N}}}\) with side length 1/k and define the finite set of indexes
Using Lemma 5.9, for each \(Q_j^k\) there exists a smooth map \(S_j^k{:}\,\Omega \rightarrow \Omega \) such that \(S_j^k=\mathrm{Id}\,\) on \(\Omega {\setminus } Q_j^k\) and
Define
Note that \(\varphi _k\in W^{1,1}(\Omega )\), \(\varphi _k=\varphi \) on \(\Omega {\setminus } A\) and by construction \(\varphi _k\rightarrow \varphi \) in \(L^1\). We now need to show that  . For, note that
. For, note that
Let \(E \subset \subset \Omega \) be a bounded Borel set such that \(|D\varphi |(\partial E)=0\). Take an open set \(U\subset A\) with \(U\supset \partial E\) such that \(|D\varphi |(U)\le \eta \) and define
Then,
where
Take k large enough so that \(j\in {\mathcal {J}}_{\partial E}^k\) implies \(Q_j^k\subset U\), and
Then, from the definition of \(\varphi _k\) and (5.11) we get
Since
by taking the limit as \(k\rightarrow +\,\infty \) in (5.12) we get
Since \(\eta >0\) is arbitrary, we conclude that
getting  .
.
Step two Let \(\phi \in BV(\Omega )\), and \(f\in L^1(\Omega ,|D\phi |)\) of the form
where \(A_1,\dots ,A_N\subset \Omega \) are pairwise disjoint open sets. A density argument (Ambrosio et al. 2000, Proposition 3.21, Theorem 3.9) provides a sequence of maps \(\{\phi _{n}\}_{n\in {\mathbb {N}}}\subset C^{\infty }( \Omega ) \cap C^0({\overline{\Omega }})\) such that
For any \(n\in {\mathbb {N}}\) and \(i=1,\dots ,N\), the previous step yields a sequence of maps \(\{\phi _{i,n}^k\}_{k\in {\mathbb {N}}}\subset W^{1,1}(\Omega )\) such that \(\phi _{i,n}^k=\phi _n\) on \(\Omega {\setminus } A_i\) and

Define
Note that
as \(k\rightarrow +\,\infty \). Since by assumption \(|D\phi |(\partial A_i)=0\) for all \(i=1,\ldots , N\), we also have
as \(n\rightarrow +\,\infty \). Therefore, a diagonalization argument allows us to conclude. \(\square \)
We are now in position to prove that the total variation is purely lower semi-continuous.
Proof of proposition 5.8
Fix \(\phi \in BV(\Omega )\), and \(f\in L^1(\Omega ,|D\phi |)\). By Lemma 5.10 applied to \(\mu =|D\phi |\), we find a sequence of \(\{f_k\}_{k\in {\mathbb {N}}} \in {\mathfrak {m}}(\Omega ,|D\phi |)\) such that \(f_k|D\phi |{\rightharpoonup ^*}\,f|D\phi |\). Then, Lemma 5.11 applied on each \(f_k\in {\mathfrak {m}}(\Omega ,|D\phi |)\) yields a sequence of maps \(\{\phi _n^k\}_{n\in {\mathbb {N}}}\subset W^{1,1}(\Omega )\) such that \(|D\phi _n^k|{\rightharpoonup ^*}\,f_k|D\phi |\), \(\phi _n^k\rightarrow \phi \) in \(L^1(\Omega )\) as \(n\rightarrow +\,\infty \). Thus, we conclude by using a diagonalization argument. \(\square \)
We can now conclude the proof of Proposition 5.7
Proof of Proposition 5.7
Properties (Ad1) and (Ad2) follow easily by the definition of \({{\mathcal {F}}}\).
In order to prove property (Ad3), we argue as follows: Let \(\phi \in BV(\Omega )\), and \(A\subset \Omega \) an open set such that \({{\mathcal {F}}}(\phi ;A)=0\). Fix \(\varepsilon >0\) and an open set \(U\subset \subset A\). Let \(x\in U\) and \(R>0\) such that \(B_R(x)\subset U\). Then \(\phi \equiv c\) on \(B_R(x)\). Let \(r\in (0,R)\) that will be chosen later and set \({\overline{\phi }}:= \phi +\mathbb {1}_{B_r(x)}\). Then
and
Taking
we get the desired result.
Finally, we show that \({{\mathcal {F}}}\) is purely lower semi-continuous. Fix \(\phi \in BV(\Omega )\), \(f\ge 1\), \(f\in L^1(\Omega , {{\mathcal {F}}}^{\phi })\). Let \(\{\phi _n\}_{n\in {\mathbb {N}}}\) be the sequence given by Proposition 5.8 such that \(\phi _n\rightarrow \phi \) in \(L^1(\Omega )\) and
We claim that
For each \(k\in {\mathbb {N}}\), consider a partition of \(\Omega \) into cubes \(\{Q_j^k\}_{j=1}^{M_k}\) such that \(|D\phi |(\partial Q_j^k)=0\) and
for all \(j=1,\dots ,M_k\). Note that, for any open set \(A\subset \subset \Omega \), the following estimates hold
Take a bounded Borel set \(E\subset \subset \Omega \) such that \({{\mathcal {F}}}^{\phi }(\partial E)=0\). Consider bounded open sets \(E_1\subset \subset E\subset \subset E_2\). Then, using (5.14), we get
By taking the limit as \(n \rightarrow +\,\infty \) on both sides, and using (5.13) and (5.14), we have
Similar computation shows also
Being the above valid for all \(k\in {\mathbb {N}}\) yields
Moreover, since \(E_1\) and \(E_2\) are arbitrary and \({{\mathcal {F}}}^{\phi }(\partial A)=0\), we conclude that
Since
we conclude that \({{\mathcal {F}}}^{\phi _n}{\rightharpoonup ^*}\,f {{\mathcal {F}}}^{\phi }\). \(\square \)
5.2.1 A Non-Local Approximation
The non-local approximation of the weighted total variation we consider in this section is the one used by Trillos and Slepčev (2016) in the context of total variation on graphs.
Let \(\eta {:}\,[0,+\,\infty )\rightarrow [0,+\,\infty )\) be a compactly supported smooth function with \(\int _0^{+\,\infty } \eta \,\mathrm {d}t =1\). For \(\varepsilon >0\), consider the energy \({{\mathcal {F}}}_{\varepsilon }{:}\,L^1(\Omega )\times {{\mathcal {A}}}(\Omega )\rightarrow [0,+\,\infty ]\) defined as
where \(\eta _{\varepsilon }(t):=\eta (t \varepsilon ^{-1})\varepsilon ^{-d}\). Fix a sequence \(\{\varepsilon _n\}_{n\in {\mathbb {N}}}\) such that \(\varepsilon _n\rightarrow 0\) as \(n\rightarrow +\,\infty \), and set \({{\mathcal {F}}}_n:={{\mathcal {F}}}_{\varepsilon _n}\). In Trillos and Slepčev (2016), the authors proved the following \(\Gamma \)-convergence result.
Theorem 5.12
It holds that \({{\mathcal {F}}}_n{\mathop {\rightarrow }\limits ^{\Gamma }}{{\mathcal {F}}}\) with respect to the \(L^1\) convergence, where
and
Moreover, if \(\{\phi _n\}_{n\in {\mathbb {N}}}\subset L^1(\Omega )\) is a sequence for which
then, up to a not relabeled subsequence, \(\phi _n\rightarrow \phi \) in \(L^1(\Omega )\), where \(\phi \in BV(\Omega )\)
It is possible to improve the above \(\Gamma \)-convergence result and obtain the following.
Proposition 5.13
The sequence \(\{{{\mathcal {F}}}_n\}_{n\in {\mathbb {N}}}\) is a good approximating sequence for \({{\mathcal {F}}}\).
Proof
Property (GA1) follows from the liminf inequality of Theorem 5.12, while property (GA2) is immediate from the definition of \({{\mathcal {F}}}_n\).
In order to prove property (GA3), we follow the same steps used in the proof of Theorem 5.12 (Trillos and Slepčev 2016, Section 4.2), that we briefly report here for the reader’s convenience. Given \(\phi \in BV(\Omega )\), we extended it to a BV function defined in the whole \({\mathbb {R}}^d\) in such a way that the extension, still denoted by \(\phi \), is such that \(|D\phi |(\partial \Omega )=0\). For any \(\delta >0\), having set
let \(\{\phi _n\}_{n\in {\mathbb {N}}}\subset C^\infty (\Omega _{\delta })\) be a sequence such that \(\phi _n\rightarrow \phi \) in \(L^1(\Omega _{\delta })\), and
Let \(E\subset \subset \Omega \) be a Borel set with \(|D\phi |(\partial E)=0\). Assume [0, M] is the support of \(\eta \). Then it holds that
where we used the change of variable \(h:=\frac{x-y}{\varepsilon _n}\) and \(z=x+t(y-x)\). In the case \(\rho \) is Lipschitz, it is possible to prove that
for some constant \(C>0\) independent of k. Therefore,
\(\square \)
The result of Proposition 5.13 allows us to apply Theorem 5.7 to get the following.
Proposition 5.14
Let \(\psi :[0,+\,\infty )\rightarrow (0,+\,\infty )\) be a Borel function with \(\inf \psi >0\). For \(\varepsilon >0\), consider the functional
if \(\phi \in L^1(\Omega )\), \(\mu \in {\mathcal {M}}^+(\Omega )\) such that
and \(+\,\infty \) otherwise on \(L^1(\Omega )\times {\mathcal {M}}^+(\Omega )\). Then \({\mathcal {G}}_\varepsilon {\mathop {\rightarrow }\limits ^{\Gamma }}\mathcal {G}\) with respect to the \(L^1\times w^*\) topology, where
where we write \(\mu =u\left( \sigma _{\eta }\rho ^2|D\phi |\right) +\mu ^{\perp }\).
5.3 Relaxation of the p-Dirichlet Energy
In this last section, we would like to note that the choice of the \(L^1\) convergence is not fundamental for the validity of the main results of this paper. Indeed, Theorem 3.8 holds also if the \(L^1\) converge is replaced by the \(L^p\) convergence. Of course, in Definitions 3.1 and 3.4 one also has to replace the \(L^1\) convergence with the \(L^p\) one.
As an example of application of our results in the \(L^p\) case, we consider, for \(p>1\), the energy \({{\mathcal {F}}}{:}\,L^p(\Omega )\times \mathcal {A}(\Omega )\rightarrow [0,+\,\infty )\) given by
when \(\phi \in W^{1,p}(\Omega )\), and \(+\,\infty \) otherwise.
Proposition 5.15
For any \(p>1\), \({{\mathcal {F}}}\in \mathrm {Ad}\).
Proof
It is easy to see that assumptions (Ad1),(Ad2) and (Ad3) are satisfied. Thus, \({{\mathcal {F}}}\in \mathrm {Ad}\). The fact that \({{\mathcal {F}}}\) is purely lower semi-continuous is obtained by using a slight variation of the proof of Proposition 5.8 by applying Lemma 5.9 for \(p>1\), Lemma 5.10 on \(\mu =|\nabla \phi |^p{{\mathcal {L}}}^n\) and Lemma 5.11 suitably adapted. \(\square \)
Noting that the constant sequence \({{\mathcal {F}}}_n:= {{\mathcal {F}}}\) is a good approximating sequence for \({{\mathcal {F}}}\) and using Corollary 3.10 we obtain the following Proposition.
Proposition 5.16
The \(L^p\times w^*\) lower semi-continuous envelope of \({\mathcal {G}}^{{{\mathcal {F}}}}(\phi ,\mu )\) is
where we write \(\mu =u|\nabla \phi |^p{{\mathcal {L}}}^n+\mu ^{\perp }\).
References
Acerbi, E., Bouchitté, G.: A general class of phase transition models with weighted interface energy. Ann. Inst. H. Poincaré Anal. Non Linéaire 25, 1111–1143 (2008)
Alicandro, R., Cicalese, M., Sigalotti, L.: Phase transitions in presence of surfactants: from discrete to continuum. Interfaces Free Bound. 14, 65–103 (2012)
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems, Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, New York (2000)
Baía, M., Barroso, A.C., Matias, J.: A model for phase transitions with competing terms. Q. J. Math. 68, 957–1000 (2017)
Braides, A.: Gamma-Convergence for Beginners, vol. 22. Clarendon Press, Oxford (2002)
Bresson, X., Laurent, T., Uminsky, D., von Brecht, J.H.: Multiclass total variation clustering. In: Proceedings of the 26th International Conference on Neural Information Processing Systems (NIPS), pp. 1421–1429 (2013)
Burger, M.: Surface diffusion including adatoms. Commun. Math. Sci. 4, 1–51 (2006)
Buttazzo, G.: Semicontinuity, Relaxation and Integral Representation in the Calculus of Variations, vol. 207 of Pitman Research Notes in Mathematics Series, Longman Scientific & Technical, Harlow; copublished in the United States with John Wiley & Sons, Inc., New York (1989)
Buttazzo, G., Freddi, L.: Functionals defined on measures and applications to non-equi-uniformly elliptic problems. Ann. Mat. Pura Appl. 4(159), 133–149 (1991)
Calatroni, L., van Gennip, Y., Schönlieb, C.-B., Rowland, H.M., Flenner, A.: Graph clustering, variational image segmentation methods and Hough transform scale detection for object measurement in images. J. Math. Imaging Vis. 57, 269–291 (2017)
Caroccia, M., Cristoferi, R., Dietrich, L.: Equilibria configurations for epitaxial crystal growth with adatoms. Arch. Ration. Mech. Anal. 230, 785–838 (2018)
Caroccia, M., Chambolle, A., Mumford Slepčev, D.: Mumford-Shah functionals on graphs and their asymptotics. Preprint (2020)
Chambolle, A., Giacomini, A., Lussardi, L.: Continuous limits of discrete perimeters. M2AN Math. Model. Numer. Anal. 44, 207–230 (2010)
Cristoferi, R., Thorpe, M.: Large data limit for a phase transition model with the p-Laplacian on point clouds, to appear on European Journal of Applied Mathematics, ArXiv preprint ArXiv:1802.08703 (2018)
Dal Maso, G.: An Introduction to \(\Gamma \)-Convergence. Progress in Nonlinear Differential Equations and their Applications, vol. 8. Birkhäuser, Boston (1993)
De Lellis, C.: Rectifiable sets, densities and tangent measures. In: Zurich Lectures in Advanced Mathematics, European Mathematical Society (EMS), Zürich (2008)
Fonseca, I., Leoni, G.: Modern Methods in the Calculus of Variations: \(L^p\) Spaces, Springer Monographs in Mathematics. Springer, New York (2007)
Fonseca, I., Fusco, N., Leoni, G., Morini, M.: Equilibrium configurations of epitaxially strained crystalline films: existence and regularity results. Arch. Ration. Mech. Anal. 186, 477–537 (2007a)
Fonseca, I., Morini, M., Slastikov, V.: Surfactants in foam stability: a phase-field model. Arch. Ration. Mech. Anal. 183, 411–456 (2007b)
Fonseca, I., Fusco, N., Leoni, G., Millot, V.: Material voids in elastic solids with anisotropic surface energies. J. Math. Pures Appl. 9(96), 591–639 (2011)
Fonseca, I., Fusco, N., Leoni, G., Morini, M.: Motion of elastic thin films by anisotropic surface diffusion with curvature regularization. Arch. Ration. Mech. Anal. 205, 425–466 (2012)
Fonseca, I., Fusco, N., Leoni, G., Morini, M.: Motion of three-dimensional elastic films by anisotropic surface diffusion with curvature regularization. Anal. PDE 8, 373–423 (2015)
Fried, E., Gurtin, M.E.: A unified treatment of evolving interfaces accounting for small deformations and atomic transport with emphasis on grain-boundaries and epitaxy. Adv. Appl. Mech. 40, 1–177 (2004)
García Trillos, N., Slepčev, D.: On the rate of convergence of empirical measures in \(\infty \)-transportation distance. Can. J. Math. 67, 1358–1383 (2015)
García Trillos, N., Slepčev, D.: A variational approach to the consistency of spectral clustering. Appl. Comput. Harmonic Anal. 45(2), 239–281 (2016)
Maggi, F.: Sets of Finite Perimeter and Geometric Variational Problems, vol. 135 of Cambridge Studies in Advanced Mathematics, Cambridge University Press, Cambridge (2012). An introduction to geometric measure theory
Modica, L.: Gradient theory of phase transitions with boundary contact energy. Annales de l’Institut Henri Poincare (C) Non Linear Anal. 4, 487–512 (1987)
Modica, L., Mortola, S.: Il limite nella \(\Gamma \)-convergenza di una famiglia di funzionali ellittici. Boll. Un. Mat. Ital. A 5(14), 526–529 (1977)
Rätz, A., Voigt, A.: A diffuse-interface approximation for surface diffusion including adatoms. Nonlinearity 20, 177 (2006)
Sandier, E., Serfaty, S.: Gamma-convergence of gradient flows with applications to Ginzburg–Landau. Commun. Pure Appl. Math. 57, 1627–1672 (2004)
Serfaty, S.: Gamma-convergence of gradient flows on Hilbert and metric spaces and applications. Discrete Contin. Dyn. Syst. 31, 1427–1451 (2011)
Spencer, B., Tersoff, J.: Asymmetry and shape transitions of epitaxially strained islands on vicinal surfaces. Appl. Phys. Lett. 96, 073114 (2010)
Szlam, A., Bresson, X.: Total variation and Cheeger cuts. In: Proceedings of the 27th International Conference on International Conference on Machine Learning (ICML), pp. 1039–1046 (2010)
Thorpe, M., Slepčev, D.: Transportation \(L^p\) distances: properties and extensions, In preparation (2017)
Thorpe, M., Theil, F.: Asymptotic analysis of the Ginzburg–Landau functional on point clouds, to appear in the Proceedings of the Royal Society of Edinburgh Section A: Mathematics, arXiv preprint arXiv:1604.04930 (2017)
Thorpe, M., Park, S., Kolouri, S., Rohde, G.K., Slepčev, D.: A transportation \(L^p\) distance for signal analysis, to appear in the Journal of Mathematical Imaging and Vision, arXiv preprint arXiv:1609.08669 (2017)
Trillos, N.G., Slepčev, D.: Continuum limit of total variation on point clouds. Arch. Ration. Mech. Anal. 220, 193–241 (2016)
van Gennip, Y., Schönlieb, C.-B.: Introduction: big data and partial differential equations. Eur. J. Appl. Math. 28, 877–885 (2017)
Acknowledgements
The authors are grateful to Irene Fonseca and Giovanni Leoni for having introduced them to the study of the problem. The work of R.C. has been supported by the National Science Foundation under Grant No. DMS-1411646 during the period at Carnegie Mellon University, and by the Grant EP/R013527/2 “Designer Microstructure via Optimal Transport Theory” of David Bourne while at Heriot-Watt University. The work of M.C has been supported by the Fundação para a Ciência e a Tecnologia (Portuguese Foundation for Science and Technology) through the Carnegie Mellon Portugal Program under Grant 18316.1.5004440 while in Lisbon, and by the grant “Calcolo delle variazioni, Equazione alle derivate parziali, Teoria geometrica della misura, Trasporto ottimo” co-founded by Scuola Normale Superiore and the university of Florence during the last part of the work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Irene Fonseca.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
We here provide some technical results that have been used in the development of our arguments.
The first is a technical result, a Crumble Lemma, namely a tool that allows us to disintegrate the domain of a non-atomic measure \({{\mathcal {F}}}\) in sub-domains containing, asymptotically, a certain percentage of the total mass \({{\mathcal {F}}}\). This result plays a key role in the proof of Proposition 4.6.
Lemma 6.1
(Crumble Lemma) Let \(\mu \) be a non-atomic positive Radon measure on \(Q:=(-\frac{1}{2},\frac{1}{2})^d\), and \(\{\mu _n\}_{n\in {\mathbb {N}}}\) be a sequence of Radon measure on Q. Then, for any \(\lambda \in (0,1)\) there exists a sequence of Borel sets \(\{R_j\}_{j\in {\mathbb {N}}}\), with \(R_j\subset Q\) such that
- (a)
 ;
; - (b)
 ;
; - (c)
\(\mu _n(\partial R_j)=0\) for all \(n,j\in {\mathbb {N}}\).
Proof
Fix \(j\in {\mathbb {N}}\). It is possible to find \(x_j\in {\mathbb {R}}^d\) such that \(G_{x_j,1/j}\) is such that \(\mu (\partial G_{x_j,1/j})=0\). Let \(\{Q_i^j\}_{j=1}^{M_j}\) denote the elements of the grid. For every \(i=1,\dots ,M_j\), since \(\mu \) is not atomic, it is possible to use (Fonseca and Leoni 2007, Proposition 1.20) in order to find a \(\mu \)-measurable set \(S_i^j\subset Q^j_i\) such that \(\mu (S^j_i)=\lambda \mu (Q^j_i)\). We claim that there exists \({\widetilde{S}}_i^j\subset Q^j_i\) such that \(\mu (\partial {\widetilde{S}}^j_i)=0\)
Indeed, consider the measure  , and let \(f_n:=\mu ^j_i*\rho _n\), where \(\{\rho _n\}_{k\in {\mathbb {N}}}\) is a sequence of mollifiers. Let n be large enough so that
, and let \(f_n:=\mu ^j_i*\rho _n\), where \(\{\rho _n\}_{k\in {\mathbb {N}}}\) is a sequence of mollifiers. Let n be large enough so that
For \(t>0\), let \({\widetilde{S}}^j_i:=\{ f_n\ge t\}\). Using the fact that each \(\mu _n\) is a Radon measure, and thus for all but countably many \(t>0\) it holds \(\mu _n(\partial {\widetilde{S}}^j_i)=0\), it is possible to find \(t>0\) such that \(\mu _n(\partial {\widetilde{S}}^j_i)=0\) for all \(n\in {\mathbb {N}}\), and
Define, for each \(j\in {\mathbb {N}}\)
From the definition, it follows that \(\mu (\partial R_j)=0\) for all \(j\in {\mathbb {N}}\). To prove that  , take a Borel set \(E\subset Q\) with \(\mu (\partial E)=0\). Fix \(\eta >0\), and let \(U\supset \partial E\) be an open set with \(\mu (U)<\eta \). Let j large enough so that \(Q^j_i\cap \partial E\ne \emptyset \) implies \(Q^j_i\subset U\). Set \(I:=\{ i=1,\dots M_j | Q^j_i\cap \partial E\ne \emptyset \}\). Then
, take a Borel set \(E\subset Q\) with \(\mu (\partial E)=0\). Fix \(\eta >0\), and let \(U\supset \partial E\) be an open set with \(\mu (U)<\eta \). Let j large enough so that \(Q^j_i\cap \partial E\ne \emptyset \) implies \(Q^j_i\subset U\). Set \(I:=\{ i=1,\dots M_j | Q^j_i\cap \partial E\ne \emptyset \}\). Then
where we used (6.1). Therefore, we conclude by sending \(j\rightarrow +\,\infty \), and using the arbitrariness of \(\eta \). \(\square \)
The second result is a test for the weak* convergence of measures.
Lemma 6.2
Let \(\{\mu _n\}_{n\in {\mathbb {N}}}\) be a sequence of nonnegative Radon measures on an open bounded set \(\Omega \subset {\mathbb {R}}^d\) with Lipschitz boundary such that \(\mu _n(U)\rightarrow \mu (U)\) for all open sets \(U\subset \Omega \) with Lipschitz boundary such that \(\mu (\partial U)=0\). Then \(\mu _n{\rightharpoonup ^*}\,\mu \).
Proof
Let \(E\subset \Omega \) be a Borel set with \(\mu (\partial E)=0\). We want to show that \(\mu _n(E)\rightarrow \mu (E)\). Fix \(\varepsilon >0\). Using the outer regularity of \(\mu \), it is possible to find an open set \(V\supset E\) such that \(\mu (V)< \mu (E)+\frac{\varepsilon }{2}\), and an open set \(W\supset \partial E\) with \(\mu (W)<\frac{\varepsilon }{2}\). Since \(\partial E\) is compact, there exists \(r>0\) such that \(B_r(x)\subset W\) for all \(x\in \partial E\). Let \(U:=V\cup W\). Using mollification, it is possible to find an open set \(U_2\) with Lipschitz boundary, such that \(E\subset U_2\subset U\). Then
Using the inner regularity of \(\mu \), it is possible to find a compact set \(K\subset E{\setminus }\partial E\) such that \(\mu (K)>\mu (E)-\varepsilon \). Note that here we used the fact that \(\mu (\partial E)=0\). In the case \(E{\setminus }\partial E=\emptyset \), we can just take \(K=\emptyset \). Since \(K\subset E{\setminus } \partial E\), and \(\Omega \) is bounded, we have that \(\mathrm {dist}(K,\partial E)>0\). Therefore, using mollifications, it is then possible to find an open set \(U_1\) with Lipschitz boundary, such that \(K\subset U_1\subset E{\setminus }\partial E\). Then
Note that
Since by assumption we have that
Using the arbitrariness of \(\varepsilon >0\), we conclude that \(\mu _n(E)\rightarrow \mu (E)\), getting the desired result. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Caroccia, M., Cristoferi, R. On the Gamma Convergence of Functionals Defined Over Pairs of Measures and Energy-Measures. J Nonlinear Sci 30, 1723–1769 (2020). https://doi.org/10.1007/s00332-020-09623-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00332-020-09623-y




 as
as  as
as 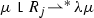 ;
; ;
;