Abstract
Heteroclinic connections are trajectories that link invariant sets for an autonomous dynamical flow: these connections can robustly form networks between equilibria, for systems with flow-invariant spaces. In this paper, we examine the relation between the heteroclinic network as a flow-invariant set and directed graphs of possible connections between nodes. We consider realizations of a large class of transitive digraphs as robust heteroclinic networks and show that although robust realizations are typically not complete (i.e. not all unstable manifolds of nodes are part of the network), they can be almost complete (i.e. complete up to a set of zero measure within the unstable manifold) and equable (i.e. all sets of connections from a node have the same dimension). We show there are almost complete and equable realizations that can be closed by adding a number of extra nodes and connections. We discuss some examples and describe a sense in which an equable almost complete network embedding is an optimal description of stochastically perturbed motion on the network.







Similar content being viewed by others
Notes
In equivariant systems, if \(\xi _i\ne \xi _j\) but they are in the same group orbit, then some authors consider the connection homoclinic. We do not make this distinction until Sect. 4.
More general heteroclinic networks, in the sense of Ashwin and Field (1999), can have higher depth connections in that they can contain trajectories that limit to connections.
Cycles are defined as simple in Krupa and Melbourne (2004) if the nodes are in different connected components of one-dimensional fixed-point spaces and the connections are in two-dimensional fixed-point spaces.
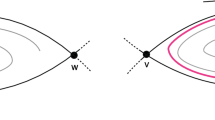
When a connection \([\xi _i \rightarrow \xi _j]\) exists, the connection \([\xi _i \rightarrow -\xi _j]\) also exists. However, under the identification of objects in the same group orbit, only \(\xi _2\) is a splitting node.
References
Armbruster, D., Stone, E., Kirk, V.: Noisy heteroclinic networks. Chaos 13(1), 71–79 (2003)
Ashwin, P., Chossat, P.: Attractors for robust heteroclinic cycles with continua of connections. J. Nonlinear Sci. 8(2), 103–129 (1998)
Ashwin, P., Field, M.J.: Heteroclinic networks in coupled cell systems. Arch. Ration. Mech. Anal. 148(2), 107–143 (1999)
Ashwin, P., Postlethwaite, C.: On designing heteroclinic networks from graphs. Physica D 265, 26–39 (2013)
Ashwin, P., Postlethwaite, C.: Designing heteroclinic and excitable networks in phase space using two populations of coupled cells. J. Nonlinear Sci. 26(2), 345–364 (2016)
Bakhtin, Y.: Noisy heteroclinic networks. Probab. Theory Relat. Fields 150(1), 1–42 (2011)
Bick, C.: Heteroclinic dynamics of localized frequency synchrony: heteroclinic cycles for small populations. J. Nonlinear Sci. (2019). https://doi.org/10.1007/s00332-019-09552-5
Brannath, W.: Heteroclinic networks on the tetrahedron. Nonlinearity 7, 1367–1384 (1994)
Castro, S.B.S.D., Lohse, A.: Stability in simple heteroclinic networks in \({\mathbb{R}}^4\). Dyn. Syst. 29(4), 451–481 (2014)
Castro, S.B.S.D., Lohse, A.: Construction of heteroclinic networks in \({\mathbb{R}}^4\). Nonlinearity 29(12), 3677–3695 (2016)
Diestel, R.: Graph theory, 3rd edn. Springer, Berlin (2005)
Field, M.J.: Heteroclinic networks in homogeneous and heterogeneous identical cell systems. J. Nonlinear Sci. 25(3), 779–813 (2015)
Field, M.J.: Patterns of desynchronization and resynchronization in heteroclinic networks. Nonlinearity 30(2), 516 (2017)
Foulds, L.R.: Graph theory applications. Springer, Berlin (1992)
Guckenheimer, J., Holmes, P.: Structurally stable heteroclinic cycles. Math. Proc. Camb. Philos. Soc. 103, 189–192 (1988)
Hoyle, R.: Pattern formation: an introduction to methods. Cambridge University Press, Cambridge (2006)
Kirk, V., Lane, E., Postlethwaite, C., Rucklidge, A.M., Silber, M.: A mechanism for switching near a heteroclinic network. Dyn. Syst. 25(3), 323–349 (2010)
Kirk, V., Postlethwaite, C., Rucklidge, A.M.: Resonant bifurcations of robust heteroclinic networks. SIAM J. Appl. Dyn. Syst. 11(4), 1360–1401 (2012)
Kirk, V., Silber, M.: A competition between heteroclinic cycles. Nonlinearity 7(6), 1605–1621 (1994)
Krupa, M.: Robust heteroclinic cycles. J. Nonlinear Sci. 7(2), 129–176 (1997)
Krupa, M., Melbourne, I.: Asymptotic stability of heteroclinic cycles in systems with symmetry. Ergod. Theory Dyn. Syst. 15(1), 121–147 (1995)
Krupa, M., Melbourne, I.: Asymptotic stability of heteroclinic cycles in systems with symmetry. II. Proc. R. Soc. Edinb. Sect. A 134, 1177–1197 (2004)
Weinberger, O., Ashwin, P.: From coupled networks of systems to networks of states in phase space. Discrete Contin. Dyn. Syst. B 23(5), 2021–2041 (2018)
Acknowledgements
We thank Chris Bick, Mike Field and Claire Postlethwaite for their insightful questions and comments. The second author was partly supported by CMUP (UID/MAT/00144/2013), funded by the Portuguese Government through the Fundação para a Ciência e a Tecnologia (FCT) with national (MEC) and European structural funds through the programs FEDER, under the partnership agreement PT2020. The second and third authors benefited from DAAD-CRUP funding through “Ação Integrada Luso-Alemã A10/17”, respectively, DAAD-project 57338573 PPP Portugal 2017, sponsored by the Federal Ministry of Education and Research (BMBF). Partial support for a visit to Exeter is gratefully acknowledged from the Centre for Predictive Modelling in Healthcare (EPSRC Grant No. EP/N014391/1).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Dr. Anthony Bloch.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Ashwin, P., Castro, S.B.S.D. & Lohse, A. Almost Complete and Equable Heteroclinic Networks. J Nonlinear Sci 30, 1–22 (2020). https://doi.org/10.1007/s00332-019-09566-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00332-019-09566-z