Differential-Geometric-Control Formulation of Flapping Flight Multi-body Dynamics

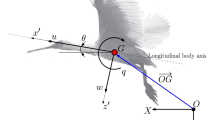
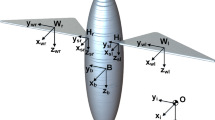
Abstract

Flapping flight dynamics is quite an intricate problem that is typically represented by a multi-body, multi-scale, nonlinear, time-varying dynamical system. The unduly simple modeling and analysis of such dynamics in the literature has long obstructed the discovery of some of the fascinating mechanisms that these flapping-wing creatures possess. Neglecting the wing inertial effects and directly averaging the dynamics over the flapping cycle are two major simplifying assumptions that have been extensively used in the literature of flapping flight balance and stability analysis. By relaxing these assumptions and formulating the multi-body dynamics of flapping-wing micro-air-vehicles in a differential-geometric-control framework, we reveal a vibrational stabilization mechanism that greatly contributes to the body pitch stabilization. The discovered vibrational stabilization mechanism is induced by the interaction between the fast oscillatory aerodynamic loads on the wings and the relatively slow body motion. This stabilization mechanism provides an artificial stiffness (i.e., spring action) to the body rotation around its pitch axis. Such a spring action is similar to that of Kapitsa pendulum where the unstable inverted pendulum is stabilized through applying fast-enough periodic forcing. Such a phenomenon cannot be captured using the overly simplified modeling and analysis of flapping flight dynamics.

Appendices

Appendix

Derivation of the Five-DOF Equations of Motion

We use the principle of virtual power (Greenwood 2003), as explained in Sect. 2, to derive the five-DOF equations of motion (2) in detail. The various terms in Eq. (1) for the body and wing are given below.

1.1 Body

The linear velocity of the reference point of the body axis system (the body’s center of gravity) and the corresponding angular velocity are written as

$$\begin{aligned} {\varvec{v}}_{\mathrm{b}} = {\dot{x}} {\varvec{i}}_{\mathrm{I}} + {\dot{z}} {\varvec{k}}_{\mathrm{I}} \text{ and } {\varvec{\omega }}_{\mathrm{b}} = {{\dot{\theta }}} {\varvec{j}}_{\mathrm{b}} = {{\dot{\theta }}} {\varvec{j}}_{\mathrm{I}}, \end{aligned}$$

where ${\varvec{i}}$, ${\varvec{j}}$, and ${\varvec{k}}$ are unit vectors along the x, y, and z directions in the axis system indicated by the subscript. Thus, one obtains

$$\begin{aligned} \frac{\partial {\varvec{v}}_{\mathrm{b}}}{\partial {\dot{x}}}&= {\varvec{i}}_{\mathrm{I}} ~~ \frac{\partial {\varvec{v}}_{\mathrm{b}}}{\partial {\dot{z}}} = {\varvec{k}}_{\mathrm{I}} ~~ \frac{\partial {\varvec{v}}_{\mathrm{b}}}{\partial {{\dot{\theta }}}} = {\varvec{0}} ~~ \frac{\partial {\varvec{v}}_{\mathrm{b}}}{\partial {{\dot{\varphi }}}} = {\varvec{0}} ~~ \frac{\partial {\varvec{v}}_{\mathrm{b}}}{\partial {{\dot{\eta }}}} = {\varvec{0}} \\ \frac{\partial {\varvec{\omega }}_{\mathrm{b}}}{\partial {\dot{x}}}&= {\varvec{0}} ~~ \frac{\partial {\varvec{\omega }}_{\mathrm{b}}}{\partial {\dot{z}}} = {\varvec{0}} ~~ \frac{\partial {\varvec{\omega }}_{\mathrm{b}}}{\partial {{\dot{\theta }}}} = {\varvec{j}}_{\mathrm{I}} ~~ \frac{\partial {\varvec{\omega }}_{\mathrm{b}}}{\partial {{\dot{\varphi }}}} = {\varvec{0}} ~~ \frac{\partial {\varvec{\omega }}_{\mathrm{b}}}{\partial {{\dot{\eta }}}} = {\varvec{0}} , \end{aligned}$$

and

$$\begin{aligned} \dot{{\varvec{v}}}_{\mathrm{b}}=\ddot{x} {\varvec{i}}_{\mathrm{I}} + \ddot{z} {\varvec{k}}_{\mathrm{I}}. \end{aligned}$$

The angular momentum vector of the body about its center of gravity and its inertial derivative are given by

$$\begin{aligned} {\varvec{h}}_{\mathrm{b}}=I_{yb}{{\dot{\theta }}} {\varvec{j}}_{\mathrm{I}}, \quad \dot{{\varvec{h}}}_{\mathrm{b}}=I_{yb}\ddot{\theta }{\varvec{j}}_{\mathrm{I}}. \end{aligned}$$

The aerodynamic contribution of the body is neglected, and hence, the body exhibits gravitational forces only with no moments. Thus, the body force in the inertial frame is written as

$$\begin{aligned} {\varvec{f}}_{\mathrm{b}}^{(\mathrm{I})}= [0,\;\; 0,\;\; m_{\mathrm{b}} g]^*. \end{aligned}$$

1.2 Wing

The linear velocity of the reference point of the wing frame (the hinge root) and its angular velocity are written as

$$\begin{aligned} {\varvec{v}}_{\mathrm{w}} = ({\dot{x}}-x_{\mathrm{h}}{{\dot{\theta }}}\sin \theta ) {\varvec{i}}_{\mathrm{I}} + ({\dot{z}}-x_{\mathrm{h}} {{\dot{\theta }}}\cos \theta ) {\varvec{k}}_{\mathrm{I}}, {\varvec{\omega }}_{\mathrm{w}} = {{\dot{\theta }}} {\varvec{j}}_{\mathrm{b}}-{{\dot{\varphi }}} {\varvec{k}}_{\mathrm{s}}+{{\dot{\eta }}}{\varvec{j}}_{\mathrm{w}}. \end{aligned}$$

Thus, one obtains

$$\begin{aligned} \frac{\partial {\varvec{v}}_{\mathrm{w}}}{\partial {\dot{x}}}&= {\varvec{i}}_{\mathrm{I}} ~&\frac{\partial {\varvec{v}}_{\mathrm{w}}}{\partial {\dot{z}}}&= {\varvec{k}}_{\mathrm{I}} ~&\frac{\partial {\varvec{v}}_{\mathrm{w}}}{\partial {{\dot{\theta }}}}&= -x_{\mathrm{h}}(\sin \theta {\varvec{i}}_{\mathrm{I}}+\cos \theta {\varvec{k}}_{\mathrm{I}}) ~&\frac{\partial {\varvec{v}}_{\mathrm{w}}}{\partial {{\dot{\varphi }}}}&= {\varvec{0}} ~&\frac{\partial {\varvec{v}}_{\mathrm{w}}}{\partial {{\dot{\eta }}}}&= {\varvec{0}} ~ \nonumber \\ \frac{\partial {\varvec{\omega }}_{\mathrm{w}}}{\partial {\dot{x}}}&= {\varvec{0}} ~&\frac{\partial {\varvec{\omega }}_{\mathrm{w}}}{\partial {\dot{z}}}&= {\varvec{0}} ~&\frac{\partial {\varvec{\omega }}_{\mathrm{w}}}{\partial {{\dot{\theta }}}}&= {\varvec{j}}_{\mathrm{I}} ~&\frac{\partial {\varvec{\omega }}_{\mathrm{w}}}{\partial {{\dot{\varphi }}}}&= -{\varvec{k}}_{\mathrm{b}} ~&\frac{\partial {\varvec{\omega }}_{\mathrm{w}}}{\partial {{\dot{\eta }}}}&= -{\varvec{j}}_{\mathrm{w}} , \end{aligned}$$

and

$$\begin{aligned} \dot{{\varvec{v}}}_{\mathrm{w}}=[\ddot{x}-x_{\mathrm{h}}\ddot{\theta }\sin \theta -x_{\mathrm{h}}{{\dot{\theta }}}^2\cos \theta ] {\varvec{i}}_{\mathrm{I}} + [\ddot{z} -x_{\mathrm{h}}\ddot{\theta }\cos \theta +x_{\mathrm{h}}{{\dot{\theta }}}^2\sin \theta ] {\varvec{k}}_{\mathrm{I}}. \end{aligned}$$

The rotation matrix from the inertial frame to the stroke plane frame is given by

$$\begin{aligned} {\varvec{R}}_\beta = \left[ \begin{array}{ccc} \cos \beta &{}\quad 0 &{}\quad -\sin \beta \\ 0 &{}\quad 1&{}\quad 0 \\ \sin \beta &{}\quad 0 &{}\quad \cos \beta \end{array} \right] , \end{aligned}$$

and rotation matrices from the stroke plane frame to the wing frame are

$$\begin{aligned} {\varvec{R}}_\varphi = \left[ \begin{array}{ccc} \cos \varphi &{}\quad -\sin \varphi &{}\quad 0 \\ \sin \varphi &{}\quad \cos \varphi &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \end{array} \right] \;\;,\;\; {\varvec{R}}_\eta = \left[ \begin{array}{ccc} \cos \eta &{}\quad 0 &{}\quad -\sin \eta \\ 0 &{}\quad 1&{}\quad 0 \\ \sin \eta &{}\quad 0 &{}\quad \cos \eta \end{array} \right] , \end{aligned}$$

and

$$\begin{aligned} {\varvec{R}}_{\mathrm{ws}} = {\varvec{R}}_\eta {\varvec{R}}_\varphi . \end{aligned}$$

The wing angular velocity vector in the wing frame is

$$\begin{aligned} {\varvec{\omega }}_{\mathrm{w}}^{(\mathrm{w})} = \left( \begin{array}{c} \omega _1 \\ \omega _2 \\ \omega _3 \end{array} \right) = {\varvec{R}}_{\mathrm{ws}} \left( \begin{array}{c} 0 \\ {{\dot{\theta }}} \\ -{{\dot{\varphi }}} \end{array} \right) + \left( \begin{array}{c} 0 \\ {{\dot{\eta }}} \\ 0 \end{array} \right) = \left( \begin{array}{c} {{\dot{\varphi }}}\sin \eta - {{\dot{\theta }}}\cos \eta \sin \varphi \\ {{\dot{\theta }}}\cos \varphi +{{\dot{\eta }}} \\ -{{\dot{\varphi }}}\cos \eta -{{\dot{\theta }}}\sin \eta \sin \varphi \end{array} \right) . \end{aligned}$$

The position vector pointing from the hinge root to the wing center of gravity is ${{\varvec{\rho _c}}}_{\mathrm{w}}=-{\hat{d}}{\varvec{i}}_{\mathrm{w}} + r_{\mathrm{cg}} {\varvec{j}}_{\mathrm{w}}$ where ${\hat{d}}$ and $r_{\mathrm{cg}}$ are the distances between the wing root hinge point and the wing center of gravity along the negative $x_{\mathrm{w}}$-axis and the $y_{\mathrm{w}}$-axis, respectively. Thus, the inertial acceleration is obtained as

$$\begin{aligned} {\ddot{{\varvec{\rho _c}}}}_{\mathrm{w}}^{(\mathrm{w})}= \left( \begin{array}{c} \ddot{\rho }_1 \\ \ddot{\rho }_2 \\ \ddot{\rho }_3 \end{array} \right) = \left( \begin{array}{c} {\hat{d}}(\omega _2^2+\omega _3^2) - r_{\mathrm{cg}}({{\dot{\omega }}}_3-\omega _1\omega _2) \\ -{\hat{d}}({{\dot{\omega }}}_3+\omega _1\omega _2) - r_{\mathrm{cg}}(\omega _1^2+\omega _3^2) \\ {\hat{d}}({{\dot{\omega }}}_2-\omega _1\omega _3) + r_{\mathrm{cg}}({{\dot{\omega }}}_1+\omega _2\omega _3) \end{array} \right) . \end{aligned}$$

Assuming the wing reference frame is fixed in the wing principal axes, the inertial time derivative of the angular momentum vector represented in the wing frame is written as

$$\begin{aligned} \dot{{\varvec{h}}}_{\mathrm{w}}^{(\mathrm{w})}= \left( \begin{array}{c} \dot{h}_1 \\ \dot{h}_2 \\ \dot{h}_3 \end{array} \right) = \left( \begin{array}{c} I_x {{\dot{\omega }}}_1 +(I_z-I_y)\omega _2\omega _3\\ I_y {{\dot{\omega }}}_y +(I_x-I_z)\omega _1\omega _3 \\ I_z {{\dot{\omega }}}_3 +(I_y-I_x)\omega _1\omega _2 \end{array} \right) . \end{aligned}$$

The wing is subject to aerodynamic and gravitational forces. Noting that the $y_b$-components of the aerodynamic force on each wing are equal and opposite, the force vector applied on the wing is written as

$$\begin{aligned} {\varvec{f}}_{\mathrm{w}}=\left( \begin{array}{c} F_x \\ 0 \\ F_z \end{array} \right) ^{(\mathrm{w})} + \left( \begin{array}{c} 0 \\ 0 \\ m_{\mathrm{w}} g \end{array} \right) ^{(\mathrm{I})}, \end{aligned}$$

where $F_x$ and $F_z$ are the aerodynamic loads along the $x_{\mathrm{w}}$ and $z_{\mathrm{w}}$ directions, respectively. The moment vector comprises three contributions: aerodynamic, gravitational, and the control torque. The aerodynamic contribution ${\varvec{M}}_{\mathrm{a}_{\mathrm{w}}}$ is determined by integrating the radial distributions of the forces $F_x$ and $F_z$ over the wing. That is, ${\varvec{M}}_{\mathrm{a}_{\mathrm{w}}}=M_x {\varvec{i}}_{\mathrm{w}}+M_y {\varvec{j}}_{\mathrm{w}}+M_z {\varvec{k}}_{\mathrm{w}}$, where

$$\begin{aligned} M_x=2\int _0^R F_z'(r) r \hbox {d}r, \;\; M_y=2\int _0^R F_z'(r) d_{\mathrm{ac}}(r) \hbox {d}r, \;\; \text{ and } \;\; M_z=-2\int _0^R F_x'(r) r \hbox {d}r, \end{aligned}$$

where $F_x'(r)$ and $F_z'(r)$ are the two-dimensional aerodynamic loads on an airfoil that is at distance r from the wing root and $d_{\mathrm{ac}}(r)$ is the distance between the hinge line and the quarter chord line (aerodynamic center) at each airfoil section along $x_{\mathrm{w}}$ direction. The gravitational contribution is written as ${\varvec{M}}_{\mathrm{g}_{\mathrm{w}}}= (-{\hat{d}}{\varvec{i}}_{\mathrm{w}}+ r_{\mathrm{cg}}{\varvec{j}}_{\mathrm{w}}) \times m_{\mathrm{w}} g{\varvec{k_{\mathrm{I}}}}$. The last contribution (the control torque) is written as ${\varvec{M}}_{\mathrm{c}_{\mathrm{w}}}= -\tau _\varphi {\varvec{k}}_{\mathrm{s}}+\tau _\eta {\varvec{j}}_{\mathrm{w}}$, where $\tau _\varphi$ and $\tau _\eta$ are the actuating torque along the flapping and pitching directions, respectively.

Constructing all the required terms to apply the principle of virtual power (1), the five-DOF equations of motion are obtained as (with obvious correspondence to the abstract form (2))

$$\begin{aligned}&m_{\mathrm{w}} \biggl (\ddot{\rho _1} \left( \cos {\beta } \cos {\eta } \cos {\varphi }-\sin {\beta } \sin {\eta }\right) +\ddot{\rho _3} \left( \cos {\beta } \sin {\eta } \cos {\varphi }+\sin {\beta } \cos {\eta }\right) \nonumber \\&\qquad +\,\ddot{\rho _2} \cos {\beta } \sin {\varphi }- x_{\mathrm{h}} \ddot{\theta } \sin {\theta }-x_{\mathrm{h}} {\dot{\theta }}^2 \cos {\theta }\biggr ) + m_{\mathrm{v}} {\dot{u}} \nonumber \\&\quad =F_x \left( \cos {\beta } \cos {\eta } \cos {\varphi }-\sin {\beta } \sin {\eta }\right) +F_z \left( \cos {\beta } \sin {\eta } \cos {\varphi }+\sin {\beta } \cos {\eta }\right) \end{aligned}$$

(32)

$$\begin{aligned}&\qquad - m_{\mathrm{w}} \biggl (\ddot{\rho _1} \left( \sin {\beta } \cos {\eta } \cos {\varphi }+\cos {\beta } \sin {\eta }\right) +\ddot{\rho _3}\left( \sin {\beta } \sin {\eta } \cos {\varphi }- \cos {\beta } \cos {\eta }\right) \nonumber \\&\qquad +\,\ddot{\rho _2} \sin {\beta } \sin {\varphi }+ x_{\mathrm{h}} \ddot{\theta } \cos {\theta }-x_{\mathrm{h}} {\dot{\theta }}^2 \sin {\theta }\biggr )+ m_{\mathrm{v}} ({\dot{w}}-g) \nonumber \\&\quad =-F_x \left( \sin {\beta } \cos {\eta } \cos {\varphi }+\cos {\beta } \sin {\eta }\right) - F_z \left( \sin {\beta } \sin {\eta } \cos {\varphi }-\cos {\beta } \cos {\eta }\right) \nonumber \\ \end{aligned}$$

(33)

$$\begin{aligned}&m_{\mathrm{w}} \biggl [-x_{\mathrm{h}} \biggl (\ddot{\theta }~ {\hat{d}} \left( \cos {\beta } \cos {\eta } \cos {\theta } \cos {\varphi }+\sin {\beta } \cos {\eta } \sin {\theta } \cos {\varphi }-\sin {\beta } \sin {\eta } \cos {\theta } \right. \nonumber \\&\qquad \left. +\,\cos {\beta } \sin {\eta } \sin {\theta }\right) - \ddot{\theta }~ r_{\mathrm{cg}} \sin {\varphi }\cos (\beta -\theta )+ {\dot{\theta }}^2 \nonumber \\&\qquad \left( -r_{\mathrm{cg}} \sin {\varphi } \sin (\beta -\theta )+{\hat{d}} \cos {\eta } \cos {\varphi } \sin (\beta -\theta )+{\hat{d}} \sin {\eta } \cos (\beta -\theta )\right) \biggr )\nonumber \\&\qquad +\, {\dot{u}} \left( -\sin {\beta }~ r_{\mathrm{cg}} \sin {\varphi }+{\hat{d}} \sin {\beta } \cos {\eta } \cos {\varphi }+{\hat{d}} \cos {\beta } \sin {\eta }\right) \nonumber \\&\qquad +\, {\dot{w}} \left( -\cos {\beta }~ r_{\mathrm{cg}} \sin {\varphi }+{\hat{d}}\cos {\beta } \cos {\eta } \cos {\varphi }-{\hat{d}} \sin {\beta } \sin {\eta }\right) \biggr ]\nonumber \\&\qquad +\, I_{y_b} \ddot{\theta }+x_{\mathrm{h}} m_{\mathrm{w}} \biggl [\ddot{\rho _3} \sin {\beta } \sin {\eta } \cos {\theta } \cos {\varphi }+\ddot{\rho _1}\left( \cos {\eta } \cos {\varphi } \sin (\beta -\theta )\right. \nonumber \\&\qquad \left. +\,\sin {\eta } \cos (\beta -\theta )\right) - \ddot{\rho _3}\left( \cos {\beta } \sin {\eta } \sin {\theta } \cos {\varphi }\right. \nonumber \\&\qquad \left. -\, \cos {\beta } \cos {\eta } \cos {\theta }- \sin {\beta } \cos {\eta } \sin {\theta }\right) +\ddot{\rho _2} \sin {\varphi } \sin (\beta -\theta )+g \cos {\theta }\nonumber \\&\qquad +\, x_{\mathrm{h}} \ddot{\theta }-{\dot{u}} \sin {\theta } -{\dot{w}} \cos {\theta } \biggr ]-\dot{h_3} \sin {\eta } \sin {\varphi }-\dot{h_1} \cos {\eta } \sin {\varphi }+\dot{h_2} \cos {\varphi }\nonumber \\&\quad = \tau _{\eta } \cos {\varphi } - F_z~ x_{\mathrm{h}} \biggl (\sin {\beta } \left( \cos {\eta } \sin {\theta }-\sin {\eta } \cos {\theta } \cos {\varphi }\right) \nonumber \\&\qquad +\,\cos {\beta } (\sin {\eta } \sin {\theta } \cos {\varphi }+\cos {\eta } \cos {\theta })\biggr )\nonumber \\&\qquad +\, F_x x_{\mathrm{h}} (\cos {\eta } \cos {\varphi } \sin (\beta -\theta )+\sin {\eta } \cos (\beta -\theta )) \nonumber \\&\qquad -\,M_x \cos {\eta } \sin {\varphi }+M_y \cos {\varphi }-M_z \sin {\eta } \sin {\varphi } \end{aligned}$$

(34)

$$\begin{aligned}&r_{\mathrm{cg}}~ x_{\mathrm{h}}~ m_{\mathrm{w}} \cos {\varphi } \biggl (\ddot{\theta } \cos {\theta } \sin {\beta }- \ddot{\theta } \sin {\theta } \cos {\beta }-2 {\dot{\theta }}^2 \cos {\theta } \cos {\beta } -2~ {\dot{\theta }}^2 \sin {\theta } \sin {\beta }\biggr )\nonumber \\&\qquad +\, r_{\mathrm{cg}}~ m_{\mathrm{w}} \cos {\varphi } \biggl ({\dot{u}} \cos {\beta }+ u~ {\dot{\theta }} \sin {\beta }- {\dot{w}}~ \sin {\beta }+ w~ {\dot{\theta }} \cos {\beta } \biggr )\nonumber \\&\qquad +\, {\hat{d}}~x_{\mathrm{h}}~ m_{\mathrm{w}} \cos {\eta } \sin {\varphi } \biggl ( \ddot{\theta } \cos {\theta } \sin {\beta } - \ddot{\theta } \sin {\theta } \cos {\beta } -2~ {\dot{\theta }}^2 \cos {\theta } \cos {\beta } \nonumber \\&\qquad -\,2~ {\dot{\theta }}^2 \sin {\theta } \sin {\beta } \biggr ) + {\hat{d}}~m_{\mathrm{w}} \cos {\eta } \sin {\varphi } \biggl ( {\dot{u}} \cos {\beta } + u~ {\dot{\theta }} \sin {\beta } - {\dot{w}}~ \sin {\beta } \nonumber \\&\qquad +\, w~ {\dot{\theta }} \cos {\beta } \biggr ) +\dot{h_1} \sin {\eta }-\dot{h_3} \cos {\eta } = \tau _{\varphi } +M_x \sin {\eta }-M_z \cos {\eta } \end{aligned}$$

(35)

$$\begin{aligned}&{\hat{d}}~x_{\mathrm{h}}~ m_{\mathrm{w}} \biggl ( \ddot{\theta } \sin {\eta } \cos {\theta } \cos {\varphi } \sin {\beta }- \ddot{\theta } \sin {\eta } \sin {\theta } \cos {\varphi } \cos {\beta } - \ddot{\theta } \cos {\eta } \cos {\theta } \cos {\beta }\nonumber \\&\qquad -\, \ddot{\theta } \cos {\eta } \sin {\theta }\sin {\beta }- 2~ {\dot{\theta }}^2 \sin {\eta } \cos {\theta } \cos {\varphi } \cos {\beta }-2~ {\dot{\theta }}^2 \sin {\eta } \sin {\theta } \cos {\varphi } \sin {\beta } \nonumber \\&\qquad -\,2~ {\dot{\theta }}^2 \cos {\eta } \cos {\theta } \sin {\beta } +2~ {\dot{\theta }}^2 \cos {\eta } \sin {\theta } \cos {\beta }\biggr )\nonumber \\&\qquad +\, {\hat{d}}~m_{\mathrm{w}} \biggl ( {\dot{u}}~ \sin {\eta } \cos {\varphi } \cos {\beta } + {\dot{u}}~ \cos {\eta } \sin {\beta } + u~ {\dot{\theta }} \sin {\eta } \cos {\varphi }\sin {\beta }\nonumber \\&\qquad -\, u~{\dot{\theta }} \cos {\eta } \cos {\beta }- \sin {\eta } \cos {\varphi } \sin {\beta }~ {\dot{w}}\nonumber \\&\qquad +\, {\dot{w}} \cos {\eta } \cos {\beta }+w~ {\dot{\theta }} \sin {\eta } \cos {\varphi } \cos {\beta }+ w~ {\dot{\theta }} \cos {\eta } \sin {\beta }\biggr )+\dot{h_2}=\tau _{\eta }+M_y, \nonumber \\ \end{aligned}$$

(36)

where $m_{\mathrm{v}}=m_{\mathrm{b}}+m_{\mathrm{w}}$.

Aerodynamic Model

The aerodynamic derivatives in Eq. (7) are defined below

$$\begin{aligned} F_{x_0}= & {} \rho \pi \left( k I_{11}-\frac{1}{4} I_{12}\right) \sin {\eta }~ {\dot{\eta }} {\dot{\varphi }}\\ F_{z_0}= & {} -\frac{1}{2} \rho ~ C_{L_\alpha } I_{21} \sin {\eta }~ {\dot{\varphi }} \left| {\dot{\varphi }}\right| -\rho \pi \left( k I_{11}-\frac{1}{4} I_{12}\right) \cos {\eta }~ {\dot{\eta }} {\dot{\varphi }}\\ M_{x_0}= & {} -\frac{1}{2} \rho ~ C_{L_\alpha } I_{31} \sin {\eta }~ {\dot{\varphi }} \left| {\dot{\varphi }}\right| -\rho \pi \left( k I_{21}-\frac{1}{4} I_{22}\right) \cos {\eta }~{\dot{\eta }} {\dot{\varphi }} \\ M_{y_0}= & {} \frac{3}{4} \biggl (-\frac{1}{2} \rho ~ C_{L_\alpha } I_{22} \sin {\eta }~ {\dot{\varphi }} \left| {\dot{\varphi }}\right| -\rho \pi \left( k I_{12}-\frac{1}{4} I_{13}\right) \cos {\eta }~{\dot{\eta }} {\dot{\varphi }} \biggr )-k~F_{z_0}\\ M_{z_0}= & {} -\rho \pi \left( k I_{21}-\frac{1}{4} I_{22}\right) \sin {\eta }~ {\dot{\eta }} {\dot{\varphi }} \\ F_{x_u}= & {} \rho \pi \left( k I_{01}-\frac{1}{4} I_{02}\right) \left( \cos {\beta } \sin {\eta } \cos {\varphi }+\sin {\beta } \cos {\eta }\right) {\dot{\eta }}\\ F_{x_w}= & {} -\rho \pi \left( k I_{01}-\frac{1}{4} I_{02}\right) \left( \sin {\beta } \sin {\eta } \cos {\varphi }-\cos {\beta } \cos {\eta }\right) {\dot{\eta }}\\ F_{x_q}= & {} \rho \pi \left( k I_{11}-\frac{1}{4} I_{12}\right) \sin {\eta } \cos {\varphi }~ {\dot{\varphi }} -\rho \pi \biggl (x_{\mathrm{h}} \left( k I_{01}-\frac{1}{4} I_{02}\right) \left( \cos {\eta } \cos {(\beta -\theta )}\right. \\&\left. -\,\sin {\eta } \cos {\varphi } \sin {(\beta -\theta )}\right) + \cos {\eta } \sin {\varphi } \left( k I_{11}-\frac{1}{4}I_{12}\right) \biggr ) {\dot{\eta }} \\ F_{x_{nl}}= & {} \rho \pi \cos {\varphi }~ {\dot{\theta }} \left( k I_{01}-\frac{1}{4} I_{02}\right) \biggl ( u \left( \cos {\beta } \sin {\eta } \cos {\varphi }+\sin {\beta } \cos {\eta }\right) \\&+\, w \left( \cos {\beta } \cos {\eta }-\sin {\beta } \sin {\eta } \cos {\varphi }\right) \biggr )\\&-\, \rho \pi \biggl (x_{\mathrm{h}} \cos {\varphi } \left( k I_{01}-\frac{1}{4} I_{02}\right) \left( \cos {\eta } \cos {(\beta -\theta )}-\sin {\eta } \cos {\varphi } \sin {(\beta -\theta )}\right) \\&+\,\cos {\eta } \sin {\varphi } \left( k I_{11}-\frac{1}{4} I_{12}\right) \biggr ) {\dot{\theta }}^2 \\ F_{z_u}= & {} -\frac{1}{2} \rho ~ C_{L_\alpha } I_{11} (2 \cos {\beta } \sin {\eta } \cos {\varphi }+\sin {\beta } \cos {\eta }) \left| {\dot{\varphi }}\right| \\&-\,\rho \pi \left( k I_{01}-\frac{1}{4} I_{02}\right) \left( \cos {\beta } \cos {\eta } \cos {\varphi }-\sin {\beta } \sin {\eta }\right) ~{\dot{\eta }} \\ F_{z_w}= & {} \rho \pi \left( k I_{01}-\frac{1}{4} I_{02}\right) \left( \sin {\beta } \cos {\eta } \cos {\varphi }+\cos {\beta } \sin {\eta }\right) ~{\dot{\eta }} \\&-\,\frac{1}{2} \rho ~ C_{L_\alpha } I_{11} \left( \cos {\beta } \cos {\eta }-2 \sin {\beta } \sin {\eta } \cos {\varphi }\right) \left| {\dot{\varphi }}\right| \\ F_{z_q}= & {} \frac{1}{2} \rho ~ C_{L_\alpha } I_{21} \cos {\eta } \sin {\varphi }~\left| {\dot{\varphi }}\right| +\\&+\, \rho ~ C_{L_\alpha } I_{11} \left| {\dot{\varphi }}\right| \biggl (x_{\mathrm{h}} \sin {\beta } \sin {\eta } \cos {\theta } \cos {\varphi }+\frac{1}{2} \cos {\beta } \left( 2 x_{\mathrm{h}} \sin {\eta } \sin {\theta } \cos {\varphi }\right. \\&\left. +\,x_{\mathrm{h}} \cos {\eta } \cos {\theta }\right) + \frac{1}{2} x_{\mathrm{h}} \sin {\beta } \cos {\eta } \sin {\theta }\biggr ) \\&+\, \rho \pi ~ x_{\mathrm{h}} \cos {\eta } \cos {\varphi } \sin (\beta -\theta ) \left( \frac{1}{4} I_{02}-k I_{01}\right) {\dot{\eta }}\\&+\,\rho \pi ~ x_{\mathrm{h}} \sin {\eta } \cos (\beta -\theta ) \left( \frac{1}{4} I_{02}-k I_{01}\right) {\dot{\eta }} - \rho \pi \sin {\eta } \sin {\varphi } \left( k I_{11}-\frac{1}{4} I_{12}\right) {\dot{\eta }}\\&-\, \rho \pi \cos {\eta } \cos {\varphi } \left( k I_{11}-\frac{1}{4} I_{12}\right) {\dot{\varphi }} \\ F_{z_{nl}}= & {} -\rho \pi ~\cos {\varphi }~ {\dot{\theta }} \left( k I_{01}-\frac{1}{4} I_{02}\right) \biggl ( u~ (\cos {\beta } \cos {\eta } \cos {\varphi }-\sin {\beta } \sin {\eta })\\&+\, w~ (\sin {\beta } \cos {\eta } \cos {\varphi }+\cos {\beta } \sin {\eta })\biggr )\\&+\, {\dot{\theta }}^2 \biggl (2 \pi \rho x_{\mathrm{h}} \cos {\varphi } \left( \frac{1}{4} I_{02}-k I_{01}\right) \left( \cos {\eta } \cos {\varphi } \sin (\beta -\theta )+\sin {\eta } \cos (\beta -\theta )\right) \\&-\, 2 \pi \rho \sin {\eta } \sin {\varphi } \cos {\varphi } \left( k I_{11}-\frac{1}{4} I_{12}\right) \biggr ) \\ M_{x_u}= & {} -\frac{1}{2} \rho ~ C_{L_\alpha } I_{21} \left( 2 \cos {\beta } \sin {\eta } \cos {\varphi }+\sin {\beta } \cos {\eta }\right) \left| {\dot{\varphi }}\right| \\&-\,\rho \pi \left( k I_{11}-\frac{1}{4} I_{12}\right) (\cos {\beta } \cos {\eta } \cos {\varphi }-\sin {\beta } \sin {\eta }) ~{\dot{\eta }} \\ M_{x_w}= & {} \rho \pi \left( k I_{11}-\frac{1}{4} I_{12}\right) \left( \sin {\beta } \cos {\eta } \cos {\varphi }+\cos {\beta } \sin {\eta }\right) ~{\dot{\eta }}\\&-\,\frac{1}{2} \rho ~ C_{L_\alpha } I_{21} (\cos {\beta } \cos {\eta }-2 \sin {\beta } \sin {\eta } \cos {\varphi }) \left| {\dot{\varphi }}\right| \\ \end{aligned}$$

$$\begin{aligned} M_{x_q}= & {} \frac{1}{2} \rho ~ C_{L_\alpha } I_{31} \cos {\eta } \sin {\varphi }~\left| {\dot{\varphi }}\right| +\rho ~ C_{L_\alpha } I_{21} \left| {\dot{\varphi }}\right| \biggl (x_{\mathrm{h}} \sin {\beta } \sin {\eta } \cos {\theta } \cos {\varphi }\\&+\, \frac{1}{2} \cos {\beta } (2 x_{\mathrm{h}} \sin {\eta } \sin {\theta } \cos {\varphi }+x_{\mathrm{h}} \cos {\eta } \cos {\theta })+\frac{1}{2} x_{\mathrm{h}} \sin {\beta } \cos {\eta } \sin {\theta }\biggr )\\&+\,\rho \pi x_{\mathrm{h}} \left( \frac{1}{4} I_{12}-k I_{11}\right) {\dot{\eta }}~ \biggl ( \cos {\eta } \cos {\varphi } \sin (\beta -\theta ) + \sin {\eta } \cos (\beta -\theta ) \biggr ) \\&-\, \rho \pi ~ \left( k I_{21}-\frac{1}{4} I_{22}\right) \biggl ( \sin {\eta } \sin {\varphi } ~{\dot{\eta }} - \cos {\eta } \cos {\varphi }~{\dot{\varphi }} \biggr ) \\ M_{x_{nl}}= & {} -\rho \pi ~ \cos {\varphi } \left( k I_{11}-\frac{1}{4} I_{12}\right) \left( \cos {\beta } \cos {\eta } \cos {\varphi }-\sin {\beta } \sin {\eta }\right) ~ {\dot{\theta }}~u\\&+\, \rho \pi ~ \cos {\varphi } \left( k I_{11}-\frac{1}{4} I_{12}\right) \left( \sin {\beta } \cos {\eta } \cos {\varphi }+\cos {\beta } \sin {\eta }\right) ~{\dot{\theta }}~w\\&+\, {\dot{\theta }}^2 \biggl (2 \rho \pi x_{\mathrm{h}} \cos {\varphi } \left( \frac{1}{4} I_{12}-k I_{11}\right) \left( \cos {\eta } \cos {\varphi } \sin (\beta -\theta )+\sin {\eta } \cos (\beta -\theta )\right) \\&-\, 2 \rho \pi \sin {\eta } \sin {\varphi } \cos {\varphi } \left( k I_{21}-\frac{1}{4} I_{22}\right) \biggr ) \\ M_{y_u}= & {} \frac{3}{4} \biggl (-\frac{1}{2} \rho ~ C_{L_\alpha } I_{12} (2 \cos {\beta } \sin {\eta } \cos {\varphi }+\sin {\beta } \cos {\eta }) \left| {\dot{\varphi }}\right| \\&-\,\rho \pi \left( k I_{02}-\frac{1}{4} I_{03}\right) (\cos {\beta } \cos {\eta } \cos {\varphi }-\sin {\beta } \sin {\eta })~{\dot{\eta }}\biggr )- k~F_{z_u} \\ M_{y_w}= & {} \frac{3}{4} \biggl (\rho \pi \left( k I_{02}-\frac{1}{4} I_{03}\right) \left( \sin {\beta } \cos {\eta } \cos {\varphi }+\cos {\beta } \sin {\eta }\right) ~{\dot{\eta }} \\&-\,\frac{1}{2} \rho ~ C_{L_\alpha } I_{12} \left( \cos {\beta } \cos {\eta }-2 \sin {\beta } \sin {\eta } \cos {\varphi }\right) \left| {\dot{\varphi }}\right| \biggr )- k~F_{z_w} \\ \end{aligned}$$

$$\begin{aligned} M_{y_q}= & {} \frac{3}{4} \biggl (\frac{1}{2} \rho ~ C_{L_\alpha } I_{22} \cos {\eta } \sin {\varphi } \left| {\dot{\varphi }}\right| +\rho ~ C_{L_\alpha } I_{12} \left| {\dot{\varphi }}\right| \biggl [x_{\mathrm{h}} \sin {\beta } \sin {\eta } \cos {\theta } \cos {\varphi }\\&+\, \frac{1}{2} \cos {\beta } \left( 2 x_{\mathrm{h}} \sin {\eta } \sin {\theta } \cos {\varphi }+x_{\mathrm{h}} \cos {\eta } \cos {\theta }\right) +\frac{1}{2} x_{\mathrm{h}} \sin {\beta } \cos {\eta } \sin {\theta }\biggr ]\\&+\, \rho \pi x_{\mathrm{h}} \cos {\eta } \cos {\varphi } \sin (\beta -\theta ) \left( \frac{1}{4} I_{03}-k I_{02}\right) {\dot{\eta }}\\&+\,\rho \pi x_{\mathrm{h}} \sin {\eta } \cos (\beta -\theta ) \left( \frac{1}{4} I_{03}-k I_{02}\right) {\dot{\eta }}\\&-\, \rho \pi \sin {\eta } \sin {\varphi } \left( k I_{12}-\frac{1}{4} I_{13}\right) {\dot{\eta }}-\rho \pi \cos {\eta } \cos {\varphi } \left( k I_{12}-\frac{1}{4} I_{13}\right) {\dot{\varphi }} \biggr )-k~F_{z_q} \\ M_{y_{nl}}= & {} \frac{3}{4} \biggl (-\rho \pi \left( k I_{02}-\frac{1}{4} I_{03}\right) \cos {\varphi }~ {\dot{\theta }} \biggl [ u~ (\cos {\beta } \cos {\eta } \cos {\varphi }\\&\qquad -\,\sin {\beta } \sin {\eta })- w~ (\sin {\beta } \cos {\eta } \cos {\varphi }+\cos {\beta } \sin {\eta }) \biggr ]\\&+\, {\dot{\theta }}^2 \biggl [2 \rho \pi x_{\mathrm{h}} \left( \frac{1}{4} I_{03}-k I_{02}\right) \cos {\varphi }~ (\cos {\eta } \cos {\varphi } \sin (\beta -\theta )+\sin {\eta } \cos (\beta -\theta ))\\&-\, 2 \rho \pi \left( k I_{12}-\frac{1}{4} I_{13}\right) \sin {\eta } \sin {\varphi } \cos {\varphi }\biggr ]\biggr )-k~F_{z_{nl}} \\ M_{z_u}= & {} - \rho \pi \left( k I_{11}-\frac{1}{4} I_{12}\right) \left( \cos {\beta } \sin {\eta } \cos {\varphi }+\sin {\beta } \cos {\eta }\right) {\dot{\eta }} \\ M_{z_w}= & {} \rho \pi \left( k I_{11}-\frac{1}{4} I_{12}\right) \left( \sin {\beta } \sin {\eta } \cos {\varphi }-\cos {\beta } \cos {\eta }\right) {\dot{\eta }} \\ M_{z_q}= & {} \rho \pi \biggl (x_{\mathrm{h}} \left( k I_{11}-\frac{1}{4} I_{12}\right) \left( \cos {\eta } \cos {(\beta -\theta )}-\sin {\eta } \cos {\varphi } \sin {(\beta -\theta )}\right) \\&+\,\cos {\eta } \sin {\varphi } \left( k I_{21}-\frac{1}{4} I_{22}\right) \biggr )~ {\dot{\eta }} - \rho \pi \left( k I_{21}-\frac{1}{4}I_{22}\right) \sin {\eta } \cos {\varphi }~ {\dot{\varphi }} \\ M_{z_{nl}}= & {} -\rho \pi \left( k I_{11}-\frac{1}{4} I_{12}\right) \cos {\varphi }~{\dot{\theta }} \biggl ( u \left( \cos {\beta } \sin {\eta } \cos {\varphi }+\sin {\beta } \cos {\eta }\right) \\&+\, w \left( \cos {\beta } \cos {\eta }-\sin {\beta } \sin {\eta } \cos {\varphi }\right) \biggr )\\&+\, \rho \pi ~ {\dot{\theta }}^2 \biggl (x_{\mathrm{h}} \cos {\varphi } \left( k I_{11}-\frac{1}{4} I_{12}\right) \left( \cos {\eta } \cos {(\beta -\theta )}\right. \\&\left. -\,\sin {\eta } \cos {\varphi } \sin {(\beta -\theta )}\right) +\cos {\eta } \sin {\varphi } \left( k I_{21}-\frac{1}{4} I_{22}\right) \biggr ), \\ \end{aligned}$$

where $k=c_r (1-x_{or})$, $c_r$ is the wing root chord, $x_{or}$ is the position of the hinge point along $x_w$ normalized by the root chord, and $x_{\mathrm{h}}$ is the distance from the vehicle center of mass to the root of the wing hinge line (i.e., the intersection of the hinge line with the $x_b$-axis). Also, $\rho$ is the air density, $C_{L_\alpha }$ is the three-dimensional lift curve slope of the wing, c(r) is the spanwise chord distribution, R is the wing radius, and $I_{mn}=2\int _0^R {r^m c^n(r) \,\hbox {d}r}$.

The Linearized Dynamics of the Averaged Three-DOF System

The linearized averaged version of the three-DOF system (8) at the trim condition can be written abstractly as

(37)

where the elements of the matrix ${\varvec{A}}$ can be written as (some elements have quite lengthy expressions, and hence, we only write their limits as the wing mass goes to zero):

$$\begin{aligned} \lim _{m_{\mathrm{w}}\rightarrow 0} A_{42}=\,&0 \\ \lim _{m_{\mathrm{w}}\rightarrow 0} A_{43}=\,&\frac{0.25 A I_{21} \rho U_1^2 \sin ^2{\alpha _m}+0.74 C_{L_\alpha } I_{21} \rho U_2^2 \sin ^2{\alpha _m}}{I_F^2 m_{\mathrm{v}} \omega ^2}\\&-\,\frac{98.86 C_{L_\alpha } I_{21} \rho U_2 \sin ^2{\alpha _m}}{I_F m_{\mathrm{v}} \omega }+\frac{3307 C_{L_\alpha } I_{21} \rho \sin ^2{\alpha _m}}{m_{\mathrm{v}}}\\ A_{44}=&\frac{1}{I_F I_{y_b} m_{\mathrm{v}} \omega } C_{L_\alpha } \rho \cos {\alpha _m} \biggl (\cos {\alpha _m} \biggl (I_{11} ({\bar{c}} {\hat{d}} k m_{\mathrm{w}} (0.98 U_2\\&-41.88 I_F \omega )+I_{y_b} (0.5 U_2-78.37 I_F \omega ))\\&+\, m_{\mathrm{w}} \left( {\bar{c}} {\hat{d}} I_{12} (31.4 I_F \omega -0.74 U_2)+I_{21} r_{\mathrm{cg}} (2.4 I_F \omega -0.02 U_2)\right) \\&+\, {\bar{c}} {\hat{d}} I_{21} m_{\mathrm{w}} \cos {\alpha _m} (0.12 U_2-19.27 I_F \omega )\biggr )\\&+\, m_{\mathrm{w}} r_{\mathrm{cg}} \left( 5.23 I_{11} I_F k \omega -0.12 I_{11} k U_2-3.92 I_{12} I_F \omega +0.09 I_{12} U_2\right) \biggr )\\ \lim _{m_{\mathrm{w}}\rightarrow 0}A_{45}=&\frac{C_{L_\alpha } I_{21} \rho U_2 \sin {\alpha _m} \cos {\alpha _m}}{I_F m_{\mathrm{v}} \omega }-\frac{42.5 C_{L_\alpha } I_{21} \rho \sin {\alpha _m} \cos {\alpha _m}}{m_{\mathrm{v}}}\\ \lim _{m_{\mathrm{w}}\rightarrow 0} A_{46}=&\frac{1}{I_F m_{\mathrm{v}} \omega } \biggl ( I_{11} k \rho (1.56 U_2-66.29 I_F \omega )+I_{12} \rho (16.57 I_F \omega -0.39 U_2)\biggr )\\ A_{52}=&\frac{1}{I_F^3 I_{y_b} \omega ^2} C_{L_\alpha } I_{y_{\mathrm{w}}} \rho \sin {\alpha _m} \sin {2 \alpha _m} \biggl (I_{21} k \left( -3230 I_F^2 \omega ^2\right. \\&\left. +\,96.6 I_F U_2 \omega -0.24 U_1^2-0.73 U_2^2\right) \\&+\, I_{22} \left( 2422 I_F^2 \omega ^2-72.43 I_F U_2 \omega +0.18 U_1^2+0.55 U_2^2\right) \\&+\, I_{31} \cos {\alpha _m} \left( -222 I_F^2 \omega ^2+10.5 I_F U_2 \omega -0.06 U_1^2-0.18 U_2^2\right) \biggr )\\ \lim _{m_{\mathrm{w}}\rightarrow 0} A_{53}=&0\\ A_{54}=&\frac{1}{I_F^2 I_{y_b} \omega } C_{L_\alpha } \rho \cos {\alpha _m} \biggl (I_{y_{\mathrm{w}}} \sin {2 \alpha _m} \biggl (-2.6 I_{11} I_F k \omega +\,0.06 I_{11} k U_2+1.96 I_{12} I_F \omega \\&{-}\,0.05 I_{12} U_2{+}\, I_{21} \cos {\alpha _m} (0.01 U_2-1.2 I_F \omega )\biggr ){+}I_{21} I_{y_b} \sin {\alpha _m} (U_2-42.5 I_F \omega )\biggr )\\ \end{aligned}$$

$$\begin{aligned} A_{55}=&\frac{1}{I_F^2 I_{y_b} \omega } C_{L_\alpha } \rho \sin {\alpha _m} \biggl (I_{y_{\mathrm{w}}} \sin {2 \alpha _m} \biggl (-12.25 I_{21} I_F k \omega \\&+\,0.12 I_{21} k U_2+9.19 I_{22} I_F \omega -0.09 I_{22} U_2\\&+\, I_{31} \cos {\alpha _m} (0.02 U_2-0.65 I_F \omega )\biggr )-I_{21} I_F I_{y_b} \omega \sin {\alpha _m}\biggr )\\ A_{56}=&\frac{1}{I_F^2 I_{y_b} \omega } \rho \sin {\alpha _m} \cos {\alpha _m} \biggl (C_{L_\alpha } I_{y_{\mathrm{w}}} \cos {\alpha _m} \left( 0.65 I_{21} I_F k \omega \right. \\&\left. -\,0.02 I_{21} k U_2-0.49 I_{22} I_F \omega +0.01 I_{22} U_2\right) \\&+\, C_{L_\alpha } I_{31} \left( 5.27 I_F I_{y_b} \omega +0.15 I_F I_{y_{\mathrm{w}}} \omega -0.12 I_{y_b} U_2-0.001 I_{y_{\mathrm{w}}} U_2\right) \\&+\, C_{L_\alpha } I_{31} I_{y_{\mathrm{w}}} \cos { 2 \alpha _m} (0.15 I_F \omega -0.001 U_2)\\&+\, I_{y_{\mathrm{w}}} \sin {\alpha _m} \biggl (k (-30 I_{11} I_F k \omega +0.19 I_{11} k U_2\\&+\, 30 I_{12} I_F \omega -0.19 I_{12} U_2)+I_{13} (0.04 U_2-5.6 I_F \omega )\biggr )\\&+\, I_{y_{\mathrm{w}}} (-2 I_{21} I_F k \omega +0.05 I_{21} k U_2+0.5 I_{22} I_F \omega -0.01 I_{22} U_2)\biggr )\\ A_{62}=&\frac{1}{I_F^2 I_{y_b} \omega ^2}C_{L_\alpha } \rho \sin {\alpha _m} \biggl (I_{21} k \left( -826 I_F^2 \omega ^2+24.7 I_F U_2 \omega -0.06 U_1^2-0.19 U_2^2\right) \\&+\,I_{22} \left( 619.6 I_F^2 \omega ^2-18.5 I_F U_2 \omega +0.05 U_1^2+0.14 U_2^2\right) \\&+\, I_{31} \cos {\alpha _m} \left( 1795 I_F^2 \omega ^2-84.4 I_F U_2 \omega +0.5 U_1^2+1.49 U_2^2\right) \biggr )\\ A_{63}=&\frac{1}{I_F^2 I_{y_b} m_{\mathrm{v}} \omega ^2}C_{L_\alpha } m_{\mathrm{w}} \rho \cos {\alpha _m} \biggl (\cos {\alpha _m} \biggl ({\bar{c}} {\hat{d}} \biggl (I_{11} k \left( -5.23 I_F U_2 \omega \right. \\&\left. +\,0.06 U_1^2+0.18 U_2^2\right) +\, I_{12} \left( 3.9 I_F U_2 \omega -0.05 U_1^2-0.14 U_2^2\right) \biggr )\\&+\,{\bar{c}} {\hat{d}}I_{21} \cos {\alpha _m} \left( U_2 (0.02 U_2-2.4 I_F \omega )+0.01 U_1^2\right) \\&+\,I_{21} r_{\mathrm{cg}} \left( U_2 (0.18 U_2-19.27 I_F \omega )+0.06 U_1^2\right) \biggr )\\&+\,r_{\mathrm{cg}} \biggl (I_{11} k \left( U_2 (1.48 U_2-41.88 I_F \omega )+0.49 U_1^2\right) \\&+\,I_{12} \left( U_2 (31.4 I_F \omega -1.1 U_2)-0.37 U_1^2\right) \biggr )\biggr )\\ \end{aligned}$$

$$\begin{aligned} A_{64}=&\frac{1}{I_F I_{y_b} \omega }C_{L_\alpha } \rho \cos {\alpha _m} \biggl (42.2 I_{11} I_F k \omega - I_{11} k U_2-31.7 I_{12} I_F \omega \\&+\,0.74 I_{12} U_2+I_{21} \cos {\alpha _m} (19.4 I_F \omega -0.12 U_2)\biggr )\\ A_{65}=&\frac{1}{I_F I_{y_b} \omega }C_{L_\alpha } \rho \sin {\alpha _m} \biggl (198 I_{21} I_F k \omega -2 I_{21} k U_2-148 I_{22} I_F \omega \\&+\,1.5 I_{22} U_2+I_{31} \cos {\alpha _m} (10.5 I_F \omega -0.25 U_2)\biggr ) \\ A_{66}=&\frac{\rho }{I_F I_{y_b} \omega } \biggl (C_{L_\alpha } \cos {\alpha _m} \left( -5.23 I_{21} I_F k \omega +0.12 I_{21} k U_2+3.9 I_{22} I_F \omega -0.09 I_{22} U_2\right) \\&+\, C_{L_\alpha } I_{31} \cos { 2 \alpha _m} (0.01 U_2-1.2 I_F \omega )-1.2 C_{L_\alpha } I_{31} I_F \omega +0.01 C_{L_\alpha } I_{31} U_2\\&+\, \sin {\alpha _m} \biggl (k (242 I_{11} I_F k \omega -1.5 I_{11} k U_2-242 I_{12} I_F \omega \\&+\,1.5 I_{12} U_2)+I_{13} (45.5 I_F \omega -0.29 U_2)\biggr )\\&+\, 16.43 I_{21} I_F k \omega -0.39 I_{21} k U_2-4.1 I_{22} I_F \omega +0.1 I_{22} U_2\biggr ). \end{aligned}$$

Hawkmoth Morphological Parameters

The morphological parameters and the wing planform for the hawkmoth, as given in Sun et al. (2007) and Ellington (1984b), are

$$\begin{aligned} R= & {} 51.9\, \mathrm {mm}, \; S=947.8\, \mathrm {mm}^2,\; {\overline{c}}=18.3\,\mathrm {mm},\\ {\hat{r}}_1= & {} 0.44,\; {\hat{r}}_2=0.525,\; f=26.3\, {\mathrm{Hz}}, \; \Phi =60.5^\circ ,\\ \alpha _m= & {} 30^\circ ,\; m_b=1.648\,\mathrm {gm},\; \text{ and }\; I_{yb}=2080\,\mathrm {mg\,cm}^2, \end{aligned}$$

where R is the semi-span of the wing, S is the area of one wing, ${\overline{c}}$ is the mean chord, f is the flapping frequency, $\Phi$ is the flapping angle amplitude, $m_b$ is the mass of the body, and $I_{yb}$ is the body moment of inertia around the body y-axis. The moments of the wing chord distribution ${\hat{r}}_1$ and ${\hat{r}}_2$ are defined as

$$\begin{aligned} I_{k1}=2\int _0^R {r^k c(r) \,\hbox {d}r}=2SR^k{\hat{r}}_k^k. \end{aligned}$$

As for the wing planform, the method of moments used by Ellington Ellington (1984b) is adopted here to obtain a chord distribution for the insect that matches the documented first two moments ${\hat{r}}_1$ and ${\hat{r}}_2$; that is,

$$\begin{aligned} c(r)=\frac{{\overline{c}}}{\beta } \left( \frac{r}{R}\right) ^{\lambda -1} \left( 1-\frac{r}{R}\right) ^{\gamma -1}, \end{aligned}$$

where

$$\begin{aligned}&\lambda ={\hat{r}}_1\left[ \frac{{\hat{r}}_1(1-{\hat{r}}_1)}{{\hat{r}}_2^2-{\hat{r}}_1^2}-1\right] \;,\; \gamma =(1-{\hat{r}}_1)\left[ \frac{{\hat{r}}_1(1-{\hat{r}}_1)}{{\hat{r}}_2^2-{\hat{r}}_1^2}-1\right] ,\\&\quad \text{ and }\;\; \beta =\int _0^1 {{\hat{r}}^{\lambda -1} (1-{\hat{r}})^{\gamma -1} \,d{\hat{r}}}. \end{aligned}$$

The mass of one wing is taken as 5.7% of the body mass according to Wu et al. (2009) and is assumed uniform with an areal mass distribution $m'$ The inertial properties of the wing are then estimated as

$$\begin{aligned}&I_x=2\int _0^R {m' r^2 c(r) \,\hbox {d}r} \;,\; I_y=2\int _0^R {m' {\hat{d}}^2 c^3(r) \,\hbox {d}r}\\&,I_z=I_x+I_y,~\text{ and }~ r_{\mathrm{cg}}=\frac{2\int _0^R {m' r c(r) \,\hbox {d}r}}{m_{\mathrm{w}}}=\frac{I_{11}}{2S}, \end{aligned}$$

where ${\hat{d}}$ is the chord-normalized distance from the wing hinge line to the center of gravity line.

Optimized Shooting Method

Periodic shooting methods have been used in the literature of FWMAVs/insects to capture the periodic orbits associated with different equilibrium configurations (e.g., hovering) (Dietl and Garcia 2008b; Wu and Sun 2012; Stanford et al. 2013; Hussein et al. 2018). The stability of these orbits are then analyzed using the Floquet theorem (Nayfeh and Balachandran 1995). Dednam and Botha (2015) provided an optimized shooting approach to capture a periodic solution of a nonlinear system. This optimized shooting approach adopts the Levenberg–Marquardt optimization algorithm to minimize the residual. This algorithm is based on two methods: the gradient descent method and the Gauss–Newton method. According to Gavin (2011), when the parameters are far from the optimal values, the Levenberg–Marquardt algorithm operates in a way similar to gradient descent. However, it operates similar to the Gauss–Newton method when approaching the optimal point.

Consider the following system of equations

$$\begin{aligned} \dot{{\varvec{x}}}(t)={\varvec{f}}({\varvec{x}}(t),{\varvec{\alpha }},t), \end{aligned}$$

(38)

where ${\varvec{x}}$$\in$$\mathbb {\mathbb {R}}^{n}$ and ${\varvec{f}}$: $\mathbb {\mathbb {R}}^{n} \times \mathbb {\mathbb {R}}^{k} \times \mathbb {\mathbb {R}}_{\ge 0}$$\rightarrow$$\mathbb {\mathbb {R}}^{n}$, and ${\varvec{\alpha }}$ are the system parameters. This system corresponds to a non-autonomous vector field. Thus, a solution ${\varvec{x}}(t)$ to the system (38) is periodic if there exists a constant $T>0$ such that

$$\begin{aligned} {\varvec{x}}(t)={\varvec{x}}(t+T). \end{aligned}$$

(39)

The optimized shooting method can be applied to any system that can be expressed in the form of (38), and, for convenience, a dimensionless time $\tau$ is introduced such that $t =\tau ~T$. Equation (38) is then written as

$$\begin{aligned} \frac{\hbox {d}{\varvec{x}}}{\hbox {d}\tau }=T{\varvec{f}}({{\varvec{x}}(\tau T),{\varvec{\alpha }},\tau T)}. \end{aligned}$$

(40)

Thus, this new variable $\tau$ allows the simplification of the boundary conditions in Eq. (39) so that $x(\tau = 0)= x(\tau = 1)$ and Eq. (40) can be integrated over one period (i.e., letting $\tau$ run from zero to one). Now, the residual can be written as

$$\begin{aligned} {\mathbf {R}}=T \int _{0}^{1} {\varvec{f}}({\varvec{x}}(\tau T), {\varvec{\alpha }},\tau T)~\hbox {d}\tau . \end{aligned}$$

(41)

According to Dednam and Botha (2015), the residual depends on the number of quantities to be optimized and can be expressed as

$$\begin{aligned} {\mathbf {R}}=\biggl ({\varvec{x}}(1)-{\varvec{x}}(0),~{\varvec{x}}(1+\varDelta \tau )-{\varvec{x}}(\varDelta \tau ),\ldots ,~{\varvec{x}}(1+(p-1)\varDelta \tau )-{\varvec{x}}((p-1)\varDelta \tau )\biggr ), \end{aligned}$$

(42)

where $\varDelta \tau$ is the integration step size and $p \in {\mathbb {N}}$. For solvability, the natural number p is chosen so that the number pn of components of the residual is greater than or equal to the number of unknowns (initial point on the periodic orbit and any unknown parameters such as the period in autonomous systems).