Near-Integrability and Recurrence in FPU Chains with Alternating Masses

Abstract

An important aspect of understanding FPU chains is the existence of invariant manifolds (called “bushes”) in FPU chains. We will focus on the classical periodic FPU chain and on the FPU chain with alternating masses where we show that also in the alternating case nested manifolds (related to bushes) exist. The use of symmetries leads to the emergence of systems of n particles as invariant manifolds of systems with a multiple of n particles. This analysis is followed by examples of existence and stability of special invariant manifolds and phase-space dynamics in the case of 4 and 8 particles. These examples are typical for periodic FPU chains with 4n or 8n particles. It turns out that in the alternating case the dynamics is strongly affected by the choice of the alternating mass m. Normal form calculations help to identify quasi-trapping regions leading to delay of recurrence. The results suggest that equipartition of energy near stable equilibrium is improbable.

1 Introduction

The Fermi–Pasta–Ulam (FPU) problem has been the subject of many papers since its formulation in 1955. For a recent study of localization, recurrence and references see Christodoulidi et al. (2010). An important aspect of understanding FPU chains is the existence of invariant manifolds (called “bushes”) in classical FPU chains; basic results are found by in Chechin and Sakhnenko (1998), Chechin et al. (2002) and Chechin et al. (2005). In these papers group-theoretical methods were used for coupled oscillator systems with special attention to $\alpha$- and $\beta$ FPU chains. See for the existence of invariant manifolds for $\beta$-chains also (Rink 2001). We will focus on the FPU chain with alternating masses (which includes the classical periodic FPU chain) to show that also in the alternating case nested manifolds (bushes) exist. This is followed by examples of existence and stability of invariant manifolds and phase-space dynamics in the case of 4 and 8 particles. These examples are typical for periodic FPU chains with 4n or 8n particles.

The alternating case was studied by Galgani et al. (1992) for a FPU chain with fixed end points using mainly numerical tools for special cases to obtain insight into the equipartition of energy, in particular between the low (acoustical) frequency and the high (optical) frequency part. The terminology acoustical–optical derives from physics. The spectrum of the linearized system scales with the alternating mass m (or its inverse) producing a natural split of the frequency spectrum. See Sect. 3.3. A preliminary but important conclusion by Galgani et al. (1992) is that for the masses considered and on long timescales no equipartition takes place; the evidence is numerical. Inspired by these results we will study the periodic FPU problem in the case of alternating masses. The emphasis will be on invariant manifolds, periodic solutions, integrability of the normal forms (near-integrability of the original system), chaos and recurrence phenomena; for recurrence see also Verhulst (2016, 2017a) for chains of FPU cells.

The periodic Fermi–Pasta–Ulam problem with alternating masses presents complicated dynamics. For the mono-atomic case of the original periodic FPU problem with all masses equal it was shown by Rink and Verhulst (2000) for up to six degrees-of-freedom (dof) and for an arbitrary number of dof by Rink (2001), that the corresponding normal forms are governed by 1 : 1 resonances and that these Hamiltonian normal forms are integrable. This explains the recurrence phenomena near stable equilibrium for long intervals of time.

Bruggeman and Verhulst (2017a) have studied the inhomogeneous FPU problem with four particles which contains many different resonance cases. In a periodic chain, for (even) n particles with arbitrary masses $m_j>0$, position $q_j$ and momentum $p_j= m_j {\dot{q}}_j, j= 1 \ldots n$, the Hamiltonian is of the form:

$$\begin{aligned} H(p, q)= \sum _{j=1}^n \left( \frac{1}{2m_j}p_j^2 + V(q_{j+1}-q_j)\right) \,\, \mathrm{{with}}\,\, V(z)= \frac{1}{2}z^2+ \frac{\alpha }{3}z^3 + \frac{\beta }{4}z^4. \end{aligned}$$

(1)

If $\alpha >0, \beta =0$ we will call this an $\alpha$-chain, if $\alpha =0, \beta >0$ a $\beta$-chain. The quadratic part of the Hamiltonian is not in diagonal form; for $n=3, 4 \ldots$ the linearized equations of motion can be written as:

$$\begin{aligned} {\left\{ \begin{array}{ll} m_1 \ddot{q}_1 +2q_1-q_2 -q_n &{} = 0,\\ m_2 \ddot{q}_2 +2q_2-q_3 -q_1 &{} = 0,\\ m_3 \ddot{q}_3 +2q_3-q_4 -q_2 &{} = 0,\\ \ldots \,\, \,\,\, \ldots &{} = 0, \\ m_n \ddot{q}_n +2q_n-q_1 -q_{n-1} &{} = 0. \end{array}\right. } \end{aligned}$$

(2)

Recurrence for the dynamics induced by system (2) is described by the Euclidean distance

$$\begin{aligned} d = \left( \sum _{i=1}^n \left( q_i(t)-q_i(0)\right) ^2 + \left( p_i(t)-p_i(0) \right) ^2\right) ^{1/2}, \end{aligned}$$

(3)

with possibly $q_i$ and $p_i$ replaced by transformed variables.

Consider the periodic FPU chain with an even number (2n) of alternating masses 1, m, 1, m, $\ldots ,$, with $m>0$, which is to some extent related to the formulation in Galgani et al. (1992) where the emphasis is on energy partition for large systems ($n=6, \ldots , 200$) with fixed end points and $0 < m \le 1$. The mass ratio m : 1 is the important parameter; we choose $a= 1/m$, $0 < a \le 1$. If $a=1$ we have the classical case of equal masses. By a symmetry argument we will leave out the case $a>1$.

The eigenvalue spectrum of system (2) will be indicated by $\lambda _i,\,i= 1, \ldots , 2n$; the corresponding frequencies of the linear normal modes are $\omega _i = \sqrt{\lambda _i}$. The numerical value of $H_2$ (for given initial conditions) is indicated by $E_0$; near stable equilibrium and assuming that m is not very large, we can rescale $p \rightarrow \varepsilon p,\, q \rightarrow \varepsilon q$ with $\varepsilon$ a small positive parameter. Dividing by $\varepsilon ^2$, we obtain from Hamiltonian (1) the Hamiltonian $H_2+ \varepsilon \alpha H_3 + \varepsilon ^2 \beta H_4$ with $H_3$ a cubic polynomial in (p, q), $H_4$ quartic in (p, q). We have clearly for the energy $E= H_2|_{t=0} + O(\varepsilon )$ for all time.

From Sect. 4 onward we will use symplectic transformations to put the linear part of the equations of motion in quasi-harmonic form. This is possible as the system induced by Hamiltonian (1) satisfies with $P_0$ a constant the momentum integral:

$$\begin{aligned} m_1 {\dot{q}}_1 + m_2 {\dot{q}}_2 + \cdots + m_n {\dot{q}}_n = P_0. \end{aligned}$$

(4)

The integral can be used to reduce the system by one dof.

The short-periodic solutions of the equations of motion linearized near the origin are called the linear normal modes of the system. One of the questions that arise are whether the linear normal modes can be continued for the system with nonlinear interactions or not. The transformation to quasi-harmonic form is natural, but may cause confusion. In position and impulse space we have the basis vectors $e_1, e_3, \ldots ,e_{2n-1}$ corresponding to particles with mass 1, and basis vectors with even index corresponding to the heavier particles with mass $m=1/a$. After symplectic transformation we have n eigenvalues that are O(a), giving the “acoustic frequencies,” and n eigenvalues that are of order 1, giving the “optical frequencies.” The description of each eigenvector (corresponding with a so-called normal mode) involves a mix of particles of mass 1 and of mass m. The behavior of the solutions within the two sets of particles cannot in a simple way be identified with the normal mode (quasi-harmonic) equations corresponding with the optical and acoustical part of the spectrum.

Note that according to Weinstein (1973) a n dof Hamiltonian system near stable equilibrium contains at least n families of periodic solutions parametrized by the energy. We will keep this in mind when looking for periodic solutions in particular systems.

In the sections on chains with 4 or 8 particles the analysis by averaging normal forms is a basic tool. For the normal form theory and results in the case of Hamiltonian systems see Sanders et al. (2007) ch. 10. In the analysis resonances in the frequency spectrum of the linearized equations of motion, generated by the quadratic part of the Hamiltonian $H_2$, play a fundamental part. The cubic part $H_3$ and if necessary the quartic part $H_4$ will be normalized to ${\bar{H}}_3, {\bar{H}}_4$.

The general theory and proofs of averaging for ODEs involve spatial variables and time with bounds (independent of $\varepsilon$) on the spatial domain and the initial conditions. It is important to note that in the case of a Hamiltonian system near stable equilibrium we have dynamics on a bounded energy manifold. The implication is that the normal form analysis and its error estimates are valid for an arbitrary number of dof if the initial energy is bounded independent of $\varepsilon$.

In Bruggeman and Verhulst (2017a) we have discussed a number of technical normal form aspects of averaging for Hamiltonian systems. In a system of n perturbed harmonic equations we will often transform to polar coordinates. If the frequencies are $\omega _j,\,1\le j \le n$ we can introduce

$$\begin{aligned} x_j \,=\, r_j \,\cos (\omega _j t+\varphi _j),\quad y_j \,=\, - r_j\,\omega _j \sin (\omega _j t+\varphi _j) \qquad (1\le j \le 7) \end{aligned}$$

(5)

to produce an equivalent first-order system in the variables

$$\begin{aligned} X\,=\,(r_1,r_2,\ldots ,r_n,\varphi _1,\ldots ,\varphi _n). \end{aligned}$$

This system is equivalent with the n dof system of perturbed harmonic equations outside the normal mode planes.

The numerical experiments were carried out by matcont under Matlab with ode code 78, for instance for Euclidean distances in phase space. The precision was increased until the picture did not change anymore with typical relative error $e^{-15}$, absolute error $e^{-15}$. Basic normal form computations were carried out using Mathematica.

In Sects. 2 and 3 we present results on periodic solutions and invariant manifolds for alternating periodic FPU chains with an even number of particles. Section 4 summarizes results for 4 particles, features that will be found again in periodic FPU chains with 4n particles. Section 5 contains the formulation of the system for 8 particles, where we find 3 invariant manifolds and study their stability. The normal form analysis of Sect. 6 produces interesting phenomena. At first-order normalization only the cases $m=2$ and $m=4/3$ give non-trivial results. In particular the analysis of the dynamics near unstable invariant manifolds for $m=4/3$ yields insight into the presence of resonance zones, recurrence and quasi-trapping phenomena. These features will be found again in periodic FPU chains with 8n particles.

2 The 2n Particles FPU Chain, Three Families of Periodic Solutions

Consider the equations of motion with alternating masses derived from Hamiltonian (1). As we shall see in Sect. 3.3, the eigenvalues $2(1+a)$, 2 and 2a of the linearized system (2) occur in the spectrum. Associated with the corresponding frequencies we can find in a 4n dof system (taken from now on for convenience instead of 2n) with alternating masses three exact families of periodic solutions:

• Solutions determined by

  $$\begin{aligned} q_{2j}(t) =0, j=1, \ldots , 2n; q_1(t)= -q_3(t)=q_5(t)=-q_7(t)= \cdots = -q_{4n-1}(t), \end{aligned}$$

  producing the equations of motion (harmonic for an $\alpha$-chain)

  $$\begin{aligned} \ddot{q}_{2j-1} + 2 q_{2j-1} =0,\, j=1, 2, \ldots , 2n. \end{aligned}$$

  (6)

  For a $\beta$-chain we add a cubic term to the equations of motion. On a given energy manifold this represents a one-parameter family of periodic solutions.

• Solutions determined by

  $$\begin{aligned} q_{2j-1}(t) =0, j=1, \ldots , 2n; q_2(t)= -q_4(t)=q_6(t)=-q_8(t)= \cdots = -q_{4n}(t), \end{aligned}$$

  producing the equations of motion (harmonic for an $\alpha$-chain)

  $$\begin{aligned} \ddot{q}_{2j} + 2a q_{2j} =0,\, j=1, 2, \ldots , 2n. \end{aligned}$$

  (7)

  For a $\beta$-chain we add a cubic term to the equations of motion. On a given energy manifold this represents a one-parameter family of periodic solutions.

• Because of the symmetry of the equations we expect that solutions exist of the form:

  $$\begin{aligned} q_1(t)=q_3(t)= \cdots = q_{4n-1},\,\, q_2(t)=q_4(t)= \cdots = q_{4n}(t). \end{aligned}$$

  For an $\alpha$-chain this leads to the linear system:

  $$\begin{aligned} {\left\{ \begin{array}{ll} \ddot{q}_1 + 2q_1 = &{} 2q_2,\\ \ddot{q}_2 + 2aq_2 = &{} 2aq_1. \end{array}\right. } \end{aligned}$$

  The eigenvalues are 0 and $2(1+a)$; the solutions exist, are periodic (harmonic) and will have frequency $\sqrt{2(1+a)}$. For a $\beta$-chain we find:

  $$\begin{aligned} {\left\{ \begin{array}{ll} \ddot{q}_1 + 2q_1 = &{} 2q_2 - 2 \varepsilon (q_1-q_2)^3,\\ \ddot{q}_2 + 2aq_2 = &{} 2aq_1 + 2a \varepsilon (q_1-q_2)^3. \end{array}\right. } \end{aligned}$$

  We conclude that $a \ddot{q}_1 + \ddot{q}_2 =0$ so that we can eliminate $q_2$. For $q_1$ we find the equation:

  $$\begin{aligned} \ddot{q}_1 + 2(1+a)q_1 = - 2 \varepsilon (1+a)^3q_1^3. \end{aligned}$$

  The solutions exist and are elliptic periodic functions.

According to Poincaré (1899), the presence of a family of periodic solutions on an energy manifold generally implies the presence of another integral of motion besides the energy. In this case, this is the momentum integral:

$$\begin{aligned} \sum _{j=1}^{2n} {\dot{q}}_{2j-1} + m \sum _{j=1}^{2n} {\dot{q}}_{2j} = \mathrm {constant}. \end{aligned}$$

(8)

We will meet these periodic solutions again when analyzing explicit FPU chains.

3 The 2n Particles FPU Chain, Invariant Manifolds

We consider the general case of the alternating periodic FPU chain with 2n particles. We will give a relation between the system with 2n particles and an invariant submanifold of the system with 2k particles for each multiple k of n.

3.1 Earlier Results

In a seminal paper Chechin and Sakhnenko (1998) group-theoretical methods were used for systems with certain symmetries. From irreducible representations of the symmetry group the authors conclude to the existence of specific dynamical regimes (called bushes) of essentially lower dimension than the dimension of the original systems. The theory was developed in Chechin and Sakhnenko (1998) both for Hamiltonian and non-Hamiltonian systems with a number of physical applications.

Independently, in Poggi and Ruffo (1997) the periodic FPU $\beta$-chain was considered for which special periodic solutions and two-mode invariant manifolds were found; the analysis in Poggi and Ruffo (1997) is by inspection of equations and not by exploiting symmetries. The paper Chechin and Sakhnenko (1998) was continued in Chechin et al. (2002) to find invariant manifolds (bushes) in classical periodic, monatomic FPU chains. The analysis leads to the existence of a wide range of multimode invariant manifolds that include the results in Poggi and Ruffo (1997). Exploiting symmetries, a number of new invariant manifolds for the classical, periodic FPU chain were given in Rink (2001).

In this section we will exploit the symmetries of the periodic FPU chain with alternating masses to obtain a great many invariant manifolds in Theorem 3.1. The proof also leads to the determination of the eigenvalues, in Proposition 3.2.

3.2 Invariant Manifolds

In the study of the alternating FPU chain with 8 particles we observed an invariant manifold equivalent to the system with 4 particles. This phenomenon turns out to be much more general, as we formulate in Theorem 3.1 below. It can be considered as an example of the theory of Chechin and Sakhenko (1998). We consider the system $\mathrm {FPU}_{2n}(a;\alpha ,\beta )$ of second-order differential equations

$$\begin{aligned} \begin{aligned} m_j \ddot{q}_j&\,=\, +(q_{j+1}-q_j) + \alpha (q_{j+1}-q_j)^2 +\beta (q_{j+1}-q_j)^3\\&\qquad \hbox {} -(q_j-q_{j-1}) -\alpha (q_j-q_{j-1})^2-\beta (q_j-q_{j-1})^3 \end{aligned}\end{aligned}$$

(9)

for $1\le j \le 2n$, with indices taken modulo 2n. The masses are $m_{2j-1}=1$ and $m_{2j}=a^{-1}$ with $a>0$. The parameters $\alpha ,\beta \in {\mathbb R}$ regulate the nonlinearity of the system. If $\alpha =\beta =0$ the system is linear, with associated matrix $-A_{2n}C_{2n}$, where $A_{2n}$ is a $2n\times 2n$ diagonal matrix with diagonal $(1,a,1,a,\ldots )$, and $C_{2n}$ has the form

$$\begin{aligned} \begin{pmatrix} 2&{}-1&{}0&{}\cdots &{}0&{}-1\\ -1&{}2&{}-1&{}\cdots &{}0&{}0\\ 0&{}-1&{}2&{}\cdots &{}0&{}0\\ \vdots &{}\vdots &{}\vdots &{}&{}\vdots &{}\vdots \\ 0&{}0&{}0&{}\cdots &{}2&{}-1\\ -1&{}0&{}0&{}\cdots &{}-1&{}2\end{pmatrix}. \end{aligned}$$

(10)

The system of differential equations (9) has the same structure if we allow $\alpha$ and $\beta$ to be complex, and $a \in {\mathbb C}{\setminus }\{0\}$. In this complex context we have the following result:

Theorem 3.1

Let $\alpha ,\beta \in {\mathbb C}$, $a\in {\mathbb C}{\setminus }\{0\}$, $n\ge 2$, and let k be a multiple of n. There is a 2n-dimensional subspace $M_{k,n}\subset {\mathbb C}^{2k}$ such that the restriction of the system $\mathrm {FPU}_{2k}(a;\alpha ,\beta )$ to $M_{k,n}$ is equivalent to the system $\mathrm {FPU}_{2n}(a;\alpha ,\beta )$.

By equivalence we mean that there is a bijective map $\Phi : {\mathbb C}^{2n}\rightarrow M_{k,n}$ such that the image $t\mapsto \Phi q(t)$ of the solution $t\mapsto q(t)$ with initial values $(q(0),q'(0))\in {\mathbb C}^{2n}$ is the solution in ${\mathbb C}^{2k}$ with initial values $\left( \Phi q(0), \Phi q'(0)\right)$.

The cyclic group of order n acts naturally on the system $\mathrm {FPU}_{2n}(a;\alpha ,\beta )$. It is generated by the shift over two particles ($j\mapsto j+2$ modulo 2n). This is the group of symmetries used in the proof of the theorem. It enters via the dual group $U_n$ of n-th roots of unity.

Proof of Theorem 3.1

Vector formulation of the system. The linear part of the system (9) can be formulated as $\ddot{q} = - A_{2n}C_{2n} q$. For the quadratic part we note that the factor of $\alpha$ has the form

$$\begin{aligned} -(2q_j-q_{j+1}-q_{j-1}) \,(q_{j-1}-q_{j+1}). \end{aligned}$$

We define $D_{2n,+}$ as the $2n\times 2n$-matrix with 1 at positions (i, j) such that $j-i \equiv 1 \bmod 2n$ and zeros elsewhere, and $D_{2n,-}=D_{2n,+}^T$. Then the quadratic term has the matrix form

$$\begin{aligned} - \alpha (A_{2n}C_{2n}q)\times \left( (D_{2n,-}q-D_{2n,+})q\right) , \end{aligned}$$

where $\times$ denotes the coordinatewise product: $(a\times b)_j=a_j b_j$.

For the coefficient of $\beta$ we proceed similarly to find the matrix form of the system, in which we use $E_{2n,+}=I_{2n}-D_{2n,+}$, $E_{2n,-}=I_{2n}-D_{2n,-}$ with the $2n\times 2n$ identity matrix $I_{2n}$.

$$\begin{aligned} \ddot{q}= & {} - AC q - \alpha \, (ACq) \times ( (D_{2n,-}-D_{2n,+}q) -\beta ( AC q)\times ( (E_+q)\nonumber \\&\quad \times (E_+q) + (E_-q)\times ( E_-q)+((D_+-D_-)q)\nonumber \\&\quad \times ((D_+-D_-)q) ). \end{aligned}$$

(11)

(To save space we suppressed the indices 2n.)

Decomposition. Let $U_n=\bigl \{ e^{2\pi i j/n}\;:\; j\bmod n\bigr \}$ denote the group of n-th roots of unity. For each $\zeta \in U_n$ we define vectors $v_{2n}(\zeta )$ and $w_{2n}(\zeta )$ in ${\mathbb C}^{2n}$ by

$$\begin{aligned} v_{2n}(\zeta )_{2j-1}\,=\,\zeta ^j,\quad v_{2n}(\zeta )_{2j}\,=\,0,\qquad w_{2n}(\zeta )_{2j-1}\,=\,0,\quad w_{2n}(\zeta )_{2j}\,=\, \zeta ^j, \end{aligned}$$

(12)

for $1\le j \le n$. Together, these vectors form a basis of ${\mathbb C}^{2n}$. This leads to a decomposition

$$\begin{aligned} {\mathbb C}^{2n} \,=\, \bigoplus _{\zeta \in U_n} X_{2n}(\zeta ),\qquad X_{2n}(\zeta ) \,=\, {\mathbb C}\ v_{2n}(\zeta )+{\mathbb C}\, w_{2n}(\zeta ).\end{aligned}$$

(13)

The importance of this decomposition is that all matrices $A_{2n}C_{2n}$, $D_{2n,\pm }$, $E_{2n,\pm }$ that occur in (11) preserve this decomposition. On the basis $v_{2n}(\zeta ), w_{2n}(\zeta )$ of $X_{2n}(\zeta )$ we have for instance the following matrix description in $X_n(\zeta )$:

$$\begin{aligned} \begin{aligned} A_{2n}C_{2n}\;\sim \; \begin{pmatrix}2&{}-(1+\zeta ^{-1}) \\ -a(1+\zeta )&{}2a \end{pmatrix},\qquad D_{2n,+}\;\sim \; \begin{pmatrix}0&{}1 \\ \zeta &{}0 \end{pmatrix}. \end{aligned} \end{aligned}$$

(14)

We do not need to know the precise form of these matrices, but it is important that these matrices do not depend explicitly on n.

The (commutative) coordinatewise product of vectors satisfies for $\zeta _1,\zeta _2\in U_n$

$$\begin{aligned} \begin{aligned} v_{2n}(\zeta _1)\times v_{2n}(\zeta _2)&\,=\, v_{2n}(\zeta _1\zeta _2),&\quad v_{2n}(\zeta _1) w_{2n}(\zeta _2)&\,=\,0, \\ w_{2n}(\zeta _1)\times w_{2n}(\zeta _2)&\,=\, w_{2n}(\zeta _1\zeta _2). \end{aligned} \end{aligned}$$

(15)

Description of the System. We write the vector q as $q=\sum _{\zeta \in U_n}x(\zeta )$ with $x(\zeta ) \in X_{2n}(\zeta )$. We arrive for each $\zeta \in U_n$ at

$$\begin{aligned} \ddot{x}(\zeta )= & {} -A_{2n}C_{2n} x(\zeta ) \nonumber \\&- \alpha \sum _{\zeta _1,\zeta _2\in U_n,\; \zeta _1\zeta _2=\zeta } T(\zeta _1,\zeta _2) - \beta \sum _{\zeta _1,\zeta _2,\zeta _3\in U_n,\; \zeta _1\zeta _2\zeta _3=\zeta } S(\zeta _1,\zeta _2,\zeta _3), \end{aligned}$$

(16)

where $T(\zeta _1,\zeta _2)$ and $S(\zeta _1,\zeta _2,\zeta _3)$ are linear combinations of products of elements of the space $X_{2n}(\zeta _j)$.

Now let k be a multiple of n. We form the linear map $\Phi _{n,k}:{\mathbb C}^{2n}\rightarrow {\mathbb C}^{2k}$ determined by $\Phi _{n,k} v_{2n}(\zeta ) = v_{2k}(\zeta )$, $\Phi _{n,k}w_{2n}(\zeta ) = w_{2k}(\zeta )$. The image of $\Phi _{n,k}$ is a linear subspace $M_{k,n}$ of ${\mathbb C}^{2k}$. This subspace is determined by the condition that $X_{2k}(\zeta ) \subset M_{kn}$ if $\zeta \in U_n\subset U_k$ and $X_{2k}(\zeta ) \cap M_{k,m}=\{0\}$ if $\zeta \in U_k{\setminus }U_n$.

Suppose $x\in M_{k,n}$. If $\zeta \in U_k{\setminus }U_n$, then $x(\zeta )=0$, and all factors in the right-hand side vanish as well, since at least one of the $\zeta _j$ has to be in $U_k{\setminus }U_n$. If $\zeta \in U_n$, then the form of the right-hand side in (16) is the same as in the system with 2n particles. If some $\zeta _j$ is not in $U_n$, then the term $T(\zeta _1,\zeta _2)$, respectively, $S(\zeta _1,\zeta _2,\zeta _3)$ is zero. So the descriptions of the system of differential equations with 2n particles and the restriction to $M_{k,n}$ of the system with 2k particles are exactly equal. $\square$

Bushes of Modes. This theorem can be seen as an example of the theory of Chechin and Sakhenko (1998). See also Chechin et al. (2002), where this theory is applied to the classical FPU chain with equal masses. For each divisor n of k the space $M_{k,n}$ is the “bush” associated with the subgroup $U_n$ of $U_k$.

For the $\beta$-chain the total group of symmetries is larger than the cyclic group used in the theorem. It is the dihedral group generated by the shift $j\mapsto j+2\bmod 2n$ and the reflection $j\mapsto 2-j \bmod 2n$. The reflection interchanges $X(\zeta )$ and $X(\zeta ^{-1})$.

Real Systems. Let $a>0$, $\alpha ,\beta \in {\mathbb R}$. The system (9) is a system of second-order differential equations in ${\mathbb R}^{2n}$. For roots of unity $\zeta$ that are not real the vectors $v_{2n}(\zeta )$ and $w_{2n}(\zeta )$ are not in ${\mathbb R}^n$, and the decomposition (13) does not respect the real structure. To get a real basis we have to consider $X_{2n}(\zeta ) \oplus X_{2n}(\bar{\zeta })$, which intersects ${\mathbb R}^{2n}$ in a space with real dimension 4. That space is invariant under the operators $A_{2n}C_{2n}$, $D_{2n,+}\cdots$.

Periodic Solutions. In Sect. 2 we mentioned periodic solutions. We now recognize them as solutions of the form $t\mapsto f(t) \, v_{2n}(-1)$ and $t\mapsto f(t)\, w_{2n}(-1)$ living in $X_{2n}(-1)$.

There are also solutions in the space $X_{2n}(1)$. One of them is the solution $f(t) \left( v_{2n}(1)+ w_{2n}(1)\right)$ with $f'=0$. It is in the translational component of the system. The third type of solution in Sect. 2 with eigenvalue $2(a+1)$ is of the form $t\mapsto f(t) \left( v_{2n}(1)-a\, w_{2n}(1) \right)$.

Invariant Manifolds. The space $M_{k,n}\subset {\mathbb C}^{2k}$ is a 2n-dimensional linear subspace of the position space ${\mathbb C}^{2k}$ of the system $\mathrm {FPU}_{2k}(a;\alpha ,\beta )$. In the context of Theorem 3.1 that seems a natural approach, since the symmetric group acts in the same way on positions and impulses of particles. The corresponding invariant manifold is a 4n-dimensional linear subspace of the phase space ${\mathbb C}^{4k}$.

3.3 Eigenvalues

Proposition 3.2

The eigenvalues of $A_{2n}C_{2n}$ are

$$\begin{aligned} 1+a \pm \sqrt{1+2a\cos (2\pi j/n)+a^2}\qquad (0\le j \le n). \end{aligned}$$

(17)

Proof

In the complex context, the eigenvalue equation of $A_{2n}C_{2n}$ is the product of the eigenvalue equations of $A_{2n}C_{2n}$ restricted to $X_{2n}(\zeta )$, where $\zeta$ runs over $U_n$. The solutions of

$$\begin{aligned} \lambda ^2-2(1+a) \lambda + a(2-\zeta -\zeta ^{-1})\,=\,0 \end{aligned}$$

give the eigenvalues in the proposition. $\square$

We note the following:

• From $\zeta =1$ we have the eigenvalues 0 and $2(a+1)$.

• If n is even (4n particles), $\zeta =-1$ is one of the possible roots leading to eigenvalues 2 and 2a.

• The other roots $\zeta ^j$ and $\zeta ^{n-j}$ with $1 \le j < n/2$ produce eigenvalues with multiplicity 2.

• The eigenvalues with $0 \le j \le n-1$ behave for $a \downarrow 0$ as

  $$\begin{aligned} 2+a\left( 1 + \cos \frac{2 \pi j}{n} \right) + O(a^2) \,\, \mathrm{and}\,\, a\left( 1- \cos \frac{2 \pi j}{n}\right) + O(a^2). \end{aligned}$$

  So, for large mass values ($a \downarrow 0$) the eigenvalue spectrum consists of two groups, one with size $2 + O(a)$ (the so-called optical group) and the second one with size O(a) (the so-called acoustical group).

The transformation of system (9) to a quasi-harmonic system of the form $\ddot{x}_i +\omega _i(a)x_i = \cdots$ with the dots representing nonlinear terms yields a more tractable system. The new variables are called phonons or quasi-particles.

4 Four Alternating Masses, a Summary

This case has been analyzed in Bruggeman and Verhulst (2017b). The dynamics of this case will be found again in systems with 8 particles, in general 4n particles.

For the $\alpha$- and $\beta$-chain we find no three dof first-order resonances in a cell with four particles. There are two dof resonances of which the normal form is integrable to a high order.

Considering large mass (a small) we find more interesting results. We have from the linear system (2) the 4 eigenvalues:

$$\begin{aligned} \lambda _i = 2(1+a), \, 2,\, 2a,\,0. \end{aligned}$$

with frequencies $\omega _i^2= \lambda _i, i =1, \ldots , 4$. After symplectic transformation using the momentum integral $\sum _1^4 m_i{\dot{q}}_i=$ constant (see also 8) we have with $\gamma = 2 \sqrt{2a(1+a)}$ for the $\alpha$-chain the quasi-harmonic equations of motion:

$$\begin{aligned} {\left\{ \begin{array}{ll} \ddot{x}_1 + 2(1+a)x_1 &{}= \gamma x_2x_3,\\ \ddot{x}_2 + 2x_2 &{}= \gamma x_1x_3,\\ \ddot{x}_3 + 2ax_3 &{}= \gamma x_1x_2. \end{array}\right. } \end{aligned}$$

(18)

Three exact families of periodic solutions are the normal modes associated with the eigenvalues $2(1+a)$, 2 and 2a. The exact solutions are harmonic.

Two of the frequencies will be near $\sqrt{2}$, one will be $\sqrt{2a}$, the associated modes will be called the optical group ($x_1,x_2$) and the acoustical group ($x_3$). System (18) is an example of a system with widely separated frequencies, see Tuwankotta and Verhulst (2003) and further references there. Following the analysis in Tuwankotta and Verhulst (2003) we apply normalization considering $x_3$ as slowly varying. We use the transformation in (5) and find that to second-order normalization the normal form has the integral of motion

$$\begin{aligned} \frac{1}{2}(r_1^2 + r_2^2) = E_1, \end{aligned}$$

(19)

$E_1$ a positive constant. A second integral of motion is with C a constant, $\chi = \phi _1- \phi _2$:

$$\begin{aligned} r_1r_2 \cos \chi = C. \end{aligned}$$

(20)

For the $\beta$-chain the equations of motion are:

$$\begin{aligned} {\left\{ \begin{array}{ll} \ddot{x}_1 + 2(1+a)x_1 &{}= -(1+a)^2x_1^3 - 3(1+a)x_1(x_2^2+ax_3^2),\\ \ddot{x}_2 + 2x_2 &{}= -x_2^3 - 3ax_2x_3^2 - 3(1+a)x_1^2x_2,\\ \ddot{x}_3 + 2ax_3 &{}= - 3ax_2^2x_3 - a^2x_3^3- 3a(1+a)x_1^2x_3. \end{array}\right. } \end{aligned}$$

(21)

The three normal modes are exact solutions (elliptic functions) of the system. Normalizing to second order we find again the normal form integrals (19) and (20).

For both the $\alpha$-chain and the $\beta$-chain special quasi-periodic solutions arise if

$$\begin{aligned} \varphi _1-\varphi _2=0\text { or }\pi .\end{aligned}$$

These solutions are unstable for the $\alpha$-chain, and stable for the $\beta$-chain, see again Bruggeman and Verhulst (2017b). At this level of approximation we find weak interaction between the optical and the acoustical group, and no equipartition.

5 A Periodic Chain with Eight Particles

The case of 8 particles in a periodic chain introduces a large number of new phenomena, typical for system with 8n particles. We find for the linear system (2) the eigenvalues numbered $\lambda _1, \ldots , \lambda _8$:

$$\begin{aligned} \lambda _i = 2(1+a),\,\,1+a + \sqrt{1+a^2} \,(\mathrm{twice}),\,\,2,\,\,2a,\,\, 1+a - \sqrt{1+a^2} \,(\mathrm{twice}),\,0, \end{aligned}$$

(22)

which for small values of a with $i=1, \ldots , 8$ satisfy:

$$\begin{aligned} \lambda _i = 2(1+a),\,\,2+ a +\frac{1}{2}a^2+O(a^4)\, (\mathrm twice),\,\, 2,\,\,2a,\,\, a -\frac{1}{2}a^2 +O(a^4)\, (\mathrm twice),\,\,0. \end{aligned}$$

The corresponding frequencies are $\omega _i = \sqrt{\lambda _i}, i =1, \ldots , 8.$ The first four modes $x_1, x_2, x_3, x_4$ will be called the optical group, the modes $x_5, x_6, x_7$ the acoustical group.

One can find a number of prominent resonances, but, as we will show below, of special interest are the cases $a = \frac{1}{2}$, $a = \frac{3}{4}$ and a near zero. The calculation of the normal forms $H_3$ and $H_4$ shows that these values of a correspond with effective resonances. The eigenvalue $\lambda =0$ corresponds with the momentum integral $\sum _1^8 m_i{\dot{q}}_i=$ constant (see 8) producing families of translations. We will use this integral to reduce the system to seven dof. For all choices of a and after this reduction there will be at least seven families of periodic solutions (Weinstein 1973).

The increased complexity of the eight particle system can be handled, but we restrict most results to $\alpha$-chains.

5.1 Symplectic Transformation

We use a symplectic transformation $p=Ky$, $q=Lx$, with $x,y\in {\mathbb R}^8$ such that the quadratic part of the Hamiltonian $H_2$ for the system with eight particles transforms to the form

$$\begin{aligned} H_2 = \frac{1}{2} y^T y + \frac{1}{2} x^T \Lambda x, \end{aligned}$$

where $\Lambda$ is the diagonal matrix with $\lambda _1,\ldots , \lambda _8$ on the diagonal. The coordinates $x_j$ and $y_j$ correspond to the eigenmodes (phonons) with eigenvalue $\lambda _j$; see also Bruggeman and Verhulst (2017a) for details.

Applying the transformation to $H_3$ and $H_4$, we arrive for $H_3$ at the expression

$$\begin{aligned} H_3&=(d_{225}x_2^2x_5 +d_{335}x_3^2x_5)+(d_{566}x_6^2x_5+d_{577}x_7^2x_5) +(d_{127}x_1x_2x_7+d_{136}x_1x_3x_6)\\&\quad \hbox {} +d_{234}x_2x_3x_4 + d_{145} x_1x_4x_5 +(d_{256}x_2x_5x_6+d_{357}x_3x_5x_7)\\&\quad \hbox {} +(d_{346}x_3x_4x_6+d_{247}x_2x_4x_7) +d_{467}x_4x_6x_7. \end{aligned}$$

Table 1 The coefficients of $H_3$, expressed in the eigencoordinates $x_j$ where $d_{\alpha \beta \gamma }$ is the coefficient of $x_\alpha x_\beta x_\gamma$

For $H_4$ we find an expression with 49 terms of the form $e_{i,j,k,l}x_ix_jx_kx_l$, among which occur all fourth powers $x_j^4$, all products $x_i^2 x_j^2$, and 21 other terms. The coefficients $d_{ijk}$ and $e_{ijkl}$ are algebraic functions of the parameter a. The coefficients $d_{ijk}$ of $H_3$ and $e_{ijkl}$ of $H_4$ are all nonzero for $0<a\le 1$; the expressions for the $d_{ijk}$ are given in Table 1.

The resulting equations of motion for the $\alpha$-chain have the following form:

$$\begin{aligned} \ddot{x}_1+2 (a+1) x_1= & {} -\alpha (x_4 x_5 d_{145}+x_3 x_6 \ d_{136}+x_2 x_7 d_{127}),\nonumber \\ \ddot{x}_2+\left( \sqrt{a^2+1}+a+1\right) x_2= & {} -\alpha (x_3 x_4 d_{234}+x_7 x_4 d_{247}+2 \ x_2 x_5 d_{225}+x_5 x_6 d_{256}\nonumber \\&\qquad \hbox {} +x_1 x_7 \ d_{127}),\nonumber \\ \ddot{x}_3+\left( \sqrt{a^2+1}+a+1\right) x_3= & {} -\alpha (x_2 x_4 d_{234}+x_6 x_4 d_{346}+2 \ x_3 x_5 d_{335}+x_1 x_6 d_{136}\nonumber \\&\qquad \hbox {} +x_5 x_7 \ d_{357}),\nonumber \\ \ddot{x}_4+2 x_4= & {} -\alpha (x_2 x_3 d_{234}+x_6 x_3 \ d_{346}+x_1 x_5 d_{145}+x_2 x_7 d_{247}\nonumber \\&\qquad \hbox {} +x_6 x_7 d_{467}),\ \nonumber \\ \ddot{x}_5+2 a x_5= & {} -\alpha \left( x_2^2 d_{225}+x_6 x_2 \ d_{256}+x_3^2 d_{335}+x_6^2 d_{665}+x_7^2 d_{775}\right. \nonumber \\&\qquad \left. \hbox {} +x_1 x_4 \ d_{145}+x_3 x_7 d_{357}\right) ,\nonumber \\ \ddot{x}_6+\left( -\sqrt{a^2+1}+a+1\right) x_6= & {} -\alpha \ (x_1 x_3 d_{136}+x_4 x_3 \ d_{346}+x_2 x_5 d_{256}+2 x_5 x_6 d_{665}\nonumber \\&\qquad \hbox {}+x_4 x_7 \ d_{467}),\nonumber \\ \ddot{x}_7+\left( -\sqrt{a^2+1}+a+1\right) x_7= & {} -\alpha (x_1 x_2 d_{127}+x_4 x_2 \ d_{247}+x_3 x_5 d_{357}+x_4 x_6 d_{467}\nonumber \\&\qquad \hbox {} +2 x_5 x_7 \ d_{775}). \end{aligned}$$

(23)

The Euclidean distance d will be based on the time evolution of $\left( x(t), \dot{x}(t) \right)$.

Inspection of the equations of motion induced by $H_2+ \alpha H_3$ yields the $x_1, x_4, x_5$ normal modes as exact solutions and three invariant manifolds that are 6-dimensional subspaces in 14-dimensional phase space:

• 1. Manifold $M_{145}$ composed by the $x_1, x_4$ and $x_5$ modes, associated with the eigenvalues $2(1+a), 2$ and 2a. The dynamics is described by:

  $$\begin{aligned} {\left\{ \begin{array}{ll} \ddot{x}_1 + 2(1+a) x_1 &{}= - \varepsilon x_4x_5 d_{145}, \\ \ddot{x}_4 + 2 x_4 &{}= - \varepsilon x_1 x_5 d_{145}, \\ \ddot{x}_5 + 2a x_5 &{}= - \varepsilon x_1 x_4 d_{145}. \end{array}\right. } \end{aligned}$$

  (24)

  For the $\alpha$-chain this system was treated already in the system with four particles; see Eq. (18). This is an example of Theorem 3.1 showing how lower-dimensional invariant manifolds emerge as invariant manifolds in systems with more particles; see Sect. 3. In the case of the $\alpha$-chain the $x_1, x_4, x_5$ normal modes are harmonic solutions.

• 2. A second 6-dimensional invariant manifold $M_{256}$ is composed from the $x_2, x_5$ and $x_6$ modes. The equations of motion are:

  $$\begin{aligned} {\left\{ \begin{array}{ll} \ddot{x}_2 + \lambda _2 x_2 &{}= - \varepsilon (2x_2 x_5 d_{225}+x_5 x_6 d_{256}), \\ \ddot{x}_5 + 2a x_5 &{}= - \varepsilon (x_2^2 d_{225}+x_6 x_2 d_{256}+x_6^2 d_{665}), \\ \ddot{x}_6 + \lambda _6 x_6 &{}= - \varepsilon (x_2 x_5 d_{256}+2 x_5 x_6 d_{665}). \end{array}\right. } \end{aligned}$$

  (25)

  The $x_5, {\dot{x}}_5$ coordinate plane contains harmonic solutions.

• 3. A third 6-dimensional invariant manifold $M_{357}$ is composed from the $x_3, x_5$ and $x_7$ modes. The equations of motion are:

  $$\begin{aligned} {\left\{ \begin{array}{ll} \ddot{x}_3 + \lambda _3 x_3 &{}= - \varepsilon (2 x_3 x_5 d_{335}+x_5 x_7 d_{357}), \\ \ddot{x}_5 + 2a x_5 &{}= - \varepsilon ( x_3^2 d_{335} +x_7^2 d_{775} +x_3 x_7 d_{357}), \\ \ddot{x}_7 + \lambda _7 x_7 &{}= - \varepsilon (x_3 x_5 d_{357}+2 x_5 x_7 d_{775}). \end{array}\right. } \end{aligned}$$

  (26)

  The $x_5, {\dot{x}}_5$ coordinate plane contains harmonic solutions.

The mode $x_5$ plays a pivotal part as it occurs in each of the three manifolds. Not too far from the origin of phase space, for fixed energy and compact energy manifold, the three invariant manifolds are slightly deformed ellipsoids, topologically $S^5$, embedded in the iso-energetic manifold of the 7 dof system (topologically $S^{13}$).

Invariant manifolds $M_{256}$ and $M_{357}$ are new; they are not a consequence of Theorem 3.1.

Fig. 1

Timeseries for an $\alpha$-chain with 8 particles, $m=8 (a= 0.125)$; with 10,000 timesteps, showing recurrence. We took $q_1(0)=1$ and the other initial values zero. Left the Euclidean distance d in phase space (vertical scale) to the initial values of the equations of motion induced by Hamiltonian (1) with $\alpha \varepsilon =0.1, \beta =0$. Right for the same initial values the Euclidean distance $d_2$ in phase space taking into account only the heavier masses 2, 4, 6, 8. Discussion. The total distance to the initial position (on the left) takes values in $[0,\, 1.8]$; the distance $d_2$ (on the right) takes values in $[0,\, 0.85]$. This indicates energy transfer to the more massive part of the chain

Fig. 2

Timeseries for $\alpha$-chains, $a= 0.75$, $\varepsilon = 0.1$, based on system (23); vertical the Euclidean distance d in phase space to the initial values of the 7 modes. On the left the initial position is in $M_{145}$, with $x_1(0)=x_4(0)=x_5(0)=0.2$ and initial velocities zero; the computation has 10,000 timesteps. On the right we add to the modes 2, 3, 6, 7 the initial position values 0.01 keeping $x_1(0)=x_4(0)=x_5(0)=0.2$, and carry out 20,000 timesteps. Discussion. On the left the solution stays in the manifold $M_{145}$. It returns fairly quickly to positions in phase space near to the initial position. On the right the solution starts near to $M_{145}$. The instability means that the solution may move far away from the manifold. We see that in 20,000 timesteps the solution does not return close to the initial position

5.2 Stability of the Invariant Manifolds

We turn to the question whether the invariant manifolds $M_{145}$, $M_{256}$ and $M_{357}$ are stable or not on the energy manifold in 14-dimensional phase space. For Hamiltonian systems the stability of solutions or manifolds is studied by linearization near the solution or manifold. The set of eigenvalues of the linearization is invariant under $\lambda \mapsto - \lambda$ and $\lambda \mapsto {\bar{\lambda }}$. There are at least two eigenvalues 0. The analysis is simple in the generic cases of two dof; the presence of eigenvalues with nonzero real part means instability, and stability occurs if the real parts of all eigenvalues are zero. For three or more dof the presence of eigenvalues with nonzero real part means instability because of the reflection invariance, but the fact that all real parts of eigenvalues are zero is inconclusive for stability. Higher-order terms may destroy the linear stability. Another complication is that if first-order normal terms vanish, we should consider higher-order resonances as instability may arise at longer timescales. Both the cases of purely imaginary eigenvalues and vanishing first-order normal forms will be indicated by quasi-stability or spectral stability. For a number of values of the mass ratio a quasi- or spectral stability of $M_{145}$, $M_{256}$ and $M_{357}$ is the rule. An important exception is that for the value $a=\frac{3}{4}$ the three invariant manifolds are unstable.

The analytical approach uses the fact that the normal modes 1, 4 and 5 are harmonic solutions in the three invariant manifolds. For $k\in \{1,4,5\}$ we consider the system near the solution $x_k(t) = p \,\cos \omega _k t$, $p>0$, $x_j=0$ for $j\ne 0$ by taking

$$\begin{aligned} x_k&= (p+u_k) \cos \omega _k t + v_k \sin \omega _k t,&\quad y_k&= -\omega _k(p+u_k) \sin \omega _k t+\omega _k v_k \cos \omega _k t,\\ x_j&= u_j \cos \omega _j t + v_j \sin \omega _j t,&\quad y_j&= -\omega _j u_j \sin \omega _j t+\omega _j v_j \cos \omega _j t\quad (j\ne k). \end{aligned}$$

with $u_j$ and $v_j$ small quantities. We linearize the resulting system in the new variables $u_j, v_j$ by omitting all occurrences of quadratic factors in the $u_j$ and $v_j$. We normalize the resulting system by averaging. By writing all goniometric functions in complex exponentials we get factors $e^{i\Omega t}$ where $\Omega$ is an integral linear combination of the frequencies $\omega _j$. The normalization is carried out by putting $e^{i\Omega t}$ equal to zero if $\Omega \ne 0$. (This is the normal form condition, see Sanders et al. 2007 Ch 10.) Since the frequencies depend on the inverse mass a, the outcome of normalization depends on a. The result for the 14-dimensional system (23) is a linear system in 14 unknowns, described by a $14\times 14$ matrix $M_{k,a}$. We carried out this lengthy process with Mathematica, with the following results:

$$\begin{aligned} \begin{array}{|c|c|c|}\hline \hbox {Mode}\ k &{} M_{k,a}=0 &{} M_{k,a}\ne 0 \\ \hline 1&{} {\mathrm{all}\ } a\in (0,1]&{}\text {none}\\ 4&{}a\in (0,1]{\setminus }\{3/4\} &{} M_{4,3/4}\ne 0\\ 5&{} a\in (0,1]{\setminus }\{1/2\} &{}M_{5,1/2}\ne 0 \\ \hline \end{array} \end{aligned}$$

(27)

The vanishing of the matrix $M_{k,a}$ does not lead to conclusions concerning spectral stability. So perturbation around mode 1 produces no results on stability.

Perturbation around mode 4 gives an unstable case $a= 0.75$ as the matrix $M_{4,3/4}$ has two positive eigenvalues $\frac{3p}{20\sqrt{2}}$, two negative eigenvalues and the eigenvalue 0 with multiplicity 10. So the system is unstable at the eigenmode 4. Inspection of the eigenvectors for the positive eigenvalues shows that the unstability is in the direction of the variables $x_6, x_7,y_6,y_7$. These directions are not in the invariant manifold $M_{145}$. Hence the manifold is unstable. The eigenmode $k=4$ is outside the invariant manifolds $M_{256}$ and $M_{357}$. The instability results are illustrated in Figs. 2, 3, and 4.

Perturbation around normal mode 5 is not conclusive as the matrix $M_{5,1/2}$ has eight purely imaginary nonzero eigenvalues and the eigenvalue 0 with multiplicity 6. From this spectral stability we cannot draw definite conclusions concerning stability.

The stability analysis thus far is restricted to linearization around the modes 1, 4, 5, it produces non-trivial results for $a= 0.5$ and 0.75 only. In the next section we obtain additional results by computing first-order normal forms for system (23).

6 Eight Particles, Normalization of the $\alpha$-Chain

Consider $0<a<1$. We rescale $x_i \rightarrow \varepsilon x_i, i = 1, \ldots , 7$ and divide the Hamiltonian by $\varepsilon ^2$. The resulting Hamiltonian $H_2 + \varepsilon H_3$ determines the equation of motion described by the vectors x en y in ${\mathbb R}^7$ (we can replace $\alpha$ by $\varepsilon$); the reduction from 8 dof to 7 dof has been obtained by using the momentum integral.

The frequencies are $\omega _j = \sqrt{\lambda _j},\,1\le j \le 7$ with $\lambda _1,\ldots ,\lambda _7$ the positive eigenvalues in (22). Introduce polar coordinates by transformation (5) to produce an equivalent first-order system in the variables

$$\begin{aligned} X\,=\,(r_1,r_2,\ldots ,r_7,\varphi _1,\ldots ,\varphi _7). \end{aligned}$$

This system is equivalent with the transformed 7 dof system outside the seven hyperplanes $x_j=y_j=0$, $1\le j \le 7$. The parameters $\omega _j$ and $d_{\alpha \beta \gamma }$ are algebraic functions of $a\in (0,1]$.

6.1 The Case $a \in (0, 1]$ with $a \ne 0.5$ and $a \ne 0.75$

We exclude $O(\varepsilon )$-neighborhoods of $a=0.5$ and $a= 0.75$, and a small interval near $a=0$. Averaging–normalization, see Sanders et al. (2007) chapter 4, using Mathematica produces that the normal form ${\bar{H}}_3=0$ which means that to first-order normalization the amplitudes $r_j$ and phases $\phi _j$ are constant. The first-order normal form in these cases is trivially integrable. To study the structural stability of this result we would have to compute higher-order normal forms.

We present a numerical example of recurrence in the FPU system induced by Hamiltonian (1) for mass ratio $1{:}8 (a= 0.125)$ in Fig. 1. A nonzero initial value is chosen only for the first mass of the chain, and the recurrence is demonstrated by computing the Euclidean distance d in 16-dimensional phase space. The regularity of the recurrence agrees with the integrability of the normal form of $H_2 + \varepsilon H_3$. However, the heavier particles at positions 2, 4, 6, 8 have zero initial values but the Euclidean distance $d_2$ of the more massive part of the chain shows variation between 0 and 0.85. This suggests excitations and interactions that are not described by the first-order normalization of $H_3$. Other choices of the mass ratio a produce similar results.

6.2 The Detuned Case $a = 0.5$

Fig. 3

Timeseries for $\alpha$-chains, $a= 0.75$, $\varepsilon = 0.1$, based on system (23). Horizontal 10,000 timesteps on the left, 20,000 timesteps on the right; vertical the Euclidean distance d in phase space to the initial values of the 7 modes. On the left the initial position is in $M_{256}$, with $x_2(0)=x_5(0)=x_6(0)=0.2$ and initial velocities zero. On the right we add to the modes 1, 3, 4, 7 the initial position values 0.01 keeping $x_2(0)=x_5(0)=x_6(0)=0.2$. Discussion. On the left, in the invariant manifold $M_{256}$, there is regular recurrence to the initial position. On the right, starting slightly away from $M_{256}$ we see no clear recurrence within 20,000 timesteps. The linearization does not lead to a conclusion concerning stability; the observation is compatible with instability

Fig. 4

Timeseries for $\alpha$-chains, $a= 0.75$, $\varepsilon = 0.1$, based on system (23). On the left 10,000 timesteps, on the right 20,000 timesteps. Vertical the Euclidean distance d in phase space to the initial values of the 7 modes. On the left the initial position is in the manifold $M_{357}$, with $x_3(0)=x_5(0)=x_7(0)=0.2$ and initial velocities zero. On the right we add to the modes 1, 2, 4, 6 the initial position values 0.01 keeping $x_3(0)=x_5(0)=x_7(0)=0.2$. Discussion. We see on the left that the solution recurs regularly close to the initial position. On the right there is no clear recurrence to the initial position in 20,000 timesteps. The linearization gave no conclusion concerning the stability. The observed behavior is compatible with instability

Fig. 5

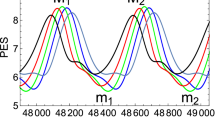
Timeseries for actions of $\alpha$-chain, $a= 0.75$, $\varepsilon = 0.1$, based on system (23) and with initial values of the unstable case in Fig. 4 (right), near $M_{357}$. Top: from left to right the actions $I_2$, $I_3$ and $I_5$; bottom: $I_4$, $I_6$ and $I_7$. The action $I_1$ shows little variation, and is not depicted. Discussion. The actions $I_2, I_3$ are intermittently in 1 : 1 resonance. We see on top that initially mode 3, located in $M_{357}$, has large energy and mode 2 has little energy. After 2000 timesteps energy is transferred from mode 3 to mode 2; the process repeats itself after 15,000 timesteps. Mode 5 is reduced in energy for a period of time after $t=$ 15,000. The modes 4, 6, 7 are in resonance according to normal form system (29). Energy is transferred to modes 4 and 6

Fig. 6

Quasi-trapping illustrated for $\alpha$-chain, $a= 0.75$, $\varepsilon = 0.1$, based on system (23) and with initial values of the unstable case in Fig. 4 (right). Left the $x_2,x_3$ modes near 1 : 1 resonance in the first 500 timesteps, middle again near a 1 : 1 resonance in 1500–2000 timesteps (note growth of $x_2$), right motion away from 1 : 1 resonance for timesteps 2000–3000

The first-order normal form of system (23) has to be reformulated in an $O(\varepsilon )$ neighborhood of $a = 0.5$. Putting $a= 0.5+ c \varepsilon$ the first seven eigenvalues $\omega _i^2$ are to $O(\varepsilon )$:

$$\begin{aligned}&3+ 2c \varepsilon ,\, \frac{1}{2}\left( 3+\sqrt{5}\right) +\left( 1+ \frac{1}{\sqrt{5}}\right) c \varepsilon \,(\mathrm{twice)},\\&\quad 2,\, 1+2c \varepsilon ,\, \frac{1}{2}\left( 3-\sqrt{5}\right) +\left( 1- \frac{1}{\sqrt{5}}\right) c \varepsilon \,(\mathrm{twice)}. \end{aligned}$$

with $O(\varepsilon )$ detuned resonances $\omega _2=\omega _5+\omega _6$ and $\omega _3\,=\,\omega _5+\omega _7$.

The combination angles that turn up in the first-order normalization

$$\begin{aligned} \chi _{256}\,=\, \varphi _2-\varphi _5-\varphi _6,\qquad \chi _{357}\,=\,\varphi _3-\varphi _5-\varphi _7, \end{aligned}$$

(28)

correspond with the sum resonances $\varphi _2=\varphi _5+\varphi _6$ and $\varphi _3=\varphi _5+\varphi _7$. In a neighborhood of $a= 0.5$ we can apply averaging–normalization using the frequencies of the exact resonance while using the $c \varepsilon$ term as a perturbation. This produces the system:

$$\begin{aligned} \dot{r}_1= & {} 0,\qquad \dot{r}_4 \,=\, 0,\qquad \dot{\varphi }_1 \,=\, \frac{c}{\sqrt{3}} \varepsilon ,\qquad {\dot{\varphi }}_4 \,=\,0,\nonumber \\ \dot{r}_2= & {} \frac{\varepsilon r_5r_6\sin \chi _{256}}{4\sqrt{15+5\sqrt{5}}},\qquad {\dot{\varphi }}_2\,=\,\frac{\varepsilon r_5 r_6 \cos \chi _{256}}{4\sqrt{15+5\sqrt{5}}\;r_2} + \frac{c}{\sqrt{5}} \varepsilon ,\nonumber \\ \dot{r}_3= & {} \frac{\varepsilon r_5r_7 \sin \chi _{357}}{4\sqrt{15+5\sqrt{5}}},\qquad {\dot{\varphi }}_3= \frac{\varepsilon r_5r_7\cos \chi _{357}}{4\sqrt{15+5\sqrt{5}}\;r_3}+ \frac{c}{\sqrt{5}} \varepsilon ,\nonumber \\ \dot{r}_5= & {} - \frac{\varepsilon (r_2r_6\sin \chi _{256}+r_3r_7\sin \chi _{357})}{4\sqrt{10}},\qquad {\dot{\varphi }}_5 \,=\, \frac{\varepsilon (r_2r_6\cos \chi _{256}+r_3r_7\cos _{357})}{4\sqrt{10}\;r_5}+ c \varepsilon ,\nonumber \\ \dot{r}_6= & {} - \frac{\varepsilon r_2r_5\sin \chi _{256}}{4\sqrt{15-5\sqrt{5}}},\qquad {\dot{\varphi }}_6 = \frac{\varepsilon r_2r_5\cos \chi _{256}}{4\sqrt{15-5\sqrt{5}}\;r_6} + \frac{c}{\sqrt{5}} \varepsilon ,\nonumber \\ \dot{r}_7= & {} -\frac{\varepsilon r_3r_5\sin \chi _{357}}{4\sqrt{15-5\sqrt{5}}},\qquad {\dot{\varphi }}_7 \,=\, \frac{\varepsilon r_3r_5\cos \chi _{357}}{4\sqrt{15-5\sqrt{5}}\;r_7} + \frac{c}{\sqrt{5}} \varepsilon . \end{aligned}$$

(29)

The system has the six independent integrals $\frac{1}{2}r_1^2=E_1$, $\frac{1}{2}r_4^2=E_4$ (already noted as exact integrals) and:

$$\begin{aligned} \sqrt{3+\sqrt{5}}r_2^2 + \sqrt{3-\sqrt{5}}r_6^2= & {} 2E_2,\\ \sqrt{3+\sqrt{5}}r_3^2 + \sqrt{3-\sqrt{5}}r_7^2= & {} 2E_3,\\ \sqrt{3+\sqrt{5}}r_2^2+\sqrt{3+\sqrt{5}}r_3^2+\sqrt{2} r_5^2= & {} 2E_5, \end{aligned}$$

and $H_2+ \varepsilon {\bar{H}}_3$; the constants $E_2, \ldots , E_5$ are positive. For integrability of the normal form one needs one more independent integral.

Short-periodic solutions of the normal form equations are found when looking for constant amplitudes; they satisfy the condition

$$\begin{aligned} \sin \chi _{357} = \sin \chi _{256} = 0. \end{aligned}$$

The equations for the combination angles are:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{1}{\varepsilon } \dot{\chi }_{357} = &{} \left( \frac{ r_5r_7\cos \chi _{357}}{4\sqrt{15+5\sqrt{5}}\;r_3} -\frac{(r_2r_6\cos \chi _{256}+r_3r_7\cos _{357})}{4\sqrt{10}\;r_5} - \frac{ r_3r_5\cos \chi _{357}}{4\sqrt{15-5\sqrt{5}}\;r_7} \right) - c , \\ \frac{1}{\varepsilon } \dot{\chi }_{256} = &{} \left( \frac{ r_5 r_6 \cos \chi _{256}}{4\sqrt{15+5\sqrt{5}}\;r_2} - \frac{(r_2r_6\cos \chi _{256}+r_3r_7\cos _{357})}{4\sqrt{10}\;r_5} - \frac{ r_2r_5\cos \chi _{256}}{4\sqrt{15-5\sqrt{5}}\;r_6} \right) - c . \end{array}\right. } \end{aligned}$$

(30)

We restrict our further discussion to the exact case $a=\frac{1}{2}$, corresponding to $c=0$.

Putting ${\dot{\chi }}_{256}={\dot{\chi }}_{357}=0$ we arrive at two equations:

$$\begin{aligned} \begin{aligned} r_2r_3r_6r_7&\,=\, \zeta \left( \sqrt{3-\sqrt{7}} r_5^2r_6^2 - r_2^2 r_6^2-\sqrt{3+\sqrt{7}} r_2^2 r_5^2\right) \\&\,=\, \zeta \left( \sqrt{3-\sqrt{7}} r_5^2r_7^2- r_3^2 r_7^2 - \sqrt{3+\sqrt{7}} r_3^2 r_5^2\right) , \end{aligned} \end{aligned}$$

(31)

with a parameter $\zeta$ satisfying $\zeta =1$ if $\chi _{256}\equiv \chi _{357}\bmod 2\pi$, and $\zeta =-1$ otherwise.) So we have in first-order normalization two resonant manifolds. They do not intersect each other in the region with positive amplitudes, which excludes double resonance.

We can continue the periodic and quasi-periodic solutions in the detuned case for c small enough.

6.3 Summary Invariant Manifolds $M_{145}, M_{256}$ and $M_{357}$ at Exact Resonance $a=0.5$

• $M_{145}$: The first-order normal form vanishes and is trivially integrable.

• $M_{256}$: The normal form Eq. (29) produces 3 normal modes, 3 integrals and 2 general position periodic solutions.

• $M_{357}$: The normal form Eq. (29) produces 3 normal modes, 3 integrals and 2 general position periodic solutions.

6.4 The Detuned Case $a = 0.75$

We find for the frequencies $\omega _i^2, i= 1,\ldots , 7$:

$$\begin{aligned} \omega _i^2= 3.5,\, 3 \,\mathrm{twice},\,2,\,1.5,\,0.5\,\mathrm{twice}. \end{aligned}$$

and to 4 decimals: $1.8708,\, 1.7321\,\mathrm{twice},\, 1.4142,\,1.2247,\, 0.7071\,\mathrm{twice}$. We replace $\alpha$ by the small positive parameter $\varepsilon$. In this case we have one combination angle $\phi _4=\phi _6+\varphi _7$. Denoting the corresponding combination angle by $\chi _{467}$ we find:

$$\begin{aligned} \dot{r}_1= & {} 0, \quad {\dot{\varphi }}_1=c\sqrt{\frac{2}{7}} \varepsilon ,\nonumber \\ \dot{r}_2= & {} 0,\quad {\dot{\varphi }}_2= c\frac{4 \varepsilon }{5 \sqrt{3}},\nonumber \\ \dot{r}_3= & {} 0,\quad {\dot{\varphi }}_3= c\frac{4 \varepsilon }{5 \sqrt{3}},\nonumber \\ \dot{r}_4= & {} \frac{3 \varepsilon r_6 r_7 \sin (\chi _{467})}{40 \sqrt{2}}\ ,\quad {\dot{\varphi }}_4=\frac{3 \varepsilon r_6 r_7 \cos (\chi _{467})}{40 \ \sqrt{2} r_4},\nonumber \\ \dot{r}_5= & {} 0,\quad {\dot{\varphi }}_5=c\sqrt{\frac{2}{3}} \varepsilon ,\nonumber \\ \dot{r}_6= & {} -\frac{3 \varepsilon r_4 r_7 \sin (\chi _{467})}{20 \ \sqrt{2}},\quad {\dot{\varphi }}_6=\frac{3 \varepsilon r_4 r_7 \cos (\chi _{467})}{20 \ \sqrt{2} r_6}+c\frac{\sqrt{2} \varepsilon }{5},\nonumber \\ \dot{r}_7= & {} -\frac{3 \varepsilon r_4 r_6 \sin (\chi _{467})}{20 \ \sqrt{2}},\quad {\dot{\varphi }}_7=\frac{3 \varepsilon r_4 r_6 \cos (\chi _{467})}{20 \ \sqrt{2} r_7}+c\frac{\sqrt{2} \varepsilon }{5}. \end{aligned}$$

(32)

Fig. 7

Projections of $x_4, x_6$ in a resonance zone of the case $m=4/3$ ($a= 0.75$), $\alpha$-chain with 8 particles reduced to system (23). We use initial values (34), $\varepsilon = 0.1$. In this case we start close to the resonance manifold described in (33). The presence of the 2 : 1 : 1 resonance of the modes 4, 6 and 7 induces transitions, and it starts near the 2 : 1 resonance as $x_7(0)=v_7(0)=0$ after which the $x_7$ mode obtains energy. We project on the plane $x_4$ and $x_6$, at the top timesteps 0–500 and 500–1000, below timesteps 1000–1500 and 1500–2000 showing the evolution of the dynamics in the resonance zone

The normal form system has the six independent integrals $r_1,r_2,r_3,r_5,2r_4^2+r_6^2=E_1 ,2r_4^2+r_7^2=E_2$ and in addition the normal form ${\bar{H}}_3$ or equivalently $H_2+ \varepsilon {\bar{H}}_3$. We conclude that the normal form $H_2+{\bar{H}}_3$ of the $\alpha$-chain for $a= 0.75$ is integrable.

In the exact case $a=\frac{3}{4}$ we find from the amplitudes that $\chi _{467}\equiv 0 \bmod \pi$ is a necessary condition for periodic solutions with constant amplitude. The condition ${\dot{\chi }}_{467}=0$ leads to the equation

$$\begin{aligned} R\;:=\; r_4^2 r_7^2+r_4^2r_6^2 - \frac{1}{2} r_6^2r_7^2 \,=\, 0, \end{aligned}$$

(33)

which describes the resonance manifold. The three invariant manifolds $M_{145}, M_{256}$ and $M_{357}$ are contained in the resonance manifold. Higher-order normalization might produce non-trivial additional results at smaller scales in $\varepsilon$.

The initial positions in the simulations that we carried out for $a=\frac{3}{4}$ are either on the resonance manifold, or near to it in the resonance zone. See Table 2.

Table 2 The quantity R in (33) describes the resonance manifold by $R=0$ in the case $a=\frac{3}{4}$

We used in Figs. 7 and 8 the initial conditions $v_i(0)=0, i=1, \ldots , 7$ with for $x_i(0), i =1 \ldots , 7$:

$$\begin{aligned} -\,0.0408248,-\,0.0547723, 0.0,-\,0.05,\,0.0,\,0.0447214,\,0.0. \end{aligned}$$

(34)

This initial position is in the resonance zone, with $R=5\times 10^{-6}$.

Figures 6, 7 and 8 illustrate the phenomenon of quasi-trapping described in Zaslavsky (2007). According to the Poincaré recurrence theorem, orbits on a compact energy manifold will return close to its initial position in phase space in a finite time. However, orbits that are not starting in a low-dimensional invariant manifold or near a stable periodic solution will in general take a very long time for this recurrence, depending on our assumption of closeness and the number of degrees of freedom. The recurrence theorem means that orbits cannot be trapped away from the initial conditions but they may linger in phase space during passage of resonance zones. In these zones we have periodic solutions, tori and unstable saddle-like manifolds that are the causes of delay. This is what we mean by quasi-trapping.

Fig. 8

The actions $I_4$, $I_6$ and $I_7$ (from left to right) for the same simulation as in Fig. 7, with $a=0.75$, 2000 timesteps, and an initial position, in (34), in the resonance zone. In the initial position $x_7(0)=0$, but mode 7 is excited.

In the case of $a= 0.5$ we have two sum resonances, in the case $a= 0.75$ we have the 2 : 1 : 1 resonance between modes 4, 6 and 7. Note that we start with zero initial value for mode 7. The dynamics in the resonance zone is illustrated in Fig. 7. First the 2 : 1 resonance of the $x_4, x_6$ modes dominates (500 timesteps), then in the timesteps for $t \ge 500$ the mode 7 is excited. The recurrent motion on tori around the periodic solution will produce exchanges of energy between the modes. In Fig. 8 we present the time series of the actions of the three modes.

7 Conclusions

• 1. The dynamics of 4 particles in a periodic FPU chain with alternating masses can be identified in a submanifold of a FPU chain with 8 particles. As is shown in Sect. 3, this is a general feature of FPU chains with 4n particles. There exist bushes (in the terminology of Chechin et al. 2002), families of invariant manifolds, for arbitrary large chains of this type with 4n particles. This also holds for the classical case $m=1$.

• 2. In the cases of 4, 8 particles, incidental resonances emerge producing periodic solutions that, in the case of stability, are associated with invariant tori. These resonances and tori occur in systems with 4n and 8n particles as well.

• 3. Quasi-trapping as formulated in Zaslavsky (2007) and demonstrated in our analysis, produces a significant delay of recurrence. The trapping regions are often associated with the primary resonances 1 : 2 or 1 : 1. The normal form approximations give precise estimates of validity for a long but finite interval of time. However, this is enough to demonstrate the phenomenon as the recurrence theorem applies to these quasi-trapping regions, the flow will return an infinite number of times arbitrarily close to the regions.

• 4. Near stable equilibrium we did not find energy equipartition in a periodic FPU chain with alternating masses. The systematic presence of nested invariant manifolds (bushes) makes equipartition less probable.