Abstract
Objective
The purpose of this study was: To test whether machine learning classifiers for transition zone (TZ) and peripheral zone (PZ) can correctly classify prostate tumors into those with/without a Gleason 4 component, and to compare the performance of the best performing classifiers against the opinion of three board-certified radiologists.
Methods
A retrospective analysis of prospectively acquired data was performed at a single center between 2012 and 2015. Inclusion criteria were (i) 3-T mp-MRI compliant with international guidelines, (ii) Likert ≥ 3/5 lesion, (iii) transperineal template ± targeted index lesion biopsy confirming cancer ≥ Gleason 3 + 3. Index lesions from 164 men were analyzed (119 PZ, 45 TZ). Quantitative MRI and clinical features were used and zone-specific machine learning classifiers were constructed. Models were validated using a fivefold cross-validation and a temporally separated patient cohort. Classifier performance was compared against the opinion of three board-certified radiologists.
Results
The best PZ classifier trained with prostate-specific antigen density, apparent diffusion coefficient (ADC), and maximum enhancement (ME) on DCE-MRI obtained a ROC area under the curve (AUC) of 0.83 following fivefold cross-validation. Diagnostic sensitivity at 50% threshold of specificity was higher for the best PZ model (0.93) when compared with the mean sensitivity of the three radiologists (0.72). The best TZ model used ADC and ME to obtain an AUC of 0.75 following fivefold cross-validation. This achieved higher diagnostic sensitivity at 50% threshold of specificity (0.88) than the mean sensitivity of the three radiologists (0.82).
Conclusions
Machine learning classifiers predict Gleason pattern 4 in prostate tumors better than radiologists.
Key Points
• Predictive models developed from quantitative multiparametric magnetic resonance imaging regarding the characterization of prostate cancer grade should be zone-specific.
• Classifiers trained differently for peripheral and transition zone can predict a Gleason 4 component with a higher performance than the subjective opinion of experienced radiologists.
• Classifiers would be particularly useful in the context of active surveillance, whereby decisions regarding whether to biopsy are necessitated.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Prostate cancer is a heterogeneous disease, with a strong relationship between aggressiveness, as characterized by Gleason grade, and survival [1]. More recently, the concept of Gleason 3 and Gleason 4 tumors representing distinct disease states has emerged [2], due to the different signatures at a genomic level [3] and the distinct survival rates encountered in large long-term follow-up studies [4, 5]. Indeed, percentage Gleason 4 has been shown to outperform traditional Gleason grading as a prognostic marker in a multivariate study of 379 prostatectomy specimens [6].
A reliable, quantitative, and non-invasive test to identify patients at risk of aggressive disease (those with a potential Gleason 4 component) would therefore have significant clinical value but does not currently exist.
Clinical parameters such as tumor volume [7] and serum prostate-specific density (PSAd) have been shown to correlate with Gleason grade [8].
While there is some evidence that the subjective opinion of radiologists interpreting multiparametric (mp) MRI can be used to estimate Gleason grade [9], quantitative measurements of signal intensity including normalized T2 signal intensity and apparent diffusion coefficient (ADC) also moderately correlate with Gleason grade [10, 11] and have been shown to differ in peripheral zone (PZ) vs. transition zone (TZ) tumors [12].
The purpose of this study was (i) to test whether machine learning classifiers for TZ and PZ (based on clinical and quantitative mp-MRI parameters) can correctly classify tumors into those with/without a Gleason 4 component and (ii) to compare the performance of the best performing classifiers against the subjective opinion of three board-certified radiologists.
Materials and methods
Our Institutional Review Board approved the study and waived the requirement for individual consent for retrospective analysis of prospectively acquired patient data collected as part of clinical trials/routine care (R&D No: 12/0195, 16 July 2012).
Patient cohorts
Two temporally separated cohorts were built: one for generating models (training cohort) and another for temporal validation (validation cohort).
For the training cohort, a trial dataset of 330 patients was interrogated. Full details of the trial have been previously reported [13]. In brief, inclusion criteria were (i) men who underwent previous transrectal ultrasound biopsy whereby suspicion remained that cancer was either missed or misclassified and (ii) men suitable for further characterization using transperineal template prostate mapping (TPM) biopsy. Exclusion criteria were (i) previous history of prostate cancer treatment and (ii) lack of complete gland sampling or inadequate sampling density at TPM.
Selection criteria for building the training cohort were (i) 3-T mp-MRI, performed between February 2012 and January 2014; (ii) Likert [14] ≥ 3/5 index lesion on mp-MRI, defined on the trial proforma following multidisciplinary tumor board discussion, whereby lesions were assigned to be of TZ or PZ origin; and (iii) TPM and targeted index lesion biopsy confirming tumor (defined as Gleason score 3 + 3 or greater). Gleason pattern 5 was not found in any samples. The index lesion was defined as the most conspicuous lesion with the highest Likert score (3, 4, or 5). This cohort consisted of 72 Gleason 4 containing lesions (38 Gleason 3 + 4, 34 Gleason 4 + 3), and 27 Gleason 3 + 3 lesions for the PZ whereas the TZ had 22 Gleason 4 containing lesions (20 Gleason 3 + 4, 2 Gleason 4 + 3), and 27 Gleason 3 + 3 lesions. A flow diagram for patient selection is shown in Fig. 1.
The validation cohort consisted of 30 consecutive men: 20 PZ (6 Gleason 3 + 4, 4 Gleason 4 + 3, and 10 Gleason 3 + 3) and 10 TZ (3 Gleason 3 + 4, 1 Gleason 4 + 3, and 5 Gleason 3 + 3) with the same selection criteria and scanning protocol as in the training cohort, performed between June and December 2015.
Table 1 shows the age, the PSA, and the gland and tumor volume of the patients in the two cohorts.
Multiparametric MRI protocol
Mp-MRI was performed using a 3-T scanner (Achieva, Philips Healthcare) and a 32-channel phased-array coil. Prior to imaging, 0.2 mg/kg (up to 20 mg) of a spasmolytic agent (Buscopan; Boehringer Ingelheim) was administered intravenously to reduce bowel peristalsis. Mp-MRI was compliant with the European Society of Uroradiology [14] guidelines. Full acquisition parameters are shown in Table 2.
Targeted biopsy
Ultrasound-guided TPM ± targeted biopsy acted as the reference standard for the training cohort using cognitive MR-guided registration. A systematic biopsy of the whole gland was performed through a brachytherapy template-grid placed on the perineum using a 5-mm sampling frame. Focal index lesions underwent cognitive MRI-targeted biopsies at the time of TPM. A genitourinary pathologist with 12 years of experience analyzed biopsy cores blinded to the MRI results. There were no instances of non-targeted samples yielding higher Gleason grades than targeted specimens.
TPM and targeted biopsies were chosen as the reference standard because they are superior to transrectal ultrasound biopsy, are the sampling method of choice in the active surveillance population, and avoid the spectrum bias associated with a prostatectomy reference standard [15], which favors patients with aggressive disease.
Multiparametric MRI review
Mp-MRI images were qualitatively assessed on an Osirix workstation by three board-certified radiologists independently (readers SP, MA, and SP). Radiologists were fellowship-trained, with 10, 2, and 3 years of experience in the clinical reporting of mp-prostate MRI, with each year comprising more than 100 mp-MRIs per year with regular attendance at weekly multidisciplinary tumor board meetings [16]. Radiologists were informed of the PSA level and subjectively evaluated whether the index lesion contained a Gleason pattern 4 component or not (i.e., a binary classification), based on their personal evaluation of imaging characteristics, as developed from years of prostate MRI reporting and pathological feedback at multidisciplinary tumor board meetings.
Radiologists were aware that high signal on b = 2000 s/mm2 DWI with corresponding low ADC value, low T2W signal, and avid early contrast enhancement compared with normal prostatic tissue suggest higher grade disease [10, 17].
Extraction of mp-MRI-derived quantitative parameters
MR datasets were analyzed with MIM Symphony Version 6.1 (MIM Software Inc), which carries out rigid translational co-registration of volumetric and axial T2W, ADC, and DCE images for semi-automatic registration, after which subsequent manual refinement can then be performed.
A fourth board-certified radiologist (EJ) with 3 years of experience in the quantitative analysis of mp-prostate MRI was blinded to the histopathology results and the opinion of the other radiologists manually contoured a volume of interest for each index lesion and recorded the mean signal intensity (SI) of each volume on the axial T2W, ADC, and DCE images at all time points. Contouring was performed on T2WI and manually adjusted on the DCE images and ADC maps to account for distortion and registration errors. A typical contoured lesion is shown in Fig. 2. In order to standardize signal intensity between subjects, normalized T2 signal intensity metrics were calculated by dividing the signal intensity of the lesion by that of the bladder urine [18].
Early enhancement (EE) and maximum enhancement (ME) metrics were derived from the DCE-MRI signal enhancement time curves. EE was defined as the first strongly enhancing postcontrast SI divided by the precontrast SI, and ME as the difference between the peak enhancement SI and the baseline SI normalized to the baseline SI [19].
Clinical features of the tumor volume, gland volume, and PSAd were also selected as features to include in the model development, whereby the first two features were measured using tri-planar measurements and the prolate ellipsoid formula [20].
Machine learning models
Five classification models were tested, namely logistic regression (LR) [21], naïve Bayes (NB) [21], support vector machine [21], random forest (RF) [22], and feed-forward neural network (FFNN) [21].
To validate each model, a fivefold cross-validation was applied, whereby data was split into five folds, with four folds being used for training and one for testing the classifiers. This was repeated for five trials with each fold used once as a test set. At each trial, a receiver operator characteristic (ROC) curve was built for both the training and test set and the corresponding AUC calculated. The values of the AUCs for the five trials were averaged to produce a single estimate, and the process was repeated for 100 rounds using a different partitioning of the data for each repetition.
Since the performance of machine learning classifiers decreases when the data used to train the model is imbalanced [23], which applies to the PZ cohort in our study (72 Gleason 4, vs. 27 Gleason 3 + 3), a resampling technique called Synthetic Minority Over-sampling TEchnique (SMOTE) [24] was applied to the PZ training cohort. Here, the minority class is over-sampled by introducing synthetic examples along the line segments joining any/all of the k minority class nearest neighbors of each minority class sample. After applying SMOTE to the PZ training cohort, 45 synthetic samples belonging to the class of 3 + 3 Gleason cancers were added and this new re-balanced data was used to generate the classifiers. SMOTE was not applied to the TZ training cohort as this cohort was sufficiently balanced.
The Statistics and Machine Learning Toolbox of MATLAB (version R2017b 9.3.0.713579, MathWorks) was used for all algorithms, using one hidden layer of 20 neurons for FFNN.
Model feature selection and internal validation
The best combination of features was derived from the training cohort dataset using the correlation feature selection (CFS) algorithm [25] for TZ and PZ lesions, denoted as SELTZ and SELPZ respectively. CFS determines (i) how each feature correlates with the presence of Gleason 4 tumor, and (ii) whether any of the selected features are redundant due to correlations between them. Redundant features were removed from the SELTZ and SELPZ feature sets.
As Fig. 3 shows, to test whether CFS was effective, we compared the performance of classifiers trained using all features (denoted ALL) with the performance of the classifiers trained using only SELTZ and SELPZ.
Flow diagram outlining the feature selection validation strategy used in the study. CFS, correlation features selection; ALL, set containing all the features; SELTZ, subset of feature selected for the TZ; SELPZ, subset of feature selected for PZ; AUCALLPZ, area under the curve obtained on PZ using all the features; AUCALLTZ, area under the curve obtained on TZ using all the features; LR, linear regression; FFNN, feed-forward neural network; SVM, support vector machine; NB, naïve Bayes; RF, random forest, AUCSELPZ, area under the curve obtained on PZ obtained using the selected feature; AUCSELTZ, area under the curve obtained on TZ obtained using the selected feature
Best model selection and temporal validation
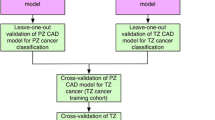
Using SELTZ and SELPZ, we applied a fivefold cross-validation to compare the classifiers and to select the best performing zone-specific models, defined by the highest AUC. A flow diagram of the comparisons is shown in Fig. 4.
Flow diagram outlining the model validation strategy used in the study. SELTZ, subset of feature selected for the transition zone; SELPZ, subset of feature selected for PZ; AUCSELPZ, area under the curve obtained on PZ obtained using the selected feature; AUCSELTZ, area under the curve obtained on TZ obtained using the selected feature; LR, linear regression; FFNN, feed-forward neural network; SVM, support vector machine; NB, naïve Bayes; RF, random forest; PZ, peripheral zone; TZ, transition zone
Once the best performing models were selected for each zone, their performance was compared with that of the three radiologists. Mean values of sensitivity and specificity were compared with that obtained by the classifiers at three cut-off points of interest on the ROC curves. In particular, we considered:
- (i)
The point characterized by a specificity of 50% (point_50), which is of interest from a clinical standpoint as we can tolerate classifying 50% of patients as false-positives provided a high level of sensitivity (i.e., low numbers of false-negatives) is maintained.
- (ii)
The point characterized by a specificity equal to the mean specificity of the three radiologists who assessed the images (point_RAD), we used this point to compare our models to the performance of an experienced radiologist.
- (iii)
The point closest to the point with sensitivity and specificity equal to 1 (point_01), we chose this point as it is characterized by the best trade-off between specificity and sensitivity. For all the three points, we derived the corresponding thresholds on the ROC curve obtained on the training set and then applied these thresholds to compute the sensitivity/specificity of the classifiers on the test set.
Finally, we applied a temporal-separated validation whereby the best performing classifier was trained on the training cohort and tested on the validation cohort. SMOTE was applied to the training set before using it to train the classifier for all the analyses performed in the PZ cohort.
Results
Model selection and internal validation
CFS selected SELPZ = {ADC, ME, PSAd} and SELTZ = {ADC, ME}. Table 3 shows the mean and standard deviation of the AUCs obtained on the test set by the classifiers using all the parameters (ALL) and the selected features (SELTZ and SELPZ).
For the PZ, the mean AUC on the test set of the models trained with SELPZ was greater than that of the models trained using ALL. However, for the TZ, only LR and NB benefitted from feature selection, while FFNN, SVM, and RF obtained slightly better AUC values when trained with ALL.
To statistically validate the comparison between classifiers trained with and without CFS, we applied the Wilcoxon signed-rank test for pairwise comparison [26] between the AUC values obtained on the test set by each classifier trained with and without feature selection. For the PZ, all the classifiers except RF obtained statistically better AUC values when trained with SELPZ than the ones trained with ALL (p value < 0.05), while for the TZ, only LR and NB obtained statistically better AUC values when trained with SELTZ.
Although some TZ classifiers did not statistically improve their performance when trained with SELTZ, the best performing models (LR, NB) obtained better results when CFS was applied. For this reason, we decided to build the models for both TZ and PZ training the classifiers with SELTZ and SELPZ, respectively.
For the PZ, LR and NB had higher AUC values followed very closely by FFNN and RF, with SVM obtaining the worst results.
The results obtained by the five classifiers on TZ were similar to the PZ, although the AUC values were generally lower. NB and LR were the best performing models, and SVM and RF were the classifiers with the lowest mean AUC values.
To compare AUC distributions obtained by the different classifiers for TZ and PZ, the Friedman [26] and Iman and Davenport tests [26] were applied. If a statistical difference was detected, the Holm test [26] was performed to compare the best performing classifier (with the lowest Friedman rank) and the remaining ones. The results for these tests are shown in Table 4, whereby the best performing classifiers were NB and LR for TZ and PZ, respectively. The Iman and Davenport statistical hypothesis of equivalence was rejected in both cases.
For the TZ, the Holm post hoc procedure stated that the AUC distributions on the test set obtained by NB are statistically better than those of all the other classifiers. For the PZ, the LR classifier achieved statistically better performance.
Radiologist comparison and temporal validation
Figure 5 shows, for the test set, the mean ROC curve along with the sensitivity and specificity mean values obtained by the three radiologists and computed at the three cut-off points over 100 rounds of fivefold cross-validation by NB and LR classifiers for TZ and PZ.
Mean ROC curve, along with the sensitivity and specificity mean values obtained by the three radiologists and computed at the three cut-off points generated on the test set following the fivefold cross-validation by the best performing classifiers (NB and LR) on TZ (left) and PZ (right). PZ, peripheral zone; TZ, transition zone; LR, linear regression; NB, naïve Bayes; ROC, receiver operator characteristic
In Table 5, the mean values of sensitivity and specificity calculated on the test set at point_50, point_01, and point_RAD are shown along with those obtained by the three radiologists.
For the PZ, at all three cut-off points, LR achieved higher values of sensitivity (0.93, 0.76, and 0.88, respectively) and specificity (0.53, 0.73, and 0.65, respectively) vs. respective sensitivity and specificity of 0.72 and 0.40 for the three radiologists.
Although the radiologists had a higher specificity in the TZ than in the PZ, their mean performance (specificity and sensitivity equal 0.82 and 0.44, respectively) was still lower than that achieved by NB, whereby point_50, point_01, and point_RAD were equal to 0.88, 0.75, and 0.92 for sensitivity, and to 0.51, 0.57, and 0.44 for specificity.
Finally, for temporal validation, the best performing classifiers (NB for TZ and LR for PZ) were trained using the training cohort and tested using the validation cohort. The AUC values obtained on the validation cohort for TZ and PZ were 0.85 and 1.00, respectively.
Discussion
Our results show that the classifiers designed to predict a Gleason 4 component in known prostate cancer are zone specific although use a similar set of features, namely {ADC, ME, PSAd} for the PZ and {ADC, ME} for the TZ. Furthermore, the best performing models were superior to the subjective opinion of radiologists at all probability thresholds and maintained their performance at temporal validation.
Several studies have previously reported logistic regression and mp-MRI-derived parameters for the prediction of Gleason grade in prostate cancer [27,28,29,30]. While our study is in agreement that ADC is a useful parameter for this purpose, our study differs from the literature in a number of ways. Firstly, all other studies excluded tumors < 0.5 ml; meaning, such data is not generalizable to smaller index lesions, which can be aggressive [31] and are often followed in active surveillance programs.
Hötker et al [27] studied 195 patients and reported a best performing univariate parameter (ADC) achieved an AUC of 0.69 for distinguishing 3 + 3 tumors from those containing a Gleason 4. A possible explanation of their lower reported AUC could be the multiscanner nature of the study and the combination of PZ and TZ cancers into a single model. Furthermore, the authors showed that Ktrans failed to add value for discriminating such tumors and the models did not undergo external validation.
The other studies in the literature [27,28,29,30] derive models based on less than 60 patients and combine DWI with spectroscopic metrics, which necessitates specialist equipment and knowledge. Indeed, all of our metrics can be extracted from the minimum protocol requirements as recommended by international consensus guidelines [14] and thus are more generalizable to non-specialist centers. Since our model uses PSAd as a predictor of Gleason 4 tumor, our study affirms that serum and imaging biomarkers can be synergistic [32]. Our results are also consistent with another group who found no additive value of the tumor volume in Gleason grade prediction [27].
In this study, we chose to analyze index lesions only, to avoid statistical clustering and because index lesions usually drive management strategy and patient outcome [33], particularly in the context of focal therapy and active surveillance. We also chose to exclude patients without evidence of cancer at biopsy since we wished to build a tool which could be used in patients who undergo MRI surveillance and would benefit from quantitative estimates of Gleason grade.
While we did not derive Tofts’ model parameters due to our institutional preference for higher spatial resolution of DCE-MRI over temporal resolution (which is required for a Tofts’ fitting), we demonstrated that ME which is a robust, semiquantitative metric [34] can improve the discriminatory ability for the prediction of Gleason 4 cancer components above ADC alone. While enhancement characteristics play a limited role in PI-RADSv2, the present study suggests these characteristics may be more beneficial in the characterization of Gleason grade rather than tumor detection.
With further work, machine learning classifiers could be used in active surveillance programs to non-invasively detect whether tumors have undergone transformation to a higher Gleason grade and thereby provoke biopsy or intervention. This potential application is particularly pertinent in light of the findings from the ProtecT study [35] which showed no significant difference in survival outcomes at 10-year follow-up in patients randomized to active surveillance, surgery or radiotherapy which is likely to impact the uptake of active surveillance as a management strategy. Indeed, mp-MRI is already advocated by the NICE in the UK as part of active surveillance programs [36].
One possible limitation is the unbalanced nature of the PZ cohort, due to a higher natural incidence of Gleason 4 containing tumors. However, this was addressed by the use of SMOTE. Although the TZ cohort was balanced, a larger cohort would be required to confirm the performance of classifiers, especially for the validation cohort. While the size of the two cohorts was limited, overfitting was avoided by feature selection which reduced the number of input variables, and by regularization which permitted a small percentage of misclassification in the training dataset to produce a less complex model. Finally, although TPM biopsy offers several advantages over transrectal ultrasound-guided biopsy, it may not be as accurate as whole-mount prostatectomy [37].
Further work could therefore consider both prospective large-scale external validation (e.g., at other centers) and the impact these predictive models have on patient outcome.
Conclusion
Machine learning classifiers combining PSAd and quantitative multiparametric MRI parameters outperform experienced radiologist opinion for the prediction of Gleason pattern 4 in prostate cancer. These classifiers could therefore harbor great potential when making management decisions in the prostate cancer pathway and would be particularly useful to inform decisions regarding patients on active surveillance programs.
Change history
10 September 2019
The original version of this article, published on 11 June 2019, unfortunately contained a mistake. The following correction has therefore been made in the original: In section “Multiparametric MRI review,” the readers mentioned in the first sentence were partly incorrect.
10 September 2019
The original version of this article, published on 11 June 2019, unfortunately contained a mistake. The following correction has therefore been made in the original: In section ���Multiparametric MRI review,��� the readers mentioned in the first sentence were partly incorrect.
Abbreviations
- ADC:
-
Apparent diffusion coefficient
- AUC:
-
Area under the curve
- CFS:
-
Correlation feature selection
- DCE:
-
Dynamic contrast-enhanced
- DWI:
-
Diffusion-weighted imaging
- EE:
-
Early enhancement
- FFNN:
-
Feed-forward neural network
- LR:
-
Logistic regression
- ME:
-
Maximum enhancement
- mp-MRI:
-
Multiparametric magnetic resonance imaging
- NB:
-
Naïve Bayes
- PSA:
-
Prostate-specific antigen
- PSAd:
-
Prostate-specific antigen density
- PZ:
-
Peripheral zone
- RF:
-
Random forest
- ROC:
-
Receiver operator characteristic
- SI:
-
Signal intensity
- SMOTE:
-
Synthetic minority over-sampling technique
- SVM:
-
Support vector machine
- TPM:
-
Transperineal template prostate mapping
- TZ:
-
Transition zone
References
Albertsen PC, Hanley JA, Fine J (2005) 20-year outcomes following conservative management of clinically localized prostate cancer. JAMA 293:2095–2101. https://doi.org/10.1001/jama.293.17.2095
Hu Y, Ahmed HU, Carter T et al (2012) A biopsy simulation study to assess the accuracy of several transrectal ultrasonography (TRUS)-biopsy strategies compared with template prostate mapping biopsies in patients who have undergone radical prostatectomy. BJU Int 110:812–820. https://doi.org/10.1111/j.1464-410X.2012.10933.x
Tomlins SA, Mehra R, Rhodes DR et al (2007) Integrative molecular concept modeling of prostate cancer progression. Nat Genet 39:41–51. https://doi.org/10.1038/ng1935
Eggener SE, Scardino PT, Walsh PC et al (2011) Predicting 15-year prostate cancer specific mortality after radical prostatectomy. J Urol 185:869–875. https://doi.org/10.1016/j.juro.2010.10.057
Tefilli MV, Gheiler EL, Tiguert R et al (1999) Should Gleason score 7 prostate cancer be considered a unique grade category? Urology 53:372–377
Stamey TA, McNeal JE, Yemoto CM, Sigal BM, Johnstone IM (1999) Biological determinants of cancer progression in men with prostate cancer. JAMA 281:1395–1400
Song SY, Kim SR, Ahn G, Choi HY (2003) Pathologic characteristics of prostatic adenocarcinomas: a mapping analysis of Korean patients. Prostate Cancer Prostatic Dis 6:143–147. https://doi.org/10.1038/sj.pcan.4500636
Verma A, St Onge J, Dhillon K, Chorneyko A (2014) PSA density improves prediction of prostate cancer. Can J Urol 21:7312–7321
Borofsky MS, Rosenkrantz AB, Abraham N, Jain R, Taneja SS (2013) Does suspicion of prostate cancer on integrated T2 and diffusion-weighted MRI predict more adverse pathology on radical prostatectomy? Urology 81:1279–1283. https://doi.org/10.1016/j.urology.2012.12.026
Wang L, Mazaheri Y, Zhang J, Ishill NM, Kuroiwa K, Hricak H (2008) Assessment of biologic aggressiveness of prostate cancer: correlation of MR signal intensity with Gleason grade after radical prostatectomy. Radiology 246:168–176. https://doi.org/10.1148/radiol.2461070057
Nowak J, Malzahn U, Baur AD et al (2016) The value of ADC, T2 signal intensity, and a combination of both parameters to assess Gleason score and primary Gleason grades in patients with known prostate cancer. Acta Radiol 57:107–114. https://doi.org/10.1177/0284185114561915
Dikaios N, Alkalbani J, Abd-Alazeez M et al (2015) Zone-specific logistic regression models improve classification of prostate cancer on multi-parametric MRI. Eur Radiol 2727–2737. https://doi.org/10.1007/s00330-015-3636-0
Simmons LA, Ahmed HU, Moore CM et al (2014) The PICTURE study -- prostate imaging (multi-parametric MRI and prostate HistoScanning™) compared to transperineal ultrasound guided biopsy for significant prostate cancer risk evaluation. Contemp Clin Trials 37:69–83. https://doi.org/10.1016/j.cct.2013.11.009
Barentsz JO, Richenberg J, Clements R et al (2012) ESUR prostate MR guidelines 2012. Eur Radiol 22:746–757. https://doi.org/10.1007/s00330-011-2377-y
Robertson NL, Emberton M, Moore CM (2013) MRI-targeted prostate biopsy: a review of technique and results. Nat Rev Urol 10:589–597. https://doi.org/10.1038/nrurol.2013.196
Brizmohun Appayya M, Adshead J, Ahmed HU et al (2018) National implementation of multi-parametric magnetic resonance imaging for prostate cancer detection - recommendations from a UK consensus meeting. BJU Int 122:13–25. https://doi.org/10.1111/bju.14361
Oto A, Yang C, Kayhan A et al (2011) Diffusion-weighted and dynamic contrast-enhanced MRI of prostate cancer: correlation of quantitative MR parameters with Gleason score and tumor angiogenesis. AJR Am J Roentgenol 197:1382–1390. https://doi.org/10.2214/AJR.11.6861
Johnston E, Punwani S (2016) Can we improve the reproducibility of quantitative multiparametric prostate MR imaging metrics? Radiology 281:652–653. https://doi.org/10.1148/radiol.2016161197
Zelhof B, Lowry M, Rodrigues G, Kraus S, Turnbull (2009) Description of magnetic resonance imaging-derived enhancement variables in pathologically confirmed prostate cancer and normal peripheral zone regions. BJU Int 104:621–627. https://doi.org/10.1111/j.1464-410X.2009.08457.x
Mazaheri Y, Goldman DA, Di Paolo PL, Akin O, Hricak H (2015) Comparison of prostate volume measured by endorectal coil MRI to prostate specimen volume and mass after radical prostatectomy. Acad Radiol 22:556–562. https://doi.org/10.1016/j.acra.2015.01.003
Bishop CM (2006) Pattern recognition and machine learning. Springer, New York
Breiman L (2001) Random forests. Mach Lear 45:5–32. https://doi.org/10.1023/A:1010933404324
López V, Fernández A, García S, Palade V, Herrera F (2013) An insight into classification with imbalanced data: empirical results and current trends on using data intrinsic characteristics. Inf Sci 250:113–141. https://doi.org/10.1016/j.ins.2013.07.007
Chawla NV, Bowyer KW, Hall LO, Kegelmeyer WP (2002) SMOTE: synthetic minority over-sampling technique. J Artif Intell Res 16:321–357
Hall MA, Smith LA (1996) Practical feature subset selection for machine learning. In: Proceedings of the 21st Australasian Computer Science Conference, Perth, 4–6 February. Springer, Berlin, pp 181–191
Sheskin DJ (2007) Handbook of parametric and nonparametric statistical procedures, 4th edn. Chapman & Hall/CRC, Boca Ranton
Hötker AM, Mazaheri Y, Aras Ö et al (2016) Assessment of prostate cancer aggressiveness by use of the combination of quantitative DWI and dynamic contrast-enhanced MRI. AJR Am J Roentgenol 1–8. https://doi.org/10.2214/AJR.15.14912
Vos EK, Kobus T, Litjens GJ et al (2015) Multiparametric magnetic resonance imaging for discriminating low-grade from high-grade prostate cancer. Invest Radiol 50:490–497. https://doi.org/10.1097/RLI.0000000000000157
Kobus T, Vos PC, Hambrock T et al (2012) Prostate cancer aggressiveness: in vivo assessment of MR spectroscopy and diffusion-weighted imaging at 3 T. Radiology 265:457–467. https://doi.org/10.1148/radiol.12111744
Nagarajan R, Margolis D, Raman S et al (2012) MR spectroscopic imaging and diffusion-weighted imaging of prostate cancer with Gleason scores. J Magn Reson Imaging 36:697–703. https://doi.org/10.1002/jmri.23676
Horninger W, Berger AP, Rogatsch H et al (2004) Characteristics of prostate cancers detected at low PSA levels. Prostate 58:232–237. https://doi.org/10.1002/pros.10325
Sciarra A, Panebianco V, Cattarino S et al (2012) Multiparametric magnetic resonance imaging of the prostate can improve the predictive value of the urinary prostate cancer antigen 3 test in patients with elevated prostate-specific antigen levels and a previous negative biopsy. BJU Int 110:1661–1665. https://doi.org/10.1111/j.1464-410X.2012.11146.x
Stamey TA, McNeal JM, Wise AM, Clayton JL (2001) Secondary cancers in the prostate do not determine PSA biochemical failure in untreated men undergoing radical retropubic prostatectomy. Eur Urol 39(Suppl 4):22–23. https://doi.org/10.1159/000052577
Buckley DL (2002) Uncertainty in the analysis of tracer kinetics using dynamic contrast-enhanced T1-weighted MRI. Magn Reson Med 47:601–606
Hamdy FC, Donovan JL, Lane JA et al (2016) 10-year outcomes after monitoring, surgery, or radiotherapy for localized prostate cancer. N Engl J Med 375:1415–1424. https://doi.org/10.1056/NEJMoa1606220
National Institute for Health and Care Excellence (2019) Prostate cancer: diagnosis and management. Available via https://www.nice.org.uk/guidance/indevelopment/gid-ng10057/consultation/html-content-2. Accessed 3 April 2019
Arumainayagam N, Ahmed HU, Moore CM et al (2013) Multiparametric MR imaging for detection of clinically significant prostate cancer: a validation cohort study with transperineal template prostate mapping as the reference standard. Radiology 268:761–769. https://doi.org/10.1148/radiol.13120641
Acknowledgments
This work was undertaken at University College London Hospital (UCLH) in collaboration with University College London (UCL). The work of EJ and SP was supported by the NIHR Biomedical Research Centre funding scheme of the UK Department of Health. Further funding for HS and SP was obtained from the Kings College London (KCL)/UCL Comprehensive Cancer Imaging Centre. Ethical approval for the study was granted by London City Road and Hampstead National research ethics committee REC reference 11/LO/1657 and the trial is registered with ClinicalTrials.gov identifier NCT01492270. The views and opinions expressed herein are those of the authors and do not necessarily reflect those of the National Health Service or the Department of Health.
Funding
This study has received funding by the NIHR Biomedical Research Centre funding scheme of the UK Department of Health.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Guarantor
The scientific guarantor of this publication is Prof Shonit Punwani.
Conflict of interest
The authors of this manuscript declare no relationships with any companies, whose products or services may be related to the subject matter of the article.
Statistics and biometry
One of the authors has significant statistical expertise.
Informed consent
Written informed consent was obtained from all subjects (patients) in this study.
Ethical approval
Institutional Review Board approval was obtained.
Study subjects or cohorts overlap
Some study subjects or cohorts have been previously reported in:
Dikaios N, Giganti F, Sidhu HS, Johnston EW, Appayya MB, Simmons L, Freeman A, Ahmed HU, Atkinson D, Punwani S. Multi-parametric MRI zone-specific diagnostic model performance compared with experienced radiologists for detection of prostate cancer. Eur Radiol. 2018 Nov 19.
Simmons LAM, Kanthabalan A, Arya M, Briggs T, Charman SC, Freeman A, Gelister J, Jameson C, McCartan N, Moore CM, van der Muelen J, Emberton M, Ahmed HU., Prostate Imaging Compared to Transperineal Ultrasound-guided biopsy for significant prostate cancer Risk Evaluation (PICTURE): a prospective cohort validating study assessing Prostate HistoScanning. Prostate Cancer Prostatic Dis. 2018 Oct 2.
Simmons LAM, Kanthabalan A, Arya M, Briggs T, Barratt D, Charman SC, Freeman A, Hawkes D, Hu Y, Jameson C, McCartan N, Moore CM, Punwani S, van der Muelen J, Emberton M, Ahmed HU. Accuracy of Transperineal Targeted Prostate Biopsies, Visual Estimation and Image Fusion in Men Needing Repeat Biopsy in the PICTURE Trial. J Urol. 2018 Dec;200(6):1227–1234. doi: https://doi.org/10.1016/j.juro.2018.07.001. Epub 2018 Jul 11.
Miah S, Eldred-Evans D, Simmons LAM, Shah TT, Kanthabalan A, Arya M, Winkler M, McCartan N, Freeman A, Punwani S, Moore CM, Emberton M, Ahmed HU. Patient Reported Outcome Measures for Transperineal Template Prostate Mapping Biopsies in the PICTURE Study. J Urol. 2018 Dec;200(6):1235–1240. doi: https://doi.org/10.1016/j.juro.2018.06.033. Epub 2018 Jun 27.
Methodology
• retrospective
• diagnostic or prognostic study
• performed at one institution
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Michela Antonelli and Edward W. Johnston are joint first authors.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Antonelli, M., Johnston, E.W., Dikaios, N. et al. Machine learning classifiers can predict Gleason pattern 4 prostate cancer with greater accuracy than experienced radiologists. Eur Radiol 29, 4754–4764 (2019). https://doi.org/10.1007/s00330-019-06244-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00330-019-06244-2