Abstract
We present a market model of a liberalized aviation market with independent decision makers. The model consists of a hierarchical, trilevel optimization problem where perfectly competitive budget-constrained airports decide (in the first level) on optimal runway capacity extensions and airport charges by anticipating long-term fleet investment and medium-term aircraft scheduling decisions taken by a set of imperfectly competitive airlines (in the second level). Both airports and airlines anticipate the short-term outcome of a perfectly competitive ticket market (in the third level). We compare our trilevel model to an integrated single-level (benchmark) model in which investments, scheduling, and market-clearing decisions are simultaneously taken by a welfare-maximizing social planner. Using a simple six airports example from the literature, we illustrate the inefficiency of long-run investments in both runway capacity and aircraft fleet which may be observed in aviation markets with imperfectly competitive airlines.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Over the past decades, many countries have liberalized their air transportation sector—see, for instance, Bowen (2002), Fu et al. (2010), or Burghouwt and de Wit (2015). This liberalization has led to the creation of markets in which different airlines compete with each other and invest in new aircraft on the basis of their expectations of the market outcomes and the corresponding profits to be made. Regulated airports, by deciding on capacity extensions and setting their charges, directly affect the outcomes of such markets while, at the same time, they rely on an anticipation of the market outcomes (as well as on the expected growth of passenger volumes) when taking long-term decisions. Such a complex investment structure involving independent decision makers whose decisions affect each other challenges traditional planning processes (see the literature review below), which do not account for the interplay of the different investment decisions made by the different players involved at different points in time and for their impact on market outcomes.
The purpose of this paper is to introduce a new model capable of providing valuable information on how to make optimal investments in a complex market environment with many market participants (airlines and airport operators), which can also be of interest to policy makers as a market-analysis tool. The model we propose features three hierarchical levels which correspond to three different decision-making stages. Focusing on a set of airports and airlines of interest in the context of a liberalized market environment, the model allows for identifying which (optimal) capacity expansion options the airports should consider (in the first level) as well as which (optimal) long-run investments in new aircraft and medium-term aircraft-scheduling decisions the airlines should make (in the second level) so as to maximize their own profits. As the investment decisions of the airlines are based on their expected future profits, our trilevel model also encompasses (in the third level) a model of the ticket market which determines the corresponding ticket sales. Assuming imperfectly competitive airlines, we quantify the investment inefficiencies of an imperfect aviation market by comparing, experimentally, the results obtained with our trilevel model to those of a single-level benchmark model with perfect competition among all players. The latter is equivalent to assuming a benevolent social planner which, as the unique decision maker, plans the whole industry in an integrated and welfare-maximizing way.
Quantitative models such as the one proposed in this paper can provide a valuable tool to evaluate and assess airport extension projects as well as their interdependent long-run effects on the airlines’ strategic decision making and policy making. Let us motivate the relevance of our model by a current example.
1.1 Example
Given the lack of sufficient runway capacity of the two existing airports of Istanbul, the Turkish authorities decided to build a third airport (Saldiraner 2013, 2014). On the one hand, the currently observed airport congestion directly limits the operations of any airline arriving at or departing from Istanbul. In particular, congestion highly affects the planning decisions of the major local airline, Turkish Airlines, which, in turn, depend on the (future) demand behavior of the passengers. On the other hand, the expected fleet expansion strategy of Turkish Airlines and the anticipated future passenger demand are the main reasons for the construction of the new airport, which will have a capacity of 150 million passengers per year with estimated construction costs of more than 32 billion Euro.
1.2 Previous works
Given the typically large-sized and computationally challenging problems in the airline industry, the operations research literature has identified different classes of real-word problems which deal with certain aspects of the airline operational and strategic planning processes—see Barnhart et al. (2003) and Jacobs et al. (2012) for an overview. Among other aspects, these problems comprise schedule design (see Teodorović and Stojković 1990; Lederer and Nambimadom 1998; Burke et al. 2010), fleet assignment (see Abara 1989; Hane et al. 1995; Rushmeier and Kontogiorgis 1997, or Rexing et al. 2000), and fleet planning (see, for instance, List et al. 2003; Clark 2007).
More recently, some authors have started to analyze integrated models which simultaneously account for several adjacent planning steps. For instance, (Lohatepanont and Barnhart 2004; Sherali et al. 2013) elaborate on optimal schedule design and fleet assignment within a single planning model. Based on these works, (Kölker and Lütjens 2015) combines network planning, scheduling, and aircraft rotation in an integrated planning approach, while (Faust et al. 2017) focuses on an integrated schedule design and aircraft maintenance routing. Cadarsoa and Marín (2011) and Cadarso and Marín (2013) propose a robust approach covering an integrated airline schedule development/design and fleet assignment.
While our work is closely related to the literature on airport capacity extensions, in the past the latter has, however, mainly built on very simplified models where, e.g., at most two airports are considered and/or airline fleet investments are completely ignored—see, for instance, (Zhang and Zhang 2006; Basso 2008; Xiao et al. 2013; Santos and Antunes 2015; Sun and Schonfeld 2015; Kidokoro et al. 2016). To the best of our knowledge, no hierarchical models of the aviation market similar to ours, which (as better explained in the remainder of the paper) involves multiple players taking sequential decisions affecting each other, are present in the literature.
1.3 Outline of our paper
Our paper is organized as follows. Section 2 describes the model framework we consider. The hierarchical, trilevel market model that we introduce is presented in Sect. 3. Our reformulation of such model and the corresponding approach that we propose for solving it are described in Sects. 4 and 5. Section 6 presents the single-level benchmark model which we use as reference. Section 7 discusses the results of a simplified case study with six airports, laying the basis for future research on larger instances. Finally, Sect. 8 summarizes the main findings of our work.
2 Model framework
In this section, we first describe the main structure of the market environment we consider and introduce the basic market participants. Secondly, we present more detailed information on these players, including their main characteristics, their corresponding key decision variables, and their profit and cost structures.
2.1 Overview of the relevant market players
Given a set of planning periods \({t}\in {T}\) of interest, we consider an inter-temporal problem where different players take decisions affecting each others’ costs and revenues.
By the set \({N}\), we model a set of airports which can decide to extend their current runway capacity. For each airport \(n \in N\), we denote the corresponding decision variable by \(x_{{n}}\in \mathbb {N}\cup \{0\}\). The latter variable measures the maximum number of takeoffs/landings that can take place at an airport within a single time period.
In an analogous way, we assume that different airlines (modeled by the set \({A}\)) can make fleet expansion decisions based on a set of possible aircraft types \({P}_{{a}}\). For each type \({p}\in {P}_{{a}}\), the variable \(y_{{a}{p}}\in \mathbb {N}\cup \{0\}\) corresponds to the number of airplanes of type p the airline decides to extend its fleet with.
We also assume that each airline can make a set of airplane-scheduling decisions. Let C be a set of connections, and let \({c}\in {C}_{{a}}\) be the subset of connections that can be served by airline a due to its exogenous business model. We refer to such connections as actual. For technical modeling reasons (which we will better explain in Sect. 3.2), we also introduce a superset of connections \(\bar{C} \supset C\), with \(\bar{C}_a \supset C_a\) for each airline \(a \in A\). \(\bar{C} {\setminus } C\) and \(\bar{C}_a {\setminus } C_a\) contain dummy connections which we will use to account for parking situations in which an aircraft stays at the same airport for one or more time steps. With each connection \(c \in \bar{C}\), we associate a departure time \(t_c^{\text {dep}}\), an arrival time \(t_c^{\text {arr}}\), a departure airport \(\ell _c^{\text {dep}}\), and an arrival airport \(\ell _c^{\text {arr}}\). Given the set \(\bar{C}\), we introduce the variable \(z_{{a}{p}{c}}\in \mathbb {N} \cup \{0\}\) to model the number of airplanes of type \(p \in P\) that airline \(a \in A\) decides to use to serve an (actual or dummy) connection \(c \in \bar{C}\).
We model the number of tickets sold by airline \({a} \in A\) on an (actual) connection \({c}\in C\) by the continuous variable \(w_{{a}{c}} \in \mathbb {R}_{\ge 0}\). Lastly, we model the connection-specific demand for each (actual) connection \(c \in C\) by the nonnegative continuous variable \(d_{{c}}\in \mathbb {R}_{\ge 0}\).
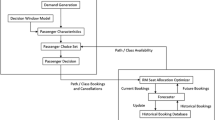
An overview of the relevant market players and their main decisions is given in Fig. 1, while Tables 6, 7, and 8 in Appendix A summarize the main sets, variables, and parameters used in this work. As Fig. 1 suggests, there is a clear temporal dimension to the decision process faced by the different players. We will further expand on such temporal dimension in the trilevel model that we propose in Sect. 3.
In order to simplify our notation, whenever a quantity such as \(x_n, y_{ap}, d_c, z_{apc},\) or \(w_{ac}\) is reported without one of its sub-/superscripts, this quantity is to be understood as a collection containing as many elements as the number of different values the missing sub-/superscript(s) can take. For instance, for each \(a \in A\), \(z_{a}\) corresponds to \((z_{apc})_{p \in P_a, c \in \bar{C}_a}\).
In the remainder of the section, we will look at the different players individually and give some more details and insights into the way we model their behavior in this paper.
2.2 Airports
2.2.1 Existing runway Capacity and airport operation costs
Given the set of airports \({N}\) of interest, we assume a given runway capacity \(\kappa _{{n}}^\text {airport}\) for each airport \({n}\in {N}\). This value corresponds to the maximum number of takeoffs and landings that can take place in that airport in a single time period before any investments take place. Such a modeling choice is in line with the assumption of runways operated in a so-called mixed mode (in which a runway is used for both landings and takeoffs), which is the case in various airports all around the world.
We assume that the airports face flight-dependent costs when operating an airport and handling arriving and departing flights, which we describe by the total variable-cost function \(\text {V}_{{n}}^\text {airport}\). In this paper, we assume a piecewise-linear total variable-cost function for each scheduled flight, an example of which is depicted in Fig. 2. The function consists of two different cost components and accounts for the total operational expenses of an airport. First, for each aircraft arriving at or departing from airport \(n \in N\), a cost of \(\alpha _{{n}}^\text {airport}\) is incurred (independently of the number of passengers on board of the respective aircraft). This cost component may, for instance, comprise taxi-in or taxi-out, parking, or gate-usage expenses. In addition, we assume that, for each passenger on board of the aircraft, airport \(n \in N\) faces additional costs of \(\beta _{{n}}^\text {airport}\), which include, e.g., baggage handling, passenger transportation, or security checking on a per-capita basis.
Let \(\delta _{n}^{\text {in}}({C}_{a})\) be the set of all (actual) ingoing connections at airport \({n}\in {N}\) of airline \({a}\in {A}\). Analogously, let \(\delta _{n}^{\text {out}}({C}_{a})\) be the corresponding set of outgoing (actual) connections. By letting \(\delta _{n}({C}_{a}):= \delta _{n}^{\text {in}}({C}_{a}) \cup \delta _{n}^{\text {out}}({C}_{a})\), the total variable-cost function for airport \({n}\in {N}\) reads:
We remark that, while we assume that both the cost for arriving and departing at an airport as well the passenger-based ones are identical, this assumption is not central to our approach and can be easily lifted without hindering the correctness of our results. Footnote 1
2.2.2 Runway capacity investment costs
As described above, we assume that each airport \({n}~\in ~{N}\) may choose to invest in additional runway capacity \(x_{{n}}\in \mathbb {N}\cup \{0\}\) with a unit investment cost of \({i_{{n}}^\text {airport}}\). Besides the actual runway construction costs, a runway capacity investment may also comprise gate or terminal extensions which might be necessary in order to handle additional flights. In line with the existing literature, throughout this paper we will assume that all investment decisions are made (and realized) at the beginning of the planning horizon—see, for instance, (Jenabi et al. 2013; Grimm et al. 2016a, b; Weibelzahl 2017). If, at a given airport, no investments are possible, we set \(x_{{n}}= 0\). We denote the total investment costs of an airport \({n}\in {N}\) by:
We note that the assumption of linearity of \(\text {I}_{{n}}^\text {airport}\) is not stringent. Indeed, since \(\text {I}_{{n}}^\text {airport}\) only shows up in the objective function of the first-level problem (see Sect. 3), the solution method we propose (see Sect. 4) in this paper is correct independently of the nature of such a function, provided that the latter can be handled by a standard spatial branch-and-bound solver (see Sect. 7.2 for more details on the solver we rely on).
2.2.3 Airport charges and budget
In this paper, we consider airport charges as a measure to recover investment and operational airport costs. Even though different types of charges may be applied in practice, we make the simplifying assumption that a passenger-based charge \(\phi _n\) be imposed on each passenger on board of an aircraft arriving at or departing from an airport \(n \in N\). Given these charges, the revenues of an airport \({n}\in {N}\) paid by an airline \({a}\in {A}\) as a function of the number of tickets (\(w_{ac}\)) it sells on each (actual) connection \(c \in C_a\) are defined as:
For similar charges that are used at different airports all around the world, see, e.g., Frankfurt Airport (2016), Heathrow Airport (2017), or Kennedy (2017). Let us remark that our model can be easily adapted in order to account for other types of airport charges (e.g., charges based on the tonnage of the airplane or on its noise category). Such charges may in general be treated either as endogenous variables or as exogenous parameters. Examples exist in the literature of both variants—see, for instance, (Jenabi et al. 2013) or (Grimm et al. 2016a). Since, in our paper, purely exogenous charges would limit and bias the investment behavior of the different airports, we model the decision on optimal airport charges as endogenous.
We express the profits of an airport as equal to its income from airport charges minus runway capacity investments and operational costs. For each airport \({n}\in {N}\), such profit can be expressed as:
2.3 Airlines
Let \({P}_{a}\) be the set of different aircraft types, e.g., A330 or Boeing 747, which an airline \({a}\in {A}\) is willing to operate or to invest in according to its exogenous business model given ex ante. The importance of the business models in the airline industry has recently been highlighted by different authors. For instance, Nataraja and Al-Aali (2011) discusses the strategy of Emirates, which mainly builds on the two aircraft types A380 and Boeing 777.
Let \(e^\text {airline}_{{a} {p}}\) be the number of aircraft of a specific type \({p}\in {P}_{a}\) the existing fleet of airline \({a}\in {A}\) is composed of at the beginning of the planning horizon. Let also \(\kappa ^\text {aircraft}_{{p}}\) be the seat capacity of each aircraft of type \({p}\in {P}_{a}\).
2.3.1 Fleet operation costs
Similarly to the airports, we assume that flight-dependent costs are described by a piecewise-linear total variable-cost function \(\text {V}_{{a}}^\text {airline}\) which depends on two different cost parameters. Independently of the number of passengers on board of the aircraft, we assume that a constant cost equal to \(\alpha _{{a} {p} {c}}^{\text {airline}}\) is incurred per completed flight due to, for instance, fuel costs of the empty aircraft \({p}\in {P}_{a}\) on an (actual) connection \({c}\in {C}_{a}\). As the total fuel costs would increase with the number of passengers, we further assume a variable per capita passenger-related cost coefficient of \(\beta _{{a} {c}}^{\text {airline}}\), which may vary between different (actual) connections \({c}\in {C}_{a}\).Footnote 2 Note that this cost may also capture further passenger-related costs like, for instance, food or beverage costs. Using this notation, the total variable-cost function for an airline \({a}\in {A}\) is:
2.3.2 Aircraft investment and fleet expansion costs
As mentioned before, we assume that the airlines can invest in new aircraft. Similarly to runway capacity extensions, we assume that aircraft investments take place at the beginning of the planning horizon. For each type of aircraft \(p \in P\), we assume a unit cost of \(i^\text {aircraft}_{{p}}\). Thanks to the decision variable \(y_{{a}{p}}\in \mathbb {N}\cup \{0\}\), which quantifies the number of additional aircraft of type \({p}\in {P}_{{a}}\) that airline \({a}\in {A}\) purchases, the total investment cost for airline \({a}\in {A}\) corresponds to:
2.4 Passengers (ticket demand, consumer surplus, and resulting revenues of airlines)
A set of (price-sensitive) passengers can buy tickets for the different (actual) flight connections \({c}\in {C}_{a}\) of an airline \({a}\in {A}\). Each (actual) connection \({c}\in C\) departs and arrives within the assumed planning horizon T. For the sake of simplicity, we only consider a single, aggregated fare class as done, for instance, in Lohatepanont and Barnhart (2004). As discussed above, we use the variable \(d_{{c}}\in \mathbb {R}_{\ge 0}\) to describe the elastic ticket demand on connection \({c}\), while we denote by \(w_{{a}{c}} \in \mathbb {R}_{\ge 0}\) the number of tickets sold by airline \({a}\in {A}\) on its flight connection \({c}\in {C}_{a}\).
We further assume non-arbitraging customers who purchase flight tickets from their origin to their destination of choice without intermediate stops (we illustrate how to partially lift this assumption in Sect. 3.4). The strictly decreasing function \(\text {P}_{{c}}^\text {con}(s)\) gives the maximum price that at least s customers are willing to pay for a ticket for connection \(c \in C\). Note that \(\text {P}_{{c}}^\text {con}\) is given as an input and it cannot be influenced by any decisions made by an airline. For the way the ticket prices are determined (they correspond, for each connection \(c \in C\), to the Lagrangian multiplier of the market-clearing constraint for that connection of the single-level welfare-maximization problem), we refer the reader to Proposition 1.
Based on the above definitions, we define the gross consumer surplus as the following integral:
By aggregating the maximum willingness to pay for \(d_c\) tickets, the gross consumer surplus corresponds to the total monetary gross benefit obtained from purchasing and eventually using \(d_c\) tickets. As we will see in Sects. 3.1 and 3.3, by subtracting the costs necessary to supply the \(d_c\) tickets from the gross consumer surplus, we arrive at the concept of welfare.
Finally, since the airline revenues are generated by ticket sales, the revenue of an airline \({a}\in {A}\) corresponds to the above-defined ticket price \(\text {P}_{{c}}^\text {con}\) multiplied by the number of tickets sold:
3 Trilevel market model
The key feature as well as the key challenge of liberalized aviation markets is that an optimal decision of a player will highly depend on the optimal decisions of all the other players. In this section, we present a market model where the optimal behavior of the players we consider is influenced by their expectations on the optimal reaction of the other players to their choices.
In more detail, the model we propose is a hierarchical game-theoretical model where three groups of players, the airports, the airlines, and the passengers, make decisions over three different levels (or stages). The order of such levels marks the different points in time in which the players’ decision-making problems arise. The actual timing of the decision-making situation we consider is depicted in Fig. 3. In it, long-term airport capacity investments are followed by long-term airline fleet investments and medium-term aircraft scheduling, which are then followed by short-term ticket trade. Planning and operation situations with a similar timing are commonly highlighted in the literature as, e.g., in Smith and Jacobs (1997) or Jacobs et al. (2012).
Key to our hierarchical model is the fact that, as mentioned before, the decisions taken by each player (either as a group or individually) affect the utility (in terms of revenues and costs) of the other players and, in turn, are affected by such decisions. For instance, the airlines’ fleet expansion decisions as well as their scheduling decisions are affected by the airports’ investments in runway capacities, while, in turn, the investments the airlines would make as a consequence of the airports’ capacity expansion choices drive the airports’ investment decisions. Assuming rational players, the optimal decisions made by a player should therefore take into account how the other players would react to it, factoring their reaction into the player’s own decision-making process so to choose a strategy which is best possible for her/him/it. Similar assumptions are made in the operations research and mathematical programming literature on bilevel (and multilevel) optimization, see Colson et al. (2007), Bolusani et al. (2020) for a survey, and are rooted in the game-theoretical literature on Stackelberg and hierarchical games, whose origin is in Von Stackelberg (1934).
As we will better explain in the following, in our hierarchical, trilevel model the airports play as a single, aggregated player (leader) in the first level while the airlines play imperfectly competitively in the second level, thereby reaching a generalized Nash equilibrium, or GNE [i.e., a Nash equilibrium with constraints, see Facchinei and Kanzow (2010) for a survey as well as the seminal paper (Nash 1951) on Nash equilibria]. The outcome (in terms of number of sold tickets) of the competitive ticket market is modeled in level three as a further optimization problem whose solution is affected by the airlines’ investment and scheduling decisions on level two (which, in turn, depend on the airports’ decisions made in level one). The latter is in line with previous works, including Barroso et al. (2006) and Pozo et al. (2013). All the modeling choices we make are better motivated in the following.
From a mathematical optimization perspective, we will cast the problem of computing an equilibrium in the game underlying our hierarchical, trilevel model as a trilevel mathematical programming problem with a single (different) decision maker in levels one and three and many competing decision makers in level two.
For the sake of a better overview, the overall trilevel market model that we consider is depicted in Fig. 4. In the remainder of the section, we describe the different problems that occur in each level of the trilevel model, their dependency on the solution that was determined in the previous levels as well as on the anticipated solution to the problems in the next levels and the way in which, in the second level, the players (airlines) imperfectly compete with each other. A mathematically equivalent single-level reformulation, which will be the key for solving the problem from an algorithmic perspective, is presented in Sect. 4.
3.1 First-level problem: airport capacity investment
In the first level, the airports choose the passenger-based charges \(\phi \) and provide the necessary infrastructure (which is used by both airlines and passengers) by taking runway capacity-extension decisions.
In a lot of countries all around the world, many airports are highly regulated by governmental authorities with complex planning and approval procedures. In Germany, for instance, the German Aviation Law (§19b) requires the airports to obtain an official permission for their charges where, among other (public interest) criteria, objectivity, transparency, and non-discrimination must be guaranteed. In addition, especially in structurally weak regions, airports are often regarded as state-infrastructure projects oriented toward public (i.e., welfare) goals, offering important infrastructure services to the public (it is often the case that airports are owned and operated by public bodies). On these and related topics, also see Basso (2008).
It is therefore natural to make (as we do in this paper) the assumption that the airports and their charges be regulated in such a way that it is in an airport’s best interest to maximize welfare—the welfare function being defined as the aggregated difference between the gross consumer surplus defined in (7) and the total investment and variable costs of the airports and airlines defined in (1)–(2) and (5)–(6). As such, welfare gives the net realized monetary gains obtained from trading and eventually using the flight tickets, having subtracted the relevant costs. It is therefore a natural objective of a regulated airport pursuing public interests.
We remark that, under the assumption of welfare-maximizing airports, the airport charges are chosen as a way to “break even,” rather than to increase an airport’s own profits by squeezing margins from the airlines.
As the welfare function is maximized by each airport \(n \in N\), we can w.l.o.g. assume that the different airports behave as a single, aggregated player in control of all the decisions that pertain the whole set of airports N. From a mathematical perspective, this has the effect of reducing the number of players in the first level of our model to just one.
Even though we assume welfare-maximizing airports, we still make the realistic assumption that the airports are budget-constrained, i.e., that their profits must always be nonnegative. Thus, we introduce the following budget constraints:
Finally, we make the following assumptions on the variables controlled by the airports:
We remark that, while the aggregated first-level decision maker, which corresponds to the airports, can only control the investment and charge variables x and \(\phi \), its objective function and its budget constraints also depend on the fleet expansion variables y, on the aircraft scheduling variables z, and on the ticket variables w. The values of these variables are determined by other players in other levels of the hierarchy. Due to the standard assumption of rationality, the aggregated first-level decision maker (the airports) makes its decisions by anticipating the optimal value that y, z, and w variables would take when the corresponding decision makers (airlines and passengers) react to the choice made by the airports for the values of the x and \(\phi \) variables. This implies that these different levels cannot be solved independently. We will formalize this aspect from a mathematical perspective in Sect. 3.5.
3.2 Second-level problem: fleet expansion and aircraft scheduling
In the second level, imperfectly competitive airlines observe the capacity-extension decisions made by the airports and (reacting to them) decide on their optimal fleet expansion by investing in new aircraft, thereby choosing the value of the y variables. For a discussion of imperfect competition in the airline industry, see, e.g., Adler (2001). The airlines also schedule their aircraft by deciding, for each time period \({t}\in {T}\), what number of aircraft of each type \(p \in {P}_{a}\) (be it new ones or old ones) should serve which (actual or dummy) connection \({c}\in \bar{{C}}_{a}\). We assume, here, that each individual airline \({a}\in {A}\) maximizes its profit \(\rho _{{a}}^{\text {airline}}\). Such value can be expressed as the difference between revenues from ticket trade in the third level and the corresponding aircraft investment cost, operational aircraft cost, and airport charges. Thus, the profit function that each imperfectly competitive airline \(a \in A\) maximizes in the second-level reads:
Once the investment in new aircraft has taken place, the airlines schedule their whole fleet (which comprises both existing and new aircraft) as described above. In particular, a decision is made by each airline as to whether or not a certain connection should be served by one of its aircraft. In this context, a connection \(c \in C\) is defined, as we mentioned before, as a tuple \((\ell _c^{\text {dep}}, \ell _c^{\text {arr}},t_c^{\text {dep}},t_c^{\text {arr}})\) describing the departure airport \(\ell _c^{\text {dep}}\) the flight starts from at a certain time \(t_c^{\text {dep}}\) and the corresponding arrival destination \(\ell _c^{\text {arr}}\) that it will reach at another point in time \(t_c^{\text {arr}}\). Note that our definition of connection is independent of the assigned aircraft type and, rather, it only depends on time–space characteristics, i.e., on the time and airport of departure and arrival. To give an example of such a connection, consider an aircraft departing from \(\ell _c^{\text {dep}}\) = Munich at \(t_c^{\text {dep}}\) = 1 p.m. and reaching \(\ell _c^{\text {arr}}\) = Berlin at \(t_c^{\text {arr}}\) = 2 p.m. As defined before, \({C}_{a}\) is the set of all possible (actual) connections that airline \({a}\) can decide to serve. Observe that, similarly to fleet investment decisions, \({C}_{a}\) may again be determined by an exogenous business model of airline \({a}\in {A}\) given ex ante. As we already introduced in Sect. 2.1, we also consider a superset \(\bar{C} \supset C\) containing, besides all “actual” connections in C, a set of “dummy” connections which we use to model the position in time and space of the aircraft when they are not flying.
In order to describe the aircraft scheduling constraints, we introduce a time–space graph for every pair \(({a}, {p}) \in ({A}, {P}_{a})\) to model the routes of all aircraft of type \({p}\in {P}_{a}\) of airline \({a}\in {A}\). See Fig. 5 for an illustration.
We first define a pair of dummy nodes consisting of a start node \(s_{{a}{p}}\) and a final node \(f_{{a}{p}}\). Moreover, for every airport and every time period, we introduce \(\tilde{{N}}_{{a}{p}}\) as the set of nodes corresponding to the locations the aircraft can be at.
We define start edges \(S_{{a}{p}} = \delta ^{\text {out}}(s_{ap})\) and final edges \(F_{{a}{p}} = \delta ^{\text {in}}(f_{ap})\) to connect the final and start nodes with the respective time and location-specific nodes at time \(t=1\) and \(t = |T|\). Horizontal edges define holdover edges \(e \in H_{{a}{p}}\) and model the fact that an aircraft can be in parking state for a certain amount of time. The edges in \(S_{ap} \cup F_{ap} \cup H_{ap}\) correspond to the dummy connections \(\bar{C}_{a} {\setminus } C_a\) we introduced before. Furthermore, we use the actual connections \({C}_{{a}}\) to define the flight edges \({C}_{{a}{p}}\) depending on the aircraft type \({p}\in {P}_{a}\), connecting the departure node \(\ell _{c}^{\text {dep}}\) at time \(t_c^{\text {dep}}\) to the arrival node \(\ell _{c}^{\text {arr}}\) at time \(t_{c}^{\text {arr}}\). Such edges only exist if a connection can be served by an airline given its exogenous business model specified ex ante.
Let us again refer to our example with two locations, Berlin and Munich, and three time periods \({t}_1\), \({t}_2\), and \({t}_3\), as depicted in Fig. 5. In the example, the aircraft starts in Berlin and arrives after one time period in Munich. The way back takes more time, which, for instance may be due to the flight trajectory being longer (this is the case of, e.g., Larnaca–London flights which, usually, take about half an hour more than London–Larnaca ones).
The following constraints ensure a feasible aircraft route:
In the above constraints, we have extended our delta-notation by a time index \({t}\in {T}\) with \(\delta _{{n}{t}}({C}_{a})\) so to describe the set of all ingoing and outgoing (actual) connections at airport \({n}\in {N}\) of airline \({a}\in {A}\) in time period \({t}\in {T}\). For every \((a,p) \in A \times P_a\) pair and for every edge e, the \(z_e\) variables correspond to the scheduling variables \(z_{{a}{p}{c}}\), where c is the (actual or dummy) connection corresponding to edge e. Eq. (14a) guarantees that no more than the aircraft that constitute the fleet of airline a be used, where \(e^\text {airline}_{{a} {p}}\) is the number of aircraft of type p originally available. Constraints (14b) are flow-conservation constraints enforcing that an aircraft can only serve a connection if it is available at the respective airport. Furthermore, (14c) limits the number of scheduled aircraft on each connection for each airline to one. This way, we prevent nonrealistic schedules where two or more airplanes take off at the same time from the same origin airport and land at the same time at the same destination airport.
Given the capacity expansion choice made by the airports in level one, whose variable x (due to being set in the previous level) is perceived as a constant by the airlines, we have to guarantee that the sum of all ingoing and outgoing flights of an airport \({n}\in {N}\) do not exceed its runway capacity (also accounting for possible runway capacity extensions) in any time period \({t}\in {T}\):
Observe that, while we do not model airport congestion effects via delay cost functions, our model could easily be extended to incorporate such functions explicitly. We also remark that, while all the scheduling constraints are specific to each airline, the airport capacity constraints are shared by them.
Finally, we assume the following restrictions on the decision variables controlled in this level:
We remark that, while we assume that all types of aircraft can be used on every connection, this assumption is not stringent and it can be easily lifted by introducing, for all airlines \(a \in A\), a 0 upper bound on the variables \(z_{apc}\) for each pair (p, c) corresponding to an aircraft type p and a connection c which are incompatible.
Let us highlight that, due to the assumption of imperfect competition in level two, the airlines explicitly compete for the scarce runway capacity as well as for a share of the ticket market (whose outcome is determined in level three) in order to maximize their profits. Notice that the objective function and the constraints in this level depend on variables (x, d, and w) whose value is set in either level one or three. As the value of the x variables is set in the first level, such quantities are perceived as constants by the airlines. Differently, the values of the d and w variables is determined in level three as a consequence of the decisions made in level one and two. Therefore, we assume that the airlines make their decisions by anticipating the value that such variables would take as a consequence of their choice.
Crucially, due to the assumption of imperfect competition we cannot condense all the airlines in a single player (as we did for the airports). In line with previous works including Barroso et al. (2006) and Pozo et al. (2013), we rely on the concept of generalized Nash equilibrium (GNE) and formulate the second-level problem as an equilibrium problem with |A| players, one per airline, noncooperatively seeking to maximize their individual profits subject to individual flow-conservation/airplane-trajectory constraints and joint capacity constraints imposed on their scheduling variables z. According to the notion of GNE, the airlines decide on a collection of strategies \(y = (y_1, \dots , y_{|A|})\) and \(z = (z_1,\dots ,z_{|A|})\) such that the decision \(y_a,z_a\) of each airline \(a \in A\) is best possible assuming that all the other airlines play according to their strategy in \(y_{-a}\) and \(z_{-a}\), where the latter two identify the decisions of all airlines except for airline a.
We remark that, in this level, the imperfectly competitive airlines may decide to limit their investments in order to increase their profits through higher prices on the ticket market on the third level. In particular, the airlines’ imperfectly competitive behavior does not necessarily imply an efficient (in terms of social welfare) use of airport infrastructures. We illustrate such a situation in the computational experiments we carry out in Sect. 7.
3.3 Third-level problem: ticket trade
After the airlines have invested and scheduled their flights in level two, the ticket prices that will have to be paid by the price-sensitive customers and the corresponding number of sold tickets on the different routes (which, in turn, depend on the scheduling choices of the airlines) are determined.
Especially with the emergence of various travel-fare metasearch engines and online travel agencies like Expedia, Opodo, or Momondo, the ability for customers to compare fares of different airlines has increased significantly (Egger et al. 2014). Thanks to websites that the customers can use for price monitoring, price comparison, and booking of (typically) the cheapest airline ticket on a desired route (and booking class), the pressure on the airlines is constantly increasing. As a consequence, the airlines are constantly monitoring the price level of their competitors by appropriate tools and adjust their own price levels on the different connections appropriately. Therefore, especially in times where the customers can rely on many multichannel ticket purchase possibilities, it is reasonable to model the outcome (in terms of number of tickets sold) of the ticket market by a perfectly competitive ticket-market model.Footnote 3
We formulate the ticket trade problem as an equilibrium problem involving two groups of players: the customers, aggregated as a player per connection \(c \in C\), and the different airlines. W.l.o.g., we aggregate all customers of a given connection \(c \in C\) into a single “aggregate” customer. Under the assumption of perfect competition, we assume exogenously given ticket prices \(\pi _c^*\) for each connection \(c \in C\).
The aggregate customer of connection c maximizes its benefit, defined as the difference between gross consumer surplus (as a function of realized demand \(d_c\)) and the ticket price that corresponds to it:
The aggregate customer only faces a nonnegativity restriction on the demand:
Each airline \(a \in A\) maximizes its profits, defined as:
To guarantee that, for each airline \({a}\in {A}\), the number of passengers on a connection \({c}\in {C}_{a}\) does not exceed the capacity of the aircraft that has been scheduled on it, we impose the following constraint to limit the number of sold tickets per connection:
Also, we assume the following restrictions on the variables of each airline:
In addition, we must ensure market clearing for each connection, i.e., we must ensure that, for each connection, the number of tickets bought by the passengers be equal to the number of tickets sold for that connection. This is achieved by imposing the following constraint:
Compactly, the ticket-market model we consider boils down to the following equilibrium problem, where the exogenous prices \(\pi _c^*\), \(c \in C\), are variables:
We remark that Problem (23a) coincides with the maximization of (17) over \(d_c \ge 0\) with a given price \(\pi ^*_c\). Due to \(P_c^\text {con}(s)\) being (by assumption) strictly decreasing, the (unique) solution to Problem (23a) coincides with setting \(d_c = \mathrm{arg\,sup}_{s \ge 0} \{P_c^\text {con}(s) \ge \pi ^*_c\}\), which indicated that every passenger with willingness to pay at least \(\pi ^*_c\) will buy a ticket.
The objective functions of the players involved in this equilibrium problem depend on the z and \(\phi \) variables, whose value is not determined in it but, rather, it is set in, respectively, the second and the first level. Therefore, these variables are all perceived as constants here. Crucially, as the third-level problem is the last problem in our hierarchical model, it does not involve any variables whose value is set in further levels and, therefore, it does not involve any anticipation.
3.4 Reformulation of the third-level problem as a (single-level) welfare-maximization problem
We now show how to recast the third-level equilibrium problem as a single-level problem in which welfare is maximized. Similar reformulations can be found in, e.g., Grimm et al. (2016a), Hobbs and Helman (2004).
Let us introduce the following third-level welfare function, defined as the difference between the gross consumer benefit and the total costs incurred by the airlines (we refer to it as \(\omega ^\text {tickets}\) to distinguish it from the welfare function \(\omega \) that is maximized by the airports in level one):
The single-level welfare-maximization problem we introduce calls for maximizing the objective function in (24) subject to constraints (20) and (22), as well as to the restrictions on the variables in (18) and (21). Similarly to the original equilibrium problem, this problem is parametric in the \(x,\phi ,y,z\) variables which, in it, behave as givens. Compactly, it reads as follows:
With the following proposition, we show that the two problems are equivalent:
Proposition 1
The solutions to the single-level welfare maximization problem (25) coincide with those to the perfect-competition equilibrium problem (23).
Proof
All of the constraints of the welfare-maximization problem in (25) are linear, which implies that constraint qualification holds everywhere on the feasible region. Since the problem calls for the maximization of a concave function, all of its KKT points are global optima, i.e., its KKT conditions are both necessary and sufficient (see, for instance, Boyd and Vandenberghe (2004)). Therefore, all of its optimal solutions satisfy the following KKT system:
Let us consider the equilibrium problem (23). For each player \(c \in C\), the KKT system of its decision-making problem reads:
For each player \(a \in A\), the KKT system of its decision-making problem reads:
Thus, every solution to (23) consists of a triple \((d,w,\pi ^*)\) satisfying (27), (28), and the market-clearing constraint (22). Letting \(\pi ^* = \mu \), \((d,w,\pi ^*)\), these equations coincide with (26). \(\square \)
In the remainder on the paper, we will solely consider the welfare maximization problem as, while the two are equivalent, the former results in a less complex problem from a computational point of view.
We remind that the welfare-maximization problem is always feasible for every choice of the first and second-level variables \((x,\phi ,y,z)\) and it always admits a finite optimal solution.
Notice that this problem can be decomposed into |C| independent problems, one per connection. From an economical perspective, this is due to the fact that we are assuming the demands for two different connections to be independent. Also observe that, in contrast to the welfare objective function \(\omega \) that is used in level one, the welfare function \(\omega ^{\text {tickets}}\) that we adopt here to model the ticket market does not account for (sunk) investment costs, but, rather, only considers variable flight-dependent costs and the relevant airport charges.
We note that, while, in our model, we assume that passengers consider each connection separately, the extension to the case with multileg trips and changeovers can be made without too much effort.Footnote 4
3.5 Complete trilevel model
We are now ready to introduce the trilevel optimization problem that we propose in this paper from a mathematical-optimization perspective. First, we present the following result:
Theorem 1
Assume that, for each airline \({a}\in {A}\), the variable-cost coefficients \(\beta _{{a} {c}}^{\text {airline}}\) are pairwise distinct for each connection \({c}\in {C}\). Then, the third-level welfare-maximization problem (25) admits a unique optimal solution.
Proof
The objective function \(\omega ^{\text {tickets}}(\phi ,z, d, w)\) of the problem features three terms: \(\sum _{{c}\in {C}} \int _{0}^{d_{{c}}}\text {P}_{{c}}^\text {con} (s) \text {d}s\), \(\sum _{{a}\in {A}} \text {V}_{{a}}^\text {airline}(z, w)\), where \(\text {V}_{{a}}^\text {airline}(z, w) = \sum _{c \in {C}_{a}} \left( \sum _{{p}\in {P}_{a}}\right. \)\(\left. \alpha _{{a} {p} {c}}^{\text {airline}} z_{{a}{p}{c}}+ \beta _{{a} {c}}^{\text {airline}} w_{{a}{c}} \right) \), and \(\sum _{{a}\in {A}} \sum _{n \in N} {\text {R}^{\text {airport}}_{{n} {a}}}(\phi , w)\), where \({\text {R}^{\text {airport}}_{{n} {a}}}(\phi , w) = \sum _{{c}\in {\delta _{n}({C}_{a})}} \phi _{{n}}w_{{a}{c}} \). The first term, due to \(\text {P}_{{c}}^\text {con} (s)\) being a strictly decreasing function, is strictly concave in d and constant in w, while the second and third term are constant in d and linear in w. The problem decomposes into |C| independent subproblems, one per connection. As each connection \(c \in C\) has a unique pair of departure and landing airports \(\ell _c^\text {dep}, \ell _c^\text {land}\), the value of \(\phi _n\) is constant in each subproblem and, thus, the third term can be ignored. Let \(d_c^*\) be the optimal demand level of the subproblem for connection \(c \in C\). Due to the assumption, we can assume, w.l.o.g., \(\beta _{ac}^\text {airline} < \beta _{a'c}^\text {airline}\) for all \(a,a' \in A: a < a'\). Any solution w with \(w_{ac} < \sum _{{p}\in {P}_{{a}}} \kappa ^\text {aircraft}_{{p}} z_{{a}{p}{c}}\) and \(w_{a'c} > 0\) for some \(a,a' \in A: a < a'\) is not optimal as shifting some of the value of \(w_{a'c}\) to \(w_{ac}\) would improve the solution value. We deduce that \(w_{ac}^*\) is optimal if and only if \(\exists \bar{a} \in A\) such that:
Clearly, such a solution is unique. Due to the objective function of each subproblem being strictly concave in \(d_c\), this implies that the overall problem admits a unique global optimum. \(\square \)
In the following, whenever it is necessary to refer to the (unique, due to Theorem 1) values that the variables w and d take for a specific choice, let us call it \(\hat{\phi }, \hat{z}\), of the \(\phi ,z\) variables which is different from the value these variables take in an equilibrium solution to the trilevel model, we will use the notation \(w(\hat{\phi }, \hat{z})\) and \(d(\hat{\phi }, \hat{z})\).
According to the standard notion of generalized Nash equilibrium, we say that a strategy profile (a collection of strategies, one per airline) (y, z) corresponds to a GNE if and only if, for every airline \(a \in A\), a unilateral deviation from a GNE which is feasible when the other airlines play their equilibrium strategy does not lead to a strictly larger profit for airline a. Denoting by \(y_{-a}\) and \(z_{-a}\) the set of subvectors of y and z containing every component except for that of airline a, the latter implies, equivalently, that, given a GNE (y, z), the (feasible) best-response strategy that each airline \(a \in A\) can adopt to react to the strategies \((y_{-a}, z_{-a})\) the other airlines play at that GNE must not yield airline a a profit strictly larger than the one the airline would make by playing the strategy \((y_a,z_a)\) that the equilibrium prescribes. Formally, we must guarantee that the following best-response constraints be satisfied for each \(a \in A\):
The right-hand side of the inequality corresponds to the problem of computing a best-response strategy \((\hat{y}_a, \hat{z}_a)\) for airline \(a \in A\), possibly different from \((y_a,z_a)\), to react to the strategy \((y_{-a}, z_{-a})\) of the other airlines. According to the standard game-theoretical terminology, we refer to it as a best-response problem. The optimal solution to this best-response problem corresponds to the largest revenue airline a could make given the airport charges \(\phi \) and under the assumption that the investment strategy and scheduling decisions of the other airlines correspond to \((y_{-a},z_{-a})\). Note that the objective function of the best-response problem depends on \(w(\phi , \hat{z}_a, z_{-a}), d(\phi , \hat{z}_a, z_{-a})\), which, according to our notation, correspond to the (unique, due to Theorem 1) values that the w, z variables would take if the all airlines but a were to play the strategy specified by y, z while airline a were to deviate from it by playing \(\hat{y}_{a}, \hat{z}_{a}\).
Formally, we require that the best response \((\hat{y}_a, \hat{z}_a)\), together with the other airlines’ strategies \((y_{-a}, z_{-a})\), satisfy constraints (14), (15), (16a), and (16b)—or, more precisely, that \(\hat{y}_a\) satisfy (16a), \(\hat{z}_a\) satisfy (16b), that \((\hat{y}_a, \hat{z}_a)\) satisfy (14), and that \(\hat{z}_a\), jointly with \(z_{-a}\) and for the given x, satisfy (15). Note that the latter are the only constraints that link the strategies of the different airlines together, i.e., they are the only constraints responsible for the problem to be a GNE problem, rather than just a Nash equilibrium problem.
By imposing best-response constraints with (29), we guarantee that the investment strategy \(y_a\) and the scheduling decision \(z_a\) of each airline \(a \in A\) be at least as profitable for that airline as the most profitable ones, which we denote by \((\hat{y}_a,\hat{z}_a)\), that the airline could make under the assumption that the other airlines’ decisions were those in (y, z).
Interestingly, we note that the right-hand side of each of constraints (29) corresponds to a bilevel programming problem (i.e., a multilevel problem with two levels). This is because, due to containing \(w(\phi , \hat{z}_a, z_{-a})\) and \(d(\phi , \hat{z}_a, z_{-a})\), each best-response problem embeds an instance of the third-level problem.
We now report, for better readability, a schematic illustration of the full trilevel model we propose:
Let us comment on the model from the bottom up:
-
Third level In its lower level, the constraints \((d,w) \in \hbox {arg}\,\hbox {max}\{\cdot \}\) impose that, given the value of the \(x,\phi \) variables chosen in level one and those of the variables y, z chosen in level two, the d, w variables be equal to the (unique, due to Theorem 1) optimal solution to the market-clearing problem.
-
Second level The constraints \(\rho ^{\text {airline}}_a(\phi , y, z, w, d) \ge \max \{\cdot \}\), together with the three linear inequalities that follow them, guarantee that, given the value of the \(x,\phi \) variables set in level one, y and z be optimal for the GNE problem in level two. In particular, this requires that, for each airline \(a \in A\), its choice of values for the \(y_a,z_a\) variables be best possible given, besides the value of the x variable chosen in level one, the choice for \(y_{-a},z_{-a}\) made by the other airlines. The \(\max \{\cdot \}\) part in the right-hand side is the best-response problem of computing the maximum revenue (with decision variables \(\hat{y}_a, \hat{z}_a\)) that is obtainable by airline a given the choices \(y_{-a},z_{-a}\) made by the other airlines—the constraint imposes that the revenue \(\rho ^{\text {airline}}_a(\phi , y, z, w, d)\) be at least as large as this value. As the choice of an airline \(a \in A\) to switch strategy from \(y_a,z_a\) to \(\hat{y}_a, \hat{z}_a\) could trigger a change in the market outcome, the best-response problem contains, as a subproblem, another instance of the third level problem with variables \(\hat{d}^a, \hat{w}^a\). Such variables model the anticipation of the market outcomes for airline a under the assumption that its strategy correspond to variables \(\hat{y}_a, \hat{z}_a\) rather than \(y_a,z_a\), while all the other variables, including the \(y_{-a}\) and \(z_{-a}\) variables of airline a, keep their original value.
-
First level Our trilevel model is concluded by its airport capacity-extension constraints and its objective function, which correspond to those we introduced in Sect. 3.1 when describing the first-level problem.
We show how to further reformulate the problem into a single-level problem in the next section.
We remark that, in this model, we have implicitly made the assumption of optimism, i.e., we have assumed that, if multiple GNE arose, a welfare-maximizing GNE would be chosen. We believe that such an assumption is appropriate as, in general, the airlines will abide by a corporate social responsibility that will not lead them to choose a solution with a welfare-diminishing effect. For instance, a responsible business practice is part of the corporate strategy of the Lufthansa Group, which aims at “meeting (its) responsibilities toward the environment and society”—see Lufthansa Group (2000).
4 Single-level problem reformulation
Multilevel problems are known to be computationally very challenging. See, for instance, (Dempe 2002; Colson et al. 2007; Dempe et al. 2014; Coniglio et al. 2017; Basilico et al. 2017, 2020; Coniglio et al. 2020) in which hardness and inapproximability results are shown for simpler problems featuring only two levels and a single player per level. For a recent survey, we refer the reader to Bolusani et al. (2020). To find a solution to the model we proposed, in this paper we develop a reformulation strategy which builds on the steps depicted in Fig. 6.
In the first step, we replace the third-level market problem by its Karush–Kuhn–Tucker (KKT) conditions. We then add such conditions (and the corresponding third-level variables) on top of the first-level problem. Then, we reformulate the best-response problem of each airline via a set of extra constraints and variables which we collectively refer to as best-response systems and which do not contain the \(\max \) operator which the original best-response constraints featured. Lastly, we add a copy of the KKT conditions to the best-response systems of each airline to model the value that the third-level variables would take as a consequence of the deviation that the best-response system looks for, thus obtaining what we refer to as explicit best-response systems. Overall, this sequence of transformations yields a single-level reformulation of the original trilevel problem.
4.1 Step 1: KKT reformulation of the third-level problem
In the trilevel hierarchy, the third-level market clearing problem is solved last, after the values of all the decision variables controlled by the airports (\(x,\phi \)) and the airlines (y, z) have been chosen. The third-level problem is, therefore, parametric in the \(x,\phi ,y,z\) variables which, in it, behave as givens. From this perspective, the problem is a maximization problem with a strictly concave quadratic objective and linear constraints and, hence, constraint qualification holds everywhere on its feasible region. Therefore, all of its KKT points are global optima, i.e., its KKT conditions are both necessary and sufficient (see for instance Dempe (2002) or Boyd and Vandenberghe (2004)). Therefore, we can replace this problem by its KKT conditions, as reported in (26).
We remind that the third-level problem is always feasible for every choice of the first and second-level variables \((x,\phi ,y,z)\) and, due to its strictly convex objective function, it always admits a finite optimal solution.
4.2 Step 2: reformulation of the generalized Nash equilibrium problem via best-response systems
We now show how to reformulate the best-response constraints (29) with a set of constraints and variables that do not require the introduction of the \(\max \) operator featured in (29). As mentioned above, we refer to this set as to a best-response system.
For each \(a \in A\), let \(D_a\) be the set of indices of all pairs of strategies \((\hat{y}_a^j, \hat{z}_a^j)\) which are feasible when considering airline a individually, that is, the indices of all pairs \((\hat{y}_a^j, \hat{z}_a^j)\) which satisfy (14), (16a), and (16b). By construction, \(D_a\) indexes a superset of the possible deviations that airline a can take from an equilibrium solution.
Without loss of generality, we can rewrite constraints (29) as the following constraint:
to be imposed for all pairs \((\hat{y}_a^j, \hat{z}_a^j)\) with \(j \in D_a\) with the property that \((\hat{y}_a^j, y_{-a},\hat{z}_a^j, z_{-a})\) is feasible for the given x and such that \((\hat{z}_a^j, z_{-a})\) satisfy (15). Given a strategy profile (y, z), for each \(a \in A\) and \(j \in D_a\) (i.e., for each deviation \((\hat{y}_a^j, \hat{z}_a^j)\)) the previous constraints is equivalent to requiring that the following disjunction be satisfied:
-
Either \((\hat{y}_a^j, y_{-a}, \hat{z}_a^j, z_{-a})\), together with the \(\phi \) and x chosen in the first level, satisfies (30) as well as (15) for all \(n \in N\) and \(t \in T\) (in this case, we refer to \((\hat{y}_a^j, y_{-a}, \hat{z}_a^j, z_{-a})\) as a feasible deviation)
-
Or \((\hat{y}_a^j, y_{-a}, \hat{z}_a^j, z_{-a})\), together with the \(\phi \) and x chosen in the first level, does not need to satisfy (30) as it violates (15) for at least a pair of indices \(n \in N\) and \(t \in T\) (in this case, we refer to \((\hat{y}_a^j, y_{-a}, \hat{z}_a^j, z_{-a})\) as an infeasible deviation).
We now show how to express this disjunction in mixed-integer quadratic terms. Let, for each \(a \in A, j \in D_a, n \in N, t \in T\), \(\zeta _{{nt}}^{{aj}} \in \{0,1\}\) be a binary variable indicating whether the instance of constraint (15) with indices n, t is satisfied by \((\hat{y}_a^j,y_{-a},\hat{z}_a^j,z_{-a})\) (i.e., \(\zeta _{{nt}}^{{aj}}=1)\) or violated (i.e., \(\zeta _{{nt}}^{{aj}}=0\)). In addition, for each \(a \in A\) and \(j \in D_a\), let the binary variable \(\xi ^{{aj}} \in \{0,1\}\) be equal to 1 if and only if constraints (15) are satisfied by \((\hat{y}_a^j,y_{-a},\hat{z}_a^j, z_{-a})\) for all \(n \in N, t \in T\). The following holds:
Theorem 2
Given a strategy profile (y, z), constraint (29) is satisfied for each \(a \in A\) if and only if the following best-response system is satisfied, i.e., if and only if there is an assignment of values to the variables \(\zeta _{{nt}}^{{aj}}\) and \(\xi ^{{aj}}\) for each \(j \in D_a\), \(n \in N\), and \(t \in T\) such that the following constraints are satisfied:





Proof
Consider each \(a \in A, j \in D_a, n \in N, t \in T\). If \(\zeta _{{nt}}^{{aj}} = 1\), (32) becomes equal to (15) and (33) is slack. If \(\zeta _{{nt}}^{{aj}} = 0\), (32) is slack and (33) imposes that (15) be strictly violated (by 1, which is the smallest possible positive violation since the constraint contains integer coefficients and integer variables only). If \(\xi ^{{aj}} = 1\), (30) is imposed as (31) becomes identical to it and, due to (34), \(\zeta _{{nt}}^{{aj}} = 1\) for all \(n \in N, t \in T\). Therefore, all of constraints (15) are imposed. If \(\xi ^{{aj}} = 0\), (30) is not imposed as (31) is slack and, due to (35), \(\zeta _{{nt}}^{{aj}} = 0\) holds for at least a pair \(n \in N, t \in T\)—which implies that, due to (33), the corresponding instance of constraint (15) is strictly violated. \(\square \)
4.3 Step 3: introduction of explicit best-response systems
Note that, to arrive at a single-level mathematical programming formulation, we should drop the two implicit functions \(w(\phi , \hat{z}_a^j, z_{-a})\) and \(d(\phi , \hat{z}_a^j, z_{-a})\) from constraints (31) and substitute, for them, an appropriate set of variables with the corresponding constraints. Recall that \(w(\phi , \hat{z}_a^j, z_{-a})\) and \(d(\phi , \hat{z}_a^j, z_{-a})\) represent the anticipation of airline a of the market outcome due to passenger charges equal to \(\phi \) and flight schedule decisions equal to \((\hat{z}_a^j,z_{-a})\).
To drop them, we introduce the variables \(\hat{w}^{aj}\) and \(\hat{d}^{aj}\) for each \(j \in D_a\) and impose \(\hat{w}^{aj} = w(\phi , \hat{z}_a^j, z_{-a})\) and \(\hat{d}^{aj} = w(\phi , \hat{z}_a^j, z_{-a})\) by relying on a set of conditions structurally similar to the KKT conditions (26). For each airline \(a \in A\) and \(j \in D_a\), such conditions read:
We introduce one such system of inequalities and variables for each pair \(a \in A, j \in D_a\). Each of them contains its own copy \(\hat{w}^{aj},\hat{d}^{aj}\) of the w, d variables, the corresponding constraints, the corresponding dual variables, and the corresponding complementarity constraints. Notice that the system features two types of z variables: the \(z_{a'pc}\) variables, which refer to the equilibrium strategy chosen by all airlines \(a' \in A {\setminus } \{a\}\), and the \(\hat{z}_{pc}^{aj}\) variables, which correspond to the deviating strategy of index \(j \in D_a\) that is considered by airline a in the original best-response system. We refer to a best-response system employing, rather than the implicit functions \(w(\phi , \hat{z}_a^j, z_{-a})\) and \(d(\phi , \hat{z}_a^j, z_{-a})\), constraints (36), as an explicit best-response system.
4.4 Final single-level problem
Applying the above reformulation steps, we arrive at a single-level problem which reads as follows. For better readability, we separate the constraints into four blocks: 1. first-level constraints, 2. explicit best-response system for the second-level problem, 3. other second-level constraints, and 4. third-level constraints.
5 Solution strategy
An obvious drawback of the above problem reformulation is the high number of explicit best-response systems (i.e., the variables and constraints appearing in the second block of reformulated model). Therefore, in this section we present a solution strategy which iteratively solves a master problem and a set of subproblems thanks to which an explicit best-response system is iteratively added at each iteration and only if needed.
5.1 Description of the algorithm
The main idea of our algorithm is to iteratively alternate between solving a master problem which only contains a (small) subset of explicit best-response systems, i.e., only featuring explicit best-response systems for a small subset of \(D_a\), for each \(a \in A\), and solving an auxiliary subproblem per airline to verify whether at least one airline \({a}\in {A}\) has an incentive to deviate from the investment and scheduling decisions y, z made when solving the master problem.

In particular, for each airline \({a}\in {A}\), the subproblem corresponds to the best-response problem of maximizing the airline’s profits subject to all the scheduling restrictions (14), (15), (16b), fleet investment constraints (16a), the KKT system (26), and fixed scheduling and investment values for all other airlines, as determined by the solution to the current master problem. If we identify a profit-enhancing strategy \((\hat{y}_{a}, \hat{z}_{a}^j)\) for an airline \({a}\) which allows it to profit by unilaterally deviating from the solution found when solving the master problem, we add a corresponding instance of the explicit best-response system (31)–(35), (36) to the master problem (substituting, as we explained, \(\hat{w}^{aj}\) for \(w(\phi , \hat{z}_a^j, z_{-a})\) and \(\hat{d}^{aj}\) for \(w(\phi , \hat{z}_a^j, z_{-a})\)), and solve it again.
At iteration one, the first master problem is obtained by relaxing all the explicit best-response systems by dropping the second block of constraints in the single-level reformulation, together with the variables which occur solely in it.
An overview of the resulting iterative solution strategy can be found in Algorithm 1.
5.2 Correctness of the algorithm
We now establish the correctness of our algorithm:
Theorem 3
Let \(|P_{{a}}| < \infty \) and assume all investment variables \(x\), \(y\) as well as airport charges \(\phi \) have a finite upper bound. Then, Algorithm 1 terminates after a finite number of iterations with an optimal solution.
Proof
Since y and z are integer variables and, by assumption, they are bounded, the number of possible strategies \((\hat{y}_a,\hat{z}_a)\) that an airline \(a \in A\) may use to deviate from a GNE is finite. Hence, the number of explicit best-response systems which can be generated is finite. Any instance of the master problem solved in Algorithm 1 is a relaxation of the trilevel problem (as it is obtained by relaxing some of the explicit best-response systems the problem features according to our reformulation). Let \((x^M,\phi ^M,y^M,z^M,w^M,d^M)\) be solution to the master problem and let, for each \(a \in A\), \((\hat{y}_a^S,\hat{z}_a^S,w^S,d^S)\) be the solution to the corresponding best-response subproblem. If, for all \(a \in A\), \(\rho ^{\text {airline}}_{{a}}(\hat{y}_a^S, y_{-a}^M, \hat{z}_a^S, z_{-a}^M, w^S, d^S) -\rho ^{\text {airline}}_{{a}}(y^M,z^M,w^M,d^M) \le \epsilon \), we conclude that no airline can obtain a strictly larger profit via a deviation. This implies that all the explicit best-response systems that have not yet been taken into account and added to the master problem are satisfied and, hence, the algorithm halts with an optimal solution. If, conversely, the subproblem produces a strictly improving deviation for at least one airline \(a \in A\), adding the corresponding explicit best-response system to the master problem guarantees that, after reoptimizing the latter, we obtain a solution \((\tilde{x}^M,\tilde{\phi }^M,\tilde{y}^M,\tilde{z}^M,\tilde{w}^M,\tilde{d}^M)\) in which either \((\tilde{y}^M_a,\tilde{z}^M_a)=(\hat{y}_a,\hat{z}_a)\) (i.e., in which the previous deviation is featured as the action chosen by airline \(a \in A\)), or the first-level solution has changed (i.e., \((\tilde{x}^M,\tilde{\phi }^M) \ne (x^M,\phi ^M)\)) and, thanks to this, \((\hat{y}_a,\hat{z}_a)\) is not anymore an improving deviation. \(\square \)
6 Theoretical benchmark: The integrated planning model
We now present an integrated planning model which allows for finding an ideal welfare-maximizing allocation of resources with the corresponding optimal investments and operational decisions. We will rely on such model as benchmark, using it as baseline to quantify the costs of liberalized and imperfect aviation markets that are obtained under our trilevel model in the case study we report in the next section. As we will see in it, such an integrated planning model may indeed yield (investment) decisions which are quite different from those identified by our trilevel model.
In the integrated planning model, we make the assumption that all of the airports’ and airlines’ investment and scheduling decisions be taken by a benevolent social planner in a globally efficient way, i.e., in such a way that the welfare of the whole industry is maximized. In this model, we assume that the airports are not limited by budget restrictions. Models similar to this one are typically referred to as “theoretical” or “first-best” benchmarks and are frequently used in the literature. See, e.g., Jenabi et al. (2013), Grimm et al. (2016a), or Weibelzahl and Märtz (2017).
From an economical point of view, the integrated planning model yields the same outcome as a variant of our market model in which welfare is maximized in each level.Footnote 5 The corresponding competitive market prices adequately reflect scarcity of resources and incentivize efficient long-run investments for the players, i.e., they align the individual profit maximization objectives of the airlines with the overall welfare maximization goal. For more details on such equivalence see, e.g., Whinston and Green (1995), Feldman (1991), Varian (2014).
Adopting the same definition of welfare as in (9), the integrated planning model corresponds to the following optimization problem:
7 Case study
In this section, we present an academic six-airport network featuring different flight connections and adopt it as case study.
Hub-and-spoke topology with demand functions according to Dobson and Lederer (1993)
7.1 Test network
The test network we consider was originally introduced in Dobson and Lederer (1993) and is used to illustrate the relevant economic effects in an intuitive way on a simple example. The instance is reported in Fig. 7. As it can be seen in the figure, the six airports are divided into the hub airport H and the destination airports 1 to 5.
Let us assume that there is no pre-existing runway capacity at the beginning of the planning horizon. Due to this assumption, the analysis we are about to carry out may be alternatively interpreted as an analysis of the residual flight demand that cannot be covered by existing runway capacities, under the assumption that any pre-existing flight schedule would not be modified after the runway capacity extensions have taken place.
Per-unit airport investment costs for the hub H and the airports 1–5 amount to $20,000 and $10,000, respectively. Furthermore, the intercept \(\alpha _{}^\text {airport}\) and the slope \(\beta _{}^\text {airport}\) of the variable-cost function for all airports amount to $5000 and $5, respectively. In order to keep our example (and the corresponding scheduling decisions) as simple as possible, we only consider five connections with takeoffs taking place in subsequent periods. In particular, the connections from the hub H to airports 1 and 2 are long-haul flights with a flight duration of three periods, while the connections with destination 3, 4, and 5 are short-haul flights with a flight duration of only one period. Therefore, in our test example we consider a total planning horizon of six periods. In addition, we assume that connections (H, 1) and (H, 3) are the two high-demand connections of the network. Note that all the five considered connections may equivalently be interpreted as return trips without affecting our analysis. As it can be seen in Fig. 7, all the demand functions we use are linear (and decreasing), which implies that the consumer surplus is a concave function.
In analogy to runway capacities, we assume that no pre-existing aircraft are available. We consider two possible candidate aircraft for fleet expansion with a seat capacity \(\kappa ^\text {aircraft}_{}\) of 300 and 600, which represent a small and a large aircraft type, respectively. Investment cost \(i^\text {aircraft}_{}\) of the “small” and “large” aircraft amount to $10,000 and $20,000. Note that the investment costs we consider here should be interpreted as annualized costs, corresponding to the costs of using an aircraft only over the planning period under consideration. Since we only consider a very short planning period of a few hours in this section, the investment costs will be relatively small when compared to the respective variable costs of a flight (see below).
We assume that all five connections can be served by each of the two aircraft. Moreover, the intercept \(\alpha _{ }^{\text {airline}}\) of the variable-cost function of the “small” aircraft is assumed to be $22,500 for the long-haul flights and $7200 for the short-haul flights. For the “large” aircraft, these values are higher and are given by $45,000 and $22,500, respectively. The slope \(\beta _{ }^{\text {airline}}\) of the variable-cost function for the long-haul flights and the short-haul flights amounts to $25 and $8, respectively. Footnote 6 Note that, similarly to the intercept values we introduced, we assume higher slope values for long-haul flights than for short-haul flights as, e.g., fuel costs or meal costs will, in general, increase with the flight time.
For the discussed test network, in the following we present the welfare optimum of the integrated planning problem as well as the equilibrium solution of our trilevel market model. In particular, for our trilevel model we analyze the effects of different degrees of competition among airlines, considering both a monopoly airline and a duopoly.
7.2 Setup
Note that, for the case of linear demand functions, our integrated planning model reduces to a mixed-integer problem with linear constraints and a concave objective, while the trilevel market model is intrinsically nonconvex—this calls for the adoption of a spatial branch-and-bound solver to achieve a globally optimal solution. All our problem instances are solved with the spatial branch-and-bound solver SCIP 3.2.1 Gamrath et al. (2016). Using our Algorithm 1, all instances of our trilevel model are solved in only a few iterations. All the computations are performed on an Intel\(^{\copyright }\) Core\(^{\mathrm{TM}}\)i5-3360M CPU with 4 cores and 2.8 GHz each and 4 GB RAM.
7.3 Discussion of main results
Let us first analyze the results obtained with the integrated planner model. As Table 1 shows, in its solution the capacity of all six airports is extended. Moreover, as shown in Tables 2 and 3, investments take place in five aircraft serving all available connections.
Two large aircraft are scheduled on the high-demand connections (H, 1) and (H, 3), whereas, on the three remaining connections, only small aircraft are used. Overall, the total welfare amounts to $553,262. We will use this value as a benchmark to assess possible market inefficiencies in the imperfect aviation market case, relying on our trilevel model—see Table 4.
We now discuss the results of our trilevel market model, which are summarized in Tables 1, 2, 3, and 4. We first assume the presence of a single airline, i.e., a monopolist, which invests in its fleet and schedules its aircraft on the second level. As expected, the monopolist reduces ticket supply in order to increase its profits. In particular, the monopolist only invests in three small aircraft that are scheduled on connections (H, 1), (H, 3), and (H, 4). Given this supply shortage based on the reduced seat capacity, welfare reduces to $364,300 when compared to the reference integrated-planning solution. The total profits of the monopolist amount to $206,800. The connection-specific profits, of $155,333, $40,733, and $10,734 for, respectively, the three connections (H, 1), (H, 3), and (H, 4), show that, indeed, all three legs are profitable for the monopolist. We remark that the observed equilibrium prices are the outcome of the competitive ticket market. This implies that the monopolist cannot charge a monopolistic price but, rather, can only affect the resulting (perfectly competitive) price through its strategic aircraft investments and scheduling decisions in level two. Therefore, for example, given a monopolist choice of investing into the small aircraft and of scheduling it on connection (H, 3) with a capacity of 300 and assuming a total of 300 passengers on that connection, the resulting market price will be \(\text {P}_{3}^\text {con} = 300\).
In a second experiment, we assume a duopoly, i.e., we consider two competing airlines on level two. In particular, we consider (i) a “large” airline that, according to its assumed airline-specific fleet portfolio, can only invest in the large aircraft type, as well as (ii) a “small” airline that can only invest in the small aircraft type. Footnote 7 As expected, the increased competition leads to a welfare of $478,800, which is higher when compared to the monopoly solution. This underlines the importance of adequate competition policy regulations—see the vast literature on competition and competition policy in the airline industry, e.g., Borenstein and Rose (1994), Mazzeo (2003), or Silva et al. (2014). The observed welfare gain is mainly driven by the fact that the “large” airline schedules one large aircraft on connection (H, 1), which increases the seat capacity on this connection by 300. In addition, we can observe a reduction of airline profits to $117,800 relative to the monopoly, whereas the consumer surplus moves in the opposite direction. In both the monopoly and in the duopoly cases, the airport profits are zero, i.e., their budget constraints are binding.
We also note that, in line with the above observations, airport charges at the hub and at airport 1 decrease in the duopoly case when compared to the monopolistic case. This is due to the fact that the airport investment and operational costs can be recovered via an increased number of passengers.
Given efficient ticket prices under the integrated planner problem (equivalent to a perfectly competitive market outcome), our trilevel market model will, in general, distort the optimal price structure of the former. In our example, for instance, the ticket prices under both the duopoly and the monopoly will be inefficiently high, which directly reflects an underinvestment in aircraft and airport capacity—see Tables 1 and 2. For instance, the price observed in the monopoly case for connection 1 in the amount of $750 is inefficiently high when compared to the price of $300 that is obtained under the benchmark model. This is because the flight capacity on this connection is reduced by the monopolist from 600 seats/tickets to only 300. In line with the current policy debate on the bankruptcy of the German carrier AirBerlin, the results obtained with our model underline that prices will, in general, tend to increase if the market concentration increases.
Finally, we note that our model may not only be used for policy analyses (carried out by, for instance, a regulator wishing to assess, e.g., the impact on the market when losing a competitor), but it can also serve as a valuable tool for business support of private actors. In particular, our model inherently allows airlines to identify an optimal strategy for a given investment and scheduling decision of its competitor(s).
Within the context of optimal airline-strategies and profitable strategy deviations, in Table 5 we present, as an example, the solutions of the last three restricted master problems and subproblems for the duopoly case.
As it can be seen in the third-last iteration, it is optimal for both airlines of the duopoly to unilaterally reduce their investments, i.e., to only invest in a single aircraft scheduled on the most profitable connections (which are connections 1 and 4, respectively). While, in the second-last iteration, there is no further unilateral and profit-enhancing deviation strategy for the large airline (which now serves connection 1), the small airline has an incentive not to offer a flight to airport 5. Adding a corresponding best-response system to the new master problem, in the last iteration no new deviation strategies are found in either subproblem and the algorithm terminates with an optimal solution, i.e., with an equilibrium.
8 Conclusion
In this paper, we have presented a trilevel market model which accounts for different economic players including airports, airlines, and passengers. In particular, we have assumed welfare-regulated airports which choose their optimal runway capacity expansion as well as an optimal airport charge in the first level, imperfectly competitive airlines which make investment in new aircraft and flight scheduling decisions in the second level, and a ticket market in the third level, in which the number of tickets that is sold is determined.
Using an integrated single-level benchmark model, we have been able to quantify the costs of imperfect markets in terms of inefficient investments in the multilevel imperfect-market model. In order to illustrate the underlying (economic) effects, as a first starting point we have analyzed a small test network that consists of six airports and five flight connections.
Due to the difference in solutions that we obtain when considering either the integrated benchmark model or our trilevel model, our results suggest the need for a careful design of (future) market structures as, otherwise, investment incentives for airports and airlines may be aligned in a way that yields severe long-run inefficiencies when implemented in practice. To this end, our model may be seen as a valuable tool to evaluate and assess different policy options on a quantitative basis in the future.
Future works include the development of algorithms for tackling instances of larger size, possibly relying on techniques of cut diversity and bound improvement for selecting the next explicit best-response system to be introduced (see Amaldi et al. (2010), Amaldi et al. (2014), Coniglio and Tieves (2015)), as well the application of techniques similar to those we developed in this paper to other multilevel decision-making problems in the airline industry.
Another interesting direction for future research is investigating under which conditions the game that is played in the second level by the airlines always admits a generalized Nash equilibrium. This could be done, for instance, by investigating whether such a game can be cast as a congestion game where the connections are interpreted as resources whose value/price is determined as a solution to the ticket-pricing game played in the third level—see, for instance, (Harks and Klimm 2012). It would also be of interest to assess the impact on the whole trilevel problem of adopting, in the generalized Nash equilibrium problem, different equilibrium-selection strategies besides the optimistic one where a welfare-maximizing equilibrium is selected.
Notes
Indeed, one could, w.l.o.g., introduce departure costs \(\alpha _n^\text {airport,dep}, \beta _n^\text {airport,dep}\) and landing costs \(\alpha _n^\text {airport,land}, \beta _n^\text {airport,land}\), and redefine \(V_n^\text {airport}(z,w)\) in Eq. (1) as follows:
$$\begin{aligned} V_n^\text {airport}(z,w)&= \sum _{a \in A} \left( \sum _{c \in \delta _n^\text {in}(C_a)} \sum _{p \in P_a} \left( \alpha _n^\text {airport,land} z_{apc} + \beta _n^\text {airport,land} w_{ac}\right) \right. \\&\quad +\left. \sum _{c \in \delta _n^\text {out}(C_a)} \sum _{p \in P_a} \left( \alpha _n^\text {airport,dep} z_{apc} + \beta _n^\text {airport,dep} w_{ac}\right) \right) . \end{aligned}$$For the sake of simplicity and in order to reduce the computational burden, we assume a cost coefficient which is independent of the aircraft type. The model can be, nevertheless, easily generalized to the case of a cost \(\beta _{apc}^{\text {airline}}\) specific to the aircraft type by extending the variable \(w_{ac}\) with an index p.
The same assumption (of perfect competition) is often made in the literature for many complex multilevel models that arise from the applications. See, e.g., Grimm et al. (2016a).
Let \(\mathcal {T}\) be a set of trips, with each trip \(\tau \in \mathcal {T}\) consisting of a collection of connections (or legs) \(C_\tau \). Rather than a demand \(d_c\) per connection \(c \in C\), let us introduce a demand \(d_\tau \) per trip \(\tau \in \mathcal {T}\). Let us redefine the gross consumer surplus per trip \(\tau \in \mathcal {T}\) as \(\int _0^{d_\tau } P_\tau ^\text {cons}(s) \mathrm{d}s\), where \(P_\tau ^\text {cons}\) is the maximum price at least s customers are willing to pay for a ticket for trip \(\tau \). From an equilibrium-problem perspective, we now have a consumer/player for each trip \(\tau \in \mathcal {T}\), rather than for each connection \(c \in C\). The market-clearing constraint becomes \(\sum _{\tau \in \mathcal {T}: c \in C_\tau } d_\tau = \sum _{a \in A} w_{ac}\) for all \(c \in C\). Assuming exogenous prices \(\pi ^*_c\) for each connection \(c \in C\) and assuming a price of \(\sum _{c \in C_\tau } \pi _c^*\) for each trip \(\tau \in \mathcal {T}\), it is not difficult to see that the result of Proposition 1 still applies, i.e., we can still solve the market-clearing problem as a single-level welfare-maximization problem with variables \(d_\tau , \tau \in \mathcal {T}\), rather than \(d_c, c \in C\), and the above-redefined willingness to pay function \(P_\tau ^\text {cons}\) and market-clearing constraint. As this has no impact on levels 1 and 2 (as only the \(w_{ac}\) variables have an impact there), the method we propose in the paper remains valid for the trip case.
In the first level, welfare is expressed as gross consumer surplus minus all investment and operational costs of both airports and airlines. In the second level, welfare equals gross consumer surplus minus fleet investment and fleet operation costs. In the third level, welfare is defined as the difference between gross consumer surplus and operational costs of the airlines. First, as all the players in the same level maximize the same objective function, they can be collapsed into a single player. Secondly, from a mathematical point of view, see, e.g., Grimm et al. (2016a), the three welfare functions we introduced are affinely equivalent. This implies that, under the assumption of optimism, it is without loss of generality to assume that all levels maximize the same welfare function as the first-level problem. Thus, the trilevel model can be solved as a single-level welfare maximization problem with a single decision maker, which is identical to our integrated planner model.
If more than a single airline is present, their costs \(\alpha _{ }^{\text {airline}}\) are made pairwise distinct by adding a small perturbation \(\epsilon \) to them—see footnote 7 for more details.
To guarantee pairwise-distinct costs, we add a positive perturbation \(\epsilon > 0\) to the cost for connections (H, 1) and (H, 2) for the small airline, and a positive perturbation by the same \(\epsilon \) for connections (H, 3), (H, 4), and (H, 5) for the large airline.
References
Abara Jeph (1989) Applying integer linear programming to the fleet assignment problem. Interfaces 19(4):20–28
Adler Nicole (2001) Competition in a deregulated air transportation market. Eur J Oper Res 129(2):337–345 A Global View of Industrial Logistics
Amaldi E, Coniglio S, Gualandi S (2010) Improving cutting plane generation with 0-1 inequalities by bi-criteria separation. In: Experimental Algorithms, 9th International Symposium, SEA 2010, Ischia Island, Naples, Italy, May 20-22, 2010. Proceedings, pp 266–275
Amaldi Edoardo, Coniglio Stefano, Gualandi Stefano (2014) Coordinated cutting plane generation via multi-objective separation. Math Program 143(1–2):87–110
Barnhart Cynthia, Belobaba Peter, Odoni Amedeo R (2003) Applications of operations research in the air transport industry. Transp Sci 37(4):368–391
Barroso Luiz Augusto, Carneiro Rafael Dix, Granville Sérgio, Pereira Mario V, Fampa Marcia HC (2006) Nash equilibrium in strategic bidding: a binary expansion approach. IEEE Trans Power Syst 21(2):629–638
Basilico Nicola, Coniglio Stefano, Gatti Nicola, Marchesi Alberto (2017) Bilevel programming approaches to the computation of optimistic and pessimistic single-leader-multi-follower equilibria. Leibniz Int Proc Inf 75:1–14
Basilico Nicola, Coniglio Stefano, Gatti Nicola, Marchesi Alberto (2020) Bilevel programming methods for computing single-leader-multi-follower equilibria in normal-form and polymatrix games. EURO J Comput Optim 8(1):3–31
Basso Leonardo J (2008) Airport deregulation: Effects on pricing and capacity. Int J Indus Organ 26(4):1015–1031
Bolusani S, Coniglio S, Ralphs TK, Tahernejad S, Dempe S, Zemkoho A (2020) A unified framework for multistage and multilevel mixed integer linear optimization. In: Bilevel Optimization, Adv. Next Challenges. Springer
Borenstein Severin, Rose Nancy L (1994) Competition and price dispersion in the us airline industry. J Polit Econ 102(4):653–683
Bowen John (2002) Network change, deregulation, and access in the global airline industry. Econom Geogr 78(4):425–439
Boyd Stephen, Vandenberghe Lieven (2004) Convex optimization. Cambridge University Press, Cambridge
Burghouwt Guillaume, de Wit Jaap G (2015) In the wake of liberalisation: long-term developments in the eu air transport market. Transp Policy 43:104–113
Burke Edmund K, De Causmaecker Patrick, De Maere Geert, Mulder Jeroen, Paelinck Marc, Berghe Greet Vanden (2010) A multi-objective approach for robust airline scheduling. Comput Oper Res 37(5):822–832
Cadarso Luis, Marín Ángel (2013) Robust passenger oriented timetable and fleet assignment integration in airline planning. J Air Transp Manag 26:44–49
Cadarsoa Luis, Marín Ángel (2011) Integrated robust airline schedule development. Procedia-Social Behav Sci 20:1041–1050
Clark Paul (2007) Buying the big jets: fleet planning for airlines. Ashgate Publishing, Ltd., UK
Colson Benot, Marcotte Patrice, Savard Gilles (2007) An overview of bilevel optimization. Ann Oper Res 153(1):235–256
Coniglio S, Gatti N, Marchesi A (2017) Pessimistic leader-follower equilibria with multiple followers. In: Proceedings of the twenty-sixth international joint conference on artificial intelligence, IJCAI 2017, Melbourne, Australia, August 19-25, 2017, pp 171–177
Coniglio Stefano, Gatti Nicola, Marchesi Alberto (2020) Computing a pessimistic stackelberg equilibrium with multiple followers: The mixed-pure case. Algorithmica 82(5):1189–1238
Coniglio S, Tieves M (2015) On the generation of cutting planes which maximize the bound improvement. In: Experimental algorithms - 14th international symposium, SEA 2015, Paris, France, June 29 - July 1, 2015, Proceedings, pp 97–109
Dempe Stephan (2002) Foundations of bilevel programming. Springer, Berlin
Dempe Stephan, Mordukhovich Boris S, Zemkoho Alain Bertrand (2014) Necessary optimality conditions in pessimistic bilevel programming. Optimization 63(4):505–533
Dobson Gregory, Lederer Phillip J (1993) Airline scheduling and routing in a hub-and-spoke system. Transp Sci 27(3):281–297
Egger R, Gula I, Walcher D (2014) Open tourism. Open innovation, crowdsourcing and collaborative consumption challenging the tourism industry
Facchinei Francisco, Kanzow Christian (2010) Generalized nash equilibrium problems. Ann Oper Res 175(1):177–211
Faust Oliver, Gönsch Jochen, Klein Robert (2017) Demand-oriented integrated scheduling for point-to-point airlines. Transp Sci 51(1):196–213
Feldman AM (1991) Welfare economics. In: The World of Economics, pp 713–726. Springer
Frankfurt Airport (2016) Airport charges at frankfurt airport
Fu X, Oum TH, Zhang A (2010) Air transport liberalization and its impacts on airline competition and air passenger traffic. Transp J, pp 24–41
Gamrath G, Fischer T, Gally T, leixner AM, Hendel G, Koch T, Maher SJ, Miltenberger M, Müller B, Pfetsch ME, Puchert C, Rehfeldt D, Schenker S, Schwarz R, Serrano F, Shinano Y, Vigerske S, Weninger D, Winkler M, Witt JT, Witzig J (2016) The SCIP Optimization Suite 3.2. techreport 15–60, ZIB
Grimm Veronika, Martin Alexander, Schmidt Martin, Weibelzahl Martin, Zöttl Gregor (2016) Transmission and generation investment in electricity markets: The effects of market splitting and network fee regimes. Eur J Oper Res 254(2):493–509
Grimm Veronika, Martin Alexander, Weibelzahl Martin, Zöttl Gregor (2016) On the long run effects of market splitting: Why more price zones might decrease welfare. Energy Policy 94:453–467
Lufthansa Group (2000) Corporate responsibility within the lufthansa group
Hane Christopher A, Barnhart Cynthia, Johnson EllisL, Marsten Roy E, Nemhauser George L, Sigismondi Gabriele (1995) The fleet assignment problem: Solving a large-scale integer program. Math Program 70(1):211–232
Harks Tobias, Klimm Max (2012) On the existence of pure Nash equilibria in weighted congestion games. Math Oper Res 37(3):419–436
Heathrow Airport (2017) Airport charges structural review
Hobbs BF, Helman U (2004) Complementarity-based equilibrium modeling for electric power markets. In: Bunn D (ed) Modeling prices in competitive electricity markets. Wiley, London
Jacobs TL, Garrow LA, Lohatepanont M, Koppelman FS, Coldren GM, Purnomo H (2012) Airline planning and schedule development. In: Cynthia B, Barry S (eds) Quantitative problem solving methods in the airline industry: a modeling methodology handbook. Springer, US, pp 35–99
Jenabi M, Fatemi Ghomi SMT, Smeers Y (2013) Bi-level game approaches for coordination of generation and transmission expansion planning within a market environment. IEEE Trans Power Syst 28(3):2639–2650
Kennedy JF (2017) International Airport. Schedule of charges for air terminals
Kidokoro Yukihiro, Lin Ming Hsin, Zhang Anming (2016) A general-equilibrium analysis of airport pricing, capacity, and regulation. J Urban Econom 96:142–155
Kölker Katrin, Lütjens Klaus (2015) Using genetic algorithms to solve large-scale airline network planning problems. Transp Res Proc 10:900–909
Lederer PhillipJ, Nambimadom Ramakrishnan S (1998) Airline network design. Oper Res 46(6):785–804
List George F, Wood Bryan, Nozick Linda K, Turnquist Mark A, Jones Dean A, Kjeldgaard Edwin A, Lawton Craig R (2003) Robust optimization for fleet planning under uncertainty. Trans Res Part E: Logist Trans Rev 39(3):209–227
Lohatepanont Manoj, Barnhart Cynthia (2004) Airline schedule planning: Integrated models and algorithms for schedule design and fleet assignment. Trans Sci 38(1):19–32
Mazzeo Michael J (2003) Competition and service quality in the us airline industry. Rev Ind Organ 22(4):275–296
Nash J (1951) Non-cooperative games. Ann Math, pp 286–295
Nataraja Sundaram, Al-Aali Abdulrahman (2011) The exceptional performance strategies of emirate airlines. Compet Rev 21(5):471–486
Pozo David, Sauma Enzo E, Contreras Javier (2013) A three-level static milp model for generation and transmission expansion planning. IEEE Trans Power Syst 28(1):202–210
Rexing Brian, Barnhart Cynthia, Kniker Tim, Jarrah Ahmad, Krishnamurthy Nirup (2000) Airline fleet assignment with time windows. Trans Sci 34(1):1–20
Rushmeier Russell A, Kontogiorgis Spyridon A (1997) Advances in the optimization of airline fleet assignment. Trans Sci 31(2):159–169
Saldiraner Yildirim (2013) Airport master planning in turkey; planning and development problems and proposals. J Air Trans Manag 32:71–77
Saldiraner Yildirim (2014) The new airport in istanbul: expectations and opportunities. J Case Res Business Econom 5:1
Santos Miguel Gueifão, Antunes António Pais (2015) Long-term evolution of airport networks: optimization model and its application to the united states. Trans Res Part E: Logist Trans Rev 73:17–46
Sherali Hanif D, Bae Ki-Hwan, Haouari Mohamed (2013) A benders decomposition approach for an integrated airline schedule design and fleet assignment problem with flight retiming, schedule balance, and demand recapture. Ann Oper Res 210(1):213–244
Silva Hugo E, Verhoef Erik T, van den Berg Vincent A C (2014) Airline route structure competition and network policy. Trans Res Part B: Methodol 67:320–343
Smith BC, Jacobs TL (1997) Airline planning and marketing in a changing environment. J Inf Syst 3(1)
Sun Yanshuo, Schonfeld Paul (2015) Stochastic capacity expansion models for airport facilities. Transp Res Part B: Methodol 80:1–18
Teodorović Dušan, Stojković Goran (1990) Model for operational daily airline scheduling. Trans Plan Technol 14(4):273–285
Varian HalR (2014) Intermediate microeconomics: a modern approach: ninth international, Student edn. WW Norton & Company, New York
Von Stackelberg Heinrich (1934) Marktform und gleichgewicht. Springer, Vienna
Weibelzahl Martin (2017) Nodal, zonal, or uniform electricity pricing: how to deal with network congestion. Front Energy 11(2):210–232
Weibelzahl M, Märtz A (2017) Optimal storage and transmission investments in a bilevel electricity market model. Ann Oper Res, pp 1–30
Whinston Michael D, Green Jerry R (1995) Microeconomic theory. Oxford University, New York
Xiao Yibin, Xiaowen Fu, Zhang Anming (2013) Demand uncertainty and airport capacity choice. Transp Res Part B: Methodol 57:91–104
Zhang Anming, Zhang Yimin (2006) Airport capacity and congestion when carriers have market power. J Urban Econom 60(2):229–247
Acknowledgements
We acknowledge funding through the DFG SFB/Transregio 154, Subproject A05. Many thanks go to the members of the International Conference on Operations Research (Berlin, 2017) and the annual meeting of the Airline Group of the International Federation of Operational Research Societies (London, 2017). Finally, we thank Richard Schumacher from Lufthansa AirPlus Servicekarten GmbH for valuable comments and discussion. We would also like to thank three anonymous referees, whose comments have helped us improve the quality of the paper, extending and clarifying its results.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Coniglio, S., Sirvent, M. & Weibelzahl, M. Airport capacity extension, fleet investment, and optimal aircraft scheduling in a multilevel market model: quantifying the costs of imperfect markets. OR Spectrum 43, 367–408 (2021). https://doi.org/10.1007/s00291-021-00621-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00291-021-00621-4