1 Introduction

Cancer is the first cause of death in The Netherlands (CBS 2016) and the second cause of death in the European Union after circulatory system diseases. Over 1.29 million people died from cancer in the 28 European Union countries in 2013: 26% of total deaths—30% of total deaths in The Netherlands. According to the World Health Organization fact sheets, 8.8 million people died from cancer worldwide in 2015, and the annual economic cost of cancer in 2010 was estimated about US$1.6 trillion (WHO 2015). The International Agency for Research on Cancer forecasts about 24 million patients to have cancer in 2035 (IARC 2017).

In modern medicine, chemotherapy is a common cancer treatment procedure next to surgery and radiotherapy. Chemotherapy drugs kill rapidly dividing cells, and cancerous cells divide rapidly. However, some healthy cells also divide rapidly, even in adults, such as bone marrow cells, the gastrointestinal tract, and hair follicles. Hence, chemotherapy is planned in multiple drug administration installments over several months.

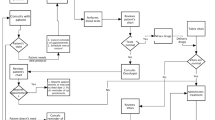
For every installment, the patient goes through the 5-step process shown in Fig. 1. Based on the laboratory results, the oncologist authorizes drug administration. If the laboratory results are satisfactory, the pharmacy prepares the drugs, and nurses administer the drugs in two steps. In the first few minutes, e.g., 15 min of drug administration, a nurse prepares the patient, sets up the infusion pump, and connects it to the patient’s body. At every moment thereafter, a nurse monitors the flow of drugs and takes care of the patient whenever needed until completion of drug administration. For setup, a nurse is exclusively assigned to the patient and does not take care of other patients. However, one nurse can simultaneously monitor up to a certain number of patients, e.g., 4 patients. At every moment, a patient is monitored by exactly one nurse, but the nurse who monitors the patient may change during drug administration. Contrarily, the same drug administration station—a combination of a chair or bed and an infusion pump—is allocated for the patient throughout the drug administration session. In contrast to the first three steps in Fig. 1, the duration of drug administration depends on the prescribed regimen, and it varies significantly from patient to patient, on a day at a clinic: from 15 min to 8 h (Turkcan et al. 2012). If the laboratory results are not satisfactory with respect to side effects or effectiveness, the oncologist postpones drug administration for a few days or continues the treatment with another regimen (protocol).

Fig. 1
figure 1

Adopted from Hesaraki et al. (2019)

Operationally relevant steps in outpatient chemotherapy.

Full size image

At oncology clinics, the staffing cost is the second largest cost, preceded by the cost of drugs (Liang and Turkcan 2016). A few studies have highlighted the importance of carefully utilizing the available nursing capacity in outpatient chemotherapy (e.g., Griffin 2014; Woodall et al. 2013). Tasks have to be carefully assigned to nurses in chemotherapy to efficiently use the available capacity while maintaining treatment effectiveness and quality of service. To that end, we focus on the last two steps in Fig. 1 (setting up and monitoring) to optimize the drug administration schedule while taking the time requirements of patients, pharmacy, and oncologists into consideration. Thus, the three prior steps for each patient are scheduled based on the drug administration appointment (Hesaraki et al. 2019). With a multi-objective formulation, we reach a trade-off among the interests of patients, nurses, and the clinic. The model we propose can be incorporated in different settings in spite of the precedence among the five consecutive steps in Fig. 1. The order in which information becomes available and scheduling decisions can be made is indicated in Fig. 2. It starts with time requirements and appointment requests. For further descriptions of the chemotherapy process and brief literature reviews of scheduling outpatient chemotherapy appointments, we refer the reader to Turkcan et al. (2012), Liang and Turkcan (2016), and Hesaraki et al. (2019).

Fig. 2
figure 2

Order in which information becomes available and scheduling decisions can be made: starting with time requirements and appointment requests

Full size image

In a prior study (Hesaraki et al. 2019), we propose a bicriterion mixed integer programming (MIP) model to generate appointment templates that can be used for the online scheduling of outpatient chemotherapy. The two criteria are flowtime and makespan, which pertain to having appointments started and ended as early as possible for the sake of patients and nurses, respectively. In this paper, we develop a quadcriterion MIP model for offline scheduling of outpatient chemotherapy. However, as information about all patients to be treated on an intended day is available a priori in offline scheduling, nurse assignment is integrated with appointment scheduling in this model. If the nurse task is scheduled consecutively after the appointment is scheduled, it will in general be inferior with respect to the optimization criteria. This is due to the exclusion of many solutions from the search space. In this paper, we focus on appointment scheduling in contrast to capacity allocation (Schütz and Kolisch 2012), which is done in the online day planning stage of Fig. 3, where the appointment days are decided as requests arrive (e.g., Gocgun and Puterman 2014).

Fig. 3
figure 3

Online versus offline appointment scheduling

Full size image

Liang and Turkcan (2016) give two separate and independent bicriterion models for functional and primary methods of delivering care in outpatient chemotherapy, which also focus on drug administration. A criterion common between their two models is the overtime. The other criteria that they consider are the direct waiting time and excess workload for the functional and primary models, respectively. However, they assume that the time that the patient is told to arrive at the clinic is already given. The waiting time is the time between that and the starting time of the drug administration appointment, which they schedule. They also assume that the start and end time of the working hours of each nurse on an intended day is already given. As a countermeasure for overtime and excess workload, their model determines the time and number of part-time nurses needed in the drug administration schedule. However, unlike primary nurses, part-time nurses are not explicitly assigned to individual patients. The drug preparation step is assumed to be included in the given appointment time.

Our model explicitly assigns nurses to patients, for all staffing ranks, e.g., full time, part-time, and primary, who are affiliated with the clinic and available on an intended day. The task schedule specifies at each timeslot of every drug administration appointment at each station, the setting up or monitoring task and the nurse assigned that task. The full-time equivalent (FTE) of nurses in the schedule can be adjusted to a desired feasible level. When a nurse takes over the monitoring of a patient from another nurse, a nurse change has taken place. The model is formulated to minimize the workload imbalance among nurses and the number of nurse changes during appointments. Allowing very few during-appointment nurse changes, in general, has higher utilization than assigning the same nurse for the entire appointment. Since the prior steps are scheduled based on the time of drug administration, our model eliminates unnecessary waiting time. Appointments are scheduled as early as possible during the day, which is desirable for chemotherapy patients (Lau et al. 2014). We develop a 3-stage heuristic to find trade-off solutions between workload imbalance among nurses and number of nurse changes for minimum deferring time of appointments with a chosen number of nurse FTEs in the schedule. These criterion points can serve as feasible solutions for warm starting the search to find other criterion points that are on efficient frontiers.

2 Problem and model formulation

In the problem that we consider, drug administration appointments have to be scheduled offline for a specific day and for a known group of P patients with the required appointment durations \(l_{p}\), \(p=1, \ldots , P\) on that day. This problem is associated with the single batch arrival process outlined by Gupta and Denton (2008): appointment scheduling decisions are not made until after observing all demand for a day; inter-arrival times are irrelevant. We make a few assumptions in developing our model. We assume that the uncertainty in appointment durations is taken into account by time buffers. Extra time is included at the end of each appointment to avoid delays for subsequent appointments while not resulting in a significant amount of idle time. Moreover, we assume that patients are available to have their drug administration at the start of the scheduled appointments, i.e., there are no late arrivals and delays. Preemption is not allowed, and we consider all stations identical. We also assume that there is no precedence among drug administration appointments.

Time is divided into timeslots of a fixed number of time units, e.g., 15 min. Thus, the opening hours of the clinic consist of T timeslots (\(t=1,\ldots ,T\)). Timeslot t is the time interval \((t-1,t]\). All appointment durations are integer numbers of timeslots. The first timeslot of the appointment duration of every patient is always scheduled for setup, and the subsequent timeslots are scheduled for monitoring the infusion progress. A patient with an appointment duration of one timeslot only has a setup timeslot in the schedule and no monitoring period. We assume that removing a patient from a station at the end of the appointment takes a small fraction of a timeslot duration, and it can be done as a monitoring task.

In solving the offline scheduling problem, we have to consider conflicting objectives. On the one hand, we have to take into account the patients’ time requirements or preferences, and on the other hand, we need high resource utilization given the scarcity of trained nurses. In our model, we refer the earliest time that patient p can and is willing to have the appointment on the day of the schedule, as the patient’s ready time. The ready time is the end of timeslot \(r_p\) in Fig. 4, and it is by default zero. However, if for whatever reason such as having another appointment, drug preparation requirements, oncologist unavailability, or commuting arrangements, the drug administration appointment cannot be scheduled before some time, then the ready time has a positive value (\(0 < r_p \leqslant T-l_p\)). Let \(s_p\) be the setup timeslot scheduled for patient p. Then, the appointment start time is \(s_p-1\). During the time between the ready time and the start time, the appointment had the opportunity to start but was deferred. We therefore refer to this period as the deferring time: \(\tau _p {:}{=}s_p-r_p-1\). We consider this quantity because of chemotherapy patients’ general preference to have their infusions as early during the day as possible (Lau et al. 2014). The time that the patient is in the clinic but involuntarily does not receive any service is the direct waiting time. When the patient is already in the clinic because of a prior appointment, the deferring time is a direct waiting time as well. For example, if the oncologist visit has to be scheduled no later than 11:00 h and the drug administration appointment is scheduled at 15:00 h, there will be a long waiting time for the patient. In contrast, some appointments may have a limiting finite due time \(d_p \leqslant T-1\) because of follow-up procedures or patients’ preferences. Unless otherwise stated, each appointment has a zero ready time and an infinite due time: \(r_p = 0,\ d_p = \infty\).

Fig. 4
figure 4

Adopted from Hesaraki et al. (2019)

Deferring time.

Full size image

It may also be desirable to have the appointments of certain patients scheduled with higher priority than others, closer to their ready times. For their appointments, the pharmacy or treating oncologist has less flexibility in scheduling their respective steps (Fig. 2). Hence, they indicate a ready time for the drug administration appointment, and by scheduling the appointment as close as possible to the ready time, there will be little direct waiting time for the patient. These priorities are formulated as weighted deferring times in the objective function. We consider two priority levels for the appointments: high and normal. These priorities are imposed by weights \(w_p\). The priority indicates the level of requirement for the appointment to start as close as possible to its ready time. The appointment start time (\(s_p-1\)) rather than its completion time (\(C_p\)) is therefore more indicative of respecting the appointment priorities.

In our model, the number of stations is a decision variable, and we assume that the clinic has a sufficient number of stations to accommodate the appointments subject to constraints imposed on other decision variables. Nevertheless, as we will demonstrate in Sect. 4, the model can be used by fixing the number of stations to a constant value. This will compromise the objective criteria, if not rendering the model infeasible for the given set of patients. We further assume that the cost of stations is insignificant; therefore, we do not include it among the objective criteria. The patient stays at the same station during the entire drug administration appointment (setup and monitoring). In the first timeslot of the appointment, one nurse prepares the patient and sets the station up. Thereafter, a nurse monitors the patient; that nurse may simultaneously monitor up to M patients who are receiving treatment. During both setting up and monitoring of each patient, only one nurse is assigned for the task. Thus, at every moment a nurse who is not taking a coffee or lunch break can set up only one station or monitor only up to M patients—but not both at the same time. This requirement is a hard constraint, in contrast to soft constraints, which are preferences that could be violated to some extent.

For the intended drug administration schedule, the clinic can choose any number of nurses from a set of N nurses who are affiliated with the clinic. We assume that on the intended day the remaining nurses of the set can be assigned to other departments of the hospital or other oncology clinics under a pooling contract. Hence, there is flexibility in adjusting the nursing FTE based on the set of patients planned for the day.

2.1 Nurse assignment

In our model, strictly speaking, an assignment \({\mathscr {A}}_a\) is a subset of the opening hour timeslots of the clinic, \({\mathscr {A}}_a \subseteq \{1, \ldots , T\}\), where the assigned nurse is available for the setup and monitoring tasks. For simplicity, we refer to the assignment by its index a. During the timeslots that are not in an assignment, the assigned nurse is either on a coffee or lunch break or not administering drugs in the clinic. Thus, numerous assignments can be defined over the opening hours. An assignment can be specified by a T-element binary vector. The ones specify the timeslots that the nurse can set up or monitor. We assume that A different assignments are defined for the day. Each assignment is specified in a row of the binary matrix \({\mathbf {H}}_{A \times T} = [h_{a,t}]_{A \times T}\) that is an input to the model and its elements \(h_{a,t}\) are defined as follows:

$$\begin{aligned} h_{a,t} = \left\{ \begin{array}{ll} 1, &{} \quad {\text {there can be a task (setup or monitor) on assignment }} a {\text { at timeslot }} t \\ 0, &{} \quad {{{\text {otherwise}}}} \end{array} \right. \end{aligned}$$

Each row in \({\mathbf {H}}_{A \times T}\) is unique and has to be effectively different from the other assignment vectors. On the one hand, having variety among assignments gives more flexibility in managing the problem with respect to time criteria, e.g., deferring time. On the other hand, with more assignments the problem becomes computationally intractable. Any of the A assignments may be chosen for any of the N nurses. However, no nurse can get more than one assignment. If \(T_{{{\text {FTE}}}}\) timeslots of work, i.e., excluding breaks, is one FTE, then a 1.0 FTE assignment has \(T_{{\text {FTE}}}\)ones in its corresponding row in \({\mathbf {H}}_{A \times T}\). Thus, for the FTE amount of assignment a, we can write the following:

$$\begin{aligned} {{\text {FTE}}}_a {:}{=}\frac{1}{T_{{\text {FTE}}}}\sum \limits _{t=1}^{T} h_{a,t}; \quad a = 1, \ldots , A \end{aligned}$$

Hence, the total number of FTEs assigned on the intended day can be written as follows:

$$\begin{aligned} \sigma _{{\text {FTE}}} {:}{=}\sum \limits _{a=1}^{A} {{\text {FTE}}}_a n_a = \frac{1}{T_{{\text {FTE}}}}\sum \limits _{a=1}^{A} \sum \limits _{t=1}^{T} h_{a,t} n_a \end{aligned}$$

where \(n_a\) is the number of nurses who get assignment a, and \(\sum _{a=1}^A n_a \leqslant N\).

In general, the assignment matrix \({\mathbf {H}}_{A \times T}\) can be an arbitrary \(A \times T\) binary matrix. Let g be the greatest common divisor among the number of ones in each row, i.e., among the total working timeslots available in each assignment:

$$\begin{aligned} g {:}{=}{{\text {gcd}}}(T_{{\text {FTE}}} {{\text {FTE}}}_1, \ldots , T_{{\text {FTE}}} {{\text {FTE}}}_A) \end{aligned}$$

Then, each \({{\text {FTE}}}_a\) can be expressed as an integer multiple of \(\Delta {{\text {FTE}}} {:}{=}g/T_{{\text {FTE}}}\). Moreover, for every given instance of a patient set, there are a minimum number of FTEs needed on the day for a feasible solution: \(\sigma _{\text {FTE,min}}\). Hence, in terms of number of FTEs, the search space can be partitioned into \(1+(N-\sigma _{\text {FTE,min}}) / \Delta {\hbox {FTE}}\) discrete values ranging from \(\sigma _{\text {FTE,min}}\) to N for the number of FTEs assigned on the day:

$$\begin{aligned} \sigma _{{\text {FTE}}} \in \left\{ \sigma _i \bigg | \sigma _i = \sigma _{\text {FTE,min}} + i \cdot \Delta {\hbox {FTE}}; \ i = 0, 1, \ldots , (N-\sigma _{\text {FTE,min}}) / \Delta {\hbox {FTE}} \right\} \end{aligned}$$

With more assignments, i.e., more rows in \({\mathbf {H}}_{A \times T}\), the optimization problem becomes larger and possibly intractable when there are several other criteria besides the nurse full-time equivalent assigned to the schedule. Hence, the assignments should be carefully defined to have enough variety for flexible and efficient use of the nursing capacity with fewer rows in \({\mathbf {H}}_{A \times T}\). To this end, it is important to have a large quantized FTE difference, \(\Delta {\hbox {FTE}}\), among assignments so that there are few discrete values for \(\sigma _{{\text {FTE}}}\) in its partitioning. This can be achieved by having the FTE of each assignment equal to a multiple of a value significantly greater than \(1/T_{{\text {FTE}}}\), e.g., \(\Delta {\hbox {FTE}} = 0.2\) FTE or 0.5 FTE.

For example, let us assume that \(N=10\) nurses are affiliated with a clinic that is open 9 h per day (36 timeslots, 15 min each), and the coffee and lunch breaks during the day are 1 h in total. Thus, one full-time equivalent of work is 8 h, i.e., \(T_{{\text {FTE}}}=32\) timeslots. We further assume that for a certain batch of patients, \(\sigma _{\text {FTE,min}}=6.5\) FTE and each assignment has one of the three durations: 32 timeslots (1 FTE), 24 timeslots (0.75 FTE), or 16 timeslots (0.5 FTE). In this case, we have \(g={\hbox {gcd}}(32,24,16)=8\) timeslots, \(\Delta FTE=g/T_{{\text {FTE}}}=8/32=0.25\) FTE. Thus, the search space is partitioned into \(1+(10-6.5)/0.25=15\) distinct values in terms of FTE to be assigned on the day.

2.2 Decision variables and the station assignment rule

The overall search space of the problem has six dimensions: patient, nurse, station, time, assignment, and task (setting up or monitoring). However, in order to reduce the complexity of problem formulation, we eliminate two dimensions (indexes). First, we note that setting up and monitoring are the only two tasks, and when a setup takes place, the remaining timeslots of the corresponding appointment are used for monitoring. Thus, rather than which task, it suffices to know when setups occur, i.e., the timeslots at which appointments start. Second, since all stations are identical, without loss of generality, we define a station assignment rule (SAR): among appointments starting at the same time, a lower indexed patient is placed at a lower indexed vacant station. This rule lets us discard the station index from the decision variables. We thus define the decision variables with indexes for patients, nurses, timeslots, and assignments:

$$\begin{aligned} x_{p,n,t}= & {} \left\{ \begin{array}{ll} 1, &{} \quad {\text {nurse }} n {\text { takes care of patient }} p {\text { at timeslot }} t \\ 0, &{} \quad {{\text {otherwise}}} \end{array} \right. \\ y_{p,n,t}= & {} \left\{ \begin{array}{ll} 1, &{} \quad {\text {nurse }} n {\text { sets-up a station for patient }} p {\text { at timeslot }} t \\ 0, &{} \quad {{\text {otherwise}}} \end{array} \right. \\ \delta _{p,n,t}= & {} \left\{ \begin{array}{ll} 1, &{} \quad {\text {nurse }} n {\text { starts taking care of patient }} p {\text { at timeslot }} t \\ 0, &{} \quad {{\text {otherwise}}} \end{array} \right. \\ v_{n,a}= & {} \left\{ \begin{array}{ll} 1, &{} \quad {\text {nurse }} n {\text { works on assignment }} a \\ 0, &{} \quad {{\text {otherwise}}} \end{array} \right. \\ \psi _{n}= & {} {\text {workload of nurse }} n {\text { in excess of the average workload per FTE}}\\ k= & {} {\text {number of stations needed for the schedule}} \end{aligned}$$

where taking care implies either setting up or monitoring, and \(p=1,\ldots ,P\); \(n=1,\ldots ,N\); \(t=1,\ldots ,T\); \(a=1,\ldots ,A\); \(k \in {\mathbb {Z}}^+\); \(\psi _{n} \in {\mathbb {R}}^+\), and \(v_{n,a} , \ x_{p,n,t} , \ y_{p,n,t} , \ \delta _{p,n,t} \in \mathbb \{0,1\}\). There are P appointments on the day with P setups. Each setup requires the nursing capacity of monitoring M patients. Hence, the total workload on the day in terms of the equivalent number of monitors is \(M\cdot P+\sum _{p=1}^{P}(l_p-1)\).

Since preemption is not allowed, using the solution to \(y_{p,n,t}\), the SAR, and the appointment durations, we can determine the stations at which appointments take place. The tasks are known from the solution to \(x_{p,n,t}\) and \(y_{p,n,t}\). Thus, the appointment schedule and the task schedule are uniquely and simultaneously determined with solutions to \(x_{p,n,t}\) and \(y_{p,n,t}\) in the same integer programming formulation in contrast to two separate formulations where the appointment schedule is determined before the task schedule. Two sets of variables are auxiliary; \(\psi _{n}\) and \(\delta _{p,n,t}\) will be used for controlling their corresponding objective criteria, and they are not needed for extracting the appointment and task schedules after solving the model.

2.3 Scheduling constraints

We impose thirteen sets of constraints to meet the appointment and task scheduling requirements for outpatient chemotherapy drug administration appointments. In the constraints, we use the following set of indexes for patient, nurse, and timeslot:

$$\begin{aligned} {\mathscr {P}}=\{1,\ldots ,P\}, \quad {\mathscr {N}}=\{1,\ldots ,N\}, \quad {\mathscr {T}}=\{1,\ldots ,T\}. \end{aligned}$$

To every nurse of the set of N nurses, at most one of the A assignments can be given:

$$\begin{aligned} \sum \limits _{a=1}^{A} v_{n,a} \leqslant 1 ; \quad \forall n \in {\mathscr {N}} \quad (\textit{assignment} \text { constraints)} \end{aligned}$$
(1)

An assignment must be given to a nurse who is taking care of a patient:

$$\begin{aligned} x_{p,n,t} \leqslant \sum \limits _{a=1}^{A} h_{a,t}v_{n,a}; \quad \forall p \in {\mathscr {P}},\quad \forall n \in {\mathscr {N}},\quad \forall t \in {\mathscr {T}} \quad (\textit{care providing} \text { constraints)} \end{aligned}$$
(2)

There must be one and only one station setup timeslot for each patient:

$$\begin{aligned} \sum \limits _{n=1}^{N} \sum \limits _{t=1}^{T} y_{p,n,t} = 1; \quad \forall p \in {\mathscr {P}} \quad (\textit{setup} \text { constraints)} \end{aligned}$$
(3)

No appointment can start before the patient’s ready time:

$$\begin{aligned} \text { if } \quad r_p > 0 \quad {{\text {then}}} \quad \sum \limits _{n=1}^{N}\sum \limits _{t=1}^{r_p} y_{p,n,t} = 0 \quad \forall p \in {\mathscr {P}} \quad (\textit{ready time} \text { constraints)} \end{aligned}$$
(4)

Each appointment must be completed before its due time and the closing time of the clinic (T):

$$\begin{aligned} \sum \limits _{n=1}^{N} \sum \limits _{t=1}^{T} (t+l_p-1) y_{p,n,t} \leqslant \min \{d_p,T\} ; \quad \forall p \in {\mathscr {P}} \quad (\textit{completion time} {\text { constraints}}) \end{aligned}$$
(5)

The number of appointments running at every moment cannot be more than the number of stations allocated for the day:

$$\begin{aligned} \sum \limits _{p=1}^{P} \sum \limits _{n=1}^{N} x_{p,n,t} \leqslant k; \quad \forall t \in {\mathscr {T}} \quad (\textit{station} {\text { constraints}}) \end{aligned}$$
(6)

Setting up a station takes as much nursing capacity as monitoring M patients, and the number of appointments running at every moment cannot exceed the total capacity of the assigned nurses:

$$\begin{aligned} \sum \limits _{p=1}^{P} \sum \limits _{n=1}^{N} \left[ x_{p,n,t} + (M-1)y_{p,n,t} \right] \leqslant M \sum \limits _{n=1}^{N} \sum \limits _{a=1}^{A} h_{a,t}v_{n,a} ; \quad \forall t \in {\mathscr {T}} \quad (\textit{nurses} {\text { constraints}}) \end{aligned}$$
(7)

For every nurse and at every moment, the patients being taken care of cannot exceed the individual nursing capacity:

$$\begin{aligned}&\sum \limits _{p=1}^{P} \left[ x_{p,n,t} + (M-1)y_{p,n,t} \right] \leqslant M \cdot \sum \limits _{a=1}^{A} h_{a,t}v_{n,a}; \quad \forall n \in {\mathscr {N}}, \quad \forall t \in {\mathscr {T}} \\&\quad (\textit{nursing capacity} {\text { constraints}}) \end{aligned}$$
(8)

Although the nurses constraints in Eq. (7) can be deduced from the nursing capacity constraints in Eq. (8) by summation over n, we keep both of them for later use in developing a 3-stage heuristic, where the criterion space is partitioned for the total number of nurse FTEs, \(\sigma _{{\text {FTE}}}\), assigned on the day.

For every patient, appointment timeslots must be fixed based on the setup timeslot. In other words, when a setup takes place for patient p at timeslot \(t'\), i.e., \(y_{p,\bullet ,t'}=1\) where \(\bullet\) signifies indifference, that timeslot and the next \(l_p-1\) timeslots must be assigned for care providing, i.e., \(x_{p,\bullet ,t' \leqslant t \leqslant t'+l_p-1}=1\). Therefore, if an appointment is running at t, i.e., \(x_{p,\bullet ,t}=1\), its setup must have happened between \(\max \{1, t-(l_p-1)\}\) and t. On the other hand, we can write the following:

$$\begin{aligned} \max \{1, t-(l_p-1)\} = \max \{t-(t-1), t-(l_p-1)\} = t - \min \{t-1, l_p-1\} \end{aligned}$$

Hence, the following set of constraints must hold at every moment for every patient:

$$\begin{aligned}&\sum \limits _{n=1}^{N} x_{p,n,t} = \sum \limits _{n=1}^{N} \sum \limits _{i=0}^{\min \{t-1, l_p-1\}} y_{p,n,t-i}; \quad \forall p \in {\mathscr {P}}, \quad \forall t \in {\mathscr {T}} \\&\quad (\textit{appointment period} {\text { constraints}}) \end{aligned}$$
(9)

For every patient and at every moment of the appointment, more than one nurse cannot be assigned:

$$\begin{aligned} \sum \limits _{n=1}^{N} x_{p,n,t} \leqslant 1 ; \quad \forall p \in {\mathscr {P}},\quad \forall t \in {\mathscr {T}} \quad (\textit{one-nurse} {\text { constraints }}) \end{aligned}$$
(10)

Constraint (10) limits the number of nurses assigned to a patient at every moment only for the care providing variable \(x_{p,n,t}\). Hence, every setup variable must be tied to its corresponding care variable to prevent two nurses being assigned during setups:

$$\begin{aligned} y_{p,n,t} \leqslant x_{p,n,t} ; \quad \forall p \in {\mathscr {P}}, \forall n \in {\mathscr {N}},\quad \forall t \in {\mathscr {T}} \quad (\textit{tying setup to care} {\text { constraints}}) \end{aligned}$$
(11)

One nursing FTE has the capacity for handling a maximum workload of \(T_{{\text {FTE}}}M\) monitors. A setup has an equivalent workload of M monitors. We would like to divide the total workload of the day among the nurses in proportion to their assignments’ FTEs. Let \(\varGamma\) denote the average workload per FTE on the day:

$$\begin{aligned} \varGamma {:}{=}\frac{(M-1)P+\mathop {\sum }\nolimits _{p=1}^{P}l_p}{\sigma _{{\text {FTE}}}} = \frac{(M-1)P+\mathop {\sum }\nolimits _{p=1}^{P}l_p}{\mathop {\frac{1}{T_{{\text {FTE}}}}}\ \mathop {\sum }\nolimits _{a=1}^{A}\ \mathop {\sum }\nolimits _{t=1}^{T}\ h_{a,t}n_a} = \frac{(M-1)P+\mathop {\sum }\nolimits _{p=1}^{P}l_p}{\mathop {\frac{1}{T_{{\text {FTE}}}}}\ \mathop {\sum }\nolimits _{a=1}^{A}\ \mathop {\sum }\nolimits _{t=1}^{T}\ \mathop {\sum }\nolimits _{n=1}^{N}h_{a,t}v_{n,a}} \end{aligned}$$

For a nurse n who is assigned to the clinic on the intended day, i.e., \(\sum _{a=1}^{A}v_{n,a}>0\), the amount of workload that she should get in an optimally balanced division of workload is \({{\text {FTE}}}_{a(n)}\varGamma\), where \({{\text {FTE}}}_{a(n)}\) is the amount of FTE of her assignment. We would like to minimize the extra workload that nurses get above this balanced share. Toward that end, we use the auxiliary variable \(\psi _n \in {\mathbb {R}}^+\) to indicate the workload of nurse n in excess of her balanced share:

$$\begin{aligned}&{\text {extra workload of nurse }} n := ({\text{workload of nurse }} n)\\&\quad - ({\text {balanced share of workload for nurse }} n) \\&\quad {\Delta WL}_{n} := WL_n - {{\text {FTE}}}_{a(n)}\varGamma \leqslant \psi _n \\&\sum \limits _{p=1}^{P}\ \sum \limits _{t=1}^{T}\ \left[ x_{p,n,t} + (M-1)y_{p,n,t} \right] - \frac{\left( \mathop {\sum }\nolimits _{a=1}^{A}\ {{\text {FTE}}}_a v_{n,a}\right) \left[ (M-1)P+\mathop {\sum }\nolimits _{p=1}^{P}l_p\right] }{\mathop {\frac{1}{T_{{\text {FTE}}}}}\ \mathop {\sum }\nolimits _{a=1}^{A}\ \mathop {\sum }\nolimits _{t=1}^{T}\ \mathop {\sum }\nolimits _{n=1}^{N}h_{a,t}v_{n,a}} \\&\quad \leqslant \psi _n; \quad \forall n \in {\mathscr {N}} \qquad (\textit{workload} {\text { constraints }}) \end{aligned}$$
(12)

In the objective function, we attempt to minimize the overall extra amount of workload among nurses, and we obviate the nonlinearity (in \(v_{n,a}\)) of the above constraint, using a 3-stage heuristic in Sect. 2.5.

Having the same nurse continuously take care of the patient, as much as possible, during drug administration is a safety and quality consideration (Condotta and Shakhlevich 2014). Using the following constraint, we can count the number of during-appointment nurse changes:

$$\begin{aligned}&x_{p,n,t+1} - x_{p,n,t} \leqslant \delta _{p,n,t+1}; \quad \forall p \in {\mathscr {P}},\quad \forall n \in {\mathscr {N}}; \\&\quad t = 1,\ldots , T-1 \quad (\textit{nurse change} {\text { constraints}}) \end{aligned}$$
(13)

where \(\delta _{p,n,t}\) is a binary variable that is one when a nurse starts taking care of a patient, except for the setups at the first timeslot of the schedule. In order to count the number of during-appointment nurse changes, we exclude setups in the corresponding objective function.

In the following (sub)sections, \({\mathcal {C}}_{13}\) denotes the feasible solutions of the above thirteen sets of constraints—Eqs. (1)–(13).

2.4 Scheduling objective criteria

In specialty-care services—in contrast to surgeries and primary care services—the preferences of both patients and care providers must be taken into account (Gupta and Denton 2008). In the integrated appointment and task scheduling model, we incorporate the following objectives:

  • reducing the nursing FTE

  • reducing the average deferring time of appointments for meeting the patients’ time preference and having little direct waiting time

  • reducing the workload imbalance among nurses, and

  • reducing the number of during-appointment nurse changes to keep the process safer and less confusing for both patients and nurses.

Toward that end, we consider the following multi-criterion objective vector:

$$\begin{aligned} {\text {``}}\min {\text {''}}({\mathbf {f}}) = {\text {``}}\min {\text {''}} \left( f_{{\text {FTE}}} , f_{{\text {DT}}} , f_{{\text {WL}}} , f_{{\text {NC}}} \right) \end{aligned}$$
(14)

where the four objective criteria are defined as follows:

$$\begin{aligned}&f_{{\text {FTE}}} {:}{=}\sum \limits _{n=1}^{N} \sum \limits _{a=1}^{A} {{\text {FTE}}}_a v_{n,a} \quad ({{\text {FTE}}})\\&f_{{\text {DT}}} {:}{=}\frac{1}{\mathop {\sum \nolimits _{p=1}^{P} w_p}} \sum \nolimits _{p=1}^{P} \sum \nolimits _{n=1}^{N} \sum \nolimits _{t=1}^{T} w_p \cdot \left( t-1-r_p\right) y_{p,n,t} \quad ({\text {weighted average deferring time}}) \\&f_{{\text {WL}}} {:}{=}\sum \limits _{n=1}^{N} \psi _n \quad ({\text {workload imbalance}}) \\&f_{{\text {NC}}} {:}{=}\left( \sum \limits _{p=1}^{P} \sum \limits _{n=1}^{N} \sum \limits _{t=1}^{T} \delta _{p,n,t} \right) - \left( P - \underbrace{\sum \limits _{n=1}^{N}\sum \limits _{a=1}^{A} h_{a,1}v_{n,a}}_{{\text {setups at }} t=1} \right) \quad ({\text {nurse change}}) \end{aligned}$$

We impose two priority levels by weighting deferring times in the objective function:

$$\begin{aligned} w_p = \left\{ \begin{array}{ll} w_h, &{} \quad \text { patient } p \text { has } high \text { priority} \\ 1, &{} \quad \text { otherwise } \end{array} \right. \end{aligned}$$

where \(w_h \in {\mathbb {Z}}^+ {\setminus } \{ 0 , 1 \}\).

2.5 Multi-criterion mixed integer programming

Equations (1)–(14) constitute the multi-criterion mixed integer programming (MCMIP) formulation that we consider for scheduling drug administration appointments:

$$\begin{aligned} \text {MCMIP:} \quad {\text {``}}\min {\text {''}} \left\{ \left( f_{{\text {FTE}}},f_{{\text {DT}}},f_{{\text {WL}}}, f_{{\text {NC}}}\right) \Big |{\mathcal {C}}_{13}\right\} \end{aligned}$$
(15)

This problem does not have any ideal solution in the decision space that optimizes all four criteria. The minimum number of FTEs needed (\(\sigma _{\text {FTE,min}}\)) for scheduling the drug administration appointments of a given set of patients can be found by relaxing several constraints in \({\mathcal {C}}_{13}\). Toward that end, we only have to keep the constraints pertaining to ready time, completion time, stations, nurse assignment, setup, and the monitoring capacity. The reason we can discard the nursing capacity constraint is that the nurses constraint imposes the setup and monitoring hard constraints, though in an aggregated way. Moreover, since for finding \(\sigma _{\text {FTE,min}}\) the individual nurse assignment is not needed, we can discard the nurse index n from the setup variables: \(y_{p,t} {:}{=}y_{p,\bullet ,t}\) instead of \(y_{p,n,t}\). Thus, \({\mathcal {C}}_{13}\) can be relaxed to the following six sets of constraints, the intersection of which we denote by \({\mathcal {C}}_{6A}\) (Hesaraki et al. (2019) use a set of constraints similar to \({\mathcal {C}}_{6A}\) with a fixed clinic capacity to generate appointment templates for online scheduling.):

$$\begin{aligned}&\sum \limits _{a=1}^{A} v_{n,a} \leqslant 1; \quad \forall n \in {\mathscr {N}} \quad ({{{\text {assignment}}}, {\mathcal {C}}_{6A} } )\\&\quad \sum \limits _{t=1}^{T} y_{p,t} = 1 ; \quad \forall p \in {\mathscr {P}} \quad ({{{\text {setup}}}, {\mathcal {C}}_{6A} }) \\&\quad {\text {if }} \quad r_p > 0 \quad {\text {then }} \quad \sum \limits _{t=1}^{r_p} y_{p,t} = 0; \quad \forall p \in {\mathscr {P}} \quad ({{\text {ready time}}, {\mathcal {C}}_{6A} } )\\&\quad \sum \limits _{t=1}^{T} (t+l_p-1) y_{p,t} \leqslant \min \{d_p,T\}; \quad \forall p \in {\mathscr {P}} \quad ({{\text {completion time}}, {\mathcal {C}}_{6A} }) \\&\quad \sum \limits _{p=1}^{P} \sum \limits _{t^{\prime }=\max \{1, t-l_p+1\}}^{t} y_{p,t^{\prime }} \leqslant k; \quad \forall t \in {\mathscr {T}} \quad ({{{\text {station}}}, {\mathcal {C}}_{6A} })\\&\quad \sum \limits _{p=1}^{P} \left[ (M-1)y_{p,t} + \sum \limits _{t^{\prime }=\max \{1,t-l_p+1\}}^{t}y_{p,t^{\prime }} \right] \leqslant M \sum \limits _{n=1}^{N} \sum \limits _{a=1}^{A} h_{a,t}v_{n,a}; \quad \forall t \in {\mathscr {T}} \quad ({{{\text {nurses}}}, {\mathcal {C}}_{6A}}) \end{aligned}$$

where in the last two sets of constraints \(\sum _{t^{\prime }=\max \{1,t-l_p+1\}}^{t}y_{p,t^{\prime }}\) indicates whether patient p is taken care of at t. The following two variable conversions were used to reach \({\mathcal {C}}_{6A}\) from \({\mathcal {C}}_{13}\):

$$\begin{aligned} \sum \limits _{n=1}^{N} y_{p,n,t}= & {} y_{p,t}\end{aligned}$$
(16)
$$\begin{aligned} \sum \limits _{n=1}^{N} x_{p,n,t}= & {} \sum \limits _{n=1}^{N} \sum \limits _{t'=\max \{1,t-l_p+1\}}^{t} y_{p,n,t'} = \sum \limits _{t'=\max \{1,t-l_p+1\}}^{t} y_{p,t'} \end{aligned}$$
(17)

Hence, the least number of FTEs needed for the given set of patients can be found by solving the following single objective integer program:

$$\begin{aligned} \text {IP1:} \quad \sigma _{\text {FTE,min}} {:}{=}\min \left( f_{{\text {FTE}}}\big | {\mathcal {C}}_{6A} \right) \end{aligned}$$

Although finding all nondominated points in the criterion space would be interesting from a combinatorial optimization point of view, many of them are not acceptable from an operations management perspective. For efficient use of resources, it does not make sense to use a substantial extra number of FTEs above the bare minimum needed for a feasible solution. We therefore consider up to 1.0 extra FTE above \(\sigma _{\text {FTE,min}}\) (though it can be a higher value, e.g., 2.5 FTE, at a higher computational cost with lower nurse utilization). Thus, the search space is partitioned into \(I = 1+1/\Delta {\hbox {FTE}}\) discrete values for the total number of FTEs to be considered for the intended day:

$$\begin{aligned} \sigma _{{\text {FTE}}} \in \left\{ \sigma _i \bigg | \sigma _i = \sigma _{\text {FTE,min}} + i \cdot \Delta {\hbox {FTE}}; \quad i=0, 1, \ldots , 1 / \Delta {\text{FTE}} \right\} \end{aligned}$$

where \(1 / \Delta FTE \in {\mathbb {Z}}^+{\setminus } \{0\}\) is a constant that is determined from the assignment matrix \({\mathbf {H}}_{A \times T}\) as explained in Sect. 2.1. The FTE partitions can be explored by adding the following constraint to the formulation for only one value of i at a time:

$$\begin{aligned} f_{{\text {FTE}}} = \overbrace{\sigma _{\text {FTE,min}} + i \cdot \Delta {\hbox {FTE}}}^{\sigma _i} \quad \text { where } \quad i \in \{0, 1, \ldots , I-1\} \quad ({\mathcal {F}}_i \text { constraint) } \end{aligned}$$

When searching within partition \({\mathcal {F}}_i\), the MCMIP in Eq. (15) is reduced to the following:

$$\begin{aligned} {\text {``}}\min {\text {''}}\{\left( f_{{\text {DT}}},f_{{\text {WL}}},f_{{\text {NC}}}\right) \big |{\mathcal {C}}_{13} \cap {\mathcal {F}}_i\} \quad \text { where } \quad i \in \{0, 1, \ldots , I-1\} \end{aligned}$$
(18)

Knowing the \(\sigma _i\) number of FTEs being assigned to the schedule, we can now calculate the average workload per FTE :

$$\begin{aligned} \varGamma _i = \frac{ (M-1)\cdot P + \mathop {\sum }\limits _{p=1}^{P} l_p}{\sigma _i} \end{aligned}$$

Unlike \(f_{{\text {FTE}}}\) that can be equal to only I values ranging from \(\sigma _{\text {FTE,min}}\) to N, \(f_{{\text {DT}}}\) can have one of many discrete values. The increment between consecutive values can be as small as 1/P, which corresponds to one timeslot reduction in the total deferring time of P patients. For example, for \(P=50\) patients all with normal priority (\(w_p=1\)) in a 15-min timeslot setting, the difference between two \(f_{{\text {DT}}}\) values can be as small as \(1/50\times 15\times 60 = 18\) s, which is quite insignificant in the context of deferring time. Therefore, searching over partitions of fixed \(f_{{\text {DT}}}\) is not computationally efficient. However, within an \({\mathcal {F}}_i\) partition it would be interesting to consider the criterion points with the minimum weighted average deferring time, denoted by \({\bar{\tau }}_{{\hbox {min}},i}\). We can find these points by solving the following single objective integer program:

$$\begin{aligned} \text { IP2: } \quad {\bar{\tau }}_{min,i} {:}{=}\min \left[ \left( 1\Big /{{\sum \limits _{p=1}^{P} w_p}} \right) \sum \limits _{p=1}^{P}\sum \limits _{t=1}^{T} w_p \cdot (t-1-r_p) \cdot y_{p,t} \Bigg | {\mathcal {C}}_{6A} \cap {\mathcal {F}}_i \right] \end{aligned}$$
(19)

Then, we add the following constraint to the reduced MCMIP of Eq. (18):

$$\begin{aligned} f_{{\text {DT}}} = {\bar{\tau }}_{{\hbox {min}},i} \quad \text { where } \quad i \in \{0, 1, \ldots , I-1\} \quad ({\mathcal {T}}_i \text { constraint)} \end{aligned}$$
(20)

Hence, the MCMIP is further reduced to the following bicriterion mixed integer program:

$$\begin{aligned} {\text {``}}\min {\text {''}}\{\left( f_{{\text {WL}}},f_{{\text {NC}}}\right) \big |{\mathcal {C}}_{13} \cap {\mathcal {F}}_i \cap {\mathcal {T}}_i \} \quad {\text {where}} \quad i \in \{0, 1, \ldots , I-1\} \end{aligned}$$
(21)

For solving the MCMIP in Eq. (21), we can use the weighted sum method (Ehrgott 2005) with various convex combinations of the two objective criteria as a single objective mixed integer program:

$$\begin{aligned}&\min \left\{ \left[ \beta f_{{\text {WL}}} + (1-\beta )f_{{\text {NC}}} \right] \Big | {\mathcal {C}}_{13} \cap {\mathcal {F}}_i \cap {\mathcal {T}}_i \ {\text {and}} \ 0< \beta < 1 \right\} \\&\quad {\text {where}} \quad i \in \{0, 1, \ldots , I-1\} \end{aligned}$$
(22)

We denote the convex combination by \(f_{\beta } {:}{=}\beta f_{{\text {WL}}} + (1-\beta )f_{{\text {NC}}}\).

3 Three-stage heuristic

The single objective MIP formulated in Eq. (22) finds nondominated points with the least weighted average deferring time for the chosen number of FTEs. However, even with commercial solver software, it takes a prohibitively long time to solve for realistic size problems, e.g., fifty patients or more. As a heuristic approach, we can use the solution to IP2 as an input to the MIP in Eq. (22). Thus, the setup moments (\({\hat{y}}_{p,t}\)) and the nurse assignments (\({\hat{v}}_{n,a}\)) are used as input constants instead of decision variables. Therefore, only the constraints that were not included in \({\mathcal {C}}_{6A}\) have to be considered. Those are formulated as the following set of constraints denoted by intersection \({\mathcal {C}}_{6B}\):

$$\begin{aligned}&x_{p,n,t} \leqslant \sum \limits _{a=1}^{A} h_{a,t}{\hat{v}}_{n,a} ; \quad \forall p \in {\mathscr {P}}, \forall n \in {\mathscr {N}}, \forall t \in {\mathscr {T}} \quad ( {\textit{care providing}, \ {\mathcal {C}}_{6B } }) \\&\quad \sum \limits _{p=1}^{P} \left[ 1 + (M-1){\hat{y}}_{p,t} \right] x_{p,n,t} \leqslant M \sum \limits _{a=1}^{A} h_{a,t}{\hat{v}}_{n,a} ; \quad \forall n \in {\mathscr {N}}, \forall t \in {\mathscr {T}} \quad ({\textit{nursing capacity}, \ {\mathcal {C}}_{6B } }) \\&\quad \sum \limits _{n=1}^{N} x_{p,n,t} = \sum \limits _{i=0}^{\min \{t-1, l_p-1\}} {\hat{y}}_{p,t-i} ; \quad \forall p \in {\mathscr {P}}, \forall t \in {\mathscr {T}} \quad ({\textit{appointment period}, \ {\mathcal {C}}_{6B } }) \\&\quad \sum \limits _{n=1}^{N} x_{p,n,t} \leqslant 1 ; \quad \forall p \in {\mathscr {P}}, \forall t \in {\mathscr {T}} \quad ({\textit{one-nurse}, \ {\mathcal {C}}_{6B } }) \\&\quad \left\{ \sum \limits _{p=1}^{P}\ \sum \limits _{t=1}^{T}\ \left[ 1 + (M-1){\hat{y}}_{p,t} \right] x_{p,n,t}\right\} - \left( \sum \limits _{a=1}^{A}\ {{\text {FTE}}}_a{\hat{v}}_{n,a}\right) \varGamma _i \leqslant \psi _n ; \quad \forall n \in {\mathscr {N}} \quad ({\textit{workload}, \ {\mathcal {C}}_{6B } }) \\&\quad x_{p,n,t+1} - x_{p,n,t} \leqslant \delta _{p,n,t+1} ; \quad \forall p \in {\mathscr {P}}, \forall n \in {\mathscr {N}}; \quad t=1, \ldots , T-1 \quad ({\textit{nurse change}, \ {\mathcal {C}}_{6B } }) \end{aligned}$$

Thus, the following single objective MIP is the last stage of the 3-stage heuristic for solving the single objective MIP in Eq. (22):

$$\begin{aligned} \text {MIP3:} \quad \min \left\{ f_{\beta } \Big | {\mathcal {C}}_{6B} \ {\text {and}} \ 0< \beta < 1 \right\} \end{aligned}$$
(23)

where \(f_{{\text {NC}}}\) and consequently \(f_\beta\) are in terms of \({\hat{v}}_{n,a}\) instead of \(v_{n,a}\).

The setup decision variables \(y_{p,t}\)—and the constant values \({\hat{y}}_{p,t}\) for that matter—do not include the nurse information. Thus, in \({\mathcal {C}}_{6B}\) it is implicitly assumed that when the setup for patient p takes place at t, i.e., \({\hat{y}}_{p,t}=1\), nurse n who is taking care of the patient, i.e., \(x_{p,n,t}=1\), is also doing the setup. Hence, the tying setup to care constraints in Eq. (11) are not needed in \({\mathcal {C}}_{6B}\).

The Venn diagram of feasible solution sets (intersections) subject to various sets of constraints is demonstrated in Fig. 5. The area between the dashed lines indicates the FTE partition, and the squares correspond to feasible solutions in \({\mathcal {C}}_{13} \cap {\mathcal {F}}_i \cap {\mathcal {T}}_i\). The intersection \({\mathcal {C}}_{13} \cap {\mathcal {F}}_i \cap {\mathcal {T}}_i\) is denoted by \(\cap {\mathcal {T}}_i\) in Fig. 5. Commercial solvers only give one optimal solution to IP2 in Eq. (19). In the Venn diagram, this corresponds to \({\mathcal {C}}_{6B}\) being limited to the small area shown within the \(\cap {\mathcal {T}}_i\) square. If all alternative optima of IP2 could be explored, then MIP3 could find nondominated points on the Pareto frontier of \(f_{{\text {WL}}}\) and \(f_{{\text {NC}}}\), which have \(\min (f_{\beta })\).

Fig. 5
figure 5

Venn diagram of various feasible solution sets and their FTE partitions (\({\mathcal {F}}_i\)), where \(\cap {\mathcal {T}}_i\) denotes \({\mathcal {C}}_{13} \cap {\mathcal {F}}_i \cap {\mathcal {T}}_i\)

Full size image

The 3-stage heuristic for finding criterion points with minimum weighted average deferring time for a chosen number of FTEs is shown in Fig. 6. The value of \(\sigma _{\text {FTE,min}}\) is found in IP1 and used in the \({\mathcal {F}}_i\)-constraint of IP2. In IP2, the solution to the setup variables \(y_{p,t}\) and the assignment variables \(v_{n,a}\) is found. Those are used as constants \({\hat{y}}_{p,t}\) and \({\hat{v}}_{n,a}\) in MIP3, and they correspond to \({\bar{\tau }}_{min,i}\). The heuristic solutions can be used as initial solutions for warm starting the solver when solving the single objective MIP in Eq. (22).

Fig. 6
figure 6

Three-stage heuristic to find criterion points with shortest weighted average deferring time for a fixed number of FTEs

Full size image

4 Numerical illustration

The computations of our numerical experiments were carried out on a 64-bit computer with Windows 10, Intel processor i7-6700HQ (2.6-3.5 GHz, 6 MB cache, 4 cores), and 16 GB of RAM. For solving the MIP models, we used Gurobi 7.0.2 in the Julia programming language using its mathematical programming package JuMP (Dunning et al. 2017).

Our numerical experiments are designed for an example clinic that is open 9 h per day from 8:00 AM to 5:00 PM. Each nurse takes a 15-min coffee break in the morning around 10:00 AM, a 30-min lunch break around 12:30, and a 15-min coffee break in the afternoon around 3:00 PM. The timeslots are 15 min long. Throughout our numerical experiments, duration of the opening hours is \(T = 36\) timeslots, and timeslots 8, 9, 17, 18, 19, 20, 28, and 29 are designated for coffee and lunch breaks. These are demarcated by six vertical lines in the plotted appointment and task schedules.

To limit the number of assignments while including enough variety among them, we consider a morning half FTE assignment, an afternoon half FTE assignment, and a one FTE assignment as shown in Fig. 7. Since every nurse takes a break in one half-period of each break, there are \(A=2\times 3=6\) assignments defined with the FTEs and breaks listed in Table 1. The total working period of each assignment defined in Fig. 7 and Table 1 is a multiple of \(\Delta {\hbox {FTE}} = 0.5\) FTE, where \(T_{{\text {FTE}}} = 32\). Hence, we only have to consider \(I=3\) partitions of \(\sigma _{{\text {FTE}}}\) to cover a 1.0 FTE range above \(\sigma _{\text {FTE,min}}\):

$$\begin{aligned}&\sigma _0 = \sigma _{\text {FTE,min}} \\&\sigma _1 = \sigma _{\text {FTE,min}} + 0.5 \\&\sigma _2 = \sigma _{\text {FTE,min}} + 1.0 \end{aligned}$$

We also report criterion points for \(\sigma _{max} = N\), besides these three values.

Fig. 7
figure 7

Time periods of 0.5 FTE and 1.0 FTE assignments. The gray timeslots are coffee and lunch breaks

Full size image
Table 1 FTE and break period of assignments
Full size table

The \({\mathcal {F}}_i \cap {\mathcal {T}}_i\) points are demonstrated with filled circles in Fig. 8. These points are nondominated for the Pareto frontier of \((f_{{\text {WL}}},f_{{\text {NC}}})\). Since there are many feasible \(f_{{\text {DT}}}\) points, they are represented by continuous lines in the figure. The thick portions of the lines correspond to weakly nondominated points for the Pareto frontier of \((f_{{\text {WL}}},f_{{\text {NC}}})\).

Fig. 8
figure 8

FTE and weighted average deferring time plane

Full size image

In our numerical experiments, the patient set of the input instance corresponds to the relative frequency histogram of drug administration appointment durations at Amphia Hospital in Breda, The Netherlands, as illustrated in Fig. 9 (Menting 2014). In this section, we assume that for each patient the appointment duration has a categorical distribution illustrated in Fig. 9.

Fig. 9
figure 9

Multinomial distribution of patients’ appointment durations with probabilities equal to the relative frequencies, e.g., \({\mathbb {P}}(l=8)=0.21\)

Full size image

The patients are numbered in ascending order of their appointment durations. The number of nurses affiliated with the clinic is \(N=15\) nurses (A, B, ..., O) for an instance with \(P=60\) patients. Patients \(p = 1, 4, 5, 11, 35, 37, 45, 49\) are given high priority with \(w_h=10\). All patients have zero ready times and infinite due times, except for the following four patients:

$$\begin{aligned}&(r_4,d_4) = (16,30) \ \text { for } \ p=4 \ \text { with } \ l_4=1 \\&(r_{11},d_{11}) = (21,\infty ) \ \text { for } \ p=11 \ \text { with } \ l_{11}=4 \\&(r_{35},d_{35}) = (9,33) \ \text { for } \ p=35 \ \text { with } \ l_{35}=12 \\&(r_{37},d_{37}) = (4,32) \ \text { for } \ p=37 \ \text { with } \ l_{37}=12 \end{aligned}$$

In the weighted sum of the objective functions for workload and nurse change, we use five values for \(\beta\): 0.01, 0.10, 0.50, 0.90, and 0.99.

The criterion points found using the 3-stage heuristic outlined in Sect. 3 are listed in Table 2. The first two stages of the heuristic are solved to optimality. IP1 is solved in a fraction of a second, and IP2 is solved within 5 min for each of the twenty cases in Table 2. MIP3 was given a relative MIP optimality gap tolerance of 5%, and the corresponding solve time is reported in the last column of Table 2. k, \(\varGamma _i\), \(f_{{\text {FTE}}}\), and \(f_{{\text {DT}}}\) are independent of \(\beta\). Increasing the number of FTEs (greater i) reduces the weighted average deferring time of appointments and the average workload per FTE while requiring more stations in the schedule. With greater \(\beta\), the task schedule has less workload imbalance as it is given a greater weight in the bicriterion objective function \(f_{\beta }\).

Table 2 Criterion points found using the 3-stage heuristic for the set of sixty patients
Full size table

Figure 10 shows appointment and task schedules for a set of \(P=60\) patients with the histogram of appointment durations shown in Fig. 11. The total workload of the patient set is equivalent to 850 monitors. However, the number of stations is fixed to \(K'=19\), which is the minimum number that is feasible for the given set of patients. This is to illustrate the impact it has on the criteria when it is an input rather than an output of the model. The solution is found for minimum weighted average deferring time with the least number of FTEs (\(\sigma _{\text {FTE,min}}=10.0\) FTEs if \(k=K'=19\)) using the 3-stage heuristic outlined in Sect. 3 with \(i=0\) and \(\beta =0.50\). IP1, IP2, and MIP3 were solved in 0.27, 1.03, and 4940 s and with MIP gaps of 0%, 0%, and 4.52%, respectively. The eight high-priority appointments are shown in dark gray in the appointment schedule. The criterion point for this solution is \((f_{{\text {FTE}}},f_{{\text {DT}}},f_{{\text {WL}}},f_{{\text {NC}}}) = (10.0,5.3,0.0,105)\). With \(\sigma _0=10.0\) FTEs, the average workload per nurse on the day is \(\varGamma _0=850/10.0=85.0\) monitors. In the task schedule, the workload of each of the ten nurses is 85 monitors. Five nurses (C, F, H, I, and O) are not assigned drug administration at the clinic on that day. More than half of the nurse changes in this schedule (57 out of 105) are because of the coffee and lunch breaks and cannot be avoided. With an average appointment duration of 11.17 timeslots or 167.5 min, a nurse change takes place on average after \(167.5/(105/60) \approx 96\) min of continuous care by the same nurse. For example, the 7-h appointment of patient-60 at station-19 has only six nurse changes while three of them are because of the breaks of nurses N and M.

Fig. 10
figure 10

Appointment schedule and task schedule for the set of sixty patients that matches the relative frequency histogram of chemotherapy drug administration appointment durations at a Dutch hospital. Patient-13 is scheduled at station-7 with the setup at \(t=1\) by nurse-L and monitored by nurse-K for the remainder of the appointment (until \(t=6\))

Full size image

Compared with the third case in Table 2, which has the same \(i=0\) and \(\beta =0.5\) setting but solved with a variable number of stations (k not fixed to a \(K'\)), the solution in Fig. 10 with 15 fewer stations uses 1.5 more nurse FTE and has 2.5 timeslots (38 min) longer weighted average deferring time. Alternatively, we can look at the difference between relaxing and constraining the number of stations from the perspective of the weighted average deferring time: while even using 0.5 FTE less nursing capacity, the weighted average deferring time can be 3.7 timeslots (56 min) shorter in the 13th case of Table 2.

For the next experiment, we drew 30 random sets of \(P=40\) appointment durations from the multinomial distribution in Fig. 9. We set the number of nurses affiliated with the clinic at \(N=9\). Besides MIP3, we gave a relative MIP optimality gap tolerance of 5% to IP2 as well. IP1 was solved to optimality within one second, and the MIP gap of IP2 dropped below 5% within 5 s in all cases. In Table 3, we report the average result of applying the 3-stage heuristic to these 30 random sets. The same trend pattern as shown in Table 2 is found in Table 3. Increasing i reduces \(f_{{\text {DT}}}\) and \(\varGamma _i\) while requiring more stations. With greater \(\beta\), \(f_{{\text {WL}}}\) becomes less as it is given a greater weight in \(f_{\beta }\).

Fig. 11
figure 11

Histograms of the instance of \(P=60\) patients used in Table 2 and Fig. 10

Full size image
Table 3 Criterion points averaged over 30 random sets of \(P=40\) after applying the 3-stage heuristic with \(N=9\)
Full size table

In order to evaluate the performance of our heuristic, we attempted to solve the MIP in Eq. (22) with \(i=0\) and \(\beta = 0.5\) (case-3 in Table 2) for the 60-patient set of Fig. 11. After 12 h, the solver could not find a feasible solution for \(\min \left\{ f_\beta | {\mathcal {C}}_{13} \cap {\mathcal {F}}_0 \cap {\mathcal {T}}_0 \ \text { and } \ \beta = 0.5 \right\}\). Next, we repeated the same experiment, but with a warm start. We loaded the solver with an initial feasible solution generated by our heuristic. However, we set the time limit for MIP3 at only 60 s, which resulted in \(f_{\beta }=62\) with a MIP3 gap of 21.8%. After 1398 s of solve time, the MIP gap for Eq. (22) was 65.1% with an incumbent of 92 and best lower bound 32.1 (the version of JuMP that we used does not pass the constant part of the objective, \(-(1-\beta )P\), to the solver; hence, the difference of \(92-62=30\) between the solver’s reported incumbent and \(f_{\beta }\)). After 12 h, it could only reach a MIP gap of 63.5% with an incumbent of 92 and best lower bound 33.6. The results are summarized in Table 4.

Table 4 Criterion points found by solving the MIP in Eq. (22) for \(i=0\) and \(\beta =0.5\) and the set of sixty patients
Full size table

5 Generalizability of the model

In this section, we give a few examples of how the model can be adjusted to meet specific requirements of a clinic. We have assumed that drug administration can begin with only one timeslot of setup for each patient. However, if an appointment is expected to need longer than the default setup, the model can be simply adjusted by adding a constraint to schedule a double duration setup. For this, an imaginary patient with an appointment duration of only one setup (no monitoring) can be scheduled right before the intended patient and with the same nurse. For example, imaginary patient-1017 with \(l_{1017}=1\) would be scheduled right before patient-17 who needs a double setup duration by imposing the following set of constraints:

$$\begin{aligned} y_{1017,n,t} = y_{17,n,t+1}, \quad \text { for } \quad t = 1, \ldots , T-1; \ n = 1, \ldots , N \end{aligned}$$

Primary nurse assignment can be done by simply removing decision variables with unacceptable nurse–patient pairs (n, p), or setting them equal to zero in the constraints:

$$\begin{aligned} x_{p',n',t} = 0 , \quad \text { for } \ (p',n') \notin \{(p,n) | n \ \text { is the primary nurse of patient } \ p\} \end{aligned}$$

When the skill level of a nurse is not enough to treat a patient, that combination can be excluded in a similar way. However, if these constraints render the model infeasible, similar to the part-time nurse addition used by Liang and Turkcan (2016), N can be increased to the smallest value for which the model is feasible.

If it is strictly required to have the same nurse assigned to the patient for the entire appointment, the model can be adjusted by constraints similar to the following while removing the nurse change constraints and criterion from the model:

$$\begin{aligned}&\sum _{t=1}^{T} x_{p,n,t} = l_pu_{p,n} , \quad \forall p \in {\mathscr {P}}, \forall n \in {\mathscr {N}}: u_{p,n} \in \{0,1\}\\&\quad (\text {1 if }n\text { takes care of }p; 0\text { otherwise})\\&\quad \sum _{n=1}^{N} u_{p,n} = 1 , \quad \forall p \in {\mathscr {P}} \end{aligned}$$

To incorporate patient acuity levels \(c_p\) in the model, we can modify the nursing capacity and workload constraints (nurses, C6A), (nursing capacity, C6B), and (workload, C6B) as follows:

$$\begin{aligned}&\sum \limits _{p=1}^{P} c_p \left[ (M-1) y_{p,t} + \sum \limits _{t^{\prime }=\max \{1,t-l_p+1\}}^{t}y_{p,t^{\prime }} \right] \leqslant M \sum \limits _{n=1}^{N} \sum \limits _{a=1}^{A} C_nh_{a,t}v_{n,a} ; \quad \forall t \in {\mathscr {T}}\\&\quad \sum \limits _{p=1}^{P} \left[ 1 + (M-1){\hat{y}}_{p,t} \right] c_px_{p,n,t} \leqslant C_nM \sum \limits _{a=1}^{A} h_{a,t}{\hat{v}}_{n,a} ; \quad \forall n \in {\mathscr {N}},\quad \forall t \in {\mathscr {T}}\\&\quad \left\{ \sum \limits _{p=1}^{P}\ \sum \limits _{t=1}^{T}\ \left[ 1 + (M-1){\hat{y}}_{p,t} \right] c_p x_{p,n,t}\right\} - \left( \sum \limits _{a=1}^{A}\ {{\text {FTE}}}_a{\hat{v}}_{n,a}\right) \varGamma _i' \leqslant \psi _n ; \quad \forall n \in {\mathscr {N}} \\&\quad \varGamma _i' = \frac{\mathop {\sum }\nolimits _{p=1}^{P} c_p\cdot (M+l_p-1)}{\sigma _i} \end{aligned}$$

where \(C_n\) is a given factor indicating the maximum amount of acuity that nurse n can handle at a timeslot, and \(\sigma _i\) is the number of FTEs assigned to the schedule.

Similar to Liang and Turkcan (2016), the start and end work time of a nurse \(n'\) can be set to given values by fixing her assignment to \(a'\) that has those start and end times: \(v_{n',a'}=1\).

6 Concluding remarks

In this paper, we have developed a multi-criterion mixed integer programming (MCMIP) model for the problem of scheduling drug administration appointments in outpatient chemotherapy where nurses are simultaneously shared among patients. In offline scheduling, we can integrate task scheduling with appointment scheduling. Hence, we can adjust the number of nurse FTEs of the intended day based on the set of appointment requests and the desired performance criteria. This helps to maintain high nurse utilization and control workload levels, despite variations in the number and workload of requests.

In the multi-step process shown in Fig. 2, we focus on appointment and task scheduling for drug administration while incorporating the strict time requirements of the prior steps into the model. The objective criteria pertain to various stakeholders: patients, nurses, and the clinic. Chemotherapy patients prefer to have their drug administration as early during the day as possible (Lau et al. 2014). Our model determines the nursing capacity and the number of stations required for scheduling drug administration appointments as early during the day as possible. It also reaches a trade-off between the least amount of workload imbalance among nurses and the least number of nurse changes during appointments. For realistic size sets of patients and nurses, the problem is too large to solve for nondominated points of the formulated MCMIP. We have therefore developed a 3-stage heuristic for finding criterion points that have a minimum weighted average deferring time of appointments for a chosen number of nurse FTEs.

6.1 Managerial implications

The time requirements of pharmacy and oncologists can be incorporated into the model via the ready times, due times, and priorities. We can consider a baseline in which all appointments have zero ready times and normal priorities. This baseline setting corresponds to an average start time for the appointments. By adjusting the ready times and weights, some start times can be shifted according to the oncologists’ and the pharmacy’s requirements. Otherwise, the patients’ direct waiting time may be long. For example, if the deferring time of a high priority appointment—for which the oncologist or the pharmacy has less flexibility—is six timeslots, either the oncologist and the pharmacy should start six timeslots later than their required time, or the patient must wait for 90 min in between. Besides helping to impose the time requirements of prior steps, the due time is an option to facilitate follow-up activities on the same day. In general, we assume that for the majority of appointments on the intended day, there is flexibility for scheduling the three prior steps based on the start times of drug administration appointments, i.e., without time requirements. If the options (ready time, priority weight, and due time) are used for too many appointments, a feasible solution cannot be found. In such cases, the model may be formulated as a weighted constraint satisfaction or fuzzy constraint problem (e.g., Kaymak and Sousa 2003; Cooper 2003).

In order to efficiently use the chemotherapy nursing capacity, the pharmacy has to prepare the drugs of as many appointments as possible before the patient arrives and allocate a sufficient number of servers (technicians or robots) based on the setup moments of the remaining appointments. Otherwise, the pharmacy’s service rate should be incorporated into the constraints of the MCMIP. This will in general result in less efficient use of the nursing resources. Moreover, for the laboratory and oncologist steps, the clinic may adopt a mixed policy using both same day and day before visits among patients. This is plausible, because on the one hand, according to prior studies in the literature (Dobish 2003; Griffin 2014; Cook and Towler 2009; Holmes et al. 2010), scheduling those two steps on the day before drug administration improves patient flow and patient satisfaction. On the other hand, some patients would prefer to have all steps on the same day as drug administration, e.g., because of transport limitations (Lau et al. 2014). Thus, a mixed policy has more flexibility for controlling the patients’ waiting times with better utilization of the nursing resources.

Although we assume that the clinic has the flexibility of choosing from a pool of resources (nurses and stations), both nurse FTE and the number of stations can be fixed as input parameters instead of variables; however, that may compromise the objective criteria if not rendering the model infeasible for the given set of patients. Also, the heuristic can be run once with the number of chairs fixed to the clinics capacity and once relaxed. The schedule with the fixed number of chairs (K) is used for the current batch of patients. The number of chairs (k) and KPIs resulting from the relaxed model are kept as a benchmark to review the clinic’s performance at a tactical level for planning and capacity adjustments. Thus, the model provides information for adjusting the capacity level in the next mid-term plan of the clinic, i.e., if there is recurrent discrepancy between the clinic’s capacity and the number of FTEs or stations determined by the model.

Further constraints can be added for imposing nurse and patient preferences. For example, some assignments can be excluded for some nurses, some assignments can be fixed for some nurses, and the appointment start time can be fixed for some patients. Of course, these extra constraints compromise the optimal solution if not rendering the problem instance infeasible.

For reliable schedules, the appointment durations should be based on data of actual infusion durations in the past, rather than those indicated in the protocols or data of scheduled appointments in the past. Accordingly, some buffer time can be calculated and added to the end of each appointment. To further mitigate the impact of uncertainties, patients who are likely to have allergic reactions that may prolong the infusion duration can be scheduled for the last appointments at stations. The parameter T can be set to one or two timeslots before the normal end of working hours, to avert overtime. Such reliability measures can be gradually taken by experience and data collection while adjusting the clinic’s capacity at a tactical level based on the information acquired using the integrated model.

6.2 Limitations and future research

Since minimizing the weighted average deferring time does not depend on the nurses assigned to the tasks, we could eliminate the nurse index from the setup binary variables (\(y_{p,n,t} \rightarrow y_{p,t}\)) in IP2. However, in order to minimize the workload imbalance or the number of nurse changes, we need to keep the nurse index of the decision variables, which makes the problem prohibitively large to solve within a comparable time limit. Hence, devising efficient heuristic methods to find criterion points that have fewer nurse changes or less workload imbalance for a desired number of FTEs than our 3-stage heuristic, are interesting follow-up research problems. Besides heuristic approaches, it would be interesting to devise large-scale exact methods for finding nondominated points that have a chosen number of FTEs.

We consider a proactive operational model (Hulshof et al. 2012; Hesaraki 2019). In follow-up research, reactive operational countermeasures, such as rescheduling policies, can be devised to handle uncertainties, e.g., delays.

Some infusion centers offer services for treatments other than chemotherapy as well, e.g., immunotherapy, rheumatherapy, ferrotherapy, and blood transfusion (Hesaraki 2019). Moreover, there are other types of services and processes where human resources can be simultaneously shared among multiple jobs, and they can be modeled with a similar station–setup–monitor setting. Examples include kidney dialysis, blood donation, computer-based standardized tests, and manufacturing. The results of this paper have the potential to improve the scheduling of those types of jobs as well.