Balance in resource allocation problems: a changing reference approach

Abstract

Fairness is one of the primary concerns in resource allocation problems, especially in settings which are associated with public welfare. Using a total benefit-maximizing approach may not be applicable while distributing resources among entities, and hence we propose a novel structure for integrating balance into the allocation process. In the proposed approach, imbalance is defined and measured as the deviation from a reference distribution determined by the decision-maker. What is considered balanced by the decision-maker might change with respect to the level of total output distributed. To provide an allocation policy that is in line with this changing structure of balance, we allow the decision-maker to change her reference distribution depending on the total amount of output (benefit). We illustrate our approach using a project portfolio selection problem. We formulate mixed integer mathematical programming models for the problem with maximizing total benefit and minimizing imbalance objectives. The bi-objective models are solved with both the epsilon-constraint method and an interactive algorithm.

Appendices

Appendix A: Alternative formulations

Recall the alternative formulations mentioned in Sect. 2.2. These are provided in this section.

1.1 IRP alternative formulations

For IRP, alternative formulation 1 is a standard formulation that writes any total benefit value as a convex combination of the threshold values with the help of continuous variables ($\lambda$) showing these coefficients and a binary variable vector $\delta$ indicating the interval that the total benefit value belongs to. Alternative formulation 2 is similar to Alternative 1 but without the $\lambda$ variables. Finally, we provide alternative formulation 3, which is similar to the proposed variant, but handles the interval fixing variables ($y_m$s) in a different way.

IRPM alternative formulation 1

$$\begin{aligned}&\max \quad \sum _{i=1}^N b_i x_i, \quad \min \quad {{\mathrm{Imbalance}}} \\&(2),(8), (10), (13)- (19) \\&\sum _{i=1}^{N}b_i x_i = \sum _{m=1}^{ M} \lambda _mT_m \end{aligned}$$

(30)

$$\begin{aligned}&\lambda _1 \le \delta _1 \end{aligned}$$

(31)

$$\begin{aligned}&\lambda _m \le \delta _{m-1}+\delta _m \quad m=2,\ldots ,M-1 \end{aligned}$$

(32)

$$\begin{aligned}&\lambda _M\le \delta _{M-1} \end{aligned}$$

(33)

$$\begin{aligned}&\sum _{m=1}^{M-1} \delta _m=1 \end{aligned}$$

(34)

$$\begin{aligned}&\sum _{m=1}^{M} \lambda _m=1 \end{aligned}$$

(35)

$$\begin{aligned}&\alpha _{k}=\sum _{m=1}^{M-1}\delta _m \alpha _{mk} \quad \forall k \in K \end{aligned}$$

(36)

$$\begin{aligned}&\delta _m \in \left\{ 0,1\right\} \quad m=1,\ldots ,(M-1) \end{aligned}$$

(37)

$$\begin{aligned}&0\le \lambda _m \le 1 \quad m=1,\ldots ,M \end{aligned}$$

(38)

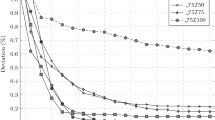
Figure 7 shows how the decision variables are set in these formulations.

Fig. 7

Indicating intervals in alternative models 1 and 2

IRPM alternative formulation 2: This formulation is the similar to Alternative 1 but without the $\lambda$ variables.

$$\begin{aligned}&\max \quad \sum _{i=1}^N b_i x_i, \quad \min \quad {{\mathrm{Imbalance}}} \\&(2),(8), (10), (13)- (19), (34),(36),(37) \\&\sum _{m=1}^{M-1}\delta _mT_m\le \sum _{i=1}^Nb_ix_i \end{aligned}$$

(39)

$$\begin{aligned}&\sum _{i=1}^Nb_ix_i \le \sum _{m=1}^{M-1}\delta _mT_{m+1} \end{aligned}$$

(40)

IRPM alternative formulation 3: This formulation is a variant of the proposed formulation, where the $y_m$ variables are set differently. We replace constraints (3)–(6) and 11 in the proposed formulation with constraints (41) and (42) and obtain the following model:

$$\begin{aligned}&\max \quad \sum _{i=1}^N b_i x_i, \quad \min \quad {{\mathrm{Imbalance}}} \\&(2), (7), (8), (10), (12)-(19) \\&y_m \le 1-\dfrac{T_{m+1}-\sum _{i=1}^Nb_ix_i}{BigM} \quad m=1,\ldots ,(M-2) \end{aligned}$$

(41)

$$\begin{aligned}&\dfrac{\sum _{i=1}^Nb_ix_i-T_{m+1}}{BigM}\le y_m \quad m=1,\ldots ,(M-2) \end{aligned}$$

(42)

where $BigM=\max _{m}\{T_{m+1}, TB-T_{m+1}\}$.

1.2 MRP alternative formulations

MRPM alternative formulation 1

MRP alternative formulation 1 is the modified version of Alternative 1 for the IRPM, for the moving reference case. For MRP, $\alpha$ is also a convex combination of threshold proportions. Hence the same coefficient variables ($\lambda$) are used to determine $\alpha$. Alternatives 2 and 3 are the modified versions of IRP Alternatives 2 and 3 for the moving reference setting, respectively.

$$\begin{aligned}&\max \quad \sum _{i=1}^N b_i x_i, \quad \min \quad {{\mathrm{Imbalance}}} \\&(2),(8), (10), (13)- (19), (30)- (35),(37),(38) \\&\alpha _{k}=\sum _{m=1}^{M-1}(\lambda _m \alpha _{mk}) + \lambda _M \alpha _{M-1k} \quad \forall k=1,\ldots , K \end{aligned}$$

(43)

MRPM alternative formulation 2

$$\begin{aligned}&\max \quad \sum _{i=1}^N b_ix_i, \quad \min \quad {{\mathrm{Imbalance}}} \\&(2),(8), (10), (13)- (19),(34), (37), (39) ,(40) \\&\alpha _{k}=\sum _{m=1}^{M-2}\delta _m \Bigg [ \frac{(\sum _ib_ix_i-T_m)(\alpha _{m+1k}-\alpha _{mk})}{\varDelta T_m}+\alpha _{mk} \Bigg ]+\delta _{M-1}\alpha _{M-1k}\quad \forall k \in K \end{aligned}$$

To linearize the multiplication: Define new continuous variables: $h_{mi}=\delta _m\times x_i$ for all $m=1,\ldots ,M-2$ and $i=1,\ldots ,N$. Add the following constraints:

$$\begin{aligned}&h_{mi}\ge x_i+\delta _m-1 \quad m=1,\ldots ,M-2, i=1,\ldots ,N \end{aligned}$$

(44)

$$\begin{aligned}&h_{mi}\le \delta _m \quad m=1,\ldots ,M-2, i=1,\ldots ,N \end{aligned}$$

(45)

$$\begin{aligned}&h_{mi}\le x_i \quad m=1,\ldots ,M-2, i=1,\ldots ,N \end{aligned}$$

(46)

$$\begin{aligned}&h_{mi}\ge 0 \quad m=1,\ldots ,M-2, i=1,\ldots ,N \end{aligned}$$

(47)

MRPM Alternative Formulation 3

$$\begin{aligned}&\max \quad \sum _{i=1}^N b_i x_i, \quad \min \quad {{\mathrm{Imbalance}}} \\&(2),(8), (10), (12)- (28), (41) ,(42) \end{aligned}$$

Tables 5 and 6 show the comparisons of alternative formulations in terms of average and maximum solution times, for IRP and MRP models, respectively. In Table 5, it is observed that all formulations have very close solution times for smaller instances of IRP. As the problems get larger, the proposed formulation performs notably better in most settings but there is no clear winner. For $N=50$, $R=100$, $K=4$ instances, the alternative formulations failed to return solutions to some of the type B and C instances, while with the proposed formulation it was possible to solve them within the time limit. It is also clearly seen in Table 6 that alternative formulations 1 and 2 perform significantly worse than MRPM. The performances of MRPM and alternative 3, which is actually quite similar to MRPM, are comparable.

Table 5 CPU time comparison among alternative IRP models

Table 6 CPU time comparison among alternative MRP models, $N=30$

Appendix B: Solution methods

We used the well-known epsilon-constraint method to obtain exact Pareto front. Additionally, we used an interactive approach to find the most preferred solution. Both methods are provided below.

Let the generic model be:

$$\begin{aligned}&\min \quad {{\mathrm{Imbalance}}}, \quad \max \quad \sum _{i=1}^{ N} b_i x_i \\&x \in X \end{aligned}$$

where x and X denote the decision variable vector and the feasible region, respectively.

We use variable fixing rules depending on the information that we obtain at each iteration on the possible total benefit levels. We provide these rules for the original formulation. Using the same idea on alternative formulations using $\delta _m$ variables instead of $y_m$ variables is straightforward.

As another variant of the epsilon-constraint algorithm, one could fix the intervals fully at each iteration, by setting an upper bound on the total benefit defined by the next interval threshold. Then all $\alpha _k$ variables can be fixed in the model. In this case, the resulting solution may not be Pareto-optimal. Hence, at the end of the algorithm, a solution set guaranteed to include the Pareto set is found. This issue, however, could be easily handled by post-processing.

For the interactive algorithm we formulate both objectives as maximization type. Let the generic model be:

$$\begin{aligned}&\max \quad z_1(x):{{\mathrm{{Balance}}}}, \quad \quad \max z_2(x):\sum _{i=1}^{ N} b_i x_i \\&x \in X \\&{{\mathrm{{Balance}}}}={{\mathrm{{Imb}}}}^{{{\mathrm{UB}}}}-{{\mathrm{Imbalance}}} \end{aligned}$$

where x and X denote the decision variable vector and the feasible region, respectively. ${{\mathrm{{Imb}}}}^{{{\mathrm{UB}}}}$ is an upper bound on the imbalance value, we set ${{\mathrm{{Imb}}}}^{{{\mathrm{UB}}}} = \sum _ib_i$.