Abstract
Responding to emergencies in Alpine terrain is quite challenging as air ambulances and mountain rescue services are often confronted with logistics challenges and adverse weather conditions that extend the response times required to provide life-saving support. Among other medical emergencies, sudden cardiac arrest (SCA) is the most time-sensitive event that requires the quick provision of medical treatment including cardiopulmonary resuscitation and electric shocks by automated external defibrillators (AED). An emerging technology called unmanned aerial vehicles (or drones) is regarded to support mountain rescuers in overcoming the time criticality of these emergencies by reducing the time span between SCA and early defibrillation. A drone that is equipped with a portable AED can fly from a base station to the patient’s site where a bystander receives it and starts treatment. This paper considers such a response system and proposes an integer linear program to determine the optimal allocation of drone base stations in a given geographical region. In detail, the developed model follows the objectives to minimize the number of used drones and to minimize the average travel times of defibrillator drones responding to SCA patients. In an example of application, under consideration of historical helicopter response times, the authors test the developed model and demonstrate the capability of drones to speed up the delivery of AEDs to SCA patients. Results indicate that time spans between SCA and early defibrillation can be reduced by the optimal allocation of drone base stations in a given geographical region, thus increasing the survival rate of SCA patients.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, tourism in the Alps has gained increased popularity through easier access to previously untouched regions for mountaineers. Simultaneously, the number of medical incidents in mountainous regions has increased sharply (https://kurier.at/chronik/oesterreich/rekordjahr-fuer-bergrettung-8-000-menschen-geborgen/232.405.161). Under these circumstances, emergency response is quite challenging, as response teams are often confronted with severe logistics challenges and weather conditions that cause long response times for life-saving support.
Among the different sets of medical emergencies (e.g., accidents while mountain biking, climbing, rafting, etc.), sudden cardiac arrest (SCA) accounts for a remarkable proportion of lethal events. For instance, in the last 10 years 707 people died in the Austrian Alps, with 37% due to SCA representing the highest proportion of all lethal incidents (https://www.alpinesicherheit.at/data/docs/presseaussendung). The immediate stop of cardiac activity during SCA leads to a rapid collapse of all vital organ processes and further, inevitably, death if untreated. The European Resuscitation Council (ERC) provides evidence-based guidelines for the best available treatment of an SCA event, namely early recognition and call for help, immediate cardiopulmonary resuscitation (CPR), as early as possible electrical defibrillation with an automated external defibrillator (AED), professional advanced life support, and standardized post-resuscitation care (Monsieurs et al. 2015). The latter two steps in this chain of survival require well-educated emergency medical service (EMS), and their effectivity is largely dependent on the previous steps, because the EMS measures will inevitably arrive after a certain time delay. However, immediate response to an SCA event can only be provided by bystanders. According to the currently valid formula from Larsen et al. (1993), survival rates decline at a rate of approximately \(8\text {-}\)16% per minute without CPR and electrical defibrillation. If CPR and electrical defibrillation are performed properly, survival rates decline less dramatically at approximately \(3\text {-}4\)% per minute. In this context, bystander use of an AED is associated with better survival and functional outcomes (Pollack et al. 2018). Particularly, the rapid use of an AED—even without CPR—seems to be beneficial and can enhance the life expectancy of SCA patients more than twofold (Capucci et al. 2016). According to Nichol et al. (1999), early defibrillation should be performed within a time interval of 6 min as survival rates up to this threshold are nearly constant and sharply decrease if no shock is provided within 6 min. In urban areas, programs that have been established to provide bystanders quick access to AEDs in public places have led to an increased number of survivors after SCA in public locations (Investigators 2004; Weisfeldt et al. 2010). Moreover, a dense EMS network guarantees best available life support with little time delay. In urban regions, recommendations set the time between EMS notification and EMS arrival to a maximum of 20 min which is almost impossible to follow in rural areas (Bos et al. 2015). However, responding to a patient with SCA in Alpine regions is often extremely challenging due to rough terrain. Difficult access to the patient’s site may lead to long response times for mountain rescue services and even ambulance helicopters, negatively affecting the chance to survive SCA events. Obviously, a reduction of the time between the SCA event and proper treatment including AED shock therapy and CPR is the only way to increase the survival rate of patients.
An emerging technology called unmanned aerial vehicles (UAV), or drones, is regarded to overcome the time criticality to respond to such emergencies in mountainous regions. Drones are flying machines that operate autonomously or are teleoperated by ground operators (Floreano and Wood 2015). The main drone types available on the market are fixed-wing systems (comparable to a miniature plane), multirotor systems, and hybrid systems with different specifications (i.e., payload, drop-off system, range) (Custers 2016). Conventional drones run on batteries to operate their engines and need to be recharged after they run out of power. Therefore, base stations are used that allow autonomous wireless recharging without the need of active user intervention (Choi et al. 2016). Aside from military applications, drones are attracting increasing attention in commercial usage, including cargo delivery, mapping, target covering, or surveillance (Dorling et al. 2017; Di Franco and Buttazzo 2015; Murray and Chu 2015). From a logistical viewpoint, they offer the clear advantage of being able to travel to areas that are inaccessible for land-based transportation at lower cost and risk compared to traditional means of transport (e.g., helicopters) (Yildrim 2017). Recently, humanitarian organizations have also become aware of these advantages, as drones can contribute to more efficient emergency operations along the entire disaster management cycle, i.e., mitigation, preparedness, response, and recovery stages (Kakaes et al. 2015; Anbaroğlu 2019). Drones can assist in damage assessment, emergency items delivery, and search and rescue missions during the immediate response to earthquakes or avalanche events (Cui et al. 2015; Doherty and Rudol 2007; Mersheeva and Friedrich 2012; Câmara 2014).
Particularly, the drones’ capability to transport various kinds of relief items to demand locations is of major interest in this study. Recent developments in drone technology enable not only the delivery of lightweight items (i.e., vaccines, blood samples, etc.) but even AEDs of heavier weight. In this regard, the drone either delivers an attached portable AED (e.g., LifeDrone AED, see Fig. 1) or both modules are merged within one technical unit [e.g., Ambulance Drone developed by TU Delft (http://www.alecmomont.com/projects/dronesforgood/)]. In practice, AED drones are activated once an alert arrives at the emergency coordination center. The required GPS (global positioning system) coordinates are either actively transmitted by the bystander via a mobile phone app to the emergency coordination center or generated by tracking the mobile phone of the caller. The GPS data are then sent to the drone base station and processed by the defibrillator drone which departs to the patient’s site. Once the bystander receives the defibrillator drone, he/she disconnects the AED from it and starts adequate treatment. The possibility to disconnect the AED from the drone ensures that it can be transported even to forest areas where trees eventually hamper safe drone landings. With video transmission between the drone and emergency operators, the bystander is guided through the whole process of providing CPR and putting electrodes on the patient’s chest. This response system could serve as an extension of ground-based (i.e., mountain rescue service) and air ambulance. It offers the clear advantage of providing faster emergency help if needed. Hence, it has the potential to reduce the time between SCA and early defibrillation, which is essential for increasing patients’ survival rates, outcomes, and quality of life (Zègre-Hemsey et al. 2018). A well-planned network of drone base stations in a given geographical region can guarantee minimal response times (referred to as travel times in this paper) to SCA patients. Particularly, in large geographical areas for which a single-drone application would not generate beneficial outcome for the patients, an optimally allocated network of defibrillator drones is required. However, the battery capacity, which limits the range of the drones, must be considered. Motivated by exploring the potentials of drone technology to speed up life-saving support, this paper considers drones as a means to deliver AEDs in Alpine terrain and presents an integer linear program for the optimal allocation of drone base stations to minimize the travel time of defibrillator drones for providing life-saving support in the minutes after SCA.
The paper is organized as follows. First, we review related papers that present models for the optimal allocation of drones for the delivery of AEDs to SCA patients. Next, we give a problem description and introduce notations along with our model assumptions. Then, we present our optimization model and illustrate its use in an example of application. A discussion on the limitations of the study and an outlook to future research conclude the paper.
2 Related work
The presented research is built upon existing works on location allocation problems in humanitarian logistics, which have been extensively researched over the past years. A broad range of different problems, including the optimal allocation of fire stations, EMS services, or medical centers were solved using heuristic and exact algorithms. These models follow the overall objectives to minimize the total distance between the demand points and candidate facility locations, to maximize the total number of demand points covered within the distance limitations, or to minimize the worst system performance (Boonmee et al. 2017). With regard to the optimal allocation of base stations of aerial vehicles (e.g., helicopters and drones), models have been proposed by Talmar (2002), Røislien et al. (2017) and Schuurman et al. (2009). Talmar (2002) focuses on optimizing the location of three rescue helicopters in South Tyrol to be able to respond to the increasing number of skiing, hiking and climbing accidents in the region. The objectives of the developed model are to minimize the maximum or worst response time to speed up emergency operations. Another model for improved helicopter response times is presented by Schuurman et al. (2009). The authors propose a location optimization model to identify where the expansion of helicopter EMS covers the greatest population in British Columbia among those people that were under-supplied during that time period. In Røislien et al. (2017) a model to estimate optimal locations for air ambulance service in Norway is proposed. The developed maximum coverage location problem (MCLP) model maximizes the population covered within a specific service distance (or time) by optimally allocating a pre-defined number of facilities. Optimal allocation of base stations that operate drones and trucks is proposed by Chowdhury et al. (2017). The proposed model determines the optimal distribution location for drones and trucks to deliver emergency items to a set of demand locations within a disaster affected area. Therefore, the model minimizes the total location-routing cost to serve the whole region by drones and trucks.
Models that are more relevant to our study and exclusively focus on the optimization of the spatial location of defibrillator drones are presented in Pulver et al. (2016), Boutilier et al. (2017) and Pulver and Wei (2018). Boutilier et al. (2017) developed an integer optimization model to determine the number of drone base stations for reducing the historical median fire, paramedic, and police response times by 1, 2, and 3 min. Aside from identifying the optimal location of drone bases stations, the authors also seek to determine the optimal number of drones for each station. Historical data including more than 53,000 SCA events that occurred between 2006 and 2014 in the eight regions of Toronto Regional RescuNET were used to test the developed optimization model. All fire, paramedic, and police stations of the region were chosen as candidate locations for defibrillator drones. The results indicate that optimized drone networks can considerably reduce response times to provide early defibrillation. In Pulver et al. (2016) a network of defibrillator drones designed to minimize the response time to SCA in Salt Lake County is presented. The objective is to have a drone at the scene within 1 min for at least 90% of SCA incidents while also minimizing implementation costs. The developed MCLP model determines the optimal configuration of the drone network by maximizing the total demand suitably covered. The results indicate that current EMS is only capable of reaching the scene within 1 min in 4.3% of all SCA incidents whereas including drones in the response system leads to 80.1% of demand being reached within 1 min. Further, installing additional launch sites would lead to 90.3% covered demand within 1 min. Pulver and Wei (2018) is based on the model proposed in Pulver et al. (2016) and presents an extended model considering backup service provision, continuously distributed demand, and empirical medical data instead of estimated incidence rates. Based on these extensions, the authors propose a new spatial optimization model, namely the backup coverage location problem with complementary coverage. The model objective is to maximize the total amount of primary and backup coverage for demand, i.e., SCA events. The model is applied in the same setting as in Pulver et al. (2016) and generates more accurate results by mitigating representation errors in locating a network of defibrillator drones.
To the best of our knowledge, no other work could be identified that addresses the optimal allocation of base stations for defibrillator drones in equal measure as presented in this paper. Our study is unique in the sense that aforementioned papers treat defibrillator drone allocation in a purely urban environment, while we introduce this concept to mountainous regions for the first time. This setting is different compared to already discussed ones due to infrastructural and geographical barriers that need to be considered in the determination of the optimal allocation of drone base stations. In terms of base station selection, our work differs to others in the sense that we cannot use EMS stations as candidate locations due to their low availability in mountainous regions. Instead, we integrate Alpine shelters and fire rescue stations as potential drone base stations. Alpine shelters are directly available within Alpine infrastructure and the only permanently installed housing structure in such rural areas. Voluntary fire rescue stations are generally much more available in Alpine infrastructure than EMS stations, as they are also maintained in really remote areas. If an SCA patient is located close to a village, a defibrillator drone departs from a close-by fire rescue station instead of an Alpine shelter hut. Travel times from a high-altitude base station would be extremely long, resulting from the differences in altitudes. Compared to other models, we primarily ignore backup supply and argue that two SCAs in a rural area at the same time are rather unlikely to occur. However, as this case cannot be completely excluded, we also extend our model such that backup supply can be considered. Finally, we compare our approach against the conventional air ambulance system in an example of application. Other papers follow a comparison with ground-based EMS that would not fit the context of this paper.
3 Optimization approach
We now introduce the integer linear program (ILP) that we use to model and analyze the allocation of drones to base stations.
Due to the characteristics of mountainous regions, the travel times of aerial vehicles, especially drones, can differ significantly even for sites that are close in terms of latitude and longitude. Peaks and cliffs form time-consuming obstacles that the drones must overcome. Hence, the coverage of a considered region is modeled by sampling a large number of patients and calculating the point-wise distances between all patients’ sites and all possible drone base stations. The considered problem is a paradigm for the well-known simple plant location problem (SPLP) that is also referred to as uncapacitated facility location problem (UFLP) (Klose and Drexl 2005; Laporte et al. 2015). Considering the analysis presented in this work, solving an ILP (introduced in Sect. 3.2) is the method of choice for the occurring problem size. For even larger problem instances, we refer to heuristic approaches from the literature (Barahona and Chudak 2005; Goldengorin et al. 2003; Jörnsten and Klose 2016; Letchford and Miller 2014; Yigit et al. 2006).
3.1 Model parameters and assumptions
Basic parameters. Formally, the problem is defined through the following parameters:
-
A set of mcandidate locations (base stations) \({\mathcal {B}}:=\{b_1,\ldots ,b_m\}\). The coordinates of a candidate location \(b \in {\mathcal {B}}\) are given by \((x_b,y_b,z_b)\) correspond to latitude, longitude, and altitude.
-
A set of qpatient’s sites\({\mathcal {P}}:=\{p_1,\ldots ,p_q\}\). The coordinates of a patient \(p \in {\mathcal {P}}\) are \((x_p,y_p,z_p)\).
-
A travel time function\(t: {\mathcal {B}} \times {\mathcal {P}} \mapsto {\mathbb {R}}^{+}\).
-
A homogeneous fleet of sdrones that must be assigned to the base stations \({\mathcal {B}}\). Clearly, \(s \le m\).
-
A maximal travel time \(t_{\mathrm{max}}\) that cannot be exceeded.
In Table 1 we summarize the used notation.
Model assumptions. In order to allow mathematical modeling of the problem, the following assumptions are made:
-
No more than one SCA happens at any one time in the same region; therefore, no backup is needed.
-
Weather and wind conditions are good enough for the selected drone models to operate. The average wind speed in the Alps is around 9.5 m/s (http://ispacevm11.researchstudio.at/index_v.html). Both drone models considered in the subsequent study can operate under these wind conditions (Table 3). In fact, drones (and also helicopters) are not always suitable to transport AEDs as wind speeds up to 34.2 m/s are possible under stormy conditions. Therefore, alternative transport solutions must be considered (e.g., AEDs are part of mountain rescue service equipment).
-
All patients \(p \in {\mathcal {P}}\) are localized on an official hiking trail. We assume this because hiking trails are the major routes that are followed by hikers; thus, the likelihood of having SCA patients in such areas is greater compared to remote areas far away from the official hiking trail network. In comparison, more than 80% of all fall-related accidents happen on marked trails (Faulhaber et al. 2017).
-
The maximal reach (battery capacity) of the considered drone is larger than the maximal distance that it can travel within the maximal travel time \(t_{\mathrm{max}}\).
We would like to highlight the fact that these assumptions are empirically based. This supports the primary objective of the study to show that such a defibrillator drone system is applicable in mountainous regions utilizing rare infrastructure.
Travel time function. We calculate the travel time between a base station \(b \in {\mathcal {B}}\) and a patient \(p \in {\mathcal {P}}\) using the following model. Therefore, we consider the largest obstacle in the direct line connecting b and p, denoted by o(b, p) having coordinates \((x_o,y_o,z_o)\). Further, we assume that the drone has a defined vertical ascending speed\(v_{\mathrm{vert}}^{+}\), a vertical descending speed\(v_{\mathrm{vert}}^{-}\), and a horizontal travel speed\(v_{\mathrm{hor}}\). Moreover, the drone needs a constant start-up time\(c_{\mathrm{start}}\), which defines the time span from receiving the alarm until take-off. The model assumes that the drone first rises vertically to the altitude of the largest obstacle \(z_o\) along its path (plus \(5 \,m\) safety distance). Then it travels horizontally following the direct line between the base station and the patient’s site, which is described by the Euclidean distance between \((x_b,y_b)\) and \((x_p,y_p)\) (Hong et al. 2018; Ehrgott 2002; Pulver et al. 2016). Finally, the drone descends vertically to the patient’s site. Hence, the travel time from b to p is given by:
where \(z_{\mathrm{max}}:=\max \{z_b,z_o+5 \,m ,z_p\}\). In Fig. 2 we illustrate the model. Clearly, for practical application a more sophisticated way to determine the flight route could result in shorter travel times.
3.2 Mathematical model
Using the notation and assumptions from the previous subsection, we now formulate the ILP. The sets of indices \([u], u \in {\mathbb {N}}\) contain the elements \(\{1,\ldots , u \}\). First, we introduce the assignment variables\(x_{ij} \in \{0,1\},~i\in [m], ~ j \in [q],\) with the following interpretation:
Moreover, we introduce variables \(y_i \in \{0,1\}, ~ i \in [m],\) such that
Consequently, we propose the following model:
The objective function (1a) allows to choose between two objectives by setting \(\alpha\) to 1 or 0. Either the model minimizes the number of used drones or the average travel time. Inequalities (1b) ensure that each patient is assigned to at least one base station. Inequalities (1c) ensure that patients are only assigned to base stations that have a drone located there. Inequalities (1d) enforce that the defined time limit to reach a patient is not exceeded, while Inequalities (1e) guarantee that the available number of drones is not exceeded. Clearly, to ensure that the model has a feasible solution, each patient must be reachable from at least one base station in \(t_{\mathrm{max}}\) or less time, i.e.,
must hold.
4 Example of application and results
In this section, we examine the applicability of a network of base stations equipped with defibrillator drones in mountainous regions. First, we focus on Val Venosta, which is the most western region of South Tyrol, Italy, covering an area of 1442 km\(^2\). The region is crossed by many valleys and dominated by high mountains, including the Ortler, with its 3.905 m making it the highest mountain in South Tyrol. Obviously, this region represents the distinctive characteristics of mountainous areas, which are the major subjects of interest in this study. Furthermore, the region of South Tyrol is served by three ambulance helicopters with base stations in Bozen, Brixen, and Gröden that are geographically decoupled from the focus region Val Venosta (highlighted in Fig. 3). This results in relatively long flight times for all three helicopters responding to patients located in Val Venosta. Installing a fleet of optimally located defibrillator drones in this region could therefore reduce the time between early defibrillation and helicopter arrival. We address this by analyzing the following two scenarios where in (1) we follow the objective to determine the optimal allocation of defibrillator drones in order to minimize the average travel times and in (2) we compare the travel times of defibrillator drones against conventional air ambulance in Val Venosta based on historical medical incidents in the region.
4.1 Data preparation
Regarding the required data, we use local hiking trail network geographic information system (GIS) data provided by the state administration of South Tyrol (http://geokatalog.buergernetz.bz.it/geokatalog/#!). For identifying available shelter huts in the region, we accessed three official databases from the tourism office of South Tyrol and extracted the locations of available shelter huts (https://www.vinschgau.net/de/aktivurlaub/wandern-bergtouren/almen-schutzhuetten.htm, https://www.suedtirol.info/de/erleben/essen-trinken/huetten-almen/, http://www.schnalstal.com/de/gletscher/huetten.html). In order to guarantee the validity of the locations of the identified shelter huts, we cross-checked them in Google Maps and OpenStreetMap and were able to locate additional shelter huts that were not included in the official databases. We derive data on fire rescue stations from the South Tyrolian association of voluntary fire brigades (https://www.lfvbz.it/bezirke/untervinschgau.html). Finally, the corresponding latitudes and longitudes (World Geodetic System 84 - WGS 84) of all locations were gathered. Elevations for both types of locations as well as the elevation of the tallest obstacle in-between them were taken from the Google Maps Elevation API. Everything was implemented in Java, and the ILPs were solved using Gurobi 8.1.0 For illustration purposes, the GIS software QGis was used. For data analysis, we used R.
4.2 Considered drone model
We operate the LifeDrone AED system as described in Claesson et al. (2017), having parameters \(v_{\mathrm{vert}}^{+}=2.5\) m/s, \(v_{\mathrm{vert}}^{-}=2.5\) m/s, and \(v_{\mathrm{hor}}=17.9\) m/s and \(c_{\mathrm{start}}=30\) s. The drone’s own weight is 5.7 kg, and it is capable of carrying an AED with a weight of 763 g. The drone is equipped with GPS and autopiloted; hence, it flies completely autonomously from the base station to the patient’s location. It is notable that in the region of South Tyrol a smart phone app is already available that allows to transmit the GPS data to the emergency coordination center (https://www.leitstelle.tirol/leistungen/zusatzleistungen/). The drone is not equipped with parachute or rope systems to supply the AED; thus, landing at the patient’s site is mandatory.
4.3 Analysis
We consider a test instance that consists of 104 base stations and 1500 patients’ sites that have been randomly sampled from points on the hiking trail network. The label \(O_{{\overline{t}}}\) denotes instances for which inequality (2) does not hold, i.e., no feasible solution can be found. When we choose to minimize the number of drones, i.e., the travel time is not part of the objective function, we calculate the travel time solely based on the selected base stations. Hence, we ignore the assignment variables \(x_{ij}\) and choose the assignment of patients to base stations \({\mathcal {B}}^* \subseteq {\mathcal {B}}\) having a drone assigned to based on the travel time, i.e., for each patient \(p \in {\mathcal {P}}\) the corresponding base station is determined as \({{\,\mathrm{arg\,min}\,}}_{b \in {\mathcal {B}}^*} t(b,p)\).
4.3.1 Optimal allocation of defibrillator drones: minimizing average travel times and number of drones
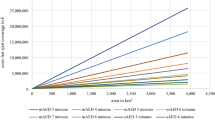
Setup. In this first scenario, we choose the minimal average travel time as objective function, i.e., \(\alpha =0\). We vary the maximal number of drones in steps of 1 and report the results in Table 2. From interval 40 to 100, we abstract the results in steps of 10 as no remarkable changes in values can be observed within this range.
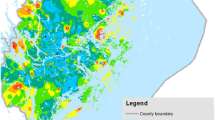
Results. We plot the results from Table 2 in Fig. 4. Hence, we choose \(s=36\) as the preferable network configuration of drone base stations, as the mean travel time of drones (05:27) is well below the 6-min threshold in which early defibrillation should be provided (Nichol et al. 1999). Further, there are no remarkable changes of the 95% quantile values for \(s>36\). We refer to this configuration as ATTs36 (average travel time with \(s=36\)) and plot the corresponding data in Fig. 5. This allocation of drone base stations in the region allows travel times of drones to the patient’s sites in an average time of 05:27. Moreover, 50% of all patients can be supplied with an AED within 05:00, which translates to a rate of survival between 50 and 70% if CPR is immediately provided. Further, 95% of the patients can be reached by an AED drone within 10:55. However, such long travel times are no more beneficial to the patients, keeping in mind the decrease of survival rate of 8–16% per minute without CPR and AED. The 99% quantile of 14:02 further underlines the insufficient performance of the subsequent drone type in ATTs36 and puts into question the benefit of this response system to the patient’s survival. We illustrate the configuration in Fig. 6 (included in Appendix). Patients that can be reached in 06:00 or less are indicated in blue, patients that can be reached between 06:00 and 11:00 are indicated in green, and patients that can not be reached in less than 11:00 are indicated in red. Potential base stations are represented by using brown circles and red cross symbols denote selected base stations according to the optimal solution of the ILP. We also illustrate the hiking trails in the region by brown lines. Analyzing the configuration in Fig. 6 reveals an accumulation of patients with travel times higher than 11:00 (colored in red) located in the most eastern part of Val Venosta. The reason for this is the low availability of potential base stations (i.e., shelter huts) in this region. Hence, it becomes obvious that travel times of drones in the analyzed setting can only be accelerated by using faster drones due to the unavailability of additional base stations in the region.
Plot of Table 2. The x-axis indicates the number of available drones s. For each value the minimal and maximal travel time between a selected base station and an assigned patient is reported. Moreover, the mean and median such as the 95% and the 99% quantiles are reported
Setup - faster drone. As the considered drone model LifeDrone AED has rather low vertical and horizontal speed, which is a major drawback when large obstacles like mountains must be overcome, we compare it against a faster drone model. Therefore, we consider the Wingcopter 178 drone, which is commercially available and capable of carrying an AED of type Philips Heartstart. This drone model has parameters of \(v_{\mathrm{vert}}^{+}=6\) m/s, \(v_{\mathrm{vert}}^{-}=6\) m/s, and \(v_{\mathrm{hor}}=36.1\) m/s and \(c_{\mathrm{start}}=20\) s (Wingcopter - Measure the future 2018). In Table 3 we summarize the parameters of both drone models considered in this work.
Results - faster drone. We compare the results of the slower drone against the faster drone in ATTs36. Using the faster drone in this setting shows remarkable improvements in terms of travel times. Firstly, \({\overline{t}}\) reduces to 06:41. Moreover, the average travel time with the faster drone type amounts to 02:36, which is an improvement of 02:51 compared to the slower one. Moreover, 50% of all patients (i.e., median value) can be reached within 02:24, which is a reduction in time of 02:36. Hence, the faster drone reaches 95% of the patients within 05:00 (compared to 10:55 using the slower drone). Improvements can also be observed with the 99% quantile that amounts to 06:23 , which indicates a time reduction of 07:39 compared to the slower drone. In Fig. 7 we again illustrate the selected base stations. When comparing Figs. 6 and 7, i.e., demand covered by LifeDrone AED and Wingcopter 178, a drastic reduction of patients with travel times higher than 11:00 (patients colored in red in Fig. 6 turned blue in Fig. 7) can be observed. In conclusion, using the same number of drones but considering a faster drone type can be beneficial for patients even in remotely located areas where no potential base station is available (Table 4).
Alternatively, we considered to minimize the number of used drones while \(t_{\mathrm{max}}\) is fixed, i.e., \(\alpha =1\). Considering the LifeDrone AED and Wingcopter 178, we vary the maximal allowed time \(t_{\mathrm{max}}\) in steps of 15 seconds, starting at \({\overline{t}}=14: 48\) and \({\overline{t}}=06: 41\), respectively. The large value of \({\overline{t}}\) implies a rather large \(t_{\mathrm{max}}\). Together with the fact that the travel time is not part of the objective, this scenario yields unacceptable results. However, the authors decided not to consider objective functions where the number of drones is weighted against the travel times due to ethical reasons. The results are reported in Tables 7 and 8, respectively, which can be found in Appendix of the paper.
Summary of the process (Pseudocode). We summarize the process (for the LifeDrone AED) of generating our results as follows:
-
1.
Collect and prepare the data as described in Sect. 4.1.
-
2.
Repeatedly solve the problem instance with changing parameters.
- For \(t_{\max }=20: 00\)\(\alpha =0\), solve the instance for \(s=1,\ldots , 104\).
-
3.
Analyze the resulting drone travel times.
4.3.2 Optimal allocation of defibrillator drones with backup
Setup - faster drone with backup. In this subsection, we discuss the unlikely event of having two SCA patients located close to each other. In this case, both SCA patients would be served from the same base station, which is clearly not possible, as the responding drone cannot visit both patients’ sites. Consequently, a defibrillator drone from another base station must be sent to one of the patients’ sites. The use of a backup drone is a reasonable choice to overcome this kind of situation. Hence, for each patient there are two drones assigned. By default, the closest drone, denoted as drone 1, responds to the patient. In case that drone 1 is not available, the second closest drone, denoted as drone 2, is sent to the patient’s site. In this work, we consider the following two approaches of assigning drone 2 to the patients:
-
B1: In this case, we stick to the original assumption that at most one drone can be assigned to each base station. Hence, drone 2 is located at a different base station than drone 1. Consequently, drone 2 is sent from the second nearest base station, i.e., we change Constraints (1b) to
$$\begin{aligned} \sum _{i\in [m]} x_{ij} \ge 2, \quad j \in [q]. \end{aligned}$$ -
B2: Here, we consider the case that a base station can be equipped with up to two drones. Now, for a given patient, there are two options. Either drone 2 is located at the same base station as drone 1, or drone 2 is located at a different base station. In order compute this scenario using Model (1), we extend the problem instance such that each potential base station is duplicated.
Results - faster drone with backup. Again, we consider the Wingcopter 178 using \(s=36\) drones and set \(t_{\mathrm{max}}= 20 : 00\). We compare the results against the setup without backup (B0) and summarize the results in Table 5. In doing so, we report the values for drone 1 and drone 2. For B1 and B2, we calculated the differences between the response times of drone 1 and drone 2 for each patient and we report the statistics in the table.
Analyzing the results shows that there is virtually no increase in the response time for drone 1 in B1 (except for outliers). However, drone 2 arrives notably later, but for 95% of the patients the use of drone 2 is still beneficial. Moreover, we notice that the response times of drone 1 in B2 are longer than for drone 1 in B1. In B1 drone 2 arrives on average 01:19 later at the same patient’s site than drone 1. In B2 this difference amounts to only 00:12. Also the 95% quantile in B2 indicates that the patients still benefit from the AED delivery. Note that in B2 we use 16 base stations equipped with 2 drones and 4 base stations equipped with 1 drone. Further, the slight decrease in the minimal response time of drone 1 in B1 and B2 (compared to B0) can be explained by the model choosing different assignments of drones to base stations. This is a valid behavior as the objective function is to minimize the average travel time.
To sum up, this analysis shows that considering backups in the assignment of drones to potential base stations enables a timely AED delivery even in the unlikely situation of simultaneously having two SCA patients closely located to each other.
4.3.3 Travel time comparison of defibrillator drones and air ambulance
Setup. In order to compare the performance of the defibrillator drone system to the conventional air ambulance, we first give a short overview of the air ambulance system in South Tyrol. In the region there are three ambulance helicopters available that are located in Bozen, Brixen and Gröden (highlighted in Fig. 3). The latter is only available in the summer season, while the others offer all-season response (https://www.heli.bz.it/de/). As previously stated, the base stations of the helicopters are geographically decoupled from Val Venosta leading to relatively long flight times to locations in this region. Interviews with experts from the mountain rescue service of South Tyrol underline this by pointing to flight times varying between 14:00 and 25:00 to locations in the most western parts of Val Venosta. Consequently, we argue that an optimally allocated fleet of drones could assist in reducing the time span between early defibrillation and helicopter arrival in case of SCA in the region. In order to learn more about helicopter flight times and to validate the expert statements, we set up a meeting with representatives of the local air ambulance provider in January 2019. The mountain rescuers’ statements were confirmed, and further insights into air ambulance service in South Tyrol were gathered. In addition, a data set including 100 flight times of the three ambulance helicopters to historical emergencies (and corresponding latitude and longitude data of the emergency locations) in Val Venosta in 2018 was provided. The data set comprises information on the responding helicopter, its departure time and arrival time on the scene. It is to be noted that the data set does not include patient related information, i.e., it is not reported what kind of medical emergency occurred. The data set validated the assumption of having most patients located on official hiking trails. Therefore, the data can be used to compare the travel times of the helicopters against the drone network. Descriptive analysis of the data set reveals flight times with a minimum of 17:00, maximum of 48:00, and mean of 26:35, which further supports the expert statements. For comparison we use the given defibrillator drone network from ATTs36 using Wingcopter 178 without backup supply. Consequently, we determine the shortest travel time for each patient based on the selected base stations and compare the generated results with the historical flight times of the data set.
Results. We report on the results of travel times of defibrillator drones against helicopters responding to historical incidents from the data set discussed before. Analyzing the generated travel times of defibrillator drones shows that flight times to all emergency locations are well below 6 min except for one patient. The helicopter cannot undercut this threshold in any case. The minimal travel time for defibrillator drones amounts to 00:22 and for the helicopter it is 17:00. The extremely short flight time for the defibrillator drone with only 00:22 is achieved by a drone departing from a fire rescue base station located really close to a patient’s location. The maximum travel time for the drone system amounts to 06:09, while it is 48:00 with the helicopter. The average flight time of defibrillator drones to patients’ sites is 02:05 and 26:35 for helicopters. The defibrillator drones reach 95% of the patients within 03:39 (compared to 36:56 with the helicopters). The 99% quantile for the defibrillator drones amounts to 05:01 and 47:00 for the helicopters. Interesting to observe is that in the worst case, the defibrillator drone requires 15.56% of the flight time of the helicopter (Table 6). We consider patients’ locations in Table 6, where the flight time of the drone is greater than 10% of the corresponding helicopter flight time. Additionally, we plot these locations in Fig. 8 (included in Appendix). All in all, we can observe remarkable reductions of the response times using the defibrillator drones compared against the existing helicopter fleet in the region.
5 Discussion and conclusion
Using our optimization model, we showed that (1) a dense network of drones allocated in a remote region like the Alps in South Tyrol could deliver AEDs to emergency patients on hiking paths, (2) the median travel time interval of the drones is 02:24 (using the Wingcopter 178), (3) that an optimally allocated network of defibrillator drones could reduce the time span between AED provision and helicopter arrival, and (4) this substantially reduced time interval may be associated with a beneficial outcome of SCA, namely a vastly improved chance of survival. Besides, the results show that considering backups in the assignment of defibrillator drones to potential base stations enables a timely AED delivery even in the unlikely situation of simultaneously having two SCA patients closely located to each other. Practitioners can benefit from this study in two respects. Firstly, we present mountain rescue services a novel approach for extending their traditional response system by an innovative means of transport. The technological features of the defibrillator drone itself can definitely increase the flexibility of response teams, thus reducing the time to provide critical support in the minutes after SCA. The developed model can provide a tool for decision makers in the field to optimally distribute defibrillator drones within local infrastructure under consideration of a given set of potential base stations. Notably, the proposed drone system should not replace air ambulance service, as the provision of intensive care medical treatment by helicopter crews is essential for the survival of the patient. From a scientific point of view, this paper is valuable in the sense that it is the first that studies the optimal allocation of defibrillator drones in mountainous regions. With this we enrich academic literature on the potential benefits, e.g., faster provision of emergency care to SCA patients, that arise from combining a transformative innovation and mathematical optimization.
There are several issues that limit this research and that are worth further consideration. First of all, environmental factors that are characteristic for Alpine regions have great influence on the drones’ performance. Huge differences in temperature and stormy conditions may have an impact on the operability of drones, e.g., less power supply by the battery if the air temperature is under \(-10^{\circ }\). In order to generate realistic data on the behavior of the considered drone model under such conditions, field experiments have to be conducted. Moreover, our study assumes that drones always fly in a straight line from the base station to the patient’s site. From the analysis it became clear that high mountains account for long vertical take-off and landing times, which have a negative impact on the overall response times. A potential solution to this problem is to let the drone circle around high mountains instead of passing over them, which could result in reduced flight times of the drones. However, this may be subject to further research.
This study solely focuses on minimizing the response time to deliver an AED to the patient’s location by using a drone. Other times and factors that might contribute to a higher survival rate of the patient are disregarded in this setting. For instance, the time of the bystander’s CPR initialization, the ability of the bystander to place the defibrillator paddles on the patient’s chest, the quality of CPR or the connectivity of the bystander’s mobile device to place an emergency call influence the survival rate. Other delays in time caused by the bystander’s potential mental overload or panic could eventually have negative impacts on the patient’s survival. It is to be noted this whole methodology only works if a bystander is on the scene.
In our model, we assume that the flight corridor of the region is adapted to the parallel use of drones and ambulance helicopters. In practice, there is the need to equip drones and helicopters with automated collision warning systems to avoid aerial conflicts that might lead to the crash of both systems. GPS guidance of the drone, as assumed in our study, is also a limiting factor due to a lack of permission to fly beyond operator line of sight in almost all countries. Further political and legal discussions related to the automated use of drones for emergency purposes have to be stimulated. In this context, the Commission of the European Union has published a new regulation to harmonize remotely controlled UAV use in the entire European Union. This regulation was released in June 2019 and will become valid from July 2020 for all member states (https://eur-lex.europa.eu/eli/reg_impl/2019/947/oj, https://eur-lex.europa.eu/eli/reg_del/2019/945/oj). Besides, in the current model it is obligatory for drones to land at the patient’s site due to safety reasons to avoid harming the bystander or patient by moving rotor blades. In case the emergency location is covered by snow or trees or is situated in a canyon, a safe landing of the drone cannot be guaranteed. Here, parachute or drop free systems, i.e., using a winch to let an AED down on a rope, could help to supply AEDs in almost every situation. This model extension will also be considered in future work.
In order to locate the drones at the defined base stations (i.e., shelter huts and fire rescue stations), infrastructural modifications must be implemented. Drones need electric power to operate. Consequently, shelter huts need to be equipped with power sources such as solar panels and accumulators that guarantee constant power supply to the drone. Autonomous take-off and landing systems also need to be installed in order to let the drone operate completely autonomously. Fire rescue stations need to be equipped with these systems too. Although we incorporate shelter huts and fire rescue stations to determine the optimal allocation of base stations, there may be other candidate locations that can be integrated in the model. Erecting new base stations at suitable locations could further reduce travel times to SCA patients. Prior to that, it has to be ensured that geographical conditions and legal regulations facilitate this. Experts (e.g., geologists, legal experts) have to be consulted, who decide which locations fulfill the desired requirements. Additionally, the installation of base stations in private homes and public institutions such as schools or post offices may be another option. Here, the number and type of base stations is mainly driven by financial considerations.
Furthermore, we run each scenario with a homogeneous fleet of drones. Future research could address the combination of different drone types in order to better react to different requirements of the response situation, i.e., using cheaper and slower drones for patients that are located close to base stations and fast and expensive ones for far away patients. Other extensions could comprise more sophisticated flight routes that could potentially result in shorter flight times. However, this would require a full 3D model of the considered region, which is not available to us. Moreover, this approach would require identifying the shortest path through the 3D environment that is also safe in terms of external parameters (e.g., thermal up and down winds, wind in general, other obstacles such as ropeways). Another model extension could comprise a general budget constraint accounting for drone hosting costs (price of electricity, space, etc.) to be included in the model. To properly estimate the costs, it needs further discussions with specialists in charge of maintaining the infrastructure on site and relevant technicians that have comprehensive knowledge on drone technology. Future work should also include a feasibility study. Bridging the gap between theory and practice by qualitative research is needed. This serves for identifying barriers and accelerators to turn the proposed concept of this study into practice. Hence, discussions with experts including mountain rescue services, EMS, and governmental stakeholders are necessary. Moreover, drone providers should also be consulted regarding the evaluation of the technological transferability of this approach. In conclusion, our model shows that drones might serve as a valuable compliment to already existing helicopter-based EMS due to theoretically achieved much faster response times.
References
Almen und Schutzhütten im Vinschgau in Südtirol (2018). https://www.vinschgau.net/de/aktivurlaub/wandern-bergtouren/almen-schutzhuetten.htm. Accessed 06 Sept 2018
Alpinunfälle in Österreich 2017 (2018). https://www.alpinesicherheit.at/data/docs/presseaussendung Accessed 07 Sept 2018
Anbaroğlu B (2019) Drones in healthcare: an extended discussion on humanitarian logistics. In: Kille T, Bates PR, and Lee SY (eds) Unmanned aerial vehicles in civilian logistics and supply chain management. IGI Global, Hershey, PA, pp 86–114
Barahona F, Chudak FA (2005) Near-optimal solutions to large-scale facility location problems. Discrete Optim 2(1):35–50. https://doi.org/10.1016/j.disopt.2003.03.001
Bezirksfeuerwehrverband Vinschgau (2018). https://www.lfvbz.it/bezirke/untervinschgau.html. Accessed 06 Sept 2018
Boonmee C, Arimura M, Asada T (2017) Facility location optimization model for emergency humanitarian logistics. Int J Disast Risk Reduct 24:485–498
Bos N, Krol M, Veenvliet C, Plass A (2015) Ambulance care in Europe: organization and practices of ambulance services in 14 European countries
Boutilier JJ, Brooks SC, Janmohamed A, Byers A, Buick JE, Zhan C, Schoellig AP, Cheskes S, Morrison LJ, Chan TC (2017) Optimizing a drone network to deliver automated external defibrillators. Circulation 135:2454–2465. https://doi.org/10.1161/CIRCULATIONAHA.116.026318
Câmara D (2014) Cavalry to the rescue: drones fleet to help rescuers operations over disasters scenarios. In: 2014 IEEE conference on antenna measurements and applications (CAMA). IEEE, pp 1–4
Capucci A, Aschieri D, Guerra F, Pelizzoni V, Nani S, Villani G, Bardy G (2016) Community-based AED only resuscitation for out of hospital cardiac arrest victims. Am Heart J 172:192–200
Choi CH, Jang HJ, Lim SG, Lim HC, Cho SH, Gaponov I (2016) Automatic wireless drone charging station creating essential environment for continuous drone operation. In: 2016 International conference on control, automation and information sciences (ICCAIS). IEEE, pp 132–136
Chowdhury S, Emelogu A, Marufuzzaman M, Nurre SG, Bian L (2017) Drones for disaster response and relief operations: a continuous approximation model. Int J Prod Econ 188:167–184
Claesson A, Bäckman A, Ringh M, Svensson L, Nordberg P, Djärv T, Hollenberg J (2017) Time to delivery of an automated external defibrillator using a drone for simulated out-of-hospital cardiac arrests vs emergency medical services. JAMA 317(22):2332–2334
Cui JQ, Phang SK, Ang KZ, Wang F, Dong X, Ke Y, Lai S, Li K, Li X, Lin F, et al. (2015) Drones for cooperative search and rescue in post-disaster situation. In: 2015 IEEE 7th international conference on cybernetics and intelligent systems (CIS) and IEEE conference on robotics, automation and mechatronics (RAM). IEEE, pp 167–174
Custers B (2016) Future of Drone use. Springer, New York
Di Franco C, Buttazzo G (2015) Energy-aware coverage path planning of UAVs. In: 2015 IEEE international conference on autonomous robot systems and competitions (ICARSC). IEEE, pp 111–117
Doherty P, Rudol P (2007) A UAV search and rescue scenario with human body detection and geolocation. In: Orgun M, Thorton J (eds) AI 2007: advances in artificial intelligence. Springer, Berlin, pp 1–13
Dorling K, Heinrichs J, Messier GG, Magierowski S (2017) Vehicle routing problems for drone delivery. IEEE Trans Syst Man Cybern Syst 47(1):70–85
Ehrgott M (2002) Location of rescue helicopters in South Tyrol. Int J Ind EngTheory Appl Pract 9(1):16–22
Faulhaber M, Pocecco E, Niedermeier M, Ruedl G, Walter D, Sterr R, Ebner H, Schobersberger W, Burtscher M (2017) Fall-related accidents among hikers in the Austrian Alps: a 9-year retrospective study. BMJ Open Sport Exerc Med 3(1):e000304. https://doi.org/10.1136/bmjsem-2017-000304
Floreano D, Wood RJ (2015) Science, technology and the future of small autonomous drones. Nature 521(7553):460
Geoportal Südtirol - Verkehrsnetz: Wanderrouten (2018). http://geokatalog.buergernetz.bz.it/geokatalog/#!. Accessed 04 Sept 2018
Goldengorin B, Ghosh D, Sierksma G (2003) Branch and peg algorithms for the simple plant location problem. Comput Oper Res 30(7):967–981. https://doi.org/10.1016/S0305-0548(02)00049-7
HELI Flugrettung Südtirol Elisoccorso Alto Adige (2018). https://www.heli.bz.it/de/. Accessed 22 Jan 2019
Hong I, Kuby M, Murray AT (2018) A range-restricted recharging station coverage model for drone delivery service planning. Transp Res Part C Emerg Technol 90:198–212
Hütten und Almen in Südtirol (2018). https://www.suedtirol.info/de/erleben/essen-trinken/huetten-almen/. Accessed 06 Sept 2018
Huttunen M (2017) Unmanned, remotely piloted, or something else? analysing the terminological dogfight. Air Space Law 42:349
Investigators PADT (2004) Public-access defibrillation and survival after out-of-hospital cardiac arrest. N Engl J Med 351(7):637–646
Jörnsten K, Klose A (2016) An improved Lagrangian relaxation and dual ascent approach to facility location problems. CMS 13(3):317–348. https://doi.org/10.1007/s10287-015-0244-z
Kakaes K, Greenwood F, Lippincott M, Dosemagen S, Meier P, Wich S (2015) Drones and aerial observation: new technologies for property rights, human rights, and global development: a primer. New America. http://www.rhinoresourcecenter.com/pdf_files/143/1438073140.pdf
Klose A, Drexl A (2005) Facility location models for distribution system design. Eur J Oper Res 162(1):4–29. https://doi.org/10.1016/j.ejor.2003.10.031
Laporte G, Nickel S, da Gama FS (eds) (2015) Location science. Springer, New York. https://doi.org/10.1007/978-3-319-13111-5
Larsen MP, Eisenberg MS, Cummins RO, Hallstrom AP (1993) Predicting survival from out-of-hospital cardiac arrest: a graphic model. Ann Emerg Med 22(11):1652–1658
Letchford AN, Miller SJ (2014) An aggressive reduction scheme for the simple plant location problem. Eur J Oper Res 234(3):674–682. https://doi.org/10.1016/j.ejor.2013.10.020
Leveraging Drone Technology to Improve Global Health (2018). http://www.alecmomont.com/projects/dronesforgood/. Accessed 07 Sept 2018
Mersheeva V, Friedrich G (2012) Routing for continuous monitoring by multiple micro UAVs in disaster scenarios. In: Proceedings of the 20th European conference on artificial intelligence. IOS Press, pp 588–593
Monsieurs KG, Nolan JP, Bossaert LL, Greif R, Maconochie IK, Nikolaou NI, Perkins GD, Soar J, Truhlar A, Wyllie J et al (2015) European resuscitation council guidelines for resuscitation 2015 section 1. Executive summary. Resuscitation 95:1–80
Murray CC, Chu AG (2015) The flying sidekick traveling salesman problem: optimization of drone-assisted parcel delivery. Transp Res Part C Emerg Technol 54:86–109
Nichol G, Stiell IG, Laupacis A, De Maio VJ, Wells GA et al (1999) A cumulative meta-analysis of the effectiveness of defibrillator-capable emergency medical services for victims of out-of-hospital cardiac arrest. Ann Emerg Med 34(4):517–525
Notfall App Leitstelle Tirol. (2018) https://www.leitstelle.tirol/leistungen/zusatzleistungen/. Accessed 06 Sept 2018
Official Journal of the European Union Commission Delegated Regulation (EU) 2019/945 of 12 March 2019 on unmanned aircraft systems and on third-country operators of unmanned aircraft systems. OJ L 152, 1–40 (2019-06-11). https://eur-lex.europa.eu/eli/reg_del/2019/945/oj
Official Journal of the European Union, Commission Implementing Regulation (EU) 2019/947 of 24 May 2019 on the rules and procedures for the operation of unmanned aircraft. OJ L 152, 45–71 (2019-06-11). https://eur-lex.europa.eu/eli/reg_impl/2019/947/oj
Pollack RA, Brown SP, Rea T, Aufderheide T, Barbic D, Buick JE, Christenson J, Idris AH, Jasti J, Kampp M et al (2018) Impact of bystander automated external defibrillator use on survival and functional outcomes in shockable observed public cardiac arrests. Circulation 137(20):2104–2113
Pulver A, Wei R (2018) Optimizing the spatial location of medical drones. Appl Geogr 90:9–16
Pulver A, Wei R, Mann C (2016) Locating AED enabled medical drones to enhance cardiac arrest response times. Prehospital Emerg Care 20(3):378–389
Rekordjahr für Bergrettung: 8.000 Menschen geborgen (2018). https://kurier.at/chronik/oesterreich/rekordjahr-fuer-bergrettung-8-000-menschen-geborgen/232.405.161. Accessed 17 Sept 2018
Røislien J, van den Berg PL, Lindner T, Zakariassen E, Aardal K, van Essen JT (2017) Exploring optimal air ambulance base locations in Norway using advanced mathematical modelling. Inj Prev 23(1):10–15
Schuurman N, Bell NJ, L’Heureux R, Hameed SM (2009) Modelling optimal location for pre-hospital helicopter emergency medical services. BMC Emerg Med 9(1):6
Skihütten und Hütten im Schnalstal in Südtirol (2018). http://www.schnalstal.com/de/gletscher/huetten.html. Accessed 15 Oct 2018
Talmar M (2002) Location of rescue helicopters in south tyrol. In: 37th Annual ORSNZ conference
Weisfeldt ML, Sitlani CM, Ornato JP, Rea T, Aufderheide TP, Davis D, Dreyer J, Hess EP, Jui J, Maloney J et al (2010) Survival after application of automatic external defibrillators before arrival of the emergency medical system: evaluation in the resuscitation outcomes consortium population of 21 million. J Am Coll Cardiol 55(16):1713–1720
Windatlas und Windpotentialstudie Österreich (2018). http://ispacevm11.researchstudio.at/index_v.html. Accessed 06 Sept 2018
Wingcopter-Measure the Future. (2018). http://geozone.ch/images/download/Wingcopter/Wingcopter. Accessed 29 Oct 2018
Yigit V, Aydin ME, Turkbey O (2006) Solving large-scale uncapacitated facility location problems with evolutionary simulated annealing. Int J Prod Res 44(22):4773–4791. https://doi.org/10.1080/00207540600621003
Yildrim ZG (2017) New approaches in supply chains: a research on the use of drone technology in logistics. J Strateg Res Soc Sci 2(4):133–142
Zègre-Hemsey JK, Bogle B, Cunningham CJ, Snyder K, Rosamond W (2018) Delivery of automated external defibrillators (AED) by drones: implications for emergency cardiac care. Curr Cardiovasc Risk Rep 12(11):25
Acknowledgements
Open access funding provided by University of Klagenfurt. This work was supported by the European Union Fund for regional development and Interreg V-A Italy Austria 2014-2020 and was carried out, while the first author was employed within the Interreg project START (Smart test of Alpine rescue technology).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wankmüller, C., Truden, C., Korzen, C. et al. Optimal allocation of defibrillator drones in mountainous regions. OR Spectrum 42, 785–814 (2020). https://doi.org/10.1007/s00291-020-00575-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00291-020-00575-z