Abstract
Climate shocks to food systems have been thoroughly researched in terms of food security and supply chain management. However, sparse research exists on the dependent nature of climate shocks on food-producing breadbasket regions and their subsequent cascading impacts. In this paper, we propose that a copula approach, combined with a multilayer network and an agent-based model, can give important insights on how tail-dependent shocks can impact food systems. We show how such shocks can potentially cascade within a region through the behavioral interactions of various layers. Based on our suggested framework, we set up a model for India and show that risks due to drought events multiply if tail dependencies during extremes drought is explicitly taken into account. We further demonstrate that the risk is exacerbated if displacement also takes place. In order to quantify the spatial–temporal evolution of climate risks, we introduce a new measure of multilayer vulnerability that we term Vulnerability Rank or VRank. We find that with higher food production losses, the number of agents that are affected increases nonlinearly due to cascading effects in different network layers. These effects spread to the unaffected regions via large-scale displacement causing sudden changes in production, employment and consumption decisions. Thus, demand shifts also force supply-side adjustments of food networks in the months following the climate shock. We suggest that our framework can provide a more accurate picture of food security-related systemic risks caused by multiple breadbasket failures which, in turn, can better inform risk management and humanitarian aid strategies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Climate-related shocks to food systems have recently emerged as a major cause for concern (Mehrabi 2020; Gaupp et al. 2020). Such shocks affect not only agriculture-dependent regions but non-agrarian regions as well through demand shocks caused by population displacement and supply shocks caused by value chain adjustments (UNDRR 2019). Highly fertile agricultural regions that produce wheat, rice or other grains are typically referred to as “breadbasket” regions. For example, Punjab region in India and Pakistan, fed by rivers in the Indo-Gangetic plain, is responsible for most of the grain productions used for consumption in South Asia, some of which is also exported. Such regions are highly prone to direct climate shocks (FAO 2018), especially droughts that can vary in degrees of magnitude and spatial coverage (CRED 2018; UNDRR 2019). Breadbasket “failures” can also occur across multiple regions as a result of weather-related inter-dependent risks. In 2010, droughts in Russia and floods in Pakistan that were physically connected through atmospheric blocking (Lau and Kim 2012) directly impacted breadbasket regions in these two countries and affected global food prices (Katsafados et al. 2014). This phenomenon, known as “Multiple Breadbasket Failures” or MBBF, has recently been highlighted as a global security concern by climate experts, agriculture economics and food security experts (Janetos et al. 2017; Gaupp et al. 2020), and with climate change, is expected to get worse in the coming decades (Gaupp et al. 2019).
Climate shocks to breadbasket regions can have several direct consequences, such as crop failure, famine and food insecurity (UNDRR 2019). They can also result in indirect outcomes like internal displacement, economic migration, disruption of food supply chains and volatility in food markets (Haraguchi and Lall 2015). For example, extended drought in the past years in the Horn of Africa caused a sever decrease in crop production, food security and job opportunities which have forced many pastoralists and rural farmers to move to urban areas in search of alternative livelihoods (Bonneau 2013). More recently, Philippines, China and India experienced recently large-scale internal displacement due to climate-related disaster events (IDMC 2018). These results are the outcome of demand-side responses driven by household behavior. For example, households in breadbasket regions affected by climate shocks are likely to lose both the ability to produce food and earn income. This can trigger different coping mechanism responses like running down savings, informal borrowing, or, with a very high likelihood, climate-induced displacement to other regions (Auffret 2003). Displacement also impacts other regions by putting a downward pressure on wages and upward pressure on prices (Naqvi 2017). If markets are not agile enough to respond to sudden demographic changes, they can cause severe fluctuations in supply chain adjustments resulting in price volatility.
In the aftermath of such climate shocks, humanitarian aid organizations and governments need to take policy response measures in a short time span, often with limited resources and imperfect information (IPCC 2018). Shocks to food systems are not new and traditionally have been addressed through mobilizing internal resources like running down food inventories and regulating markets or external support through foreign aid and food donations. However, such strategies are likely to be inadequate in case of severe and large-scale drought events happening simultaneously across multiple breadbasket regions. Traditional economic modeling techniques also provide inadequate solutions to short-term responses due to their long-run focus, lack to detailed spatial coverage and lack of feedback interactions across multiple agents (Okuyama 2007).
In order to address the above challenges, we propose combining new innovative modeling techniques to assess the risk and consequences of climate shocks to multiple breadbasket regions. First, we utilize copulas, which allows us to model the relationship of extreme climate shocks across multiple regions more accurately. The recent literature suggests that extreme climate events, such as droughts, and corresponding impacts exhibit tail dependencies (Jongman et al. 2014; Gaupp et al. 2017). If such dependencies are not accounted for, the risks of simultaneous failures can be seriously underestimated.
Second, once the risks of simultaneous climate shock events across different regions are understood, we propose to combine them with multilayer networks and agent-based models. Multilayer networks identify the different layers which connect the same set of locations or nodes. This multilayer network structure can be further endowed with behavioral rules which govern interactions across different locations and their various layers. This bottom-up approach allows us to model rapidly changing nonlinear dynamic responses of regions to climate shocks (Naqvi 2017).
We argue that such an integrated approach can more accurately capture cascading risks, which in turn can help to better inform risk management and humanitarian aid strategies, especially for large-scale events. For example, by analyzing how a shock can potentially cascade and impact other regions, aid organizations and policymakers can come up with more nuanced policies, for example, in regard to price policies and food storage decisions. This is especially relevant for low-income countries, where limited time and resources need to be efficiently allocated. We use the case of India which faced severe droughts in the past to show the usefulness of our suggested approach.
The remaining paper is structured as follows. In Sect. 2, we embed the concept of copulas, multilayer networks and agent-based models within the relevant research literature. Based on this discussion, we propose in Sect. 3, a novel framework which combines the three methodologies to estimate direct and indirect losses emerging from MBBFs. In order to estimate vulnerability, we also introduce a new multilayer network risk measure that we term Vulnerability Rank, or VRank, to capture food insecurity arising from climate shocks. We use India as a case study in Sect. 4, to calibrate and apply our suggested framework, and discuss the results. Finally, Sect. 5 provides conclusions and directions for future research.
2 Literature review
In this section, we give a brief overview of state-of-the-art modeling approaches that deal with climate shocks. We also discuss the contributions of copulas, multilayer networks and agent-based models in this context.
2.1 Economic modeling approaches
Okuyama (2007) highlights three aspects of climate shocks that models need to incorporate: time, space and nonlinear feedback effects. In the last few decades, several waves of modeling efforts have taken place that led to considerable methodological developments in the field of natural disaster analysis in that regard. This includes the early input–output (I–O) models which conducted extensive research on lifeline losses and disruption of transportation networks but focused exclusively on high-income countries like the USA and Japan (Dacy and Kunreuther 1969; Wilson 1982; Rose and Miernyk 1989; Rose et al. 1997). These models were later extended toward more developing countries and emerging economies (Okuyama 2004, 2011). Better availability of data also allowed I–O models to include regional impacts (Okuyama and Santos 2014; Cavallo et al. 2014). However, these models have been criticized for their strong assumptions of linear and fixed relationships across parameters and purely supply-side-driven adjustments.
Therefore, in addition to I–O models, computable general equilibrium (CGE) and dynamic stochastic general equilibrium (DSGE) models were developed and are now the most commonly used framework for analyzing post-shock outcomes (Cole 1995, 1998, 2004). Both CGE and DSGE models focus on long-run equilibrium using rational optimizing agents. Models in this field include national-level (Ueda et al. 2001; Rose and Guha 2004; Rose and Liao 2005) and regional- level studies (Tsuchiya et al. 2007; Hallegatte and Dumas 2009). Both CGE and DSGE models assume perfectly functioning markets, perfect foresight and smooth transitions to a new equilibrium after shocks. While they can now handle regional analysis both due to availability of better computational power and advances in numerical solutions (Ishiwata and Yokomatsu 2018), they still suffer from certain drawbacks. For example, strong assumptions of fixed and exogenously defined parameters remain unchanged during and after the shock and the exclusive focus on long-run equilibrium with little or no discussion on the transition processes. Additionally, the mathematical structure of these models makes it extremely challenging to include a large number of sectors and regions, or other nonlinear behavioral aspects, for example endogenous parameter changes (Rose 2004; Okuyama 2007).
Some recent models have taken non-mainstream approaches. For example, Hallegatte and Ghil (2008) and Hallegatte et al. (2007) introduce business cycles in a mixed demand and supply-driven framework. Albala-Bertrand 1993 shows that while impacts might be negligible at the macro level, they can completely disrupt regional economies. Albala-Bertrand 1993 also highlights the role of labor in estimating overall losses, an aspect that is missing in mainstream models which are mostly driven by capital stock accumulation through investments (Skoufias 2003; Hallegatte and Przyluski 2010).
While the above methods are relevant from a long-term policy planning perspective where economic trends are assumed to stabilize and behave “normally,” short-run outcomes, which are relevant for immediate policy response under an uncertain environment need alternative modeling tools (Skoufias 2003; Naqvi and Rehm 2014b). The above literature points out to several gaps, especially two worth noting. First, little has been done to include probabilistic climate risks in macroeconomic models with only some recent literature touching upon this topic (Hochrainer-Stigler et al. 2011; Ishiwata and Yokomatsu 2018; Poledna et al. 2018). Second, the evolution of short-run direct and indirect losses is not clearly understood with competing and conflicting views in the empirical literature (Kahn 2005; Loayza et al. 2012; Horwich 2000; Strobl 2012; Skidmore and Toya 2002; Hallegatte et al. 2007; Crespo et al. 2008; Hallegatte and Dumas 2009).
We discuss in the following subsections on how copulas and agent-based models can be used to model the short-run outcomes following climate shocks to breadbasket regions.
2.2 Copulas
While the above-mentioned models focus on economic relationships and the impact of climate shocks, copulas are especially useful to address issues of tail dependency usually not looked at in such models. For example, a copula can explicitly address the probability of a large loss in one region given another region faces a large loss (Sklar 1959; Joe 1997; Nelsen 2007). Initially developed for the financial sector (Aas 2004; Dißmann et al. 2013), copulas are now increasingly applied to the field of natural hazard and disaster risk modeling. For example, the phenomena of increasing tail dependency are noticeable in hydrological processes such as water discharge levels across basins. In the work of Jongman and colleagues (Jongman et al. 2014), it was shown that large-scale atmospheric processes can result in strongly correlated extreme discharges across river basins leading to extreme flooding across large regions over Europe. Also in the case of drought events, the risk of simultaneous large-scale events that cause drought-induced crop losses in several regions at once are found to exhibit tail dependency (Prudhomme and Genevier 2011; Ratnam et al. 2016; Vicente-Serrano and López-Moreno 2006; Gaupp et al. 2019).
Copulas are able to model nonlinear codependencies of risks as in the case of joint climate extremes. They can also be used to model the dependence structure between multiple variables such as climate indicators and crop yields. In agricultural sciences, copulas are typically used to depict the joint effects of temperature and precipitation on crop yields (Cong and Brady 2012). A common class of multivariate copulas used in this field is the so-called Vine copulas (Aas et al. 2009; Bedford and Cooke 2002; Czado et al. 2013) which consist of a cascade of bivariate conditional and unconditional pair-copulas. For our case study, we use the most advanced approach currently available, namely regular vines, or RVines, which can model complex dependencies even in large dimensions (Dißmann et al. 2013). As we will see further below, copulas are a flexible statistical tool to model the dependencies between risks. Due to Sklar’s Theorem (Sklar 1959), the underlying univariate marginal distributions, for example of individual risks, can be modeled separately from the dependence structure (Aas et al. 2009). In this way, droughts in different regions, and with varying degrees of duration, severity and distributions, can still be modeled jointly using copulas (Shiau 2006). For our case, we use logistically de-trended wheat yield data in the Indian breadbasket states to demonstrate the importance of incorporating tail dependencies in drought risk estimations. Subsequent cascading impacts are modeled through an agent-based multilayer network approach as discussed in the next section.
2.3 Multilayer networks and agent-based models (ABMs)
While inter-dependent risk can be modeled through copula approaches, economic modeling approaches, as discussed above, do not capture the intrinsic dynamics of shocks within systems, and therefore, agent-based modeling approaches are coming nowadays to the forefront (Elsner et al. 2014; Naqvi and Rehm 2014a). Agent-based models, or ABMs, are a bottom-up methodology that allows agents to make decisions based on past and current outcomes as well as on the behavior of others (Bowles 2006). ABMs have the ability to handle a large set of different agent sets allowing for heterogeneity within each agent set. Within such a framework, the interaction of agents determines meso- and macro-outcomes, which can further feedback into the micro-decision-making of individual agents resulting in nonlinear path-dependent outcomes (Arthur 2006; Elsner et al. 2014; Tesfatsion 2006). Thus, ABMs are well equipped to handle large parameter spaces, nonlinear thresholds, boundary conditions and out-of-equilibrium states thus going beyond state-of-the-art modeling tools typically used in disaster analysis (Farmer and Foley 2009; Axtell 2005).
However, it is not enough, as currently done, to look at the economic system as a single-layer entity with heterogeneous agents. We suggest applying multilayer network approaches instead (Kivelä et al. 2014; Battiston et al. 2016). Multilayer networks are represented by unique but interconnected layers. Assuming regions can be represented as nodes in a network structure, these nodes can interact with each other in different ways. For example, goods flow can be represented by trade networks and population flows by migration networks. The nodes interact with and across layers based on behavioral rules usually derived from the economic theory or empirical literature based on the region under study (Alfarano and Milaković 2009; Naqvi and Rehm 2014a; Naqvi 2017). This network structure allows us to track changes resulting from climate and economic shocks that might occur in one part of the network, but can cascade throughout the system through behavioral interactions. The specific network structure is typically determined by the number of locations or nodes, the number of layers, endowment of stocks and the strength of connections across the layers.
The multilayer approach was first applied to financial networks after the 2008 global crisis to understand how shocks cascade and can cause “systemic risk” (Bardoscia et al. 2015; Battiston et al. 2012; Poledna et al. 2015). Unlike financial networks, where all transactions are in monetary units across different types of financial institutions or assets (Hurd and Gleeson 2011; Stolbova et al. 2018), food production involves networks comprising of different monetary and non-monetary units. For example, land is used to produce a physical output of crops, which is later converted into monetary units through market transactions. Similarly, agriculture labor, which is typically a large proportion of the total population in developing countries, engages in farm work in exchange for usually low wages. A climate shock like flood or drought to such a system implies that food output is lost through less land being available. A more catastrophic shock like earthquakes can even cause high casualties reducing labor power in a region. Thus, losses in different layers cannot be treated in the same way as losses within financial networks. Additionally, unlike financial networks which are governed with relatively well-defined homogeneous rules and regulations, the agriculture–food web and its corresponding agrarian and farming population need to be set up with layer-specific behavioral rules. In order to do so, the dynamics within each dimension need to be modeled through the behavioral interaction of different agent sets belonging to different layers across a network of spatially explicit locations.
In the next section, we describe how the three methods of copulas, multilayer networks and agent-based models can be combined together to tackle the challenges addressed above, that is, how to model simultaneous risks and cascading impacts across regions.
3 Model framework
3.1 Modeling climate shocks through copulas
Copula approaches gained their importance due to Sklar’s Theorem (Sklar 1959). It states that every multivariate distribution F with margins \(F_1, \dots , F_d\) can be written as:
with C as a d-dimensional copula, a multivariate distribution on the unit hypercube \([0,1]^d\) with uniform marginal distributions. F is continuous with strictly increasing continuous marginals \(F_1, \dots , F_d\) such that:
where c is the copula density, f, the multi-dimensional probability density function of F, and \(f_k\), the marginal probability density function of \(F_k\), \(k=1,\dots ,d\). d in our example refers to the number of breadbasket states in India. The advantage of this approach is that the copula, and thereby the dependence structure, can be chosen independently from the marginal distributions. There are different copula families capturing different dependence structures (Jaworski et al. 2010) but generally speaking, any multivariate distribution can be used as the basis for a copula (Aas 2007). To structure our multivariate copula model, we used regular vines (RVines) (Aas et al. 2009; Bedford and Cooke 2002; Kurowicka and Cooke 2006; Dißmann et al. 2013), a flexible graphical model that consists of a cascade (or tree structure) of conditional and unconditional bivariate copulas that decompose the multivariate probability density. A d-dimensional RVine model consists of \(d-1\) trees. Each tree consists of nodes and edges joining the nodes. The first tree identifies \(d-1\) pairs of variables with a directly modeled distribution. The second tree identifies \(d-2\) pairs with a distribution conditional on a single variable, modeled by a pair-copula. Continuing in that way, the last tree consists of a single pair-copula with a distribution conditional on all remaining variables. For a graphical representation of a RVine tree, see (Dißmann et al. 2013) or (Brechmann and Schepsmeier 2013). The RVine tree structure in this study is selected using the maximum spanning tree approach with Kendall’s \(\tau \) as edge weights (Dißmann et al. 2013):
with \({\hat{\tau }}_{m,n}\) as pairwise empirical Kendall’s \(\tau \) (that is, a rank correlation coefficient, see Embrechts et al. 1997). As will be discussed in the results section, this approach was adopted for India on the state level, which showed large tail dependencies for some regions and therefore is an excellent example for showing the advantages of a copula approach when it comes to determine systemic risks.
3.2 The multilayer networks and agent-based models
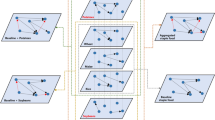
Going to the ABM modeling component, we first want to note that every ABM needs to be contextualized, that is, it must be set up for a specific purpose of analysis (Gilbert 2008; Klabunde and Willekens 2016; Naqvi 2017), which in our case are drought-related production shocks in India. A shock in the food system through a strong reduction in crop yields will cascade through the affected population as well as through the unaffected one. For example, in the case of India, a state’s economy can be assumed to produce output across different sectors that can be divided into agricultural or other goods (physical goods and services). Each state holds a stock of workers which are employed across the different sectors that interact with each other to form a simple circular flow economy. Cross-state interactions result in the exchange of goods (including food) and services. Underlying this production and trade interactions are labor markets, which determine how much labor is employed across different sectors. Like trade which is driven by price and profit signals, income differentials result in migration across locations. This, in turn, determines population and income distributions. Migration decisions are also influenced by social signals, for example social- or community-based networks. The household and the production layer combined represents a multilayer network structure as shown in Fig. 1.
Each dot in Fig. 1 represents a location divided across two layers. A production layer employs workers to produce output. This output is in demand not only in one location but in other locations as well. The second layer represents the demand side, where households contribute via two channels: by providing labor for production in exchange for income and demand for consumption purchased through income and savings. Labor can also move around based on market signals or when faced with high-distress scenarios as in the case of shocks.
3.2.1 A multilayer network
In order to operationalize this framework for India, we set up a multilayer network model, where the 36 Indian states are represented as nodes and two layers shown in Fig. 1. The first layer represents low-income households, and a goods layer represents the production of food and other goods (see Fig. 1). Each node is calibrated using actual data to determine the level of production of food and other goods in each state (see Table 1 in “Appendix A”).
The nodes which produce food are subjected to a supply-side breadbasket failure shock, which means simultaneous production losses in multiple Indian states. In our case, two specific shock scenarios are tested, (a) a shock assuming independence between food production across states and (b) a copula-based shock derived from a probability distributions that includes production inter-dependencies across the states. In the copula scenario, the number of agents affected simultaneously increases with the intensity of the production shock. This impacts other layers as well through employment, income and consumption decisions. For both shocks, we simulate a no-migration and a migration scenario to test the impact of the shock across the region. The no-migration scenario represents a single-layer simulation where only the production side (or the supply-side) is simulated.
Summarizing, our approach represents two improvements the over existing literature. First, shocks are not assumed to be independent, uncorrelated events, but follow a copula-based structure. Second, food production shocks impact other layers, notably the household layer, resulting in a transmission of the shock to non-affected regions. The ABM model itself is discussed in more detail next.
It should be noted that for the sake of simplicity, the model assumes that all layers adjust completely to demand and supply interactions. Mismatch in markets is corrected through prices and all output, and income is fully exhausted such that there are no leftover stocks. This mimics a general equilibrium framework where prices drive the model outcomes. In a more realistic setting, path dependencies and institutional barriers will also very likely play a role as well. Thus, a full adjustment model is a best-case scenario model and distributions resulting from the simulations shown here therefore represent a lower bound for the level of disparities created from the climate shocks.
3.2.2 The agent-based model
In order to operationalize the model, we need to endow the nodes and links with behavioral rules. These are introduced in the model in a very basic form using standard economic assumptions described below.
Each node i is endowed with land and capital stock that allows for a maximum production of food (F) and other consumable goods (G), respectively. The production level of each node is derived from Table 1. Assuming j is the index of goods produces at each location i, which in our model is \(j={F,G}\), the value of the total output produced at a node i equals
This two-good model framework can be easily extended to include a larger set of goods. To produce these goods, all the labor supply \(L_i\) available at each node is employed. Assuming each unit is produced at a cost \(\rho \), the total wage bill is simply \(\rho y_i\). The wage rate (\(w_i\)) of workers at a node i equals the total wage bill over the total labor supply, or
The income earned by workers is fully spent on the goods produced at the node where a fraction \(\alpha \) is spent on food F and \(1-\alpha \) on other goods G. Or more formally, the consumption of each good at a location i is defined as:
From this, the price of the two goods can be derived as:
For the sake of simplicity, the average price at location i, \(p_i\), is taken as a simple arithmetic average of the two prices. This can be made more complex to represent goods baskets with price weights to generate average price indices at different locations.
In nominal terms, the value of the total output produced at a node i can be derived as
If the nodes are allowed to interact, then a gravity model-like specification determines how much is exchanged across the nodes (Anderson 1979). This is estimated in the model as a logistic function \(\Pi _{iq}\) between node i and its q connected neighbors following a joint probability distribution of the type:
In short, the probability of moving to a connected neighbor q or \(\Pi _{iq}\) is positively affected by relative economic gains, \(\Pi _{iq}^h\), at destination q. For migration, the economic gains are determined by real-income differences (\(h=w_q/w_i\)) and for trade by potential profit gains defined by relative prices (\(h=p_q/p_i\)). The choice of destination q is also negatively affected by distance \(\Pi _{iq}^r\) to neighbor q. The generic logistic function is of the type:
where a and b are shape parameters of the logistic function. Additional migration–decision factors can also be added, for example community at destination and other social linkages (see (Naqvi 2017) for the full model specification).
Two thresholds are introduced in the model to make the post-shock decision-making behavior more realistic. First, households adjust their propensity to consume food relative to a minimum consumption value \({\bar{c}}\). If their income goes down or food prices go up, then \(\alpha \) will adjust endogenously to ensure that they stay at least at the \({\bar{c}}\) level. Formally,
Since households cannot spend more than what they earn, \(\alpha \) is bounded such that \({\bar{\alpha }} \le \alpha \le 1\). Like households, firms only sell in markets which give them positive profits. Unlike households, they can diversify their portfolio to sell in several markets. This also allows them to dynamically adjust their supply to changes in demand in their vicinity. Since firms have production costs (wages in this model), the difference between the costs and the market prices determines the profit margins. Since the unit cost of production equals \(\rho \) and the market price equals \(p_{i}^j\), then the condition \(p_{i}^j \ge \rho \) defines the sorting for selling in markets. If some markets fall below this threshold, or \(p_{i}^j < \rho \), then they are excluded from the list. These two thresholds evolve dynamically since all variables are time indexed.
3.2.3 A multilayer vulnerability index
Following the advances in multi-dimensional network measures (Magnani et al. 2013; Kivelä et al. 2014; Gemmetto et al. 2016), a similar measure is adapted here to estimate multilayer vulnerability. Vulnerability is simply defined as the populations falling below the minimum consumption threshold (\({\bar{c}}\)). In spirit of DebtRank, a key centrality measure of multilayer systemic risk in financial networks (Bardoscia et al. 2015; Battiston et al. 2012; Thurner and Poledna 2013) that itself is shaped after Google’s PageRank (Brin and Page 1998; Halu et al. 2013), we develop a new vulnerability measure to represent multilayer food insecurity, a key issue in disaster-prone regions (FAO 2015). We will call this measure Vulnerability Rank or VRank, which is estimated as follows:
In other words, the vulnerability of a node i is not only defined as the purchasing power of food of populations at that node, but also all its neighboring q nodes. The parameter \(\beta \) is the dampening factor, typically set at \(\beta =0.8\), which determines the impact of the neighbors on node i. This formula captures two key aspects. First, it encapsulates the dependence of one node on another in terms of food supply. For example, a node which does not produce any food would be considered vulnerable in isolation, but if it is connected by several food-producing regions that can service it in times of shocks, it should have a much lower vulnerability than a food-producing node that is completely isolated. Second, it captures the displacement-based linkages as well. A node that produces enough food for its current population might see a sudden influx of populations from shocked neighbors, making it potentially very vulnerable in the short-run following the climate shock.
4 Results
In this section, we now integrate our suggested modeling approach as discussed above to the case of India. The country serves very well for our purpose. Around 55% of the Indian workforce lists agriculture and associated activities as their primary source of employment. Agriculture also contributed 17.4% to India’s real gross values added (GVA) in 2016–17 (Department of Agriculture India 2018). In rural areas, agriculture still generates more than half of the total income (Kadiyala et al. 2014). After rice, wheat is the most important cereal in India (40%) with cereals accounting for 94% of total food grains (Department of Agriculture India 2018). Only around 50% of sown area are irrigated which means that agriculture is still largely dependent on monsoon rainfall which occurs, depending on the region, between June and September. Additionally, in dry years low reservoir levels and fuel shortages can hamper irrigation efforts (Krishna Kumar et al. 2004). Winter crops such as wheat benefit from the monsoon rainfall through residual soil moisture. If the monsoon fails, India experiences risks of crop failure in wide parts of the country.
4.1 Risk assessment of a MBBF in India
To give an understanding of the underlying principle of dependent crop losses, we start with an example of two dependent Indian states, namely Uttar Pradesh and Rajasthan, both part of the Indian wheat breadbasket. Figure 2 shows the univariate marginal distributions of logistically de-trended (Gaupp et al. 2017) wheat yields in Uttar Pradesh and Rajasthan. Both de-trended yields follow a normal distribution tested with the Shapiro–Wilk test.
In the middle, their scatter plot is shown as well as the contour plot of the Frank copula which was selected as the bestfitting copula type. It joins the marginals of de-trended wheat yields in Uttar Pradesh and Rajasthan and has the following form:
with \(\theta \) as the copula parameter determining the strength of tail dependence. To stress the importance of dependence, we take a look at the 1974 food crisis in India. A combination of adverse weather conditions and a rise in oil prices with consequent shortages of petroleum-based fertilizer led to unexpectedly low yields in India (Weinraub 1974a, b; Joerin and Joerin 2013). Based on our data, the likelihood of yields as low as the 1974 yields occurring simultaneously in Uttar Pradesh and Rajasthan equals \(C_\theta [F_\mathrm{{UP}}(-0.29), F_\mathrm{{R}}(-0.16)] = 0.027\). If we would not take into account the dependence structure between the two states, the likelihood of both states experiencing a 1974-type event would be \(F_\mathrm{{UP}}(-0.29), F_\mathrm{{R}}(-0.16)= 0.007\). To estimate the joint probability of all eight breadbasket states, we use an RVine tree structure as described in the methods section. Figure 3 shows the first tree of the de-trended wheat yields in the Indian breadbasket. Edges are labeled with the copula families connecting the nodes via bivariate copulas.
The full tree structures which include all conditional copulas are shown in Fig. 7 in “Appendix B”. In 2003, following the 2002 monsoon failure, India experienced a major wheat yield shock (with shock defined as deviation from the long-term logistic trend). Based on our analysis in eight breadbasket states (see Table 2), the wheat yield shock in 2003 in the Indian breadbasket was a 1-in-17 years event. The importance of not only considering the yield distributions in the different states in an agricultural risk analysis but also the dependence structure between them becomes clear when we compare the return period of the 2003 yield shock with the return period if we would ignore the dependencies. If we assume independence between the states, the likelihood of a 2003 event would decrease to a 1-in-370 years event, a 20-fold increase in the magnitude. Therefore, by ignoring linkages between the production in different states, the risks of crop failure are underestimated dramatically. In addition, further spillover effects of those spatially inter-dependent yield shocks have to be modeled to fully grasp the systemic risks of our current food system.
The above framework is applied to India to estimate the impact of a breadbasket failure on internal displacement. Figure 4b shows the states of India of which eight (shown as green dots) are major food crop producing states.This represents 40–45% of all employment in India, most of which is at extremely low end of the income distribution. The 2003 crop failure resulted in a rise in food prices. Since India is not a net importer of food items, the loss in crops resulted in an internal market adjustment to the climate shock.
4.2 Simulating the effects of a MBBF in India
We conduct four experiments to show the usefulness of our approach, using a combination of no-displacement and displacement scenarios and independent and copula-based probability distributions. The displacement scenario allows populations to move from one state to another if they see better real-income opportunities. Due to a lack of state-to-state migration or displacement data, which can allow us to calculate migration propensities, all states are given equal weights in terms of destination choices, where the only negative factor is average distance where farther away locations are considered less attractive than nearby ones. In a more real-world scenario, propensity to move would also be determined by community and language ties, work opportunities and other social and cultural factors (Black et al. 2013; Klabunde and Willekens 2016; Cattaneo and Peri 2016). Thus, our displacement scenarios represent a highly stylized baseline outcome, which, in reality, is likely to be much worse. The 36 states are set up in the simulation model using data from Table 1 for calibration. The table provides information on low-income populations, total output produced in each sector, and the share of agriculture in this output. Low-income workers are divided into these sectors accordingly. The simulations run till states achieve stable trends in prices and population distributions (Fig. 4b).
The breadbasket states, shown in green in Fig. 4, are subjected to a production shock to simulate the drought event. As described above, the shocks can either be modeled as independent or follow an inter-dependent copula structure. The probabilities of changes in yields using both independent probability distributions and a copula-based probability distribution for a 100 year production shock event are estimated and provided in Table 1. Figure 5 shows the temporal trends for the four scenarios for four different indicators: real income, average consumption, marginal propensity to consume and the VRank index. Figure 5a shows that the real income, or the price of labor relative to the price of food, falls across all scenarios. The independent, no-displacement scenario shows the smallest change, while the copula with displacement scenario shows the highest impact. This can be explained by the fact that wheat yields are strongly positively correlated between the states which means that a shock in one state leads to a shock in surrounding states with a high probability. A copula-based shock shows on average a larger decline in relative price changes. Since income falls, and food becomes more expensive, due to an overall decline in output, the average consumption levels, shown in Fig. 5b, also fall.
As consumption levels decline, households allocate more of their income toward food in order to stay above the minimum consumption threshold. Figure 5a, b indicates that including and excluding dependencies between states have a much higher impact than with or without displacement. Figure 5c shows the development of this indicator, which rises steeply if one assumes tail dependence with displacement. This scenario also takes the longest to stabilize. Figure 5d shows the VRank index, which on average increases for all scenarios with the copula scenarios showing the highest increase. This last graph highlights that underestimating both the joint probability risk and the multilayer displacement effects can result in underestimating the full extent of the shocks. Figure 6 shows the results as spatial choropleth maps at the end of the six- month simulation period, when the indicators stabilize. The graphs show changes relative to the baseline no-shock scenario. Displacement scenarios, shown on the right column in Fig. 6, exhibit a relatively higher vulnerability as the shock spreads from the affected states to the non-affected states through migration. In the non-displacement scenario, the copula- based distribution of the shock shows a higher increase in vulnerability.
The results provide important insights in terms of dynamics as well as policy-wise. For example, while an aggregated macroeconomic performance measure such as the GDP exhibits similar patterns across two displacement scenarios they can completely differ in the distributional effects. Furthermore, such different outcomes also imply that completely different policy responses are needed to tackle such risk. As recently suggested by Pflug and Pichler (2018), the difference in distributional impacts across the dependent and independent case can be used for determining the share of systemic risk (due to the dependency between states) to overall risk. If we conducted a complete probabilistic assessment of all possible agriculture-related climate risk scenarios, which in principle is possible as both the copula and marginal distributions are available, it would be possible to apply classic risk management strategies as well as to analyze humanitarian aid responses. However, this would be extremely difficult to operationalize in short time span due to the high computational requirements (for example, thousand of risk distributions need to be generated and analyzed via the ABM model). Alternatively, so-called risk-layer approaches which focus on risk reduction for more frequent risks and risk financing for infrequent ones (Mechler et al. 2014) can provide guidance on best strategies forward. As we were looking at independence and 100-year event cases, from a risk perspective, these events would still belong to the “relatively frequent” set. Therefore, risk reduction measures such as crop storage or subsidies during time of crisis could be, in principle, applied and studied with our approach. However, there are limitations due to data scarcity, especially as displacement patterns on such large scales are difficult to be empirically tested and validated. Nevertheless, current efforts are underway to get a more complete picture (Kc et al. 2018).
While these results are derived from a highly stylized model, where adjustments in markets are perfect, a fully calibrated model would include more frictions where the results would show much worse outcomes and distributions. Thus, our model results can be taken as an upper bound for disaster impacts in a best-case scenario.
Model calibration and application to countries are always a challenge for agent-based models. A model on a subregional level, for example provinces or states, has relatively abundant data, allowing for calibration since such regions typically represent standard administrative units (like provinces or districts) at which data are collected. Thus, a subregional level allows the model to be flexible enough to be adopted to different countries. The model can be scaled further down, for example to the village or even household level, but data limitations and the model scale would make the results both highly intractable and potentially subject to extensive sensitivity testing (Naqvi 2017).
5 Conclusions and directions for future research
Climate shocks result in humanitarian crises that usually affect locations beyond the areas of direct impact. Understanding and responding to these events, given limited resources, are critical for policymakers and aid organizations that are typically making decisions under uncertainty and in a short span of time. State-of-the-art modeling tools usually deal with long-run outcomes and are not adequate to explain short-run nonlinear dynamics that emerge from complex interactions following a climate shock scenario.
To close this research gap, in this paper we proposed that risks associated with climate shocks and their subsequent outcomes can be modeled by combining copulas with multilayer networks and agent-based models. Copulas provide the dependent structures of climate risks across multiple regions, multilayer networks describe how these regions are interconnected, and agent-based models allow us to embed behavioral rules that define socioeconomic interactions. While most of the advances in the above three methods evolved mainly in the fields of banking and finance, they have strong applications in the domain of humanitarian operations.
We discussed how such a model can be constructed and applied to drought shocks in agriculture-dependent breadbasket regions in India where weather-related interlinked dependencies across various Indian states can result in multiple breadbasket failures (MBBFs). Through the modeling exercise, we explored how these shocks can spread across other regions. Using the copula approach, we showed that with higher food production losses, the number of agents that were affected increased nonlinearly which led to cascading spillover effects in other locations via network layers through employment, income and consumption decisions. The simulation results showed large-scale displacement which led to large-scale demand and supply-side adjustments in the months following the climate shock. We summarized the food insecurity arising from interactions across the multilayer economic linkages through a new risk measure, Vulnerability Rank or VRank, which showed that risk increases significantly if inter-dependent structure of climate shocks and the resulting displacement are fully accounted for. Such a modeling framework can be easily applied and calibrated to low-income countries using regional-level data that is typically available from statistical offices. While the current model focused on the short-run (that is, the six-month transition phase that can occur after shocks), it can also be extended to include long-term effects of disaster financing (Mechler et al. 2008) and demographic shifts resulting from long-term displacement or permanent migration.
The suggested framework can be used for testing and employing traditional, as well as, novel risk management strategies, for example food storage and insurance schemes, respectively. It can also be used to quickly identify highly vulnerable locations which require humanitarian aid. Thus, our suggested framework, if effectively utilized, for example in the case of MBBFs, can help minimize or prevent secondary-level post-shock outcomes like displacement and food shortages.
A coupla-based multilayer agent-based model can also be deployed to simulate different policy scenarios, for example price controls, allowing policymakers to be better informed about the positive and negative economic and human impacts, changes in risks over time, as well as how to address such issues in the future. These applications are not just limited to climate shocks to agricultural regions but can also be extended to various other aspects of humanitarian crises, for example water and energy issues, early warning systems, potential market failures, spread of diseases, demographic shifts and spending on reconstruction and rehabilitation. We suggest that in all of these domains, where operations research is a key management tool, such modeling innovations can be utilized to manage and minimize various forms of systemic and interconnected risks.
References
Aas K (2004) Modelling the dependence structure of financial assets: a survey of four copulas. NR note no. SAMBA/22/04. Norwegian Computing Center, Oslo, Norway
Aas K (2007) Statistical modeling of financial risk. PhD Thesis, Norwegian Institute of Science and Technology, Trondheim, Norway
Aas K, Czado C, Frigessi A, Bakken H (2009) Pair-copula constructions of multiple dependence. Insur: Math Econ 44(2):182–198. https://doi.org/10.1016/j.insmatheco.2007.02.001
Albala-Bertrand JM (1993) Natural disaster situations and growth: a macroeconomic model for sudden disaster impacts. World Dev 21(9):1417–1434. https://doi.org/10.1016/0305-750X(93)90122-P
Alfarano S, Milaković M (2009) Network structure and N-dependence in agent-based herding models. J Econ Dyn Control 33(1):78–92. https://doi.org/10.1016/j.jedc.2008.05.003. http://linkinghub.elsevier.com/retrieve/pii/S0165188908000833
Anderson JE (1979) A theoretical foundation for the gravity equation. Am Econ Rev 69(1):106–116
Arthur WB (2006) Out-of-equilibrium economics and agent-based modeling. In: Tesfatsion L, Judd KL (eds) Handbook of computational economics, volume 2: agent-based computational economics. Elsevier, chap 32, pp 1551–1564. http://ideas.repec.org/h/eee/hecchp/2-32.html
Auffret P (2003) High consumption volatility: the impact of natural disasters? Tech. Rep. January, The World Bank. https://doi.org/10.1596/1813-9450-2962
Axtell R (2005) The complexity of exchange. Econ J 115(504):F193–F210. http://ideas.repec.org/a/ecj/econjl/v115y2005i504pf193-f210.html
Bardoscia M, Battiston S, Caccioli F, Caldarelli G (2015) DebtRank: a microscopic foundation for shock propagation. PLoS ONE 10(6):1–13. https://doi.org/10.1371/journal.pone.0130406. arXiv:1504.01857
Battiston S, Puliga M, Kaushik R, Tasca P, Caldarelli G (2012) DebtRank: too central to fail? Financial networks, the FED and systemic risk. Sci Rep 2(1):541. https://doi.org/10.1038/srep00541. http://www.nature.com/articles/srep00541
Battiston F, Nicosia V, Latora V (2016) Efficient exploration of multiplex networks. New J Phys 18(4). https://doi.org/10.1088/1367-2630/18/4/043035. arXiv:1505.01378
Bedford T, Cooke RM (2002) Vines–a new graphical model for dependent random variables. Ann Stat. https://doi.org/10.1214/aos/1031689016
Black R, Arnell NW, Adger WN, Thomas D, Geddes A (2013) Migration, immobility and displacement outcomes following extreme events. Environ Sci Policy. https://doi.org/10.1016/j.envsci.2012.09.001
Bonneau P (2013) Drought and internal displacements of pastoralits in Northern Kenya in 2012: an assessment. In: Gemenne F, Brucker P, Lonesco D (eds) The state of environmental migration 2013: a review of 2012. Institute for Sustainable Development and International and Geneva, International Organization for Migration, Paris
Bowles S (2006) Microeconomics : behavior, institutions, and evolution. https://doi.org/10.1177/0486613406293231. arXiv:1011.1669v3
Brechmann EC, Schepsmeier U (2013) Modeling dependence with C- and D-vine copulas: the R package CDVine. J Stat Softw 52(3):1–27. https://doi.org/10.18637/jss.v052.i03. http://www.jstatsoft.org/v52/i03/. arXiv:0908.3817v2
Brin S, Page L (1998) The anatomy of a large scale hypertextual Web search engine. Comput Netw ISDN Syst 30(1/7):107–17. https://doi.org/10.1016/S0169-7552(98)00110-X. arXiv:1111.6189v1
Cattaneo C, Peri G (2016) The migration response to increasing temperatures. J Dev Econ 122:127–146. https://doi.org/10.1016/j.jdeveco.2016.05.004. http://linkinghub.elsevier.com/retrieve/pii/S0304387816300372. arXiv:1011.1669v3
Cavallo A, Cavallo E, Rigobon R (2014) Prices and supply disruptions during natural disasters. Rev Income Wealth 60:S449–S471. https://doi.org/10.1111/roiw.12141
Cole S (1995) Lifelines and livelihood: a social accounting matrix approach to calamity preparedness. J Conting Crisis Manag 3(4):228–246
Cole S (1998) Decision support for calamity preparedness: socioeconomic and interregional impacts. In: Shinozuka M, Rose A, Eguchi RT (eds) Engineering and socioeconomic impacts of earthquakes, multidisciplinary center for earthquake engineering research, Buffalo and NY, pp 125–153
Cole S (2004) Geohazards in social systems: an insurance matrix approach. In: Okuyama Y, Chang SE (eds) Modeling spatial and economic impacts of disasters. Springer, Berlin, pp 103–118
Cong RG, Brady M (2012) The interdependence between rainfall and temperature: copula analyses. Sci World J 2012:1–11. https://doi.org/10.1100/2012/405675
CRED (2018) Economic losses, disasters, poverty: 1998–2017. Tech. rep., Centre for Research on the Epidemiology of Disasters (CRED)
Crespo J, Hlouskova J, Obersteiner M (2008) Natural disasters as creative destruction? Evidence from developing countries. Econ Inq 46(2):214–226. https://doi.org/10.1111/j.1465-7295.2007.00063.x
Czado C, Brechmann EC, Gruber L (2013) Selection of vine copulas. In: Jaworski P, Durante F, Härdle WK (eds) Mathematical and quantitative finance. Springer, Berlin, pp 17–37. https://doi.org/10.1007/978-3-642-35407-6_2
Dacy DC, Kunreuther H (1969) The economics of natural disasters. The Free Press, New York
Department of Agriculture India (2018) Statistical database
Dißmann J, Brechmann E, Czado C, Kurowicka D (2013) Selecting and estimating regular vine copulae and application to financial returns. Comput Stat Data Anal 59:52–69. https://doi.org/10.1016/j.csda.2012.08.010. https://linkinghub.elsevier.com/retrieve/pii/S0167947312003131
Elsner W, Heinrich T, Schwardt H (2014) The microeconomics of complex economies: evolutionary, institutional, and complexity perspectives. Academic Press, London . https://doi.org/10.1016/C2012-0-06498-8
Embrechts P, Klüppelberg C, Mikosch T (1997) Modelling extremal events. Springer, Berlin. https://doi.org/10.1007/978-3-642-33483-2. http://link.springer.com/10.1007/978-3-642-33483-2
FAO (2015) The impact of disasters and crises on agriculture and food security. Tech. rep., Food and Agriculture Organization of the United Nations
FAO (2018) The state of food and agriculture: migration, agriculture, and rural development. Tech. rep., Food and Agriculture Organization of the United Nations (FAO), Rome, Italy
Farmer JD, Foley D (2009) The economy needs agent-based modelling. Nature 460(August):685–686. https://doi.org/10.1038/460685a. http://www.nature.com/doifinder/10.1038/460685a, arXiv:0028-0836
Gaupp F, Pflug G, Hochrainer-Stigler S, Hall J, Dadson S (2017) Dependency of crop production between global breadbaskets: a copula approach for the assessment of global and regional risk pools. Risk Anal 37(11):2212–2228. https://doi.org/10.1111/risa.12761
Gaupp F, Hall J, Mitchell D, Dadson S (2019) Increasing risks of multiple breadbasket failure under 1.5 and 2 C global warming. Agric Syst. https://doi.org/10.1016/j.agsy.2019.05.010
Gaupp F, Hall J, Hochrainer-Stigler S, Dadson S (2020) Changing risks of simultaneous global breadbasket failure. Nat Clim Change 10(1):54–57. https://doi.org/10.1038/s41558-019-0600-z
Gemmetto V, Squartini T, Picciolo F, Ruzzenenti F, Garlaschelli D (2016) Multiplexity and multireciprocity in directed multiplexes. Phys Rev E 94(4):1–20. https://doi.org/10.1103/PhysRevE.94.042316. arXiv:1411.1282
Gilbert N (2008) Agent-based models (quantitative applications in the social sciences), annotated edn. Sage Publications, Inc. http://www.worldcat.org/isbn/1412949645
Hallegatte S, Dumas P (2009) Can natural disasters have positive consequences? Investigating the role of embodied technical change. Ecol Econ 68(3):777–786. https://doi.org/10.1016/j.ecolecon.2008.06.011
Hallegatte S, Ghil M (2008) Natural disasters impacting a macroeconomic model with endogenous dynamics. Ecol Econ 68(1–2):582–592. https://doi.org/10.1016/j.ecolecon.2008.05.022
Hallegatte S, Przyluski V (2010) The economics of natural disasters. CESifo Forum 11(2):14–24. https://doi.org/10.1146/annurev-resource-073009-104211
Hallegatte S, Hourcade JC, Dumas P (2007) Why economic dynamics matter in assessing climate change damages: illustration on extreme events. Ecol Econ 62(2):330–340. https://doi.org/10.1016/j.ecolecon.2006.06.006. http://linkinghub.elsevier.com/retrieve/pii/S0921800906003041
Halu A, Mondragón RJ, Panzarasa P, Bianconi G (2013) Multiplex pagerank. PLoS ONE 8(10):1–10. https://doi.org/10.1371/journal.pone.0078293. arXiv:1306.3576
Haraguchi M, Lall U (2015) Flood risks and impacts: a case study of Thailand’s floods in 2011 and research questions for supply chain decision making. Int J Disaster Risk Reduct. https://doi.org/10.1016/j.ijdrr.2014.09.005
Hochrainer-Stigler S, Patnaik U, Kull D, Singh P, Wajih S (2011) Disaster financing and poverty traps for poor households: realities in Northern India. Int J Mass Emerg Disasters 29(1):57–82
Horwich G (2000) Economic lessons of the Kobe earthquake. Econ Dev Cult Change 48(3):521–542. https://doi.org/10.1086/452609. http://www.journals.uchicago.edu/doi/10.1086/452609
Hurd TR, Gleeson JP (2011) A framework for analyzing contagion in banking networks pp 1–23. https://doi.org/10.2139/ssrn.1945748. arxiv:1110.4312
IDMC (2018) GRID: global report on internal displacement 2018. Tech. rep., Internal Displacement Monitoring Center, Geneva, Switzerland. http://www.internal-displacement.org/global-report/grid2018/
IPCC (2018) An IPCC special report on the impacts of global warming of 1.5C above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change. Tech. rep., Inter-governmental Panel on Climate Change
Ishiwata H, Yokomatsu M (2018) Dynamic stochastic macroeconomic model of disaster risk reduction investment in developing countries. Risk Anal 38(11):2424–2440. https://doi.org/10.1111/risa.13144
Janetos A, Justice C, Jahn M, Obersteiner M, Glauber J, Mulhern W (2017) The risks of multiple breadbasket failures in the 21st century: a science research agenda. Tech. Rep. March, Knowledge Systems for Sustainability (KSS) and the Frederick S. Pardee Center for the Study of the Longer-Range Future (BU), Boston, Massachussetts
Jaworski P, Durante F, Härdle WK, Rychlik T (eds) (2010) Copula theory and its applications, vol 198. Lecture notes in statistics. Springer, Berlin
Joe H (1997) Multivariate models and multivariate dependence concepts. CRC Press, Boca Raton
Joerin J, Joerin R (2013) Reviewing the similarities of the 2007-08 and 1972-74 food crisis. Tech. Rep. September
Jongman B, Hochrainer-Stigler S, Feyen L, Aerts JC, Mechler R, Botzen WJ, Bouwer LM, Pflug G, Rojas R, Ward PJ (2014) Increasing stress on disaster-risk finance due to large floods. Nat Clim Change 4(4):264–268. https://doi.org/10.1038/nclimate2124
Kadiyala S, Harris J, Headey D, Yosef S, Gillespie S (2014) Agriculture and nutrition in India: mapping evidence to pathways. Ann New York Acad Sci 1331(1):43–56. https://doi.org/10.1111/nyas.12477
Kahn ME (2005) The death toll from natural disasters: the role of income, geography and institutions. Rev Econ Stat 87(2):271–284
Katsafados P, Papadopoulos A, Varlas G, Papadopoulou E, Mavromatidis E (2014) Seasonal predictability of the 2010 Russian heat wave. Nat Hazards Earth Syst Sci. https://doi.org/10.5194/nhess-14-1531-2014
Kc S, Wurzer M, Speringer M, Lutz W (2018) Future population and human capital in heterogeneous India. Proc Natl Acad Sci 115(33):8328–8333. https://doi.org/10.1073/pnas.1722359115
Kivelä M, Arenas A, Barthelemy M, Gleeson JP, Moreno Y, Porter MA (2014) Multilayer networks. J Complex Netw 2(3):203–271. https://doi.org/10.1093/comnet/cnu016. arXiv:1309.7233
Klabunde A, Willekens F (2016) Decision-making in agent-based models of migration: state of the art and challenges. Eur J Popul 32(1):73–97. https://doi.org/10.1007/s10680-015-9362-0
Krishna Kumar K, Rupa Kumar K, Ashrit RG, Deshpande NR, Hansen JW (2004) Climate impacts on Indian agriculture. Int J Climatol 24(11):1375–1393. https://doi.org/10.1002/joc.1081
Kurowicka D, Cooke RM (2006) Uncertainty analysis with high dimensional dependence modelling. Wiley, New York
Lau WKM, Kim KM (2012) The 2010 Pakistan flood and Russian heat wave: teleconnection of hydrometeorological extremes. J Hydrometeorol. https://doi.org/10.1175/JHM-D-11-016.1
Loayza NV, Olaberría E, Rigolini J, Christiaensen L (2012) Natural disasters and growth: going beyond the averages. World Dev 40(7):1317–1336. https://doi.org/10.1016/j.worlddev.2012.03.002
Magnani M, Monreale A, Rossetti G, Giannotti F (2013) On multidimensional network measures. In: Italian conference on sistemi evoluti per le Basi di Dati (SEBD) pp 1–8. arXiv:1703.10511v1
Mechler R, Hochrainer S, Kull D, Chopde S, Singh P, Wajih S (2008) Risk to Resillience Study Team (2008) Uttar Pradesh drought cost benefit analysis: from risk to resillience working paper no. 5
Mechler R, Bouwer LM, Linnerooth-Bayer J, Hochrainer-Stigler S, Aerts JCJH, Surminski S, Williges K (2014) Managing unnatural disaster risk from climate extremes. Nat Clim Change 4(4):235–237. https://doi.org/10.1038/nclimate2137
Mehrabi Z (2020) Food system collapse. Nat Clim Change 10(1):16–17. https://doi.org/10.1038/s41558-019-0643-1
Naqvi A (2017) Deep impact: geo-simulations as a policy toolkit for natural disasters. World Dev 99:395–418. https://doi.org/10.1016/j.worlddev.2017.05.015
Naqvi A, Rehm M (2014a) A multi-agent model of a low income economy: simulating the distributional effects of natural disasters. J Econ Interact Coord 9(2):275–309. https://doi.org/10.1007/s11403-014-0137-1
Naqvi A, Rehm M (2014b) Simulating natural disasters—a complex systems framework. In: 2014 IEEE conference on computational intelligence for financial engineering & economics (CIFEr), IEEE, London, UK, pp 414–421. https://doi.org/10.1109/CIFEr.2014.6924103
Nelsen RB (2007) An introduction to copulas. Springer, Berlin
Okuyama Y (2004) Modeling spatial economic impacts of an earthquake: input–output approaches. Disaster Prev Manag: Int J 13(4):297–306. https://doi.org/10.1108/09653560410556519
Okuyama Y (2007) Economic modeling for disaster impact analysis: past, present, and future. Econ Syst Res 19(2):115–124. https://doi.org/10.1080/09535310701328435
Okuyama Y (2011) Critical review of methodologies on disaster impact estimation. UN Assessment on the Economics of Disaster Risk Reduction pp 1–27. https://doi.org/10.1007/s13398-014-0173-7.2. arXiv:9809069v1
Okuyama Y, Santos JR (2014) Disaster impact and input–output analysis. Econ Syst Res 26(1):1–12. https://doi.org/10.1080/09535314.2013.871505
Pflug GC, Pichler A (2018) Systemic risk and copula models. Cent Eur J Oper Res 26(2):465–483. https://doi.org/10.1007/s10100-018-0525-z
Poledna S, Molina-Borboa JL, Martínez-Jaramillo S, van der Leij M, Thurner S (2015) The multi-layer network nature of systemic risk and its implications for the costs of financial crises. J Financ Stab 20:70–81. https://doi.org/10.1016/j.jfs.2015.08.001. arXiv:1505.04276
Poledna S, Miess M, Thurner T (2018) Economic forecasting with an agent-based model
Prudhomme C, Genevier M (2011) Can atmospheric circulation be linked to flooding in Europe? Hydrol Process 25(7):1180–1190. https://doi.org/10.1002/hyp.7879
Ratnam JV, Behera SK, Ratna SB, Rajeevan M, Yamagata T (2016) Anatomy of Indian heatwaves. Sci Rep. https://doi.org/10.1038/srep24395
Rose A (2004) Defining and measuring economic resilience to disasters. Disaster Prevent Manag 13(4):307–314. https://doi.org/10.1108/09653560410556528
Rose A, Guha GS (2004) Computable general equilibrium modeling of electric utility lifeline losses from earthquakes. In: Okuyama Y, Chang SE (eds) Modeling spatial and economic impacts of disasters. Springer, New York, pp 119–141
Rose A, Liao SY (2005) Modeling regional economic resilience to disasters: a computable general equilibrium analysis of water service disruptions. J Region Sci 45(1):75–112. https://doi.org/10.1111/j.0022-4146.2005.00365.x. http://doi.wiley.com/10.1111/j.0022-4146.2005.00365.x
Rose A, Miernyk W (1989) Input–output analysis: the first fifty years. Econ Syst Res 1(2):229–272. https://doi.org/10.1080/09535318900000016. http://www.tandfonline.com/doi/full/10.1080/09535318900000016
Rose A, Benavides J, Chang SE, Szezesniak P, Lim D (1997) The regional economic impact of an earthquake: direct and indirect effects of electricity lifeline disruptions. J Region Sci 37(3):437–458
Shiau JT (2006) Fitting drought duration and severity with two-dimensional copulas. Water Resour Manag 20(5):795–815. https://doi.org/10.1007/s11269-005-9008-9
Skidmore M, Toya H (2002) Do natural disasters promote long-run growth? Econ Inq 40(4):664–687. https://doi.org/10.1093/ei/40.4.664
Sklar M (1959) Fonctions de répartition à n dimensions et leurs marges. Université Paris 8
Skoufias E (2003) Economic crises and natural disasters: coping strategies and policy implications. World Dev 31(7):1087–1102. https://doi.org/10.1016/S0305-750X(03)00069-X
Stolbova V, Monasterolo I, Battiston S (2018) A financial macro-network approach to climate policy evaluation. Ecol Econ 149:239–253. https://doi.org/10.1016/j.ecolecon.2018.03.013
Strobl E (2012) The economic growth impact of natural disasters in developing countries: evidence from hurricane strikes in the Central American and Caribbean regions. J Dev Econ 97(1):130–141. https://doi.org/10.1016/j.jdeveco.2010.12.002
Tesfatsion L (2006) Agent-based computational economics: a constructive approach to economic theory. In: Tesfatsion L, Judd KL (eds) Handbook of computational economics, general handbooks in economics, vol 2. Elsevier, Amsterdam, pp 831–880
Thurner S, Poledna S (2013) DebtRank-transparency: controlling systemic risk in financial networks. Sci Rep 3:1888. https://doi.org/10.1038/srep01888. arXiv:1301.6115v1
Tsuchiya S, Tatano H, Okada N (2007) Economic loss assessment due to railroad and highway disruptions. Econ Syst Res 19(2):147–162. https://doi.org/10.1080/09535310701328567
Ueda T, Koike A, Iwakami K (2001) Economic damage assessment of catastrophes in high speed rail network. In: Proceedings of the 1st workshop on ’comparative study of urban earthquake disaster management’, pp 13–19
UNDRR (2019) Global assessment report on disaster risk reduction. Tech. rep., United Nations Office on Disaster Risk Reduction
Vicente-Serrano SM, López-Moreno JI (2006) The influence of atmospheric circulation at different spatial scales on winter drought variability through a semi-arid climatic gradient in Northeast Spain. Int J Climatol 26(11):1427–1453. https://doi.org/10.1002/joc.1387
Weinraub B (1974a) India Requesting Food Aid from U.S
Weinraub B (1974b) India, slow to grasp oil crisis, now fears severe economic loss
Wilson R (1982) Earthquake vulnerability analysis for economic impact assessment. Tech. rep., Federal Emergency Management Agency (FEMA), Information Resources Management Office, Washington DC
Acknowledgements
Open access funding provided by International Institute for Applied Systems Analysis (IIASA).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This paper was partly funded by the IIASA-IDMC-OFDA Grant No. AID-OFDA-G-17-00285 and by the Austrian Climate Research Program (ACRP) Grant No. KR15AC8K12597.
Appendices
Appendix A: Data and calibration
Appendix B: Copula trees
A nested set of trees depicts the decomposition of the joint density of de-trended wheat yields. Each tree consists of a set of nodes connected by edges. The nodes in tree \(T_j\) determine the labels of the edges in tree \(T_{j+1}\). Trees help to identify the different pair-copula decomposition of an RVine copula (Fig. 7).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Naqvi, A., Gaupp, F. & Hochrainer-Stigler, S. The risk and consequences of multiple breadbasket failures: an integrated copula and multilayer agent-based modeling approach. OR Spectrum 42, 727–754 (2020). https://doi.org/10.1007/s00291-020-00574-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00291-020-00574-0