Abstract
During collaboration between neighboring pickers in a bucket brigade order picking, the downstream picker frequently experiences productivity loss in the form of a hand-off delay while waiting for a new tote from the upstream picker. This paper proposes an analytical model to quantify the hand-off delay of downstream pickers under non-deterministic pick times and non-instantaneous walk times of the upstream pickers. Numerical analyses show the effects of the magnitude of pick time, the variation of pick time, and the forward walk time on the hand-off delay, and simulation models show the effects of the number of pickers and their skill differences. We conclude that stable pick times are especially important to reduce hand-off delays and that slowest-to-fastest picker assignments offset hand-off delays with the blocking delays.

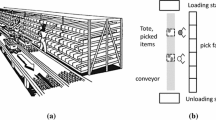
(Adapted from Bartholdi and Eisenstein (1996a))











Similar content being viewed by others
References
Bartholdi JJ, Eisenstein DD (1996a) Bucket brigades: a self-organizing order-picking system for a warehouse. Sch Ind Syst Eng. https://doi.org/10.1287/opre.49.5.710.10609
Bartholdi JJ, Eisenstein DD (1996b) A production line that balances itself. Oper Res 44(1):21–34
Bartholdi JJ, Eisenstein DD (2005) Using bucket brigades to migrate from craft manufacturing to assembly lines. Manuf Serv Oper Manag 7(2):121–129. https://doi.org/10.1287/msom.1040.0059
Bartholdi JJ, Eisenstein DD, Foley RD (2001) Performance of bucket brigades when work is stochastic. Oper Res 49(5):710–719
Bartholdi JJ, Eisenstein DD, Lim YF (2006) Bucket brigades on in-tree assembly networks. Eur J Oper Res 168(3):870–879
Bartholdi JJ, Eisenstein DD, Lim YF (2009) Deterministic chaos in a model of discrete manufacturing. Naval Res Logist (NRL) 56(4):293–299. https://doi.org/10.1002/nav.20337
Bartholdi JJ, Eisenstein DD, Lim YF (2010) Self-organizing logistics systems. Ann Rev Control 34(1):111–117. https://doi.org/10.1016/j.arcontrol.2010.02.006
Gue KR, Meller RD, Skufca JD (2006) The effects of pick density on order picking areas with narrow aisles. IIE Trans 38(10):859–868
Hong S (2014) Two-worker blocking congestion model with walk speed m in a no-passing circular passage system. Eur J Oper Res 235(3):687–696. https://doi.org/10.1016/j.ejor.2013.10.013
Hong S, Johnson AL, Peters BA (2015) Quantifying picker blocking in a bucket brigade order picking system. Int J Prod Econ 170(Part C):862–873. https://doi.org/10.1016/j.ijpe.2015.04.012
Hong S, Johnson AL, Peters BA (2016) Order batching in a bucket brigade order picking system considering picker blocking. Flex Serv Manuf 28(3):425–441. https://doi.org/10.1007/s10696-015-9223-5
Hopp WJ, Spearman ML (2008) Factory physics. The McGraw-Hill/Irwin series operations and decision sciences, 3rd edn. McGraw-Hill/Irwin, New York
Koo P-H (2009) The use of bucket brigades in zone order picking systems. OR Spectr 31(4):759–774. https://doi.org/10.1007/s00291-008-0131-x
Lim YF (2011) Cellular bucket brigades. Oper Res 59(6):1539–1545. https://doi.org/10.1287/opre.1110.0958
Lim YF (2012) Order-picking by cellular bucket brigades: a case study. In: Warehousing in the global supply chain: advanced models, tools and applications for storage systems. Springer, pp 71-85
Lim YF (2017) Performance of cellular bucket brigades with hand-off times. Prod Oper Manag. https://doi.org/10.1111/poms.12739
Lim YF, Wu Y (2014) Cellular bucket brigades on U-lines with discrete work stations. Prod Oper Manag 23(7):1113–1128. https://doi.org/10.1111/poms.12091
Lim YF, Yang KK (2009) Maximizing throughput of bucket brigades on discrete work stations. Prod Oper Manag 18(1):48–59
Parikh PJ, Meller RD (2009) Estimating picker blocking in wide-aisle order picking systems. IIE Trans 41:232–246
Parikh PJ, Meller RD (2010) A note on worker blocking in narrow-aisle order picking systems when pick time is non-deterministic. IIE Trans 42(6):392–404
Ross SM (2010) Introduction to probability models, 10th edn. Academic Press, Boston. https://doi.org/10.1016/B978-0-12-375686-2.50001-6
Acknowledgements
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2014R1A1A2053550).
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 The interdependency in the hand-off location and the hand-off delay
Let X i be the ith hand-off. Then, we evaluate the interdependency in the hand-off location and the hand-off delay. We conduct a simulation to observe the hand-off location and the hand-off delay between ith hand-off and i + 1st hand-off. Figure 13 shows the scatter plot of ith hand-off and the i + 1st hand-off. Figure 13a indicates the correlation between the hand-off locations, which is about − 0.47 correlation value. The correlation coefficient is relatively high as shown in the scatter plot comparison. Vice versa, in the scatter plot of the hand-off delay between ith hand-off and i + 1st hand-off, we look for a clear linear trend, which is close to a relative randomness. The correlation coefficient appears smaller than 0.1.
The autocorrelation analysis in Fig. 14 generalizes the result above. In Fig. 14a, the autocorrelation analysis of the hand-off location shows relatively high autocorrelation values and patterns over the increase in lags. However, in Fig. 14b, the autocorrelation analysis of the hand-off delay shows smaller values and it appears that there is little likelihood of dependence between delays.
An experiment over larger p and other pick time distribution in Figs. 15 and 16 confirms the observations. We consider an exponential pick time situation with higher pick probability. The similar results repeat over the hand-off locations and the hand-off delay. Consistently, the scatter plots and autocorrelation plots show a relatively high dependency in the hand-off location and a relatively high randomness in the hand-off delay.
In conclusion, the dependency in the hand-off location does not affect the hand-off delay under the stochastic pick time and the finite walk time. Intuitively, hand-off locations “remember” their last hand-offs while the arrival times of downstream pickers do not repeat the previous hand-off times in the stochastic picking.
1.2 Detailed calculation of the expected waiting time (E[W])
Excess-time model The expected waiting time (E[W]) is E[PT2]/2E[PT] when pickers return randomly, the walk speed is infinite, and there is no blocking delay.
Proof
The renewal process is derived based on the definition in Ross (2010). It follows that there is a renewal process {N(t), t ≥ 0} having inter-arrival times PT n , n ≥ 1, and assuming a hand-off when a downstream picker meets an upstream picker. We assume the hand-off to be a reward. We define W(t) to equal the time from t until the next stop, a renewal, and, as such, it represents the remaining (residual or excess) life of the pick at time t. Over the renewal process {PT(t), t ≥ 0}, we measure the time of W(t) as the excess time Y(t) = An+1(t) – t.
Then, according to the renewal reward process (Ross 2010), the time to completion at time t is the time from t until the next renewal and becomes the remaining time to completion at time t. We assume the new waiting time t 0 be a reward during a renewal cycle. We write the average value of the excess as,
In addition, over the given cycle length PT, we obtain the following expected value,
The expectation for the overall PT ranges from 0 to infinite and PT has a distribution F,
where \( \, E\left[ {\int_{0}^{X} {\left( {X - t} \right) \cdot {\text{d}}t} } \right] \, = \, \int_{0}^{\infty } {\int_{0}^{X} {\left( {X - t} \right) \cdot {\text{d}}t} \cdot {\text{d}}F\left( X \right)} \).
The time of a pick cycle is an inter-arrival time between the picks having the distribution function F. Then, \( E\left[ {{\text{Pick}}\;{\text{time}}\;{\text{of}}\;{\text{a}}\;{\text{stop}}} \right] = E\left[ {PT} \right] \).
Thus, we express the expected waiting time (E[W]) as,
□.
1.3 Proof of Theorem 1
When a downstream picker returns randomly and meets an upstream picker who is picking, the expected waiting time of the downstream picker (E[HD p ]) is
Proof
The expected delay time per hand-off occurrence (HD p ) is derived when an upstream picker is picking by replacing W with HD p in Fig. 5. First, we estimate E[PT]. Given these pick and walk decision patterns, the expected pick time as a stop (PT) is equal to the expected number of picks at a pick face · unit pick time (τ) = the expected number of picks at a pick face. Formulate E[PT] as:
Second, E[PT2] becomes
Finally, we obtain the expected hand-off delay during picking(HD p ) as
□.
1.4 Calculation of Eq. (8)
E[HD w ] becomes
1.5 Calculation of Eq. (9)
The expected delay time per hand-off occurrence and the expected delay time per order are derived when there are instantaneous walk times, a large number of picks, and no picker blocking. Obtain the expected hand-off delay as
1.6 Proof of Theorem 3
From Eq. (9), we define the lower bound and upper bound of the HD. The lower bound inequality holds by simplifying \( E[PT^{2} ] = \sum\nolimits_{i = 1}^{m} {i^{2} \cdot p^{i} q} + m^{2} p^{m + 1} \ge m^{2} p^{m + 1} \) as follows:
The following limiting property shows that the lower bound is bounded by (m + ft)/2.
Similarly, the upper bound inequality holds by replacing \( E[PT^{2} ] = \sum\nolimits_{i = 1}^{m} {i^{2} \cdot p^{i} q} + m^{2} p^{m + 1} \le q\sum\nolimits_{i = 1}^{m} {i^{2} } + m^{2} p^{m + 1} \) as follows:
The upper bound also is bounded by (m + ft)/2 (see “Proof of Theorem 3” section in Appendix for details):
As both the lower bound (Eq. (14) and the upper bound (Eq. (15)) converge to the same value (m + ft)/2, E[HD] results in (m + ft)/2:
□.
1.7 General distributions and calculation steps of Eq. (11)
1.8 General distributions and calculation steps
If the pick duration follows the uniform distribution of Unif(a,b) where b ≥ a ≥ 0.
If the pick duration follows the exponential distribution of mean = a where a > 0.
If the pick duration follows the triangular distribution of triangular(a,b,c) where a ≥ c ≥ b ≥ 0.
There are numerical examples of three pick time distributions: Uni = uniform [min,max] = uniform [a,b] = [0.0, 2.0]; Exp = exponential [mean] = exp[a] = [1.0]; and Tri = triangular [min, mode, max] = triangular [a, b, c] = [0.5, 1.0, 1.5], where the time unit represents the time spent to retrieve an item.
Rights and permissions
About this article
Cite this article
Hong, S. The effects of picker-oriented operational factors on hand-off delay in a bucket brigade order picking system. OR Spectrum 40, 781–808 (2018). https://doi.org/10.1007/s00291-018-0523-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00291-018-0523-5