Multi-species viscous models for tissue growth: incompressible limit and qualitative behaviour

Abstract

We introduce two 2D mechanical models reproducing the evolution of two viscous tissues in contact. Their main property is to model the swirling cell motions while keeping the tissues segregated, as observed during vertebrate embryo elongation. Segregation is encoded differently in the two models: by passive or active segregation (based on a mechanical repulsion pressure). We formally compute the incompressible limits of the two models, and obtain strictly segregated solutions. The two models thus obtained are compared. A striking feature in the active segregation model is the persistence of the repulsion pressure at the limit: a ghost effect is discussed and confronted to the biological data. Thanks to a transmission problem formulation at the incompressible limit, we show a pressure jump at the tissues’ boundaries.

Appendices

Derivation of the transmission problem

This section is devoted to the derivation of the transmission problems in ${\mathbb {R}}^2$. We first do the complete computations of the derivation of the transmission problem in the case of a single species for simplicity. Similar rigorous computations (though not shown in this paper) hold for the transmission problems $(T_2)$ and $(T_{VM})$ respectively for the L-ESVM for a given $q^\infty$ and for the L-VM. We then present a formal version of the transmission problem when $q^{\infty }$ is a stationary solution of (32)–(33) (and not anymore a given $L^2$ function as in the simplified framework of Sects. 3.25).

1.1 Derivation of the transmission problem for the single species case

If we take either densities ($n_1$ or $n_2$) equal to zero in the VM, we obtain a single species model (SS) for the density and the velocity. The system (SS) is as follows: for all $(t,x) \in [0;+\infty )\times {\mathbb {R}}^{d}$,

$$\begin{aligned}&\partial _{t}n+ \nabla \cdot (nv)=nG(p_{\epsilon }), \end{aligned}$$

(75)

$$\begin{aligned}&-\beta \Delta v+v=-\nabla p_{\epsilon }, \end{aligned}$$

(76)

$$\begin{aligned}&p_{\epsilon }=\epsilon \frac{n}{1-n}. \end{aligned}$$

(77)

Notice here that this system, with the general form of the velocity we consider, includes the system in (Perthame and Vauchelet 2015) where the velocity is of gradient form. In this case, we can also obtain the incompressible limit by taking $\epsilon \xrightarrow {} 0$, and the limiting system can be easily deduced from (23)–(29) by taking either $n_1^\infty$ or $n_2^\infty$ equal to zero, and $q^\infty =0$.

A stationary transmission problem can also be formalized, and we obtain, as a straightforward consequence of the two-species case, the well-posedness and the elliptic regularity results (Theorem 3.8) as well as the expression of the pressure jump (Proposition 3.12). Note that the one-species system is elliptic for any $\beta >0$ and $g>0$, so that the results apply without any supplementary condition on these parameters.

The stationary system on the velocity in the single species case is posed in a bounded domain $\Theta \subset {\mathbb {R}}^2$. We assume $\Omega \subset \Theta$ to be a smooth bounded subdomain with $\overline{\Omega }\subset \Theta$.

The one-species problem coupled with homogeneous Dirichlet boundary conditions on $v^\infty$ is as follows,

$$\begin{aligned} (S_1) \;\; \left\{ \begin{array}{ll} -\beta \Delta v^{\infty }+v^{\infty }=- \nabla [(p^{*}-\frac{1}{g}\nabla \cdot v^{\infty })\chi _{\Omega }]&{} \;\text { on }\; \Theta , \\ v^{\infty }=0&{} \;\text { on }\; \partial \Theta , \end{array} \right. \end{aligned}$$

with $\chi _{\Omega }$ the indicator function of the domain $\Omega$.

Proposition A.1

(Transmission problem, one species) Let $\Omega$ be a smooth bounded domain with $\overline{\Omega }\subset \Theta$, and let $\Gamma {:=}\partial \Omega$ and $\Omega ^c{:=}\Theta \backslash \overline{\Omega }$. Let $\beta >0$, $g>0$ and $p^*>0$.

Then the solution of system $(S_1)$ solves the following transmission problem $(T_1)$,

$$\begin{aligned} (T_1) \;\; \left\{ \begin{array}{ll} -\beta \Delta v^{\infty } +v^{\infty } -\frac{1}{g} \nabla (\nabla \cdot v^{\infty })= 0 &{} \;\text { in }\; \Omega , \\ -\beta \Delta v^{\infty } +v^{\infty }=0 &{} \;\text { in }\; \Omega ^c, \\ \beta [(\nabla v^{\infty })_{\Omega }- (\nabla v^{\infty })_{\Omega ^c}]\vec {\nu } = [p^{*}-\frac{1}{g}(\nabla \cdot v^{\infty })_{\Omega }] \vec {\nu } &{} \;\text { on }\; \Gamma ,\\ (v^{\infty })_{\Omega }=(v^{\infty })_{\Omega ^c} &{} \;\text { on }\; \Gamma , \\ v^{\infty }=0 &{} \;\text { on }\; \partial \Theta , \end{array} \right. \end{aligned}$$

with $\vec {\nu }$ the outward normal on $\Gamma$ and with the notations $(\cdot )_\Omega$ and $(\cdot )_{\Omega ^c}$ defined in (41).

Remark A.2

Note that in the following proof we only use the $C^{1}$ regularity of $v^\infty$ in each subdomain (up to the boundary) ${\overline{\Omega }}$ and $\overline{\Omega ^c}$. This ensures that the proof remains valid for the case of more than one species, thanks to Theorem 3.3.

Proof

We consider the weak formulation of $(S_1)$,

$$\begin{aligned}&\beta \int _{\Theta } \nabla v^\infty :\nabla \phi \, dx+ \int _{\Theta } v^\infty \cdot \phi \, dx+\int _{\Theta }\left( p^*-\frac{1}{g}\nabla \cdot v^\infty \right) \chi _{\Omega }\nabla \cdot \phi \, dx=0, \nonumber \\&\quad \qquad \text { for all } \phi \; \in {\mathcal {C}}^\infty _c(\Theta )^2, \end{aligned}$$

(78)

where the Frobenius inner product is used in the first integral. Then by extension of test functions $\phi \in {\mathcal {C}}^{\infty }_{c}(\Omega )^2$ (by 0 outside $\Omega$) we obtain,

$$\begin{aligned} -\beta \Delta v^{\infty } -\frac{1}{g}\nabla (\nabla \cdot v^{\infty })+v^{\infty }=0 \; \;\text { in } {\mathcal {D}}'(\Omega ). \end{aligned}$$

Similarly, by extension of test functions $\phi \in {\mathcal {C}}^{\infty }_{c}(\Omega ^c)^2$ (by 0 outside $\Omega ^c$) we obtain,

$$\begin{aligned} -\beta \Delta v^{\infty } +v^{\infty }=0 \; \; \text { in } {\mathcal {D}}'(\Omega ^c). \end{aligned}$$

It remains to obtain the transmission conditions at the interface. For this, we use a sequence of smooth functions $(\chi _n)_n$ that are localized around the interface. More precisely these functions satisfy the following properties,

$$\begin{aligned} \chi _n \in C^\infty (\Theta ), \qquad \text {for all }n\ge 0 \text { large enough}, \end{aligned}$$

(79)

as well as,

$$\begin{aligned} \chi _{n} \xrightarrow [n \rightarrow \infty ]{L^{p}(\Theta )}0, \quad \text {for all } p \in [1,\infty ), \end{aligned}$$

(80)

and finally, for any function $w\in C(\overline{\Omega }) \cap C(\overline{\Omega ^c})$,

$$\begin{aligned} \lim _{n \rightarrow +\infty } \int _\Theta w \cdot \nabla \chi _{n}\, dx = \int _{\Gamma } (w)_{\Omega ^c} \cdot \vec {\nu }\, d\sigma (x)- \int _{\Gamma } (w)_\Omega \cdot \vec {\nu }\, d\sigma (x), \end{aligned}$$

(81)

with the notations of (41), with $\vec {\nu }$ the normal vector to $\Gamma$ and $d\sigma (x)$ the surface measure along $\Gamma$. Such sequence can be constructed explicitly.

Now, we consider a test function $\phi \in {\mathcal {C}}^{\infty }_{c}(\Theta )^2$, which does not necessarily vanish close to $\Gamma$, and define ${\tilde{\phi }}_{n}{:=}\phi \chi _n$. We insert the test function ${\tilde{\phi }}_{n}$ in (78) and get,

$$\begin{aligned} \beta \int _{\Theta }\nabla v^{\infty } :\nabla {\tilde{\phi }}_{n} \, dx +\int _{\Theta } v^{\infty } \cdot {\tilde{\phi }}_{n} \, dx = \int _{\Theta }(p^{*}-\frac{1}{g}\nabla \cdot v^{\infty }) \chi _{\Omega }\nabla \cdot {\tilde{\phi }}_{n}\, dx, \end{aligned}$$

(82)

which we rewrite,

$$\begin{aligned}&\beta \int _{\Theta } \chi _n \nabla v^{\infty } :\nabla \phi \, dx+ \beta \int _{\Theta }\nabla v^{\infty } :(\nabla \chi _n \otimes \phi ) \, dx +\int _{\Theta } v^{\infty } \cdot \phi \chi _n \, dx \end{aligned}$$

(83)

$$\begin{aligned}&\quad = \int _{\Theta } \chi _n (p^{*}-\frac{1}{g}\nabla \cdot v^{\infty }) \chi _{\Omega }\nabla \cdot \phi \, dx + \int _{\Theta }(p^{*}-\frac{1}{g}\nabla \cdot v^{\infty }) \chi _{\Omega }(\nabla \chi _n) \cdot \phi \, dx.\nonumber \\ \end{aligned}$$

(84)

Now using the convergences (80) and (81) together with the $C^1$ regularity of $v^\infty$ on each subdomain $\overline{\Omega }$ and $\overline{\Omega ^c}$ (up to the boundaries), we can pass to the limit $n\longrightarrow \infty$ and get,

$$\begin{aligned} \beta \int _{\Gamma } \left( \left( \nabla v^{\infty }\right) _{\Omega ^c} -\left( \nabla v^{\infty }\right) _{\Omega }\right) :(\vec {\nu } \otimes \phi ) \, d\sigma (x) = - \int _{\Gamma }(p^{*}-\frac{1}{g}\left( \nabla \cdot v^{\infty }\right) _\Omega ) \phi \cdot \vec {\nu } \, d\sigma (x). \end{aligned}$$

As this is verified for all $\phi \in {\mathcal {C}}^{\infty }_{c}(\Theta )^{2}$, particularly by extension of $\phi \in {\mathcal {C}}^{\infty }_{c}(\Gamma )^{2}$, we have the following condition on the interface,

$$\begin{aligned} \beta [(\nabla v^{\infty })_{\Omega }- (\nabla v^{\infty })_{\Omega ^c}]\cdot \vec {\nu } = [p^{*}-\frac{1}{g}(\nabla \cdot v^{\infty })_{\Omega }]\vec {\nu } \;\text { on }\; \Gamma . \end{aligned}$$

(85)

Then we see that a solution to the variational problem $(S_1)$, using the regularity result and the computations above, is a solution to $(T_1)$, where the continuity condition comes from the fact that $v^{\infty }$ is in $H^{1}(\Theta )^{2}$ and is then continuous across any hypersurface of $\Theta$. $\square$

This section was dedicated to the rigorous derivation of the transmission problem in the single-species case. Similar computations can be made for the two-species case by adapting the choice of the test function $\tilde{\phi _n}$ to be localized on the interface between the two tissues and on their outer boundaries.

1.2 A formal transmission problem for the general two species case

We now present the transmission problem one can obtain formally for the stationary L-ESVM, when $\Theta$, $\Omega _1$, $\Omega _2$ are chosen as in (34)–(37). Contrarily to the simplified framework of Sects. 3.2 and 5, where q is considered given, q is here a stationary solution of (32)–(33). We can rewrite these equations as in (58) in $\Omega _1$ and (59) in $\Omega _2$. Then, supposing that q is smooth enough inside each subdomain $\Omega _1$ and $\Omega _2$, the limiting model defined by the Eqs. (23)–(33) is equivalent at equilibrium to the following transmission problem $(T_2^*)$ considered on $\Theta$, and coupled with Dirichlet boundary conditions on $\partial \Theta$,

$$\begin{aligned}&(T_{2,\Omega _1}^*) \left\{ \begin{array}{ll} -\beta _1 \Delta v_1+v_1-\frac{1}{g_1}\nabla \nabla \cdot v_1=0 &{} \text { in } \Omega _1, \\ -\beta _2 \Delta v_2+v_2-\frac{1}{g_1}\nabla \nabla \cdot v_1=-\nabla q &{} \text { in } \Omega _1,\\ \nabla \cdot (\log (q+1)v_2)=g_2\log (q+1)[p_2^{*}-(p_1^{*}-\frac{1}{g_1}\nabla \cdot v_1 +q)] &{} \text { in } \Omega _1. \end{array} \right. \\&(T_{2,\Omega _2}^*)\left\{ \begin{array}{ll} -\beta _1 \Delta v_1+v_1-\frac{1}{g_2}\nabla \nabla \cdot v_2=-\nabla q &{} \text { in } \Omega _2, \\ -\beta _2 \Delta v_2+v_2-\frac{1}{g_2}\nabla \nabla \cdot v_2=0 &{} \text { in } \Omega _2, \\ \nabla \cdot (\log (q+1)v_1)=g_1\log (q+1)[p_1^{*}-(p_2^{*}-\frac{1}{g_2}\nabla \cdot v_2 +q)] &{} \text { in } \Omega _2. \end{array} \right. \\&(T_{2,\Omega ^c}^*) \left\{ \begin{array}{ll} -\beta _1 \Delta v_1+v_1=0 &{} \text { in } \Omega ^c,\\ -\beta _2 \Delta v_2+v_2=0 &{} \text { in } \Omega ^c.\\ \end{array} \right. \\&(T_{2,\Gamma _1}^*)\left\{ \begin{array}{ll} \beta _1 [(\nabla v_1)_{\Omega _1}-(\nabla v_1)_{\Omega ^c}]\cdot \vec {\nu }=[p_1^{*}-\frac{1}{g_1}(\nabla \cdot v_1)_{\Omega _1}] \vec {\nu } &{} \text { on } \Gamma _1,\\ \beta _2 [(\nabla v_2)_{\Omega _1}-(\nabla v_2)_{\Omega ^c}]\cdot \vec {\nu }=[p_1^{*}+(q)_{\Omega _1}-\frac{1}{g_1}(\nabla \cdot v_1)_{\Omega _1}] \vec {\nu } &{} \text { on } \Gamma _1,\\ (v_1)_{\Omega _1}=(v_1)_{\Omega ^c}, \quad (v_2)_{\Omega _1}=(v_2)_{\Omega ^c}, \quad (v_2q)_{\Omega _1}\cdot \vec {\nu }=0 &{} \text { on } \Gamma _1. \end{array} \right. \\&(T_{2,\Gamma _2}^*)\left\{ \begin{array}{ll} \beta _1 [(\nabla v_1)_{\Omega _2}-(\nabla v_1)_{\Omega ^c}]\cdot \vec {\nu }=[p_2^{*}+(q)_{\Omega _2}-\frac{1}{g_2}(\nabla \cdot v_2)_{\Omega _2}]\vec {\nu } &{} \text { on } \Gamma _2,\\ \beta _2 [(\nabla v_2)_{\Omega _2}-(\nabla v_2)_{\Omega ^c}]\cdot \vec {\nu }=[p_2^{*}-\frac{1}{g_2}(\nabla \cdot v_2)_{\Omega _2}]\vec {\nu } &{} \text { on } \Gamma _2,\\ (v_1)_{\Omega _2}=(v_1)_{\Omega ^c}, \quad (v_2)_{\Omega _2}=(v_2)_{\Omega ^c}, \quad (v_1q)_{\Omega _2}\cdot \vec {\nu }=0 &{} \text { on } \Gamma _2. \end{array} \right. \\&(T_{2,\Gamma }^*)\left\{ \begin{array}{ll} \beta _1 [(\nabla v_1)_{\Omega _1}-(\nabla v_1)_{\Omega _2}]\cdot \vec {\nu }=[(p_1^{*}-p_2^{*})-(q)_{\Omega _2}+\frac{1}{g_2}(\nabla \cdot v_2)_{\Omega _2}-\frac{1}{g_1}(\nabla \cdot v_1)_{\Omega _1}] \vec {\nu } &{} \text { on } \Gamma ,\\ \beta _2 [(\nabla v_2)_{\Omega _1}-(\nabla v_2)_{\Omega _2}]\cdot \vec {\nu }=[(p_1^{*}-p_2^{*})+(q)_{\Omega _1}+\frac{1}{g_2}(\nabla \cdot v_2)_{\Omega _2}-\frac{1}{g_1}(\nabla \cdot v_1)_{\Omega _1}]\vec {\nu } &{} \text { on } \Gamma ,\\ (v_1)_{\Omega _1}=(v_1)_{\Omega _2}, \quad (v_2)_{\Omega _1}=(v_2)_{\Omega _2},\quad v_1\cdot \vec {\nu }=v_2\cdot \vec {\nu }, \quad (q)_{\Omega _1}=(q)_{\Omega _2} &{} \text { on } \Gamma . \end{array} \right. \end{aligned}$$

This transmission problem gives us some insight on the behaviour of the system. It shows on the one hand that q does not have a jump on $\Gamma _1, \Gamma _2, \Gamma$, unlike the pressure p. On the other hand we can observe that the jumps of the gradients of the velocities of the two species at the interface $\Gamma$ are not equal in general.

Complementary numerical simulations

1.1 Segregation in the ESVM for initially mixed densities

In this section we exhibit the role of the repulsion pressure in the ESVM in segregating initially mixed densities. We consider initially two mixed densities $n_1$ and $n_2$ such that $n_1^{{ini}}(x)=~0.7\chi _{\{X \in {\mathbb {R}}^2; \Vert X\Vert \le 0.3\}}$ and $n_2^{{ini}}(x)=0.2\chi _{\{X=(x,y) \in {\mathbb {R}}^2 ; (x-0.4)^2+y^2\le 0.3\}}$, with $\chi$ the indicator function, see Fig. 6a. We use the following parameters $m=30, \alpha =0.001, \epsilon =0.1$, and choose the growth functions and viscosities as in (20). At initial time, the densities share a mixing region $n_1n_2$ represented in Fig. 6c. At $t=0.1$ we observe the segregation of the densities $n_1$ and $n_2$, see Fig. 6b. In Fig. 6d, we represent the mixing region between the densities at $t=0.1$ and notice that the maximum of $n_1n_2$ is largely reduced compared to $n_1^{{ini}}n_2^{{ini}}$.

Fig. 6

Segregation of two initially mixed population densities in the ESVM. The top panels represent the densities $n_1$ and $n_2$ respectively at time $t=0$ in Panel (a) and $t=0.1$ in Panel (b). The bottom panels represent the mixing region $n_1n_2$ respectively at $t=0$ in Panel (c) and $t=0.1$ in Panel (d)

These simulations highlight the role of the repulsion pressure in segregating the densities in finite time. This segregation is not perfect as some mixing still appears at the interface between the densities. At the incompressible limit we recover full segregation as proven in Sect. 4.

1.2 Effects of $\epsilon$, $\alpha$, and m on the solution of the ESVM

In this section we investigate the role of each of the parameters $\epsilon$, $\alpha$, and m on the solution of the ESVM in the case of the vertebrate embryo. In Fig. 7, we represent the densities $n_1$ and $n_2$ in the left panels and the mixing region (the product $n_1n_2$) in the right panels for different sets of parameters $(m,\alpha ,\epsilon )$ in the ESVM, at final time $t=0.1$.

Fig. 7

The left panels illustrate the densities $n_1$ (in green) and $n_2$ (in red) and the right panels illustrate the mixing region $n_1n_2$ at $t=~0.1$ in the ESVM with different sets of parameters $(m, \alpha ,\epsilon )$ (color figure online)

In Figs. 7a, b the ESVM is simulated with the parameters $(m,\alpha ,\epsilon )=~(30,0.001,0.1)$ , similar to those used in Sect. 2.3. In Fig. 7b, we notice the very thin region of mixing at the interface between the densities.

In Figs. 7c, d we change the value of the repulsion parameter to $m=10$ (with $\alpha$ and $\epsilon$ unchanged). We notice that the densities’ shapes are affected and the density overlap is more significant. Decreasing the parameter m then results in a concentrated mixing around the interface.

When changing the parameter $\alpha$ as in Figs. 7e, f where we set it to $\alpha =0.01$, the width of the mixing region increases significantly compared to 7b. This shows that large values of $\alpha$ result in the mixing of the densities on a larger region. Changing $\alpha$ also appears to affect the shape of the densities, with the PSM (density in red) enveloping posteriorly the NT (green species) compared to Fig. 7a. We note here that our choice of the parameter $\alpha$ is sufficient to maintain the stability of the system ESVM. We refer the reader to Chertock et al. (2019) where authors exhibit in dimension 1 (and with Darcy’s law for the velocities) the role of small values of $\alpha$ in creating instabilities with the appearance of alternating population densities.

Finally, we change the parameter $\epsilon$ and set it to 1 in Figs. 7g, h. The mixing between the densities is qualitatively not affected. The densities $n_1$ and $n_2$ reach a maximum of around 0.87 (lighter colors on the colorbar) compared to the other simulations where $\epsilon =0.1$ and the maximum is reached at around 0.98. A smaller $\epsilon$ increases the densities which become closer to the maximal density 1 as per our choice of pressure law (4). This observation exhibits the role of the parameter $\epsilon$ in controlling the congestion of the densities.

We note here that $\alpha$ and m cannot independently tend to their respective asymptotic limits as they are both involved in the segregation of the densities. In fact, $\alpha$ cannot be taken too small when m is large as it balances the instability of the system ESVM caused by the segregation pressure.

Overall, the observed effects of $\epsilon , \alpha$ and m on the ESVM in this preliminary parameter study are aligned with those observed in (Chertock et al. 2019).

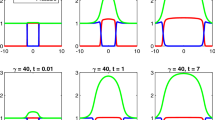
1.3 Segregation in the VM and in the L-VM

In this section we support our conjecture in Remark 3.10 by exhibiting numerical simulations of the VM with $\epsilon =1$, and the VM in asymptotic regime with $\epsilon =0.1$ in dimension 1 for clarity. The densities are initially segregated with ${n_1}^{{ini}}(x)=0.8\chi _{[0.3;1]}(x)$ (in green) and ${n_2}^{{ini}}(x)=0.8\chi _{[-1;-0.3]}(x)$ (in red) and the viscosities are taken as $(\beta _1,\beta _2)=(3,1)$. In Figs. 8a–c we show the initial data $n_1, n_2, p_\epsilon$ respectively in the VM with $\epsilon =1$ and in the VM with $\epsilon =0.1$. At $t=10$, the green and red densities appear to maintain their segregation throughout their evolution in the case $\epsilon =1$, see Fig. 8b, and $\epsilon =0.1$, see Fig. 8d. The pressure $p_\epsilon$ in orange is continuous (Figs. 8b–d) as expected as it is a function of the total density $n=n_1+n_2$, but its gradient exhibits sharp discontinuities at the interface.

To sum up, these simulations are strongly in favor of our conjecture (Remark 3.10) that the VM and the L-VM propagate segregation from initial data.

Fig. 8

Left: initial conditions for the densities $n_1, n_2$ and the pressure $p_\epsilon$ in the VM for $\epsilon =1$ (top) and $\epsilon =0.1$ (bottom). Right: the densities and the pressure at $t=10$ in the VM for $\epsilon =1$ (top) and $\epsilon =0.1$ (bottom) (color figure online)

Numerical scheme for the L-VM

The numerical simulations of the L-VM are performed in Freefem++ (Hecht 2012) using a finite element scheme. The densities are initialized as indicator functions,

$$\begin{aligned} {n_1}^{{ini}}(x)=\chi _{\Omega _1^{{ini}}}(x) \quad \text{ and } \quad {n_2}^{{ini}} (x)=\chi _{\Omega _2^{{ini}}}(x), \end{aligned}$$

with $\Omega _1^{{ini}} = [-1/3;1/3]\times [-1; 0]$ and $\Omega _2^{{ini}} = ([-1;-1/3]\cup [1/3;1])\times [-1;0]$. We consider solutions under the form of an indicator function and therefore:

$$\begin{aligned} {n_1}(x,t)=\chi _{\Omega _1(t)}(x) \quad \text{ and } \quad {n_2}(x,t)=\chi _{\Omega _2(t)}(x). \end{aligned}$$

The growth functions are considered linear as in (39). At the initialization a triangular mesh is generated by Freefem++. At each time step the velocity is computed according to the variational formulation of (47)–(48), combined with the complementary relation (50). Thus for all $(\phi _1, \phi _2) \in {\mathcal {C}}_c^\infty (\Theta )$ we have,

$$\begin{aligned}&\beta _1 \int _{\Theta } \nabla v_1^\infty :\nabla \phi _1 + \int _{\Theta } v_1^\infty \cdot \phi _1 \\&\quad = \int _{\Omega _1(t)} \left( p^*_1-\frac{1}{g_1} \nabla \cdot v_1^\infty \right) ~\nabla \cdot \phi _1 + \int _{\Omega _2(t)} \left( p^*_2-\frac{1}{g_2} \nabla \cdot v_2^\infty \right) ~\nabla \cdot \phi _1,\\&\beta _2 \int _{\Theta } \nabla v_2^\infty :\nabla \phi _2 + \int _{\Theta } v_2^\infty \cdot \phi _2 \\&\quad = \int _{\Omega _1(t)} \left( p^*_1-\frac{1}{g_1} \nabla \cdot v_1^\infty \right) ~\nabla \cdot \phi _2 + \int _{\Omega _2(t)} \left( p^*_2-\frac{1}{g_2} \nabla \cdot v_2^\infty \right) ~\nabla \cdot \phi _2. \end{aligned}$$

The solutions of this system with Dirichlet boundary conditions are easily computed in Freefem++ using piecewise constant discontinuous finite element (P0 element). We then compute the new domains $\Omega _1$ and $\Omega _2$ by moving the mesh with the new velocities. Note that the movement of the mesh needs to be carefully performed to ensure triangles are not flipping over.