Theoretical modeling of collaterally sensitive drug cycles: shaping heterogeneity to allow adaptive therapy

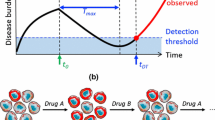
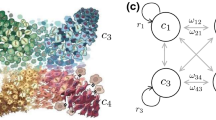
Abstract

In previous work, we focused on the optimal therapeutic strategy with a pair of drugs which are collaterally sensitive to each other, that is, a situation in which evolution of resistance to one drug induces sensitivity to the other, and vice versa. Yoona (Bull Math Biol 8:1–34,Yoon et al. 2018) Here, we have extended this exploration to the optimal strategy with a collaterally sensitive drug sequence of an arbitrary length, N. To explore this, we have developed a dynamical model of sequential drug therapies with N drugs. In this model, tumor cells are classified as one of N subpopulations represented as $\{R_i|i=1,2,...,N\}$. Each subpopulation, $R_i$, is resistant to ‘$Drug\ i$’ and each subpopulation, $R_{i-1}$ (or $R_N$, if $i=1$), is sensitive to it, so that $R_i$ increases under ‘$Drug\ i$’ as it is resistant to it, and after drug-switching, decreases under ‘$Drug\ i+1$’ as it is sensitive to that drug(s). Similar to our previous work examining optimal therapy with two drugs, we found that there is an initial period of time in which the tumor is ‘shaped’ into a specific makeup of each subpopulation, at which time all the drugs are equally effective ($\mathcal {R}^*$). After this shaping period, all the drugs are quickly switched with duration relative to their efficacy in order to maintain each subpopulation, consistent with the ideas underlying adaptive therapy. West(Canver Res 80(7):578–589Gatenby et al. 2009) and Gatenby (Cancer Res 67(11):4894–4903West et al. 2020). Additionally, we have developed methodologies to administer the optimal regimen under clinical or experimental situations in which no drug parameters and limited information of trackable populations data (all the subpopulations or only total population) are known. The therapy simulation based on these methodologies showed consistency with the theoretical effect of optimal therapy .

Appendices

Appendix A Differential system of instantaneous drug switch

Definition

In addition to the definitions from Table 1, we defines further notations to facilitate the descriptions on proofs.

Table 1 Definitions of parameters and variables related to System (1)

$\mathcal {D}_i:=\mathcal {D}(i) \in \mathbb {R}^{N \times N}$, $\mathcal {M}_i(t):=\left( m_{j,k}^i(t)\right) \in \mathbb {R}^{N \times N}$, $\mathcal {L}_{i,\epsilon }:=\mathcal {M}_i(f_i \ \epsilon )$

with

$$\begin{aligned} m_{j,k}^i(t)=\left\{ \begin{array}{ll} e^{\lambda _r^i \ t} &{} \text {if} \ j=k=i \\ e^{\lambda _s^i \ t} &{} \text {if} \ j=k=i' \\ e^{\lambda _0^i \ t} &{} \text {if} \ j=k \not \in \{i,i'\} \\ \frac{g_0^i \ g_s^i \ e^{\lambda _0^i t} \left( e^{\lambda _r^i t}-1\right) \left( 1-e^{-\left( \lambda _0^i-\lambda _s^i\right) t}\right) }{\lambda _r^i \left( \lambda _0^i-\lambda _s^i\right) } &{} \text {if} \ j=i \text { and } k=i' \\ \frac{g_0^i \ e^{\lambda _0^i t} \left( e^{\lambda _r^i t}-1\right) }{\lambda _r^i} &{} \text {if} \ j=i \text { and } k \not \in \{i,i'\} \\ \frac{\overline{g_0^i}\left( e^{\lambda _0^i t}-e^{\lambda _s^i t}\right) }{\lambda _0^i-\lambda _s^i} &{} \text {if} \ k=i' \text { and } j \not \in \{i,i'\} \\ 0 &{} \text {otherwise} \end{array} \right. \end{aligned}$$

Also, we will use the following notation of product of an arbitrary sequence of matrices, $\mathcal {A}_i$, $\mathcal {A}_{i+1}$, $\ldots$, $\mathcal {A}_j$.

$$\begin{aligned} \overset{\curvearrowleft }{\displaystyle \prod ^{j}_{k=i}}\mathcal {A}_k=\mathcal {A}_j \mathcal {A}_{j-1} \cdots \mathcal {A}_{i+1}\mathcal {A}_i \end{aligned}$$

Proposition A.1

Under the therapy with $Drug \ i$:

$$\begin{aligned} \mathcal {R}'(t) = \mathcal {D}_i \ \mathcal {R}(t), \ \mathcal {R}(t_0+\Delta t) = \mathcal {M}_i(\Delta t) \ \mathcal {R}(t_0). \end{aligned}$$

Proposition A.2

$\left. {\mathcal {L}_{i,\epsilon }} \right| _{\epsilon =0} = I_N$ for all $1 \le i \le N$.

Proposition A.3

$\left. {\displaystyle \frac{d}{d\epsilon } \mathcal {L}_{i,\epsilon }} \right| _{\epsilon =0} = \displaystyle f_i \ \mathcal {D}_i$, for all $1 \le i \le N$

Lemma A.4

$\displaystyle \frac{d}{d\epsilon } \left( \overset{\curvearrowleft }{\displaystyle \prod ^{i}_{k=1}} \mathcal {L}_{k,\epsilon } \right) =\sum _{k=1}^i f_k \ \mathcal {D}_k$ for all $1 \le i \le N$

Proof

$$\begin{aligned} \displaystyle \frac{d}{d\epsilon } \left( \overset{\curvearrowleft }{\displaystyle \prod ^{i}_{k=1}} \mathcal {L}_{k,\epsilon } \right)&= \sum _{k=1}^i \left( \overset{\curvearrowleft }{\displaystyle \prod ^{i}_{j=k-1}} \mathcal {L}_{j,\epsilon } \right) \left( \frac{d}{d\epsilon }\mathcal {L}_{k,\epsilon } \right) \left( \overset{\curvearrowleft }{\displaystyle \prod ^{k+1}_{j=1}} \mathcal {L}_{j,\epsilon } \right) \\&= \sum _{k=1}^i \left( \overset{\curvearrowleft }{\displaystyle \prod ^{i}_{j=k-1}}I_N \right) \left( f_k \ \mathcal {D}_k \right) \left( \overset{\curvearrowleft }{\displaystyle \prod ^{k+1}_{j=1}}I_N \right) \quad \text {(by Propositions A.2,A.3)} \\&= \sum _{k=1}^i f_k \ \mathcal {D}_k \end{aligned}$$

$\square$

Lemma A.5

For any positive integer, n, and an any integer, i, in [1, N]

$$\begin{aligned}&\displaystyle \lim _{\epsilon \rightarrow 0} \displaystyle \frac{\mathcal {L}_{i,\eta \epsilon } \left( \overset{\curvearrowleft }{\displaystyle \prod ^{i-1}_{k=1}} \mathcal {L}_{k,\epsilon } \right) \left( \overset{\curvearrowleft }{\displaystyle \prod ^{N}_{k=1}} \mathcal {L}_{k,\epsilon } \right) ^n - I_N}{(n + \sum _{k=1}^{i-1} f_k + \eta f_i) \epsilon } \\ =&\displaystyle \frac{1}{n + \sum _{k=1}^{i-1} f_k + \eta f_i} \left( n \sum _{k=1}^N f_k \ \mathcal {D}_k + \sum _{k=1}^{i-1} f_k \ \mathcal {D}_k + \eta \ f_i \ \mathcal {D}_i\right) , \end{aligned}$$

where $\eta$ is some number in [0, 1) and $0 \le f_k \le 1$ with $\sum _{k=1}^N f_k=1$.

Proof

$$\begin{aligned}&\displaystyle \lim _{\epsilon \rightarrow 0} \displaystyle \frac{\mathcal {L}_{i,\eta \epsilon } \left( \overset{\curvearrowleft }{\displaystyle \prod ^{i-1}_{k=1}} \mathcal {L}_{k,\epsilon } \right) \left( \overset{\curvearrowleft }{\displaystyle \prod ^{N}_{k=1}} \mathcal {L}_{k,\epsilon } \right) ^n - I_N}{(n + \sum _{k=1}^{i-1} f_k + \eta f_i) \epsilon } \\&= \displaystyle \lim _{\epsilon \rightarrow 0} \displaystyle \frac{\frac{d}{d\epsilon } \left( \mathcal {L}_{i,\eta \epsilon } \left( \overset{\curvearrowleft }{\displaystyle \prod ^{i-1}_{k=1}} \mathcal {L}_{k,\epsilon } \right) \left( \overset{\curvearrowleft }{\displaystyle \prod ^{N}_{k=1}} \mathcal {L}_{k,\epsilon } \right) ^n - I_N\right) }{\frac{d}{d\epsilon } (n + \sum _{k=1}^{i-1} f_k + \eta f_i)\epsilon } \,\,\text {(by L'Hospital's Rule)} \\&= \displaystyle \lim _{\epsilon \rightarrow 0} \displaystyle \frac{ \mathcal {L}_{i,\eta \epsilon } \left( \overset{\curvearrowleft }{\displaystyle \prod ^{i-1}_{k=1}} \mathcal {L}_{k,\epsilon } \right) \ \frac{d}{d\epsilon } \left( \overset{\curvearrowleft }{\displaystyle \prod ^{N}_{k=1}} \mathcal {L}_{k,\epsilon } \right) ^n + \mathcal {L}_{i,\eta \epsilon } \frac{d}{d\epsilon } \left( \overset{\curvearrowleft }{\displaystyle \prod ^{i-1}_{k=1}} \mathcal {L}_{k,\epsilon } \right) \left( \overset{\curvearrowleft }{\displaystyle \prod ^{N}_{k=1}} \mathcal {L}_{k,\epsilon } \right) ^n + \cdots }{n + \sum _{k=1}^{i-1} f_k + \eta f_{i}} \nonumber \\&\cdots + \frac{d}{d\epsilon }\left( \mathcal {L}_{i,\eta \epsilon }\right) \left( \overset{\curvearrowleft }{\displaystyle \prod ^{i-1}_{k=1}} \mathcal {L}_{k,\epsilon } \right) \left( \overset{\curvearrowleft }{\displaystyle \prod ^{N}_{k=1}} \mathcal {L}_{k,\epsilon } \right) ^n \\&= \displaystyle \lim _{\epsilon \rightarrow 0} \displaystyle \frac{ n \sum _{k=1}^N f_k \ \mathcal {D}_k + \sum _{k=1}^{i-1} f_k \ \mathcal {D}_k + \eta \ f_i \ \mathcal {D}_{i+1} }{n + \sum _{k=1}^{i-1} f_k + \eta f_{i}} \,\\&\quad \text {(by Proposition A.2,A.3 and Lemma A.4)} \\&= \displaystyle \frac{1}{n + \sum _{k=1}^{i-1} f_k + \eta f_i} \left( n \sum _{k=1}^N f_k \ \mathcal {D}_k + \sum _{k=1}^{i-1} f_k \mathcal {D}_k + \eta \ f_i \ \mathcal {D}_i\right) \end{aligned}$$

$\square$

Theorem A.6

If Drug1, Drug2, ..., DrugN, are prescribed in a cycle, and are switched instantaneously with relative duration of $0 \le f_1$, $f_2$, ..., $f_N \le 1$ (where $\sum _{k=1}^N f_k=1$), respectively, $\mathcal {R}$ obeys

$$\begin{aligned} \displaystyle \frac{d\mathcal {R}}{dt} = \sum _{k=1}^N f_k \ \mathcal {D}_k \mathcal {R} \end{aligned}$$

Proof

For any time point $t_0$, let us define $\mathcal {R}_\epsilon (t)$ as a vector-valued function of $R_1(t)$, $R_2(t)$,..., and $R_N(t)$ describing the cell population dynamics under a periodic therapy starting at $t_0$ with $Drug \ i$ assigned for $t_0+\left( m+\sum _{k=1}^{i-1} f_i\right) \ \epsilon \le t < t_0+\left( m+\sum _{k=1}^i f_i\right) \epsilon$ where m is any non-negative integer and i is any integer in [1, N].

For any $\Delta t>0$, there uniquely exist $n\in \{0,1,2,...\}$ and $\eta \in [0,1)$ such that $\Delta t = \left( n + \sum _{k=1}^{i-1} f_k + \eta f_i\right) \ \epsilon$. Then, by Proposition A.1 and the definitions of $\mathcal {L}_i$s,

$$\begin{aligned} \mathcal {R}_\epsilon (t)&=\mathcal {R}_\epsilon \left( t_0+\left( n+\sum _{k=1}^{i-1} f_k +\eta f_i\right) \epsilon \right) \\&= \eta f_i \mathcal {L}_i\left( \overset{\curvearrowleft }{\displaystyle \prod ^{i-1}_{k=1}} f_k \mathcal {L}_{k,\epsilon } \right) \left( \overset{\curvearrowleft }{\displaystyle \prod ^{N}_{k=1}} f_k \mathcal {L}_{k,\epsilon } \right) ^n \ \mathcal {R}(t_0) \cdots (*1) \end{aligned}$$

where $\mathcal {R}(t_0)=\left( \begin{array}{cccc} R_1(t_0)&R_2(t_0)&\cdots&R_N(t_0) \end{array} \right) ^T$. And, $\mathcal {R}_0(t)$ represents instantaneous drug switching.

$$\begin{aligned} \left. \frac{d}{dt}\mathcal {R}_0\right| _{t=t_0}=&\displaystyle \lim _{\Delta t \rightarrow 0} \displaystyle \frac{\mathcal {R}_0\left( t_0+\Delta t\right) -\mathcal {R}(t_0)}{\Delta t} \\ =&\displaystyle \lim _{\Delta t \rightarrow 0} \lim _{\epsilon \rightarrow 0} \displaystyle \frac{\mathcal {R}_{\epsilon }\left( t_0+\left( n(\Delta t, \epsilon )+\sum _{k=1}^{i-1} f_k + \eta (\Delta t, \epsilon ) \ f_i \right) \epsilon \right) -\mathcal {R}(t_0)}{\left( n(\Delta t, \epsilon )+\sum _{k=1}^{i-1} f_k + \eta (\Delta t, \epsilon ) \ f_i \right) \epsilon } \\ =&\displaystyle \lim _{\Delta t \rightarrow 0} \lim _{\epsilon \rightarrow 0} \displaystyle \frac{\eta (\Delta t, \epsilon ) \mathcal {L}_{i,\epsilon } \left( \overset{\curvearrowleft }{\displaystyle \prod ^{i-1}_{k=1}} \mathcal {L}_{k,\epsilon } \right) \left( \overset{\curvearrowleft }{\displaystyle \prod ^{N}_{k=1}} \mathcal {L}_{k,\epsilon } \right) ^{n(\Delta t, \epsilon )}-I_N}{\left( n(\Delta t, \epsilon )+\sum _{k=1}^{i-1} f_k + \eta (\Delta t, \epsilon ) \ f_i \right) \epsilon }\mathcal {R}(t_0) \\ =&\displaystyle \lim _{\Delta t \rightarrow 0} \lim _{\epsilon \rightarrow 0} \displaystyle \frac{1}{n + \sum _{k=1}^{i-1} f_k + \eta f_i} \left( n \sum _{k=1}^N f_k \ \mathcal {D}_k + \sum _{k=1}^{i-1} f_k \ \mathcal {D}_k + \eta \ f_i \ \mathcal {D}_i\right) \mathcal {R}(t_0) \\&\,\,\,\,\,\,\,\,\,\,\,\,\text {(by Lemma A.5)} \\ =&\displaystyle \lim _{\Delta t \rightarrow 0} \lim _{n \rightarrow \infty } \displaystyle \frac{1}{n + \sum _{k=1}^{i-1} f_k + \eta f_i} \left( n \sum _{k=1}^N f_k \ \mathcal {D}_k + \sum _{k=1}^{i-1} f_k \ \mathcal {D}_k + \eta \ f_i \ \mathcal {D}_i\right) \mathcal {R}(t_0) \\ =&\sum _{k=1}^N f_k \ \mathcal {D}_k \mathcal {R}(t_0). \end{aligned}$$

Therefore,

$$\begin{aligned} \displaystyle \left. \frac{d}{dt} \mathcal {R}_0 \right| _{t=t_0} = \sum _{k=1}^N f_k \ \mathcal {D}_k \mathcal {R}(t_0) \quad \,\,and\quad \,\, \displaystyle \frac{d\mathcal {R}}{dt} = \sum _{k=1}^N f_k \ \mathcal {D}_k \mathcal {R}. \end{aligned}$$

$\square$

Theorem A.7

The population makeup at which all the drugs are equally effective is

$$\begin{aligned} \mathcal {R}^*=\displaystyle \frac{\mathcal {C}}{||\mathcal {C}||_1} \text {\,where \,} \mathcal {C}=\left( \begin{array}{c} (\mathcal {P}^1)^T\\ (\mathcal {P}^2)^T\\ \vdots \\ (\mathcal {P}^N)^T \end{array} \right) ^{-1} \varvec{1}, \end{aligned}$$

where $\{\mathcal {P}^1,\mathcal {P}^2,\ldots ,\mathcal {P}^N\}$ is linearly independent.

Proof

By the definition (4), the effect of $Drug \ i$ is

$$\begin{aligned} ef_k=\mathcal {P}^i \cdot \mathcal {R}=(\mathcal {P}^i)^T \mathcal {R}. \end{aligned}$$

Then, at a specific population makeup with balanced drug effects, denoted by $\mathcal {R}^*$,

$$\begin{aligned} (\mathcal {P}^1)^T \mathcal {R}^*=(\mathcal {P}^2)^T \mathcal {R}^*=\cdots =(\mathcal {P}^N)^T \mathcal {R}^*:=k \Longleftrightarrow \left( \begin{array}{c} (\mathcal {P}^1)^T\\ (\mathcal {P}^2)^T\\ \vdots \\ (\mathcal {P}^N)^T \end{array} \right) \mathcal {R}^* = k \left( \begin{array}{c} 1\\ \vdots \\ 1 \end{array} \right) \end{aligned}$$

where k is a constant representing the level of balanced drug effect. Since $\{\mathcal {P}^1,\mathcal {P}^2,\ldots ,\mathcal {P}^N\}$ is linearly independent, we can isolate $\mathcal {R}^*$ with an inverse matrix.

$$\begin{aligned} \mathcal {R}^* = k \left( \begin{array}{c} (\mathcal {P}^1)^T\\ (\mathcal {P}^2)^T\\ \vdots \\ (\mathcal {P}^N)^T \end{array} \right) ^{-1} \varvec{1}, \end{aligned}$$

Also, $||\mathcal {R}^*||_1=1$, therefore

$$\begin{aligned} k=\displaystyle \frac{1}{||\mathcal {C}||_1} \,\,\, \text {where}\,\, \,\mathcal {C}=\left( \begin{array}{c} (\mathcal {P}^1)^T\\ (\mathcal {P}^2)^T\\ \vdots \\ (\mathcal {P}^N)^T \end{array} \right) ^{-1} \varvec{1} \end{aligned}$$

and

$$\begin{aligned} \mathcal {R}^*=\displaystyle \frac{\mathcal {C}}{||\mathcal {C}||_1} \end{aligned}$$

Corollary A.8

When the drugs are symmetric, the population makeup at which all the drugs are equally effective is

$$\begin{aligned} \mathcal {R}^* = \displaystyle \frac{1}{N} \ \varvec{1}, \end{aligned}$$

where $\{\mathcal {P}^1,\mathcal {P}^2,\ldots ,\mathcal {P}^N\}$ is linearly independent.

Proof

Similar to the proof of Theorem A.7, there exists unique solution of $\mathcal {R}^*$ and k satisfying

$$\begin{aligned} \left( \begin{array}{c} (\mathcal {P}^1)^T\\ (\mathcal {P}^2)^T\\ \vdots \\ (\mathcal {P}^N)^T \end{array} \right) \mathcal {R}^* = k \ \varvec{1} \,\,\, \text {and}\,\, \,||\mathcal {R}^*||_1=1. \end{aligned}$$

If we plug in $\mathcal {R}^* = \displaystyle \frac{1}{N} \ \varvec{1}$ to the equation,

$$\begin{aligned}&\left( \begin{array}{c} (\mathcal {P}^1)^T\\ (\mathcal {P}^2)^T\\ \vdots \\ (\mathcal {P}^N)^T \end{array} \right) \mathcal {R}^*= \displaystyle \frac{1}{N} \left( \begin{array}{c} (\mathcal {P}^1)^T\\ (\mathcal {P}^2)^T\\ \vdots \\ (\mathcal {P}^N)^T \end{array} \right) \varvec{1} =\displaystyle \frac{1}{N} \left( \begin{array}{c} p_r+p_s+(N-2)p_0\\ \vdots \\ p_r+p_s+(N-2)p_0 \end{array} \right) \nonumber \\ =&\displaystyle \frac{p_r+p_s+(N-2)p_0}{N} \ \varvec{1} = k \ \varvec{1} \,\,\, \text {with}\,\, \,k=\displaystyle \frac{p_r+p_s+(N-2)p_0}{N}. \end{aligned}$$

Therefore, proved.

Theorem A.9

$\{\mathcal {P}^1,\mathcal {P}^2,\ldots ,\mathcal {P}^N\}$ is linearly dependent, if the drugs are symmetric (i.e., $\{p_r^i,p_s^i,p_0^i\}=\{p_r,p_s,p_0\}$ for all i) and $p_r+p_s+(N-2)p_0=0$.

Proof

It suffices to show that there exists a linear combination of $\mathcal {P}^i$s that equals to a zero vector. Let the general form of a linear combination be $\sum _{i=1}^N a_i\mathcal {P}^i$, where $a_i$s are constants. If $a_i=1$ for all i, $\sum _{i=1}^N \mathcal {P}^i=(p_r+p_s+(N-2)p_0)\varvec{1}=0 \cdot \varvec{1}=0$. Therefore, $\{\mathcal {P}^1,\mathcal {P}^2,\ldots ,\mathcal {P}^N\}$ is linearly dependent.

Theorem A.10

Under instantaneously switching of symmetric drug cycle, total population with equal drug duration $(f_1=f_2=...=f_N=1/N)$, TP, is changing exponentially with the growth/decay rate,

$$\begin{aligned} \lambda = \displaystyle \frac{p_r+p_s+(N-2)p_0}{N} . \end{aligned}$$

Proof

The derivative of total population, TPD, is the summation of the vector, $\frac{d\mathcal {R}}{dt}$.

$$\begin{aligned} TPD\,=\,&sum\left( \displaystyle \frac{d\mathcal {R}}{dt} \right) = sum\left( \displaystyle \frac{1}{N} \sum _{k=1}^N \mathcal {D}_k \mathcal {R}\right) \,\, \text {(by Theorem A.6)} \\ \,=\,&\displaystyle \frac{1}{N} \sum _{k=1}^N \left( sum\left( \mathcal {D}_k \mathcal {R}\right) \right) = \displaystyle \frac{1}{N} \sum _{k=1}^N \left( \mathcal {P}^k \cdot \mathcal {R} \right) = \displaystyle \frac{1}{N} \left( \sum _{k=1}^N \mathcal {P}^k \right) \cdot \mathcal {R} \\ \,=\,&\displaystyle \frac{1}{N} \left( \begin{array}{c} p_r+p_s+(N-2)p_0\\ \vdots \\ p_r+p_s+(N-2)p_0 \end{array} \right) \cdot \mathcal {R} = \displaystyle \frac{p_r+p_s+(N-2)p_0}{N} \left( \varvec{1} \cdot \mathcal {R} \right) \\ \,=\,&\displaystyle \frac{p_r+p_s+(N-2)p_0}{N} \sum _{k=1}^N R_k = \lambda \ TP \end{aligned}$$

$\square$

Appendix B Shannon entropy of periodic sequences

Shannon entropy is a measure of diversity of a heterogeneous collection. If there are k different types of elements in the multiset, and if we represent the proportions of the types as $f_1$, $f_2$, $\ldots$ $f_k$ ($\sum _{i=1}^k f_i=1$), respectively, its Shannon entropy is

$$\begin{aligned} -\sum _{i=1}^k f_i \log f_i. \end{aligned}$$

If the multiset is composed by one identical element, its Shannon entropy is 0. Otherwise, if the multiset is composed by all distinct k elements, its Shannon entropy is $\log k$.

We used this concept of the entropy to explore the level of periodicity shown on sequences. For a sequence $a=(a_i)_{i\in \mathbb {N}}$, we define an associated sequence $(h_i|a)_{i\in \mathbb {N}}$ such that $h_i$ is the entropy of the first part of the sequence, $(a_j)_{j=1}^i$. With any arbitrary $(a_i)_{i\in \mathbb {N}}$, $h_1=0$. If $(a_i)_{i\in \mathbb {N}}$ is entirely periodic with the periodicity k, $h_k=h_{2k}=\cdots =h_{nk}=\cdots (:=h)$, and $\lim _{k \rightarrow \infty }h_{i}=h$. Figure 10 describes $(h_j|a)_{i\in \mathbb {N}}$ of an example of periodic sequence $a=(a_i)_{i\in \mathbb {N}}$.

Fig. 10

Entropy sequence evaluated from an example sequence periodic with the repeating terms of 1, 2, 2, 3, 3, 3

Such idea of entropy evaluation was applied for all the stages (4 stages in total) of the drug sequences in the exercise of optimal therapy simulation shown on Fig. 6. (Figure   11) The first stage is comprised by only one type of drug, therefore the entropy stays 0. In each of other stages, the corresponding sequence of entropy is nonzero, and is stabilized to the entropy level of the entire sequences of the stage. Also, we can see the periodic oscillations as the sequence proceeds. This observation is not quantified, however we believe it is sufficient to say the drug sequence within each stage is almost" periodic. As expected, such pattern is not observed, when we randomly shuffle and rearrange the drug sequences within stages (Fig. 12a), or rearrange the drugs in the order of $Drug\ 1$, $Drug\ 2$, $Drug\ 3$ and $Drug\ 4$ (Fig. 12b).

Fig. 11

Entropy sequences of the 4 stages of drug sequences of Fig. 6. The horizontal gray lines present the entropy values of the entire sequence of the 4 stages

Fig. 12

Entropy sequences with the rearranged drug sequence. a Rearrangement each stage by random shuffling. b Rearrangement in the order of $Drug\ 1$, $Drug\ 2$, $Drug\ 3$ and $Drug\ 4$