Counting phylogenetic networks of level 1 and 2

Abstract

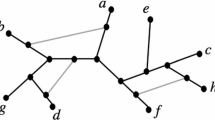
Phylogenetic networks generalize phylogenetic trees, and have been introduced in order to describe evolution in the case of transfer of genetic material between coexisting species. There are many classes of phylogenetic networks, which can all be modeled as families of graphs with labeled leaves. In this paper, we focus on rooted and unrooted level-k networks and provide enumeration formulas (exact and asymptotic) for rooted and unrooted level-1 and level-2 phylogenetic networks with a given number of leaves. We also prove that the distribution of some parameters of these networks (such as their number of cycles) are asymptotically normally distributed. These results are obtained by first providing a recursive description (also called combinatorial specification) of our networks, and by next applying classical methods of enumerative, symbolic and analytic combinatorics.

Appendix

1.1 Case analysis for unrooted level-2 generators

In the pictures below, we use thick lines to represent paths containing at least 2 internal nodes incident with a cut-edge which is incident with another pointed unrooted level-2 network. We use # to represent the fictitious root in the pointed network, v to denote its neighbour, and ${\mathcal {U}}$ to represent any pointed network.

1.1.1 Case 1: One edge with an attached network

One edge of the generator carries a sequence of at least two incident cut-edges. Because multiple edges are not allowed, it cannot be one of the two edges incident to v. So, it can be only one of the two edges not incident to v (which are not distinguished). The sequence is unorie of symmetry, explaining the factor $\tfrac{1}{2}$ below.

$$\begin{aligned} \frac{{U}^2}{2(1- {U})} \end{aligned}$$

1.1.2 Case 2: Two edges with attached networks

Case 2A: Two edges of the generator carry exactly one incident cut-edge. Since multiple edges are not allowed, it can either be one edge incident to v and one not, or both edges not incident to v. In the latter case, the two edges should not be distinguished, hence the factor $\tfrac{1}{2}$.

$$\begin{aligned} {U}^2+\dfrac{{U}^2}{2} = \frac{3}{2}{U}^2 \end{aligned}$$

Case 2B: One edge of the generator carries a single incident cut-edge and another edge carries a sequence of at least two incident cut-edges. Again, these cannot be the two edges incident to v. The only case where symmetries need to be taken care of is when the two edges are those not incident to v: in this case, the sequence is not oriented, hence the factor $\tfrac{1}{2}$. In all other cases, the orientation of the sequence is determined by the presence of the fictitious root or the outgoing arc from the other edge with and attached network.

$$\begin{aligned} \dfrac{{U}^3}{1-{U}}+\dfrac{{U}^3}{1-{U}}+\dfrac{{U}^3}{2(1-{U})} = \frac{5{U}^3}{2(1- {U})} \end{aligned}$$

Case 2C: Two edges of the generator (but not the two incident to v, as before) carry a sequence of at least two incident cut-edges. If one arc is incident to v and the other not, then both sequences are oriented and there is no symmetry factor. If the two arcs are those not incident to v, then the two sequences they carry can be seen as an unordered pair of oriented sequences, seen up to symmetry w.r.t. the vertical axis. This yields a factor $\tfrac{1}{2}$ since the pair is unordered, and another factor $\tfrac{1}{2}$ to account for the symmetry w.r.t. the vertical axis.

$$\begin{aligned} \dfrac{{U}^4}{(1-{U})^2}+\dfrac{{U}^4}{4(1-{U})^2} = \frac{5{U}^4}{4(1- {U})^2} \end{aligned}$$

1.1.3 Case 3: Three edges with attached networks

Case 3A: Three edges of the generator carry exactly one incident cut-edge. The unused edge can either be incident with v or not. In both cases, we have a factor $\tfrac{1}{2}$ because of symmetry.

$$\begin{aligned} \dfrac{{U}^3}{2}+\dfrac{{U}^3}{2} = {U}^3 \end{aligned}$$

Case 3B: Two edges of the generator carry a single incident cut-edge and one carries a sequence of at least two incident cut-edges. The only cases where a symmetry comes into play here are when the edges carrying a single incident cut-edge are either the two edges incident to v or the two edges not incident to v. This yield the factor $\tfrac{1}{2}$ in these two cases. Moreover, all sequences are oriented, because of the presence of the fictitious root or the single incident cut-edges.

$$\begin{aligned} \dfrac{{U}^4}{1-{U}}+\dfrac{{U}^4}{1-{U}}+\dfrac{{U}^4}{2(1-{U})}+\dfrac{{U}^4}{2(1-{U})} = \frac{3{U}^4}{1-{U}} \end{aligned}$$

Case 3C: One edge of the generator carries a single incident cut-edge and two edges carry a sequence of at least two incident cut-edges. Similarly to the previous case, we obtain a factor $\tfrac{1}{2}$ for symmetry reasons when the two edges carrying sequences are either the two edges incident to v or the two edges not incident to v. Moreover, all sequences are oriented, because of the presence of the fictitious root or the single incident cut-edge.

$$\begin{aligned} \dfrac{{U}^5}{(1-{U})^2}+\dfrac{{U}^5}{(1-{U})^2}+\dfrac{{U}^5}{2(1-{U})^2}+\dfrac{{U}^5}{2(1-{U})^2} = \frac{3{U}^5}{(1- {U})^2} \end{aligned}$$

Case 3D: Three edges of the generator carry a sequence of at least two incident cut-edges. In both cases, we have a factor $\tfrac{1}{2}$ for symmetry reason, but all sequences are oriented by the presence of the fictitious root, or of the sequence on the edge(s) incident to v.

$$\begin{aligned} \dfrac{{U}^6}{2(1-{U})^3}+\dfrac{{U}^6}{2(1-{U})^3} = \frac{{U}^6}{(1- {U})^3} \end{aligned}$$

1.1.4 Case 4: Four edges with attached networks

Case 4A: The four edges of the generator each carry exactly one incident cut-edge. In this case, the two edges incident to v can be exchanged without modifying the network, and the same holds for the two edges not incident to v. This yields a factor $\tfrac{1}{2} \cdot \tfrac{1}{2} = \tfrac{1}{4}$ due to symmetries.

$$\begin{aligned} \dfrac{{U}^4}{4} \end{aligned}$$

Case 4B: Three edges of the generator carry a single incident cut-edge and the fourth one carries a sequence of at least two incident cut-edges. If this fourth edge is one incident to v, then the sequence it carries is oriented by the presence of the fictitious root, but the two arcs pending on the edges not incident to v are symmetric, hence a factor $\tfrac{1}{2}$. If on the contrary the edge carrying the sequence is not incident to v, then the sequence is also oriented, this time because of the arcs attached to the edges incident to v. Moreover, the picture has a symmetry w.r.t. the vertical axis, hence a factor $\tfrac{1}{2}$.

$$\begin{aligned} \dfrac{{U}^5}{2(1-{U})}+\dfrac{{U}^5}{2(1-{U})} = \frac{{U}^5}{1- {U}} \end{aligned}$$

Case 4C: Two edges carry a single incident cut-edge and the two others carry a sequence of at least two incident cut-edges. In all cases, the sequences are oriented, by the presence of either the fictitious root or of the single arcs attached to edges. If the edges carrying sequences are one incident to v and the other not incident to v, all edges are in addition distinguished from each other. In the other two cases, both edges incident to v form an unordered pair, as well as the two edges not incident to v. In each case, we therefore have a factor $\tfrac{1}{4}$.

$$\begin{aligned} \dfrac{{U}^6}{(1-{U})^2}+\dfrac{{U}^6}{4(1-{U})^2}+\dfrac{{U}^6}{4(1-{U})^2} = \frac{3{U}^6}{2(1- {U})^2} \end{aligned}$$

Case 4D: One edge of the generator carries a single incident cut-edge and three edges carry a sequence of at least two incident cut-edges. As in the previous case, all sequences are oriented. However, if the two edges incident to v carry a sequence, the picture has a symmetry w.r.t. the vertical axis, hence a factor $\tfrac{1}{2}$. If on the contrary the two edges not incident to v carry a sequence, these two edges are indistinguishable, hence a factor $\tfrac{1}{2}$ also in this case.

$$\begin{aligned} \dfrac{{U}^7}{2(1-{U})^3}+\dfrac{{U}^7}{2(1-{U})^3} = \frac{{U}^7}{(1- {U})^3} \end{aligned}$$

Case 4E: All four edges of the generator carry a sequence of at least two incident cut-edges. Then all sequences are oriented, but the two edges not incident to v are indistinguishable. The picture has in addition a symmetry w.r.t. the vertical axis. This yields a factor $\tfrac{1}{4}$.

$$\begin{aligned} \dfrac{{U}^8}{4(1-{U})^4} \end{aligned}$$

1.2 Case analysis for the rooted level-2 generator 2b

In the pictures below, we use thick lines to represent paths containing at least one internal node incident with a cut arc which is incident with the root of another rooted level-2 network. All arcs are directed downwards. We use ${\mathcal {L}}$ to represented any rooted level-2 network.

1.2.1 Case 1

Only one arc of the generator carries a sequence of at least one outgoing arc. This arc can only be e or $e'$ (and these cases are indistinguishable), since otherwise the network would contain multiple arcs, and this is not allowed.

$$\begin{aligned} {L} \frac{{L}}{1-{L}} \end{aligned}$$

1.2.2 Case 2

Exactly two arcs of the generator carry a sequence of at least one outgoing arc. To avoid multiple arcs, either these two arcs are e and $e'$ (and those two arcs are symmetric, hence the factor $\frac{1}{2}$), or one of them is e or $e'$ (which are not distinguished) and the other arc is chosen among the three arcs different from e and $e'$.

$$\begin{aligned} \frac{1}{2} {L} \left( \dfrac{{L}}{1-{L}}\right) ^2 + 3 {L} \left( \dfrac{{L}}{1-{L}}\right) ^2 = \frac{7}{2} {L} \left( \dfrac{{L}}{1-{L}}\right) ^2 \end{aligned}$$

1.2.3 Case 3

Exactly three arcs of the generator carry a sequence of at least one outgoing arc. Here, there are two possibilities. Either both e and $e'$ are among those three arcs (and those two arcs are symmetric, hence the factor $\frac{1}{2}$). Or, to avoid multiple arcs, we must choose one of e and $e'$ (which are not distinguished from each other), and two additional arcs among the three remaining arcs.

$$\begin{aligned} \frac{3}{2} {L} \left( \dfrac{{L}}{1-{L}}\right) ^3 + 3 {L} \left( \dfrac{{L}}{1-{L}}\right) ^3 = \frac{9}{2} {L} \left( \dfrac{{L}}{1-{L}}\right) ^3 \end{aligned}$$

1.2.4 Case 4

Exactly four arcs of the generator carry a sequence of at least one outgoing arc. Either both e and $e'$ are among those four arcs (and those two arcs are symmetric, hence the factor $\frac{1}{2}$), so the last two are chosen among the three other arcs of the generator. Or we choose the three arcs of the generator other than e and $e'$, and e (which is undistinguishable from $e'$).

$$\begin{aligned} \frac{\left( {\begin{array}{c}3\\ 2\end{array}}\right) }{2} {L} \left( \dfrac{{L}}{1-{L}}\right) ^4 + {L} \left( \dfrac{{L}}{1-{L}}\right) ^4 = \frac{5}{2} {L} \left( \dfrac{{L}}{1-{L}}\right) ^4 \end{aligned}$$

1.2.5 Case 5

All five arcs of the generator carry a sequence of at least one outgoing arc. The fact that e and $e'$ are symmetric explains the factor $\frac{1}{2}$.

$$\begin{aligned} \frac{1}{2} {L} \left( \dfrac{{L}}{1-{L}}\right) ^5. \end{aligned}$$

1.3 Exact enumeration formulas

1.3.1 Unrooted level-2 networks

Proposition 13

For any $n \ge 1$, the number $u_n$ of unrooted level-2 phylogenetic networks with $(n+1)$ leaves is given by

$$\begin{aligned} u_n = (n-1)! \mathop {\sum }\limits _{\begin{array}{c} 0\le s \le q \le p \le k \le i \le n-1 \\ j=n-1-i-k-p-q-s \ge 0 \\ i\ne 0 \\ {{n+i-1}\atopwithdelims (){i}} {{4i+j-1}\atopwithdelims (){j}} {{i}\atopwithdelims (){k}} {{k}\atopwithdelims (){p}} {{p}\atopwithdelims (){q}} {{q}\atopwithdelims (){s}} \\ \qquad \times \left( 3\right) ^i \left( \frac{-15}{6}\right) ^k \left( -\frac{16}{15}\right) ^p \left( -\frac{1}{2}\right) ^q \left( -\frac{3}{16}\right) ^{s}. \end{array}} \end{aligned}$$

Proof (Sketch)

Recall that $U(z)=z \phi (U(z))$ with $\phi (z) = \frac{1}{1-\frac{3z^5-16z^4+32z^3-30z^2+12z}{4(1-z)^4}}$. Using first the classical development of $(1-z)^{-n}$ in series (see Eq. (2)), and then the binomial theorem, we have

$$\begin{aligned} \phi (z)^n&= \sum _{i \ge 0} {{n+i-1} \atopwithdelims (){i}} \left( \frac{12z}{4(1-z)^4}+ \frac{- 30z^2 +32z^3-16z^4+3z^5}{4(1-z)^4}\right) ^i \\&= \sum _{i \ge 0} \sum _{k=0}^i {{n+i-1} \atopwithdelims (){i}} {{i} \atopwithdelims (){k}} \left( \frac{12z}{4(1-z)^4}\right) ^{i-k} \left( \frac{- 30z^2 +32z^3-16z^4+3z^5}{4(1-z)^4}\right) ^k \text {.} \end{aligned}$$

We continue applying the binomial theorem inside the above formula, isolating each time the term with the lowest degree in the numerator (that is, first $\tfrac{- 30z^2}{4(1-z)^4}$, second $\tfrac{32z^3}{4(1-z)^4}$, ...). This yields

$$\begin{aligned}&\phi (z)^n = \sum _{i \ge 0} \sum _{k=0}^i \sum _{p=0}^k \sum _{q=0}^p \sum _{s=0}^q \\&\qquad \times {{n+i-1} \atopwithdelims (){i}} {{i} \atopwithdelims (){k}} {{k} \atopwithdelims (){p}} {{p} \atopwithdelims (){q}} {{q} \atopwithdelims (){s}} \left( \frac{12z}{4(1-z)^4}\right) ^{i-k} \left( \frac{- 30z^2}{4(1-z)^4}\right) ^{k-p} \\&\qquad \left( \frac{32z^3}{4(1-z)^4}\right) ^{p-q} \left( \frac{-16z^4}{4(1-z)^4}\right) ^{q-s} \left( \frac{3z^5}{4(1-z)^4}\right) ^{s}\\&\quad = \sum _{i \ge 0} \sum _{k=0}^i \sum _{p=0}^k \sum _{q=0}^p \sum _{s=0}^q {{n+i-1} \atopwithdelims (){i}} {{i} \atopwithdelims (){k}} {{k} \atopwithdelims (){p}} {{p} \atopwithdelims (){q}} {{q} \atopwithdelims (){s}} \nonumber \\&\quad \frac{ (3)^{i} (\tfrac{-15}{6})^{k} (\tfrac{-16}{15})^{p} (\tfrac{-1}{2})^{q} (\tfrac{-3}{16})^{s}}{(1-z)^{4i}}\\&\qquad \times z^{i+k+p+q+s} \text {.} \end{aligned}$$

The result then follows from developing of $(1-z)^{-4i}$ in series as $(1-z)^{-4i} = \sum _{j \ge 0} {{4i+j-1} \atopwithdelims (){j}} z^j$ and using the Lagrange inversion formula. $\square$

1.3.2 Rooted level-2 networks

Proposition 14

For any $n \ge 1$, the number $\ell _n$ of rooted level-2 phylogenetic networks with n leaves is given by

$$\begin{aligned} \ell _n = (n-1)! \mathop {\sum }\limits _{\begin{array}{c} 0 \le t \le m \le s \le q \le p \le k \le i \le n-1 \\ j=n-1-i-k-p-q-s-m-t \ge 0 \\ {i\ne 0} \\ {{n+i-1}\atopwithdelims (){i}} {{6i+j-1}\atopwithdelims (){j}} {{i}\atopwithdelims (){k}} {{k}\atopwithdelims (){p}} {{p}\atopwithdelims (){q}} {{q}\atopwithdelims (){s}}{{s}\atopwithdelims (){m}} {{m}\atopwithdelims (){t}} \\ \qquad \times \left( 9\right) ^i \left( \frac{-17}{6}\right) ^{k} \left( \frac{-53}{34}\right) ^p \left( \frac{-148}{159}\right) ^q \left( \frac{-81}{148}\right) ^s \left( \frac{-8}{27}\right) ^m \left( \frac{-1}{8}\right) ^t. \end{array} } \end{aligned}$$

Proof (Sketch)

This follows again from the Lagrange inversion formula, using the equation ${L}(z)= z\phi ( {L}(z))$ for the function $\phi$ given in Theorem 6. The computations involve the usual development of $(1-z)^{-n}$ given by Eq. (2) and the binomial formula, applied following exactly the same steps as in the proof of Proposition 13. Details of the computations are left to the reader. $\square$