Fluctuating-rate model with multiple gene states

Abstract

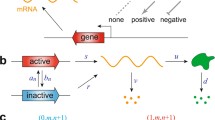
Multiple phenotypic states of single cells often co-exist in the presence of positive feedbacks. Stochastic gene-state switchings and low copy numbers of proteins in single cells cause considerable fluctuations. The chemical master equation (CME) is a powerful tool that describes the dynamics of single cells, but it may be overly complicated. Among many simplified models, a fluctuating-rate (FR) model has been proposed recently to approximate the full CME model in the realistic intermediate region of gene-state switchings. However, only the scenario with two gene states has been carefully analysed. In this paper, we generalise the FR model to the case with multiple gene states, in which the mathematical derivation becomes more complicated. The leading order of fluctuations around each phenotypic state, as well as the transition rates between phenotypic states, in the intermediate gene-state switching region is characterized by the rate function of the stationary distribution of the FR model in the Freidlin–Wentzell-type large deviation principle (LDP). Under certain reasonable assumptions, we show that the derivative of the rate function is equal to the unique nontrivial solution of a dominant generalised eigenvalue problem, leading to a new numerical algorithm for obtaining the LDP rate function directly. Furthermore, we prove the Lyapunov property of the rate function for the corresponding deterministic mean-field dynamics. Finally, through a tristable example, we show that the local fluctuations (the asymptotic variance of the stationary distribution at each phenotypic state) in the intermediate and rapid regions of gene-state switchings are different. Finally, a tri-stable example is constructed to illustrate the validity of our theory.

Appendices

Appendix A: Results related to dominant generalised eigenvalue problem

• $G>0$: matrix dimension/size.

• ${\mathcal {G}}:=\left\{ 1,2,3,\cdots ,G\right\}$.

• $B=\left( b_{i,j}\right) _{G\times G}$: general $G\times G$ matrix.

• $B^{{\mathcal {S}}_1,{\mathcal {S}}_2}$ for ${\mathcal {S}}_1,{\mathcal {S}}_2\subset {\mathcal {G}}$: principal submatrix of B formed by rows in ${\mathcal {S}}_1$ and columns in ${\mathcal {S}}_2$. Particularly, $B^{{\mathcal {S}}}:=B^{{\mathcal {S}},{\mathcal {S}}}$ for ${\mathcal {S}}\subset {\mathcal {G}}$.

• ${\bar{i}}:={\mathcal {G}}{\setminus }\left\{ i\right\}$.

• $|b_{\cdot ,j}|:=\sum _{i\ne j}|b_{i,j}|$.

• Z: $G\times G$ Z-matrix (real matrix such that off-diagonal elements are nonpositive) in the normal form (block upper-triangular form with each diagonal block irreducible).

• ${\mathcal {I}}$: indices of irreducible diagonal blocks of Z.

• $Z_i$ for $i\in {\mathcal {I}}$: irreducible diagonal blocks of Z.

• M: $G\times G$ M-matrix (Z-matrix such that all eigenvalues have nonnegative real parts) in the normal form. Note that we allow singular M-matrix.

• D: $G\times G$ real diagonal matrix.

• $D_i$ for $i\in {\mathcal {I}}$: diagonal blocks of D corresponding to $Z_i$.

• $d_i$ for $i\in {\mathcal {G}}$: the ith diagonal element of D.

• ${\mathcal {G}}_0:=\left\{ i\in {\mathcal {G}}|d_i=0\right\}$. ${\mathcal {G}}_+:=\left\{ i\in {\mathcal {G}}|d_i>0\right\}$. ${\mathcal {G}}_-:=\left\{ i\in {\mathcal {G}}|d_i<0\right\}$.

• $r\left( Z\right)$: dominant eigenvalue (the eigenvalue with smallest real part, which must be real by the Perron–Frobenius theorem) of Z.

• $m\left( D\right)$ and $n\left( D\right)$: the number of positive and negative diagonal elements of D. $D\ne 0$ means $m\left( D\right) +n\left( D\right) >0$.

• $O\left( o,\rho \right) :=\left\{ z\in {\mathbb {C}}||z-o|\le \rho \right\}$, where $o\in {\mathbb {C}}$ and $\rho \ge 0$.

In this “Appendix”, we state results without proofs. Their proofs are given in “Appendix B”. We always assume $D\ne 0$.

Definition A1

Denote the real part of $\lambda \in {\mathbb {C}}$ by $\mathfrak {R}(\lambda )$. Define

$$\begin{aligned}&\varLambda \left( B|D\right) :=\left\{ \lambda \in {\mathbb {C}}|\det \left( B-\lambda D\right) =0\right\} ,\\&\varLambda _+\left( B|D\right) :=\left\{ \lambda \in \varLambda \left( B|D\right) |\mathfrak {R}\left( \lambda \right) >0\right\} ,\\&\varLambda _-\left( B|D\right) :=\left\{ \lambda \in \varLambda \left( B|D\right) |\mathfrak {R}\left( \lambda \right) <0\right\} ,\\&\varLambda _0\left( B|D\right) :=\left\{ \lambda \in \varLambda \left( B|D\right) |\mathfrak {R}\left( \lambda \right) =0\right\} . \end{aligned}$$

$\lambda \in \varLambda \left( B|D\right)$ is called the generalised eigenvalue (GE) of B on D (Chu 1987; Ikramov 1993). For $\lambda _0\in \varLambda \left( B|D\right)$, let $c\left( \lambda _0|B|D\right)$ be the multiplicity of $\lambda _0$ as a root of $\det \left( B-\lambda D\right) =0$. We define $R\left( Z|D\right) :=\left\{ \lambda \in {\mathbb {R}}|r\left( Z-\lambda D\right) =0\right\}$, and call $\lambda \in R\left( Z|D\right)$ the dominant generalised eigenvalue (DGE) of Z on D. Define $\varXi \left( Z-\lambda D\right) :=\det \left( Z-\lambda D\right) /r\left( Z-\lambda D\right)$, which is analytic even for $\lambda \in R\left( Z|D\right)$ because they are removable singular points.

Lemma A1

Assume that M is irreducible.

• 1. If $n\left( D\right) =0$, then $R\left( M|D\right) =\left\{ \mu _+\right\}$ with $\mu _+\ge 0$ and $c\left( \mu _+|M|D\right) =1$. $r\left( M-\lambda D\right) >0$ for $\lambda <\mu _+$ and $r\left( M-\lambda D\right) <0$ for $\lambda >\mu _+$.

• 2. If $m\left( D\right) =0$, then $R\left( M|D\right) =\left\{ \mu _-\right\}$ with $\mu _-\le 0$ and $c\left( \mu _-|M|D\right) =1$. $r\left( M-\lambda D\right) >0$ for $\lambda >\mu _-$ and $r\left( M-\lambda D\right) <0$ for $\lambda <\mu _-$.

• 3. Otherwise, $R\left( M|D\right) =\left\{ \mu _-,\mu _+\right\}$ with $\mu _+\ge 0\ge \mu _-$. $c\left( \mu _{\pm }|M|D\right) =1$ unless $\mu _{\pm }=0$, at which $c\left( \mu _{\pm }|M|D\right) =c\left( 0|M|D\right) =2$. $r\left( M-\lambda D\right) >0$ for $\mu _-<\lambda <\mu _+$ and $r\left( M-\lambda D\right) <0$ for $\lambda <\mu _-$ or $\lambda >\mu _+$.

Lemma A1 justifies Definition A2.

Definition A2

For irreducible M, define $\mu _+\left( M|D\right) :=\max _{\lambda \in R\left( M|D\right) }\lambda$ for $m\left( D\right) >0$, and $\mu _-\left( M|D\right) :=\min _{\lambda \in R\left( M|D\right) }\lambda$ for $n\left( D\right) >0$.

Definition A2 can be explained as follows. By Lemma A1, for $m\left( D\right) >0$ and $n\left( D\right) =0$, there is only a nonnegative DGE for M on D, which is denoted by $\mu _+\left( M|D\right)$. Similarly, for $m\left( D\right) =0$ and $n\left( D\right) >0$, there is only a nonpositive DGE, which is denoted by $\mu _-\left( M|D\right)$. If $m\left( D\right) >0$ and $n\left( D\right) >0$, then there are both a nonnegative DGE and a nonpositive DGE, which are respectively denoted by $\mu _+\left( M|D\right)$ and $\mu _-\left( M|D\right)$.

Since $r\left( M-\lambda D\right) =\min _{i\in {\mathcal {G}}}r\left( M_i-\lambda D_i\right)$, the results in Lemma A1 can be generalised to reducible M (see Corollary A1) if for any irreducible diagonal block $i\in {\mathcal {I}}$ such that $D_i=0$, $M_i$ is nonsingular. Lemma A2 provides a sufficient condition for this.

Lemma A2

${\mathcal {K}}_0^{\mathrm{sin}}:=\left\{ i\in {\mathcal {I}}|m\left( D_i\right) =n\left( D_i\right) =0,\det \left( M_i\right) =0\right\} =\emptyset$ if and only if $\det \left( M^{{\mathcal {G}}_0}\right) \ne 0$.

Corollary A1

Assume that $\det \left( M^{{\mathcal {G}}_0}\right) \ne 0$.

• 1. If $n\left( D\right) =0$, then $R\left( M|D\right) =\left\{ \mu _+\right\}$ with

  $$\begin{aligned} \mu _+=\mu _+\left( M|D\right) :=\min _{i:m\left( D_i\right) >0}\mu _+\left( M_i|D_i\right) , \end{aligned}$$

  $r\left( M-\lambda D\right) <0$ for $\lambda >\mu _+$, and $r\left( M-\lambda D\right) >0$ for $\lambda <\mu _+$.

• 2. If $m\left( D\right) =0$, then $R\left( M|D\right) =\left\{ \mu _-\right\}$ with

  $$\begin{aligned} \mu _-=\mu _-\left( M|D\right) :=\max _{i:n\left( D_i\right) >0}\mu _-\left( M_i|D_i\right) , \end{aligned}$$

  $r\left( M-\lambda D\right) <0$ for $\lambda <\mu _-$, and $r\left( M-\lambda D\right) >0$ for $\lambda >\mu _-$.

• 3. Otherwise, $R\left( M|D\right) =\left\{ \mu _-,\mu _+\right\}$ with

  $$\begin{aligned}&\mu _+=\mu _+\left( M|D\right) :=\min _{i:m\left( D_i\right)>0}\mu _+\left( M_i|D_i\right) ,\\&\mu _-=\mu _-\left( M|D\right) :=\max _{i:n\left( D_i\right) >0}\mu _-\left( M_i|D_i\right) , \end{aligned}$$

  $r\left( M-\lambda D\right) <0$ for $\lambda <\mu _-$ or $\lambda >\mu _+$, and $r\left( M-\lambda D\right) >0$ for $\mu _-<\lambda <\mu _+$.

Corollary A1 extends Definition A2 to reducible M, and gives Lemma A3.

Lemma A3

Assume that $M\left( \theta \right)$ is a continuous $G\times G$ M-matrix function of $\theta$, $D\left( \theta \right)$ is a continuous $G\times G$ diagonal matrix function of $\theta$ with constant ${\mathcal {G}}_{\pm }$ and ${\mathcal {G}}_0$ $\forall \theta$, and $\det \left[ M^{{\mathcal {G}}_0}\left( \theta \right) \right] \ne 0$ $\forall \theta$.

• 1. If $m\left[ D\left( \theta \right) \right] >0$, then $\mu _+\left( \theta \right) :=\mu _+\left( M|D\right) \left( \theta \right)$ is continuous.

• 2. If $n\left[ D\left( \theta \right) \right] >0$, then $\mu _-\left( \theta \right) :=\mu _-\left( M|D\right) \left( \theta \right)$ is continuous.

Lemma A4

• 1. Assume that $|b_{j,j}|\ge |b_{\cdot ,j}|$ $\forall j\in {\mathcal {G}}_0$, $B^{{\mathcal {G}}_0}$ is irreducible, and $\exists j_0\in {\mathcal {G}}_0$ such that $|b_{j_0,j_0}|>\sum _{i\in {\mathcal {G}}_0{\setminus }\left\{ j_0\right\} }|b_{i,j_0}|$. Then

  $$\begin{aligned} \bigcup _{j\in {\mathcal {G}}{\setminus }{\mathcal {G}}_0}O\left( b_{j,j}/d_j,|b_{\cdot ,j}|/|d_j|\right) =:{\mathcal {O}}\left( B|D\right) \supset \varLambda \left( B|D\right) . \end{aligned}$$

• 2. Under the assumptions in statement 1, further assume that $b_{j,j}\ge 0$ for $j\notin {\mathcal {G}}_0$ and B is diagonally dominant for all columns. Then

  $$\begin{aligned} \sum _{\lambda \in \left[ \varLambda \cap {\mathcal {O}}_+\right] \left( B|D\right) }c\left( \lambda |B|D\right) \ge m\left( D\right) ,\quad \sum _{\lambda \in \left[ \varLambda \cap {\mathcal {O}}_-\right] \left( B|D\right) }c\left( \lambda |B|D\right) \ge n\left( D\right) , \end{aligned}$$

  where ${\mathcal {O}}_{\pm }\left( B|D\right) :=\bigcup _{j\in {\mathcal {G}}_{\pm }}O\left( b_{j,j}/d_j,|b_{\cdot ,j}|/d_j\right)$.

Lemma A4 generalises the Gershgorin circle theorem to GEs.

Definition A3

Let $T=\left( t_{i,j}\right) _{G\times G}$ be a Z-matrix with $\sum _{i\in {\mathcal {G}}} t_{i,j}=0$ $\forall j\in {\mathcal {G}}$. T is called a negative transition rate matrix. Let $m\left( T|D\right) :=\sum _{\lambda \in \varLambda _+\left( T|D\right) }c\left( \lambda |T|D\right)$ and $n\left( T|D\right) :=\sum _{\lambda \in \varLambda _-\left( T|D\right) }c\left( \lambda |T|D\right)$.

Lemmas A5 and A6, and Theorem A1 connect the signs of the real parts of GEs with the signatures of D for negative transition rate matrix T step by step. Since T is diagonally dominant, it is not hard to prove by the Gershgorin circle theorem that T is a singular M-matrix. Applying Lemma A4 to T, we have Lemma A5.

Lemma A5

Assume that $T^{{\mathcal {G}}_0}$ is irreducible, and $\exists j_0\in {\mathcal {G}}_0$ such that $|t_{j_0,j_0}|>\sum _{i\in {\mathcal {G}}_0{\setminus }\left\{ j_0\right\} }|t_{i,j_0}|$. Then $\varLambda _0\left( T|D\right) \subset \left\{ 0\right\}$, and exact one of the following happens.

• 1. $m\left( T|D\right) =m\left( D\right)$.

• 2. $n\left( T|D\right) =n\left( D\right)$.

• 3. $m\left( T|D\right) <m\left( D\right)$, $n\left( T|D\right) <n\left( D\right)$.

If T is irreducible, Lemma A5 becomes Lemma A6 by Lemma A1.

Lemma A6

Assume that T is irreducible, $T^{{\mathcal {G}}_0}$ is irreducible, and $\exists j_0\in {\mathcal {G}}_0$ such that $|t_{j_0,j_0}|>\sum _{i\in {\mathcal {G}}_0{\setminus }\left\{ j_0\right\} }|t_{i,j_0}|$. Then exact one of the following happens.

• 1. $m\left( T|D\right) =m\left( D\right)$, $n\left( T|D\right) =n\left( D\right) -1$, $\mu _-\left( T|D\right) =0$, $c\left( \mu _-|T|D\right) =1$. If $m\left( D\right) >0$, $\mu _+\left( T|D\right) >0$ and $c\left( \mu _+|T|D\right) =1$.

• 2. $m\left( T|D\right) =m\left( D\right) -1$, $n\left( T|D\right) =n\left( D\right)$, $\mu _+\left( T|D\right) =0$, $c\left( \mu _+|T|D\right) =1$. If $n\left( D\right) >0$, $\mu _-\left( T|D\right) <0$ and $c\left( \mu _-|T|D\right) =1$.

• 3. $m\left( T|D\right) =m\left( D\right) -1$, $n\left( T|D\right) =n\left( D\right) -1$, $\mu _{\pm }\left( T|D\right) =0$, $c\left( \mu _{\pm }|T|D\right) =1$.

Theorem A1 generalises Lemma A6 to reducible T, and concretizes Lemma A5.

Theorem A1

Assume that $T^{{\mathcal {G}}_0}$ is irreducible, and $\exists j_0\in {\mathcal {G}}_0$ such that $|t_{j_0,j_0}|>\sum _{i\in {\mathcal {G}}_0{\setminus }\left\{ j_0\right\} }|t_{i,j_0}|$. Then exact one of the following happens.

• 1. $m\left( T|D\right) =m\left( D\right)$, $\mu _-\left( T|D\right) =0$. If $m\left( D\right) >0$, $\mu _+\left( T|D\right) >0$.

• 2. $n\left( T|D\right) =n\left( D\right)$, $\mu _+\left( T|D\right) =0$. If $n\left( D\right) >0$, $\mu _-\left( T|D\right) <0$.

• 3. $m\left( T|D\right) <m\left( D\right)$, $n\left( T|D\right) <n\left( D\right)$, $\mu _{\pm }\left( T|D\right) =0$.

Definition A4

$T^{{\mathcal {G}}_0}$ is irreducible. $\exists j_0\in {\mathcal {G}}_0$ such that $|t_{j_0,j_0}|>\sum _{i\in {\mathcal {G}}_0{\setminus }\left\{ j_0\right\} }|t_{i,j_0}|$. For $m\left( D\right) ,n\left( D\right) >0$, define

$$\begin{aligned} \mu \left( T|D\right) :=\left\{ \begin{array}{c@{\quad }c} \mu _+\left( T|D\right) , &{} \mu _+\left( T|D\right) >0,\\ \mu _-\left( T|D\right) , &{} \mu _+\left( T|D\right) =0, \end{array}\right. \end{aligned}$$

as the nontrivial DGE of T on D.

By Theorem A1, at least one of $\mu _{\pm }\left( T|D\right)$ is zero. Therefore, the nontrivial DGE in Definition A4 is obtained by always choosing the nonzero DGE if possible.

Theorem A2

Assume that $T=T\left( \theta \right)$ is a continuous $G\times G$ negative transition rate matrix function of $\theta$, $D\left( \theta \right)$ is a continuous $G\times G$ diagonal matrix function of $\theta$ with constant ${\mathcal {G}}_{\pm }$ and ${\mathcal {G}}_0$ $\forall \theta$, and $\det \left[ T^{{\mathcal {G}}_0}\left( \theta \right) \right] \ne 0$ $\forall \theta$. Then $\mu \left( \theta \right) :=\mu \left( T|D\right) \left( \theta \right)$ is continuous.

Theorem A2 proves the continuity of $\mu \left( T|D\right)$ by Lemma A3.

Lemma A7

For $\epsilon >0$ and $j_0\in {\mathcal {G}}$, let $Z^\epsilon :=\left( z^\epsilon _{i,j}\right) _{G\times G}$ with $z^\epsilon _{i,j_0}:=\epsilon z_{i,j_0}$ and $z^\epsilon _{i,j}:=z_{i,j}$ for $j\ne j_0$. Then ${{\,\mathrm{sgn}\,}}\left[ r\left( Z^\epsilon \right) \right] \equiv {{\,\mathrm{sgn}\,}}\left[ r\left( Z\right) \right]$, where ${{\,\mathrm{sgn}\,}}$ is the sign function.

Lemma A8

Assume that T is irreducible. Then $v=\left( v_j\right) _{G\times 1}\ne 0$ satisfies $Tv=0$ iff

$$\begin{aligned} \frac{v_1}{\det \left( T^{{\bar{1}}}\right) }=\frac{v_2}{\det \left( T^{{\bar{2}}}\right) }=\frac{v_3}{\det \left( T^{{\bar{3}}}\right) }=\cdots =\frac{v_G}{\det \left( T^{{\bar{G}}}\right) }. \end{aligned}$$

Appendix B: Proofs of results in “Appendix A”

Proof of Lemma A1.

Proof

Case 1: Since $r\left( M-\lambda D\right)$ has the smallest real part among all eigenvalues of $M-\lambda D$, it is not hard to show by the Gershgorin circle theorem that $\lim _{\lambda \rightarrow +\infty }r\left( M-\lambda D\right) =-\infty$. By $r\left( M\right) \ge 0$, $\exists \mu _+\ge 0$ such that $r\left( M-\mu _+ D\right) =0$. Because $D>0$, $\lambda <\mu _+ \Rightarrow M-\lambda D>M-\mu _+ D \Rightarrow r\left( M-\lambda D\right) >r\left( M-\mu _+ D\right) =0$. $\frac{dr\left( M-\lambda D\right) }{d\lambda }|_{\lambda =\mu _+}<0$ since otherwise, by $\frac{d^2r\left( M-\lambda D\right) }{d\lambda ^2}<0$ (Deutsch and Neumann 1984), $r\left( M-\lambda D\right) <0$ for $\lambda <\mu _+$, conflicts. By $\frac{d^2r\left( M-\lambda D\right) }{d\lambda ^2}<0$, $r\left( M-\lambda D\right) <0$ for $\lambda >\mu _+$. $\varXi \left( M-\mu _+ D\right) >0$ because it is the product of nondominant eigenvalues of irreducible M-matrix $M-\mu _+ D$. Therefore,

$$\begin{aligned} \frac{d\det \left( M-\lambda D\right) }{d\lambda }\bigg |_{\lambda =\mu _+}= & {} \frac{dr\left( M-\lambda D\right) \varXi \left( M-\lambda D\right) }{d\lambda }\bigg |_{\lambda =\mu _+}\nonumber \\= & {} \frac{dr\left( M-\lambda D\right) }{d\lambda }\varXi \left( M-\lambda D\right) \bigg |_{\lambda =\mu _+}\nonumber \\&+\,r\left( M-\lambda D\right) \frac{d\varXi \left( M-\lambda D\right) }{d\lambda }\bigg |_{\lambda =\mu _+}\nonumber \\= & {} \frac{dr\left( M-\lambda D\right) }{d\lambda }\bigg |_{\lambda =\mu _+}\varXi \left( M-\mu _+ D\right) <0, \end{aligned}$$

(A1)

i.e. $c\left( \mu _+|M|D\right) =1$.

Case 2: Similar as case 1.

Case 3: Resembling case 1, $\lim _{\lambda \rightarrow \pm \infty }r\left( M-\lambda D\right) =-\infty$. If $r\left( M\right) >0$, $\exists \mu _+>0>\mu _-$ such that $r\left( M-\mu _{\pm } D\right) =0$. Because $\frac{d^2r\left( M-\lambda D\right) }{d\lambda ^2}<0$, we have

$$\begin{aligned} \frac{dr\left( M-\lambda D\right) }{d\lambda }|_{\lambda =\mu _+}<0<\frac{dr\left( M-\lambda D\right) }{d\lambda }|_{\lambda =\mu _-}, \end{aligned}$$

$r\left( M-\lambda D\right) >0$ for $\mu _-<\lambda <\mu _+$, and $r\left( M-\lambda D\right) <0$ for $\lambda <\mu _-$ or $\lambda >\mu _+$. By Eq. (A1), $\frac{d\det \left( M-\lambda D\right) }{d\lambda }|_{\lambda =\mu _+}<0<\frac{d\det \left( M-\lambda D\right) }{d\lambda }|_{\lambda =\mu _-}$. Thus, $c\left( \mu _{\pm }|M|D\right) =1$.

If $r\left( M\right) =0$ and $\frac{dr\left( M-\lambda D\right) }{d\lambda }\big |_{\lambda =0}>0$ ($\frac{dr\left( M-\lambda D\right) }{d\lambda }\big |_{\lambda =0}<0$), $\exists \mu _-=0<\mu _+$ ($\mu _-<0=\mu _+$) such that $r\left( M-\mu _{\pm } D\right) =0$ since $\lim _{\lambda \rightarrow \pm \infty }r\left( M-\lambda D\right) =-\infty$. The subsequent proofs are the same as $r\left( M\right) >0$. If $\frac{dr\left( M-\lambda D\right) }{d\lambda }\big |_{\lambda =0}=0$, since $\frac{d^2r\left( M-\lambda D\right) }{d\lambda ^2}<0$, $r\left( M-\lambda D\right) <0$ for $\lambda \ne 0$, and $c\left( 0|M|D\right) =2$. $\square$

Proof of Lemma A2.

Proof

Sufficiency: Define ${\mathcal {K}}_0^{\mathrm{non}}:=\left\{ i\in {\mathcal {I}}|m\left( D_i\right) =n\left( D_i\right) =0,\det \left( M_i\right) \ne 0\right\}$. $\forall i\in {\mathcal {K}}_0^{\mathrm{sin}}\cup {\mathcal {K}}_0^{\mathrm{non}}$, $M_i$ is a principal submatrix of the nonsingular M-matrix $M^{{\mathcal {G}}_0}$, thereby nonsingular. Thus, $i\in {\mathcal {K}}_0^{\mathrm{non}}$, which means ${\mathcal {K}}_0^{\mathrm{sin}}=\emptyset$.

Necessity: Assume without loss of generality that $M^{{\mathcal {G}}_0}$ is in the normal form. Any irreducible diagonal block $M_j^{{\mathcal {G}}_0}$ of $M^{{\mathcal {G}}_0}$ is either an irreducible diagonal block $M_i$ of M, or a principal submatrix of that. For the former, $M_j^{{\mathcal {G}}_0}$ is nonsingular since ${\mathcal {K}}_0^{\mathrm{sin}}=\emptyset$. For the latter, $M_j^{{\mathcal {G}}_0}$ is nonsingular since $M_i$ is an irreducible M-matrix. In summary, $M^{{\mathcal {G}}_0}$ is nonsingular. $\square$

Proof of Lemma A3.

Proof

Case 1: Prove by contradiction that $\lim _{\theta \rightarrow \theta _0}\mu _+\left( \theta \right) =\mu _+\left( \theta _0\right)$. Otherwise, since $\mu _+\left( \theta \right)$ is bounded near $\theta _0$, $+\infty>\varlimsup _{\theta \rightarrow \theta _0}\mu _+\left( \theta \right)>\varliminf _{\theta \rightarrow \theta _0}\mu _+\left( \theta \right) >-\infty$. Let $\lim _{i\rightarrow +\infty }\theta _i=\theta _0$ be a sequence such that

$$\begin{aligned} \lim _{i\rightarrow +\infty }\mu _+\left( \theta _i\right) =\varliminf _{\theta \rightarrow \theta _0}\mu _+\left( \theta \right) . \end{aligned}$$

By continuity of $r\left( M-\lambda D\right)$,

$$\begin{aligned} 0= & {} \lim _{i\rightarrow +\infty }r\left[ M\left( \theta _i\right) -\mu _+\left( \theta _i\right) D\left( \theta _i\right) \right] =r\left[ M\left( \theta _0\right) -\lim _{i\rightarrow +\infty }\mu _+\left( \theta _i\right) D\left( \theta _0\right) \right] \\= & {} r\left[ M\left( \theta _0\right) -\varliminf _{\theta \rightarrow \theta _0}\mu _+\left( \theta \right) D\left( \theta _0\right) \right] . \end{aligned}$$

So $\varliminf _{\theta \rightarrow \theta _0}\mu _+\left( \theta \right) \in R\left( M|D\right) \left( \theta _0\right)$. Similarly, $\varlimsup _{\theta \rightarrow \theta _0}\mu _+\left( \theta \right) \in R\left( M|D\right) \left( \theta _0\right)$. Since $\varliminf _{\theta \rightarrow \theta _0}\mu _+\left( \theta \right) \ne \varlimsup _{\theta \rightarrow \theta _0}\mu _+\left( \theta \right)$, the only possibility is that

$$\begin{aligned} \mu _+\left( \theta _0\right) =\varlimsup _{\theta \rightarrow \theta _0}\mu _+\left( \theta \right) >\varliminf _{\theta \rightarrow \theta _0}\mu _+\left( \theta \right) =\lim _{i\rightarrow +\infty }\mu _+\left( \theta _i\right) =\mu _-\left( \theta _0\right) . \end{aligned}$$

For i large enough, $\mu _+\left( \theta _i\right) <\left[ \mu _+\left( \theta _0\right) +\mu _-\left( \theta _0\right) \right] /2=:{\overline{\mu }}\left( \theta _0\right)$. By Corollary A1, $r\left[ M\left( \theta _0\right) -{\overline{\mu }}\left( \theta _0\right) D\left( \theta _0\right) \right] >0$ since $\mu _-\left( \theta _0\right)<{\overline{\mu }}\left( \theta _0\right) <\mu _+\left( \theta _0\right)$, and for i large enough, $r\left[ M\left( \theta _i\right) -{\overline{\mu }}\left( \theta _0\right) D\left( \theta _i\right) \right] <0$ since ${\overline{\mu }}\left( \theta _0\right) >\mu _+\left( \theta _i\right)$. By the continuity of $r\left( M-\lambda D\right)$,

$$\begin{aligned} 0\ge \lim _{i\rightarrow +\infty }r\left[ M\left( \theta _i\right) -{\overline{\mu }}\left( \theta _0\right) D\left( \theta _i\right) \right] =r\left[ M\left( \theta _0\right) -{\overline{\mu }}\left( \theta _0\right) D\left( \theta _0\right) \right] >0, \end{aligned}$$

conflicts. Thus, $\mu _+\left( \theta \right)$ is continuous, and similarly, $\mu _-\left( \theta \right)$ is continuous.

Case 2: Similar as case 1. $\square$

Proof of Lemma A4.

Proof

$\forall \lambda \in \varLambda \left( B|D\right)$, $\exists v=\left( v_1,v_2,\cdots ,v_G\right)$ such that $v\left( B-\lambda D\right) =0$. Prove by contradiction that $\exists i_1\notin {\mathcal {G}}_0$ such that $|v_{i_1}|=\max _{i'\in {\mathcal {G}}}|v_{i'}|$. Otherwise, $|v_{i_2}|=\max _{i'\in {\mathcal {G}}}|v_{i'}|$ for some $i_2\in {\mathcal {G}}_0$. Because $B^{{\mathcal {G}}_0}$ is irreducible, there exists a path $i_2={\widehat{i}}_1,{\widehat{i}}_2,\cdots ,{\widehat{i}}_a=j_0\in {\mathcal {G}}_0$ such that $b_{{\widehat{i}}_{a'+1},{\widehat{i}}_{a'}}>0$ $\forall a'\in \left[ 1,a-1\right]$. Because $d_j=0$ and $|b_{j,j}|\ge |b_{\cdot ,j}|$ $\forall j\in {\mathcal {G}}_0$, by consecutively vanishing components ${\widehat{i}}_1,{\widehat{i}}_2,\cdots ,{\widehat{i}}_{a}$ of $v\left( B-\lambda D\right)$, $|b_{{\widehat{i}}_{a'},{\widehat{i}}_{a'}}|=|b_{\cdot ,{\widehat{i}}_{a'}}|$ and $|v_{{\widehat{i}}_{a'}}|=\max _{i'\in {\mathcal {G}}}|v_{i'}|$ $\forall a'\in \left[ 1,a\right]$. Since $|b_{j_0,j_0}|>\sum _{i\in {\mathcal {G}}_0{\setminus }\left\{ j_0\right\} }|b_{i,j_0}|$, $\exists i_1\notin {\mathcal {G}}_0$ such that $b_{i_1,j_0}\ne 0$. So $|v_{i_1}|=\max _{i'\in {\mathcal {G}}}|v_{i'}|$, conflicts.

Since component $i_1$ of $v\left( B-\lambda D\right)$ vanishes, $v_{i_1}\left( \lambda d_{i_1}-b_{i_1,i_1}\right) =\sum _{i\ne i_1}v_ib_{i,i_1}$. Thus,

$$\begin{aligned}&|\lambda - b_{i_1,i_1}/d_{i_1}|=\left| \left( \sum _{i\ne i_1}\frac{v_i}{v_{i_1}}b_{i,i_1}\right) \Bigg / d_{i_1}\right| \le \left( \sum _{i\ne i_1}\left| \frac{v_i}{v_{i_1}}b_{i,i_1}\right| \right) \Bigg / |d_{i_1}|\\&\le \left( \sum _{i\ne i_1}\left| b_{i,i_1}\right| \right) \Bigg / |d_{i_1}|=|b_{\cdot ,i_1}|/|d_{i_1}|. \end{aligned}$$

Therefore, $\lambda \in O\left( b_{i_1,i_1}/d_{i_1},|b_{\cdot ,i_1}|/|d_{i_1}|\right) \subset {\mathcal {O}}\left( B|D\right)$. This is statement 1.

Let $B^{\epsilon }=\left( b^{\epsilon }_{i,j}\right) _{G\times G}$ for $\epsilon \in \left[ 0,1\right]$. $b^{\epsilon }_{i,j}=\epsilon b_{i,j}$ for $j\notin {\mathcal {G}}_0$ and $i\ne j$; otherwise, $b^{\epsilon }_{i,j}=b_{i,j}$. $B^{\epsilon }$ satisfies conditions in statement 1. Define ${\mathcal {G}}_+^0:=\left\{ j|j\in {\mathcal {G}},d_j>0,b_{j,j}=0\right\}$ and ${\mathcal {G}}_-^0:=\left\{ j|j\in {\mathcal {G}},d_j<0,b_{j,j}=0\right\}$. For $\epsilon =0$, $\varLambda \left( B^\epsilon |D\right) =\left\{ b_{j,j}/d_j|j\notin {\mathcal {G}}_0\right\}$. For $\epsilon <1$,

$$\begin{aligned}&\bigcup _{j\in {\mathcal {G}}_+^0\cup {\mathcal {G}}_-^0}O\left( b_{j,j}/d_j,\epsilon |b_{\cdot ,j}|/d_j\right) \equiv \left\{ 0\right\} ,\\&\left[ \bigcup _{j\in {\mathcal {G}}_+{\setminus } {\mathcal {G}}_+^0}O\left( b_{j,j}/d_j,\epsilon |b_{\cdot ,j}|/d_j\right) \right] \cap \left[ \bigcup _{j\in {\mathcal {G}}_-{\setminus } {\mathcal {G}}_-^0}O\left( b_{j,j}/d_j,\epsilon |b_{\cdot ,j}|/d_j\right) \right] =\emptyset . \end{aligned}$$

By statement 1 and the continuity of $\varLambda \left( B^{\epsilon }|D\right)$ on $\epsilon$,

$$\begin{aligned}&m\left( D\right) +|{\mathcal {G}}_-^0|\le \sum _{\lambda \in \left[ \varLambda \cap {\mathcal {O}}_+\right] \left( B|D\right) }c\left( \lambda |B|D\right) ,\\&n\left( D\right) +|{\mathcal {G}}_+^0|\le \sum _{\lambda \in \left[ \varLambda \cap {\mathcal {O}}_-\right] \left( B|D\right) }c\left( \lambda |B|D\right) . \end{aligned}$$

This is statement 2. $\square$

Proof of Lemma A5.

Proof

By Lemma A4, $\sum _{\lambda \in \left[ \varLambda \cap {\mathcal {O}}_+\right] \left( T|D\right) }c\left( \lambda |T|D\right) \ge m\left( D\right)$. $\left[ \varLambda _-\cap {\mathcal {O}}_+\right] \left( T|D\right) =\emptyset$ and $\sum _{\lambda \in \varLambda \left( T|D\right) }c\left( \lambda |T|D\right) =m\left( D\right) +n\left( D\right)$, so $n\left( T|D\right) \le n\left( D\right)$. Similarly, $m\left( T|D\right) \le m\left( D\right)$. Thus, if both cases 1 and 2 fail, then $m\left( T|D\right) < m\left( D\right)$ and $n\left( T|D\right) < n\left( D\right)$. So at least one of the three cases happens. Obviously, case 3 cannot happen simultaneously with any of cases 1 and 2. Because $0\in \varLambda \left( T|D\right)$, cases 1 and 2 cannot happen simultaneously. In summary, exact one of the three cases happens. By Lemma A4, $\varLambda _0\left( T|D\right) \subset {\mathcal {O}}\left( T|D\right)$. So $\varLambda _0\left( T|D\right) \subset {\mathcal {O}}\left( T|D\right) \cap \left\{ z\in {\mathbb {C}}|\mathfrak {R}\left( z\right) =0\right\} =\left\{ 0\right\}$. $\square$

Proof of Lemma A6.

Proof

Case 1: Starting from case 1 in Lemma A5, $m\left( T|D\right) =m\left( D\right)$. $T^{{\mathcal {G}}_0}$ is a nonsingular M-matrix. So $\det \left( T^{{\mathcal {G}}_0}\right) >0$. For $0<\lambda <\min _{\lambda '\in \varLambda _+\left( T|D\right) }\mathfrak {R}\left( \lambda '\right)$,

$$\begin{aligned} \det \left( T-\lambda D\right)= & {} \det \left( T^{{\mathcal {G}}_0}\right) \prod _{i\notin {\mathcal {G}}_0}\left( -d_i\right) \left( \lambda -\lambda _i\right) \\= & {} \det \left( T^{{\mathcal {G}}_0}\right) \prod _{i\notin {\mathcal {G}}_0}\left( -1\right) ^{m\left( D\right) }|d_i|\left( -1\right) ^{m\left( T|D\right) }|\lambda -\lambda _i|\\= & {} \det \left( T^{{\mathcal {G}}_0}\right) \prod _{i\notin {\mathcal {G}}_0}|d_i||\lambda -\lambda _i|>0, \end{aligned}$$

where $\lambda _i$ are the roots of $\det \left( T-\lambda D\right) =0$. Moreover, since T is an irreducible M-matrix, $\varXi \left( T\right) >0$ because it is the product of nondominant eigenvalues of M-matrix T. So for $\lambda >0$ small enough, $\varXi \left( T-\lambda D\right) >0$. In conclusion, $r\left( T-\lambda D\right) =\det \left( T-\lambda D\right) /\varXi \left( T-\lambda D\right) >0$. By Lemma A1, if $m\left( D\right) >0$, $0<\lambda <\mu _+\left( T|D\right)$. Since $r\left( T\right) =0$, $\mu _-\left( T|D\right) =0$. Finally, $c\left( \mu _{\pm }|T|D\right) =1$ by Lemma A1. Together with $\varLambda _0\subset \left\{ 0\right\}$ by Lemma A5, there is $n\left( Z|D\right) =n\left( D\right) -1$,

Case 2: Similar as case 1.

Case 3: Starting from case 3 in Lemma A5, $m\left( T|D\right) <m\left( D\right)$ and $n\left( T|D\right) <n\left( D\right)$. Because $c\left( 0|T|D\right) \le 2$ by Lemma A1, the only possibility is $m\left( T|D\right) =m\left( D\right) -1$, $n\left( T|D\right) =n\left( D\right) -1$, and $\mu _{\pm }\left( T|D\right) =0$. $\square$

Proof of Theorem A1.

Proof

Case 1: Starting from case 1 in Lemma A5, $m\left( T|D\right) =m\left( D\right)$. $T_i$ is irreducible and diagonally dominant in columns, so $T_i$ is singular iff it has vanishing column sums. Also, since $T^{{\mathcal {G}}_0}$ is irreducible, it is either an irreducible block of T, or a principal submatrix of that. As a result, singular $T_i$ satisfies all conditions in Lemma A6. So there are three types of singular $T_i$.

• 1. $m\left( T_i|D_i\right) =m\left( D_i\right)$, $n\left( T_i|D_i\right) =n\left( D_i\right) -1$, $\mu _-\left( T_i|D_i\right) =0$. If $m\left( D_i\right) >0$, $\mu _+\left( T_i|D_i\right) >0$.

• 2. $m\left( T_i|D_i\right) =m\left( D_i\right) -1$, $n\left( T_i|D_i\right) =n\left( D_i\right)$, $\mu _+\left( T_i|D_i\right) =0$. If $n\left( D_i\right) >0$, $\mu _-\left( T_i|D_i\right) <0$.

• 3. $m\left( T_i|D_i\right) =m\left( D_i\right) -1$, $n\left( T_i|D_i\right) =n\left( D_i\right) -1$, $\mu _{\pm }\left( T_i|D_i\right) =0$.

Since $m\left( T|D\right) =m\left( D\right)$, only type 1 can happen. By Lemma A1, $r\left( T_i-\lambda D_i\right) >0$ for $0=\mu _-\left( T_i|D_i\right)<\lambda <\mu _+\left( T_i|D_i\right)$ if $m\left( D_i\right) >0$; otherwise, $r\left( T_i-\lambda D_i\right) >0$ for $0=\mu _-\left( T_i|D_i\right) <\lambda$. On the other hand, $r\left( T_i-\lambda D_i\right) >0$ for nonsingular $T_i$ and $\lambda >0$ small enough. In summary, $r\left( T-\lambda D\right) >0$ for $\lambda >0$ small enough. Because $T^{{\mathcal {G}}_0}$ is nonsingular, by Corollary A1, $\mu _+\left( T|D\right)>\lambda >0$ if $m\left( D\right) >0$. Finally, $\mu _-\left( T|D\right) =0$ since $r\left( T\right) =0$.

Case 2: Similar as case 1.

Case 3: Starting from case 3 in Lemma A5, $m\left( T|D\right) <m\left( D\right)$ and $n\left( T|D\right) <n\left( D\right)$. If there exists singular $T_i$ of type 3, then by Lemma A1, $r\left( T_i-\lambda D_i\right) <0$ for $\lambda \ne 0$, thereby $r\left( T-\lambda D\right) <0$ for $\lambda \ne 0$. Thus, $\mu _{\pm }\left( T|D\right) =0$ by Corollary A1. Otherwise, by $m\left( T|D\right) <m\left( D\right)$, there exists singular $T_i$ of type 2. By Lemma A1, $r\left( T_i-\lambda D_i\right) <0$ for $\lambda >\mu _+\left( T_i|D_i\right) =0$, thereby $r\left( T-\lambda D\right) <0$ for $\lambda >0$. Similarly, by $n\left( T|D\right) <n\left( D\right)$, there exists singular $T_i$ of type 1, thereby $r\left( T-\lambda D\right) <0$ for $\lambda <0$. In summary, $r\left( T-\lambda D\right) <0$ for $\lambda \ne 0$. Thus, $\mu _{\pm }\left( T|D\right) =0$ by Corollary A1. $\square$

Proof of Theorem A2.

Proof

By Lemma A3, $\mu _{\pm }\left( \theta \right)$ are continuous. If $\mu _+\left( \theta _0\right) >\mu _-\left( \theta _0\right)$, by continuity, $\exists \delta >0$ such that $\mu _+\left( \theta _1\right) >\mu _-\left( \theta _2\right)$ $\forall \theta _1,\theta _2\in \left( \theta _0-\delta ,\theta _0+\delta \right)$. Therefore, either $\mu _+\left( \theta \right) \equiv 0$ or $\mu _-\left( \theta \right) \equiv 0$ in $\left( \theta _0-\delta ,\theta _0+\delta \right)$. Thus, either $\mu \left( \theta \right) \equiv \mu _-\left( \theta \right)$ or $\mu \left( \theta \right) \equiv \mu _+\left( \theta \right)$ in $\left( \theta _0-\delta ,\theta _0+\delta \right)$. Then $\mu \left( \theta \right)$ is continuous at $\theta _0$.

If $\mu _{\pm }\left( \theta _0\right) =0$, then since $\mu \in \{\mu _+,\mu _-\}$,

$$\begin{aligned} \mu \left( \theta _0\right) =\mu _{\pm }\left( \theta _0\right) =0=\lim _{\theta \rightarrow \theta _0}\mu _{\pm }\left( \theta \right) =\lim _{\theta \rightarrow \theta _0}\mu \left( \theta \right) . \end{aligned}$$

$\square$

Proof of Lemma A7.

Proof

First prove the case of irreducible Z.

• 1. Assume $r\left( Z\right) =0$. Since Z is irreducible, $\exists v>0$ such that $vZ=0$. Thus, $vZ^{\epsilon }=0$. Because $Z^{\epsilon }$ is irreducible and $v>0$, $r(Z^{\epsilon })=0$.

• 2. Assume $r\left( Z\right) \ne 0$. Prove by contradiction that ${{\,\mathrm{sgn}\,}}\left[ r\left( Z\right) \right] ={{\,\mathrm{sgn}\,}}\left[ r\left( Z^\epsilon \right) \right]$. Otherwise, by continuity, $\exists \epsilon '>0$ such that $r\left( Z^{\epsilon '}\right) =0$. By case 1, $r\left( Z\right) =0$, conflicts.

If Z is reducible,

$$\begin{aligned}&{{\,\mathrm{sgn}\,}}\left[ r\left( Z\right) \right] ={{\,\mathrm{sgn}\,}}\left[ \min _{i\in {\mathcal {I}}}r\left( Z_i\right) \right] =\min _{i\in {\mathcal {I}}}{{\,\mathrm{sgn}\,}}\left[ r\left( Z_i\right) \right] \\&=\min _{i\in {\mathcal {I}}}{{\,\mathrm{sgn}\,}}\left[ r\left( Z^\epsilon _i\right) \right] ={{\,\mathrm{sgn}\,}}\left[ \min _{i\in {\mathcal {I}}}r\left( Z^\epsilon _i\right) \right] ={{\,\mathrm{sgn}\,}}\left[ r\left( Z^{\epsilon }\right) \right] . \end{aligned}$$

$\square$

Proof of Lemma A8.

Proof

Sufficiency: Because column sums of T vanish, the following three steps transform $T^{{\bar{i}},{\bar{j}}}$ to $T^{{\bar{j}},{\bar{j}}}$ for $i>j$.

• 1. Sum all rows of $T^{{\bar{i}},{\bar{j}}}$ except row j to row j.

• 2. Multiply row j by $-1$.

• 3. Exchange row j with rows $j+1,j+2,\cdots ,i-1$ one by one.

During which there are totally $i-j$ changes of sign. So $T^{{\bar{j}},{\bar{j}}}=\left( -1\right) ^{i-j}T^{{\bar{i}},{\bar{j}}}=\left( -1\right) ^{i+j}T^{{\bar{i}},{\bar{j}}}$ for $i>j$. There are similar statements for $i<j$ as well. Then component i of Tv satisfies

$$\begin{aligned} \sum _{j=1}^G t_{i,j}T^{{\bar{j}},{\bar{j}}}=\sum _{j=1}^G \left( -1\right) ^{i+j}t_{i,j}T^{{\bar{i}},{\bar{j}}}=\det \left( T\right) =0. \end{aligned}$$

Necessity: Because T is irreducible, its dominant eigenvalue 0 is simple, and the corresponding eigenvector space is of dimension 1. $\square$

Appendix C: Extension of Theorem 1

Theorem A3

For $i\in \left[ 2,G-1\right]$, if $\widehat{{\widetilde{H}}}\left( x\right)$ is continuous at $x_i^*$, $\lim _{x\rightarrow x_i^*}\frac{\widehat{{\widetilde{h}}}_{i,\cdot }\left( x\right) }{|x-x_i^*|}=+\infty$, and $\lim _{x\rightarrow x_i^*}\frac{\widehat{{\widetilde{h}}}_{i,j}\left( x\right) }{\widehat{{\widetilde{h}}}_{i,\cdot }\left( x\right) }$ exists $\forall j\ne i$, then:

• 1. There exists a single root $\lambda _{\infty }\left( x\right)$ of $\det \left[ \widehat{{\widetilde{H}}}\left( x\right) -\lambda A\left( x\right) \right] =0$ near $x_i^*$ such that $\widehat{{\widetilde{h}}}_{i,\cdot }\left( x_i^*\right) =\lim _{x\rightarrow x_i^*}\gamma \left( x_i^*-x\right) \lambda _{\infty }\left( x\right)$.

• 2. ${\mathbb {H}}_i:=\lim _{x\rightarrow x_i^*}\widehat{{\widetilde{H}}}\left( x\right) I_i\left[ 1/\widehat{{\widetilde{h}}}_{i,\cdot }\left( x\right) \right]$ satisfies that $\forall \lambda$,

  $$\begin{aligned} \lim _{x\rightarrow x_i^*}p\left( x\right) \left( \lambda \right) =\det \left[ {\mathbb {H}}_i-\lambda A\left( x_i^*\right) \right] \Bigg /\left[ \prod _{i'\ne i}\gamma \left( x_i^*-x_{i'}^*\right) \right] , \end{aligned}$$

  where $I_i\left[ 1/\widehat{{\widetilde{h}}}_{i,\cdot }\left( x\right) \right]$ is obtained by replacing the ith diagonal element of the identity matrix by $1/\widehat{{\widetilde{h}}}_{i,\cdot }\left( x\right)$, and for $x\in \bigcup _{i'=1}^{G-1}\left( x_{i'+1}^*,x_{i'}^*\right)$,

  $$\begin{aligned} p\left( x\right) \left( \lambda \right) :=\det \left[ \widehat{{\widetilde{H}}}\left( x\right) -\lambda A\left( x\right) \right] \Bigg /\left\{ \left[ \lambda -\lambda _{\infty }\left( x\right) \right] \prod _{i'=1}^G\gamma \left( x-x_{i'}^*\right) \right\} . \end{aligned}$$

  (A2)

• 3. $\lim _{x\rightarrow x_i^*}\mu \left( x\right) =\mu _i:=\mu \left[ {\mathbb {H}}_i|A\left( x_i^*\right) \right]$.

Under the assumption of Theorem A3, it is possible that $\widehat{{\widetilde{h}}}_{i,\cdot }\left( x_i^*\right) =0$. Then the characteristic polynomial of GEs degenerates, i.e. $\det \left[ \widehat{{\widetilde{H}}}\left( x_i^*\right) -\lambda A\left( x_i^*\right) \right] \equiv 0$ $\forall \lambda \in {\mathbb {C}}$. This explains the importance of irreducibility of $\widehat{{\widetilde{H}}}\left( x\right)$, which promises $\widehat{{\widetilde{h}}}_{i,\cdot }\left( x_i^*\right) >0$ in Theorem 1. By Theorem A1, $\mu \left( \widehat{{\widetilde{H}}}|A\right) \left( x\right)$ is still well-defined for $x\in \bigcup _{i=1}^{G-1}\left( x_{i+1}^*,x_{i}^*\right)$, and we define $\mu \left( x\right) :=\mu \left( \widehat{{\widetilde{H}}}|A\right) \left( x\right)$. Nevertheless, $\mu \left( x_i^*\right)$ no longer equals to $\mu \left( \widehat{{\widetilde{H}}}|A\right) \left( x_i^*\right)$.

Proof

For $x\in \bigcup _{i'=1}^{G-1}\left( x_{i'+1}^*,x_{i'}^*\right)$, $A\left( x\right)$ is nonsingular, thereby

$$\begin{aligned} \det \left[ \widehat{{\widetilde{H}}}\left( x\right) -\lambda A\left( x\right) \right] =\det \left[ \widehat{{\widetilde{H}}}\left( x\right) A^{-1}\left( x\right) -\lambda I\right] \det \left[ A\left( x\right) \right] , \end{aligned}$$

and the GEs of $\widehat{{\widetilde{H}}}\left( x\right)$ on $A\left( x\right)$ are the eigenvalues of $\widehat{{\widetilde{H}}}\left( x\right) A^{-1}\left( x\right)$. $\forall \lambda$,

$$\begin{aligned} \lim _{x\rightarrow x_i^*}\det \left[ \gamma \left( x_i^*-x\right) \widehat{{\widetilde{H}}}\left( x\right) A^{-1}\left( x\right) -\lambda I\right] =\left( -1\right) ^G\lambda ^{G-1}\left[ \lambda -\widehat{{\widetilde{h}}}_{i,\cdot }\left( x_i^*\right) \right] , \end{aligned}$$

so as $x\rightarrow x_i^*$, $G-1$ eigenvalues (count multiplicity) of $\gamma \left( x_i^*-x\right) \widehat{{\widetilde{H}}}\left( x\right) A^{-1}\left( x\right)$ tend to 0, and one tends to $\widehat{{\widetilde{h}}}_{i,\cdot }\left( x_i^*\right)$. The eigenvalues of $\gamma \left( x_i^*-x\right) \widehat{{\widetilde{H}}}\left( x\right) A^{-1}\left( x\right)$ are just those of $\widehat{{\widetilde{H}}}\left( x\right) A^{-1}\left( x\right)$ multiplying $\gamma \left( x_i^*-x\right)$, so we have statement 1.

Multiply both sides of Eq. (A2) by $\left[ \lambda -\lambda _{\infty }\left( x\right) \right] \prod _{i'=1}^G\gamma \left( x-x_{i'}^*\right) /\widehat{{\widetilde{h}}}_{i,\cdot }\left( x\right)$.

$$\begin{aligned}&\left[ \prod _{i'\ne i}\gamma \left( x-x_{i'}^*\right) \right] \gamma \left( x-x_i^*\right) \left[ \lambda -\lambda _\infty \left( x\right) \right] /\widehat{{\widetilde{h}}}_{i,\cdot }\left( x\right) P\left( x\right) \left( \lambda \right) \\&\quad =\det \left\{ \left[ \widehat{{\widetilde{H}}}\left( x\right) -\lambda A\left( x\right) \right] I_i\left[ 1/\widehat{{\widetilde{h}}}_{i,\cdot }\left( x\right) \right] \right\} . \end{aligned}$$

Because ${\mathbb {H}}_i:=\lim _{x\rightarrow x_i^*}\widehat{{\widetilde{H}}}\left( x\right) I_i\left[ 1/\widehat{{\widetilde{h}}}_{i,\cdot }\left( x\right) \right]$, $\lim _{x\rightarrow x_i^*}\gamma \left( x_i^*-x\right) /\widehat{{\widetilde{h}}}_{i,\cdot }\left( x\right) =0$, and $\lim _{x\rightarrow x_i^*}\gamma \left( x_i^*-x\right) \lambda _{\infty }\left( x\right) =\widehat{{\widetilde{h}}}_{i,\cdot }\left( x_i^*\right)$, for any fixed $\lambda$,

$$\begin{aligned}&\left[ \prod _{i'\ne i}\gamma \left( x_i^*-x_{i'}^*\right) \right] \lim _{x\rightarrow x_i^*}P\left( x\right) \left( \lambda \right) \\&\quad =\lim _{x\rightarrow x_i^*}\left[ \prod _{i'\ne i}\gamma \left( x-x_{i'}^*\right) \right] \gamma \left( x-x_i^*\right) \left[ \lambda -\lambda _\infty \left( x\right) \right] /\widehat{{\widetilde{h}}}_{i,\cdot }\left( x\right) P\left( x\right) \left( \lambda \right) \\&\quad =\lim _{x\rightarrow x_i^*}\det \left\{ \left[ \widehat{{\widetilde{H}}}\left( x\right) -\lambda A\left( x\right) \right] I_i\left[ 1/\widehat{{\widetilde{h}}}_{i,\cdot }\left( x\right) \right] \right\} =\det \left[ {\mathbb {H}}_i-\lambda A\left( x_i^*\right) \right] . \end{aligned}$$

This is statement 2.

The trace of $\widehat{{\widetilde{H}}}\left( x\right) A^{-1}\left( x\right)$ tends to $+\infty$ as $x\rightarrow x_i^*-$ because

$$\begin{aligned} \lim _{x\rightarrow x_i^*-}\frac{\widehat{{\widetilde{h}}}_{i,\cdot }\left( x\right) }{\gamma \left( x_i^*-x\right) }=+\infty . \end{aligned}$$

Since the GEs are the eigenvalues of $\widehat{{\widetilde{H}}}\left( x\right) A^{-1}\left( x\right)$ for $x\in \bigcup _{i'=1}^{G-1}\left( x_{i'+1}^*,x_{i'}^*\right)$, the sum of all GEs is the trace of $\widehat{{\widetilde{H}}}\left( x\right) A^{-1}\left( x\right)$, thereby tending to $+\infty$ as $x\rightarrow x_i^*-$. By statement 2, GEs other than $\lambda _{\infty }\left( x\right)$ have finite limits as $x\rightarrow x_i^*$. So $\lim _{x\rightarrow x_i^*-}\lambda _{\infty }\left( x\right) =+\infty$. Similarly, $\lim _{x\rightarrow x_i^*+}\lambda _{\infty }\left( x\right) =-\infty$. Because $m[A(x_i^*)],n[A(x_i^*)]>0$, some diagonal element of $\widehat{{\widetilde{H}}}\left( x\right) -\lambda _{\infty }\left( x\right) A\left( x\right)$ tends to $-\infty$ as $x\rightarrow x_i^*$. By the Gershgorin circle theorem (Gershgorin 1931), $\lim _{x\rightarrow x_i^*}r\left[ \widehat{{\widetilde{H}}}\left( x\right) -\lambda _{\infty }\left( x\right) A\left( x\right) \right] =-\infty$. Thus, $\mu \left( x\right) \ne \lambda _{\infty }\left( x\right)$ for x near $x_i^*$. By statement 2, the roots of $\det \left[ \widehat{{\widetilde{H}}}\left( x\right) -\lambda A\left( x\right) \right] =0$ except $\lambda _\infty \left( x\right)$ tend to the $G-1$ roots of $\det \left[ {\mathbb {H}}_i-\lambda A\left( x_i^*\right) \right]$ as $x\rightarrow x_i^*$, thereby continuous at $x_i^*$ and bounded near $x_i^*$; thus, $-\infty<\varliminf _{x\rightarrow x_i^*}\mu \left( x\right) \le \varlimsup _{x\rightarrow x_i^*}\mu \left( x\right) <+\infty$. Let $\lim _{j\rightarrow +\infty }y_j=x_i^*$ be a sequence such that

$$\begin{aligned} \lim _{j\rightarrow +\infty }\mu \left( y_j\right) =\varlimsup _{x\rightarrow x_i^*}\mu \left( x\right) . \end{aligned}$$

For j large enough, $\widehat{{\widetilde{h}}}_{i,\cdot }\left( y_j\right) >0$ because $\lim _{x\rightarrow x_i^*}\frac{\widehat{{\widetilde{h}}}_{i,\cdot }\left( x\right) }{|x-x_i^*|}=+\infty$. By Lemma A7,

$$\begin{aligned}&r\left[ \widehat{{\widetilde{H}}}\left( y_j\right) -\mu \left( y_j\right) A\left( y_j\right) \right] =0\\&\quad \Rightarrow r\left\{ \left[ \widehat{{\widetilde{H}}}\left( y_j\right) -\mu \left( y_j\right) A\left( y_j\right) \right] I_i\left[ 1/\widehat{{\widetilde{h}}}_{i,\cdot }\left( y_j\right) \right] \right\} =0. \end{aligned}$$

As a result,

$$\begin{aligned}&r\left[ {\mathbb {H}}_i-\varlimsup _{x\rightarrow x_i^*}\mu \left( x\right) A\left( x_i^*\right) \right] \\&\quad =\lim _{j\rightarrow +\infty }r\left\{ \left[ \widehat{{\widetilde{H}}}\left( y_j\right) -\mu \left( y_j\right) A\left( y_j\right) \right] I_i\left[ 1/\widehat{{\widetilde{h}}}_{i,\cdot }\left( y_j\right) \right] \right\} =0. \end{aligned}$$

Thus, $\varlimsup _{x\rightarrow x_i^*}\mu \left( x\right)$ is a DGE of ${\mathbb {H}}_i$ on $A\left( x_i^*\right)$, and so is $\varliminf _{x\rightarrow x_i^*}\mu \left( x\right)$. Prove by contradiction that $\varlimsup _{x\rightarrow x_i^*}\mu \left( x\right) =\varliminf _{x\rightarrow x_i^*}\mu \left( x\right)$. Otherwise, $\varlimsup _{x\rightarrow x_i^*}\mu \left( x\right)$ and $\varliminf _{x\rightarrow x_i^*}\mu \left( x\right)$ are the only two DGEs of ${\mathbb {H}}_i$ on $A\left( x_i^*\right)$ by Corollary A1, and one must be 0 by Theorem A1. Assume without loss of generality that $0=\varlimsup _{x\rightarrow x_i^*}\mu \left( x\right) >\varliminf _{x\rightarrow x_i^*}\mu \left( x\right)$. Let ${\bar{\mu }}:=\varliminf _{x\rightarrow x_i^*}\mu \left( x\right) /2<0$. By Corollary A1, $r\left[ {\mathbb {H}}_i-{\bar{\mu }} A\left( x_i^*\right) \right] >0$ since $\varliminf _{x\rightarrow x_i^*}\mu \left( x\right)<{\bar{\mu }}<\varlimsup _{x\rightarrow x_i^*}\mu \left( x\right)$. For j large enough, ${\bar{\mu }}<\mu \left( y_j\right)$. Then

$$\begin{aligned} r\left\{ \left[ \widehat{{\widetilde{H}}}\left( y_j\right) -{\bar{\mu }}A\left( y_j\right) \right] I_i\left[ 1/\widehat{{\widetilde{h}}}_{i,\cdot }\left( y_j\right) \right] \right\} <0 \end{aligned}$$

by Corollary A1 since ${\bar{\mu }}<0$ and ${\bar{\mu }}<\mu (y_j)$. As $j\rightarrow +\infty$, $r\left[ {\mathbb {H}}_i-{\bar{\mu }} A\left( x_i^*\right) \right] \le 0$, conflicts. Therefore,

$$\begin{aligned} \varlimsup _{x\rightarrow x_i^*}\mu \left( x\right) =\varliminf _{x\rightarrow x_i^*}\mu \left( x\right) . \end{aligned}$$

Define $\mu \left( x_i^*\right) :=\lim _{x\rightarrow x_i^*}\mu \left( x\right)$. Then, $\mu \left( x\right)$ is continuous at $x_i^*$.

Now we show that $\mu \left( x_i^*\right) =\mu _i$. If $\mu _i=0$, then by Definition A4, 0 is the only DGE of ${\mathbb {H}}_i$ on $A\left( x_i^*\right)$. Then $\mu \left( x_i^*\right) =0$ because $\mu \left( x_i^*\right)$ is a DGE. Otherwise, assume without loss of generality that $\mu _i>0$. By Theorem A1, $m\left[ {\mathbb {H}}_i|A\left( x_i^*\right) \right] =m\left[ A\left( x_i^*\right) \right] =i-1$. By continuity, $\exists \delta >0$ such that for $x\in \left( x_i^*-\delta ,x_i^*\right)$, the $i-1$ roots of $\det \left[ {\mathbb {H}}_i-\lambda A\left( x_i^*\right) \right] =0$ with positive real parts at $x_i^*$ still have positive real parts at x. By $\lim _{x\rightarrow x_i^*-}\lambda _\infty \left( x\right) =+\infty$, it is possible to decrease $\delta$ such that $\lambda _\infty \left( x\right) >0$, thereby $m\left( \widehat{{\widetilde{H}}}|A\right) \left( x\right) \ge i$ for $x\in \left( x_i^*-\delta ,x_i^*\right)$. Conversely, for $x\in \left( x_{i+1}^*,x_i^*\right)$, $m\left( \widehat{{\widetilde{H}}}|A\right) \left( x\right) \le m\left[ A\left( x\right) \right] =i$ by Theorem A1. Therefore, $m\left( \widehat{{\widetilde{H}}}|A\right) \left( x\right) =m\left[ A\left( x\right) \right] =i$. By Theorem A1, $\mu \left( x\right) >0$ for $x\in \left( x_i^*-\delta ,x_i^*\right)$. Prove by contradiction that $\mu \left( x_i^*\right) =\mu _i$. Otherwise, $\mu \left( x_i^*\right) =0$. By continuity, the i roots of $\det \left[ \widehat{{\widetilde{H}}}\left( x\right) -\lambda A\left( x\right) \right] =0$ with positive real parts in $\left( x_i^*-\delta ,x_i^*\right)$, i.e. the $i-1$ roots of $\det \left[ {\mathbb {H}}_i-\lambda A\left( x_i^*\right) \right] =0$ with positive real parts at $x_i^*$ and $\lambda _{\infty }\left( x\right)$, are different from $\mu \left( x\right)$ for $x\in \left( x_i^*-\delta ',x_i^*\right)$ with $0<\delta '<\delta$ small enough. Thus, $m\left( \widehat{{\widetilde{H}}}|A\right) \left( x\right) \ge i+1>i=m\left[ A\left( x\right) \right]$, conflicts. Thus, we have statement 3. $\square$

Similar to Corollary 1, we have Corollary A2.

Corollary A2

Assume $\widehat{{\widetilde{H}}}\left( x\right)$ is continuous in $\left( x_G^*,x_1^*\right)$, $\lim _{x\rightarrow x_i^*}\frac{\widehat{{\widetilde{h}}}_{i,\cdot }\left( x\right) }{|x-x_i^*|}=+\infty$ $\forall i\in \left[ 2,G-1\right]$, and $\lim _{x\rightarrow x_i^*}\frac{\widehat{{\widetilde{h}}}_{i,j}\left( x\right) }{\widehat{{\widetilde{h}}}_{i,\cdot }\left( x\right) }$ exists $\forall j\ne i$. Let $\mu \left( x_i^*\right) :=\mu _i$ for $i\in \left[ 2,G-1\right]$. Then, $\mu \left( x\right)$ is continuous in $\left( x_G^*,x_1^*\right)$.

Remark A1

Assume $\widehat{{\widetilde{h}}}_{i,\cdot }\left( x_i^*\right) >0$. Then the characteristic polynomial of GEs is nondegenerate. Since $\left[ \widehat{{\widetilde{H}}}\left( x_i^*\right) -\lambda A\left( x_i^*\right) \right] I_i\left[ 1/\widehat{{\widetilde{h}}}_{i,\cdot }\left( x\right) \right] ={\mathbb {H}}_i-\lambda A\left( x_i^*\right)$, we have $\det \left[ {\mathbb {H}}_i-\lambda A\left( x_i^*\right) \right] =\det \left[ \widehat{{\widetilde{H}}}\left( x_i^*\right) -\lambda A\left( x_i^*\right) \right] /\widehat{{\widetilde{h}}}_{i,\cdot }\left( x\right)$. By Lemma A7, $\forall \lambda$, $r\left[ \widehat{{\widetilde{H}}}\left( x_i^*\right) -\lambda A\left( x_i^*\right) \right] =0$ iff $r\left[ {\mathbb {H}}_i-\lambda A\left( x_i^*\right) \right] =0$. Thus, GEs and DGEs of $\widehat{{\widetilde{H}}}\left( x_i^*\right)$ on $A\left( x_i^*\right)$ are the same as those of ${\mathbb {H}}_i$ on $A\left( x_i^*\right)$. So $\mu \left( \widehat{{\widetilde{H}}}|A\right) \left( x_i^*\right) =\mu \left[ {\mathbb {H}}_i|A\left( x_i^*\right) \right] =\mu _i$. In summary, the statements in Theorem A3 are equivalent to those in Theorem 1 for $\widehat{{\widetilde{h}}}_{i,\cdot }\left( x_i^*\right) >0$. Since $\widehat{{\widetilde{h}}}_{i,\cdot }\left( x_i^*\right) >0$ for irreducible $\widehat{{\widetilde{H}}}\left( x_i^*\right)$, Theorem A3 implies Theorem 1.