Adaptive dynamics of saturated polymorphisms

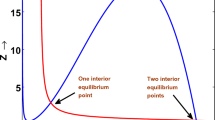
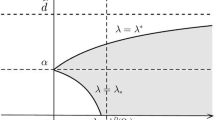
Abstract

We study the joint adaptive dynamics of n scalar-valued strategies in ecosystems where n is the maximum number of coexisting strategies permitted by the (generalized) competitive exclusion principle. The adaptive dynamics of such saturated systems exhibits special characteristics, which we first demonstrate in a simple example of a host–pathogen–predator model. The main part of the paper characterizes the adaptive dynamics of saturated polymorphisms in general. In order to investigate convergence stability, we give a new sufficient condition for absolute stability of an arbitrary (not necessarily saturated) polymorphic singularity and show that saturated evolutionarily stable polymorphisms satisfy it. For the case $n=2$, we also introduce a method to construct different pairwise invasibility plots of the monomorphic population without changing the selection gradients of the saturated dimorphism.

Appendices

Appendix A

In the main text, we assume that the resident population dynamics attain an asymptotically stable equilibrium. If the resident system exhibits non-equilibrium dynamics such that the environmental feedbacks vary in time, then the environment is characterized by the functions $t \mapsto E_1(t),\ldots ,E_n(t)$ and is therefore infinite dimensional unless there exists an alternative, finite-dimensional characterization. In this Appendix, we show how such finite-dimensional representations can be found and be used to extend the results of Sect. 3 to some non-equilibrium systems.

In the main text, we assume that the invasion fitness can be written as a function of the invading strategy and numbers $\hat{E}_1,\ldots ,\hat{E}_n$ that represent the environment, such that $\hat{E}_1,\ldots ,\hat{E}_n$ depend on the resident strategies but not on the invading strategy. Assume that the focal strategies have unstructured populations. The invasion fitness of the mutant $x_{mut}$ is then given by the time average of its population growth rate, i.e., by

$$\begin{aligned} \langle r(x_{mut},E_1(t),\ldots ,E_n(t),\psi (t)) \rangle \end{aligned}$$

where the angle brackets $\langle \cdot \rangle$ denote the time average and we assume that the expectation exists (Metz et al. 1992). We included a new (possibly vector-valued) argument $\psi (t)$ of the population growth rate r to accommodate non-autonomous population dynamics, i.e., the possible effect of temporal fluctuations in the physical environment such as the weather. For the present argument, it does not matter whether the environmental feedbacks vary in time due to endogeneous non-equilibrium dynamics or due to external fluctuations.

If $r(x_{mut},E_1,\ldots ,E_n,\psi )$ is linear in $E_1,\ldots ,E_n$ and in $\psi$, then the invasion fitness simplifies to

$$\begin{aligned} \langle r(x_{mut},E_1(t),\ldots ,E_n(t),\psi (t)) \rangle = r(x_{mut},\langle E_1(t) \rangle ,\ldots ,\langle E_n(t) \rangle ,\langle \psi (t) \rangle ) \end{aligned}$$

(26)

such that the resident population affects the invasion fitness only via the time averages $\langle E_1(t) \rangle ,\ldots ,\langle E_n(t) \rangle$ of the environmental feedback variables. Equation (7) are then equivalent to

$$\begin{aligned} r(x_1,\langle E_1(t) \rangle ,\ldots ,\langle E_n(t) \rangle ,\langle \psi (t) \rangle )= & {} 0 \nonumber \\&\vdots \\ r(x_n,\langle E_1(t) \rangle ,\ldots ,\langle E_n(t) \rangle ,\langle \psi (t) \rangle )= & {} 0 \nonumber \end{aligned}$$

and all results of Sect. 3 are valid with $\hat{E}_i=\langle E_i(t) \rangle$ for $i=1,\ldots ,n$.

There is considerable freedom in how the environmental feedback variables are defined in a given model, and in simple models it is often possible to chose the environmental feedback variables and $\psi$ such that r is linear in them and (26) applies. In the remainder of this Appendix, we show several examples based on the host–pathogen–predator model in Sect. 2.

Suppose first that in the model of Sect. 2, the natural mortality rate $\mu$ depends on time (e.g. varies with the seasons). Since the population growth rate

$$\begin{aligned} r(\alpha _{mut},S,P,\mu )=\beta (\alpha _{mut}) S - (\alpha _{mut} + \mu + \nu ) - (c+ \phi (\alpha _{mut})) P \end{aligned}$$

(27)

is linear in S and in P and also in $\mu$, we can apply (26) directly with $E_1(t)=S(t)$, $E_2(t)=P(t)$ and $\psi (t)=\mu (t)$. In other words, we can use $\langle S(t) \rangle$ and $\langle P(t) \rangle$ in place of $\hat{S}$ and $\hat{P}$, respectively, throughout the analysis of the model. In particular, the values of $\langle S(t) \rangle$ and $\langle P(t) \rangle$ in a resident population of strains $\alpha _1$ and $\alpha _2$ are the same as $\hat{S}(\alpha _1,\alpha _2)$ and $\hat{P}(\alpha _1,\alpha _2)$ in (5), respectively, in a population at equilibrium with $\mu$ constant at the value of $\langle \mu (t) \rangle$. Therefore, the adaptive dynamics of dimorphic populations would not be affected by the fluctuations (Fig. 1 would remain the same). Many simple models of unstructured populations based on mass action are similar to this example. In Lotka–Volterra models, it is well known that the time averages of population densities equal to their equilibrium values also if the system does not converge to the equilibrium; the same principle applies here.

Suppose now that predators interfere with each other when hunting for the prey, such that the presence of a second predator decreases the capture rate of the first. A somewhat sloppy way to include predator interference is to replace Eq. (1) with

$$\begin{aligned} \frac{dI_j}{dt}=\left[ \beta (\alpha _j) S(t) - (\alpha _j + \mu (t) + \nu ) - (1-e(\alpha _j) P(t)) (c+ \phi (\alpha _j))P(t) \right] I_j \end{aligned}$$

where the factor $(1-e(\alpha _j)P(t))$ is the probability that a hunting predator is not disturbed, and e may depend on $\alpha _j$ because hosts much weakened by the pathogen may be captured faster by the predator, giving less opportunity for interference. This introduces a quadratic term with $P^2$ into the population growth rate

$$\begin{aligned} r(\alpha _{mut},S,P,\mu )= & {} \beta (\alpha _{mut}) S - (\alpha _{mut} + \mu + \nu ) - (c+ \phi (\alpha _{mut})) \\&+\, e(\alpha _{mut}) (c+ \phi (\alpha _{mut})) P^2 \end{aligned}$$

In this case, we can define three environmental feedback variables, $E_1(t)=S(t)$, $E_2(t)=P(t)$ and $E_3(t)=[P(t)]^2$. r is linear of each of these, so that (26) applies. Note that through the quadratic term, fluctuations introduce a new feedback, essentially the variance of P(t). It remains to be seen whether three strains can coexist in this system or the number of environmental feedback variables has been inflated without increasing the maximum number of coexisting strains. This depends on the trade-off structure of the pathogen; if $\phi$ and e are constants, then $E_2$ and $E_3$ combine into a single environmental feedback variable $E(t)=(1-e P(t)) (c+ \phi )P(t)$, of which r is a linear function, and therefore no more than two strains can coexist.

Suppose next that the natural mortality rate $\mu$ depends also on the total density of the host population, N. Then the population growth rate is the same as in (27), but next to $E_1(t)=S(t)$ and $E_2(t)=P(t)$, we have $E_3(t)=\mu (N(t),t)$ as a new environmental feedback variable chosen such that (26) applies. In this case, the explicit time-dependence of $\mu$ is absorbed into $E_3(t)$.

As a final example, assume that the predator has Holling II functional response and $\mu$ depends only on t again. Then the population growth rate

$$\begin{aligned} r(\alpha _{mut},S,P,\mu )= & {} \beta (\alpha _{mut}) S - (\alpha _{mut} + \mu + \nu )\nonumber \\&- \,(c+ \phi (\alpha _{mut})) \frac{P}{1+T \left( c S+ \sum _k (c+ \phi (\alpha _k))I_k \right) } \end{aligned}$$

is linear in the environmental feedback variables $E_1(t)=S(t)$ and

$$\begin{aligned} E_2(t)=\frac{P(t)}{1+T \left( c S(t)+ \sum _k (c+ \phi (\alpha _k))I_k(t) \right) } \end{aligned}$$

so that (26) applies.

Note that in general, it need not be possible to choose a finite number of environmental feedback variables such that the population growth rate r is linear in them; Geritz et al. (2007) is an example where this is not possible. In these cases, non-equilibrium systems have infinite dimensional feedbacks, which does not constrain the number of coexisting strategies.

Appendix B

In this Appendix, we first give a sufficient condition for absolute stability of an arbitrary k-morphic singularity, where the polymorphism is not necessarily saturated. Next, we show that this condition is always satisfied at a generic evolutionarily stable singularity of a saturated polymorphism.

To describe non-smooth evolutionary trajectories, we consider a differential inclusion approximation of a trait substitution sequence with small mutation steps. Let $\mathbf {x}=(x_1,\dots ,x_k)$ be a vector of $k \le n$ coexisting one-dimensional resident strategies, and let $s_{\mathbf {x}}(y)$ denote the invasion fitness of an initially rare mutant strategy y. The selection gradient $\partial _ys_{\mathbf {x}}(y)|_{y=x_i}$ for the resident strategy $x_i$ and the evolutionary change $\mathrm {d}x_i/\mathrm {d}t$ of the same strategy always have the same sign, i.e.,

$$\begin{aligned} \frac{\mathrm {d}x_i}{\mathrm {d}t} \cdot \partial _ys_{\mathbf {x}}(y)|_{y=x_i} \ge 0 \quad {\text {for }} i=1,\ldots ,k. \end{aligned}$$

(28)

A function $t \mapsto \mathbf {x}(t)=(x_1(t),\dots ,x_k(t))$ is a solution of the differential inclusion (28) if it is continuous, piecewise differentiable and satisfies (28) in every point where it is differentiable. A point $\mathbf {x}^*=(x_1^*,\dots ,x_k^*)$ is called absolutely stable if for every open neighbourhood U of $\mathbf {x}^*$ there exists an open neighbourhood $V \subset U$ of $\mathbf {x}^*$ such that every solution of (28) that starts in V will stay in U for all $t \ge 0$. One readily sees that if $\mathbf {x}^*$ is absolutely stable, then it is a singular point, i.e.,

$$\begin{aligned} \partial _ys_{\mathbf {x}}(y)|_{y=x_i} = 0 \quad {\text {for }} i=1,\ldots ,k. \end{aligned}$$

Linearisation of (28) at a singularity $\mathbf {x}^*$ gives

$$\begin{aligned} \frac{\mathrm {d}x_i}{\mathrm {d}t} \cdot \sum _{j=1}^{k} b_{ij}(x_j-x_j^*) \ge 0 \quad {\text {for }} i=1,\ldots ,k. \end{aligned}$$

(29)

where

$$\begin{aligned} b_{ij} =\partial _y^2 s_{\mathbf {x}}(y) \delta _{ij} + \partial _{x_j}\partial _y s_{\mathbf {x}}(y) \end{aligned}$$

(30)

evaluated for $y=x_i^*$ and $\mathbf {x}=\mathbf {x}^*$, and where $\delta _{ij}$ is the Kronecker delta. Note that $b_{ij}$ in (30) is the same as in (15) of the main text.

Proposition 15

Let $\mathbf {x}^*=(x_1^*,\dots ,x_k^*)$ be a singular point. If the matrix $B=(b_{ij})$ is strictly negative diagonally dominant, i.e., if there exists $d_1,\dots ,d_k>0$ such that

$$\begin{aligned} \frac{b_{ii}}{d_i} < -\sum _{j \ne i} \frac{|b_{ij}|}{d_j} \quad \forall i, \end{aligned}$$

(31)

then $\mathbf {x^*}$ is absolutely stable for the dynamics given by (29).

Proof

Let $\mathbf {x} \ne \mathbf {x^*}$ and take $i_0\in \{1,\dots ,k\}$ such that

$$\begin{aligned} d_{i_0}|x_{i_0}-x_{i_0}^*| = \max _j d_j|x_j-x_j^*| > 0. \end{aligned}$$

(32)

Then in particular $x_{i_0}-x_{i_0}^* \ne 0$, and so we can rewrite (29) as

$$\begin{aligned} \frac{\mathrm {d}(x_{i_0}-x_{i_0}^*)^2}{\mathrm {d}t} \cdot \left( b_{i_0i_0}+\sum _{j \ne i_0}\frac{ b_{i_0j}(x_j-x_j^*)}{x_{i_0}-x_{i_0}^*}\right) \ge 0. \end{aligned}$$

(33)

Moreover, from the diagonal dominance (31) and property (32) we have

$$\begin{aligned} \frac{b_{i_0i_0}}{d_{i_0}}< & {} - \sum _{j \ne i_0} \frac{|b_{i_0j}|}{d_j} \le - \sum _{j \ne i_0} \frac{|b_{i_0j}|}{d_j}\frac{d_j|x_j-x_j^*|}{d_{i_0}|x_{i_0}-x_{i_0}^*|}\\\le & {} -\frac{1}{d_{i_0}} \sum _{j \ne i_0} \frac{b_{i_0j}(x_j-x_j^*)}{x_{i_0}-x_{i_0}^*}, \end{aligned}$$

and hence

$$\begin{aligned} b_{i_0i_0} + \sum _{j \ne i_0} \frac{b_{i_0j}(x_j-x_j^*)}{x_{i_0}-x_{i_0}^*} < 0. \end{aligned}$$

From this inequality and the differential inclusion (33), we get that ${\mathrm {d}(x_{i_0}-x_{i_0}^*)^2}/{\mathrm {d}t} \le 0$ and hence also ${\mathrm {d}(d_{i_0}|x_{i_0}-x_{i_0}^*|)}/{\mathrm {d}t} \le 0$, which, by property (32), is equivalent to

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t} \left( \max _j d_j|x_j-x_j^*|\right) \le 0. \end{aligned}$$

(34)

The nested sets $V_\varepsilon = \{(x_1,\dots ,x_k):\;\max _j d_j|x_j-x_j^*|<\varepsilon \}$ for different values of $\varepsilon >0$ are therefore forward invariant for the differential inclusion (29). From this it immediately follows that $\mathbf {x}^*$ is absolutely stable. For example, in the definition of absolute stability for given but otherwise arbitrary neighbourhood U any $V=V_\varepsilon$ for $\varepsilon >0$ sufficiently small such that $V_\varepsilon \subset U$ suffices. $\square$

For the special case of $k=2$ coevolving strategies, the conditions for absolute stability have been determined by Matessi and Pasquale (1996) and presented by Kisdi (2006) in the form $b_{11}, b_{22}<0$ and $b_{11} b_{22} > |b_{12} b_{21}|$. These are equivalent to condition (31) for $k=2$. Leimar (2009) considered the absolute stability of monomorphic singularities of multidimensional traits. This is different from the present situation because several traits of the same strategy can be affected by a single mutation whereas the traits of several strategies cannot; the differential inclusion (28) applies to the latter.

Next, we apply the above proposition to saturated polymorphisms ($k=n$). In the notation of the main text, (30) is

$$\begin{aligned} b_{ij} =\partial _{11} r(x_i,\hat{E}_1,\ldots ,\hat{E}_n) \delta _{ij} + \sum _{l=1}^n \partial _{1,l+1} r(x_i,\hat{E}_1,\ldots ,\hat{E}_n) \frac{\partial \hat{E}_l}{\partial x_j} \end{aligned}$$

where $\hat{E}_1,\ldots ,\hat{E}_n$ are evaluated at the singularity and, in accordance with the main text, we have dropped the star that denoted the singularity earlier in this Appendix. By Proposition 2, $\frac{\partial \hat{E}_i}{\partial x_j}=0$ for all i and j at a singularity of a saturated polymorphism, and hence we have $b_{ii}=\partial _{11} r(x_i,\hat{E}_1,\ldots ,\hat{E}_n)$ and $b_{ij}=0$ for all $i \ne j$. At a generic evolutionarily stable singularity, $b_{ii} < 0$ (cf. (11)). This implies that (31) is satisfied for any positive $d_1,\ldots ,d_n$, and therefore a generic evolutionarily stable singularity of a saturated polymorphism is also absolutely stable. In the special case of $n=2$, Svennungsen and Kisdi (2009) used the same argument with the stability condition given in Kisdi (2006) to prove that every generic evolutionarily stable dimorphism is absolutely stable.

Appendix C

Proof of Proposition 10

We start with proving part (ii) of the proposition. The first step is to derive the limiting value of $\bar{E}'_i(\epsilon )$ as $\epsilon \rightarrow 0$. From implicit differentiation of (20) with respect to $\epsilon$, we obtain

$$\begin{aligned} \mathbf {A}(\epsilon ) \left[ \begin{array}{c} \bar{E}'_1(\epsilon )\\ \vdots \\ \bar{E}'_n(\epsilon ) \end{array} \right] = \left[ \begin{array}{c} - \xi _1 \partial _1 r(x_0+\epsilon \xi _1,\bar{E}_1(\epsilon ),\ldots ,\bar{E}_n(\epsilon ))\\ - \xi _2 \partial _1 r(x_0+\epsilon \xi _2,\bar{E}_1(\epsilon ),\ldots ,\bar{E}_n(\epsilon ))\\ 0\\ \vdots \\ 0 \end{array} \right] \end{aligned}$$

(35)

where $\mathbf {A}(\epsilon )$ is as defined in (12), i.e., $a_{ij}=\partial _{j+1} r(x_i,\bar{E}_1(\epsilon ),\ldots ,\bar{E}_n(\epsilon ))$, with $x_1=x_0+\epsilon \xi _1$ and $x_2=x_0+\epsilon \xi _2$. Let $\mathbf {A}_i(\epsilon )$ denote the matrix obtained by replacing the ith column of $\mathbf {A}(\epsilon )$ with the vector on the right hand side of (35). By Cramer’s rule, the solution of (35) is

$$\begin{aligned} \bar{E}'_i(\epsilon )=\frac{\det {\mathbf {A}_i(\epsilon )}}{\det {\mathbf {A}(\epsilon )}} \end{aligned}$$

Because the derivatives on the right hand side of (35) are zero at $\epsilon =0$ (cf. (21)), $\mathbf {A}_i(0)$ is singular. $\mathbf {A}(0)$ is singular because its first two rows are the same. Hence to take the limit $\epsilon \rightarrow 0$, we use L’Hôpital’s rule,

$$\begin{aligned} \bar{E}'_i(0) = \lim _{\epsilon \rightarrow 0}\bar{E}'_i(\epsilon )=\lim _{\epsilon \rightarrow 0} \frac{\frac{d}{d \epsilon } \det {\mathbf {A}_i(\epsilon )}}{\frac{d}{d \epsilon } \det {\mathbf {A}(\epsilon )}} \end{aligned}$$

(36)

We derive the limit of the numerator and that of the denominator of (36) in turn. We first expand the determinant $\det {\mathbf {A}_i(\epsilon )}$ using its ith column, which is the vector on the right hand side of Eq. (35):

$$\begin{aligned} \det {\mathbf {A}_i(\epsilon )}= & {} (-1)^{i+1} \left[ \xi _1 \partial _1 r(x_0+\epsilon \xi _1, \bar{E}_1(\epsilon ),\ldots , \bar{E}_n(\epsilon )) \det {\mathbf {A}_{1i}(\epsilon )}\right. \\&\left. - \xi _2 \partial _1 r(x_0+\epsilon \xi _2, \bar{E}_1(\epsilon ),\ldots , \bar{E}_n(\epsilon )) \det {\mathbf {A}_{2i}(\epsilon )}\right] \end{aligned}$$

Differentiating with respect to $\epsilon$ and taking the limit $\epsilon \rightarrow 0$, we obtain

$$\begin{aligned}&\lim _{\epsilon \rightarrow 0} \frac{d}{d \epsilon } \det {\mathbf {A}_i(\epsilon )} \nonumber \\&\quad = (-1)^{i+1} \left[ (\xi _1^2 - \xi _2^2) \partial _{11}r + (\xi _1 - \xi _2) \sum _{l=1}^n \partial _{1,l+1} r \, \bar{E}'_l(0) \right] \det {\mathbf {A}_{1i}(0)} \end{aligned}$$

(37)

where all derivatives of r are evaluated at $(x_0,\bar{E}_1(0),\ldots ,\bar{E}_n(0))$. Here we used that $\partial _1 r(x_0, \bar{E}_1(0),\ldots ,\bar{E}_n(0))=0$ (cf. (21)) and because the first two rows of $\mathbf {A}(0)$ are the same, $\mathbf {A}_{1i}(0)= \mathbf {A}_{2i}(0)$.

Next, we expand $\det {\mathbf {A}(\epsilon )}$ using its first two rows (i.e., using minors of order 2 rather than elements of a single row):

$$\begin{aligned} \det {\mathbf {A}(\epsilon )}=\sum _{j=1}^{n-1} \sum _{k=j+1}^n (-1)^{1+2+j+k} D_{jk}(\epsilon ) \det {\mathbf {A}_{(1,2),(j,k)}(\epsilon )} \end{aligned}$$

where $\mathbf {A}_{(1,2),(j,k)}(\epsilon )$ is obtained from $\mathbf {A}(\epsilon )$ by deleting its first two rows and the jth and kth columns when $n>2$ and $\det {\mathbf {A}_{(1,2),(j,k)}(\epsilon )}$ is replaced with 1 when $n=2$; and

$$\begin{aligned}&D_{jk}(\epsilon ) \\&\quad = \det { \left( \begin{array}{cc} \partial _{j+1}r(x_0+\epsilon \xi _1, \bar{E}_1(\epsilon ),\ldots , \bar{E}_n(\epsilon )) &{} \partial _{k+1}r(x_0+\epsilon \xi _1, \bar{E}_1(\epsilon ),\ldots , \bar{E}_n(\epsilon ))\\ \partial _{j+1}r(x_0+\epsilon \xi _2, \bar{E}_1(\epsilon ),\ldots , \bar{E}_n(\epsilon )) &{} \partial _{k+1}r(x_0+\epsilon \xi _2, \bar{E}_1(\epsilon ),\ldots , \bar{E}_n(\epsilon )) \end{array} \right) }. \end{aligned}$$

Note that $D_{jk}(0)=0$ for all j, k, and

$$\begin{aligned} \lim _{\epsilon \rightarrow 0}\frac{d D_{jk}(\epsilon )}{d \epsilon }= & {} \left( \xi _1 \partial _{1,j+1} r + \sum _{l=1}^ n \partial _{l+1,j+1} r \, \bar{E}'_l(0) \right) \partial _{k+1} r\\&+ \left( \xi _2 \partial _{1,k+1} r + \sum _{l=1}^ n \partial _{l+1,k+1} r \, \bar{E}'_l(0) \right) \partial _{j+1} r\\&- \left( \xi _2 \partial _{1,j+1} r + \sum _{l=1}^ n \partial _{l+1,j+1} r \, \bar{E}'_l(0) \right) \partial _{k+1} r\\&- \left( \xi _1 \partial _{1,k+1} r + \sum _{l=1}^ n \partial _{l+1,k+1} r \, \bar{E}'_l(0) \right) \partial _{j+1} r\\= & {} (\xi _1 - \xi _2) \left( \partial _{1,j+1} r \, \partial _{k+1} r \, - \partial _{1,k+1} r \, \partial _{j+1} r \right) \end{aligned}$$

where all derivatives of r are evaluated at $(x_0,\bar{E}_1(0),\ldots ,\bar{E}_n(0))$. Using these identities, we obtain

$$\begin{aligned}&\lim _{\epsilon \rightarrow 0} \frac{d}{d \epsilon } \det {\mathbf {A}(\epsilon )} \nonumber \\&\quad = (\xi _1 - \xi _2) \sum _{j=1}^{n-1} \sum _{k=j+1}^n (-1)^{j+k+1} \left( \partial _{1,j+1} r \, \partial _{k+1} r - \partial _{1,k+1} r \, \partial _{j+1} r \right) \det {\mathbf {A}_{(1,2),(j,k)}(0)}\nonumber \\ \end{aligned}$$

(38)

Substituting (37) and (38) into (36) and cancelling the factor $(\xi _1-\xi _2)$ (recall that $\xi _1 \ne \xi _2$) yields the result

$$\begin{aligned} \bar{E}'_i(0)=\frac{(-1)^i \left[ (\xi _1+\xi _2) \partial _{11} r + \sum _{l=1}^n \partial _{1,l+1} r \, \bar{E}'_l(0) \right] \det {\mathbf {A}_{1i}} }{\sum _{j=1}^{n-1} \sum _{k=j+1}^n (-1)^{j+k} \left[ \partial _{1,j+1}r \, \partial _{k+1}r - \partial _{1,k+1}r \, \partial _{j+1}r \right] \det {\mathbf {A}_{(1,2),(j,k)}} } \end{aligned}$$

(39)

for $i=1,\ldots ,n$, where all derivatives of r are evaluated at $(x_0,\bar{E}_1(0),\ldots ,\bar{E}_n(0))$. We assume that the non-degeneracy condition

(A8) $\sum _{j=1}^{n-1} \sum _{k=j+1}^n (-1)^{j+k} \left[ \partial _{1,j+1}r \, \partial _{k+1}r - \partial _{1,k+1}r \, \partial _{j+1}r \right] \det {\mathbf {A}_{(1,2),(j,k)}} \ne 0$

holds.

(39) is a system of linear equations for $\bar{E}'_i(0)$. With the particular choice $\xi _2=-\xi _1$, (39) is homogeneous and therefore $\bar{E}'_i(0)=0$ for all i. This corresponds to the fact that $\hat{E}_i(x_1,\ldots ,x_n)$ is invariant under the permutation of its arguments (the labelling of the strategies is arbitrary), so that the environmental feedback contours of Fig. 1 are symmetric about the diagonal.

If $\bar{E}'_i(0)=0$ holds for all $\xi _1, \xi _2$ for some i, then $\partial _{11} r(x_0,\bar{E}_1(0),\ldots ,\bar{E}_n(0))$ must be zero for (39) to hold. This means that $x_0 \in X^c$. Furthermore, (39) is then homogeneous, and therefore $\bar{E}'_i(0)=0$ holds for all i, so that each environmental feedback attains a critical point as a function of $x_1$ and $x_2$. Conversely, if $x_0 \in X^c$, then (39) is homogeneous and it follows immediately that $\bar{E}'_i(0)=0$ for all i and for all $\xi _1, \xi _2$, so that all environmental feedbacks attain a critical point on the diagonal as functions of $x_1$ and $x_2$. This proves part (ii) of Proposition 10.

To prove part (i), take a first order Taylor expansion of (9) to obtain

$$\begin{aligned} \partial _1 r(x_0+\epsilon \xi _1,\bar{E}_1(\epsilon ),\ldots ,\bar{E}_n(\epsilon ))= & {} \left[ \xi _1 \partial _{11} r + \sum \nolimits _{l=1}^n \partial _{1,l+1} r \, \bar{E}'_l(0) \right] \epsilon + O(\epsilon ^2)\\ \partial _1 r(x_0+\epsilon \xi _2,\bar{E}_1(\epsilon ),\ldots ,\bar{E}_n(\epsilon ))= & {} \left[ \xi _2 \partial _{11} r + \sum \nolimits _{l=1}^n \partial _{1,l+1} r \, \bar{E}'_l(0) \right] \epsilon + O(\epsilon ^2) \end{aligned}$$

where all derivatives of r on the right hand side are evaluated at $(x_0,\bar{E}_1(0),\ldots ,$ $\bar{E}_n(0))$. Choose $x_0=\frac{x_1+x_2}{2}$ such that $\xi _2=-\xi _1$. With this choice, it follows from Eq. (39) that $\bar{E}'_l(0)=0$ for all l. Then, up to order $\epsilon$, the vector of selection gradients of the first two strategies is

$$\begin{aligned} \left[ \begin{array}{c} 1 \\ -1 \end{array} \right] \xi _1 \partial _{11} r(x_0,\bar{E}_1(0),\ldots ,\bar{E}_n(0)) \epsilon \end{aligned}$$

(40)

These two selection gradients vanish simultaneously, and vanish if and only if $x_0 \in X^c$. This proves part (i) of Proposition 10.

Proof of Proposition 12

When $n=2$, the vector in (40) is the vector of all selection gradients. This vector is perpendicular to the diagonal $x_2=x_1$, and its direction is determined by the sign of $\partial _{11} r(x_0,\bar{E}_1(0),\ldots ,\bar{E}_n(0))$.

Appendix D

In this Appendix, we prove Propositions 13 and 14 concerning the common points of isoclines and invasion boundaries.

Proof of Proposition 13 for the general case $n \ge 2$. Let the n-vector $\mathbf {x}_{mj}$ denote the vector obtained from $\mathbf {x}=(x_1,\ldots ,x_n)$ by replacing its mth entry with the value of $x_j$. The point $\mathbf {x}_{mj}$ is therefore on the diagonal $x_m=x_j$. With a slight abuse of notation, let $\bar{E}_i(\mathbf {x}_{mj})$ denote the limiting value of $\hat{E}_i(\mathbf {x})$ on the diagonal. If $\mathbf {x}$ is on the $x_j$-isocline of the n-morphism, then, by Proposition 9, $\hat{E}_i(\mathbf {x})=\bar{E}_i(\mathbf {x}_{mj})$ for $i=1,\ldots ,n$. If $\mathbf {x}$ is also on the $x_m$-invasion boundary, then, by Lemma 2 in Sect. 4.1, the diagonal point $\mathbf {x}_{mj}$ must also be on the $x_m$-invasion boundary. This implies that the diagonal point is a point of the $x_j$-isocline of the $(n-1)$-morphic population. Conversely, if the diagonal point $\mathbf {x}_{mj}$ is an $x_j$-isocline point of the $(n-1)$-morphism, then it is on the $x_m$-invasion boundary of the n-morphism. By Lemma 2, every point $\mathbf {x}$ which differs from $\mathbf {x}_{mj}$ only in its $x_m$-coordinate and at which $\hat{E}_i(\mathbf {x})=\bar{E}(\mathbf {x}_{mj})$ holds for $i=1,\ldots ,n$ must also be on the $x_m$-invasion boundary. By Proposition 9, these points are on the $x_j$-isocline of the n-morphism.

Proof of Proposition 14

Define the column vector $\mathbf {x_{\lnot m}}=(x_1,\ldots ,x_{m-1},$ $x_{m+1},\ldots ,x_n)^T$ as the $(n-1)$-vector obtained from $(x_1,\ldots ,x_n)$ by deleting $x_m$, define $\mathbf {N_{\lnot m}}$ analogously, and let $\mathbf {Z}=(Z_1,\ldots ,Z_k)^T$. We can then rewrite Eq. (23) in the form

$$\begin{aligned} \mathbf {G}(\mathbf {x_{\lnot m}},x_m,\mathbf {N_{\lnot m}},\mathbf {Z})=\mathbf {0} \end{aligned}$$

(41)

where $\mathbf {G}(\mathbf {x_{\lnot m}},x_m,\mathbf {N_{\lnot m}},\mathbf {Z}) \in \mathbb {R}^{n+k}$ contains

$$\begin{aligned} G_i (\mathbf {x_{\lnot m}},x_m,\mathbf {N_{\lnot m}},\mathbf {Z})= & {} F_i(x_1,\ldots ,x_n,\hat{E}_1(\mathbf {x}),\ldots ,\hat{E}_n(\mathbf {x}),N_1,\ldots ,N_{m-1},0,\\&N_{m+1},\ldots ,N_n,Z_1,\ldots ,Z_k) \end{aligned}$$

Note that $F_i$ does not depend on its mth argument due to assumption (A3), but still depends on $x_m$ via $\hat{E}_1(\mathbf {x}),\ldots ,\hat{E}_n(\mathbf {x})$, which are given by the solution of (7) irrespectively of whether $N_m$ is zero or not.

First we determine the hyperplane tangent to the $x_m$-invasion boundary at an arbitrary point. Implicit differentiation of (41) yields

$$\begin{aligned} \left[ \mathbf {B}, \mathbf {C} \right] \left[ \begin{array}{c} d \mathbf {x_{\lnot m}} \\ d x_m \\ d \mathbf {N_{\lnot m}} \\ d \mathbf {Z} \end{array} \right] = \mathbf {B} \left[ d \mathbf {x_{\lnot m}} \right] + \mathbf {C} \left[ \begin{array}{c} d x_m \\ d \mathbf {N_{\lnot m}} \\ d \mathbf {Z} \end{array} \right] =\mathbf {0} \end{aligned}$$

(42)

where the blocks $\mathbf {B}$, $\mathbf {C}$ of the Jacobian matrix are

$$\begin{aligned} \mathbf {B}=\left[ \frac{\partial \mathbf {G}}{\partial \mathbf {x_{\lnot m}}} \right] \quad {\text {and}} \quad \mathbf {C}=\left[ \frac{\partial \mathbf {G}}{\partial x_m}, \frac{\partial \mathbf {G}}{\partial \mathbf {N_{\lnot m}}}, \frac{\partial \mathbf {G}}{\partial \mathbf {Z}} \right] \end{aligned}$$

By Cramer’s rule, (42) yields

$$\begin{aligned} dx_m = \frac{ \det \left[ -\mathbf {B} d \mathbf {x_{\lnot m}}, \frac{\partial \mathbf {G}}{\partial \mathbf {N_{\lnot m}}}, \frac{\partial \mathbf {G}}{\partial \mathbf {Z}} \right] }{\det \left[ \mathbf {C} \right] } \end{aligned}$$

(43)

The hyperplane tangent to the $x_m$-invasion boundary at a given point is the hyperplane $a_1 x_1 + \ldots + a_n x_n=c$ with the coefficients chosen such that $\sum _i a_i dx_i=0$ for any choice of $d \mathbf {x_{\lnot m}}$ and with $dx_m$ from (43). By choosing the unit vectors $d \mathbf {x_{\lnot m}}=\mathbf {e_i}$ and $d \mathbf {x_{\lnot m}}=\mathbf {e_j}$ with $i,j \ne m$, we obtain

$$\begin{aligned} \frac{a_i}{a_j}=\frac{\det \left[ \mathbf {B} \mathbf {e}_i, \frac{\partial \mathbf {G}}{\partial \mathbf {N_{\lnot m}}}, \frac{\partial \mathbf {G}}{\partial \mathbf {Z}} \right] }{\det \left[ \mathbf {B} \mathbf {e}_j, \frac{\partial \mathbf {G}}{\partial \mathbf {N_{\lnot m}}}, \frac{\partial \mathbf {G}}{\partial \mathbf {Z}} \right] } \end{aligned}$$

(44)

which determines all coefficients except $a_m$ up to a constant. Let the $(n-1)$ column vector $\mathbf {a_{\lnot m}}$ contain these coefficients. $a_m$ is then given by

$$\begin{aligned} a_m= - \left[ \mathbf {a}^T_\mathbf {\lnot m} d \mathbf {x_{\lnot m}} \right] \frac{\det [ \mathbf {C}]}{\det \left[ -\mathbf {B} d \mathbf {x_{\lnot m}}, \frac{\partial \mathbf {G}}{\partial \mathbf {N_{\lnot m}}}, \frac{\partial \mathbf {G}}{\partial \mathbf {Z}} \right] } \end{aligned}$$

(45)

The hyperplane tangent to the $x_m$-invasion boundary at a given point is determined by (44) and (45), with all derivatives evaluated at the point of tangency.

Suppose now that the point $(x_1,\ldots ,x_n)$ is both on the $x_m$-invasion boundary and on the $x_m$-isocline. By Proposition 1, we then have $\frac{\partial \hat{E}_1}{\partial x_m}=\ldots =\frac{\partial \hat{E}_n}{\partial x_m}=0$, and this implies $\frac{\partial \mathbf {G}}{\partial x_m}=\mathbf {0}$. Because the first column of $\mathbf {C}$ is zero, its determinant vanishes and we get $a_m=0$ in (45). Hence the normal of the $x_m$-invasion boundary, $(a_1,\ldots ,a_n)$, is perpendicular to the mth unit vector.

Appendix E

Here we derive $\hat{h}_1(x_1,x_2;\kappa )$ in Eq. (25) of the main text. Although this derivation is in the same spirit as the one in Appendix D, we detail it here since it is easier to follow it when presented explicitly.

Let $\hat{N}_1(x_1,x_2)$ and $\hat{Z}_1(x_1,x_2),\ldots ,\hat{Z}_k(x_1,x_2)$ denote the values of respectively $N_1$ and $Z_1,\ldots ,Z_k$ that satisfy the $k+1$ equations $F_2=\cdots =F_{k+2}=0$ in (24) and recall the definition $\hat{f}(x_1,x_2)=f(x_1,x_2,\hat{E}_1(x_1,x_2),\hat{E}_2(x_1,x_2),$ $\hat{N}_1(x_1,x_2),0,\hat{Z}_1(x_1,x_2),\ldots ,\hat{Z}_k(x_1,x_2))$. By implicit differentiation of (24) with respect to $x_1$ and using that, by assumption (A3), $\partial _2 \tilde{F}_1 =\partial _2 F_2 =\cdots = \partial _2 F_{k+2}=0$ on the invasion boundary, we obtain

(46)

where $\kappa =\frac{dx_2}{dx_1}$ is the slope of the invasion boundary, $y_0=\frac{\partial \hat{N}_1}{\partial x_1}+\frac{\partial \hat{N}_1}{\partial x_2} \kappa$, $y_i=\frac{\partial \hat{Z}_i}{\partial x_1}+\frac{\partial \hat{Z}_i}{\partial x_2} \kappa$ for $i=1,\ldots ,k$, and all derivatives of $\tilde{F}_1, F_2,\ldots ,F_{k+2}$ are evaluated at the arguments

$$\begin{aligned} (x_1,x_2,\hat{E}_1(x_1,x_2),\hat{E}_2(x_1,x_2), \hat{N}_1(x_1,x_2),0,\hat{Z}_1(x_1,x_2),\ldots ,\hat{Z}_k(x_1,x_2)) \end{aligned}$$

and, in the case of $\tilde{F}_1$, $\hat{h}_0(x_1,x_2)$. These equations are satisfied when $h'(\hat{f}(x_1,x_2))=\hat{h}_1(x_1,x_2;\kappa )$ where

$$\begin{aligned}&\hat{h}_1(x_1,x_2;\kappa )=- \frac{\partial _1 \tilde{F}_1 + \sum _{i=1}^2 \partial _{i+2} \tilde{F}_1 \, \left( \frac{\partial \hat{E}_i}{\partial x_1}+ \frac{\partial \hat{E}_i}{\partial x_2} \kappa \right) + \partial _{5} \tilde{F}_1 \, y_0 + \sum _{i=1}^k \partial _{6+i} \tilde{F}_1 \, y_i}{\partial _{k+7} \tilde{F}_1\, \left( \frac{\partial \hat{f}}{\partial x_1}+ \frac{\partial \hat{f}}{\partial x_2} \kappa \right) } \end{aligned}$$

(47)

with the values of $y_0,\ldots ,y_k$ that satisfy the last $k+1$ equations of (46). (Since the denominator of (47) vanishes for $\kappa =-\frac{\partial \hat{f}}{\partial x_1} / \frac{\partial \hat{f}}{\partial x_2}$, this particular slope of the invasion boundary cannot be achieved.)

In the remainder of this Appendix, we consider the special cases when (i) the point $(x_1,x_2)$ is on the $x_2$-isocline and (ii) $(x_1,x_2)=(x_0,x_0)$ with $x_0 \in X^c$.

If the $x_2$-invasion boundary intersects the $x_2$-isocline away from the diagonal, then, by Proposition 14, the invasion boundary must be tangent to a vertical line; hence one cannot choose the function h such that the invasion boundary would have an arbitrary slope $\kappa$. Consider (46) as a system of $k+2$ linear equations for the unknowns $\kappa , y_0, y_1,\ldots ,y_n$. The point $(x_1,x_2)$ is on the $x_2$-isocline if and only if $\frac{\partial \hat{E}_1}{\partial x_2}=\frac{\partial \hat{E}_2}{\partial x_2}=0$ (see Proposition 1). As we show in the next paragraph, this implies $\frac{\partial \hat{f}}{\partial x_2}=0$. As a result, the coefficient of $\kappa$ vanishes in each equation of (46), i.e., the matrix of this linear system is singular, and therefore the implicit function theorem does not apply.

To show that $\frac{\partial \hat{E}_1}{\partial x_2}=\frac{\partial \hat{E}_2}{\partial x_2}=0$ indeed implies $\frac{\partial \hat{f}}{\partial x_2}=0$, note that the terms containing $\kappa$ in the last $k+1$ equations of (46) all vanish, so that these equations can be solved for $y_0,\ldots ,y_n$ independently of $\kappa$. Since $y_0=\frac{\partial \hat{N}_1}{\partial x_1}+\frac{\partial \hat{N}_1}{\partial x_2} \kappa$ and $y_i=\frac{\partial \hat{Z}_i}{\partial x_1}+\frac{\partial \hat{Z}_i}{\partial x_2} \kappa$, this implies $\frac{\partial \hat{N}_1}{\partial x_2}=0$ and $\frac{\partial \hat{Z}_i}{\partial x_2}=0$ for $i=1,\ldots ,k$. By definition, the derivative $\frac{\partial \hat{f}}{\partial x_2}$ is given by

$$\begin{aligned} \frac{\partial \hat{f}}{\partial x_2}=\partial _2 f+ \partial _3 f \frac{\partial \hat{E}_1}{\partial x_2}+\partial _4 f \frac{\partial \hat{E}_2}{\partial x_2}+\partial _5 f \frac{\partial \hat{N}_1}{\partial x_2}+\sum _{i=1}^k \partial _{6+i} f \frac{\partial \hat{Z}_i}{\partial x_2} \end{aligned}$$

Hence all but the first terms vanish when $\frac{\partial \hat{E}_1}{\partial x_2}=\frac{\partial \hat{E}_2}{\partial x_2}=0$; and since the derivative is evaluated at $(x_1,x_2,\hat{E}_1(x_1,x_2),\hat{E}_2(x_1,x_2),\hat{N}_1(x_1,x_2),0,$ $\hat{Z}_1(x_1,x_2),\ldots ,$ $\hat{Z}_k(x_1,x_2))$, $\partial _2 f$ is zero by assumption (A7).

Suppose now that we wish to have a monomorphic singularity at a point $x_0 \in X^c$, i.e., we take $(x_1,x_2)=(x_0,x_0)$. By the definition of the set $X^c$, $C_{00}=0$ at such a singularity, i.e., it is at a bifurcation point between being uninvadable and invadable. By Proposition 10, the limiting values of the equilibrium feedbacks attain a critical point at $(x_0,x_0)$. Hence the above argument applies with $\hat{E}_i(x_1,x_2)$ substituted with its limiting value at all points, and we obtain, as above, that the matrix of the linear system that determines $\kappa$ for any given function h is singular. Therefore generically there is no solution for $\kappa$, and the invasion boundary is tangent to a vertical line at the singularity.