Construction of multiple trade-offs to obtain arbitrary singularities of adaptive dynamics

Abstract

Evolutionary singularities are central to the adaptive dynamics of evolving traits. The evolutionary singularities are strongly affected by the shape of any trade-off functions a model assumes, yet the trade-off functions are often chosen in an ad hoc manner, which may unjustifiably constrain the evolutionary dynamics exhibited by the model. To avoid this problem, critical function analysis has been used to find a trade-off function that yields a certain evolutionary singularity such as an evolutionary branching point. Here I extend this method to multiple trade-offs parameterized with a scalar strategy. I show that the trade-off functions can be chosen such that an arbitrary point in the viability domain of the trait space is a singularity of an arbitrary type, provided (next to certain non-degeneracy conditions) that the model has at least two environmental feedback variables and at least as many trade-offs as feedback variables. The proof is constructive, i.e., it provides an algorithm to find trade-off functions that yield the desired singularity. I illustrate the construction of trade-offs with an example where the virulence of a pathogen evolves in a small ecosystem of a host, its pathogen, a predator that attacks the host and an alternative prey of the predator.

Appendices

Appendix A

In this Appendix, I show that the population dynamical equilibrium of the model in (10) is asymptotically stable if $b'(N) \rightarrow - \infty$; the same holds when $b'(N)$ is sufficiently large negative. $b'(N) \rightarrow - \infty$ implies that the total host density $N$ is constant, and therefore (10) can be replaced with the 3-dimensional system

$$\begin{aligned} \frac{dI}{dt}&= \left[ \beta (N-I) -(k \alpha + \mu +\nu ) - (c+\phi ) P \right] I \end{aligned}$$

(33a)

$$\begin{aligned} \frac{dZ}{dt}&= \left[ \rho (1-Z/K)-\zeta P \right] Z \end{aligned}$$

(33b)

$$\begin{aligned} \frac{dP}{dt}&= \left[ \gamma c N + \gamma \phi I + \theta \zeta Z - \delta \right] P \end{aligned}$$

(33c)

The characteristic equation of this system is

$$\begin{aligned} - \det \left[ \begin{array} {c@{\quad }c@{\quad }c} - \beta I-\lambda &{}\quad 0 &{}\quad -(c+\phi ) I\\ 0 &{}\quad - \rho Z/K - \lambda &{}\quad -\zeta Z\\ \gamma \phi P &{}\quad \theta \zeta P &{}\quad -\lambda \end{array} \right] = \lambda ^3+a_1 \lambda ^2 + a_2 \lambda + a_3 =0\nonumber \\ \end{aligned}$$

(34)

where

$$\begin{aligned} a_1&= \beta I+\frac{\rho Z}{K}\\ a_2&= \beta I \frac{\rho Z}{K}+ \theta \zeta ^2 PZ+ \gamma \phi (c+\phi ) PI\\ a_3&= \beta I \theta \zeta ^2 PZ+ \gamma \phi (c+\phi ) PI \frac{\rho Z}{K} \end{aligned}$$

By the Routh–Hurwitz criteria, all eigenvalues of the Jacobian have negative real parts if $a_1>0, a_3>0$, and $a_1 a_2>a_3$. The first two of these conditions obviously hold. For the last, it is easy to verify that

$$\begin{aligned} a_1 a_2 - a_3 = \left( \beta I+\frac{\rho Z}{K} \right) \beta I \frac{\rho Z}{K} + \beta I \cdot \gamma \phi (c+\phi ) PI + \frac{\rho Z}{K} \theta \zeta ^2 PZ \end{aligned}$$

which is always positive.

Appendix B

Here I give the elements of matrix $\mathbf {E}$ for the application in Sect. 4. To find the interior equilibria of the feedback variables, it is convenient to rewrite equations (10) using $N=S+I$ into the form

$$\begin{aligned} \frac{dN}{dt}&= b(N)N-(\mu + c P) N- (k \alpha + \phi P) I =0 \end{aligned}$$

(35a)

$$\begin{aligned} \frac{1}{I} \frac{dI}{dt}&= \beta (N-I) -(\mu +\nu + k \alpha ) - (c+\phi ) P =0 \end{aligned}$$

(35b)

$$\begin{aligned} \frac{1}{Z} \frac{dZ}{dt}&= \rho (1-Z/K)-\zeta P =0 \end{aligned}$$

(35c)

$$\begin{aligned} \frac{1}{P} \frac{dP}{dt}&= \gamma cS + \gamma (c+\phi )I + \theta \zeta Z - \delta =0 \end{aligned}$$

(35d)

Equations (35b)–(35d) are linear and thus easily solved for $I, Z$ and $P$ in terms of the still unknown $N$. Substituting the solution into (35a) yields a single nonlinear equation (35a*) for $N$ (not shown), which can be solved only when the density-dependent birth rate function $b$ is specified. Assuming $b(N)=b_0-q N$ (i.e., a logistic host), (35a*) is only quadratic, but its solution is an unruly formula.

The elements of $\mathbf {E}$ are the derivatives of the feedback variables $S=N-I$ and $P$ with respect to the traits $\alpha , \beta$ and $\phi$. To obtain these, I differentiate (35a*) implicitly with respect to a trait (e.g. with respect to $\alpha$ to obtain $dN/d \alpha$) and obtain the derivatives of the feedbacks (e.g. $dS/d \alpha = dN/d \alpha - dI/d \alpha$ and $dP/d \alpha$) by differentiating the explicit solution from (35b)–(35d) and substituting the derivative of $N$ from the implicit differentiation. The calculations were done in Mathematica 9.0 and yield $e_{ij}$ in the form

$$\begin{aligned} e_{ij}=A_{ij}/B_i \end{aligned}$$

with $A_{ij}$ and $B_i$ given below [note that $k$ and $\gamma$ have been factored out in (14)].

$$\begin{aligned} A_{11}&= -\left( K \rho \theta \zeta ^2 (c+\phi ) (\gamma (\alpha c k+c (\mu +\nu )-\phi \nu )+\beta \gamma N (c+\phi )-\beta \delta )\right. \\&+\,\, \beta K ^2 \theta ^2 \zeta ^4 (\alpha k+\mu )-K \theta \zeta ^2 \left( N b'(N)+b(N)\right) \left( \beta K \theta \zeta ^2+\phi \gamma \rho (c+\phi )\right) \\&\left. +\,\, \beta K ^2 \rho \theta ^2 \zeta ^3 (c\!+\!\phi )\!+\!c \gamma \rho ^2 (c+\phi )^2 (\gamma N (c+\phi )-\delta )+c \gamma K \rho ^2 \theta \zeta (c+\phi )^2 \right) \\&\times \, \left( \beta K \theta \zeta ^2+\phi \gamma \rho (c+\phi )\right) \\ A_{12}&= -\left( \left( K \theta \zeta ^2 (\alpha k+\mu +\nu )+\rho (c+\phi ) (\gamma N (c+\phi )-\delta )+K \rho \theta \zeta (c+\phi )\right) \right. \\&\times \, \left( -K \rho \theta \zeta ^2 (c+\phi ) (-\phi \gamma (\alpha k+\mu +2 \nu )+2 \beta \gamma N (c+\phi )-\beta \delta )\right. \\&-\,\, \beta K ^2 \theta ^2 \zeta ^4 (\alpha k+\mu )+K \theta \zeta ^2 \left( N b'(N)+b(N)\right) \left( \beta K \theta \zeta ^2+\phi \gamma \rho (c+\phi )\right) \\&-\, \left. \left. \beta K ^2 \rho \theta ^2 \zeta ^3 (c+\phi )-\delta \phi \gamma \rho ^2 (c+\phi )^2+\phi \gamma K \rho ^2 \theta \zeta (c+\phi )^2 \right) \right) \\ A_{13}&= -\left( \rho \left( \left( N b'(N)+b(N)\right) \left( \beta K \theta \zeta ^2+\phi \gamma \rho (c+\phi )\right) \right. \right. \\&\times \, \left( K \theta \zeta ^2 (\gamma (c+2 \phi ) (\alpha k+\mu +\nu )+\beta (\delta -2 \gamma N (c+\phi )))\right. \\&\left. -\, \beta K ^2 \theta ^2 \zeta ^3+ \gamma \rho (c+\phi )^2 (c \gamma N-\delta )+\gamma K \rho \theta \zeta (c+\phi )^2\right) \\&+\,\, \beta ^2 K \theta \zeta ^2 (2 \gamma N (c+\phi )-\delta +K \theta \zeta ) \\&\times \, \left( K \theta \zeta ^2 (\alpha k+\mu )+\rho (c+\phi ) (\gamma N (c+\phi )-\delta )+K \rho \theta \zeta (c+\phi )\right) \\&+\,\,\beta \gamma \left( -K \rho \theta \zeta ^2 (c+\phi ) \left( \alpha k (\gamma N (c+\phi ) (c+2 \phi )-\delta (c+3 \phi ))\right. \right. \\&+\,\, c^2 \gamma \mu N+ c (\phi (3 \gamma \mu N+4 \gamma N \nu +K \rho \theta )-\delta \mu )+\phi (-3 \delta (\mu +\nu )\\&\left. +\,\, 2 \phi \gamma N (\mu +2 \nu )+\phi K \rho \theta )\right) - K ^2 \rho \theta ^2 \zeta ^3 (c+\phi ) ((c+3 \phi ) (\alpha k+\mu )+3 \phi \nu )\\&-\, K ^2 \theta ^2 \zeta ^4 (c+2 \phi ) (\alpha k+\mu ) (\alpha k+\mu +\nu )\\&\left. -\,\, \phi K \rho ^2 \theta \zeta (c+\phi )^2 (\gamma N (c+\phi )-2 \delta )+\delta \phi \rho ^2 (c+\phi )^2 (\gamma N (c+\phi )-\delta )\right) \\&-\, \,\phi \gamma ^2 \rho (c+\phi ) \left( \rho (c+\phi ) (c (\alpha k+\mu ) (\gamma N (c+\phi )-\delta )+\delta \phi \nu )\right. \\&\left. \left. \left. +\, K \rho \theta \zeta (c\!+\!\phi ) (\alpha c k+c \mu \!-\!\phi \nu )\!+\!K \theta \zeta ^2 (\alpha k\!+\!\mu +\nu ) (\alpha c k+c \mu -2 \phi \nu )\right) \right) \right) \\ A_{21}&= -\left( \rho \left( \rho (c+\phi ) (\phi \gamma (\alpha c k-\phi \mu )+\beta (c+\phi ) (c \gamma N-\delta ))\right. \right. \\&+\, \,\beta K \theta \zeta ^2 (\alpha k (2 c+\phi )-c (\beta N-\mu -\nu )+\phi (\nu -\beta N))\\&\left. \left. +\,\,\phi \left( N b'(N)+b(N)\right) \left( \beta K \theta \zeta ^2+\phi \gamma \rho (c+\phi )\right) +\beta K \rho \theta \zeta (c+\phi )^2\right) \right) \\ A_{22}&= \rho \left( \alpha c k+\phi N b'(N)+\phi b(N)-\phi \mu \right) \\&\times \, \left( K \theta \zeta ^2 (\alpha k+\mu +\nu )+\rho (c+\phi ) (\gamma N (c+\phi )-\delta )+K \rho \theta \zeta (c+\phi )\right) \\ A_{23}&= \rho \Big (\rho \big (\alpha ^2 c \phi \gamma k^2+\alpha \phi k (\gamma (c (\mu +\nu )-\phi \mu )-\beta \delta )-\mu \big (\beta \delta (c+2 \phi )\\&-\, \beta \gamma N (c+\phi )^2+\phi ^2 \gamma (\mu +\nu )\big )\big )+\left( N b'(N)+b(N)\right) \\&\times \, \big (\rho \left( \phi ^2 \gamma (\alpha k+\mu +\nu )+\beta \delta (c+2 \phi )-\beta \gamma N (c+\phi )^2\right) \\&+\, \beta K \theta \zeta ^2 (\beta N-\alpha k-\mu -\nu )-\beta K \rho \theta \zeta (c+2 \phi )\big ) \\&+\,\beta K \rho \theta \zeta (\alpha \phi k+\mu (c+2 \phi ))+ \beta K \theta \zeta ^2 (\alpha k+\mu ) (\alpha k-\beta N+\mu +\nu )\Big )\\ B_1&= \left( \beta K \theta \zeta ^2+\phi \gamma \rho (c+\phi )\right) B_2\\ B_2&= -\beta ^2 K \theta \zeta ^2 \left( K \theta \zeta ^2 (\alpha k+\mu )+\rho (c+\phi ) (2 \gamma N (c+\phi )-\delta )+K \rho \theta \zeta (c+\phi )\right) \\&+\, \beta \gamma \rho (c+\phi ) \left( K \theta \zeta ^2 (\alpha k (c+\phi )+2 \phi \nu )-\delta \phi \rho (c+\phi )+\phi K \rho \theta \zeta (c+\phi )\right) \\&+\,\, \phi \gamma ^2 \rho ^2 (c+\phi )^2 (\alpha c k-\phi \mu )\!+\!\,\,\left( N b'(N)\!+\!b(N)\right) \left( \beta K \theta \zeta ^2+\phi \gamma \rho (c\!+\!\phi )\right) ^2 \end{aligned}$$

Appendix C

The quantities that appear in (19) are as follows (with $(bN)'=b'(N)N+b(N)$ and $\sigma =K \theta \zeta ^2/ \rho$):

$$\begin{aligned} D_1&= \frac{\beta ((c+\phi ) \gamma N+K \theta \zeta -\delta )-\gamma \phi (k \alpha +\mu +\nu )}{(c+\phi )^2 \gamma N+\phi K \theta \zeta +\sigma (k \alpha +\mu +\nu )+c (K \theta \zeta -\delta ) - \phi \delta }\\ D_2&= \phi \gamma ^2 (c+\phi )^2 (\phi \mu -k \alpha c)\\&\quad +\, \beta ^2 \sigma \left[ (c+\phi ) (2 (c+\phi ) \gamma N+K \theta \zeta -\delta )+\sigma (k \alpha +\mu ) \right] \\&\quad -\, \beta \gamma (c+\phi ) \left[ \phi (c+\phi ) (K \theta \zeta - \delta ) + \sigma (k \alpha (c+\phi ) + 2 \phi \nu ) \right] \\*&\quad -\, (bN)' (\phi \gamma (c+\phi )+\beta \sigma )^2\\ D_3&= \left[ (bN)'-k \alpha -\mu \right] \left[ (c+\phi ) (c \gamma N+K \theta \zeta -\delta )-\sigma (\beta N-k \alpha -\mu -\nu ) \right] \end{aligned}$$

Appendix D

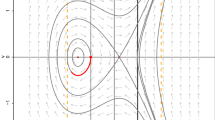
In this Appendix, I explain how the evolutionary singularity in Fig. 2a bifurcates into the one in Fig. 2b with increasing $\epsilon$ (note in particular that the singularity in Fig. 2a is an evolutionary repellor, whereas the branching point in Fig. 2b is convergence stable). This bifurcation is not directly relevant to the construction method, because the construction first fixes the value of $\epsilon$ and only then chooses the coefficients of the quadratic terms in (24), the choice depending on $\epsilon$.

The construction method starts with ${\mathbf {f'}}(x)$ such that $x$ is singular with $\mathcal {M}=0$, and then replaces ${\mathbf {f'}}(x)$ with ${\mathbf {f'}}(x)+\varDelta {\mathbf {f'}}(x)$ such that $\mathcal {M}$ becomes negative; in the example of (24), the latter is done by replacing $\epsilon =0$ with $\epsilon >0$. By the same replacement, the value of $\mathcal {E}$ changes with

$$\begin{aligned} \varDelta {\mathcal {E}} =\sum _{i=1}^m \sum _{j=1}^m s_{i,j} (\varDelta f'_i \cdot f'_j + f'_i \cdot \varDelta f'_j ) \end{aligned}$$

(36)

(cf. (7)). In general, $\varDelta \mathcal {E}$ may have any sign depending on $s_{i,j}$, the second derivatives of the invasion fitness with respect to traits; this is the reason why ${\mathbf {f''}}(x)$ has to be chosen after fixing $\varDelta {\mathbf {f'}}(x)$ (or $\epsilon$), such that the final sign of $\mathcal {E}$ is as required by the desired singularity.

In the simple model of Sect. 4, however, the invasion fitness (12) is linear in the traits, such that $s_{i,j}=0$ for all $i,j$ and ${\mathcal {E}}=\sum _{i=1}^m s_i f''_i$ is independent of $\varDelta {\mathbf {f'}}(x)$. Increasing $\epsilon$ therefore decreases $\mathcal {M}$ but does not change $\mathcal {E}$. Since the desired singularity is an evolutionary branching point, ${\mathbf {f''}}(x)$ is chosen such that $\mathcal {E}>0$ (cf. Table 1). At $\epsilon =0$, the singularity has $\mathcal {M}=0$ and since $\mathcal {E}+\mathcal {M}>0$, the singularity is not convergence stable (Fig. 2a). When $\epsilon =\epsilon _{TR}=0.07524$, then $\mathcal {M}=-\mathcal {E}$ and the singularity is not hyperbolic. Because $\varDelta {\mathbf {f'}}(x)/||\varDelta {\mathbf {f'}}(x)||$ (the direction of $\varDelta {\mathbf {f'}}(x)$) is chosen such that the location of the singularity is fixed, convergence stability changes through a transcritical bifurcation (see Fig. 3). When $\epsilon > \epsilon _{TR}, {\mathcal {E}}+{\mathcal {M}}<0$ and the singularity is convergence stable; and since the value of $\mathcal {E}$ is constant positive for any $\epsilon$, the singularity is a branching point (Fig. 2b).

Fig. 3

The transcritical bifurcation connecting the two pairwise invasibility plots in Fig. 2. The outermost panels are identical to Fig. 2a and b, respectively. The transcritical bifurcation occurs approximately at $\epsilon =0.07524$. All parameters are as in Fig. 2, except $\epsilon$ as shown in the panels