An analytical framework in the general coalescent tree setting for analyzing polymorphisms created by two mutations

Abstract

This paper presents an analytical framework for analyzing polymorphisms created by two mutation events in samples of DNA sequences modeled in the general coalescent tree setting. I developed the framework by deriving analytical formulas for the numbers of the topologies of the genealogies with two mutation events. This approach gives an advantage to analyze polymorphisms in large samples of DNA sequences at a non-recombining locus under vicarious evolutionary scenarios. Particularly the framework allows to estimate the probability of polymorphism data created by two mutation events as well as the ages of the events. Based on these results I extended the definition of the site frequency spectrum by classifying pairs of polymorphic sites into groups and presented analytical expressions for computing the expected sizes of these groups. Within the framework I also designed a Bayesian approach for inferring the haplotype of the most recent common ancestor at two polymorphic sites. Lastly, the framework was applied to polymorphism data from human APOE gene region under various demographic scenarios for ancestral human population and explored the signature of linkage disequilibrium for inferring the ancestral haplotype at two polymorphic sites. Interestingly enough, the results show that the most frequent haplotype at two completely linked polymorphic sites is not always the most likely candidate for the haplotype of the most recent common ancestor.

Appendix

1.1 The proof of Lemma 1

I first derive expressions for the numbers $N_{1}(k,m;b,c,a)$ and $N_{2}(k,m;a,c,b)$ when $a, b, c$ are positive. In the derivations I use an additional condition that the the sequences in the sample are labeled and in a particular order. To remove this condition for completing the proof, the derived numbers must be multiplied by $\genfrac(){0.0pt}0{a+b+c}{a\ \ b\ \ c}.$

Since $N_{1}(k,m;b,c,a)$ represents possible topologies of the genealogies with two mutations that are consistent with the data $(a,b,c)$ when the ancestral haplotype at the two sites is $TT,$ transition history at early and late mutation events is $H_1=(TT\rightarrow TC\rightarrow CC)$, and the number of ancestral lineages at the early and late mutation events are $k$ and $m$, respectively; from the definition of $(k,m)$ follows that $3 \le m \le b+a+1$, $k$ is less than or equal to $m-1$, and $2\le k \le a+1$, consequently $2 \le k \le \min (a+1,m-1).$

The genealogies satisfying the above conditions can be represented as a combination of three parts determined by the early and late mutation events. The first part of the genealogy is between sampling time point and the late mutation event; the second part is the part of the genealogy between the late and early mutation events; the third part is between the early mutation event and the time of the most recent common ancestor of the sample. The numbers of possible topologies in the three parts of the genealogy determine $N_{1}(k,m;b,c,a)$.

For this purpose I consider the sample as combination of three groups of sequences determined by the haplotypes $TT, TC, CC.$ In the first part of the genealogy the lineages coalesce only with the lineages of their groups, in other words the groups do not share an ancestor up to the time of the late mutation event. At this time point the number of the lineages associated with the group $CC$ is 1. Let the numbers of the lineages for the groups of $TC$ and $TT$ label by $m_1$ and $m_2,$ respectively. The number of topologies of the genealogies conditioned on $\{m_1, m_2\},$ is a product of the numbers of possible topologies in the three parts of the genealogy. I provide in details the derivation of the number of possible topologies in the first part of the genealogy.

The coalescent events occur one at a time in consecutive order back in time, and the total number of such events on this part of the genealogy is $a+b+c-m.$ These coalescent events are distributed among the genealogies of the groups $CC, TC$, and $TT$ as $c-1$, $b-m_1$, and $a-m_2,$ respectively. Consequently, the number of ways of distributing the coalescent events for the groups is

$$\begin{aligned} \genfrac(){0.0pt}0{a+b+c-m}{c-1,\ b-m_1,\ a-m_2}. \end{aligned}$$

For a given sequence of the coalescent events among the groups, the topologies of the genealogies of the groups have random joining structure, therefore the numbers of the possible topologies of the genealogies of the groups $TT, TC, CC$ are computed based on the following formula: If $i$ lineages are traced back in time and stopped when the number of lineages is $j$ by randomly joining two lineages at each coalescent event, the number of all possible generated topologies is equal to

$$\begin{aligned} \gamma (i,j)\equiv \genfrac(){0.0pt}0{i}{2}\genfrac(){0.0pt}0{i-1}{2}\cdots \genfrac(){0.0pt}0{j+1}{2},\ j\le i-1. \end{aligned}$$

From this observation follows that the number of all possible topologies for the first part of the genealogy conditional on $\{m_1, m_2\},$ is equal to

$$\begin{aligned} \genfrac(){0.0pt}0{a+b+c-m}{c-1,\ b-m_1,\ a-m_2}\gamma (c,1)\gamma (b,m_1)\gamma (a,m_2). \end{aligned}$$

The same type of approach one can use to compute the numbers of the topologies for the second and third parts of the genealogy (details not shown). These numbers are equal to

$$\begin{aligned} \genfrac(){0.0pt}0{m-k}{m_1}\gamma (m_1+1,1)\gamma (m_2,k-1) \end{aligned}$$

and

$$\begin{aligned} \gamma (k,1), \end{aligned}$$

respectively. Thus, after multiplying the above three expressions and simplifying the product, the following formula holds for the number of the topologies of the genealogies conditional on $m_1, m_2$:

$$\begin{aligned} N(a,b,c)\genfrac(){0.0pt}0{m-m_2}{2}\genfrac(){0.0pt}0{k}{2} \genfrac(){0.0pt}0{a+b+c-m}{c-1}\genfrac(){0.0pt}0{a+b+1-m}{a-m_2} \genfrac(){0.0pt}0{m-k}{m_2-k+1}, \end{aligned}$$

where

$$\begin{aligned} N(a,b,c)\equiv \frac{a!(a-1)!}{2^{a-1}}\frac{b!(b-1)!}{2^{b-1}}\frac{c!(c-1)!}{2^{c-1}}. \end{aligned}$$

From the definition of $m_1$ and $m_2,$ the following inequalities hold

$$\begin{aligned} m_1+m_2+1=m,\ 1\le m_1 \le b, \ 1\le m_2 \le a,\ \text {and}\ 2\le k\le m_2+1, \end{aligned}$$

and from these conditions follows that $m_2$ satisfies

$$\begin{aligned} m-b-1\le m_2 \le m-2, \end{aligned}$$

and

$$\begin{aligned} \max (m-b-1,1) \le m_2 \le \min (m-2,a), \end{aligned}$$

consequently

$$\begin{aligned} \max (m-b-1,k-1) \le m_2 \le \min (m-2,a). \end{aligned}$$

(33)

From the above derivations and the boundary conditions in (33) follows that the labeled and particularly ordered version of $N_{1}(k,m;b,c,a)$ can be represented as the sum

$$\begin{aligned}&N(a,b,c)\genfrac(){0.0pt}0{a+b+c-m}{c-1}\genfrac(){0.0pt}0{k}{2}\nonumber \\&\quad \times \sum _{m_2=\max (k-1,m-b-1)}^{\min (a,m-2)}\frac{(m-m_2)(m-m_2-1)}{2} \genfrac(){0.0pt}0{a+b+1-m}{a-m_2}\genfrac(){0.0pt}0{m-k}{m_2-k+1}\nonumber \\ \end{aligned}$$

(34)

Note that changing the range for $m_2$ in the above sum to $\max (k-1,m-b-1) \le m_2 \le \min (a,m-1)$ does not change the result of the sum because the term corresponding to $m_2=m-1$ is zero.

To compute this sum the following identity is used:

$$\begin{aligned} (m-m_2)(m-m_2-1)&= (a-m_2)(a-m_2-1)\nonumber \\&+2(m-a)(a-m_2)+(m-a)(m-a-1).\qquad \end{aligned}$$

(35)

After applying this to the above sum, it can be expressed as

$$\begin{aligned}&\sum _{\max (k-1,m-b-1)}^{\min (a,m-1)}\genfrac(){0.0pt}0{a+b+1-m}{a-m_2} \genfrac(){0.0pt}0{m-k}{m_2-k+1}\frac{(m-m_2)(m-m_2-1)}{2}\\&\quad =\frac{1}{2}\sum _{\max (k-1,m-b-1)}^{\min (a,m-1)} \genfrac(){0.0pt}0{a+b+1-m}{a-m_2}\genfrac(){0.0pt}0{m-k}{m_2-k+1}\\&\qquad \times ((m-a)(m-a-1)+2(m-a)(a-m_2)+(a-m_2)(a-m_2-1))\\&\quad =J_1+J_2+J_3. \end{aligned}$$

For computing $J_i,\ i=1,2,3,$ the following formula [see Feller (1970)] is used:

$$\begin{aligned} \sum _{i=\max (0,c-b)}^{\min (a,c)}\genfrac(){0.0pt}0{a}{i}\genfrac(){0.0pt}0{b}{c-i}= \genfrac(){0.0pt}0{a+b}{c}. \end{aligned}$$

After applying this formula to $J_1$ the following formula holds

$$\begin{aligned} J_1&\equiv \genfrac(){0.0pt}0{m-a}{2}\sum _{m_2=\max (k-1,m-b-1)}^{\min (a,m-1)} \genfrac(){0.0pt}0{a+b+1-m}{a-m_2}\genfrac(){0.0pt}0{m-k}{m_2-k+1}\\&= \genfrac(){0.0pt}0{m-a}{2}\sum _{i=\max (0,a-m+1)}^{\min (a-k+1,a-m+b+1)} \genfrac(){0.0pt}0{a+b+1-m}{i}\genfrac(){0.0pt}0{m-k}{a-k+1-i}\\&= \genfrac(){0.0pt}0{m-a}{2}\genfrac(){0.0pt}0{a+b+1-k}{a-k+1}. \end{aligned}$$

Applying the same formula to $J_2$ and $J_3$ the following equations hold:

$$\begin{aligned} J_2&= (m-a)\sum _{m_2=\max (k-1,m-b-1)}^{\min (a,m-1)}\frac{(a-m_2)(a+b+1-m)!}{ (a-m_2)!(b+1-m+m_2)!}\genfrac(){0.0pt}0{m-k}{m_2-k+1}\\&= (m-a)(a+b+1-m)\sum _{m_2=\max (k-1,m-b-1)}^{\min (a,m-1)} \genfrac(){0.0pt}0{a+b-m}{a-m_2-1} \genfrac(){0.0pt}0{m-k}{m_2-k+1}\\&= (m-a)(a+b+1-m)\genfrac(){0.0pt}0{a+b-k}{a-k} \end{aligned}$$

and

$$\begin{aligned} J_3&= \sum _{m_2=\max (k-1,m-b-1)}^{\min (a,m-1)}\genfrac(){0.0pt}0{a-m_2}{2}\genfrac(){0.0pt}0{a+b+1-m}{a-m_2}\genfrac(){0.0pt}0{m-k}{m_2-k+1} \\&= \genfrac(){0.0pt}0{a+b+1-m}{2}\sum _{m_2=\max (k-1,m-b-1)}^{\min (a,m-1)}\genfrac(){0.0pt}0{a+b-k-1}{a-m_2-2}\genfrac(){0.0pt}0{m-k}{m_2-k+1}\\&= \frac{1}{2}(a+b+1-m)(a+b-m)\genfrac(){0.0pt}0{a+b-k-1}{a-k-1}. \end{aligned}$$

Combining $J_i,\ i=1,2,3,$ together completes the proof of the formula for $N_{1}(k,m;b,c,a).$

Derivation of the formula for $N_{2}(k,m;a,c,b)$ is very similar to the proof of the previous case. I again consider the genealogy as a combination of three parts determined by the early and late mutation events. The first part of the genealogy is between the sampling time point and the late mutation event, and it is a combination of the genealogies for the groups $TT, TC, CC$ that do not share ancestor between the groups. The numbers of the ancestral lineages of these groups at the late mutation event are equal to $m_2, m_1, 1,$ respectively. Note that $m_2$ and $m_1$ satisfy $m=1+m_1+m_2$ and

$$\begin{aligned} 1\le m_2 \le a\ \text {and}\ 1\le m_1 \le b, \ k-2\le m_1. \end{aligned}$$

As a result of these conditions, the following boundary conditions hold for $m_2\!:$

$$\begin{aligned} \max (1,m-1-b)\le m_2 \le \min (m-2,m-k+1,a), \end{aligned}$$

$m$ and $k$ satisfy conditions $3 \le m \le a+b+1$ and $2 \le k \le m.$

Based on the similar arguments as in the previous case, the number of the topologies of the genealogies with two mutations conditional on $(m_1, m_2)$ is

$$\begin{aligned} N(a,b,c)\genfrac(){0.0pt}0{k}{2}\genfrac(){0.0pt}0{m-m_2}{2} \genfrac(){0.0pt}0{a+b+c-m}{c-1}\genfrac(){0.0pt}0{a+b-m+1}{a-m_2} \genfrac(){0.0pt}0{m-k}{m_2-1}. \end{aligned}$$

The sum of these numbers is equal to $N_{2}(k,m;a,c,b)\!:$

$$\begin{aligned}&N(a,b,c)\genfrac(){0.0pt}0{a+b+c-m}{c-1}\genfrac(){0.0pt}0{k}{2}\nonumber \\&\quad \times \frac{1}{2}\sum _{m_2=\max (1,m-1-b)}^{\min (m-2,m-k+1,a)} \genfrac(){0.0pt}0{a+b-m+1}{a-m_2}\genfrac(){0.0pt}0{m-k}{m_2-1}(m-m_2)(m-m_2-1).\nonumber \\ \end{aligned}$$

(36)

The range for $m_2$ in the above sum can be changed to $\max (1,m-1-b)\le m_2 \le \min (m-k+1,a)$ because $2 \le k$ and the term corresponding to $m_2=m-1$ is zero. Using the following identity

$$\begin{aligned} (m-m_2)(m-m_2-1)&= (a-m_2)(a-m_2-1)\\&+2(m-a)(a-m_2)+(m-a)(m-a-1), \end{aligned}$$

the sum in the expression (36) can be represented as

$$\begin{aligned}&\sum _{m_2=\max (1,m-1-b)}^{\min (m-k+1,a)}\genfrac(){0.0pt}0{a+b-m+1}{a-m_2}\genfrac(){0.0pt}0{m-k}{m_2-1}\\&\qquad \times ((a-m_2)(a-m_2-1)+2(m-a)(a-m_1)+(m-a)(m-a-1))\\&\quad =I_1+I_2+I_3. \end{aligned}$$

To compute $I_i,\ i=1,2,3,$ I use the same approach as for $J_i,\ i=1,2,3$. Thus, the following formulas hold

$$\begin{aligned} I_1&= \sum _{m_2=\max (1,m-1-b)}^{\min (m-k+1,a)}\genfrac(){0.0pt}0{a+b+1-m}{a-m_2}\genfrac(){0.0pt}0{m-k}{m_2-1}(a-m_2)(a-m_2-1)\\&= (a+b+1-m)(a+b-m)\sum _{m_2=\max (1,m-1-b)}^{\min (m-k+1,a)}\genfrac(){0.0pt}0{a+b-m-1}{a-m_2-2}\genfrac(){0.0pt}0{m-k}{m_2-1} \end{aligned}$$

and

$$\begin{aligned} I_1=(a+b+1-m)(a+b-m)\genfrac(){0.0pt}0{a+b-k-1}{a-3}. \end{aligned}$$

For $I_2$ and $I_3$ the following formulas hold

$$\begin{aligned} I_2=2(m-a)(a+b+1-m)\genfrac(){0.0pt}0{a+b-k}{a-2} \end{aligned}$$

and

$$\begin{aligned} I_3=(m-a)(m-a-1)\genfrac(){0.0pt}0{a+b-k+1}{a-1}. \end{aligned}$$

Combining the formulas for $I_i$, $i=1,2,3$, completes the proof of the formula for $N_{2}(k,m;a,c,b).$ The arguments for deriving the formulas when $b=0$ are very similar. The details are not provided.

1.2 The proof of Theorem 1

The probabilities of $r_n$ and $h_n$: To show that $h_n$ and $r_n$ are independent of the topology of the genealogy, it is enough to show that the statement holds for $r_n.$ I use an induction with respect to $n$. Obviously, the statement holds for $n=2$ and $n=3$. Assuming that the statement holds for any $k$ less than $n, n> 3$, it needs to be shown that the statement also holds for $n$.

For $n$ sequences, let $E_{2r}(G_n)$ be the set of genealogies $G_n$ with two mutation events occurred on same lineage. This set $E_{2r}(G_n)$ can be partitioned into disjoint sets $E_{2r}(G_n, \ell )$ determined by the condition that the late mutation event occurred on branch $\ell .$ Each of these genealogies can be considered as a result of a branching event at time $T_n$ from a lineage of a genealogy $G_{n-1}$ that has $n-1$ leaves and coalescence waiting times equal to $(T_{n-1}+T_n, T_{n-2},\ldots , T_2).$ Let $\ell _0$ be the branch of $G_{n-1}$ on which the branching event occurred. I label the three branches of $G_n$ created by the branching event as $\ell _1, \ell _2, \ell _3$ and their lengths (for which I use the same notation as for the branches) satisfy the equations $\ell _1=\ell _2=T_n$ and $\ell _3=\ell _0-T_n$. Since mutation events occur independently on different branches of the genealogy according to a Poisson process with rate $\theta /2,$ it is easy to see that $\mathrm{I}\!\mathrm{P}(E_{2r}(G_n, \ell )) = \mathrm{I}\!\mathrm{P}(E_{2r}(G_{n-1}, \ell ))$ if $\ell \ne \ell _i, i=1,2,3,$ and

$$\begin{aligned} \mathrm{I}\!\mathrm{P}(E_{2r}(G_n, \ell _i))&= (\theta _0/2)^2\left( \frac{ T_n^2}{2}+T_nZ_{n-1}\right) e^{-\theta _0/2L_n},\quad i=1, 2,\\ \mathrm{I}\!\mathrm{P}(E_{2r}(G_n, \ell _3))&= (\theta _0/2)^2\left( \frac{(\ell _0-T_n)^2}{2}+ (\ell _0-T_n)(Z_{n}-\ell _0)\right) e^{-\theta _0/2L_n}, \end{aligned}$$

and

$$\begin{aligned} \mathrm{I}\!\mathrm{P}(E_{2r}(G_{n-1}, \ell _0)) = (\theta _0/2)^2 \left( \frac{\ell _0^2}{2}+\ell _0(Z_{n}-\ell _0)\right) e^{-\theta _0/2L_n}, \end{aligned}$$

where, $Z_i$ are defined as $\sum _{j=2}^i T_j.$

After combining all the equations above the following equation holds

$$\begin{aligned} \mathrm{I}\!\mathrm{P}(E_{2r}(G_n))=\mathrm{I}\!\mathrm{P}(E_{2,r}(G_{n-1}))+(\theta _0/2)^2\left( \frac{ T_n^2}{2}+T_nZ_{n-1}\right) . \end{aligned}$$

Since the first term in the above sum is independent from the topology of the genealogy based on the inductive assumption and the second term is also independent from the topology, it follows that the probability of $E_{2,r}(G_n)$ is independent from the topology of $G_n$.

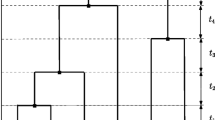
Derivation of the expression for $r_n$: Since the above results show that the value of $r_n$ is the same for any topology of the genealogy, I derive the expression for $r_n$ by considering a genealogy in which the all $n-1$ coalescent events occur along a single lineage. The branch lengths of this genealogy are equal to $T_n, T_{n-1}\ldots , T_2, S_{n},\ldots , S_2,$ where $S_i=\sum _{j=i}^n T_j$. Figure 6 shows an example of a such genealogy for the case of $n=5.$

Fig. 6

The genealogy of five sequences with a specific topology in which the 4 coalescent events occur on the same lineage. The coalescence times and waiting times between consecutive coalescent events $(S_i$ and $T_i, i=2,\ldots , 5)$ represent the branch lengths of the genealogy

Using the same partitioning for $E_{2r}(G_n)$ as described in the above proof, all possibilities for $E_{2r}(G_n, \ell )$ can be easily explored for the special type of genealogy: If the late mutation event is on the branch $\ell =T_i$, the early mutation event can be on that branch or on the part of the lineage connecting the beginning of that branch to the root of the genealogy. The probability of $E_{2r}(G_n, \ell )$ in this case is

$$\begin{aligned} (\theta _0/2)^2\left( \frac{T_i^2}{2}+T_i(S_2-S_{i})\right) e^{-\theta _0/2L_n}. \end{aligned}$$

Similarly, if the late mutation event is on the branch $\ell = S_i,$ the probability of $E_{2r}(G_n, \ell )$ is

$$\begin{aligned} (\theta _0/2)^2\left( \frac{S_i^2}{2}+S_i(S_2-S_{i})\right) e^{-\theta _0/2L_n}. \end{aligned}$$

Adding the above expressions for all the cases, the probability of two mutation events occurring on same lineage is equal to

$$\begin{aligned} \frac{(\theta _0/2)^2\left( \sum _{i=2}^n T_i^2+2T_i(S_2-S_{i})+S_i^2+2S_i(S_2-S_{i})\right) e^{-\theta _0/2L_n}}{2}. \end{aligned}$$

After simplifying the above expression, the following equation holds

$$\begin{aligned} \mathrm{I}\!\mathrm{P}(E_{2r}(G_n))=\frac{(\theta _0/2)^2\left( nS_2^2-\sum _{i=2}^{n} (S_2- S_i)^2\right) e^{-\theta _0/2L_n}}{2}. \end{aligned}$$

Combining the above expression with the representation

$$\begin{aligned} r_n = \frac{\mathrm{I}\!\mathrm{E}\mathrm{I}\!\mathrm{P}(E_{2r}(G_n))}{\mathrm{I}\!\mathrm{E}\mathrm{I}\!\mathrm{P}(E_2)}, \end{aligned}$$

the following formula holds

$$\begin{aligned} r_n =\frac{\mathrm{I}\!\mathrm{E}\left( (nS_2^2-\sum _{i=2}^{n}(S_2-S_{i})^2)e^{-\theta _0 L_n/2}\right) }{\mathrm{I}\!\mathrm{E}(L_n^2e^{-\theta _0 L_n/2})}. \end{aligned}$$

The proof of the inequality $h_n > r_n, n>2$: I use a mathematical induction to prove that $h_n-r_n >0$ if $n>2$. From the previous results follows that the difference $h_n - r_n$ can be represented as

$$\begin{aligned} h_n - r_n =\frac{\mathrm{I}\!\mathrm{E}\left( (L_n^2-2nS_2^2+2\sum _{i=2}^{n}(S_2-S_{i})^2)e^{-\theta _0 L_n/2}\right) }{\mathrm{I}\!\mathrm{E}(L_n^2e^{-\theta _0 L_n/2})}. \end{aligned}$$

(37)

The following notations are needed $Z_{i}=\sum _{j=2}^{i} T_j$ and $\phi _n=L_n^2-2nZ_n^2+2\sum _{i=2}^{n-1}Z_{i}^2,$ which is equal to $L_n^2-2nS_2^2+2\sum _{i=2}^{n}(S_2-S_{i})^2.$ For $n=3$, it is easy to check that

$$\begin{aligned} \phi _3=L_3^2-6Z_3^2+2Z_2^2 =3T_3^2>0. \end{aligned}$$

Assume that $\phi _k>0$ if $k=n-1,$ I prove that this inequality also holds if $k=n.$ Since $L_n=\sum _{j=2}^n jT_j$, it can be represented as $nT_n+L_{n-1}$ as well as $nZ_n-\sum _{i=2}^{n-1}Z_i.$ Thus, the following formula holds

$$\begin{aligned} \phi _n-\phi _{n-1} = n(n-2)T_n^2+2nT_n\left( (n-3)Z_{n-1}-\sum _{i=2}^{n-2}Z_i\right) . \end{aligned}$$

As a result, the inequality

$$\begin{aligned} \phi _n > 0. \end{aligned}$$

holds since $\phi _{n-1}$ is greater than 0 and

$$\begin{aligned} (n-3)Z_{n-1}-\sum _{i=2}^{n-2}Z_i > 0. \end{aligned}$$

Derivations of the formulas for $\mathrm{I}\!\mathrm{P}(E_{2r,s}\mid E_2)$ and $\mathrm{I}\!\mathrm{P}(E_{2h,c}\mid E_2)$: I derive the formulas using the following representations for the probabilities $\mathrm{I}\!\mathrm{P}(E_{2r,s}\mid E_2)$ and $\mathrm{I}\!\mathrm{P}(E_{2h,c}\mid E_2)\!:$

$$\begin{aligned} \mathrm{I}\!\mathrm{P}(E_{2r,s}\mid E_2)=\sum _{a=1}^n \mathrm{I}\!\mathrm{P}\left( (a,0,n-a)\mid TT, H_1, E_2\right) \end{aligned}$$

and

$$\begin{aligned} \mathrm{I}\!\mathrm{P}(E_{2h,c}\mid E_2)=\sum _{a=1}^n \mathrm{I}\!\mathrm{P}\left( (a,0,n-a)\mid TC, H_2, E_2\right) , \end{aligned}$$

which I modify based on the Eq. (9) and changing the orders of the terms in sums. Thus, the following equations hold

$$\begin{aligned}&\mathrm{I}\!\mathrm{P}(E_{2r,s}\mid E_2)\\&\quad =\frac{ \sum _{m=2}^n\sum _{k=2}^m \left( \sum _{a=m-1}^{n-1} N_{1}(k,m;0,n-a,a)\right) d_{m,k}\mathrm{I}\!\mathrm{E}(T_k T_m e^{-\theta _0 L_n/2})}{N(n)\mathrm{I}\!\mathrm{E}\left( (L_{n}^2/2) e^{-\theta _0 L_n/2}\right) } \end{aligned}$$

and

$$\begin{aligned} \mathrm{I}\!\mathrm{P}(E_{2h,c}\mid E_2)=\frac{ \sum _{m=2}^n \left( \sum _{a=m-1}^{n-1} N_{2}(k,m;a,n-a,0)\right) d_{m,k}\mathrm{I}\!\mathrm{E}(T_k T_m e^{-\theta _0 L_n/2})}{N(n)\mathrm{I}\!\mathrm{E}\left( (L_{n}^2/2) e^{-\theta _0 L_n/2}\right) }. \end{aligned}$$

The above sums I simplify further using the formulas for $N_1()$ and $N_2()$ and the identity

$$\begin{aligned} \sum _{r=v}^w \genfrac(){0.0pt}0{r}{v}=\genfrac(){0.0pt}0{w+1}{v+1}. \end{aligned}$$

Hence, the following formulas hold

$$\begin{aligned} \sum _{a=m-1}^{n-1}\frac{N_{1}(k,m;0,n-a,a)}{N(n)}&= \frac{k(k-1)(n-m)!(m-2)!}{(n-1)!} \sum _{a=m-1}^{n-1} \genfrac(){0.0pt}0{a-1}{m-2}\\&= \frac{k(k-1)}{m-1} \end{aligned}$$

and

$$\begin{aligned} \sum _{a=m-1}^{n-1} \frac{N_{2}(k,m;a,n-a,0)}{N(n)}=\frac{2(m-2)!(n-m)!}{(n-1)!}\sum _{a=m-1}^{n-1} \genfrac(){0.0pt}0{a-1}{m-2}=\frac{2}{m-1}. \end{aligned}$$

The proof of Theorem 1 is complete.

1.3 The proof of Theorem 2

I represent the probability $\mathrm{I}\!\mathrm{P}( D_{n}\mid \alpha , H_{\alpha }, E_2)$ as a ratio of probabilities:

$$\begin{aligned} \mathrm{I}\!\mathrm{P}( D_{n}\mid \alpha , H_{\alpha }, E_2)=\frac{\mathrm{I}\!\mathrm{P}( D_{n},\alpha , H_{\alpha }, E_2)}{\mathrm{I}\!\mathrm{P}(\alpha , H_{\alpha }, E_2)}. \end{aligned}$$

To derive expressions for the probabilities in the numerator and denominator, I use the framework for generating polymorphisms in samples of DNA sequences in the general coalescent tree setting. The coalescence waiting times are determined by the random variables $T_n,\ldots , T_2,$ and mutation events are added along the lineages of the genealogy according to a Poisson process with rate $\theta _0/2.$ Because of these properties, the probability in the denominator can be represented as

$$\begin{aligned} \mathrm{I}\!\mathrm{P}(\alpha , H_{\alpha }, E_2)=\mathrm{I}\!\mathrm{P}(\alpha , H_{\alpha }) \mathrm{I}\!\mathrm{E}((\theta _0^2 L_n^2/8)e^{-\theta _0 L_n/2}), \end{aligned}$$

where $L_n$ is the total branch length of the genealogy. Using a similar approach described by Sargsyan (2010), the probability in the numerator can be represented as the sum

$$\begin{aligned} \mathrm{I}\!\mathrm{P}( D_{n},\alpha , H_{\alpha }, E_2)=\sum _{(k,m)\in {\varDelta }_j(e)}\mathrm{I}\!\mathrm{E}\mathrm{I}\!\mathrm{P}({\varGamma }(k,m) \cong D_{n}\mid {\varGamma }(k,m)), \end{aligned}$$

where ${\varGamma }(k,m)$ represent genealogies with two mutation events satisfying the following conditions: (1) The number of ancestral lineages at the early and late mutation events are $k$ and $m$, respectively. (2) The $\alpha$ is the haplotype of the most recent common ancestor, and $H_{\alpha }$ is the transition history at early and late mutation events. The symbol “$\cong$” means that the genealogy with two mutations is consistent with $D_n.$ Each term of this sum can be represented as a sum based on the definition of the conditional expectation. Thus,

$$\begin{aligned} \mathrm{I}\!\mathrm{E}\mathrm{I}\!\mathrm{P}({\varGamma }(k,m) \cong D_{n}\mid {\varGamma }(k,m)) = \sum _{ {\varGamma }(k,m)} \mathrm{I}\!\mathrm{P}({\varGamma }(k,m) \cong D_{n}\mid {\varGamma }(k,m))\mathrm{I}\!\mathrm{P}({\varGamma }(k,m)), \end{aligned}$$

where the probability of ${\varGamma }(k,m)$ is equal to

$$\begin{aligned} \mathrm{I}\!\mathrm{P}({\varGamma }(k,m))=\mathrm{I}\!\mathrm{P}(\alpha , H_{\alpha })d_{m,k}\frac{\theta _0 T_k}{2}\frac{\theta _0 T_m}{2} e^{-\theta _0 L_n/2} \end{aligned}$$

and

$$\begin{aligned} \mathrm{I}\!\mathrm{P}({\varGamma }(k,m) \cong D_{n}\mid {\varGamma }(k,m))=\frac{N_{j}(k,m;e)}{N(n)}, \end{aligned}$$

the values of $j$ and $e$ are determined by $\alpha , H_{\alpha }$ and the frequencies $(a,b,c)$ of the haplotypes $TT, TC, CC.$ The quantity N(n) represents the number of all possible topological trees with $n$ leaves and it is equal to $=n!(n-1!)/2^{n-1},$ which can be easily derived based on tracing and joining two lineages at each coalescent event. Combining the above equations completes the proof.

1.4 The proof of Lemma 2

First I derive the asymptotic formula when $TT$ is the ancestral haplotype. Factoring out some of the terms in Eq. (7), the following holds

$$\begin{aligned}&N_{1}(k,m;b,c,a)\\&\quad =\genfrac(){0.0pt}0{a+b+c}{a\ \ b\ \ c}N(a,b,c)\genfrac(){0.0pt}0{a+b+c-m}{c-1}\frac{k(k-1)}{2} \frac{(a+b-k-1)!}{b!(a+1-k)!}\\&\qquad \quad \times \left( \frac{1}{2}(m-a)(m-a-1)(a+b+1-k)(a+b-k)\right. \\&\qquad \quad +\,(m-a)(a + b + 1 - m)(a + b - k)(a - k + 1)\\&\qquad \quad \left. +\,\frac{1}{2}(a + b + 1 - m)(a + b - m)(a - k + 1)(a - k)\right) . \end{aligned}$$

and

$$\begin{aligned} \frac{N_{1}(k,m;b,c,a)}{\frac{N(n)}{n^2}}&= \frac{n^24(a-1)!(a+b+c-m)!\frac{k(k-1)}{2}(a+b-k-1)!}{(a+1-k)!(a+b+c-1)!(a+b+1-m)!b}\\&\left( \frac{1}{2}(m-a)(m-a-1)(a+b+1-k)(a+b-k)\right. \\&\quad +(m-a)(a + b + 1 - m)(a + b - k)(a - k + 1)\\&\quad \left. +\frac{1}{2}(a + b + 1 - m)(a + b - m)(a - k + 1)(a - k)\right) \!. \end{aligned}$$

To approximate this ratio under the limits $a/n\rightarrow x,$ $b/n\rightarrow y,$ $c/n\rightarrow z$ as $a,b,c$ tend to $\infty ,$ first the following limit is derived

$$\begin{aligned} \frac{(a-1)!}{(a+1-k)!(a+b+c)^{k-2}}\rightarrow x^{k-2}, \end{aligned}$$

which follows from the representation

$$\begin{aligned} \frac{(a-1)!}{(a+1-k)!(a+b+c)^{k-2}}= \frac{(a-k+2)}{(a+b+c)}\cdots \frac{(a-1)}{(a+b+c)}. \end{aligned}$$

Using similar approach the following limits hold:

$$\begin{aligned} \frac{(a+b-k-1)!}{(a+b+1-m)!(a+b+c)^{m-k-2}}\rightarrow (x+y)^{m-k-2}, \end{aligned}$$

and

$$\begin{aligned} \frac{(a+b+c-m)!(a+b+c)^{m-1}}{(a+b+c-1)!}\rightarrow 1. \end{aligned}$$

After expanding the expression

$$\begin{aligned}&\left( \frac{1}{2}(m-a)(m-a-1)(a+b+1-k)(a+b-k)\right. \\&\quad +(m-a)(a + b + 1 - m)(a + b - k)(a - k + 1)\\&\quad \left. + \frac{1}{2}(a + b + 1 - m)(a + b - m)(a - k + 1)(a - k)\right) \end{aligned}$$

to

$$\begin{aligned} -\frac{bk}{2}-\frac{b^2k}{2}-bak+\frac{bk^2}{2}+\frac{b^2k^2}{2}+\frac{bm}{2}+ \frac{b^2m}{2}+bam-b^2km-\frac{bm^2}{2}+\frac{b^2m^2}{2}, \end{aligned}$$

it is asymptotically equal to $(a+b+c)^2\frac{y}{2}(m-k)(2x+y(m-k+1)))$. After combining these results the following limit holds

$$\begin{aligned} \frac{N_{1}(k,m;b,c,a)}{\frac{N(n)}{n^2}}\rightarrow \frac{k(k-1)(m-k)(2x^{k-1}+x^{k-2}y(m-k+1))}{(x+y)^{k-m+2}}. \end{aligned}$$

Note that the above approach can be applied similarly to derive the asymptotic formula for $N_{2}(k,m;a,c,b)$. The proof of the lemma is complete.

1.5 The proof of Theorem 3

In the standard coalescent setting $T_i$, $i=2,\ldots ,n$, are pairwise independent exponential random variables with rates $2/(i(i-1))$, therefore the following equations hold:

$$\begin{aligned} \mathrm{I}\!\mathrm{E}(T_kT_m) = \frac{4}{k(k-1)m(m-1)},\ m\ne k, \end{aligned}$$

and

$$\begin{aligned} \mathrm{I}\!\mathrm{E}(T_m^2) =\frac{8}{(m(m-1))^2}. \end{aligned}$$

Using these formulas and the approximations in Lemma 2, I compute the limit of the expression

$$\begin{aligned} \frac{n^2}{N(n)}\sum _{m=3}^{b+a+1}\sum _{k=2}^{\min (m-1,a+1)}N_{1}(k,m;b,c,a) d_{m,k}\mathrm{I}\!\mathrm{E}(T_kT_m) \end{aligned}$$

under the conditions $a/n\rightarrow x,$ $b/n\rightarrow y,$ $c/n\rightarrow z$ as $a,b,c$ tend to $\infty ,$ by substituting the ratio

$$\begin{aligned} \frac{N_{1}(k,m;b,c,a)}{\frac{N(n)}{n^2}}d_{m,k}\mathrm{I}\!\mathrm{E}(T_kT_m) \end{aligned}$$

with

$$\begin{aligned} D_1(y,k;z,m)\frac{4}{m(m-1)k(k-1)} \end{aligned}$$

and showing that the following identity holds

$$\begin{aligned} \sum _{m=3}^{\infty }\sum _{k=2}^{m-1}D_1(y,k;z,m)\frac{4}{m(m-1)k(k-1)} = F(z). \end{aligned}$$

Similar to this approach the following equations hold for the other cases

$$\begin{aligned} \sum _{m=3}^{\infty }\sum _{k=2}^{m}D_2(x,k;z,m)\frac{4}{m(m-1)k(k-1)}&= \left( \frac{4}{z(x+z)}-F(z)\right) ,\\ \sum _{m=3}^{\infty }\sum _{k=2}^{m}D_2(z,k;x,m)\frac{4}{m(m-1)k(k-1)}&= \left( \frac{4}{x(x+z)}-F(x)\right) . \end{aligned}$$

Note that if $m=k$ then

$$\begin{aligned} \sum _{m=3}^{\infty }D_2(x,m;z,m)\frac{8}{m^2(m-1)^2}= 2F(1-y). \end{aligned}$$

For the derivations of these formulas I used Wolfram Mathematica Software and the formulas

$$\begin{aligned} \sum _{i=0}^{\infty }t^i=\frac{1}{1-t}, \end{aligned}$$

and

$$\begin{aligned} \sum _{i=1}^{\infty }\frac{t^i}{i}=-\log (1-t). \end{aligned}$$

Under the limits $\frac{a}{n}\rightarrow x, \frac{b}{n}\rightarrow y, c/n\rightarrow z$, as $a,b,c$ tend to $\infty$ the following limits hold in the standard coalescent setting:

$$\begin{aligned} \frac{n^2}{N(n)}\sum _{m=3}^{b+a+1}\sum _{k=2}^{\min (m-1,a+1)}N_{1}(k,m;b,c,a) d_{m,k}\mathrm{I}\!\mathrm{E}(T_kT_m)&\rightarrow F(z),\\ \frac{n^2}{N(n)}\sum _{m=3}^{b+c+1}\sum _{k=2}^{\min (m-1,c+1)}N_{1}(k,m;b,a,c) d_{m,k}\mathrm{I}\!\mathrm{E}(T_kT_m)&\rightarrow F(x),\\ \frac{n^2}{N(n)}\sum _{m=3}^{a+b+1}\sum _{k=2}^{\min (m,b+2)}N_{2}(k,m;a,c,b) d_{m,k}\mathrm{I}\!\mathrm{E}(T_kT_m)&\rightarrow {\varDelta }(z,x,y),\\ \frac{n^2}{N(n)}\sum _{m=3}^{b+c+1}\sum _{k=2}^{\min (m,b+2)}N_{2}(k,m;c,a,b) d_{m,k}\mathrm{I}\!\mathrm{E}(T_kT_m)&\rightarrow {\varDelta }(x,z,y), \end{aligned}$$

where

$$\begin{aligned} {\varDelta }(z,x,y)\equiv \left( \frac{4}{z(x+z)}-F(z)\right) \end{aligned}$$

and

$$\begin{aligned} F(x)\equiv \frac{4(1-x^2+2x\log (x))}{x(1-x)^3}. \end{aligned}$$

Based on Eq. (6) and (17) the following holds

$$\begin{aligned} \mathrm{I}\!\mathrm{P}(TT\mid (x,y,z), E_2)&\propto \mathrm{I}\!\mathrm{P}((x,y,z)\mid TT, H_1,E_2)\pi _{TT},\\ \mathrm{I}\!\mathrm{P}(TC\mid (x,y,z), E_2)&\propto (\mathrm{I}\!\mathrm{P}((x,y,z)\mid \textit{TC}, H_2,E_2) \!+\! \mathrm{I}\!\mathrm{P}((x,y,z)\mid \textit{TC},H_3, E_2))\pi _{TC},\\ \mathrm{I}\!\mathrm{P}(CC\mid (x,y,z), E_2)&\propto \mathrm{I}\!\mathrm{P}((x,y,z)\mid CC, H_4,E_2)\pi _{CC}. \end{aligned}$$

Combining these equations with the above limits the proof of the theorem is complete.

1.6 The proof of Theorem 4

Derivations here are very similar to the approach used by Sargsyan (2010), for more details see that paper. First I represent the joint distribution of the ages of $\xi _1, \xi _2,$ and $\xi$ as the ratio of two probabilities:

$$\begin{aligned}&\mathrm{I}\!\mathrm{P}(\xi _1 \le t_1 , \xi _2 \le t_2, \xi \le t\mid D_{n}, \alpha , H_{\alpha }, E_2)\\&\quad =\frac{\mathrm{I}\!\mathrm{P}(\xi _1 \le t_1 , \xi _2 \le t_2, \xi \le t, D_{n}, \alpha , H_{\alpha }, E_2)}{\mathrm{I}\!\mathrm{P}( D_{n}, \alpha , H_{\alpha }, E_2)}. \end{aligned}$$

The denominator in the above equation can be substituted by the expression in Theorem 2. To derive an expression for the probability in the numerator one can use very similar approach as in Theorem 2. After determining $j$ and $e$ based on $\alpha , H_{\alpha }$ and $(a,b,c)$ (the frequencies of the haplotypes $TT, TC, CC)$ the following equation holds:

$$\begin{aligned}&\mathrm{I}\!\mathrm{P}(\xi _1 \le t_1 , \xi _2 \le t_2, \xi \le t, D_{n}, \alpha , H_{\alpha }, E_2)\\&\quad =\sum _{(k,m)\in {\varDelta }_{j}(e)}\mathrm{I}\!\mathrm{E}\mathrm{I}\!\mathrm{P}(\xi _1 \le t_1 , \xi _2 \le t_2, \xi \le t, {\varGamma }(k,m) \cong D_{n}\mid {\varGamma }(k,m)), \end{aligned}$$

where ${\varGamma }(k,m)$ has distribution

$$\begin{aligned} \mathrm{I}\!\mathrm{P}({\varGamma }(k,m))=\mathrm{I}\!\mathrm{P}(\alpha , H_{\alpha })d_{m,k}T_k T_m e^{-\theta _0 L_n/2}. \end{aligned}$$

The probabilities in the above sum can be written as

$$\begin{aligned}&\mathrm{I}\!\mathrm{P}(\xi _1 \le t_1 , \xi _2 \le t_2, \xi \le t, {\varGamma }(k,m) \cong D_{n}\mid {\varGamma }(k,m))\nonumber \\&\quad =\mathrm{I}\!\mathrm{P}(\xi _1 \le t_1 , \xi _2 \le t_2, \xi \le t \mid {\varGamma }(k,m)) \mathrm{I}\!\mathrm{P}( {\varGamma }(k,m) \cong D_{n}\mid {\varGamma }(k,m)). \end{aligned}$$

(38)

Each of the factors in the above product are evaluated separately:

$$\begin{aligned} \mathrm{I}\!\mathrm{P}({\varGamma }(k,m) \cong D_{n}\mid {\varGamma }(k,m))=\frac{N_{j}(k,m;e)}{N(n)}, \end{aligned}$$

and conditional on ${\varGamma }(k,m)$, $\xi _1$ and $\xi _2$ and $\xi$ are respectively equal to $S_{k+1}+U_0 T_{k}$, $S_{m+1}+U_1 T_{m}$, and $S_2,$ in distribution, where $S_i$ is $\sum _{j=i}^n T_j$, and if $k\ne m$ then $U_1=U_{00}$ and $U_2=U_{01}$ where $U_{00}, U_{01}$ are independent uniform random variables on $(0,1)$, if $k=m$ then $U_2=\min (U_{00}, U_{01})$ and $U_1=\max (U_{00}, U_{01})$. Thus, if $k\ne m$ then the following equation holds

$$\begin{aligned}&\mathrm{I}\!\mathrm{P}(\xi _1 \le t_1 , \xi _2 \le t_2, \xi \le t \mid {\varGamma }(k,m))\nonumber \\&\quad =\left( 1\wedge \left( \frac{t_1-S_{k+1}}{T_{k}}\right) _{+}\right) \left( 1\wedge \left( \frac{t_2-S_{m+1}}{T_{m}}\right) _{+}\right) \mathbf {I}\{S_2\le t\}; \end{aligned}$$

(39)

recall that $1\wedge r = \min (1,r)$ and $(a)_{+}$ is equal to $a$ if $a>0$, otherwise it is 0. If $k=m$ and $t_1<t_2$

$$\begin{aligned}&\mathrm{I}\!\mathrm{P}(\xi _1 \le t_1 , \xi _2 \le t_2, \xi \le t \mid {\varGamma }(k,m))\nonumber \\&\quad =\left( 1\wedge \left( \frac{t_1-S_{k+1}}{T_{k}}\right) _{+}\right) ^2 \mathbf {I}\{S_2\le t\}; \end{aligned}$$

(40)

if $t_2<t_1$ then the following holds

$$\begin{aligned}&\mathrm{I}\!\mathrm{P}(\xi _1 \le t_1 , \xi _2 \le t_2, \xi \le t \mid {\varGamma }(k,m))\nonumber \\&\quad =\left( 2\left( 1\wedge \left( \frac{t_1-S_{k+1}}{T_{k}}\right) _{+}\right) \left( 1\wedge \left( \frac{t_2-S_{k+1}}{T_{k}}\right) _{+}\right) -\left( 1\wedge \left( \frac{t_2-S_{k+1}}{T_{k}}\right) _{+}\right) ^2\right) \nonumber \\&\quad \quad \quad \times \, \mathbf {I}\{S_2\le t\}. \end{aligned}$$

(41)

From the steps in the proof of Theorem  2 the following equation holds

$$\begin{aligned} \mathrm{I}\!\mathrm{P}( D_{n}, \alpha , H_{\alpha }, E_2)=\mathrm{I}\!\mathrm{P}(\alpha , H_{\alpha })\sum _{(k,m)\in {\varDelta }_j(e)}\frac{N_{j}(k,m;e)}{N(n)}d_{m,k}T_k T_m e^{-\theta _0 L_n/2}. \end{aligned}$$

After combining the above results the proof of the theorem is complete.

1.7 The proof of Theorem 5

To derive expressions in the theorem, I use Eq. (26) under the limits $\theta _0\rightarrow 0,$ $a/n\rightarrow x, b/n\rightarrow y,$ $c/n\rightarrow z$ as $a,b,c$ tend to $\infty .$ Using the properties of the coalescence waiting times in the standard coalescent setting, the following formulas hold

$$\begin{aligned} \mathrm{I}\!\mathrm{E}\left( T_mT_k(0.5T_m+S_{m+1})\right)&= \frac{8}{k(k-1)m(m-1)^2},\\ \mathrm{I}\!\mathrm{E}\left( T_mT_k(0.5T_k+S_{k+1})\right)&= \frac{8}{(m(m-1))^2k(k-1)}+\frac{8}{k(k-1)^2m(m-1)},\\ \mathrm{I}\!\mathrm{E}\left( T_mT_m(0.5T_m+S_{m+1})\right)&= \frac{8(2m+1)}{(m(m-1))^3}. \end{aligned}$$

I use these formulas in Eq. (26) combined with the limits in Lemma 2 to derive analytical expressions for the expected ages of $\xi _1$ and $\xi _2,$ conditional on $\alpha =TT,$ $H_1,$ and $(x,y,z).$ In the case of $\alpha =TC$ and transition histories $H_2$ and $H_3,$ two type of substations occur $TC\rightarrow TT$ and $TC\rightarrow CC.$ I infer the expected ages of these two substation events instead of the ages of the early and late mutation events. Before using Eq. (26) in this case, I first derive an expression for computing the expected age of $\xi _{TC, TT}.$ Similar steps can be done for the expected age of $\xi _{TC, CC}.$ Hence, the following holds

$$\begin{aligned}&\mathrm{I}\!\mathrm{E}(\xi _{TC, TT}\mid (x,y,z), TC, H_2 or H_3)\\&\quad =\mathrm{I}\!\mathrm{E}(\xi _{TC, TT}\mid (x,y,z), TC, H_2)\frac{\mathrm{I}\!\mathrm{P}((x,y,z), TC, H_2)}{\mathrm{I}\!\mathrm{P}((x,y,z), TC, H_2 or H_3)}\\&\quad \quad +\mathrm{I}\!\mathrm{E}(\xi _{TC, TT}\mid (x,y,z), TC, H_3)\frac{\mathrm{I}\!\mathrm{P}((x,y,z), TC, H_3)}{\mathrm{I}\!\mathrm{P}((x,y,z), TC, H_2 or H_3)}. \end{aligned}$$

Note that

$$\begin{aligned} \mathrm{I}\!\mathrm{E}(\xi _{TC, TT}\mid (x,y,z), TC, H_2)=\mathrm{I}\!\mathrm{E}(\xi _1\mid (x,y,z), TC, H_2) \end{aligned}$$

and

$$\begin{aligned} \mathrm{I}\!\mathrm{E}(\xi _{TC, TT}\mid (x,y,z), TC, H_3)=\mathrm{I}\!\mathrm{E}(\xi _2\mid (x,y,z), TC, H_3). \end{aligned}$$

Now under the limits $a/n\rightarrow x, b/n\rightarrow y,$ $c/n\rightarrow z$ as $a, b, c$ tend to $\infty$ I derive the formulas for the experted conditional ages of $\xi _1$ and $\xi _2$ by using the limits in Lemma 2 for

$$\begin{aligned} \frac{N_{j}(k,m;e)}{\frac{N(n)}{n^2}} \end{aligned}$$

and compute the following sums

$$\begin{aligned} D_{1,0}(x,y,z)&\equiv \sum _{m=3}^\infty \sum _{k=2}^{m-1} D_1(y,k;x,m)\mathrm{I}\!\mathrm{E}\left( T_mT_k(0.5T_m+S_{m+1})\right) \\&= \frac{-8x((1+x)\log (x)-2x+2)}{(1-x)^3}, \end{aligned}$$

$$\begin{aligned} D_{1,1}(x,y,z)&\equiv \sum _{m=3}^\infty \sum _{k=2}^{m-1} D_1(y,k;x,m)\mathrm{I}\!\mathrm{E}\left( T_mT_k(0.5T_k+S_{k+1})\right) \\&= \frac{16\log (1-z)\log (x)}{(1-x)^3}+\frac{16}{(1-x)^3} \int _0^1\log (1-(y+z)t)\\&\times \left( \frac{z}{1-zt}-\frac{1}{t}\right) dt +\frac{8(x^2-y^2)\log (1-z)}{yzx(1-x)}\\&+\frac{8\log (x)(2y-x(1-x))}{y(1-x)^3},\\ D_{2,0}(x,y,z)&\equiv \sum _{m=3}^\infty \sum _{k=2}^m D_2(y,k;x,m)\mathrm{I}\!\mathrm{E}\left( T_mT_k(0.5T_k+S_{k+1})\right) \\&= -\frac{8(y^2+(1-z)(1-x)^2)\log (1-z)}{yz^3(1-x)}\\&-\frac{16}{z^2}+ \left( \frac{x}{y}-\frac{2}{1-x}\right) \frac{8\log (x)}{(1-x)^2}\\&\quad -\frac{16\mathrm{PolyLog}(2,1-x)}{(1-x)^3}+\frac{8z}{(1-x)^2}\int _0^1 \frac{G(x)-G(1-zt)}{(1-zt-x))}dt, \end{aligned}$$

where

$$\begin{aligned} G(t)&\equiv \frac{1-t^2+2t\log (t)}{t(1-t)};\\ D_{2,1}(x,y,z)&\equiv \sum _{m=3}^\infty \sum _{k=2}^m D_2(y,k;x,m)\mathrm{I}\!\mathrm{E}\left( T_mT_k(0.5T_m+S_{m+1})\right) \\&= \frac{8}{1-x}-\frac{8z\log (x)}{y(1-x)^2}+\frac{8(1-x^2+2x\log (x))}{(1-x)^3}+ \frac{8\log (1-z)}{yz}\\&\quad -\frac{40}{z^2}+\frac{8(-3+2z)\log (1-z)}{z^3}+\frac{16\mathrm{PolyLog}(2,z)}{z^3}. \end{aligned}$$

If $m=k$, the following formula holds

$$\begin{aligned} D_{2,2}(z)&\equiv \sum _{m=3}^\infty D_2(y,m;x,m)\mathrm{I}\!\mathrm{E}\left( T_m ^2(0.5T_m+S_{m+1})\right) \\&= -\frac{56}{z^2}-\frac{8(5-3z)\log (1-z)}{z^3}+\frac{16\mathrm{PolyLog}(2,z)}{z^3}. \end{aligned}$$

The derivations of the above formulas are tedious and are not shown in details. For this purpose I used Wolfram Mathematica 3.0 as helping tool. The derivations are based on the computation of the power series by transforming them into a geometric series. For example, to derive a formula for the series $\sum \frac{t^i}{i^2}$ the coefficients $1/i^2$ in the terms can be replaced by the integral $\int _0^1\int _0^1 w^{i-1} v^{i-1}dwdv$ and the summation and integration order can be changed because the terms in the series are non-negative, that is

$$\begin{aligned} \sum \frac{t^i}{i^2}=\sum t^i\int _0^1\int _0^1 w^{i-1} v^{i-1}dwdv =\int _0^1\int _0^1 t\left( \sum (tvw)^{i-1}\right) dwdv. \end{aligned}$$

Thus, the series inside of the integral is a geometric series.