Pattern formation in auxin flux

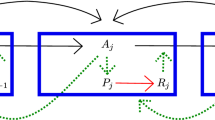
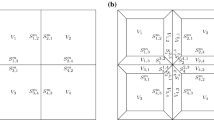
Abstract

The plant hormone auxin is fundamental for plant growth, and its spatial distribution in plant tissues is critical for plant morphogenesis. We consider a leading model of the polar auxin flux, and study in full detail the stability of the possible equilibrium configurations. We show that the critical states of the auxin transport process are composed of basic building blocks, which are isolated in a background of auxin depleted cells, and are not geometrically regular in general. The same model was considered recently through a continuous limit and a coupling to the von Karman equations, to model the interplay of biochemistry and mechanics during plant growth. Our conclusions might be of interest in this setting, since, for example, we establish the existence of Lyapunov functions for the auxin flux, proving in this way the convergence of pure transport processes toward the set of equilibrium points.

Appendix: A

1.1 A.1 Proof of the existence of the solution (Proposition 1)

In the following, we use the notation $\dot{{\varvec{a}}}$ instead of $\frac{\mathrm{d}{\varvec{a}}}{\mathrm{d}t}$.

System (2) can be written as

$$\begin{aligned} \dot{a}_i=D\sum _{k\sim i}a_k+T\sum _{k\sim i}\left(\frac{a_k}{\kappa +\sum _{j\sim k}a_j}-\frac{a_k}{\kappa +\sum _{j\sim i}a_j}-\frac{D}{T}\right)a_i. \end{aligned}$$

(30)

Let ${\varvec{a}}$ be a solution of (30) with ${\varvec{a}}(0)\in \mathbb R ^L_{\ge 0}$.

We say that the function $f:\mathbb R _+\rightarrow \mathbb R$ is instantaneously positive (i.p.) if there exists $\delta >0$ so that $f$ is strictly positive over $(0,\delta )$. If $f(0)>0$ and $f$ is continuous to the right at $0$, then $f$ is i.p.. It is also clear that if $f$ admits a strictly positive right-hand derivative at $0$, then it is i.p..

Let $U$ be the open set $U=\{{\varvec{x}}=(x_1,x_2,\ldots ,x_L)\in \mathbb R ^L;-\frac{\kappa }{2L}<x_i\}$. Since the right-hand member of (30) is continuous over $U$, the general theory of o.d.e.’s provides the existence of a solution defined over a maximal interval $0\in J^+\subset \mathbb R _+$ for any initial condition ${\varvec{a}}(0)\in U$. Moreover, the solution is unique because the right-hand member of (30) locally lipschitzian. Set for convenience

$$\begin{aligned} h_i(t)&= D\sum _{k\sim i}a_k(t)\quad \text{ and} \\ g_i(t)&= T\sum _{k\sim i}\left(\frac{a_k(t)}{\kappa +\sum _{j\sim k}a_j(t)}-\frac{a_k(t)}{\kappa +\sum _{j\sim i}a_j(t)}-\frac{D}{T}\right). \end{aligned}$$

The variation of constants formula allows us to write , $\forall t\in J^+$,

$$\begin{aligned} a_i(t)=a_i(0)e^{\int _0^tg_i(s)ds}+\int \limits _0^t h_i(u)e^{-\int _u^tg_i(v)dv}du. \end{aligned}$$

(31)

Since $a_i(0)\ge 0$, the first term in (31) is non-negative. Moreover if $a_k(t)$ is i.p. for some $k\sim i$, then according to (31), the same property holds for $a_i(t)$. In particular, if $a_k(0)>0$ for some $k\sim i$, then by continuity $a_k(t)$ is i.p. and thus also $a_i(t)$.

The case $D>0$:

Clearly, if ${\varvec{a}}(0)= {\varvec{0}}$, then the unique solution is identically $0$. Otherwise, there exists $1\le i_0\le L$ with $a_{i_0}(0)>0$ and $\forall j\sim i_0, a_j(t)$ is i.p.. Since our graph is supposed to be connected, every $i$ admits a neighbour $k\sim i$ with $a_k(t)$ i.p.. Hence, $a_i(t)$ is i.p. $\forall i,1\le i\le L$.

The preceding arguments show that for any initial condition ${\varvec{a}}(0)\in \mathbb R _{\ge 0}^L\subset U$, all components of the solution of (30) are i.p.. Let us suppose that one of them admits the value $0$ in $J^+$. Since all components are continuous and their number is finite, there exists a first time $t_0>0$ for which at least one component $a_{i_0}(t_0)=0$ and all of them are strictly positive over $(0,t_0)$. According to (31), we have

$$\begin{aligned} a_{i_0}(t_0)=0=a_i(0)e^{\int _0^{t_0}g_i(s)ds}+\int \limits _0^{t_0}h_i(u)e^{-\int _u^{t_0}g_i(v)dv}du. \end{aligned}$$

Clearly $h_i(t)>0$ over $J^+\backslash \{0\}$ and since the first term is non-negative, we conclude to $a_{i_0}(t_0)>0$, a contradiction. Therefore all $a_i(t)$ are strictly positive over $J^+\backslash \{0\}$.

The case $D=0$: If $a_i(0)>0$ , $a_i(t)$ is i.p. by continuity. In that case $a_i(t)=a_i(0)e^{\int _0^tg_i(s)ds}>0$ over $J^+$. If $a_i(0)=0$, the homogeneous equation for $a_i(t)$ admits only the zero solution, and we remove the related $i$th component from (30).

The preceding modification implies that, in both cases, solution of (30) have strictly positive components over $J^+\backslash \{0\}$. We also proved that $\forall t \in J^+$ we have:

$$\begin{aligned} \sum _{1\le i\le L}a_i(t)=\sum _{1\le i\le L}a_i(0). \end{aligned}$$

As a consequence the solution of (30) is bounded and thus the unique solution of our problem is defined over $J^+=[0,+\infty )$.

We easily check that the system $\dot{{\varvec{a}}}=f({\varvec{a}})$ is conservative, as

$$\begin{aligned} \sum _i \dot{a}_i (t)&= D \sum _i\sum _{k \sim i} (a_k -a_i)+T \sum _i \sum _{k\sim i}a_k a_i\left(\frac{N_i-N_k}{N_k N_i}\right)\\&= D \sum _i(d_i a_i-d_i a_i)+\frac{1}{2} T \sum _i\sum _{k\sim i}\frac{a_k a_i}{N_k N_i}((N_i-N_k)+(N_k-N_i))=0, \end{aligned}$$

where $N_k=\kappa +\sum _{j\sim k}a_k$, and where $d_i$ is the degree of $i$ (that is the number of neighbours of $i$).$\square$

1.2 A.2 Proof of the Jacobian matrix in the irreducible case (Proposition 3)

We first give the Jacobian, for an arbitrary ${\varvec{a}}$. We have

$$\begin{aligned} \frac{\partial f_i({\varvec{a}})}{\partial a_j} =\frac{a_i}{N_j}-\frac{a_i}{N_i}+\sum _{k\sim i}\frac{a_i a_k}{N_i^2}-\sum _{k\sim i, k\sim j}a_k \frac{a_i}{N_k^2}, \end{aligned}$$

(32)

(where the last term is due to the triangles in the graph) when $j\sim i$, that is, $i$ and $j$ are nearest neighbours. When $i=j$, one gets

$$\begin{aligned} \frac{\partial f_i({\varvec{a}})}{\partial a_i} =\sum _{k\sim i}\frac{a_k}{N_k}-a_i\sum _{k\sim i}\frac{a_k}{N_k^2} -\frac{\sum _{k\sim i}a_k}{N_i}. \end{aligned}$$

(33)

The remaining non-vanishing partial derivatives correspond to nodes $j$ located at distance 2 of $i$ in the graph, that is, to nodes $j$ such that $j\sim k$ for some $k\sim i$, $j\ne i$ but $i\not \sim j$. Then

$$\begin{aligned} \frac{\partial f_i({\varvec{a}})}{\partial a_j} =-\sum _{j\sim k,\ k\sim i}\frac{a_i a_k}{N_k^2}. \end{aligned}$$

(34)

When $N_i = N$, $\forall i$, these expressions simplify to

$$\begin{aligned} \frac{\partial f_i({\varvec{a}})}{\partial a_j} =\sum _{k\sim i}\frac{a_i a_k}{N_i^2}=\frac{N-\kappa }{N^2}a_i-\frac{a_i}{N^2}\sum _{k\sim i, k\sim j}a_k. \end{aligned}$$

If $j\sim i$,

$$\begin{aligned} \frac{\partial f_i({\varvec{a}})}{\partial a_i}=-\frac{N-\kappa }{N^2}a_i, \end{aligned}$$

and

$$\begin{aligned} \frac{\partial f_i({\varvec{a}})}{\partial a_j} =-\sum _{k\sim i, k\sim j}\frac{a_i a_k}{N_k^2}=-\frac{a_i}{N^2}\sum _{k\sim i, k\sim j}a_k, \end{aligned}$$

if $j\sim k$ for some $k\sim i$, $j\ne i$ but $i\not \sim j$.

Consider the sub-matrix ${\varvec{M}}$ given by ${\varvec{M}}=(\partial f_i({\varvec{a}})/\partial a_j)_{j\sim i}$. Let $\text{ diag}({\varvec{a}})$ be the diagonal matrix whose diagonal elements are given by ${\varvec{a}}$. The perturbation associated with the triangles contained in the graph is represented by the term $-\frac{a_i}{N^2}\sum _{k\sim i, k\sim j}a_k$ in $\frac{\partial f_i({\varvec{a}})}{\partial a_j}$ for $j\sim i$, and the related matrix is given by

$$\begin{aligned} \!\!\!\!\!\! \left(-\frac{a_i}{N^2}\sum _{k\sim i, k\sim j}a_k\right)\gamma _{ij}&= \left(-\frac{a_i}{N^2}\sum _{k}\gamma _{ik}a_k\gamma _{kj}\right)\gamma _{ij}\\ \quad&= \left( -\frac{1}{N^2}\left(\text{ diag}({\varvec{a}}){\varvec{\varGamma }} \text{ diag}({\varvec{a}}){\varvec{\varGamma }}-\mathrm{diag}( \text{ diag}({\varvec{a}}){\varvec{\varGamma }} \text{ diag}({\varvec{a}}){\varvec{\varGamma }})\right)_{ij}\right)\gamma _{ij}\\ \quad&= \left( -\frac{1}{N^2}(\text{ diag}({\varvec{a}}){\varvec{\varGamma }} \text{ diag}({\varvec{a}}){\varvec{\varGamma }})_{ij}+\frac{N-\kappa }{N^2}\text{ diag}({\varvec{a}})_{ij}\right)\gamma _{ij}.\\ \end{aligned}$$

The matrix ${\varvec{M}}$ is now given by

$$\begin{aligned} {\varvec{M}}=\frac{\text{ diag}({\varvec{a}})}{N^2}(N-\kappa )({\varvec{\varGamma }}-\mathbf{id})- \frac{1}{N^2}(\text{ diag}({\varvec{a}}){\varvec{\varGamma }} \text{ diag}({\varvec{a}}) {\varvec{\varGamma }}-(N-\kappa )\text{ diag}({\varvec{a}}))\circ {\varvec{\varGamma }}, \end{aligned}$$

where $\circ$ represents the matrix Hadamard product, i.e. the multiplication component by component.

Similarly, the perturbation of ${\varvec{M}}$ by $\left(\frac{\partial f_i({\varvec{a}})}{\partial a_j}\right)_{i\sim k, k\sim j, i\not \sim j, i\ne j}$ can be written as

$$\begin{aligned}&\left(-\frac{a_i}{N^2}\sum _{\begin{array}{c} k\sim i, k\sim j,\\ \ i \not \sim j, i\ne j \end{array}} a_k \right)\gamma _{ij}= \left(-\frac{a_i}{N^2}\sum _{k}\gamma _{ik}a_k\gamma _{kj}\right)(1-\gamma _{ij}-\mathbf{id}_{ij})\\&\qquad = \left( -\frac{1}{N^2}(\text{ diag}({\varvec{a}}){\varvec{\varGamma }} \text{ diag}({\varvec{a}}){\varvec{\varGamma }})_{ij}+\frac{N-\kappa }{N^2}\text{ diag}({\varvec{a}})_{ij}\right)(1-\gamma _{ij}-\mathbf{id}_{ij}).\\ \end{aligned}$$

The related Jacobian is thus given by ${\varvec{M}}+\left(\frac{\partial f_i({\varvec{a}})}{\partial a_j}\right)_{i\sim k, k\sim j, i\not \sim j, i\ne j}$, that is

$$\begin{aligned} \mathrm{d}f({\varvec{a}})&= \frac{\text{ diag}({\varvec{a}})}{N^2}(N{-}\kappa )({\varvec{\varGamma }}{-}\mathbf{id}){-} \frac{1}{N^2}\left(\text{ diag}({\varvec{a}}){\varvec{\varGamma }} \text{ diag}({\varvec{a}}) {\varvec{\varGamma }}-(N-\kappa )\text{ diag}({\varvec{a}})\right) \circ {\varvec{\varGamma }}\\&- \frac{1}{N^2}\left(\text{ diag}({\varvec{a}}){\varvec{\varGamma }} \text{ diag}({\varvec{a}}) {\varvec{\varGamma }}-(N-\kappa )\text{ diag}({\varvec{a}})\right) \circ ({\varvec{1}}-{\varvec{\varGamma }}-\mathbf{id})\\&= \frac{\text{ diag}({\varvec{a}})}{N^2}(N{-}\kappa )({\varvec{\varGamma }}-\mathbf{id})- \frac{1}{N^2}\left(\text{ diag}({\varvec{a}}){\varvec{\varGamma }} \text{ diag}({\varvec{a}}) {\varvec{\varGamma }} -(N-\kappa )\text{ diag}({\varvec{a}})\right) \circ ({\varvec{1}}-\mathbf{id})\\&= \frac{\text{ diag}({\varvec{a}})}{N^2}(N-\kappa )({\varvec{\varGamma }}-\mathbf{id})- \frac{1}{N^2}(\text{ diag}({\varvec{a}}){\varvec{\varGamma }} \text{ diag}({\varvec{a}}) {\varvec{\varGamma }}-(N-\kappa )\text{ diag}({\varvec{a}})),\\ \end{aligned}$$

where ${\varvec{1}}$ is the matrix composed of ones only. The last equality is a consequence of the fact that the diagonal of $\text{ diag}({\varvec{a}}){\varvec{\varGamma }} \text{ diag}({\varvec{a}}) {\varvec{\varGamma }}-(N-\kappa )\text{ diag}({\varvec{a}})$ vanishes. Hence,

$$\begin{aligned} \mathrm{d}f({\varvec{a}})=\frac{\text{ diag}({\varvec{a}}){\varvec{\varGamma }}}{N^2}((N-\kappa )\mathbf{id}-\text{ diag}({\varvec{a}}){\varvec{\varGamma }} ) =\frac{\text{ diag}({\varvec{a}}){\varvec{\varGamma }}}{N^2}( c\ \mathbf{id}-\text{ diag}({\varvec{a}}){\varvec{\varGamma }} ), \end{aligned}$$

proving the result.

1.3 A.3 Proof of the spectrum in the reducible case (Proposition 4)

Set $I=\{i \in \varLambda : a_i=0\}$, and consider the subgraphs $\gamma _p$ of $G$ induced by the nodes of $J=\varLambda \setminus I$, with $\gamma _p=(\varLambda _p,E_p)$, $1 \le p \le P$. For any related equilibrium point ${\varvec{a}}$, the restrictions ${\varvec{a}}\vert _{\gamma _p}$ satisfy the linear systems ${\varvec{\varGamma }}_{\gamma _p}{\varvec{a}}\vert _{\gamma _p}=c_{\gamma _p} {\varvec{1}}\vert _{\gamma _p}$. Set $N_{\gamma _p}=c_{\gamma _p}+ \kappa$.

Equations (32)–(34) allow the computation of the entries of the Jacobian matrix. By first looking at the diagonal entries, for $i\in \varLambda _p$, one has

$$\begin{aligned} \frac{\partial f_i({\varvec{a}})}{\partial a_i} = - a_i \frac{N_{\gamma _p}-\kappa }{N_{\gamma _p}^2}, \end{aligned}$$

providing the diagonal entry of the Jacobian of $f\vert _{\gamma _p}({\varvec{a}}\vert _{\gamma _p})$. When $i\not \in \varLambda _p$, a similar computation yields

$$\begin{aligned} \frac{\partial f_i({\varvec{a}})}{\partial a_i} = \sum _{k\sim i} \frac{a_k}{N_k} - \frac{N_i-\kappa }{N_i}. \end{aligned}$$

We then compute the entries $(i,j)$ for $j \sim i$, $i,j \in \varLambda _p$ and $1\le p \le P$:

$$\begin{aligned} \frac{\partial f_i({\varvec{a}})}{\partial a_j} =a_i \frac{N_{\gamma _p} - \kappa }{N_{\gamma _p}^2}-\sum _{k\sim i, k\sim j} a_k \frac{a_i}{N_k^2} = a_i \frac{N_{\gamma _p} - \kappa }{N_{\gamma _p}^2}-\sum _{k\sim i, k\sim j, k \in \varLambda _p} \frac{a_k a_i}{N_{\gamma _p}^2} , \end{aligned}$$

This corresponds to the $(i,j)$ entry of the Jacobian of $f\vert _{\gamma _p}({\varvec{a}}\vert _{\gamma _p})$. Similarly, when $i \in \varLambda _p$ for some $p$ and $j \not \in \varLambda _p$

$$\begin{aligned} \frac{\partial f_i({\varvec{a}})}{\partial a_j} = \frac{a_i}{N_j}- \frac{a_i}{N_{\gamma _p}} {+} \sum _{k\sim i} \frac{a_i a_k}{N_{\gamma _p}^2}{-}\sum _{\begin{array}{c} k\sim i, k\sim j, \\ k \in \varLambda _p \end{array}} \frac{a_k a_i}{N_{\gamma _p}^2} = \frac{a_i}{N_j} - a_i \frac{\kappa }{N_{\gamma _p}^2} - \frac{a_i}{N_{\gamma _p}^2} \sum _{\begin{array}{c} k\sim i, k\sim j,\\ k \in \varLambda _p \end{array}} a_ k . \end{aligned}$$

Finally, when $i,j \not \in \cup _p\varLambda _p$, or equivalently when both $i$ and $j$ belongs to $I$

$$\begin{aligned} \frac{\partial f_i({\varvec{a}})}{\partial a_j}=0. \end{aligned}$$

We next consider $(i,j)$ entries where $j$ is at a distance 2 of $i$ in the graph $G$, that is when $j$ is such that $j\sim k$ for some $k\sim i$, $j\ne i$ and $j \not \sim i$. For $i,j,k \in \varLambda _p$

$$\begin{aligned} \frac{\partial f_i({\varvec{a}})}{\partial a_j}=-a_i \sum _{j \sim k, k \sim i} \frac{a_k}{N_{\gamma _p}^2}. \end{aligned}$$

This is the $(i,j)$ entry of the Jacobian of $f\vert _{\gamma _p}({\varvec{a}}\vert _{\gamma _p})$.

Similarly, for $i,k \in \varLambda _p, j\not \in \varLambda _p$ ($\Rightarrow j \in I$)

$$\begin{aligned} \frac{\partial f_i({\varvec{a}})}{\partial a_j}=-a_i \sum _{j \sim k, k \sim i} \frac{a_k}{N_{\gamma _p}^2} . \end{aligned}$$

Next, for $i \, \text{ or} \, k \not \in \varLambda _p, \forall j \in \varLambda$

$$\begin{aligned} \frac{\partial f_i({\varvec{a}})}{\partial a_j}=0. \end{aligned}$$

Permuting conveniently the indices, the Jacobian $\mathrm{d}f({\varvec{a}})$ can be written as

$$\begin{aligned} \mathrm{d}f({\varvec{a}}) = \begin{pmatrix} {\varvec{d}_n}&{\varvec{0}} \\ *&\mathrm{d}f^{\gamma } \end{pmatrix} \end{aligned}$$

where ${\varvec{d}_n}$ is a diagonal matrix $n \times n$ with entries $\lambda _i:= \sum _{k\sim i} \frac{a_k}{N_k} - \frac{N_i-\kappa }{N_i}$, for $i \in I$, and $\mathrm{d}f^{\gamma }$ is a block diagonal matrix, each block being equal to the Jacobian of $f$ restricted on each subgraph $\gamma _p$. The permutation allows grouping of all indices $i \in I$ in the same block, and all indices related to the subgraphs $\gamma _p$ are also arranged together. It follows that the spectrum of $\mathrm{d}f({\varvec{a}})$ is :

$$\begin{aligned} \mathrm{spec}(\mathrm{d}f({\varvec{a}}))= \bigcup _{p=1}^P \mathrm{spec}\left(\mathrm{d}f\vert _{\gamma _p}({\varvec{a}}\vert _{\gamma _p})\right) \cup \left\{ \sum _{k\sim i} \frac{a_k}{N_k} - \frac{N_i-\kappa }{N_i}, i\in I \right\} . \end{aligned}$$

1.4 A.4 Proof of Proposition 5

To prove the Proposition 5, we will use the following Proposition, see Gabriel et al. (1989).

Proposition 9

Let $f:\mathbb R _+\rightarrow \mathbb R$ be twice differentiable and bounded together with $\ddot{f}$. If, as $n\rightarrow +\infty$, $t_n\uparrow +\infty$ and $f(t_n)\rightarrow \liminf _{t\rightarrow +\infty } f(t)$ (or $f(t_n)\rightarrow \limsup _{t\rightarrow +\infty } f(t)$), then $\dot{f}(t_n)\rightarrow 0$.

Proof

If $a_k(0)=0$ for all $1\le k\le L$, then the unique solution is identically zero. Otherwise $\sum _{k=1}^L a_k(0)>0$. Let us suppose that for some $i\in \{1,\ldots ,L\}$,

$$\begin{aligned} \liminf _{t\rightarrow +\infty }a_i(t)=0. \end{aligned}$$

Let us introduce the notation $\underline{a}_i=\liminf _{t\rightarrow +\infty }a_i(t)$. Since $a_i(t)$ is bounded together with its second derivative, the preceding proposition applies and for any sequence $t_n\uparrow +\infty$ such that $a_i(t_n)\rightarrow \underline{a}_i$, we have $\dot{a}_i(t_n)\rightarrow 0$ as $n\rightarrow +\infty$. Every $a_k(t_n)$ being bounded in the right-hand member of the equation for $\dot{a}_i(t_n)$, we conclude that $\lim _{n\rightarrow +\infty }D\sum _{k\sim i}a_k(t_n)=0$. The non-negativity of each $a_k(t_n)$ entails $\lim _{n\rightarrow +\infty }a_k(t_n)=0=\underline{a}_k$ for every ${k\sim i}$. According to the above proposition, $\lim _{n\rightarrow +\infty }\dot{a}_k(t_n)=0$ for every ${k\sim i}$ and since the graph is connected, repeating the same argument provides $\lim _{n\rightarrow +\infty }\dot{a}_j(t_n)=0$ for every $j\in \{1,\ldots ,L\}$. Thus $0=\lim _{n\rightarrow +\infty }\sum _{1\le j\le L}a_j(t_n)=\sum _{k=1}^L a_k(0)>0$, a contradiction. $\square$