Introduction

Groundwater access from the Ogallala aquiferFootnote 1 is the game-changer for semi-arid Texas High Plains (THP) agriculture overcoming the uncertainty associated with irrigation (Hornbeck and Keskin 2014). Currently, THP produces ~ 55% of the Texas corn and > 20% of the US cotton (USDA-NASS 2021), making this region a vital production hub for both food and fiber. Here, crop irrigation alone accounts for as high as 90% of total groundwater withdrawals. The withdrawals arise due to two main reasons: first, irrigation boosts crop yield by more than twofold compared to dryland farming (Lascano and Sojka 2007); second, private pumping cost is less than the social cost of water withdrawal (Peterson et al. 2003). This stimulated the ‘tragedy of commons’ in groundwater use in THP, depleting water levels by more than 50 m since the 1950s (McGuire 2014).Footnote 2 Furthermore, high dependence on irrigation and episodic droughts in THP drains aquifer and affects crop production (Nie et al. 2018), thus subjecting irrigated agriculture to increasing risks. Increasing irrigation water demand and depleting groundwater corroborated by reduced rainfall, megadroughts, and higher temperatures from changing weather patterns will likely aggravate future impacts (Cook et al. 2015; Nielsen‐Gammon et al. 2020). This presents enormous challenges to adaptation to future water needs in agriculture and other competing sectors such as households and industries. Thus, strengthening agricultural resiliency to such impacts exacerbated by climate changes is essential for sustainability of aquifer levels and irrigation-dependent agricultural production in the THP.

Both anthropogenic and climate-induced shifts will bring changes in irrigation water availability, and subsequently, the shadow price of water (Yoo et al. 2014). Hence, understanding farmers’ capacity to adjust to the changes mentioned above necessitates insight into the responsiveness of irrigation water demand to price changes. Moreover, knowledge of how water demand and subsequent crop production vary is essential for assessing feasible policy solutions for THP concerning its irrigated agriculture. Against this backdrop, estimating the price elasticity of irrigation water demand could provide valuable economic insight to determine the usefulness of price-related policy alternatives aiding in water conservation.

This study is conducted with two objectives: (1) to estimate the elasticity of water demand in the THP region for two major irrigated crops—corn and cotton, and (2) to assess the influence of water price on major inputs used in irrigated corn and cotton. To accomplish these objectives, we apply normalized, restricted translog profit function and corresponding, derived demand functions to the data of irrigated corn and cotton from the THP. Here, we show that the water price serves as a critical tool in determining irrigation water demand in corn and cotton. There are two main contributions to the existing literature. First, although several papers have reported the price elasticity of water demand, few have directly estimated the elasticities using a longer timeframe, which is essential for policy building. Here, we provide an empirical estimate of elasticity using annual county-level data from 1998 to 2020. Second, estimates of input use elasticities for highly valued crops such as corn and cotton are not available using long-run data. Here we provide input demand elasticities for these two major crops in the THP. Given the knowledge gap about crop-specific input use elasticities and increasing cotton bandwagon from higher expected profit and relatively lower water demand (Ledbetter 2020), our paper will serve as a useful reference. On the policy front, our analysis provides empirical results for output supply and input demand functions, especially of water, which complements the water conservation-related policymaking process.

The rest of the paper proceeds as follows: the next section provides an overview of elasticity and irrigation water demand. “Data and methods” section provides a detailed description about the study area, data sources, and empirical specification. “Results and discussion” section reports main results along with discussion about the findings. “Conclusion and policy implications” section concludes the paper with policy implications.

Overview of elasticity and irrigation water demand

Price elasticity of demand (η) measures how the quantity demanded of a factor changes with its price change. The price elasticity of irrigation water demand assesses how the relative profit-maximizing amount of irrigation water demanded changes as relative water price changes (Lu et al. 2004). Like demand elasticity for any factor, the price elasticity of irrigation water demand is measured in absolute terms, which indicates the magnitude of effect induced by the change in water price on farmers’ irrigation water use.Footnote 3 Previous studies have employed mathematical programming approaches (Scheierling et al. 2004), field experiments (Hooker and Alexander 1998), and econometric techniques (Hendricks and Peterson 2012) to estimate the price elasticity of irrigation water demand. Existing elasticity estimates are either based on aggregate (state or county-level) or field-level data (Frank and Beattie 1979; Hendricks and Peterson 2012; Nieswiadomy 1985).

Most studies on the elasticity of irrigation water demand demonstrate a negative relationship between the cost of water and its intra-seasonal use (Gonzalez-Alvarez et al. 2006; Ogg and Gollehon 1989). A study on row crop farmers of Georgia by Mullen et al. (2009) reports that irrigation water demand is moderately affected by water price with elasticity ranging from – 0.01 to – 0.17. Schoengold et al. (2006) show that the own-price elasticity of water is – 0.787, implying that irrigation water demand is more elastic to water price than indicated by other studies. Similarly, based on data from the THP region, Adusumilli et al. (2011) report water demand elasticity as – 0.138 and 0.003 for corn and cotton, respectively. Most studies report water demand elasticity in the inelastic range, maybe due to the data representing a shorter time frame. However, it is long-run elasticities that matter for policy purposes, and they are larger than the mean estimates of the short-run elasticities (Scheierling et al. 2006). Based on ten years of acreage data from two South Central Idaho counties, Elbakidze et al. (2017) estimated the average short and long-run price elasticities for irrigation water demand and reported that short-run demand is less elastic than long-run demand. They report price elasticities ranging from – 1.12 up to – 4.9 for the short run and long run, respectively. Similarly, de Bonviller et al. (2020) use long-run market data and show that groundwater demand is price elastic (η = – 1.05).

Understanding the price elasticity of irrigation water demand could guide policymakers in speculating the ramifications of proposed irrigation pricing policies and gauge the efficacy of those policies in promoting water conservation (Bruno and Jessoe 2021b; Grafton et al. 2020; Njuki and Bravo-Ureta 2018). According to Chu and Grafton (2020), water pricing can significantly reduce water use (~ 84%) with a relatively lesser impact on the average profit (~ 17%) of farmers in water-scarce areas. The usefulness of price intervention to lessen groundwater use (~ 33%) is also demonstrated by Smith et al. (2017). Apart from pricing, water use restrictions through quota can also lower water use (~ 26%) (Drysdale and Hendricks 2018). However, considerations of perverse consequences, irrigation efficiency, institutional incentives, and externalities are equally important to designing groundwater use policy (Lin 2016). Besides that, providing normative appeals and social comparisons could have a sustained impact on water demand (Ferraro et al. 2011). For instance, providing farmers with water use reports which include social comparisons could promote prosocial behavior and significantly bring down average water use for irrigation. Optimal management likely increases gains (~ 30%) under climate change and technical progress.

The physical scarcity of water supplies for agricultural use and the rising cost to pump water reinforces the need to estimate farmers' responses to relative water prices credibly. Water price also influences the adoption of water-saving technology (Dinar and Yaron 1992). However, several studies, including Adusumilli et al. (2011), Hendricks and Peterson (2012), Mullen et al. (2009), and Suárez et al. (2018), report that elasticity estimates of irrigation water demand are inelastic to water price. The authors assert a lack of incentives to opt for water conservation and rational use (i.e., using water to meet the general objective of economic efficiency and environmental conservation). Interestingly, there are claims that below a threshold price, irrigation water demand is inelastic but elastic above that level where farmers respond by decreasing water use through substitution or shifting to high value-added crops, or implementing dryland farming (Varela-Ortega et al. 1998; Yang et al. 2003). For water-intensive crops, an increase in water price above a certain level makes it non-optimal for status-quo cultivation practices and redirects the farmers to management actions (Weinberg et al. 1993). These studies further reinforce that a comprehensive understanding of region-specific irrigation water demand is essential to designing an effective water use policy.

Data and methods

Study area

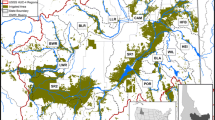
The study area includes 39 counties of Northern and Southern High Plains agricultural districts in Texas (Fig. 1).Footnote 4 These include major parts of High Plains Underground Water Conservation District (HPWD), Panhandle Groundwater Conservation District, and North Plains Groundwater Conservation District on Ogallala aquifer, Texas. Major crops here include corn, cotton, wheat, and sorghum. Due to the semi-arid climate, farmers rely on irrigation for higher yields (Segarra and Feng 2016). This region is chosen due to its dependence on non-renewable groundwater of the Ogallala aquifer for the irrigation of major summer crops, including corn and cotton. THP signals depleting well yield and surging pumping cost owing to increasing lift and annual extraction limits. These pressing issues provide the impetus to evaluate the effect of pricing and related policy solutions on promoting the sustainable use of groundwater (Adusumilli et al. 2011).

Fig. 1
figure 1

Map of Texas showing counties in the High Plains region

Full size image

Data

The study of irrigation water demand would be more promising with actual farm-level input use and corresponding output production data. However, such micro-data are not publicly available owing to privacy concerns. Therefore, we pursue this study based on annual county-level data of two major irrigated crops—corn and cotton—in the THP for the crop years 1998–2020.

We obtained annual data on crop acreage and irrigation water use in the THP counties from the historical agricultural irrigation water use estimates provided by the Texas Water Development Board (TWBD 2021). There is currently no direct evidence of an explicit groundwater irrigation water price in Texas agriculture due to the ‘absolute ownership’ doctrine or ‘rule-of-capture.’ Therefore, the price of irrigation water is attributed to the expense of energy required to extract an acre-inch of water from the underground water table to the surface. We use energy cost per acre-inch of irrigation as the water price in this study following Hendricks and Peterson (2012), Pfeiffer and Lin (2014), and Sampson et al. (2021). Irrigation cost is equal to the energy cost, which is a function of pumping water level, pressure head, pumping efficiency, and energy-use efficiency (Mieno and Brozović 2017). Thus, the per acre-inch cost of irrigation reflects both the well-depth and changes in energy price. We use energy cost per acre-inch of irrigation as the water price data from the irrigated corn and cotton production budgets provided by the Texas A&M AgriLife Extension (2020).

Furthermore, fertilizer use and fertilizer price data were obtained from the Economic Research Service of the US Department of Agriculture (USDA-ERS 2019). Fertilizer price in the case of corn was calculated as the weighted average price of three commonly used fertilizers: liquid phosphorus (P), anhydrous ammonia (ANH3), and liquid nitrogen. We considered the weighted average price of liquid phosphorus (P) and liquid nitrogen as the fertilizer price for cotton. Labor wage data for corn and cotton enterprise were obtained at the county level from the US Bureau of Labor Statistics (BLS 2021). Labor input comprised all forms of labor: irrigation labor, machinery labor (tractors/self-propelled), and other labor. Labor hours data for irrigated corn and cotton were obtained from crop and livestock budgets (1998–2020) of Texas A&M AgriLife Extension (2020). Similarly, crop price and county-level yield data were obtained from the National Agricultural Statistics Service database (NASS 2020). All prices and revenues were converted into 2015 dollars based on historical GDP deflator data from the USDA Economic Research Service.Footnote 5 Precipitation and heating degree days (HDD)Footnote 6 data for corn and cotton cropping seasonFootnote 7 in the THP region used in this study is based on the Parameter-elevation Regressions on Independent Slopes Model (PRISM) Climate Database (PRISM Climate Group 2021).

All costs, revenues, and profits were calculated on a per-county basis. Variable costs were obtained by summing major input costs—fertilizer cost, water cost, and labor cost. Restricted profit was obtained by subtracting the total variable cost from total revenue. We restrict our analysis to Bt corn for grain and cotton that are irrigated using natural gas because natural gas is a common irrigation fuel in the THP. The observations lacking acreage and water use data for corn and cotton were dropped before further analysis. The THP counties reporting > 1000 acres area under corn or cotton production were only considered during the final analysis. The variables used in the study are listed in Table 1.

Table 1 Summary statistics of variables used in the study
Full size table

Model

We model each county as if it is a perfectly competitive firm under an assumption that a set of producers within a given county act akin to a price-taking, profit-maximizing firm with a county-level production function. The county-level production function is represented by:

$$q = f\left( {x,z} \right),$$
(1)

where q is the output quantity and x and z denote the vector of variable and exogenous factors, respectively. Under rationality condition, the general profit function can be expressed as:

$$\pi = pq- w^{\prime} x,$$
(2)

where π denotes profit, p is the output price, and w′ denotes a transposed vector of input prices. A rational producer always chooses the level of variable factors and output that will maximize the profit of the firm. This profit maximization problem can be algebraically expressed as:

$${}_{x, q}^{\max } pq - w^{\prime}x\,{\text{subject to}}\,q = f(x,z).$$
(3)

The solution of Eq. (3) provides a set of input demand and output supply functions as:

$$x = x\left( {p,w,z} \right)\,{\text{for input demand, and}}$$
(4)
$$q = q\left( {p,w,z} \right)\,{\text{for output supply}}.$$
(5)

Substituting the values from Eqs. (4) and (5) in (2), we get the profit maximization level of input use and output supply as:

$$\pi = p.q(p,w,z) -w^{\prime} .x\left( {p,w,z} \right).$$
(6)

By differentiating this profit function with respect to variable input price (\(w_i\)) and output price (p), we obtain the inverse input demand function and output supply function as:

$$x_i^* = - \frac{\partial \pi }{{\partial w_i }} = x^* \left( {p, w, z} \right),$$
(7)
$$q^* = \frac{\partial \pi }{{\partial p}} = q^* \left( {p, w, z} \right).$$
(8)

We assume irrigation water demand for given crops in the THP region as a function of its own price, price of output, price of other variable inputs, and exogenous factors. We use a flexible functional form to measure the price elasticity of irrigation water demand. The framework is mostly based on the classical work of Sidhu and Baanante (1981) and is explained below.

Translog profit function

The translog production function is a widely used flexible specification to quantify the relationship between inputs and outputs. The widespread use of translog function in the empirical analysis is due to its underlying simplicity and no imposition of a priori restrictions on elasticities of substitution and returns to scale (Kim 1992). This flexibility allows elasticities of factors to depend on factor level, unlike the Cobb–Douglas function, where factor demand elasticities are constant across given input (Christensen et al. 1973). Moreover, it satisfies the assumption of price homogeneity by imposing restrictions on the estimated parameters (Reynaud 2003). Homogeneity relies on the fact that only relative prices matter than the actual price of inputs and output.

Here, we employ a translog profit function to assess the responsiveness of inputs and output to prices and other exogenous factors as there is a dual association between a profit function and an intrinsic production function (Lau 1978). The profit function model is also advantageous because it is framed as a function of prices and fixed factors, which are exogenous. Hence, they are shielded from likely endogeneity problems associated with a given production function model (Lau and Yotopoulos 1972). The empirical specification of the translog profit function used in our study is as follows (Christensen et al. 1973; Diewert 1974):

$$\begin{aligned} \ln \pi^{\prime} & = \alpha_0 + \mathop \sum \limits_{i = 1}^3 \alpha_i \ln P_i^{\prime} + \frac{1}{2}\mathop \sum \limits_{i = 1}^3 \mathop \sum \limits_{h = 1}^3 \gamma_{ih} \ln P_i^{\prime} \ln P_h^{\prime} \\ & \quad + \frac{1}{2}\mathop \sum \limits_{i = 1}^3 \mathop \sum \limits_{k = 1}^2 \delta_{ik} \ln P_i^{\prime} \ln Z_k + \mathop \sum \limits_{k = 1}^2 \beta_k \ln Z_k \\ & \quad + \frac{1}{2}\mathop \sum \limits_{k = 1}^2 \mathop \sum \limits_{j = 1}^2 \theta_{kj} \ln Z_k \ln Z_j + \varphi *D + \tau *T + v, \\ \end{aligned}$$
(9)

where \(\pi^{\prime}\) = restricted profit normalized by the price of output (\(P_y\)); \(P_i^{\prime}\) = price of ith input (\(P_i\)) normalized by the output price (\(P_y\)); i = 1: fertilizer price, i = 2: water price, i = 3: labor wage; \(Z_k\) = quantity of exogenous input (k), k = 1: total precipitation, k = 2: total heating degree days above threshold temperature; D = county dummy; T = time trend; v = random error; ln = natural logarithm; and \(\alpha_0\), \(\alpha_i\), \(\gamma_{ih}\), \(\delta_{ik}\), \(\beta_k\), \(\theta_{kj}\), \(\varphi\), \(\tau\) are the parameters to be estimated.

Using Shepherd’s Lemma, we obtain derived demand equations. The corresponding share equations for different inputs are expressed as (Sidhu and Baanante 1981):

$$S_i = - \frac{P_i X_i }{\pi } = \frac{\delta \ln \pi^{\prime} }{{\delta P_i^{\prime} }} = \alpha_i + \mathop \sum \limits_{h = 1}^3 \gamma_{ih} \ln P_h^{\prime} + \mathop \sum \limits_{k = 1}^2 \theta_{ik} \ln Z_k .$$
(10)

Similarly,

$$S_y = \frac{P_y X_y }{\pi } = 1 + \frac{\delta \ln \pi^{\prime} }{{\delta P_y }} = 1 - \mathop \sum \limits_{i = 1}^3 \alpha_i - \mathop \sum \limits_{i = 1}^3 \mathop \sum \limits_{h = 1}^3 \gamma_{ih} \ln P_i^{\prime} - \mathop \sum \limits_{i = 1}^3 \mathop \sum \limits_{k = 1}^2 \theta_{ik} \ln Z_k ,$$
(11)

where \(S_i\) is the share of ith input, \(S_y\) is the share of output, \(X_i\) denotes the quantity if the input is i, and y is the level of output. Different input and output shares form a singular system of equations (by definition, \(S_y - \sum S_i = 1\)); therefore, we dropped the output share from the equation. The profit function and variable input share equations are estimated simultaneously using seemingly unrelated regression (SURE) (Zellner 1962) with iterations to ensure consistent parameter estimates. The use of iterations provides maximum likelihood estimates. We also impose 18 symmetry constraints across equations to ensure the equality of parameters.

The own-price elasticity of demand for ith variable input (\(\eta_{ii}\)) is calculated as (Sidhu and Baanante 1981):

$$\eta_{ii} = - S_i - \frac{{\gamma_{ii} }}{S_i } - 1,\,{\text{for all}}\,i,$$
(12)

where \(S_i\) represents ith share equation at the sample mean.

Similarly, the cross-price elasticity of demand for ith variable input in reference to the price of hth variable input (\(\eta_{ih}\)) is calculated as:

$$\eta_{ih} = - S_h - \frac{{\gamma_{ih} }}{S_i },\,{\text{for}}\,i \ne h .$$
(13)

The elasticity of demand for ith variable input with output price \(P_y\) (\(\eta_{iy}\)) is calculated as:

$$\eta_{iy} = S_y + \mathop \sum \limits_{i = 1}^m \frac{{\gamma_{ih} }}{S_i } ,$$
(14)

where \(S_y\) denotes the output share at the sample mean.

The elasticity of demand for ith variable input relating to kth fixed factor (\(\eta_{ik}\)) is calculated as:

$$\eta_{ik} = \left( {\beta_k + \delta_{ik} \ln P_i^{\prime} + \mathop \sum \limits_{k = 1}^2 \theta_{kj} \ln Z_j } \right) - \frac{{\delta_{ik} }}{S_i } .$$
(15)

Likewise, the elasticity of output supply concerning kth fixed input (\(\eta_{yk}\)) is calculated as:

$$\eta_{yk} = \left( {\beta_k + \mathop \sum \limits_{i = 1}^3 \delta_{ik} \ln P_i^{\prime} + \mathop \sum \limits_{k = 1}^2 \theta_{kj} \ln Z_j } \right) + \frac{{\sum_{i = 1}^3 \delta_{ik} }}{S_y } .$$
(16)

The elasticity of output supply regarding the price of ith variable input (\(\eta_{yi}\)) is calculated as:

$$\eta_{yi} = - S_i - \frac{{\sum_{i = 1}^3 \gamma_{ih} }}{S_y }.$$
(17)

Finally, the elasticity of output supply with its own price \(P_y\) (\(\eta_{yy}\)) is calculated as:

$$\eta_{yy} = \mathop \sum \limits_{i = 1}^3 S_i + \frac{{\sum_{i = 1}^3 \sum_{h = 1}^3 \gamma_{ih} }}{S_y }.$$
(18)

Results and discussion

The summary statistics of the different variables used in our study are presented in Table 1. The values of variables such as restricted profit, total variable costs, precipitation, and yield are widely dispersed revealing high heterogeneity in costs, returns, and output production in the THP. The relative shares of different variable inputs in corn and cotton production along with their relative price are presented in Figs. 2 and 3. These figures show that the irrigation water cost constitutes one of the major shares of corn (~ 0.28) and cotton (~ 0.43) production inputs. Regarding the natural properties of the translog profit function, homogeneity in prices was auto imposed because of the use of the normalized specification. Monotonicity holds when the estimated output share is positive and the input share is negative in a translog model. This holds in our case with output shares equal to 1.58 and 1.80 for corn and cotton, respectively (Table 2). Moreover, all estimated input shares are negative at chosen approximation point. We also check for convexityFootnote 8 and find that this property holds for most of the output prices. We impose symmetry restrictions and conclude that sufficient evidence is available on the farmers’ profit-maximizing nature with respect to normalized prices of the variable inputs following Sidhu and Baanante (1981).

Fig. 2
figure 2

Changes in (a) factor cost-share and (b) factor price in Texas High Plains corn production

Full size image
Fig. 3
figure 3

Changes in (a) factor cost-share and (b) factor price in Texas High Plains cotton production

Full size image
Table 2 Shares of different variable inputs and output in corn and cotton production
Full size table

Table 3 presents the parameter estimates of the translog profit function estimated jointly with three variable input share equations using the iterated SURE procedure. For corn and cotton, eight variables are significantly different from zero at a 10% significance level. The coefficients of all variable inputs, except water price in cotton, are less than unity in the profit function, implying that restricted profit is inelastic to changes in input price. This also implies that the percentage change in profit from corn and cotton production is less than the percentage change in variable inputs’ price. Similarly, the negative values of variable input price coefficients in Table 3 indicate that lower prices of such inputs increase profit levels from corn and cotton production. We conduct a statistical test to test for the Cobb–Douglas hypothesis—that is, all second-order coefficients, \({\upgamma }_{ih}\) and \(\delta_{ik}\), in Eq. (9) be zero. We reject the null hypothesis as per the result obtained from χ2-test for both corn (χ2 (12) = 2046.27***) and cotton (χ2 (12) = 116.61***). The estimated results suggested that the translog model performs better than the Cobb–Douglas model for the given data and specification. The elasticities are the functions of the share of variable inputs, prices of variable inputs, levels of exogenous factors, and the estimated parameters of the translog profit function (Eqs. 12–18). All elasticities are analyzed at arithmetic means of input shares \(\left( {S_i } \right)\). The elasticity estimates for corn and cotton derived from the translog profit function are presented in Tables 4 and 5, respectively. The elasticity estimates of factor demand and output supply could serve as reference measures for policy actions as elasticities provide a picturesque of aggregate responsiveness of factors to changes in price and fixed input(s).

Table 3 Restricted parameter estimates of the translog profit function for corn and cotton
Full size table
Table 4 Elasticity estimates for different inputs of corn from restricted normalized translog profit model
Full size table
Table 5 Elasticity estimates for different inputs of cotton from restricted normalized translog profit model
Full size table

We compare elasticities obtained from translog profit function parameters and find the non-symmetric impact of different inputs and exogenous factors across variable input demand functions which is at par with theoretical expectation and more logical—that is, different factors have a different level of impact.

Effect of input price on input demand

The effects of price are logical and in line with the routine hypotheses in this study. Demand for inputs is increasing with an increase in output price and is consistent with standard expectations. The higher estimates of price elasticities of input demand, especially for cotton, may be attributed to the highly commercialized THP cotton system constituting ~ 4% of the world’s cotton and cottonseed production where input use is intensive, homogenous, and responds substantially to prices. The existence of both negative and positive values of cross-price elasticities of variable input demand in the translog model (Tables 4, 5) underpins that some inputs are complements while others are substitutes in corn and cotton production in the THP region.

Own price elasticities of variable inputs demanded hover around the moderately inelastic range for corn, implying that corn farmers are relatively less sensitive to the changes in the market price of inputs. However, own-price elasticities are in the elastic range for input demand in cotton production, which implies that cotton farmers are much more responsive to changes in the price of variable inputs than corn farmers. Our input demand elasticity estimates, especially that of water, (Tables 4, 5) are relatively higher. Similar estimates have been reported by de Bonviller et al. (2020) and Burlig et al. (2021). However, our estimates differ from those reported by Bruno and Jessoe (2021a), Hendricks and Peterson (2012), and Scheierling et al. (2006). One reason behind this is that the use of the production, profit, or cost function approach yields different results, and the estimates are not necessarily dual to each other (Hamermesh and Grant 1979). In addition, the choice of the functional form also varies with the study affecting the magnitude of elasticity estimates. However, the price elasticity of irrigation water demand for corn in this study (– 0.81) is almost similar to – 0.79 that was reported by Schoengold et al. (2006). Our results contrast with Adusumilli et al. (2011) for two reasons: first, we emphasize variable inputs in the translog model, unlike using land allocation models to estimate elasticities. Second, our study includes data spanning 23 years, unlike most studies that account for a shorter time frame. Elbakidze et al. (2017) calculated the arc elasticities over a range of prices under different scenarios from the lowest price range between $0 and $30 per acre-foot to the highest price range of $270 and $300 per acre-foot. The authors confirmed that long-run elasticities are greater than short-run elasticities (up to – 9.29 at the price range between $180 and $210 per acre-foot under long-run no deficit irrigation scenario).

Irrigation water demand and water price

The results show that the price elasticity of irrigation water demand for corn is – 0.805, implying that a 10% increase in water price results in an 8.05% decrease in water demanded for irrigation. However, irrigation water demanded for cotton is price elastic with an elasticity of – 1.582. The change in the quantity of water demanded for irrigation resulting from the change in water price is significant at a 1% level as given in Tables 4 and 5. We also find substantial responsiveness of water demand in both corn and cotton to a rise in output price. Nevertheless, the change in the quantity of water demanded due to changing water price is different for corn and cotton. Irrigation water demanded in cotton is more sensitive to changes in water price than in corn. Corn is a relatively water-demanding crop requiring ~ 24–30 inches of water and due to its higher sensitivity to water stress conditions, especially during the early reproductive growth phase, farmers might be reluctant to make changes in water application amounts. The incentive offered by the Renewable Fuel Standard (RFS) might be another reason behind the price-inelastic nature of corn water demand. The enaction of the RFS in the 2000s drove corn prices up by 30% resulting in the expansion of US corn acreage by 8.7% to supplement corn grain ethanol production (Lark et al. 2022). In contrast, cotton is relatively drought-tolerant and requires only ~ 12 to 24 inches of water which is almost 30% lower than that required by corn. Depleting groundwater level, the high opportunity cost of water, and irrigation water being a major input constituting more than one-third of the total variable costs in cotton production (Figs. 2, 3) are other supporting factors for the elastic nature of water demanded to irrigate cotton in the THP region. The higher value of price elasticity of water demand in cotton than that of corn may also be due to the substantially increasing cotton acreage in the THP since the early 2010s as a result of the difficulty in meeting full crop water demand for corn owing to diminishing well capacities.

As irrigation water demand changes with water price, a price increase will increase elasticity with more responsive feedback between farmers and irrigation water-related markets (Qin et al. 2010). For example, if water cost is much lower than the cost of adopting a water-saving technology, no water-saving effort will emerge from increasing water prices. However, if the cost of water can send an appropriate signal for water management, new irrigation technology will come forward, and conservation can occur (Zhou et al. 2015). Due to the high price elasticity of irrigation water demand, especially for cotton in the THP region, implementing price instruments as a policy measure may influence sustainable choices in using water from the Ogallala aquifer. Pricing policy likely affects crop selection, acreage allocation through switching or fallowing, and ultimately groundwater demand (Pfeiffer and Lin 2014). As an effective instrument, a pricing policy could provide a necessary trigger for farmers to use irrigation water efficiently at higher price levels (Scheierling et al. 2006; Smith et al. 2017). However, due to the varying sensitivity of corn and cotton to changes in water price, a non-uniform pricing policy could be more promising in attaining the goals of efficient water use in the THP.

Effect of output price on input demand and output supply

A rise in output price leads to a significant increase in demand for variable inputs for producing corn and cotton in the THP (Tables 4, 5). The results show that cotton producers respond more to changes in output price by altering input usage than corn producers. The supply response of corn farmers to a rise in corn price is positive, consistent with the theory. A 1% increase in corn price increases corn supply by 0.452%. The supply response of cotton farmers to an increase in cotton price is also positively inelastic with estimates being 0.919. According to standard economic theory, the positive elasticity of output supply to output price is due to farmers’ inherent nature to supply more at a higher price and vice-versa.

Effect of exogenous factors on input demand and output supply

We find that increase in precipitation increases corn supply (η = 0.288) and the effect is significant at 5% significance level. However, we did not find any significant effect of precipitation on the cotton supply. The demand for all three inputs is not significantly varying due to changes in precipitation. Input demand and output supply elasticities to rainfall are in the inelastic range (Tables 4, 5), implying that the effect of precipitation is minimal in input demand and output supply. The precipitation effect is also reported as insignificant in another study on the High Plains aquifer (Suarez et al. 2015). The relative insignificance of precipitation is due to the irrigation dominant crop production system in the THP (Schlenker and Roberts 2009).

Similarly, an increase in HDD (> 29 °C for corn and > 32 °C for cotton) has a mixed influence on the output supply of corn and cotton. A 1% increase in HDD during the corn growing season reduces corn output supply by 0.65% and this effect is significant at the 1% level of significance. Contrary to our expectations, cotton output supply is positively inelastic to changes in HDD; however, the effect is not significant. Moreover, an increase in HDD is also associated with a significant decrease in demand for all inputs—fertilizers, irrigation water, and labor—in both corn and cotton (Tables 4, 5). Schlenker and Roberts (2009) report that HDD has a severe impact on crop yield. Here, we provide evidence that input usage is also greatly impacted by HDD. The significant effect of HDD on input demand provides evidence that farmers are highly responsive to changes in temperatures above the critical threshold in the THP. Our results also demonstrate that cotton farmers are more responsive to HDD than corn farmers. This aligns with the profit-maximizing nature of farmers who are inclined to reduce input usage when the length of HDD is already high enough with potentially detrimental and non-recoverable impacts on crop yield.

Our analysis, however, is not without limitations. The energy used to pump irrigation water reflects a substantial cost, which varies with the amount of water pumped, energy price, geographic sites, and the pump and fuel characteristics. Furthermore, energy prices affect not only water use but also other farm production decisions. In this respect, the price effects estimated here may reflect the effect of water price on water use and the effect of pumping costs on production activities. The impact of energy price might limit the possible implications for the estimated magnitudes of elasticities when non-economic factors such as peer pressure and socio-behavioral aspects also have a remarkable influence on groundwater extraction and usage. At the farm level, farmers are highly likely to face varying irrigation water prices due to heterogeneity in farm type, source of energy, groundwater availability, soil moisture condition, and alike. These aspects could have been masked due to the aggregate nature of our data. Therefore, we also acknowledge the limitations of using county-level data instead of the actual farm-level dataset to make inferences.

Conclusion and policy implications

In the context of increasing groundwater demand and limited supply, determining the price elasticity of irrigation water demand using an appropriate model provides a better hint for formulating an effective water use policy. Estimating the price elasticity of water demand is more important when climate change and anthropogenic impacts such as increased temperature, droughts, higher pumping rate, and alike are straining the non-renewable Ogallala aquifer. This research demonstrates the relationship between irrigation water price and farmers’ resource allocation decisions in producing irrigated summer crops such as corn and cotton in the THP region; the empirical results also follow standard economic theory and statistical fit.

Our empirical analysis shows that demand for irrigation water is relatively inelastic for corn (ηcorn = – 0.805) but elastic for cotton (ηcotton = – 1.582) at observed price levels. These results imply that an increase in water price, as a policy alternative, can significantly reduce the demand for irrigation water and promote the adoption of water conservation technology, especially in the THP cotton production. The responsiveness of corn and cotton to water price is quite different, suggesting that a uniform pricing policy will not have a similar effect in bringing water conservation in both crops; however, the relatively significant value of price elasticity of irrigation water demand provides an impetus for using price mechanisms for water conservation. The influence of water price on farmers’ resource allocation decisions generates some space for groundwater conservation policy through price levying; however, a reasonable price in any form must demonstrate its market value while considering farmers' income and tolerance levels simultaneously. Policy on groundwater use should account for its long-term goal of conserving water and incorporate short-run profit-maximizing goals of farmers to avoid the counterproductive consequence of potential policy. One such unintended consequence may be a higher water depletion from the plan targeted to bring down water use (Ward and Pulido-Velazquez 2008).

Since the costs associated with corn and cotton irrigation are substantial, there is a caveat that an increase in water price may hurt farmers’ motivation for production and they may not be motivated towards conservation efforts fearing a likely decline in output. However, irrigation-related costs comprise < 20% of the total revenue, thus signaling that there is a chance for water pricing to serve as a policy tool in the THP region. Here, water conservation can come either from restricting water quantity, increasing water use efficiency, or identifying a conservation-oriented water price. As the elasticity estimates for two crops are quite different, a crop-specific pricing policy for irrigation water use will likely have unequal, yet promising, water conservation benefits for corn and cotton; however, this needs further investigation, possibly with farm-level micro-data.

As Zhou et al. (2015) and Berbel et al. (2018) suggest, there is always a trade-off between reducing water consumption and regional agriculture and economic development based on price response, which can negatively impact agricultural income and wealth of farmers. Therefore, implementing complementary policies for compensating farmers’ income loss while making efforts to conserve water is essential. For example, in addition to the financial incentives available through the Natural Resources Conservation Service for voluntary adoption of water conservation technology, a region-specific program providing additional incentives to foster water conservation initiatives with meaningful and measurable improvement could supplement some of the economic losses to agricultural income. We suggest that a policy should balance profit maximization with sustainable natural resource use and other climate-related adaptation strategies. Extending our analysis with micro-data over several other crops and under varying irrigation technologies may provide further evidence concerning prospective pricing policies and their potential for THP groundwater conservation.