Introduction

Tourmalines are a mineral supergroup of complex borosilicates occurring in different geological settings, from diagenetic stages to ultra-high-pressure (UHP) environments (e.g., Henry and Dutrow 1996; Dutrow and Henry 2011; Lussier et al. 2016). Such an extensive stability field is due both to the capacity of tourmaline to adjust its composition depending upon the formation environment and to its crystal structure (discussed below).

The general chemical formula of tourmaline is: XY3Z6T6O18(BO3)3V3W, where X = Na+, K+, Ca2+, □ (= vacancy); Y = Al3+, Fe3+, Cr3+, V3+, Mg2+, Fe2+, Mn2+, Li+; Z = Al3+, Fe3+, Cr3+, V3+, Mg2+, Fe2+; T = Si4+, Al3+, B3+; B = B3+; V = (OH)−, O2−; W = (OH)−, F−, O2−. The non-italicized letters X, Y, Z, T and B represent groups of cations at the [9]X, [6]Y, [6]Z, [4]T and [3]B crystallographic sites (italicized letters), and the letters V and W represent groups of anions accommodated at the [3]-coordinated O3 and O1 crystallographic sites, respectively. Tourmaline-supergroup minerals are primarily classified into three groups, vacant, alkali and calcic, based on the X-site occupancy (Henry et al. 2011). A further level of classification into subgroups is based on charge arrangements at the Y and Z sites. Tourmalines are also distinguished by the dominant anion at the W position of the general formula into hydroxy-, fluor- and oxy-species.

Tourmaline structure is inextricably built over the triangular planar (BO3) group, which is bonded to the trigonal antiprism XO9 and to YO6 octahedron. Each one of the XO9 antiprisms is linked to a ring of six tetrahedra [T6O18]. All those structural elements of tourmaline constitute separate islands that extend along c crystallographic axis. Finally, the structural backbone of tourmaline is made by ZO6 polyhedra that tie the islands together thus giving tourmaline the mechanical properties that makes it a very resistant mineral in clastic sediments and UHP environments (e.g., Bosi 2018). Also for this reason, tourmaline is able to give inferences about the chemical conditions of its formation (Dutrow and Henry 2011). Thus, tourmaline is stable in a variety of geological setting, including where crustal material is recycled through subduction zones down to the upper mantle (Henry and Dutrow 1996; Ota et al. 2008a,b; Shimizu and Ogasawara 2013). Tourmaline can also form in subduction environments in presence of B-bearing aqueous fluids, when the other phases in paragenesis with it reach their breakdown conditions and some elements are recycled in tourmaline’s structure which is stable at those depths, so that it may form, or overgrow (if it was pre-existing in the recycled material) with a new composition, depending upon the elements available to be incorporated. At greater depths, tourmaline itself experiences breakdown, and aqueous fluids are released and may escape once again going metasomatize the surrounding rocks, reducing both their solidus temperature and the viscosity of possibly associated melt (Pichavant 1981; Dingwell et al. 1992).

If subducting serpentinites are strictly coupled with carbonaceous (meta)sediments, the release of Ca-rich metasomatic fluids along the slab is likely to occur as a consequence of dehydration reactions, going for example to form strongly Ca-enriched patches and layers of hybrid rocks (lawsonite-bearing) in metagabbro matrix (Tartarotti et al. 2019). Those Ca-rich metasomatic fluids may also lead to the formation of Ca-bearing tourmaline that acts as Ca-carrier at greater depths until the breakdown conditions are reached. In some cases, tourmaline can experience an extreme chemical evolution that ends up with a change in its nomenclature, for example from alkali to calcic, following the possible substitution scheme for Ca incorporation into tourmaline reported in Henry and Dutrow (1990).

The breakdown conditions of tourmaline are composition-dependent and a reference diagram of tourmaline stability field is reported in van Hinsberg et al. (2011), mainly regarding alkali tourmalines (schorl and dravite) and vacant ones (magnesio-foitite).

The occurrence of Ca-rich tourmalines in nature was experimentally demonstrated to be a function of pressure, temperature and metamorphic fluids composition (Berryman et al. 2016), but calcic tourmalines remain so far the less investigated in terms of thermal behaviour, dehydration and breakdown products, also because uvite, ideally CaMg3(Al5Mg)(Si6O18)(BO3)3(OH)3(OH), was only recently officially approved by the International Mineralogical Association’s Commission on Nomenclature and Classification as a new mineral species of tourmaline supergroup (Bosi et al. 2022).

The present work aims at investigating the thermal behaviour and stability of the calcic tourmaline uvite, at room pressure (RP). The holotype of uvite from San Piero in Campo (Elba Island, Italy), described by Bosi et al. (2022) with formula X(Ca0.61Na0.35□0.04)Σ1.00 Y(Mg1.51Fe2+0.47Al0.70Fe3+0.14Ti0.18)Σ3.00 Z(Al4.54Fe3+0.18V3+0.02Mg1.27)Σ6.01 T(Si5.90Al0.10)Σ6.00 (BO3)3 V(OH)3 W[(OH)0.55F0.05O0.40]Σ1.00, was studied by in situ high-temperature powder X-ray diffraction (HT-PXRD) up to the structural breakdown.

Experimental

A fragment of an uvite crystal was gently ground in an agate mortar under ethanol. The resulting powder was loaded in a 0.7 mm-diameter SiO2-glass capillary kept open at one side. To avoid unwanted movements of the powder along the capillary, some kaolin wool-glass was used as a stopper at the open side. Finally, the capillary was fixed to a hollow corundum tube using an HT cement. In situ HT-PXRD experiments were performed using a heating chamber for capillaries, developed by MRI and Bruker AXS, placed along the beam path of the diffractometer. Relevant features and details of the thermal calibration procedure of the chamber may be found in Ballirano and Melis (2007).

Data were measured, using CuKα radiation, on a Bruker AXS D8 Advance, operating in θ/θ geometry in transmission mode, fitted with focussing multilayer graded (Göbel) mirrors placed along the incident beam and Soller slits on both the incident (2.3° opening angle) and diffracted (radial) beams. Intensities were collected by a position sensitive detector (PSD) VÅntec-1 set at an opening angle of 6° 2θ.

At the end of the heating run, the capillary was cooled back at room temperature (RT) within the chamber with a 10 °C/min rate. The powder was removed from the capillary, re-homogenized and loaded in a new borosilicate-glass capillary following the same procedure, aimed at reducing the possible effect of textured recrystallization at the walls of the capillary, adopted by Celata et al. (2021) and Ballirano et al. (2022). Data collection was performed keeping the sample outside the chamber using the same angular range, step-scan size, and counting time of the HT measurements (see Table 1).

Table 1 Miscellaneous data of the data collection and Rietveld refinements
Full size table

Data were evaluated by the Rietveld method using Topas V.6 (Bruker AXS 2016) which implements the Fundamental Parameters Approach (FPA: Cheary and Coelho 1992) to describe the peak shape. Absorption correction for a cylindrical sample was performed using the equation of Sabine et al. (1998) and the procedure described by Ballirano and Maras (2006) was applied for handling the correlation existing between displacement parameters and absorption. The isotropic displacement parameters were constrained as follows: BY = BZ = BB = BT; BO1 = BO2 = BO3 = BO4 = BO5 = BO6 = BO7 = BO8; BH1 = BH3 = 1.2* BO1. Texture effects were corrected using spherical harmonics (8th-order, nine refinable parameters), selecting the number of appropriate terms by using the approach of Ballirano (2003). Starting structural data were taken from Bosi et al. (2022) and each refined structure at a given non-ambient T was used as input for the subsequent T. Experimental conditions and miscellaneous information regarding the refinements are listed in Table 1, a magnified 3D-plot of the full data set is shown in Fig. 1, and a representative example of Rietveld plots is shown in Fig. 2. CIFs of the uvite structure refined at the various T are given in online resource.

Fig. 1
figure 1

Magnified 7–40° 2θ 3D-view of the full data set collected in the 30–900 °C thermal range

Full size image
Fig. 2
figure 2

Representative example of the Rietveld plots of the diffraction pattern collected at 175 °C. Blue: experimental; red: calculated; grey: difference; vertical bars: position of calculated Bragg reflections of the uvite studied

Full size image

Results and discussion

Breakdown products of uvite

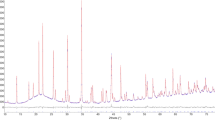
The first evidence of uvite structural breakdown was observed at 800 °C owing to the occurrence of weak diffraction reflections that were subsequently assigned with the help of the diffraction pattern collected on the material cooled to RT. The breakdown was completed at the T of 900 °C. The diffraction pattern of the sample cooled down at RT (Fig. 3) was refined by the Rietveld method keeping fixed all structural parameters to reference data except for unit-cell parameters. Therefore, the resulting quantitative phase analysis (QPA) must be considered as semi-quantitative. Data indicate the occurrence of prevailing indialite, ideally Mg2Al3[AlSi5O18] (Balassone et al. 2004), plus yuanfuliite, ideally Mg(Fe3+,Al)O(BO3) (Appel et al. 1999), plagioclase, a “boron-mullite” phase (labelled as Al4B2O9 in the graph; Fischer et al. 2008) and hematite as breakdown products of uvite. According to various determinative methods (Kroll 1983) and considering the relatively large standard uncertainty of the refined cell parameters, plagioclase composition could be restrained to the 75–90 An mol% range. All these phases were also identified in the HT diffraction patterns collected at T ≥ 800 °C, indicating that they were not produced during the cooling process. Furthermore, no intensity variation of the broad bump centred at ~ 22° 2θ, due to the capillary glass, was observed at the end of the thermal heating run testifying the absence of relevant amounts of amorphous material.

Fig. 3
figure 3

Magnified 7–60° 2θ view of the Rietveld plots of the products of breakdown of the uvite studied. Blue: experimental; red: calculated; grey: difference; vertical bars: position of calculated Bragg reflections of (from above to below) plagioclase, indialite, hematite, yuanfuliite and “boron mullite”. The contribution of “boron mullite” (labelled as Al4B2O9 in the legend) is indicated as a continuous magenta line

Full size image

The observed assemblage of phases is significantly different with respect to that resulting from the thermal breakdown of both Fe-rich fluor-elbaite (Celata et al. 2021) and Mn-bearing fluor-elbaite (Ballirano et al. 2022). In particular, the mullite-like phase reported as the prevailing crystalline product of Fe-rich fluor-elbaite and Mn-bearing fluor-elbaite breakdown is replaced by indialite. This is due to the occurrence of significant Mg and lower Al content of the pristine uvite sample (5.24 atoms per formula unit, apfu) as compared to the fluor-elbaite ones (5.96 and 7.81 apfu, respectively).

Moreover, the absence of abundant B-rich amorphous material is justified by the occurrence, among the breakdown products of uvite, of two different phases (yuanfuliite and boromullite) where B may be accommodated.

Owing to the limited amount of “boron mullite” in mixture, it was not possible to derive reliable unit-cell parameters to characterize in detail its chemistry as it was done for the Al2O3–B2O3–SiO2 (ABS) phases arising from the breakdown of fluor-elbaite samples (Celata et al. 2021; Ballirano et al. 2022).

Thus, after uvite breakdown, Ca is hosted in plagioclase (75–90% An) and allegedly in both indialite and yuanfuliite (< 0.10 apfu). No melt was observed, so, at these conditions, no B–Ca-bearing aqueous fluids are produced.

Our experimental results can be intended as a preliminary study of the lower limit of uvite’s stability field, setting the stage for future HP–HT experiments aimed to mimic the conditions of a subducting slab to better understand the role and behaviour of Ca–tourmaline in dehydration processes and release of Ca-bearing metasomatic fluids.

Thermal expansion and HT structure modifications

Variation of unit-cell parameter values at each T for the uvite sample is reported in Table 2, and shown in a graphical way in Fig. 4. The dependence of the unit-cell parameters from T was modelled using the Berman equation (Berman 1988). This approach indicated the occurrence of a discontinuity at 450 °C, and for this reason, the fitting was limited to a maximum T of 425 °C. The corresponding functions are shown as continuous red lines in Fig. 4. Table 3 lists the relevant parameters of the fitted functions that are compared to those of Fe-rich fluor-elbaite (Celata et al. 2021) and Mn-bearing fluor-elbaite (recalculated from the published data of Ballirano et al. 2022). Data indicate that the c-parameter is softer than the a-parameter against T. It is worth noting that uvite expands at a rate slightly greater than that of both Fe-rich fluor-elbaite and Mn-bearing fluor-elbaite.

Table 2 Refined cell parameters of the studied uvite at the various temperatures
Full size table
Fig. 4
figure 4

Variation of unit-cell parameters with T for the studied uvite. The continuous red lines represent the fitted Berman functions for a, c and vol. Parameters of the corresponding functions are listed in Table 3

Full size image
Table 3 Relevant parameters of the fitting procedure by the Berman equation of the unit-cell parameters vs T data, up to oxidation, of different tourmaline samples
Full size table

The dependence of the normalized unit-cell parameters with T is reported in Fig. 5. The trend is very similar to that observed in both Fe-rich fluor-elbaite and Mn-bearing fluor-elbaite (Celata et al. 2021; Ballirano et al. 2022).

Fig. 5
figure 5

Dependence of the normalized unit-cell parameters from T for uvite. For comparison purpose, data from Fe-rich fluor-elbaite (Celata et al. 2021) and Mn-bearing fluor-elbaite (Ballirano et al. 2022) are also reported

Full size image

The first deviation from the regularly increasing trend of the a-parameter occurs at 450 °C and it ends at 625 °C; above this T, the a-parameter increases again with approximately the same rate observed below 450 °C. The c-parameter shows a discontinuity at the same T (450 °C) consisting in a very small inflexion before regaining the same expansion rate. The data measured at T = 900 °C, during the onset of the breakdown, apparently deviate from the trends, but they are affected by a high standard uncertainty value. It is worth noting that Mn-bearing fluor-elbaite shows a diverging behaviour for the a- and c-parameter at T exceeding 750 °C that may be related to the onset of the intracrystalline order–disorder reaction YLi + ZAl → ZLi + YAl (Ballirano et al. 2022).

Based on reference data (Celata et al. 2021; Ballirano et al. 2022), the discontinuity of the unit-cell parameters’ dependence from T observed in the 450–625 °C thermal range is caused by the onset of the transition elements (TEs) oxidation process which is coupled to deprotonation at the H1 and/or H3 sites. In the case of uvite, the equation describing the process takes the form of (Fe2+) + (OH)− → (Fe3+) + (O2−) + 1/2H2(g), (Bosi et al. 2019). In fact, such a discontinuity is similar to that observed in Fe-rich fluor-elbaite and Mn-bearing fluor-elbaite (Celata et al. 2021; Ballirano et al. 2022); the magnitude of the contraction of the cell parameters is consistent with the corresponding amounts of TEs (Fe-rich fluor-elbaite: 1.12 apfu Fe2+  + Mn2+; uvite, 0.47 apfu Fe2+; Mn-bearing fluor-elbaite, 0.12 apfu Mn2+).

As far as the structural modifications are referred to, the < X–O > mean bond distance is characterized by a regular increase with T which is nicely fitted by a linear dependence (Fig. 6).

Fig. 6
figure 6

Variation of < X–O > bond distance with T for the studied uvite

Full size image

The dependences of < Y–O > and < Z–O > bond distances from T display contrasting behaviours (Figs. 7, 8). The < Y–O > bond distance increases in a fairly regular way from 2.045 to 2.065 Å. Minor dispersion of the data from the linear trend may be possibly related to the effect of the minor TEs’ oxidation. Differently, this behaviour is evident in the case of Fe-rich fluor-elbaite, whose TEs’ content is significantly higher than that of uvite. In fact, a contraction of the < Y–O > bond distance, in the thermal range where the TEs’ oxidation occurs (Celata et al. 2021), is observed and ascribed to the smaller ionic radius of Fe3+ than that of Fe2+. Differently, the < Z–O > bond distance shows a very minor decrease, from 1.935 to 1.929 Å, as a function of T. It is unclear whether the decrease is significant or not as it is of a magnitude comparable to the standard uncertainty of individual Z–O bond distances. Such a variation could be possibly attributed to minor intracrystalline order–disorder reaction such as YFe + ZAl → ZFe + YAl described by Ballirano et al. (2022) for Mn-bearing fluor-elbaite. However, analysis of the mean atomic number (man; Hawthorne et al. 1995) at both Y and Z sites (Fig. 9) shows that the small, constant reduction of man at Z, is not counterbalanced by a proportional increase at Y. This reduction may hence be related to the simplification adopted to constrain the displacement parameters of atoms at the Y, Z, B and T sites to be equal throughout the various refinements.

Fig. 7
figure 7

Dependence of < Y–O > bond distances from T for the studied uvite

Full size image
Fig. 8
figure 8

Dependence of < Z–O > bond distances from T for the studied uvite

Full size image
Fig. 9
figure 9

Evolution with T of mean atomic number (man) at the Y (upper panel) and Z (lower panel) sites for the studied uvite. Thick black lines indicate the average values, whereas the dotted lines indicate the 1σ level

Full size image

Conclusions

The thermal behaviour of uvite was investigated for the first time up to structural breakdown through in situ HT-PXRD.

Well before the breakdown, heating the uvite at 450 °C in air was enough to set the Fe oxidation out, counterbalanced by the deprotonation reaction: (Fe2+) + (OH)− → (Fe3+) + (O2−) + 1/2H2(g).

Tourmaline breakdown products have been identified as indialite (prevalent) yuanfuliite, plagioclase, a “boron-mullite” phase, and hematite. No melt was produced after uvite breakdown and Ca is stored in plagioclase (75–90% An).