Abstract
The crystal structure and crystal chemistry of meyerhofferite, ideally CaB3O3(OH)5·H2O, was investigated by a multi-methodological approach based on titrimetric determination of boron, gravimetric determination of calcium, determination of fluorine by ion selective electrode, determination of water content by heating, other minor elements by inductively coupled plasma atomic emission spectroscopy, along with single-crystal synchrotron X-ray and neutron diffraction. The concentration of more than 50 chemical elements was measured. The combination of these techniques proves that the composition of meyerhofferite approaches the ideal one (i.e., (Ca1.012Mg0.003) (B2.984Si0.001)O3(OH)5·1.018H2O), with only a modest fraction of Mg (with MgO ≈ 0.03 wt%) replacing Ca, and with Si the only potential substituent of tetrahedral B (with SiO2 ≈ 0.02 wt%). The content of REE and other minor elements is, overall, not significant, including that of fluorine as a potential OH− substituent (i.e., < 0.01 wt%). These findings have some relevant geochemical and technical implications, here discussed. The X-ray and neutron structure model obtained in this study prove that the building units of the structure of meyerhofferite consist of: two BO2(OH)2 tetrahedra and one BO2(OH) triangle, linked by corner-sharing to form [B3O3(OH)5]2− rings, and distorted Ca-polyhedra (with CN = 8, CaO3(OH)4(OH2)), linked by edge-sharing to form infinite chains along [001]. The B3O3(OH)5 rings are connected to the Ca-polyhedra chains by corner- and edge-sharing, on two sides of the chains. These heteropolyhedral chains, made by Ca-polyhedra and B3O3(OH)5 rings, are mutually connected through hydrogen bonding only, giving rise to the tri-dimensional edifice of meyerhofferite. The neutron structure refinement showed no evidence of static or dynamic disorder pertaining to the H sites; their libration regime was found to be significantly anisotropic. At least seven of the nine oxygen sites of the structure are involved in H-bonding, as donors or as acceptors. The role played by the H-bonding scheme on the physical properties of meyerhofferite is discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Boron is a chemical element with an average low concentration in the Earth’s crust (~ 0.00086 wt%), and natural borates represent the main source for this element. Demand for B has increased rapidly in the last 20 years, due to the wide use of this element in a series of technological processes (e.g., glass, ceramics, electronics, metallurgy, textile, cosmetics, fertilizers and chemicals). In 2000, the world production of borates was estimated to be about 4.5 million tons; in 2020 the production raised to more than 7–8 Mtons (source: U.S.G.S., 2021). Due to the elevated ability of 10B to absorb thermal neutrons (Carter et al. 1953; Palmer and Swihart 1996; Rauch and Waschkowski 2002), natural borates are also being used for the production of radiation-shielding concretes, used in nuclear energy plants or in facilities for scientific research or medical applications (e.g., Yarar and Bayülken 1994; Kinno et al. 2002; Okuno et al. 2009, 2013; Gatta et al. 2010, 2013; Korkut et al. 2010; Uysal et al. 2018). The most common natural borates (i.e., borax Na2(B4O5) (OH)4·8H2O, ulexite NaCa[B5O6(OH)6]·5H2O) produce a drastic effect on setting and hardening of Portland cements, with a consequent lowering of strength development and durability of concretes (e.g., Kula et al. 2001; Derun and Kipcak 2012; Içelli et al. 2013; Erdogmus 2014; Glinicki et al. 2018). In addition, these minerals release sodium, when dissolved into the paste, which can activate harmful reactions for the durability of Portland cement concretes. In the framework of a long-term project to select new B-bearing aggregates, as potential substituents of borax and ulexite in cement concretes, we have re-investigated the crystal chemistry, chemical stability and low/high-temperature and pressure behaviour of a series of natural borates: colemanite (CaB3O4(OH)3·H2O, Lotti et al. 2017a,b; 2019), kernite (Na2B4O6(OH)2·3H2O, Comboni et al. 2020a; Gatta et al. 2020), kurnakovite (MgB3O3(OH)5·5H2O, Gatta et al. 2019; Pagliaro et al. 2021) and inyoite (Ca2B6O6(OH)10·8H2O, Comboni et al. 2021a). This study extends our investigation to meyerhofferite, which is a Na-free borate, ideally CaB3O3(OH)5·H2O (or Ca2B6O6(OH)10·2H2O), and contains up to 46.7 wt% B2O3.
Despite the geochemical and the industrial interest on borates, only a few studies were so far devoted to this mineral. Meyerhofferite was recognised as a new mineral species by Schaller (1916). Palache (1938) provided the first crystallographic data of meyerhofferite. The crystal structure of this mineral was solved by Christ and Clark (1956) by single-crystal X-ray diffraction data, in the space group P-1 with a ~ 6.6, b ~ 8.3, c ~ 6.5 Å, α ~ 90.5°, β ~ 102.3°, γ ~ 87.2°, and then re-investigated by Burns and Hawthorne (1993). Its principal building units are represented by: two Bϕ4-tetrahedra (where ϕ: O, OH) and one Bϕ3-triangle, linked by corner-sharing to form [B3O3(OH)5]2− rings (Fig. 1), and Ca-polyhedra (with CN = 8), linked by edge-sharing to form infinite chains along [001]. The Ca-polyhedra chains link, by corner-sharing and edge-sharing, the B3O3(OH)5 rings to two sides of the chains (Fig. 1). These heteropolyhedral chains, made by Ca-polyhedra and B3O3(OH)5 rings, are connected through hydrogen bonding only.
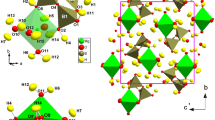
Principal building units of the structure of meyerhofferite, i.e., B3O3(OH)5 rings and distorted CaO3(OH)4(OH2) polyhedra, the heteropolyhedral chains (made by B3O3(OH)5 rings and Ca-polyhedra) running along [001], and a view of the structure down to [001]. Model based on the neutron structure refinement of this study. Displacement ellipsoid probability factor: 50%
The type locality of meyerhofferite is the Monte Blanco deposit (Black Mountains, Amargosa Range, Inyo Co., California, USA). Other important occurrences reported in the literature are: the Furnace Creek Mining District (Furnace Creek Borate Mining District) and the Kramer borate deposit (Boron, Kern Co.) in California; Mesa del Almo (Sonora), in Mexico; Anita mine (Sijes district) and Tincalayu borax deposit (Salta Province) in Argentina; several deposits of the Bigadiç borate district (Balıkesir Province) and the Killik and Espey borate mines (Emet, Kütahya Province) in Turkey; the Inder borate deposit, in Kazakhstan. To the best of our knowledge, no synthetic counterpart of meyerhofferite is available in the market, despite its synthesis route is known (i.e., Parkenson 1963, US3337292A patent).
There are some open questions pertaining to the crystal chemistry of meyerhofferite: (1) due to the absence of chemical data based on modern standards, the potential B- or Ca-substituents are largely unknown; (2) the H-bonding network in meyerhofferire is complex and pervasive (as this mineral contains ~ 28 wt% H2O), and it was described on the basis of X-ray data only; (3) its non-ambient conditions behaviour (i.e., low- and high-T, high-P) is presumably strongly controlled by the H-bonding network of the structure. In this light, the aim of this study is a reinvestigation of the crystal chemistry and crystal structure of meyerhofferite by a multi-methodological approach: titrimetric determination of boron, gravimetric determination of calcium, determination of fluorine by ion selective electrode, determination of water content by heating, other minor elements by inductively coupled plasma atomic emission spectroscopy, single-crystal synchrotron X-ray and neutron diffraction. The combination of these techniques is expected to provide:
-
a.
A description of the crystal chemistry of this mineral based on modern analytical protocols, with a particular attention to the potential B- and Ca-substituents;
-
b.
An unambiguous location of all the proton sites and the description of the complex H-bonding network expected in meyerhofferite structure, along with the anisotropic displacement parameters of all the atomic sites, including the H-sites;
-
c.
a more robust description of B-coordination environment (e.g., aplanarity of the Bϕ3-group, tetrahedral distortion of the Bϕ4-groups).
The results of this multi-methodological study will be pivotal to describe the chemical, thermal and compressional behaviour of meyerhofferite, along with potential T- or P-induced phase transitions, coupled with the mechanisms, at the atomic scale, which govern any potential structure transformations. Such experiments are in progress, and the first experimental findings on the compressional behaviour of meyerhofferite have been recently published (Comboni et al. 2020b, 2021b). The experimental data of this study are crucial for any potential technical utilization of meyerhofferite in radiation-shielding concretes.
Sample description and occurrence
The sample of meyerhofferite used in this study belongs to the collection of the Museum of Mineralogy of the University of Padua (catalogue number MM5990). Centimetric, white, platy-prismatic crystals, collected at the main borate deposit at Bigadiç, Marmara region, Turkey, make the hand specimen. The Bigadiç borate deposit represents the largest colemanite and ulexite high-grade deposit in the world. Bigadiç is located in the Western Anatolia, associated with several other borate deposits including Emet, Kestelek and Kirka. The Bigadiç volcano-sedimentary stratigraphic sequence of Neogenic age consists of a borates-bearing non-marine basin, composed of lower volcanic units, clays, limestone, tuff and a first borate zone separated by an upper unit of tuff, a second borate zone and olivine basalts. The borate minerals, formed in the lower and upper zone, are separated by tuff beds, the latter is locally replaced by montmorillonite, chlorite and zeolites minerals. Colemanite and ulexite predominate in both borate zones: other borates including howlite, probertite, and hydroboracite are in the lower borate zone, while meyerhofferite, inyoite, priceite, hydroboracite, howlite and tunellite, are located in the upper borate zone.
The Bigadiç borate non-marine deposits were fed by thermal springs, associated with local volcanic activity under arid climatic conditions. The radiometric data revealed that the formation of the Bigadic volcano-sedimentary succession is restricted to a period between 20.6 and 17.8 My (Helvaci 1995, 2015, 2019; Helvaci and Alonso 2000).
Experimental methods
Chemical characterisation
Titrimetric determination of boron
A mass of 80–100 mg of a sample of meyerhofferite was placed in a 50 ml plastic test tube, along with 5 ml of water and 3 ml of hydrochloric acid 1 M; the plastic test tube was then covered and transferred in an ultrasound bath for 1–2 h. The resulting clear solution was transferred in a 200–300 ml beaker with water up to about 100 ml of the total solution.
A combined glass electrode (InLab® Routine Pro—Mettler Toledo) was immersed in the solution, and the pH was adjusted to 5.5–6.5 with solutions of HCl 0.1–1 M and NaOH 0.1–1 M. 5–6 g of mannitol were added and stirred until the complete dissolution of the solid. The solution was then titrated with NaOH 0.1 M up to pH 8.3–8.7.
The content of titrated acid was entirely due to the presence of boric acid in solution, as the sample does not contain elements capable to hydrolyze the medium, or in general able to influence its acidity. The measured fraction of B2O3 was 46.3(2) wt%.
Gravimetric method of calcium
A mass of 200–300 mg of meyerhofferite was placed in a 200 ml beaker, acidified with 40 ml of hydrochloric acid 0.5 N. After complete dissolution, the solution was treated two times with 10 ml of ethyl alcohol and boiled for 15 min. Heating the solution (at temperature below the boiling point), 10 ml of concentrated ammonium hydroxide were added, followed by 5 ml of 20% sodium tungstate dihydrate solution dropwise. After 1 h, the white precipitate was collected on a preweight 30 ml sintered-glass filtering crucible (m1) (porosity n. 4), washed 10 times with 10 ml of 1:10 ammonium hydroxide solution. The crucible was dried at 105 °C, until a constant weight (m2) was measured. The difference of weight (m2–m1) represents the total calcium content of the mineral, expressed as CaWO4. The measured fraction of CaO was 25.2(2) wt%.
Determination of fluorine by ion selective electrode
A mineral sample of 20 mg in mass was placed in a 50 ml plastic test tube, along with 5 ml of water and 3 ml of hydrochloric acid 1 M; the plastic test tube was covered and transferred in an ultrasound bath for 1–2 h. 2–3 ml of Total Ionic Strength Adjustment Buffer (Commercial solution TISAB III) were added to the clear solution and diluted to 20 ml with water. The F content was then determined using perfectION™ Combination Fluoride Ion Selective Electrode (Mettler Toledo), adopting the method of standard addition. Solutions of fluorine from 0.1 to 5.0 mg/l were prepared by Certified Reference Material—CRM 1000 mg/l of fluorine. The resulting F fraction was < 0.01 wt% (uncertainty not determined).
Determination of water content by heating
A sample of 1000 mg was placed in a quartz crucible with lid, and gradually heated in a muffle furnace from ambient temperature up to 800 °C. Assuming that the mass loss represents the total amount of H2O, the estimated fraction of H2O of the sample was 28.4(2) wt%.
Determination of minor elements by inductively coupled plasma atomic emission spectroscopy (ICP/AES)
All measurements were performed in axial view mode for REE and radial view mode for the other minor elements with a Perkin Elmer Optima 7000DV ICP/AES spectrometer.
Determination of REE concentration
A mass of 50 mg of mineral sample was placed in a 50 ml plastic test tube, along with 5 ml of water and 3 ml of hydrochloric acid 1 M; the plastic test tube was covered and transferred in an ultrasound bath for 1–2 h. The resulting clear solution was then transferred and diluted with water in a 50 ml volumetric flask. A calibration protocol was performed with a blank solution and series of solutions prepared with similar fractions of calcium and boron as those of the sample under investigation and REE concentrations from 0.001 to 0.050 mg/l for each element (using CRM multi-elemental standard mix for ICP).
Results and instrumental parameters are listed in Table 1.
Determination of other minor elements concentration
For the non-REE minor elements determination, two different protocols were used.
Protocol 1
A mass of 10–20 mg of mineral sample was placed in a 50 ml plastic test tube, along with 5 ml of water and 3 ml of hydrochloric acid 1 M; the plastic test tube was covered and transferred in an ultrasound bath for 1–2 h. The resulting clear solution was transferred and diluted with water in a 25 ml volumetric flask, containing 2.5 ml of scandium solution 100 mg/l as internal standard. A calibration protocol was performed with a blank solution and a series of 5 solutions prepared with concentration from 0.05 to 1.0 mg/l for each element (using CRM multi-elemental standard mix for ICP).
Only the Cs concentration was measured with a Varian SpectrAA 220FS air-acetylene flame atomic emission spectrometer and some modification to the Procol 1: 50 mg of mineral was used, 150 mg of potassium nitrate were added, instead of the scandium solution, and the calibration solutions were prepared with concentration from 1 to 20 mg/l of Cs.
Protocol 2
10–20 mg of mineral sample were decomposed by alkaline fusion in a platinum crucible with 100 mg of sodium carbonate or potassium carbonate in a muffle furnace at 1000 °C for 5 min, followed by dissolution in 10 ml of water and 1 ml of sulfuric acid 1 M or 1 ml of hydrochloric acid 1 M. The clear solution was then transferred and diluted with water in a 25 ml volumetric flask containing 2.5 ml of scandium solution 100 mg/l as internal standard. A calibration protocol was performed with a blank solution and a series of 5 solutions prepared with concentration from 0.05 to 1.0 mg/l for each element (using CRM multi-elemental standard mix for ICP).
Results and instrumental parameters are listed in Table 2.
Determination of carbon, nitrogen, hydrogen by thermal decomposition and detection by Infrared absorption (C,H) and thermal conductivity (N)
200–300 mg of mineral sample were decomposed at 950 °C in an elementary analyzer LECO Truspec CHN, in excess of oxygen for 90 s. The products of decomposition were transferred to a second furnace (Afterburner) at 850 °C for a further oxidation and particulate removal. The gases, after collection and homogenization in a container of 4.5 l at 50 °C, were analyzed by infrared absorption for the measurement of CO2 and H2O (C was measured in the form of CO2 and the H2 as H2O). An aliquot of the gas was instead transferred in a stream of helium through a warm copper catalyst and filtered to convert NOX to N2 and to remove oxygen, carbon dioxide and water. Finally, a thermal conductivity detector was used to determine the nitrogen content. As calibration standards, EDTA, sodium tetraborate decahydrate, boric acid, calcium carbonate, sodium nitrate, and dihydrate oxalic acid were used. The resulting concentrations were: C < 0.02 wt%, N < 0.02 wt%, and H = 3.08(2) wt%.
The general chemical composition of the meyerhofferite sample used in this study, considering major and minor components (with a significant concentration), is given in Table 3. The calculated unit formula, based on 3O + 5OH apfu, is: (Ca1.012Mg0.003) (B2.984Si0.001)O3(OH)5·1.018H2O, or Ca1.01B2.98O3(OH)5·1.02H2O.
Structural characterisation
Synchrotron X-ray diffraction
A crystal of size ~ 50 × 30 × 20 μm3 was selected for the X-ray diffraction experiment. Single-crystal synchrotron X-ray diffraction data were collected at the ID15-b beamline, at the ESRF, Grenoble (France). A convergent monochromatic beam (E ~ 30 keV, λ ~ 0.414 Å) was used for the diffraction experiment. The diffraction patterns were collected by an Eiger2 9 M CdTe detector, positioned at about 180 mm from the sample position. Sample-to-detector distance was calibrated using a Si standard and a vanadinite (Pb5(VO4)3Cl) crystal. Further details on the beamline setup are reported in Merlini and Hanfland (2013). The data collection strategy consisted in a pure ω-scan (− 75° ≤ ω ≤ + 75°), with 0.4° step width and 0.5 s exposure time per step. Indexing of the diffraction peaks and integration of their intensities (corrected for Lorentz-polarization effects) was performed using the CrysAlis package (Rigaku Oxford Diffraction 2018). The lattice was found to be metrically triclinic (Table 4), and consistent with the previous experimental findings of meyerhofferite reported in the literature (e.g., Christ and Clark 1956, Burns and Hawthorne 1993). A total number of 3840 reflections were collected (with −9 ≤ h ≤ + 10, −11 ≤ k ≤ + 11 and −10 ≤ l ≤ + 11), out of which 2457 were unique according to the Laue class -1 (RFriedel = 0.0134) and 2409 with Fo > 4σ(Fo), with dmin ~ 0.56 Å (Table 4). The Wilson plot and the statistics of distributions of the normalized structure factors suggested that the structure is centrosymmetric. Further details pertaining to synchrotron X-ray data collection are listed in Table 4.
Anisotropic crystal-structure refinement based on the X-ray intensity data was performed in the space group P-1, using the SHELXL-2018/3 software (Sheldrick 2008, 2014), starting from the structure model of Burns and Hawthorne (1993), without any H atom. The X-ray neutral scattering factors of Ca, B, O and H were taken from the International Tables of X-ray Crystallography. Secondary isotropic extinction effect was corrected according to the formalism of Larson (1967), as implemented in the SHELXL package. Convergence was rapidly reached after the first cycles of refinement, with a series of positive residual peaks in the final difference–Fourier map of the electron density, which were then implemented in the further cycles of refinement as (isotropic) H sites (Table 5). At the end of the refinement (with R1(F) = 0.0278 for 2457 reflections with FO > 4σ(FO) and 140 refined parameters), the convergence was achieved with all the principal mean-square atomic displacement parameters positive. Further details pertaining to structure refinement are given in Table 4. Site coordinates and atomic displacement parameters are listed in Tables 5 and 6; selected interatomic distances and angles are given in Table 7. CIF is available upon request to the corresponding author.
Neutron diffraction
The neutron diffraction experiment was performed at the single-crystal diffractometer SXD (Keen et al. 2006) at the ISIS spallation neutron source (UK), with the Laue method in time-of-flight (TOF). Bragg intensities were collected using polychromatic radiation (0.3 < λ < 8 Å), with an array of eleven 2D position-sensitive TOF detectors statically placed around the sample. A series of 7 orientations around the vertical axis of the instrument, with a counting time of ~ 10 h each, were used. Data were initially indexed with the unit cell available from the X-ray measurement. Integrated intensities were extracted using the 3D-profile fitting method implemented in the SXD2001 software (Gutmann 2017) and corrected for the Lorentz effect. An absorption correction was applied to the data with an in-house SXD-software package that reconstructs the three-dimensional shape of the crystal via image-processing of a 360° panoramic, and calculates the exact path-length of neutrons through the crystal for characteristic diffraction shape nodes (de Meulenaer and Tompa 1965). The transmission factor was, than, calculated via analytic solution of the integral of diffraction centres across the whole crystal volume, according to diffraction angles and neutron wavelengths (Leonardi and Capelli 2022, in preparation). Final unit cell parameters were refined against the fitted positions of the Bragg peaks after the 3D profile integration. The starting model for structural refinement was based on the atomic coordinates of the non-hydrogen atoms from the X-ray structure, while all hydrogen atoms were located from Fourier-difference maps of the nuclear density function. Structure was refined by full matrix least squares on F2 using the SHELXL-2018/3 software (Sheldrick 2008, 2014). The neutron scattering lengths of Ca, B, O and H were taken from Sear (1986). Convergence was rapidly reached, and the H positions obtained by X-ray data were substantially confirmed, but modelled anisotropically (Table 5). A careful inspection of the difference-Fourier maps of the nuclear density showed no evidence of positional or dynamic disorder of the H sites. At the end of the refinements, the variance–covariance matrix showed no significant correlation among the refined variables, with all the principal mean-square atomic displacement parameters positive, H included. Further details pertaining to structure refinement are given in Table 4. Site coordinates and displacement parameters are listed in Tables 5 and 6; selected interatomic distances and angles are given in Table 7. CIF is available upon request to the corresponding author.
Results and discussion
The complex multi-methodological approach of this study, aimed at describing the chemical composition of the meyerhofferite sample, corroborates previous findings about the ideal formula of this mineral, that is CaB3O3(OH)5·H2O. A very modest fraction of Mg (with MgO ≈ 0.03 wt%, Tables 2 and 3) can replace Ca. The only potential substituent of B, in tetrahedral coordination, is Si (with SiO2 ≈ 0.02 wt%, Tables 2 and 3); however, the measured fraction of Si could represent the effect of minor mineral impurities (e.g., quartz or clay minerals) in the sample of meyerhofferite used for the wet chemical analysis. The content of REE and other minor elements is, overall, not significant (Table 1), including that of fluorine as a potential OH− substituent (i.e., < 0.01 wt%). These findings have some relevant geochemical and technical implications: (i) we can infer that meyerhofferite does not behave as a geochemical trap of industrially relevant elements (e.g., Li, Be or REE) and (ii) its almost ideal composition makes this borate a potential B-rich aggregate in Portland concretes, which does not release undesirable elements (e.g., Na) able to activate deleterious reactions for the durability; however, the effects of meyerhofferite on testing and hardening of Portland cement are still unknown. An open question is whether the unusual purity of meyerhofferite is governed by the absence of potential substituents in the growing environment or is dictated by crystallochemical reasons. If we consider the mineral assemblages of the Bigadiç borate deposit, described in one of the previous sections, we are inclined to exclude that potential substituents, especially for Ca, were not available. For any evaporitic basin, we might expect an available source of many fluid–mobile elements (both during formation and later diagenesis), and especially for Mg, Na and K. In addition, the Bigadiç non-marine deposits were fed by thermal springs, associated with local volcanic activity (e.g., Helvaci 1995, 2015, 2019 and references therein; Helvaci and Alonso 2000). Therefore, the availability of potential substituents, at least for Ca, is highly likely. We have recently studied the crystal-chemistry of a series of natural borates, potentially suitable as B-bearing aggregates, and we have reported similar findings for other minerals: colemanite (ideally CaB3O4(OH)3·H2O), kurnakovite (ideally MgB3O3(OH)5·5H2O) and kernite (ideally Na2B4O6(OH)2∙3H2O). For all of those, no significant isomorphic substituents were observed (Lotti et al. 2017a,b, 2019; Gatta et al. 2019, 2020). Considering that the aforementioned borates are from different deposits (colemanite: Bigadiç Mine, Balikesir Province, Marmara Region, Turkey; kurnakovite and kernite: Kramer Deposit, Kern County, California), we are inclined to believe that the surprisingly high level of purity cannot be a peculiarity of meyerhofferite from the Bigadiç borate deposit, but it is rather a common feature of all the borates formed in lacustrine deposits under hydrothermal activity. In this light, we cannot exclude that, in this particular geological environment, crystal nucleation and growth promote purification by iterated dissolution and recrystallization. However, more evidence is required to corroborate this potential mechanism. Furthermore, the configuration of the distorted Ca2+ polyhedron (with CN = 8) likely limits substitution of Ca2+ for ions such as Na+, K+, Mg2+ or Sr2+ due to the resulting significant local distortion of the structure. Even the potential substituents of B, at least in tetrahedral coordination, e.g., Al3+ or Si4+, would generate significant chemical strain. Therefore, we can consider that there are, nonetheless, crystallochemical reasons for the high purity of meyerhofferite.
The X-ray and neutron structure model obtained in this study is consistent with that previously reported by Christ and Clark (1956) and Burns and Hawthorne (1993), by single-crystal X-ray intensity data. The building units of the structure of meyerhofferite consist of: two BO2(OH)2 tetrahedra and one BO2(OH) triangle, linked by corner-sharing to form B3O3(OH)5 rings, and distorted Ca-polyhedra (with CN = 8, CaO3(OH)4(OH2)), linked by edge-sharing to form infinite chains along [001]. The B3O3(OH)5 rings are connected to the Ca-polyhedra chains by corner- and edge-sharing, on two sides of the chains (Fig. 1). These heteropolyhedral chains, made by Ca-polyhedra and B3O3(OH)5 rings, are mutually connected through hydrogen bonding only, giving rise to the tri-dimensional edifice of meyerhofferite (Fig. 2).
More specifically, the structure refinements showed that:
-
1.
The triangular BO2(OH) unit has an almost ideal geometrical configuration, with Δ(B1 O)max ~ 0.01 Å (i.e., here defined as the difference between the longest and the shortest bond distances; X-ray data), O–B1–O angles ranging between ~ 115° and ~ 123°, and aplanarity < 1° (here defined as the average angle described by the plane on which the 3-oxygen sites lie and each of the three independent B1–On vectors) (Table 7). The tetrahedral BO2(OH)2 units show only a modest distortion, with Δ(B2–O)max ~ 0.03 Å and Δ(B3–O)max ~ 0.04 Å, and both with average O–B–O angle of ~ 109.5° (Table 7). The CaO3(OH)4(OH2) polyhedron is more distorted, with Δ(Ca–O)max ~ 0.17 Å (Table 7). As expected, the Ca–O and B–O distances of the same polyhedron are slightly different even in response to the bonding configuration of the oxygen site (i.e., oxygen of an OH− group, H2O molecule or as a bridging site between adjacent polyhedra).
-
2.
The neutron structure refinement shows no evidence of static or dynamic disorder pertaining to the H sites, which is not unusual in this class of material (e.g., in colemanite, Lotti et al. 2017a,b; in kernite, Gatta et al. 2020). Their libration regime is significantly anisotropic, as can be deduced by the Uij tensors, but still acceptable (Table 7, Fig. 2). At least seven of the nine oxygen sites of the structure (i.e., all excluding O3 and O5) are involved in H-bonding, as donors or as acceptors (Table 7).
-
3.
The unique H2O molecule (i.e., H6–O7–H7; Table 7) shows an almost ideal geometry with the H–O–H angle of ~ 105° (neutron data, Table 7). The O–H distances, corrected for “riding motion effect” (following Busing and Levy 1964), range between 0.983 and 1.003 Å (Table 7, neutron data). The two H-bonds of the H2O molecule show Odonor–H…Oacceptor angles ≥ 168° (Table 7), with an energetically favourable configuration (i.e., approaching linearity, Steiner 1998, Gatta et al. 2021), and the Odonor…Oacceptor distances ranging between 2.68 and 2.87 Å with H…Oacceptor between 1.7 and 1.9 Å (Table 7). Concerning the hydroxyl groups (i.e., O2–H1, O4–H2, O6–H3, O8–H4, O9–H5, Table 7), all the O–H distances corrected for “riding motion effect” range between 0.97 and 1.00 Å, Odonor…Oacceptor distances between 2.8 and 2.9 Å, H…Oacceptor between 1.85 and 1.96 Å and Odonor–H…Oacceptor > 156°, excluding the O9–H5 that shows H…Oacceptor ~ 2.26 Å and O9–H5…O2 angle ~ 123° (Table 7). Therefore, all the H-bonds, in which H2O or OH-groups are involved, are relatively strong, excluding the O9–H5…O2 one, which is relatively weak.
-
4.
As the heteropolyhedral chains are mutually connected only via hydrogen bonding, the H-bonds scheme plays a crucial role on the physical properties of the crystal. In particular, the higher number of strong H-bonds have major components along [100] (i.e., O2–H1…O7, O4–H2…O9 and O6–H2…O1, Table 7, Fig. 2) followed by [010] (i.e., O8–H4…O2 and O7–H6…O8, Table 7, Fig. 2). Conversely, along [001] (i.e., the direction of the chains) only the weak O9–H5…O2 and the strong O7–H7…O8 occur (Table 7, Fig. 2). It is worth to note that the weakest O9–H5…O2 bond is actually an “intra-chain” bond. Its configuration is energetically unfavourable (with Odonor–H…Oacceptor ~ 123°); however, no other acceptor is actually available to establish a more favourable interaction. Our recent high-pressure study on meyerhofferite by Comboni et al. (2020b, 2021b) shows that this mineral is relatively soft, with the isothermal bulk modulus KV0 = 31.6(5) GPa, and a marked anisotropic compressional pattern, with mutual relationships of the linearised bulk moduli: K(a)0: K(b)0: K(c)0 ~ 1.5: 1: 3. The lowest compressibility of the structure along [001] is clearly due to the orientation of the heteropolyhedral chains, which act as “pillars” hindering the compression along that direction. On the ab plane, the structure is more compressible along [010] than along [100] (difference of ca. 50%), and this is governed by the H-bonding scheme. All the Odonor…Oacceptor distances were found to decrease significantly with increasing pressure, with a rate ranging between 0.02 and 0.06 Å/GPa, toward a P-induced phase transition bracketed between 3.1 and 3.5 GPa. The transition is a first-order iso-symmetric transformation, marked by an increase in the coordination number of the boron B1 site, from III to IV, leading to a more interconnected and less compressible structure (Comboni et al. 2021b). We can presume that any potential structural destabilization in response to environmental variables (i.e., under chemical, compressional and thermal stress) would affect the H-bonding network first.
-
5.
The H-bonding scheme obtained in this study can explain the complex Raman and IR spectra of meyerhofferite, pertaining to the OH stretching region, given in Frost et al. (2013, 2017) and in the RRUFF database (https://rruff.info/Meyerhofferite). Frost et al. (2013) reported distinct OH stretching Raman peaks at ~ 3400, ~ 3480 and ~ 3610 cm−1, which emerge from a broad band, likely made by the convolution of more active modes. In addition, the IR spectrum available in the RUFF database shows at least five independent active modes ascribable to the OH stretching modes (at ~ 3040, ~ 3300, ~ 3430, ~ 3480, and ~ 3600 cm−1), which are likely superimposed to additional weak ones. The similar geometric configuration of a series of the H-bonds here described on the basis of the neutron structure refinement, in terms of Odonor…Oacceptor and H…Oacceptor (Table 7), can explain the convolution of the vibrational signals.
References
Burns PC, Hawthorne FC (1993) Hydrogen bonding in meyerhofferite : an X-ray and structure energy study. Can Mineral 31:305–312
Busing WR, Levy HA (1964) The effect of thermal motion on the estimation of bond lengths from diffraction measurements. Acta Crystallogr 17:142–146
Carter RS, Palevsky H, Myers VW, Hughes DJ (1953) Thermal neutron absorption cross sections of boron and gold. Phys Rev 92:716–721
Christ CL, Clark JR (1956) The structure of meyerhofferite, Ca2O3B2O3·7H2O, a P-1 crystal, determined by the direct method of Hauptman & Karle. Acta Crystallogr 9:830–830
Comboni D, Pagliaro F, Gatta GD, Lotti P, Milani S, Merlini M, Battiston T, Glazyrin K, Liermann HP (2020a) High-pressure behavior and phase stability of Na2B4O6(OH)2·3H2O (kernite). J Am Ceramic Soc 103:5291–5301
Comboni D, Pagliaro F, Gatta GD, Lotti P, Battiston T, Garbarino G, Hanfland M (2020b) High-pressure behaviour and phase stability of Ca2B6O6(OH)10·2(H2O) (meyerhofferite). Phys Chem Minerals 47:50
Comboni D, Battiston T, Lotti P, Gatta GD, Garbarino G, Hanfland M (2021a) High-pressure behaviour and atomic-scale deformation mechanisms in inyoite, CaB3O3(OH)5·4H2O. Phys Chem Minerals. https://doi.org/10.1007/s00269-021-01173-3
Comboni D, Poreba T, Pagliaro F, Battiston T, Lotti P, Gatta GD, Garbarino G, Hanfland M (2021b) Crystal structure of the high-P polymorph of Ca2B6O6(OH)10·2(H2O) (meyerhofferite). Acta Crystallogr B 77:6
de Meulenaer J, Tompa H (1965) The absorption correction in crystal structure analysis. Acta Crystallogr 19:1014–1018
Derun EM, Kipcak AS (2012) Characterization of some boron minerals against neutron shielding and 12 year performance of neutron permeability. J Radioanal Nucl Chem 292:871–878
Erdogmus E (2014) Combined effect of waste colemanite and silica fume on properties of cement mortar. Sci Eng Compos Mater 21:369–375
Frost RL, López A, Xi Y, Scholz R, Magela Da Costa G, Belotti FM, Malena R, Lima F (2013) Vibrational spectroscopy of the mineral meyerhofferite CaB3O3(OH)5·H2O-an assessment of the molecular structure. Spectrochim Acta A 114:27–32
Frost RL, Scholz R, Ruan X (2017) Thermal analysis, X-ray diffraction and infrared emission spectroscopy of the borate mineral meyerhofferite CaB3O3(OH)5·H2O. J Ther Anal Calorim 128:601–604
Gatta GD, Rotiroti N, Fisch M, Armbruster T (2010) Stability at high pressure, elastic behavior and pressure-induced structural evolution of ‘“Al5BO9”’, a mullite-type ceramic material. Phys Chem Minerals 37:227–236
Gatta GD, Lotti P, Merlini M, Liermann HP, Fisch M (2013) High-pressure behavior and phase stability of Al5BO9, a mullite-type ceramic material. J Am Ceramic Soc 96:2583–2592
Gatta GD, Guastoni A, Lotti P, Guastella G, Fabelo O, Fernandez-Diaz MT (2019) A multi-methodological study of kurnakovite: a potential B-rich aggregate. Am Mineral 104:1315–1322
Gatta GD, Guastoni A, Lotti P, Guastella G, Fabelo O, Fernandez-Diaz MT (2020) A multi-methodological study of kernite, a mineral commodity of boron. Am Mineral 105:1424–1431
Glinicki MA, Antolik A, Gawlicki M (2018) Evaluation of compatibility of neutron shielding boron aggregates with Portland cement in mortar. Constr Build Mater 164:731–738
Gutmann MJ (2017) A 3D profile function suitable for integration of neutron time-of-flight single crystal diffraction peaks. Nucl Instrum Meth A848:170–173
Helvaci C (1995) Stratigraphy, mineralogy, and genesis of the Bigadiç deposits, western Turkey. Econ Geol 90:1237–1260
Helvaci C (2015) Geological features of neogene basins hosting borate deposits: on overview of deposits and future forecasts, Turkey. Bull Miner Res Explor 151:169–215
Helvaci C (2019) Turkish Borate Deposits: Geological Setting, Genesis and Overview of the Deposits. In: Pirajno F, Ünlü T, Dönmez C, Şahin M (eds) Mineral Resources of Turkey Modern Approaches in Solid Earth Sciences, vol 16. Springer, Cham. https://doi.org/10.1007/978-3-030-02950-0_11
Helvaci C, Alonso RN (2000) Deposits of Turkey and Argentina; a summary and geological comparison. Turk J Earth Sci 9:1–27
Içelli O, Mann KS, Yalçın Z, Orak S, Karakaya V (2013) Investigation of shielding properties of some boron compounds. Ann Nucl Energy 55:341–350
Keen DA, Gutmann MJ, Wilson CC (2006) SXD – the single-crystal diffractometer at the ISIS spallation neutron source. J Appl Crystallogr 39(5):714–722
Kinno M, Kimura K, Nakamura T (2002) Raw materials for low-activation concrete neutron shields. J Nucl Sci Technol 39:1275–1280
Korkut T, Űn A, Demir F, Karabulut A, Budak G, Şahin R, Oltulu M (2010) Neutron dose transmission measurements for several new concrete samples including colemanite. Ann Nucl Energy 37:996–998
Kula I, Olgun A, Erdogan Y, Sevinc V (2001) Effects of colemanite waste, cool bottom ash, and fly ash on the properties of cement. Cem Concr Res 31:491–494
Larson AC (1967) Inclusion of secondary extinction in least-squares calculations. Acta Crystallogr 23:664–665
Lotti P, Gatta GD, Demitri N, Guastella G, Rizzato S, Ortenzi MA, Magrini F, Comboni D, Guastoni A, Fernandez-Diaz MT (2017a) Crystal-chemistry and temperature behavior of the natural hydrous borate colemanite, a mineral commodity of boron. Phys Chem Minerals 45:405–422
Lotti P, Gatta GD, Comboni D, Guastella G, Merlini M, Guastoni A, Liermann HP (2017b) High-pressure behavior and P-induced phase transition of CaB3O4(OH)3·H2O (colemanite). J Am Ceram Soc 100:2209–2220
Lotti P, Comboni D, Gigli L, Carlucci L, Mossini E, Macerata E, Mariani M, Gatta GD (2019) Thermal stability and high-temperature behavior of the natural borate colemanite: an aggregate in radiation-shielding concretes. Constr Build Mater 203:679–686
Merlini M, Hanfland M (2013) Single-crystal diffraction at megabar conditions by synchrotron radiation. High Press Res 33:511–522
Okuno K, Kawai M, Yamada H (2009) Development of novel neutron shielding concrete. Nucl Technol 168:545–552
Okuno K, Matsue H, Miyata S, Kiyanagi Y (2013) Neutron activation property of colemanite-peridotite concrete. Nucl Sci Eng 173:139–149
Pagliaro F, Lotti P, Battiston T, Comboni D, Gatta GD, Cámara F, Milani S, Merlini M, Glazyrin K, Liermann HP (2021) Thermal and compressional behavior of the natural borate kurnakovite, MgB3O3(OH)5·5H2O. Constr Build Mater 266:121094
Palache C (1938) Crystallography of Meyerhofferite. Am Mineral 23:644–648
Palmer M, Swihart G (1996) Boron isotope geochemistry An overview. In: Anovitz L, Grew E (eds) Boron: Mineralogy, Petrology, and Geochemistry. Mineralogical Society of America, Washington, pp 709–744
Parkerson CR (1963) Hydrothermal synthesis of hydrated calcium borates. Report of the Defence Technical Information Center, Fort Belvoir, VA 22060–6218. Report Date: 1963-04-30, Accession Number: AD0410863
Rauch H, Waschkowski W (2002) Neutron scattering lengths. In: Dianoux AJ, Lander G (eds) Neutron Data Booklet, 1st edn. Institut Laue Langevin, Grenoble, pp 1–18
Rigaku Oxford Diffraction (2018) CrysAlisPro Software system, version 1.171.38.46. Rigaku Corporation, Oxford
Schaller WT (1916) Inyoite and meyerhofferite, two new calcium borates. U.S. Geol Survey Bull 610:35–55
Sears VF (1986) Neutron Scattering Lengths and Cross-Sections. In: Sköld K, Price DL (eds) Neutron Scattering, Methods of Experimental Physics, vol 23A. Academic Press, New York, pp 521–550
Sheldrick GM (2008) A short history of SHELX. Acta Crystallogr A 64:112–122
Sheldrick GM (2014) SHELXL-2014. University of Göttingen, Germany, Programs for crystal structure determination and refinement
Steiner T (1998) Opening and narrowing of the water H-O-H angle by hydrogen-bonding effects: re-inspection of neutron diffraction data. Acta Crystallogr B 54:464–470
U.S.G.S. (2021) U.S. Geological Survey - U.S. Department of the Interior. Mineral Commodity Summaries 2000–2021. Reston, Virginia (USA). https://www.usgs.gov/centers/national-minerals-information-center/mineral-commodity-summaries.
US3337292A (1967) Preparation of hydrates of 2CaO·3B2O3. United States Patent Office 3,337,292
Uysal M, Al-Mashhadani MM, Aygörmez Y, Canpolat O (2018) Effect of using colemanite waste and silica fume as partial replacement on the performance of metakaolin-based geopolymer mortars. Constr Build Mater 176:271–282
Yarar Y, Bayülken A (1994) Investigation of neutron shielding efficiency and radioactivity of concrete shields containing colemanite. J Nucl Mater 212–215:1720–1723
Acknowledgements
The authors thank the ESRF (Grenoble, France) and the ISIS STFC Rutherford Appleton Laboratory (UK) for the allocation of the beamtime. The support of the Italian Ministry of Education (MIUR) through the projects “PRIN2017—Mineral reactivity, a key to understand large-scale processes” (2017L83S77) and “Dipartimenti di Eccellenza 2018–2022: LE GEOSCIENZE PER LA SOCIETA': RISORSE E LORO EVOLUZIONE” is also acknowledged. Two anonymous reviewers and the Editor Earl F. O'Bannon are thanked for the revision of the manuscript.
Funding
Open access funding provided by Università degli Studi di Milano within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gatta, G.D., Guastella, G., Capelli, S.C. et al. On the crystal-chemistry of meyerhofferite, CaB3O3(OH)5·H2O. Phys Chem Minerals 49, 22 (2022). https://doi.org/10.1007/s00269-022-01199-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00269-022-01199-1