Abstract
Here, we present a comprehensive study that encompasses changes within the crystal and magnetic structure in the brownmillerite-type phase Ca2Fe2O5 induced by the substitution of Fe3+ with Ga3+. 61 synthetic single-crystal samples of Ca2Fe2−xGaxO5 0.00 ≤ x ≤ 1.328 have been investigated by single-crystal X-ray diffraction at 25 °C. We find that pure Ca2Fe2O5 and samples up to x ~ 1.0 have space group Pnma, Z = 4, whereas samples with x > 1.0 show I2mb symmetry, Z = 4. The Raman spectroscopic measurements exhibit that the change from Pnma to I2mb space group symmetry is reflected by a significant shift of two Raman modes below 150 cm−1. These Raman modes are obviously linked to changes in the Ca–O bond lengths at the phase transition. 57Fe Mössbauer spectroscopy was used to characterize the cation distribution and magnetic structure as a function of composition and temperature. Thereby, the strong preference of Ga3+ for the tetrahedral site is verified, as an independent method besides XRD. At room-temperature, Ca2Fe2−xGaxO5 solid solution compounds with 0 ≤ x ≤ 1.0 are antiferromagnetic ordered, as revealed by the appearance of magnetically split sextets in the Mössbauer spectra; samples with higher Ga3+ contents are paramagnetic. Over and above, the substitution of Fe3+ by Ga3+ results in the appearance of sharp, additional magnetic hyperfine split sextets, which can be attributed to cluster configurations within the individual tetrahedral chains. The temperature-dependent (20–720 K) Mössbauer study reveals a transition from the magnetically ordered to the paramagnetic state at a temperature of about 710 K for the Ca2Fe2O5 end-member.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Brownmillerite-type compounds with the general formula A2B’xB2−xO5, where A = alkaline earth metals (e.g. Ca, Sr, Ba) and B’/B = group III or transition-metal atoms (e.g. Al, Ga, Cr, Mn, Co, Fe, and In), are among the most frequently studied oxygen-deficient perovskites. (Abakumov et al. 2004; Anderson et al. 1993; Parsons et al. 2009; Tilley 2016). The group of compounds is named after the mineral Brownmillerite, Ca2FeAlO5, first described by Hansen and Brownmiller (1928). As a solid solution series, Ca2Fe2−xAlxO5 is one of the four most common components of ordinary Portland cement clinkers [e.g., Taylor (1997), Hansen (1928)].
In recent years, the interest in Brownmillerite compounds has risen considerably, as these are handled as promising candidates for oxygen ion conductors, which operate at moderate temperatures for the use as electrodes in solid oxygen fuel cells (SOFC), ceramic membranes for oxygen separation, or catalysts for oxidation of hydrocarbons (Saib et al. 2017; Tsuji et al. 2017). In addition, large magnetoresistance effects have been described in Mn-based brownmillerite-type compounds (Battle et al. 2002, 2004).
The crystal structure of pure Ca2Fe2O5 was first described by Bertaut et al. (1959) and refined later on by Colville (1970) and Berggren et al. (1971). According to Smith (1962), the iron end-member belongs to space group Pnma with a = 5.429(1), b = 14.771(2) and c = 5.599(1) Å. Soon, it was found that the brownmillerite solid solution series Ca2(Fe,Al)2O5 is not isostructural but transforms to I2mb with higher Al substitutional rates (Colville and Geller 1971, 1972; Geller et al. 1973; Kahlenberg and Fischer 2000). In a detailed investigation, the chemically induced phase change in Ca2Fe2−xAlxO5 was investigated by Redhammer et al. (2004) with X-ray diffraction on single crystals; the transition point between the Pnma and the I2mb structure at 298 K was fixed at x = 0.56. At high temperature, superstructure reflections appeared in pure and doped Ca2Fe2O5 pointing to incommensurately modulated high-temperature structures. This issue was investigated in detail by Kruger and Kahlenberg (2005), Kruger et al. (2009, 2011), and Lazic et al. (2008).
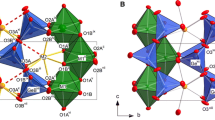
In general, the orthorhombic brownmillerite structure consists of alternating layers of corner sharing BO6 octahedra and single chains of B’O4 tetrahedra stacked along the b-axis. The large cations located in the interstitial sites between the layers are coordinated by eight oxygen atoms, forming distorted bicapped trigonal prisms. In both space groups, the general structural building units are the same; the structural difference depends exclusively on the symmetry relation between the tetrahedral chains. A detailed outline of structural differences is given in the electronic supporting information (ESI) text and Figs. S1–S4.
Contrary to the relatively well-studied Al/Fe solid solution series Ca2Fe2−xAlxO5, the substitution of Ga3+ in the Brownmillerite-type phase Ca2Fe2O5 is far less frequently described in literature. To the best of our knowledge, a corresponding phase transition within the Ga/Fe solid solution series has not been documented in the literature. Kahlenberg and Fischer (2000) investigated a Ga3+-substituted Ca2Fe2O5 sample with x = 0.556. The sample was synthesized by flux growth techniques, belonging to space group Pnma with an amount of about 23% of the total Gallium content in the octahedral site. Their results are contradictory to the studies of Arpe et al. (1974) and Geller et al. (1971a). Both articles stated that Ga3+ is ordered at the tetrahedral site and no Ga3+ is found at the octahedral position up to x = 1.0, respectively; all tetrahedra are filled with Gallium. Grosvenor et al. (2009) synthesized three samples of Ca2Fe2−xGaxO5 (x = 0.5, 1.0, 1.5) by solid-state ceramic sintering techniques, also stating that they belong to Pnma structure type. In this study, XANES and EELS have been applied to characterize the solid solution series, and one of their main results is that more covalent O–Ga bonds are formed (Grosvenor et al. 2009). However, from a preliminary study, it is known that, also within the Ca2Fe2−xGaxO5 series, the chemical-driven phase change from Pnma to I2mb takes place (Redhammer et al. 2005). A comparative and systematic crystal chemical study of changes in structural parameters with variation of the Ga/Fe ratio is unfortunately absent up to now and providing this is one goal of the present study.
Since the early days of Brownmillerite research, also 57Fe Mössbauer spectroscopy has been used to characterize cation distribution, valence state, and magnetic structures. The early work is reviewed by Geller et al. (1971a). Kim et al. (1995) as well as Redhammer et al. (2005) studied a series of Al3+-substituted Ca2Fe2−xAlxO5. It was found that samples up to x = 1.00 are antiferromagnetically ordered at room temperature, and can be evaluated by one octahedral and one tetrahedral magnetically split subspectra. With increasing temperature or increasing Al3+ content, respectively, the local magnetic fields decrease and finally collapse (TN = 518 K for x = 0.0 and TN = 298 K for x = 1.06). Despite the change of space group symmetry, quadrupole splitting at both positions increases almost linearly with increasing Al3+ content. Even at low Al3+ contents, there is always a distribution of Fe3+ and Al3+ over the tetrahedral and octahedral positions with Fe3+ preferring the octahedral positions (Redhammer et al. 2005).
Raman spectroscopy is a versatile and quick tool to receive information about the atomic dynamics within a solid. On this way, Raman spectroscopy enables one to draw appropriate conclusions about phase transitions or the change of symmetry, respectively. Thus, it is surprising that, in contrast to the multitude of structural investigations, only a handful of vibrational spectroscopic studies on Brownmillerite compounds appear in the literature (Bielecki et al. 2014; Gangopadhayay et al. 2009; Glamazda et al. 2015; Islam et al. 2015; Lazic et al. 2008; Mahboub et al. 2012; Piovano et al. 2015; The-Long et al. 2018). Very recently, The-Long et al. (2018) have reported on the change of the Raman modes in Ca2Fe2O5 induced by the substitution of Fe3+ with Al3+. They have succeeded to make a connection between individual Raman modes and the phase transition from Pnma and the I2mb space group. The change in symmetry has especially a significant effect on the Raman peaks below a wavenumber of 150 cm−1, assigned to the movements of the Ca2+ cation (Piovano et al. 2015; The-Long et al. 2018).
This work should contribute to an understanding of the driving forces of tetrahedral chain ordering in Brownmillerite when substituting the more electronegative metal Ga3+ for Fe3+, by performing comprehensive structural and spectroscopic investigations and comparing the results with already published papers, including the results of substituting a less electronegative metal such as Al3+ (Redhammer et al. 2004). Samples along the Ca2Fe2−xGaxO5 series were synthesized using ceramic sintering route; in addition, slow cooling of stoichiometric melts and flux technique were applied to obtain single crystals. X-ray diffraction experiments (XRD), both on polycrystalline powdered ceramic samples (P) and single crystals (SC), scanning electron microscopy (SEM), electron microprobe analyses (EMPA), Mössbauer spectroscopy (MBS), as well as Raman spectroscopy (RS) were applied.
Experimental
Synthesis
Polycrystalline samples of Ca2Fe2−xGaxO5 with 0 ≤ x ≤ 2.0, in steps of x = 0.1, were synthesized using the conventional solid-state sinter reactions. The stoichiometric amounts of CaCO3 (Alfa), Fe2O3 (Merck), and Ga2O3 (Alfa) were mixed and homogenized in an agate mortar under alcohol. The mixtures of the powders were pressed to pellets, put into a Pt crucible and slowly heated up with 120 K/h to 1273 K, and kept there for 12 h in air and cooled down to room temperature with 300 K/h. After this calcination step, the powder samples were crushed, homogenized in a mortar, and pressed to pellets again. During a second heat treatment, the pellets were sintered at 1373 K for 480 h in open Pt crucibles, with one intermediate grinding step. Optically, the material turned from hematite red to dark brown—beige colored—depending on the Ga content, a flowchart of sintering experiments is given in the ESI Fig. S5.
Single crystals were synthesized by two different methods, flux growth and slow cooling from the melt. For the flux growth, stoichiometric mixtures of CaCO3, Fe2O3, and Ga2O3 were weighed and homogenized in an agate mortar. The CaCl2 (melting point 1045 K) was first heated at 130 K for 2 h to remove absorbed water and subsequently added to the starting materials in a ratio of 1:3 (flux: sample). The compounds were mixed again and a 4 g batch of the mixture was placed in a Pt crucible with a Pt cover. The flux growth technique was applied to starting materials with x = 0.1–1.6. The mixture was heated from room temperature to 1323 K with a heating rate of 90°/h and held at this temperature for 24 h to homogenize the melt. Afterwards, the melt was cooled down to 1173 K at a rate of 5 K/h and immediately quenched to room temperature by removing the platinum crucible from the furnace.
The method of obtaining single crystals by slow cooling from the melt was successfully applied by Redhammer et al. (2004) for the series Ca2Fe2−xAlxO5 and was used in a similar way also for this solid solution series. The starting materials (calcined in a previous step) were placed in small Pt tube, welded tight on one side with the other side left open. The tubes were put into a resistance furnace and heated in air up to 1773 K with a heating rate of 60 K/h and held for 10 h, and then cooled down to 1273 K at a rate of 0.1 K/min. The specific arrangement of Pt tubes fixed in larger corundum crucibles is shown in the ESI, Fig. S6.
Electron microprobe analysis (EMPA) and scanning electron microscopy (SEM)
The chemical composition of selected Ca2Fe2−xGaxO5 samples was determined by EMPA using a JEOL JXA 8600 microprobe, acceleration voltage 15 kV, beam current 30 nA, and beam diameter focused to 3 μm. For that purpose, crystals were embedded in epoxy resin, polished, covered with carbon, and analyzed. At least five points from rim to core to rim were measured for each grain, and about ten analyses were performed for each synthesis batch and merged to give the final chemical composition of the sample. The chemical compositions (wt% and structural formula) are reported in Table 1.
X-ray diffraction
For qualitative and quantitative phase analysis of synthesis products, step-scan powder X-ray diffraction data were collected at room temperature in coupled Theta–Theta mode on a Bruker D8 Advance with DaVinci design diffractometer, having a goniometer radius of 280 mm and being equipped with a fast-solid-state Lynxeye detector and an automatic sample changer. Data acquisition was done using Cu Kα1,2 radiation between 5° and 85° 2Θ, with a step size of 0.01°, integration time of 1 s, with the divergence slits opened at 0.3°, while the anti-scatter slit was opened fully at 4°; a primary and secondary side 2.5° soller slit was used to minimize axial divergence, and the detector window opening angle was chosen as 2.93°. Data handling and qualitative phase analysis was done with the Bruker software DIFFRAC.EVA™ V2.1, while, for quantitative phase content determination, the Rietveld program TOPAS™ 4.2 was used (Bruker 2012a, b).
Single-crystal X-ray diffraction data on a total of 61 crystals were collected on a Bruker SMART APEX CCD diffractometer. A single crystal was selected on the basis of its optical properties (sharp extinctions, regular shape, and homogeneity in color) and glued on top of a glass capillary (0.1 mm in diameter). Intensity data were collected with graphite-monochromatized Mo Kα X-ray radiation (50 kV, 30 mA). The crystal-to-detector distance was 30 mm and the detector positioned at − 28° 2Θ using an ω-scan mode strategy at four different ϕ positions (0°, 90°, 180°, and 270°). 630 frames with Δω = 0.3° were acquired for each run. Three-dimensional data were integrated and corrected for Lorentz-, polarization, and background effects using the APEX3 software (Bruker 2015). Structure solution using direct methods and subsequent weighted full-matrix least-squares refinements on F2 were carried out with SHELX-2012 (Sheldrick 2015) as implemented in the program suite WinGX 2014.1 (Farrugia 2012).
Mössbauer spectroscopy
Transmission 57Fe Mössbauer spectra were collected using a Mössbauer apparatus (HALDER electronics, Germany) in horizontal arrangement (57Co/Rh single-line thin source, constant acceleration mode, symmetric triangular velocity shape, multi-channel analyzer with 1024 channels, velocity scale calibrated to α-iron). For Mössbauer—absorber preparation—samples were carefully ground under ethanol, filled into Cu-rings (inner diameter 10 mm and covered with a high-purity Al-foil on one side), and mixed with epoxy resin to fix the sample. The folded spectra were analyzed using classical full-static Hamiltonian site analysis (using Lorentzian shaped doublets) or a Voigt-based hyperfine-field distribution method as implemented in the program RECOIL (Rancourt and Ping 1991).
Raman spectroscopy
The polycrystalline brownmillerite Ca2Fe2−xGaxO5 samples were examined at room temperature by Raman spectroscopy with laser excitation at 532 nm and 780 nm. The Raman measurements were done using a Thermo DXR Raman microscope (Thermo, Madison, USA) equipped with a confocal microscope BX41 (Olympus Corp., Japan), the spectrometer running with the Thermo Omnic 8.0 acquisition software. The diameter of the laser spot due to a 10× microscope objective (NA = 0.25) was approximately 2.5 μm, and the laser power on the samples 1 mW at both excitation wavelengths. The Raman data set was acquired using a high-resolution grating (50–1800 cm−1), and a 50 μm pinhole-like entrance slit to the spectrometer, resulting in an apparatus function with full width at half maximum in the range of 2 cm−1. All measurements were performed with an exposure time of 90 s and four accumulations. For each polycrystalline brownmillerite sample, Raman spectra were collected in at least two different positions.
Results and discussion
Synthesis and materials’ chemistry
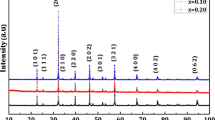
Phase pure polycrystalline sample material of the Ca2Fe2−xGaxO5 series was obtained up to x = 1.5, at higher substitutional rates increasing amounts of CaGa2O4 appeared pointing to a limited substitution rate. Different to Grosvenor et al. (2009), there are several evidences in the PXRD data for a compositional driven Pnma → I2mb phase change. The Bragg peaks 111, or 131, appearing between 23–24° and 29–30° 2θ, can be used to detect the phase transition from Pnma to a body-centered cell. These h + k + l = 2n + 1 reflections are forbidden in the body-centered cell of the I2mb space group. As depicted in Fig. 1, these Bragg peaks are clearly visible up to x = 1.0, decrease in intensity for samples with x = 1.1 and 1.2 and are completely absent in the phase pure samples with x > 1.3. These later data can only be indexed assuming I2mb symmetry. The presumption of a phase transition is confirmed by single-crystal X-ray diffraction data (see “Single-crystal X-ray diffraction”).
Flux growth experiments resulted in idiomorphic, cuboid-to-prismatic black crystals. Very thin translucent crystals or crystal splinter show a reddish-brown color. The crystal habitus changes depending on the composition of the starting materials. The Brownmillerite crystals grown from starting mixtures with x = 0.1–0.9 are exclusively cuboid shaped with up to 0.5 mm edge length. A higher content of Ga3+ in the mixture results in platy-shaped crystals with an edge length up to 2 mm (see Fig. 2). EDX and SC-XRD results show that the amount of Ga3+ substitution for Fe3+ is significantly lower than expected from the starting material and below x < 0.8 in all cases. An initially assumed relationship between the phase transition and the change in crystal habitus, thus, cannot be confirmed.
Due to the fact that it was not possible to obtain a continuous Ga/Fe solid solution series by growth from a flux, crystals were directly synthesized by slow cooling of melts with starting materials with 0.1 ≤ x ≤ 1.6. For Fe-rich starting materials, large idiomorphic crystals up to 0.3 mm could be obtained from coarse-grained crystallized melts. With increasing Ga3+ content, crystals became smaller with less developed faces and a more non-isometric, platy habitus. Single crystals from selected compositions were analyzed with EMPA and the results are given in Table 1 (wt% and structural formula). These are in excellent agreement with those obtained from single-crystal refinements. Backscattered electron micrographs reveal homogeneous crystals (uniform color of the SEM-BSE images) for most of the series, ESI Fig. S7.
Figure 3 summarizes a comparison of nominal vs. observed Ga3+ content in the samples, determined from SC-XRD via site occupation refinement and from EMPA of melt grown crystals. It is evident that both flux-grown and melt grown crystals generally have smaller Ga3+ contents than expected from the starting material. This may be due to loss of Ga3+ to the Pt crucibles or due to evaporation of Ga2O3. While, for the high-temperature melt grown crystals, no saturation is observed up to maximum Ga3+ contents of ~ 1.3 atoms per formula units (apfu), for CaCl2 flux-grown crystals, the maximum amount of Ga3+ incorporations is limited to ~ 0.7 apfu. For small Ga3+ contents, different crystals have very similar compositions, indicating the formation of homogeneous substitutions; the scatter in individual crystal compositions is larger at high Ga3+ contents, which points to some different Ga/Fe distribution during crystal formation.
Comparison of nominal vs. effective Ga3+ content of single crystals of the Ca2Fe2−xGaxO5 solid solution series. Blue crossed squares = single crystals obtained from CaCl2 flux growth, filled red squares = single crystals obtained from high-temperature melt growth; the dashed line would correspond to the formation of ideal crystals corresponding to starting material
Single-crystal X-ray diffraction
Up to now, it was assumed that the substitution of Ga3+, in contrast to Al3+, in the Brownmillerite-type phase Ca2Fe2O5 will not lead to a change in space group symmetry. From SC-XRD experiments, the change from the primitive Pnma to the body-centered I2mb cell takes place at x ~ 1.0 at 25 °C. The change in space group is derived by the analysis of systematic extinctions and intensity statistics and subsequent structure refinements; data from Redhammer et al. (2004) were taken as starting values. Intensity statistics exhibits that samples up to Ca2Fe1.10Ga0.90O5 are centrosymmetric with \(\left|{E}^{2}-1\right|=0.864-0.933\), close to the statistical expectation value of 0.968. For samples with x ≥ 0.99, a notable change of \(\left|{E}^{2}-1\right|=0.673-0.716\) (expected value for non-centrosymmetric structures is 0.736) and the systematic absence support the assignment of the acentric space group I2mb. The appearance of this phase for the Ca2Fe2−xGaxO5 solid solution series was not mentioned in the literature so far. Refinements in Pnma or I2mb converge to low wR2-values and lead to chemical compositions close to the values obtained by EDX and EMPA. The structure refinements of a total of 61 crystals with anisotropic atomic displacement parameters and consideration of substitutional disorder converged to final R1 (all data) values below 5% and final wR2 (all data) values below 7% (data sets corrected for absorption effects); only 6 samples show higher values. These data have x values of 1.0–1.05 and hint that, in this range, a regular intergrowth of the Pnma and the I2mb structure is present, similar to the one described recently by Piovano et al. (2015). These authors modeled this intergrowth using an intermediate Imma model; however, we did not succeed in applying the Imma model to these data.
Experimental details on data collection and results of structure refinement of selected samples are given in Table 2; the fractional atomic coordinates, and anisotropic and equivalent isotropic atomic displacement parameters are compiled in Table 3, while Table 4 gives selected bond lengths and additional secondary structural parameters. The electronic supporting information displays a set of plots showing the variation of various structural parameters with total Gallium content; the full set of data is also available as CIF, while various diagrams for variations of structural parameters with total Ga3+ content are compiled in the electronic supporting information (ESI).
The equivalent isotropic displacement parameters (Ueq) slightly decrease for all atoms with increasing Ga3+ substitution (see ESI Fig. S8). The isotropic as well as the anisotropic displacement parameters do not show any variation at the phase transition and are in good agreement with the values usually observed for inorganic compounds. The largest Ueq is observed for the O2 atom, which links the octahedral layer with the tetrahedral chain. The smallest equivalent atomic displacement parameters are found for the M (octahedral) and T (tetrahedral) cations. The O2, O3, and Ca atoms have nearly the same values. This and the low R values hint that all the samples exhibit tetrahedral chain ordering, either the one of the Pnma (LRLR…) or the one of the I2mb structures (LL or RR) but no mixture/ intergrowth of them with a disordered average structure. A proof for this, however, would only be possible by HRTEM.
The asymmetric unit of the Pnma structure is composed of the following: one Ca atom found on the general position 8d; three different O atoms, of which O1 and O2 are on general position 8d and O3 is on the special position 4c (site symmetry m); the Fe and Ga atoms are distributed on two different crystallographic sites: the M-site cations Fe1/Ga1 on special position 4a (site symmetry \(\stackrel{-}{1}\)) and the T-site cations Fe2/Ga2 on special position 4c. The phase transition results in a symmetry reduction to the orthorhombic non-centrosymmetric space group I2mb, with the asymmetric unit composed of one Ca atom found on the general position 8c; three different O atoms, of which O1 and O2 are on general position 8c and O3 is on the special position 4b (site symmetry m); the Fe and Ga atoms are randomly distributed on two different crystallographic sites: the M-site cations Fe1/Ga1 on special position 4a (site symmetry 2) and the T-site cations Fe2/Ga2 on special position 4b. The framework of the Brownmillerite in the Pnma and the I2mb modification in different orientations is compared and displayed in Fig. 4; the main differences are outlined in the ESI.
Lattice parameters
Substitution of Ga3+ for slightly larger Fe3+ atoms in Ca2Fe2O5 leads to a decrease of the lattice parameters a and b. In contrast to that, the c unit-cell parameter vs. Ga3+ content (Fig. 5) shows a linear increase up to x ~ 1.0 and a decrease afterwards. At x ~ 1.0, discontinuities appear in all three unit-cell parameters and in the unit-cell volume. The change in symmetry is, therefore, also clearly reflected as discontinuities in the variation of lattice parameters. The data for the samples produced by ceramic sintering are also included and show excellent agreement with those of SC-XRD. The plot of a unit-cell parameter vs. Ga3+ content is a straight line within the centrosymmetric phase, and the same is true for the b unit-cell parameter. The a- and b-lattice parameter decrease strongly by 0.032 and 0.072 Å from x = 0.0 to x = 0.989, whereas the c-lattice parameter slightly increases by 0.012 Å in the same x range. Above the discontinuity point, the a-lattice parameter decreases more sharply by 0.015 Å with increasing amount of Ga3+, while b decreases with a smaller slope as well by 0.015 Å, than within the Pnma phase. Data from the literature are approximately consistent with our results. Our data, however, give rise to smooth variations with compositions, which go beyond to what can be learned from literature so far. This especially accounts for the change in slope direction for the c unit-cell parameter at the phase transition composition.
Compositional variations of unit-cell parameters for the Ca2Fe2−xGaxO5 solid solution series at 25 °C. Linear regression curves are fitted to the data and serve as guides to the eye; red triangles represent data for samples, synthesized by slow cooling from the melt in the Pnma symmetry, green squares = flux growth samples in Pnma, orange diamonds = melt grown samples in I2mb, open blue circles = data from powder samples synthesized at 1373 K, and open crossed squares = data from the literature (Arpe et al. 1974; Kahlenberg and Fischer 2000; Grosvenor 2009); if not visible, the estimated standard deviations are smaller than the symbols
As outlined above, the phase change occurs at Ga3+ contents of x ~ 1.0; however, in PXRD data, body-centered forbidden Bragg peaks are observed up to x ~ 1.2. Similar observations have been made for the brownmillerite-phase Ca2MnGa1−xAlxO5 by Abakumov and coworkers and are interpreted as the co-existence of the two space groups Pnma and I2mb within one crystallite (Abakumov et al. 2004, 2005). By high-resolution electron microscopy, they were able to show that the compounds consist of closely intermixed phases with the I2mb and Pnma space symmetry, forming separate crystallites together with narrow I2mb domains in the Pnma matrix. This narrow I2mb domains embedded into the Pnma matrix can be identified as coalescence of translational interfaces, the so-called antiphase boundaries.
Cation distribution
By refining the site occupation factors for the octahedral and tetrahedral site, it was possible to determine the cation distribution of Fe3+ and Ga3+ over the corresponding positions. Our results show that the distribution is far from random and that Ga3+ strongly prefers the tetrahedral site. For samples, crystallized directly from the melt, Ga3+ ions just enter the tetrahedral coordinated site up to a total Ga3+ content of x ~ 0.5; for the flux-grown samples, this behavior is found up to x ~ 0.3. Above these values, there is a distribution of Ga3+ and Fe3+ over the octahedral and tetrahedral site, still with a preference of the tetrahedral site; the slope of the data is close to the one of an equal distribution, meaning that additional Ga3+ distributes equally over both sites within the Pnma phase. After the phase transition, the trend of the data points for \({\text{Ga}}_{\text{tot}}^{3+}\) vs. \({\text{Ga}}_{\text{oct}. \text{site}}^{3+}\) first follows the same straight line; however, it starts to deviate slightly with a slope greater than that for a random distribution. This finding shows that, above \(x\left({\text{Ga}}_{\text{tot}}^{3+}\right)=1.2,\) additional Gallium preferentially fills the octahedral site. The site distribution, which was calculated from the Mössbauer data, fits very well the one of the samples, crystallized directly from the melt, extending the data range to higher total Ga3+ values.
The results are contrary to the findings of Arpe et al. (1974), who postulated an octahedral site substitution of Ga3+ only after all tetrahedra have already been filled. Already, Kahlenberg and Fischer (2000) published crystallographic data of one single crystal, synthesized by flux growth method, which is consistent with our results. Their structure refinement yields the chemical composition Ca2(Fe0.874Ga0.126)oct(Fe0.570Ga0.430)tetrO5, which is similar to the cation distribution in our sample with Ca2(Fe0.828Ga0.172)oct(Fe0.509Ga0.491)tetrO5. The atomic displacement parameters, which are very sensitive parameters for the correctness of cation distribution, have the same order of magnitude in both the samples.
The octahedral site
At the octahedral site, two groups of individual M–O bond lengths can be distinguished. In pure Ca2Fe2O5, there are two symmetry non-equivalent pairs of bond distances M–O1 in the range 1.961(2)–1.969(2) Å, and the equatorial O1 atoms are related to each other by a center of inversion in Pnma. The longer distances have lengths of 2.121(2) Å and correspond to the apical O2 atoms, bridging the octahedral sheet with the tetrahedral chains along the b-axis. In pure Ca2Fe2O5, the average out of the <Fe–O> has a value of about 2.017(1) Å and it remains almost constant with increasing overall Ga3+ content within the Pnma phase but decreases in the I2mb phase. This is due to the fact that Ga3+ mainly enters the tetrahedral site first in the Pnma phase, but also substitutes in distinct amounts to the octahedral site within I2mb as observed from the site occupation numbers.
In particular, substituting the smaller Ga3+ cation [6]r = 0.62 Å for the slightly larger Fe3+ cation [6]r = 0.6645 Å (Shannon and Prewitt 1969) results in a linearly decrease of the M–O1 bond distances and an increase of the M–O2 bond distances by ~ 0.5% within the Pnma phase, thereby elongating the octahedra to some extent. At the phase transition, a significant jump in one of the equatorial bond lengths and the apical bond lengths to lower values is observed. The jump stems from the reduction of the symmetry resulting in a small movement of the M-site cation in x-direction within the (0 1 0) plane. The M cation, located at 0, 0, 0 in Pnma, is slightly displaced along the a direction in I2mb with coordinates x, 0, 0. Within the equatorial plane of the octahedron, the bond lengths between Ga3+/Fe3+ and the O1 atoms (I2mb phase) decrease with a larger slope with increasing total Ga3+ content, by 0.2 and 0.3% from x = 0.989 to x = 1.328. The course of the long M–O2 bonds vs. total Ga3+ content data changes the slope direction after phase transition, so that the initial value (x = 0) and the final value (x = 1.328) for the bond lengths are nearly identical. As a consequence, the Pnma to I2mb phase transition is associated with a decrease of the MO6-polyhedral volume. For the M–O bond lengths, there are several alterations also for the O1–O1 and O1–O2 distances, defining the edges of the (Fe3+, Ga3+)O6 octahedron. The average O–O edge lengths at first stay constant with increasing Ga3+ content. However, the phase transition is associated with a marked drop and a variation in slope, so the average O–O edge decreases linearly with increasing Ga3+ content within the I2mb. In general, the alterations of the O–O edges are more pronounced both in the course of Ga3+ substitution and reach up to 1.5% of the values in pure Ca2Fe2O5 (see ESI) (Fig. 6).
Content of Ga3+ at the octahedral site, indicating a distinct preference of Ga3+ for the tetrahedral site for samples of the Ca2Fe2 −xGaxO5 solid solution series at 25 °C. Quadratic regression curves are fitted to the data and serve as guides to the eye; blue crossed squares = flux gown samples, red filled squares = melt grown samples in Pnma, orange diamonds = melt grown samples in I2mb, and dark blue circles = data from Mössbauer spectroscopy in the paramagnetic state
Octahedral bond angels O–M–O range between 86.6° and 93.4° in Ca2Fe2O5. The incorporation of Ga3+ slightly modifies them within both crystallographic phases. The changes are moderate and less than ~ 0.5° in the Pnma phase and not appreciable in the I2mb phase. By the reduction of the octahedron´s symmetry from \(\stackrel{-}{1}\) to 2, the central M cation is allowed to move freely along the a-axis, whereby jumps and drops of the bond angles were established. One of the O1–M–O1 bond angles splits up like the corresponding M–O1 bonds and decreases or increases by 1.1°. The O1–M–O2 alter their angles in range between 0.7° and 4.2°. For more details, the reader is referred to the ESI. A sketch of the different geometry of the equatorial plane of the octahedra is shown in Fig. 7.
The degree of polyhedral distortion expressed by the bond-length distortion parameter (BLD) and the octahedral angle variance (OAV) is shown in Fig. 8e, f. Within the Pnma phase, they deviate from regularity and become more distorted with increasing Ga3+ content. Similar can be seen from the edge length distortion parameter (ELD). The ELD index (in the range of 2.4–3.0%) indicates a weaker distortion of the octahedron edges in comparison to the related BLD index (in the range of 3.5–3.9%). It should be noted, here, that there is no change in slope or discontinuity in any of the three parameters within Pnma. With the change from Pnma to I2mb, OAV and ELD increase; increasing the substitutional rate of Ga3+ does not change the BLD, while it slightly decreases OAV and ELD. These observations have some important significance for the interpretation of Mössbauer data (Fig. 9).
Variation of structural parameters at the octahedral site for the Ca2Fe2 −xGaxO5 solid solution series at 25 °C. Average (a) and individual M–O bond lengths (b–d) as well as bond-length distortion (BLD) values. Linear regression curves are fitted to the data and serve as guides to the eye; blue squares and green circles = data for samples synthesized by flux growth and slow cooling of the melt in Pnma symmetry, respectively; red triangles = data for samples synthesized by slow cooling of the melt in I2mb symmetry of the samples
Variation of structural parameters at the tetrahedral site for the Ca2Fe2 -xGaxO5 solid solution series at 25 °C. Average (a) and individual M–O bond lengths (b–d) as well as bond-length distortion (BLD) values. Symbols as in Fig. 8
The tetrahedral site
In Ca2Fe2O5, two groups of bond distances can be distinguished within the tetrahedra: first, 1.838 Å for the T–O2 bonds and, second, two different T–O3 bond lengths in the range of 1.908–1.920 Å. With increasing Ga3+ substitution, all T–O bonds decrease distinctly following a linear trend for the Pnma phase and also for the I2mb phase, but with a change in slope (Fig. 9a). This shortening is a direct indication for the Ga3+ substitution. The shorter T–O2 bonds connecting the tetrahedral chain with the octahedral layer decrease by 1.1% from x = 0.0 to x = 0.902. After the phase transition, the T–O2 bond stays at the same value. The longer T–O3 bonds connect the tetrahedra to chains, running along [1 0 0]: both bonds shorten by nearly the same magnitude, namely 0.7% and 0.9%, within the Pnma phase, but behave differently after the phase transition. The shorter of the two T–O3 bonds remains more or less unchanged, whereas the other bond increases the downward slope. According to the BLD index, the distortion of the T –O bonds in the tetrahedral is less than in the octahedra. It slightly increases toward the phase transition, but decreases again; afterwards, the overall changes, however, are small.
Average Ca–O bond lengths and bond-length distortion (BLD) values for Ca polyhedron in the Ca2Fe2−xGaxO5 solid solution series at 25 °C. Errorbars are smaller than the symbols, if not visible. Symbols as in Figure 8
The O–O interatomic distances in Ca2Fe2O5, defining the edges of the tetrahedron, can also be divided into two groups. Three out of the four independent edges are within 3.002(1) Å and 3.047(1) Å, but the fourth distance (O2–O2) is distinctly longer at 3.29(1) Å. The O2–O2 distance runs parallel [0 1 0] and directly represents the distance between the tetrahedral layers. As illustrated in Fig. 9b, the distance decreases in a linear way for the I2mb phase, while, for the Pnma phase, the reduction in the O2–O2 edge is absent. This correlates well with the observed variation of the b-lattice parameter, which has a smaller decrease in the I2mb phase. With increasing total Ga3+ content, the O2–O3 interatomic distances linear decrease, with the same slope in both phases, overall by 0.7% and 1.6%. As a result, both O2–O3 distances have nearly the same value at x = 1.328; all in all, the difference decreases from 0.0304 Å (x = 0) to 0.0055 Å (x = 1.328). In the Pnma phase, the O3–O3 edge of the tetrahedron becomes distinctly shorter. At the phase transition, a small jump towards higher values can be seen. All these changes cause the ELD to decrease somewhat with increasing Ga3+ towards the phase transition, while, in the body-centered cell, it is positively correlated with the total Ga3+ content.
Generally spoken, a regular tetrahedron is composed of four threefold rotation axes, whereby the axis together each form an angle of 109.47°. The average O–T–O angle in the Ca2Fe2 −xGaxO5 compounds is close to this value and comes as close as 0.15° to the ideal angle, at the phase transition. The individual bond angles, however, differ widely one from another, in a range between 105.51° and 122.3° in Ca2Fe2O5. The largest value occurs for the tetrahedral cation T and the two O2 atoms, which form the link between the tetrahedral chains and the octahedral layers. The variation of O–T–O angles with composition is inhomogeneous: For angles below 109.47°, they increase with increasing Ga3+ or remain nearly constant; the large O2–T–O2 decreases. In contrast to the others, the O3–T–O3 bond angle slightly jumps upon the transition from the primitive to the body-centered cell. Apart from that, the O3–T–O3 angle increases linearly and with the same slope within the whole solid solution series. This behavior is in contradiction with the reduction of the O3–O3 distance and will be compensated by the decrease of the T–O3 bond lengths. The big differences in the individual tetrahedral angles are mirrored by the quadratic tetrahedral angle variance (TAV), which, however, decreases within the Pnma phase, revealing the tetrahedron to become more and more regular with increasing Ga3+ content. This is, however, not valid any more in the I2mb phase, where ELD and TAV parameters increase again.
Depending on the Ga3+ concentration of the Ca2(Fe2 −xGax)O5 solid solution series, the tetrahedral chain will be stretched or compressed by the tilting of the TO4 polyhedron. In Ca2Fe2O5, the kinking angle is 125.8° and deviates substantially from the straight configuration (O3–O3–O3 = 180°). With increasing Ga3+ content, the kinking stays at the same value. After a small jump, at the phase transition, increasing Ga3+ causes a small decrease of the O3–O3–O3 angle, i.e., the tetrahedral chain becomes more compressed. The length of the a-axis is directly related to changes in the length of the O3–O3 tetrahedral edge and O3–O3–O3 kinking angle. Within the Pnma phase, exclusively, the decrease of the O3–O3 distance is responsible for the reduction of the length of the a-axis.
The interstitial site
Manipulating the B/B’-cation composition is also reflected in the geometry of the Ca2+-site. The calcium ion is surrounded by an irregular polyhedron of eight oxygen atoms, forming a distorted bicapped trigonal prism. In Ca2Fe2O5, the Ca–O distances range from 2.323 to 3.001 Å. The distorted bicapped trigonal prism shares with the adjacent polyhedrons, three common octahedron faces, one common O1–O1 octahedron edge, and one common O2–O3 tetrahedron edge. The mean of the eight different Ca–O bond lengths decreases linearly with increasing Ga3+ for both the Pnma and the I2mb phase, however, with different slopes and a slight jump at the phase transition. Overall, the <Ca–O> decreases by 0.0174 Å (0.69%) from x = 0.0 to x = 1.33, as an effect of decreasing octahedral and tetrahedral size. The individual Ca–O bond lengths show different compositional variation in the Pnma and I2mb phase, which are displayed in the ESI. The bond-length distortion index takes all Ca-O bond lengths into account and becomes smaller for Ga3+-rich compositions. It reduces from 6.37 to 4.97% with the most marked change at the phase transition; within both phases, the BLD index stays nearly constant.
The Ca–O2 bonds connect the Ca2+ cation to both the tetrahedral chain and the octahedral sheet. As the Ga3+ content increases, the shortest Ca–O2 bond becomes slightly shorter, while the intermediate Ca–O2 bond length stays unchanged and the longest bond becomes significant shorter. The difference between the shortest and the longest Ca–O2 bond decreases from 0.676 Å at x = 0 to 0.628 Å at x = 1.328. After the phase transition, all Ca–O bonds stay nearly at the same level, excluded the longest Ca–O2 bond. It seems that the higher content of Ga3+ at the octahedral site above x = 0.5, for flux-grown crystals, has a measurable impact to some of the Ca–O bonds.
Mössbauer spectroscopy
At room temperature, Ca2Fe2 −xGaxO5 solid solution compounds with 0 ≤ x ≤ 1.0 are antiferromagnetic ordered, as revealed by the appearance of magnetically split sextets in the Mössbauer spectra, samples with higher Ga3+ contents are paramagnetic. For pure end-member Ca2Fe2O5, the magnetic structure was described several times to be antiferromagnetic with the magnetic moments being directed approximately along the c-axis (Berastegui et al. 1999; Ceretti et al. 2012; Geller et al. 1970, 1971b, 1973). In a recent study, Auckett et al. (2015) re-refined the structure to be a canted G-type antiferromagnet, with the moments still directed approximately to the c-axis, however, with a small tilt of ~ 15° and ~ 9° away from c for the octahedral and tetrahedral sites, respectively. There are no components of the magnetic moment along b; this magnetic spins are within the a–c plane. Using this information, model building for data evaluation of Mössbauer spectra of pure Ca2Fe2O5 is reported first in the following paragraph.
End-member Ca2Fe2O5
At T < 700 K, pure Ca2Fe2O5 shows 11 lines in its Mössbauer spectrum, arising from the presence of both magnetic dipole as well as electric quadrupole interactions (Fig. 12a, b). The lines correspond to two different magnetically split hyperfine spectra of high spin Fe3+ in octahedral and tetrahedral coordination, respectively. Symmetry restrictions give first aids for data evaluation. The point symmetries of the octahedral and tetrahedral sites are \(\stackrel{-}{1 }\) and m, respectively. Therefore, the electric field gradient (EFG), which is a second rank tensor with the diagonal elements \(\left|{V}_{zz}\right|\ge \left|{V}_{yy}\right|\ge \left|{V}_{xx}\right|,\) has no symmetry restrictions at the octahedral site. At the tetrahedral site, however, one principal axis of the EFG has to be perpendicular to the a–c mirror plane, thus restricting the other 2 EFG-axes to it. From this, the polar angle θ, which defines the angle between \({V}_{zz}\) and the direction of the internal magnetic field \({H}_{\text{f}}\), has to be 0° or 90° for the tetrahedral site (Geller et al. 1971a). The best results in data evaluation were obtained when θ = 90°, i.e., \({V_{zz}}\left\| b \right.\), consistent with the magnetic spin structure and \({H}_{\text{f}}\) is in the (0 1 0) plane for both sites. Even if allowed to refine freely, also for the octahedral site, the angle θ ~ is 90° and thus is in agreement with the magnetic structure.
In addition, the analysis of paramagnetic spectra at temperatures above 720 K shows the \(\varDelta {E}_{\text{q}}\) splitting values on octahedral and tetrahedral sites to be large but having similar values of ~ 1.4–1.5 mm/s. Using this information gives restrictions to the value of the angle φ on the octahedral site during the refinement process: it must be close to zero, thereby giving \(\varDelta {E}_{\text{q}}\) ~ 1.45 mm/s and η ~ 0.25. Starting with η ~ 90° during refinements gives \(\varDelta {E}_{\text{q}}\) values of ~ 1.1 mm/s and η ~ 0 over the whole T range inspected. However, a jump in \(\varDelta {E}_{\text{q}}\) at the magnetic-to-paramagnetic transition by more than 0.3 mm/s is unusual and not reliable, and thus, this model was dismissed. For some spectra, it was also possible to get good refinements with \(\varDelta {E}_{\text{q}}\) ~ 1.45 mm/s, and a combination of larger η ~ 0.4, resulting in larger values of ~ 30° for the angle ϕ with the two later parameters being highly correlated. On the statistical basis, these sets of refinements are equal. Finally—on the basis of consistency over all spectra, we have chosen the more simple model, and the Mössbauer spectra were evaluated consistently over the whole T range between 20 and 720 K with a strategy being in concordance with (Geller et al. 1971a), the fitting results are compiled in Table 5. The fitting strategy and the definitions of Mössbauer parameters are also summarized in the ESI Table S1.
In analogy with earlier studies (Geller et al. 1971a; Kim et al. 1995; Redhammer et al. 2004, 2005), the magnetic sub-spectrum with the smaller isomer shift δ = 0.175 mm/s at 298 K is assigned to the tetrahedral site, the sub-spectrum with the larger one (δ = 0.355 mm/s at 298 K) to the octahedral site. Within the experimental error, the area ratio of the subspectra is 1:1 over the whole T range, according to the chemical formula. From this, it can be concluded that the recoil free fractions of Fe3+ at both positions are equal within the experimental error.
The local magnetic field \({H}_{\text{f}}\) is smaller at the tetrahedral sites (\({H}_{\text{f}}\) = 428 kOe at 298 K) than at the octahedral sites (\({H}_{\text{f}}\) = 505 kOe at 298 K). For the tetrahedral site, the asymmetry parameter η is zero (cf. Table 5), meaning that the EFG has axial symmetry (Vxx = Vyy, η = 0). At the octahedral site, it has a small value of ~ 0.25, showing it to be almost axial symmetric. There is no evident change of η with temperature. For both sites, the angle θ refined to values very close to 90° and did not change with temperature, and thus, in final refinements, the angle was fixed to 90° to keep refinements more stable. From θ = 90°, Vzz is oriented in a plane perpendicular to \({H}_{\text{f}}\). Because the easy direction of magnetization is parallel to the c-axis in Pnma symmetry (Auckett et al. 2015), Vzz is parallel to the b-axis for the octahedral and the tetrahedral sites, respectively. In addition, the angle ϕ between Vxx and the projection of \({H}_{\text{f}}\) on the xy plane of the EFG was allowed to refine. For both sites, it slightly deviates from zero, i.e., tilted away from the c-axis by ~ 5° for the tetrahedral and ~ 10° for the octahedral site; however, these angles scatter as a function of temperature and are highly correlated with \(\varDelta {E}_{\text{q}}\) and η, especially for the octahedral site. Nevertheless, the orientation of the EFG suggests the magnetic moments to lie in the a–c plane and is mostly oriented along the c-axis with a slight spin canting. This model is in perfect agreement with the refined magnetic structure of Ca2Fe2O5. A small discontinuity in magnetization data (Zhou and Goodenough 2005), which was assumed to be due to a possible spin rotation, could not be resolved from our data.
With increasing temperature of the absorber, the magnetic fields at both positions decrease, and between 713 and 718 K, there is the transition to the paramagnetic state (Fig. 11c, d). The variation of the internal magnetic field is shown in Fig. 12a for both sites. It was fitted with a phenomenological power law to extract the saturation magnetic fields, critical exponents, and ordering temperatures. These are H0 = 477(2) kOe and 536(2) kOe, TN = 716.7(8) K and 717.1(9) K, and β = 0.36(1) and 0.39(1) for the tetrahedral and the octahedral site, respectively.
Consistently with the literature (Geller et al. 1971a), the quadrupole splitting \(\varDelta {E}_{\text{q}}\) is large and exhibits only a slight temperature variation. It remains almost constant at the octahedral site and increases somewhat for the tetrahedral site (Fig. 12b). Here, there is a small discontinuity at the demagnetization temperature which hints some effects of magneto-elastic coupling. As, for Fe3+, there is a positive correlation of local environment distortion around the probe nucleus and the size of \(\varDelta {E}_{\text{q}}\), this would correspond to a more regular site environment in the paramagnetic state. In general, the large \(\varDelta {E}_{\text{q}}\) values for both sites in Ca2Fe2O5 are indications for distinctly distorted polyhedra, which are in line with the distortion parameters, derived from structure analysis. As is expected from theory, the isomer shift increases with decreasing temperature and saturates at low T. The smooth trend is seen as an indication of the correctness of our model of data evaluation.
Our Mössbauer parameters contrast to some details the findings of (Kagomiya et al. 2017), who found η = 0.36 and 0.41 for tetrahedral and octahedral sites, respectively, and thus, some different values for polar angles are retrieved. However, as the \(\varDelta {E}_{\text{q}}\) value of, especially, the octahedral site is large in their study (1.698 mm/s at 287 K) and drops to 1.360 mm/s at 750 K, which is not observed to take place in our data; we assume that there are some severe correlations between \(\varDelta {E}_{\text{q}}\), η, and ϕ leading to a local, but not global minimum.
The Ca2Fe2−xGaxO5 solid solution series
Mössbauer spectra were collected on polycrystalline samples synthesized at 1373 K at 298 K. The substitution of Fe3+ by Ga3+ has some major influence on the appearance of the Mössbauer spectra: additional, magnetically split components arise first at the tetrahedral site, at higher substitutional rates also on the octahedral site; in addition, the spectra become broadened due to magnetic relaxation effects, especially in the vicinity of the magnetic/ paramagnetic transition. Magnetic ordering breaks down around x ~ 1.0; above this composition, the spectra appear as simple two-line spectra, which could be evaluated with two quadrupole doublets and which allow the extraction of more precise hyperfine parameter variation with composition; these are compiled in Table 6.
For the magnetically ordered spectra, data evaluation was done in two different ways; the corresponding hyperfine parameters are given in Table S2 of the SI. The first approach applies a Voigt line-based fitting method using hyperfine-field distributions (HFD) as proposed by Rancourt and Ping (1991). Besides allowing for a field distribution, which is fortune here for introducing additional hyperfine-field components both at tetrahedral and octahedral sites, also ratios of the spectral areas of the low energy peak (A1) to the high energy peak A3/A1 and A2/A1can be varied. Ideally, these are 3 and 2; however, with increasing magnetic relaxation, the innermost lines of a sextet become more intense, which can be encountered for by these two refinement parameters. Quadrupole interactions are taken into account by refining the quadrupole shift ε, merging \(\varDelta {E}_{\text{q}}\), polar angles ϕ and θ and η into one parameter. Selected spectra refined in this way are displayed in Fig. 13. The second approach uses the classical full-static Hamiltonian site analysis (FSHA), which could satisfactorily be applied up to x = 0.6 and which allows, in principle, the refinement of η, θ, and ϕ independently.
One striking feature of the Mössbauer spectra of the solid solution series compounds at 298 K is the aforementioned appearance of additional magnetically split components at the tetrahedral site. A first additional sextet is already present at x = 0.1 and has a hyperfine field, which is smaller by ~ 30 kOe as compared to the main one; a second one is observable for samples with x = 0.3 whose hyperfine field is smaller by ~ 80 kOe (Fig. 14a). This is consistently observed both in HFD and FSHA analyses. The relative area fractions of these three components change with Ga3+ substitution: the one with the largest hyperfine field gradually decreases on the extent of the other ones, for x > 0.6, only two components are present, the one with the large hyperfine field has diminished (Fig. 14b). For x = 0.8, the relative fractions of the intermediate and small hyperfine-field component are reversed, and for x = 0.9 only, one broad component could be resolved. In general, the size of internal magnetic field of the different components at the tetrahedral site decreases with increasing Ga3+ content. The presence of these different components is explained from different clusters around a tetrahedral site: A central site has two neighboring tetrahedral and two octahedral sites, and as Ga3+ exclusively enters the tetrahedral site up to x ~ 0.5, it is the occupation of the two neighboring tetrahedral sites within the tetrahedral chain, which seems to cause different internal magnetic field strengths: the component with the largest field results from a Fe3+–Fe3+–Fe3+ configuration, the one with the intermediate field from Fe3+–Fe3+–Ga3+, and the one with the lowest field from Ga3+–Fe3+–Ga3+. The isomer shift values (yielding the same values for both evaluation approaches within estimated standard deviation) as well as quadrupole shifts ε stay constant for the tetrahedral site within the magnetically ordered region.
Variation in 57Fe hyperfine parameters for compounds of the Ca2Fe2−xGaxO5 series: a variation of the internal magnetic field, b relative area fractions of different magnetic split components at the tetrahedral site, c variation of the quadrupole shift ε with Ga3+ content for magnetic split subspectra, and d variation of the isomer shift
For the octahedral site, an asymmetric broadening—which has to be overcome by introducing a second HFD component—is observed for x = 0.7 and the internal magnetic field is smaller by ~ 50 kOe. In addition, for the octahedral site, the hyperfine field is decreasing with Ga3+. While the isomer shift is constant up to x = 1.0, a striking feature is observed for the quadrupole shift ε. It is constant at ~ − 0.27 mm/s up to x = 0.5, but then changes significantly to ~ − 0.42 mm/s for x > 0.5 (Fig. 5c). This hints that, within the series, there is a change in one or more of the parameters \(\varDelta {E}_{q}\), η, θ, or ϕ. This cannot be deduced from the HFD analysis but must come from a classic static Hamiltonian site analysis; the results are reported below.
At the tetrahedral site, in analogy to the end-member, the EFG has axial symmetry (η ~ 0), and the angle θ ~ 0. For the octahedral site, η > 0, the polar angle θ ~ 90°, and high correlations of \(\varDelta {E}_{\text{q}}\), η, and ϕ are present. However, with the assumption that \(\varDelta {E}_{\text{q}}\) should be in the range 1.45–1.55 mm/s, based on information from the paramagnetic region, consistent data could be obtained up to x = 0.6 (see Table S2). For higher Ga3+ contents, spectra become too broad and overlapping, and area ratios of the sextets are too far away from ideal 3: 2: 1 ratio due to magnetic relaxation to extract reliable information with this approach. The data suggest that \(\varDelta {E}_{\text{q}}\) at the octahedral site increases by 0.05 mm/s, while the asymmetry parameter stays almost constant. This is what could be expected also from the polyhedral distortion parameters. The marked difference in the refined parameters between x = 0.5 and 0.6 is a distinct rotation of the EFG, i.e., the angle ϕ changes from small values around 10°–45°. Other combinations of parameters with a jump in the \(\varDelta {E}_{\text{q}}\) to 0.9 mm/s and an increase of η to 0.7 were also observed but excluded on basis of smooth variations in ELD and OAV from the structure refinements. This means that the magnetic structure changes jump-like from an almost collinear to a distinct spin-canting structure x > 0.5.
For the paramagnetic region, the spectra consist of two slightly asymmetric resonant absorption lines with a slight shoulder at the left side (∼ 0.80 mm/s) of the high-velocity absorption line. A fit with two doublets, corresponding to the octahedral and tetrahedral sites, respectively, with \(\varDelta {E}_{\text{q}}\) values of ~ 1.45 mm/s for both sites, gives statistically acceptable results (Table S2). The isomer shift and QS value for paramagnetic spectra fit well into the trends extracted from the magnetically split spectra; in addition, some more trends are valid in the paramagnetic region: QS for the tetrahedral site increases, the one on the octahedral site decreases. The decrease of the QS at the octahedral site for samples with high overall Gallium contents corresponds to a decreasing polyhedral distortion, which is in good agreement with what was observed from the distortion parameters QAV and ELD. As it was observed previously for Fe3+, it is the ELD and the OAV around the probe nucleus, which controls the size of the quadrupole splitting and correlates positively with it, rather than the bond-length distortion.
From the relative area ratios for Fe3+ on octahedral and tetrahedral sites, extracted from the HFD approach in the magnetic and classical doublet fits in the paramagnetic region, it can be concluded that Ga3+ prefers the tetrahedral site even at high overall Ga3+ contents, as the amount of Fe3+ on the tetrahedral site steadily decreases. In general, the site distribution, calculated on basis of the area fractions of Mössbauer data, fits excellently the trends, observed also form site occupation factor refinements in single-crystal structure refinements; the two different methods give consistent results.
Raman spectroscopy
The Ca2Fe2O5 Brownmillerite compound is orthorhombic and belongs to the space group Pnma, with the general point group D2h (mmm). At the center of the Brillouin zone, the symmetry assignment of the 108 normal modes of Ca2Fe2O5 Brownmillerite is as follows:
There are, therefore, after removal of the three translations, 48 Raman active modes, 43 IR- active modes, and 14 IR- and Raman-silent Au modes. For the simple factor group analysis, the Bilbao Crystallographic Server was used (Kroumova et al. 2003; Piovano et al. 2015). The following discussion takes into account that isomorphic brownmillerites have similar atomic arrangements and, consequently, comparable Raman spectra. Any differences in the spectra may, therefore, be reduced to discrepancies in the short-range structure (Bielecki et al. 2014; Glamazda et al. 2015).
Non-polarized Raman spectra were collected for polycrystalline powders of the Ca2Fe2 −xGaxO5 series, in a wavenumber range of 50–1800 cm−1 with the laser excitation at 780 nm. The goal was to probe variations in the spectrum caused by the successive replacement of Fe3+ by Ga3+ and the change of symmetry within the solid solution series. The Raman spectrum taken for the Ca2Fe2O5 end-member is shown in Fig. 15. The obtained spectrum is in good agreement with the data published so far (Piovano et al. 2015; The-Long et al. 2018).
The effect of the Ga3+ versus Fe3+ substitution is presented in Fig. 16. Comparing our results with the very recently reported Raman spectroscopic investigations of the Ca2Fe2−xAlxO5 solid solution series, we observe marked variations of the lower wavenumber peaks. For both solid solution series, the disappearance of the 131 reflection in the X-ray powder pattern, as shown in Fig. 1 and in The-Long et al. (2018), is accompanied by the changes of the vibrational modes below 150 cm−1. The region of interest is highlighted by a blue bar, as can be seen in Fig. 17. In these spectral ranges, the modes of vibration involve the motion of the Ca2+ ion, at the interstitial site (Piovano et al. 2015). This concurs to the findings, detected in our structure refinements based on single-crystal X-ray diffraction data. At the phase transition, individual Ca–O bonds significantly change their length, as illustrated in Fig. 10 for the substitution of Fe3+ by Ga3+ and Fig. 17 (Redhammer et al. 2004) for the substitution of Fe3+ by Al3+.
In a proceeding paper, we will report in more detail on orientation-dependent polarized Raman spectra of single crystalline material of the Ca2Fe2 −xGaxO5 series, which—together with DFT calculations—will give deeper insight into lattice dynamics with Fe3+ by Ga3+ replacement and with change of symmetry from Pnma to I2mb.
Conclusion
Single crystals of Ca2Fe2−xGaxO5 could be obtained through flux growth techniques and slow cooling of melts. Using single-crystal X-ray diffraction, it was possible to draw an accurate picture of changes in structural parameters with variation of the Ga/Fe ratio. In contrast to earlier expectations, we found a change from the primitive Pnma to a body-centered I2mb cell taking place at x ~ 1.0 at 25 °C. By refining the site occupation number for the octahedral and tetrahedral sites, it was possible to determine a strong preference of Ga3+ for the tetrahedral site and also monitor slight differences in cation distribution for crystals grown directly from the melt and those grown with flux methods. A former and stronger preference of Ga3+ for the octahedra site, i.e., more equal distribution, for samples grown with flux methods is observed. The different distribution of Ga3+ over the corresponding sites at the same \({\text{Ga}}_{\text{tot}}^{3+}\) concentration is mainly reflected by differences in one Ca–O1, one Ca–O2, and one Ca–O3 bond length.
When comparing the Ca2Fe2−xAlxO5 and the Ca2Fe2 −xGaxO5 solid solution series with each other, several similar data trends can be observed, even if these are more pronounced for the Al substitutional series due to larger differences in ionic radii between Fe3+ and Al3+ (0.10 Å and 0.115 Å) for tetrahedral and octahedral coordinations, respectively, as compared to the difference between Fe3+ and Ga3+ (0.02 Å and 0.025 Å). Due to smaller difference, the phase change composition is shifted to higher substitutional rates.
It is astounding that the maximum Ga3+ or Al3+ content found in the Brownmillerite lattice, for single crystals synthesized under normal conditions, is both time x ~ 1.33, regardless of their ionic radii. The reason for this result may be the preferred occupation of the tetrahedral site by both ions Al3+ and Ga3+, which is already occupied by 80% Fe3+/Ga3+ ions at high x values. The unit-cell volumes are generally declining with increasing Ga3+ or Al3+ contents. The comparison of the bond lengths and angles shows nearly identical behavior for both solid solution series. Worth mentioning are the very similar M–O and T–O bond lengths at the phase transition for the Al and Ga compounds. Within the I2mb phase, the bond lengths of the Ca2Fe2−xAlxO5 solid solution series decrease strongly on the basis of the differences in the ionic radii. Significant differences at the phase transition can be observed for the Ca–O bond lengths and the octahedral angles, which are closely related at a structural point of view.
In 2005, Abakumov put forth the idea that dipole–dipole interactions between the tetrahedral chains are a possible driving force causing various patterns of tetrahedral chain ordering (Abakumov et al. 2005). The model of dipole stabilization by twisting the tetrahedral chains was developed by (Hadermann et al. 2007) who added the influence of the separation between tetrahedral layers (half the length of the b-axis). Parsons et al. (2009) rationalized these arguments into a “structure map” by plotting the tetrahedral chain distortion from 180° against the interlayer separation. The comparison of the Ga3+- and Al3+-doped \({\text{Ca}}_{2}{\text{Fe}}_{2}{\text{O}}_{5}\) series with the “structure map” indicates good agreement for the Ca2Fe2 −xAlxO5 compounds. However, the Ca2Fe2−xAlxO5 series has a change in space group with increasing x, in contrast to the structure map predicted Pnma structure for the whole solid solution series. The failure of the model can be found in the constant O3–O3–O3 kinking angle within the Pnma phase. Our findings show discrepancies in this structure map and indicate that there must be additional effects for stabilizing a specific space group.
From Mössbauer spectroscopy, it was possible to verify the site occupation with an independent method. From the magnetic split spectra of pure Ca2Fe2O5 and samples with low substitutional rates, the proposed spin structure could be confirmed. For both sites, the magnetic moments are aligned along the a-axis with a small spin canting of ~ 5°–10° towards the c-axis; no moment is along b, both for the octahedral and the tetrahedral site. The substitution of Fe3+ by Ga3+ results in the appearance of sharp, additional magnetic hyperfine split sextets for the tetrahedral site, which can be attributed to cluster configurations where a central tetrahedral site has two, one, or non-Fe3+ tetrahedron neighboring within the tetrahedral chain. This assumption is supported by the decreasing intensity of a Fe–Fe–Fe cluster, while those with Ga–Fe–Ga are dominating at high substitutional rates. The magnetic moment orientation on the tetrahedral sites seems to remain unaffected by the Ga3+ incorporation, while, on the octahedral site, a prominent spin reorientation takes place indicated by a change in the quadrupole shift and—in full-static Hamiltonian site analyses—an increase of the azimuthal angle from ~ 10° to 50° within the a–c plane. The final proof for this can only come from neutron diffraction experiments, which are under progress.
To the best of our knowledge, the Raman spectrum of Ga3+-doped Ca2Fe2O5 had not been described in the literature before. The change from Pnma to I2mb space group could be indicated, by the significant change of the Raman modes below 150 cm−1. Theory and our structural investigations suggest that these modes are linked to changes of the Ca–O bond lengths at the phase transition. Our Raman measurements are, therefore, consistent with a recent study on Ca2Fe2−xAlxO5 (The-Long et al. 2018) and correspond with the results obtained from the X-ray diffraction analyses.
References
Abakumov AM, Rozova MG, Antipov EV (2004) Complex manganese oxides with the brownmillerite structure: synthesis, crystal chemistry and properties. Usp Khim 73:917–931
Abakumov AM, Kalyuzhnaya AS, Rozova MG, Antipov EV, Hadermann J, Van Tendeloo G (2005) Compositionally induced phase transition in the Ca2MnGa1−xAlxO5 solid solutions: ordering of tetrahedral chains in brownmillerite structure. Solid State Sci 7:801–811. https://doi.org/10.1016/j.solidstatesciences.2005.01.020
Anderson MT, Vaughey JT, Poeppelmeier KR (1993) Structural similarities among oxygen-deficient perovskites. Chem Mater 5:151–165. https://doi.org/10.1021/cm00026a003
Arpe R, Schenck RV, Mullerbu H (1974) Oxogallates of alkaline-earth metals. 6. Ca2FeGao5, a contribution to crystal-chemistry of M2/2 + ME3/3 + O5 compounds. Z Fur Anorg Allg Chem 410:97–103. https://doi.org/10.1002/zaac.19744100202
Auckett JE, McIntyre GJ, Avdeev M, Bruyn H, Tan TT, Li S, Ling CD (2015) Neutron Laue diffraction study of the complex low-temperature magnetic behaviour of Brownmillerite-type Ca2Fe2O5. J Appl Crystallogr 48:273–279. https://doi.org/10.1107/s1600576714027976
Battle PD et al (2002) Crystal structure and magnetic properties of SrCaMnGaO5 + delta. J Solid State Chem 167:188–195. https://doi.org/10.1006/jssc.2002.9641
Battle PD et al (2004) Ca2.5Sr0.5GaMn2O8: diamagnetic Ga in control of the structural and electronic properties of a bilayered manganate. J Am Chem Soc 126:12517–12527. https://doi.org/10.1021/ja0485000
Berastegui P, Eriksson SG, Hull S (1999) A neutron diffraction study of the temperature dependence of Ca2Fe2O5. Mater Res Bull 34:303–314. https://doi.org/10.1016/s0025-5408(99)00007-0
Berggren J (1971) Refinement of crystal-structure of dicalcium, ferrite, CA2Fe2O5. Acta Chem Scand 25:3616. https://doi.org/10.3891/acta.chem.scand.25-3616
Bertaut EF, Blum P, Sagnieres A (1959) Structure Du ferrite bicalcique et de la Brownmillerite. Acta Crystallogr 12:149–159. https://doi.org/10.1107/s0365110x59000433
Bielecki J, Parker SF, Ekanayake D, Rahman SMH, Borjesson L, Karlsson M (2014) Short-range structure of the brownmillerite-type oxide Ba2In2O5 and its hydrated proton-conducting form BaInO3H. J Mater Chem A 2:16915–16924. https://doi.org/10.1039/c4ta03213f
Bruker (2012a) Diffrac.EVA V2.1 (version 2012). Bruker AXS Inc, Madison
Bruker (2012b) Topas V4.1 (version 2012). Bruker AXS Inc, Madison
Bruker (2015) APEX3 (version 2015. 10.0). Bruker AXS Inc, Madison
Ceretti M et al (2012) Growth and characterization of large high quality brownmillerite CaFeO2.5 single crystals. Crystengcomm 14:5771–5776. https://doi.org/10.1039/c2ce25413a
Colville AA (1970) Crystal structure of Ca2FeO5 and its relation to nuclear electric field gradient at iron sites. Acta Crystallogr Sect B Struct Crystallogr Cryst Chem B 26:1469. https://doi.org/10.1107/s056774087000434x
Colville AA, Geller S (1971) Crystal structure of Brownmillerite, Ca2FeAlO5. Acta Crystallogr Sect B Struct Crystallogr Cryst Chem B 27:2311. https://doi.org/10.1107/s056774087100579x
Colville AA, Geller S (1972) Crystal–structures of Ca2Fe1.43Al0.57O5 and Ca2Fe1.28Al0.72O5. Acta Crystallogr Sect B Struct Sci B 28:3196–3260. https://doi.org/10.1107/s0567740872007733
Farrugia L (2012) WinGX and ORTEP for windows: an update. J Appl Crystallogr 45:849–854. https://doi.org/10.1107/S0021889812029111
Gangopadhayay S, Inerbaev T, Masunov AE, Altilio D, Orlovskaya N (2009) Structural characterization combined with the first principles simulations of barium/strontium cobaltite/ferrite as promising material for solid oxide fuel cells cathodes and high-temperature oxygen permeation membranes. ACS Appl Mater Interfaces 1:1512–1519. https://doi.org/10.1021/am900182p
Geller S, Grant RW, Fullmer LD (1970) Magnetic structures in Ca2Fe2-xAlxO5 system. J Phys Chem Solids 31:793. https://doi.org/10.1016/0022-3697(70)90213-1
Geller S, Grant RW, Gonser U (1971a) Crystal chemistry and magnetic structures of substituted Ca2[Fe](Fe)O5 Progress in. Solid State Chemistry 5:27
Geller S, Grant RW, Gonser U (1971b) Crystal chemistry and magnetic structures of substituted Ca2[Fe](Fe)O5 Progress in. Solid State Chemistry 5:1–26. https://doi.org/10.1016/0079-6786(71)90015-X
Geller S, Grant RW, Colville AA (1973) Magnetic structures in Ca2Fe2–xALxO5 System. J Phys Chem Solids 34:107–110. https://doi.org/10.1016/0022-3697(73)90065-6
Glamazda A, Choi K-Y, Lemmens P, Choi WS, Jeen H, Meyer TL, Lee HN (2015) Structural instability of the CoO4 tetrahedral chain in SrCoO3—δ thin films. J Appl Phys 118:085313. https://doi.org/10.1063/1.4929659
Grosvenor AP, Ramezanipour F, Derakhshan S, Maunders C, Botton GA, Greedan JE (2009) Effects of bond character on the electronic structure of brownmillerite-phase oxides, Ca2B′xFe2–xO5 (B′ = Al, Ga): an X-ray absorption and electron energy loss spectroscopic study. J Mater Chem 19:9213–9220. https://doi.org/10.1039/b914983j
Hadermann J et al (2007) Synthesis and crystal structure of the Sr2Al1.07Mn0.93O5 Brownmillerite. J Mater Chem 17:692–698. https://doi.org/10.1039/b614168d
Hansen WC (1928) Further studies on Portland cement compounds by the X-ray diffraction method. J Am Ceram Soc 11:68–78. https://doi.org/10.1111/j.1151-2916.1928.tb16854.x
Hansen WC, Brownmiller LT (1928) Equilibrium studies on alumina and ferric oxide, and on combinations of these with magnesia and calcium oxide. Am J Sci 15:225–242
Islam MA, Xie YJ, Scafetta MD, May SJ, Spanier JE (2015) Raman scattering in La1-xSrxFeO3-delta thin films: annealing-induced reduction and phase transformation. J Phys Condensed Matter. https://doi.org/10.1088/0953-8984/27/15/155401
Kagomiya I et al (2017) Weak ferromagnetic ordering in brownmillerite Ca2Fe2O5 and its effect on electric field gradients. Phys Chem Chem Phys 19:31194–31201. https://doi.org/10.1039/c7cp04520d
Kahlenberg V, Fischer RX (2000) Crystal growth and cation distribution in doped dicalcium ferrite Ca2(Fe1-xMex)(2)O5(Me = Al3+,Ga3+). Eur J Miner 12:129–135
Kim GY, Roh KS, Yo CH (1995) Structural and magnetic-properties of the Brownmillerite Ca2Al_xFe{2-X}O_5 system. Bull Korean Chem Soc 16:934–938
Kroumova E, Aroyo MI, Perez-Mato JM, Kirov A, Capillas C, Ivantchev S, Wondratschek H (2003) Bilbao crystallographic server: useful databases and tools for phase-transition. Stud Phase Transit 76:155–170. https://doi.org/10.1080/0141159031000076110
Kruger H, Kahlenberg V (2005) Incommensurately modulated ordering of tetrahedral chains in Ca2Fe2O5 at elevated temperatures. Acta Crystallogr Sect B Struct Sci 61:656–662. https://doi.org/10.1107/s0108768105026480
Kruger H, Kahlenberg V, Petricek V, Phillipp F, Wertl W (2009) High-temperature structural phase transition in Ca2Fe2O5 studied by in-situ X-ray diffraction and transmission electron microscopy. J Solid State Chem 182:1515–1523. https://doi.org/10.1016/j.jssc.2009.03.027
Kruger H, Stober S, Welberry TR, Withers RL, Gerald JDF (2011) Stacking faults and superstructures in a layered brownmillerite. Acta Crystallogr Sect B Struct Sci 67:476–485. https://doi.org/10.1107/s0108768111042005
Lazic B, Kruger H, Kahlenberg V, Konzett J, Kaindl R (2008) Incommensurate structure of Ca2Al2O5 at high temperatures—structure investigation and Raman spectroscopy. Acta Crystallogr Sect B Struct Sci 64:417–425. https://doi.org/10.1107/s0108768108016029
Mahboub MS, Zeroual S, Boudjada A (2012) Synthesis of homogeneous Ca0.5Sr0.5FeO2.5 + δ compound using a mirror furnace method. Mater Res Bull 47:370–374. https://doi.org/10.1016/j.materresbull.2011.11.001
Parsons TG, D’Hondt H, Hadermann J, Hayward MA (2009) Synthesis and structural characterization of La(1-x)A(x)MnO(2.5) (A = Ba, Sr, Ca) phases: mapping the variants of the Brownmillerite structure. Chem Mater 21:5527–5538. https://doi.org/10.1021/cm902535m
Piovano A, Ceretti M, Johnson MR, Agostini G, Paulus W, Lamberti C (2015) Anisotropy in the Raman scattering of a CaFeO2. 5 single crystal and its link with oxygen ordering in Brownmillerite frameworks. J Phys Condens Matter. https://doi.org/10.1088/0953-8984/27/22/225403
Rancourt DG, Ping JY (1991) Voigt-based methods for arbitrary-shape static hyperfine parameter, distributions in Mossbauer-spectroscopy. Nucl Instrum Methods Phys Res Sect B Beam Interact Mater Atoms 58:85–97 https://doi.org/10.1016/0168-583x(91)95681-3
Redhammer GJ, Tippelt G, Roth G, Amthauer G (2004) Structural variations in the brownmillerite series Ca2(Fe2-xAlx)O5: single-crystal X-ray diffraction at 25 degrees C and high-temperature X-ray powder diffraction (25 degrees C < = T < = 1000 degrees C. Am Miner 89:405–420
Redhammer GJ, Amthauer G, Tippelt G, Lottermoser W, Roth G (2005) Fe-57 Mossbauer spectroscopic investigations on the browntnillerite series Ca2(Fe2–x,Alx)O5. In: Gracia M, Marco JF, Plazaola F (eds) Industrial applications of the Mossbauer effect, vol 765. Aip conference proceedings, pp 179–184. https://doi.org/10.1063/1.1923651
Saib F, Mekiri M, Bellal B, Chibane M, Trari M (2017) Photoelectrochemical properties of the brownmillerite Sr2Fe2O5: application to electrochemical oxygen evolution Russian. J Phys Chem A 91:1562–1570. https://doi.org/10.1134/s0036024417080295
Shannon RD, Prewitt CT (1969) Effective ionic radii in oxides and fluorides. Acta Crystallogr Sect B 25:925–946. https://doi.org/10.1107/S0567740869003220
Sheldrick G (2015) Crystal structure refinement with SHELXL. Acta Crystallogr Sect C 71:3–8. https://doi.org/10.1107/S2053229614024218
Smith DK (1962) Crystallographic changes with substitution of aluminum for iron in dicalcium ferrite. Acta Crystallogr 15:1146. https://doi.org/10.1107/s0365110x62003011
Taylor HFW (1997) Cement chemistry. Thomas Telford, London, p 459
The-Long P et al (2018) Electronic structure and magnetic properties of Al-doped Ca2Fe2O5 brownmillerite compounds. J Am Ceram Soc 101:2181–2189. https://doi.org/10.1111/jace.15357
Tilley RJD (2016) Perovskites: structure-property relationships. Wiley, Hoboken, p 328
Tsuji E et al (2017) Brownmillerite-type Ca2FeCoO5 as a practicable oxygen evolution reaction catalyst. Chemsuschem 10:2864–2868. https://doi.org/10.1002/cssc.201700499
Zhou HD, Goodenough JB (2005) Rotation of magnetocrystalline easy axis in Ca2Fe2O5. Solid State Sci 7:656–659. https://doi.org/10.1016/j.solidstatesciences.2004.11.011
Acknowledgements
Open access funding provided by Paris Lodron University of Salzburg. We would like to thank Manfred Bernroider for help with the EMPA analysis and Prof. Maurizio Musso (University of Salzburg) for the fruitful discussions regarding the interpretation of the Raman results.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Stahl, Q.E., Redhammer, G.J., Tippelt, G. et al. Structural and spectroscopic characterization of the brownmillerite-type Ca2Fe2−xGaxO5 solid solution series. Phys Chem Minerals 46, 271–298 (2019). https://doi.org/10.1007/s00269-018-1003-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00269-018-1003-9