Crystal structures of NiSO₄·9H₂O and NiSO₄·8H₂O: magnetic properties, stability with respect to morenosite (NiSO₄·7H₂O), the solid-solution series (Mg_xNi_1−x)SO₄·9H₂O

Abstract

Since being discovered initially in mixed-cation systems, a method of forming end-member NiSO₄·9H₂O and NiSO₄·8H₂O has been found. We have obtained powder diffraction data from protonated analogues (with X-rays) and deuterated analogues (using neutrons) of these compounds over a range of temperatures, allowing us to determine their crystal structures—including all H-atoms—and to characterise the transitions on warming from 220 to 278 K; glass → 9-hydrate → 8-hydrate + ice → 7-hydrate + ice → partial melt (7-hydrate + liquid). NiSO₄·8D₂O is triclinic, space-group $P\bar {1}$, Z = 2, with unit cell parameters at 150 K, a = 6.12463(8) Å, b = 6.8401(1) Å, c = 12.5339(2) Å, α = 92.846(1)°, β = 97.822(1)°, γ = 96.627(1)° and V = 515.58(1) Å³. The structure consists of two symmetry-inequivalent Ni(D₂O)₆ octahedra on sites of $\bar {1}$ symmetry. These are directly joined by a water–water H-bond to form chains of octahedra parallel with the c-axis at x = 0. Two interstitial water molecules serve both to bridge the Ni(D₂O)₆ octahedral chains in the b–c plane and also to connect with the SO₄²⁻ tetrahedral oxyanion. These tetrahedra are linked by the two interstitial water molecules in a reticular motif to form sheets perpendicular to c. NiSO₄·9D₂O is monoclinic, space-group P2₁/c, Z = 4, with unit-cell parameters at 150 K, a = 6.69739(6) Å, b = 11.8628(1) Å, c = 14.5667(1) Å, β = 94.9739(8)° and V = 1152.96(1) Å³. The structure is isotypic with the Mg analogue described elsewhere (Fortes et al., Acta Cryst B 73:47‒64, 2017b). It shares the motif of H-bonded octahedral chains with NiSO₄·8D₂O, although in the enneahydrate these run parallel with the b-axis at x = 0. Three interstitial water molecules bridge the Ni(D₂O)₆ octahedra to the SO₄²⁻ tetrahedral oxyanion. The tetrahedra sit at x ≈ 0.5 and are linked by two of the three interstitial water molecules in a pentagonal motif to form ribbons parallel with b. A solid-solution series exists between Mg and Ni enneahydrate end-members where we observe preferential partitioning of Ni²⁺ into the octahedral sites on the 2c Wyckoff positions rather than the 2a sites. The solution is slightly non-ideal, as indicated by the small positive excess volume of mixing. Measurements of the DC magnetisation of quenched NiSO₄ solutions reveal anomalies in the molar susceptibility on warming through the region from 221 to 225 K, probably due to devitrification of the (assumed) glassy specimen into a mixture of NiSO₄·9H₂O + ice Ih. Further temperature-dependent measurements on repeated warming and cooling provide no evidence of magnetic ordering and indicate a weak ferromagnetic coupling between neighbouring Ni²⁺ ions, likely via super-exchange through the H-bond between neighbouring Ni(H₂O)₆ octahedra.

Introduction

Background

Crystalline hydrates having the general formula NiSO₄·nH₂O with n = 1, 2, 3, 4, 5, 6, and 7 are well known (Chrétien and Rohmer 1934), some of which occur naturally as the minerals dwornikite (n = 1, with ~ 10 atom % Fe²⁺), retgersite and nickelhexahydrite (tetragonal and monoclinic polymorphs with n = 6), and morenosite (n = 7), respectively. As part of a broader programme of research into water-rich cryohydrates, we attempted to synthesise compounds having n > 7 with the specific aims of identifying a hypothetical Ni-analogue of meridianiite (MgSO₄·11H₂O) or of isolating hitherto unknown hydrates with 7 < n < 11. Whilst we failed to form the NiSO₄·11H₂O end-member, we succeeded instead in producing a novel hydrate with n = 9 in systems containing mixtures of Ni, Zn or Fe with Mg, and a new hydrate with n = 8 in pure NiSO₄ (Fortes et al. 2012a, b). Since then, we have been able to form end-member 9-hydrates from each of MgSO₄, NiSO₄ and ZnSO₄. However, it remains the case that the octahydrate has been observed solely in NiSO₄-bearing mixtures.

There have been a few prior reports in the literature concerning octahydrates of divalent metal sulfates, including Mg²⁺ (Takegami 1922) and Fe²⁺ (Viola 1923) although these were shown subsequently to be either irreproducible or due to errors of analysis (Benrath and Schröder 1927; D’Ans 1933). In light of this, we were quite cautious in our assertion that the newly identified hydrate of NiSO₄ was an octahydrate based solely on molar volume considerations. Since we consider the formation of a single-phase and ice-free specimen of NiSO₄·8H₂O to be practically impossible by flash-freezing of a stoichiometric aqueous solution, and since the metastability of this phase precludes growth, extraction or handling of even small crystals suitable for either X-ray single-crystal diffraction or thermogravimetric analysis, the only way to confirm the stoichiometry is to solve the structure from mixed-phase powder diffraction data. In achieving that goal we will show that this phase is indeed an octahydrate; along with the structure refinement of nickel sulfate enneahydrate reported in this work, these are the first new NiSO₄ hydrate structures to be established with certainty in over 80 years.

Characterising the structures, properties and phase behaviour of these new cryohydrates sheds fresh light on a little-explored but pertinent area of (principally extraterrestrial) mineralogy. Exploration of Mars and of the outer solar system over the past five decades has revealed the importance of aqueous solutions, or brines, which result in the possible deposition of a great variety of polyhydrated inorganic salts on planetary surfaces. Since these environments are typically much colder than the Earth’s mean surface temperature, the behaviour of such brines when crystallised at low temperatures—even flash frozen, as may occur on extrusion or spraying into the ultra-cold surface environment of an outer solar system body—is important to understand. This is reflected in the efforts of the planetary science community to determine experimentally which stable or metastable phases appear when different brine compositions are frozen at different rates (e.g., Hennings et al. 2013; Schmidt et al. 2013; Toner et al. 2014; Vu et al. 2016, 2017; Thomas et al. 2017) or when salt hydrates are exposed to elevated relative humidities at low temperatures (Leftwich et al. 2013). Our work on divalent metal sulfate cryohydrates adds a small piece to this larger picture.

This work forms the final part of a series of three closely related papers. The first deals with the high-pressure behaviour of meridianiite (MgSO₄·11H₂O) and its decomposition to MgSO₄·9H₂O (Fortes et al. 2017a): the second paper reports on the structure and thermoelastic properties of MgSO₄·9H₂O (Fortes et al. 2017b). This third paper deals purely with the structures and properties of NiSO₄·9H₂O and NiSO₄·8H₂O.

Experimental objectives

The objectives of this work are: (i) to refine the crystal structure of NiSO₄·9H₂O, including all hydrogen positions, based on the recently determined structure of MgSO₄·9H₂O; (ii) to determine the crystal structure of NiSO₄·8H₂O; (iii) to establish the relative stability of these phases with respect to one another and to NiSO₄·7H₂O as a function of temperature; (iv) to characterise the variation in unit cell parameters across the solid-solution series between MgSO₄·9H₂O and NiSO₄·9H₂O and relate this to the site distribution of Ni²⁺ in the structure, and (v) to characterise the magnetic properties, where possible, of these hydrates for comparison with literature data on the hepta- and hexahydrates.

Experimental methods

Sample synthesis

Aqueous solutions for the X-ray powder diffraction measurements were prepared from NiSO₄·7H₂O (Sigma–Aldrich 72285, purum > 99.0 wt%) dissolved in H₂O (Alfa-Aesar, ACS Reagent Grade, 36645); for the neutron powder diffraction measurements, solutions were prepared from anhydrous NiSO₄ (Aldrich 656895, 99.99% trace metals basis) dissolved in D₂O (Aldrich 151882 99.9 atom % D). Additionally, mixtures of anhydrous powder with the composition (Mg_xNi_1−x)SO₄ were prepared in the range 1 < x < 0.1 in increments of 0.1, which were also dissolved in D₂O. All of the solutions were prepared with a concentration of 25 wt% anhydrous solid. These liquids were pipetted as droplets directly into ~ 30 cm³ of liquid nitrogen held in a steel cryomortar (∅ = 60 mm, depth 20 mm), producing glassy solid spherules in the region of 2–4 mm in diameter. The amorphous spherules were pulverised with a nitrogen-chilled steel pestle and mortar and then transferred to an appropriate sample holder. This work was carried in the UCL Earth Sciences Cold Rooms at an air temperature of around 260 K.

X-ray powder diffraction

X-ray powder diffraction data were obtained using a PANanalytical X’Pert Pro multipurpose powder diffractometer with germanium monochromated CoKα₁ radiation (λ = 1.788996 Å, and an X’Celerator multi-strip detector). Data were collected with variable divergence and receiving slits, converted to fixed-slit geometry with the proprietary X’Pert Pro HighScore Plus software package, and exported in an appropriate format for analysis in the GSAS/Expgui package (Larsen and Von Dreele 2000; Toby 2001).

Low-temperature measurements were achieved using a thermoelectrically cooled sample stage (Wood et al. 2012). The cold stage was held in a plastic box filled with dry-ice pellets whilst the powder specimen was prepared and loaded. Powder samples were transferred to the cold stage and packed down to form a top-loaded pressed-powder specimen.

Measurements of quench-frozen [Mg_xNi_1−x]SO₄ cryohydrates were made at temperatures between 258 and 261 K. The limitations imposed by the operating temperature of the Peltier stage meant that only mixtures containing ≥ 90 atom % Ni formed the triclinic crystal that we inferred (on the basis of molar volume considerations) to be an octahydrate; lower nickel concentrations produced a monoclinic enneahydrate and eventually, for Ni < 40 atom %, the triclinic (Mg,Ni)SO₄·11H₂O (Ni-meridianiite). A representative X-ray powder diffraction pattern from NiSO₄·8H₂O is shown in Fig. 1.

Fig. 1

Representative X-ray powder diffraction pattern of NiSO₄·8D₂O measured at 260 K. Filled red circles report the observed data, solid green lines the calculated fit based on a joint refinements of the X-ray and neutron diffraction data (see text); the purple line underneath is Obs-Calc. Tick marks for NiSO₄·8D₂O are uppermost and those for water ice are below them. A small excluded region near 2θ = 28° covers an ill-fitted ice Bragg peak

The analysis of these X-ray data is largely presented in our earlier work (Fortes et al. 2012a, b). Following the neutron diffraction and computational studies described in the following sections, we have re-evaluated some of the X-ray data, in particular the dataset measured at 259.95 K on end-member NiSO₄·8H₂O (Fig. 1) and the 40 wt% Ni dataset measured at 257.75 K (see Fig. 9).

Neutron powder diffraction

Neutron powder diffraction data were collected using the high resolution powder diffractometer (HRPD) (Ibberson et al. 1992; Ibberson 2009) at the STFC ISIS spallation neutron source, Rutherford Appleton Laboratory, UK, which is ideally suited to rapid, accurate and precise determination of unit-cell parameters by virtue of its long neutron flight path (95 m) and essentially Q-independent resolution; Δd/d ≈ 6 × 10^− 4 in the backscattering detectors, 2θ = 168.33°.

Samples of NiSO₄·8D₂O + ice were prepared by quenching of large globules of aqueous NiSO₄ in liquid nitrogen to form solid ‘buttons’ with a diameter of ~ 20 mm and a thickness of ~ 5 mm. These were stored overnight in a freezer at 255 K before being powdered under liquid nitrogen in a steel cryomortar and then loaded into a pre-cooled sample holder mounted on a cryostat centre stick. The sample holder consisted of an aluminium frame with a slab-geometry cavity of width 18 mm, height 23 mm and depth (parallel to the incident beam) 15 mm. Steel-framed vanadium windows were screwed to the front and back of the holder, the exposed Al and steel components on the front face being masked by Gd and Cd foils. After installation on the beamline, the temperature was reduced to 150 K. The specimen was measured for 8 h in HRPD’s 30–130 ms time-of-flight (t-o-f) window, taken off the beamline and stored in dry-ice for 1 day whilst another sample was studied, and then re-loaded at 150 K for a 3.25 h measurement in the 100–200 ms t-o-f window.

Shorter annealing times in the freezer (< 1 h) were found to produce samples containing principally NiSO₄·9D₂O. We considered it useful, therefore, to observe the annealing process in situ as a function of temperature. To this end, a solid quench sample was loaded into a slab-can at liquid nitrogen temperatures and neutron powder diffraction data were collected as it was warmed up to the point of devitrification (220 K). At this point the sample was observed to consist of a phase mixture, comprising ice Ih and NiSO₄·9D₂O. Data were subsequently collected on warming in 5 K increments to 260 K and then 2 K increments up to 278 K for 1 h each in the 100–200 ms t-o-f window.

Complementary datasets were obtained from flash-frozen mixtures of aqueous MgSO₄ with NiSO₄. These were prepared and loaded under liquid nitrogen in the same manner as above and mounted in a cryostat on HRPD at 150 K. Warming to ca. 220 K induced crystallisation of (Mg_1 − xNi_x)SO₄·9D₂O. Solutions prepared with x varying from 0 to 1 in 0.1 atom-fraction increments were crystallised as outlined previously and then cooled to 150 K for acquisition of 1 h datasets in HRPD’s 100–200 ms time window. Above x = 0.3, these specimens comprised (Mg_1 − xNi_x)SO₄·9D₂O + ice; samples with x = 0.4, 0.5 and 0.8 contained small but non-negligible contributions from the octahydrate, (Mg_1 − xNi_x)SO₄·8D₂O.

All powder diffraction data were normalised to the incident spectrum and corrected for detector efficiency using data from a vanadium standard. Representative neutron powder diffraction patterns from NiSO₄·9D₂O are shown in Fig. 2. A summary of the neutron powder diffraction datasets used in this work is provided in Table 1.

Fig. 2

Rietveld refinement of the NiSO₄·9D₂O structure against neutron powder diffraction data obtained at 150 K in HRPD’s 30–130 ms window. The left-hand panel shows the data measured in the backscattering detector banks and the right-hand panel shows data from the 90° detectors in the same time window. Filled red circles report the observed data, solid green lines the calculated fit and the purple line underneath is Obs-Calc. Tick marks for NiSO₄·9D₂O are uppermost and those for water ice are below them

Table 1 Details of the experimental conditions for each neutron powder diffraction dataset

Magnetic property measurements

Measurements of the magnetic properties of (inferred) NiSO₄·9H₂O + ice mixtures were obtained using a commercial SQUID magnetometer (Quantum Design MPMS-7T, McElfresh 1994). Approximately 200 mg of aqueous solution containing 27.14 wt% NiSO₄ was loaded into a gelatine capsule (mass ≈ 37 mg) and mounted on the SQUID sample stick inside a polyethylene straw. The specimen capsule was then inserted into the instrument chamber where it was immersed in He exchange gas at 80 K; our in situ diffraction observations, outlined in “Neutron powder diffraction”, led us to believe that this would result in a glassy specimen, which would devitrify on warming through 220 K.

DC mass-susceptibility measurements were then made in a 1 kOe applied field as the sample temperature was reduced to 2 K (at 3 K min^− 1), increased from 2 to 200 K at the same rate and then warmed more slowly from 200 to 240 K (1 K min^− 1). A significant drop in the susceptibility was observed between 224 and 227 K (Fig. 3), which we attribute to the crystallisation of NiSO₄·9H₂O from a glassy precursor. In order to test this hypothesis, the temperature program was repeated, cooling to 2 K and back up to 240 K; no further anomalies were detected, supporting our interpretation of the susceptibility drop as a signature of devitrification.

Fig. 3

Expanded view of the inverse magnetic susceptibility in the temperature region where the diffraction data indicate that devitrification takes place. The data for sample #2 are to be read from the right-hand axis, whereas samples #1 and #3 are to be read from the left-hand axis

A second and third loading of the same aqueous solution was carried out to evaluate the effect of a larger applied field and of different temperature ramp rates. Sample #2 was studied in a 10 kOe field, being cooled from 80 to 2 K and then warmed from 2 to 220 K at 3 K min^− 1. Over the range where we expected devitrification to occur (220–230 K), the ramp was reduced to 0.2 K min^− 1. As in Sample #1, there was a drop in the susceptibility, but the feature was much narrower and at a slightly lower temperature, peaking at 221.3 K and extending from 220.4 to 222.0 K. As before, continued temperature cycling revealed no further anomalies.

Sample #3 was measured in a 1 kOe applied field, but data acquisition was done with a thermal equilibration wait time at each datum instead of measuring on a continuous temperature ramp. The effect of this was to reproduce the lower temperature of the devitrification anomaly seen in Sample #2 but to greatly reduce its magnitude. Finally, a magnetic hysteresis loop was measured at 2 K in the range ± 70 kOe.

Data were corrected for the susceptibility of the gel capsule and the core diamagnetism of NiSO₄ (Bain and Berry 2008) and ice (Senftle and Thorpe 1962) in the specimen and converted to inverse molar susceptibility, 1/χ_m, for further analysis.

Density functional theory calculations

In order to aid in the interpretation of some of our experimental data we carried out a series of first-principles calculations using density functional theory, DFT, and the plane-wave pseudopotential method (Hohenberg and Kohn 1964; Kohn and Sham 1965). The calculations were carried out using CASTEP (Payne et al. 1992; Segall et al. 2002; Clark et al. 2005) in conjunction with the analysis tools in the Materials Studio software package (http://accelrys.com). Tests for convergence of the total energy and of structural parameters were done by varying the basis-set cut-offs and the reciprocal-space sampling. As described in our earlier paper (Fortes et al. 2017b), we found that the recently developed Wu–Cohen GGA functional (Wu and Cohen 2006) gives more accurate structural parameters than PBE for these materials, changing the ~ 5% over-estimation of molar volume to a ~ 1% under-estimation.

Using the WC GGA with ultrasoft pseudopotentials (non-linear core-corrected for Ni) with a basis-set cut-off of 1200 eV and a 4 × 2 × 2 $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {k}$-point grid for the 9-hydrate and a 3 × 3 × 2 $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {k}$-point grid for the 8-hydrate (~ 0.04 Å⁻¹ reciprocal lattice spacing in both cases) achieved a satisfactory convergence of the total energy.

Spin-polarised calculations were done for the Ni-bearing compounds so as to allow degenerate d-orbitals to adopt differing energy levels, these being done for a variety of ferromagnetic and antiferromagnetic initial spin configurations. For simplicity, the quantisation axis (or spin direction) was fixed so as to correspond with the H-bonded chains of octahedra, along the b-axis in the 9-hydrate and along the c-axis in the 8-hydrate. For the supercells described later, we were forced to adopt ferromagnetic structures in order to avoid further increasing the supercell dimensions or further lowering the symmetry since the calculations for the very large low-symmetry spin-polarised supercells are computationally expensive.

Lastly, as is well-known, DFT does not properly treat the Coulomb interactions of highly localised d and f electrons in transition metal elements (Hubbard 1963). A straightforward correction of the on-site Coulomb interaction (U) and the on-site exchange interaction (J) to the Hohenberg–Kohn–Sham Hamiltonian is achieved by the use of a Hubbard interaction parameter. The CASTEP implementation adopts the U_eff = U − J approach of Dudarev et al. (1998) and we use a value of U_eff = 5.96 eV for Ni taken from Madsen and Novak (2005). Although the value of Hubbard U will vary from one compound to another, and indeed from one crystallographic site to another in given material (Cococcioni 2012), we do not expect small deviations to alter the structural parameters in these hydrates significantly. In fact, the very similar degree of over-binding seen in both MgSO₄·9H₂O (where this issue does not occur) and the NiSO₄·9H₂O analogue supports this hypothesis. The same value, U = 5.96 eV, was adopted by Fang et al. (2015) in their recent study of NiSO₄ hydrate, assuring complementarity with this work. The DFT calculation of elastic constants in tetragonal NiSO₄·6H₂O (retgersite) did not report the use of a Hubbard correction (Arbeck et al. 2010).

Structural relaxations of the 8- and 9-hydrate under zero-pressure athermal conditions were carried out, starting from the experimental crystal structures [see “Structure determination and completion (8-hydrate)” and “Structure determination and completion (9-hydrate)”], using the BFGS method (Pfrommer et al. 1997). The relaxations were considered to have converged when the forces on each atom were less than 5 × 10^− 3 eV Å⁻¹ and each component of the stress tensor was smaller than 0.005 GPa. Details of how other specific properties were calculated are given in subsequent sections.

Some additional calculations were done to characterise the solid-solution series MgSO₄·9H₂O–NiSO₄·9H₂O, evaluating the variation in unit-cell parameters and energetic favourability of distributing Ni²⁺ in various ways across the two octahedral sites. The cations occupy two symmetry-inequivalent octahedral sites (Fig. 4), one of which (M1) has a metal-coordinated water molecule that donates a hydrogen bond to the other octahedral site (M2). Hence the difference between the two sites can be simplified to the M1 sites (on Wyckoff positions 2a) being “H-bond donors” and the M2 sites (on positions 2c) being “H-bond acceptors”.

Fig. 4

Illustration of the H-bonded chains of NiO₆ octahedra running along the b-axis in NiSO₄·9H₂O. Symmetry codes: (i) x, 1 + y, z; (ii) − x, 1 − y, −z; (iii) − x, −y, −z. Drawn using Diamond (Putz and Brandenburg 2006)

In addition to the end-member calculations, geometry optimisations were done for compositions corresponding to (Mg_0.5Ni_0.5)SO₄·9H₂O with Ni²⁺ distributed either entirely on the M1 sites or entirely on the M2 sites. The situation in which Ni²⁺ is evenly distributed between the two sites required the construction of (at least) a 2 × 1 × 1 supercell which, provided the Ni²⁺ is arranged in such a way as to maximise the Ni–Ni distance, retains P2₁/c symmetry. In this supercell, the M1 sites are those on Wyckoff positions 2a (at 0, 0, 0) and 2b (at ½, 0, 0) and the M2 sites are now on positions 2c (0, ½, 0) and 2d (½, ½, 0). The model used to describe the 50:50 distribution of Mg²⁺ and Ni²⁺ is not a particularly good description of the real crystal since it exhibits both short- and long-range order, having a unit cell that would lead to experimentally observable superlattice reflections. However, it is not currently possible to do spin-polarised calculations with partially occupied sites via CASTEP’s Virtual Crystal Approximation.

Results

Structure determination and completion (8-hydrate)

From prior work (Fortes et al. 2012a, b) it was known that NiSO₄·8H₂O is triclinic, space-group $P\bar {1}$, with unit-cell parameters at 260 K a = 6.13 Å, b = 6.86 Å, c = 12.63 Å, α = 92.9°, β = 97.7°, γ = 96.6° and V = 522 Å³. Since the packing of the coordination polyhedra is likely, to a first approximation, to be similar to that in other related cryohydrates, such as MgSO₄·9H₂O and NiSO₄·9H₂O, a rather obvious trial structure can be generated with Ni(H₂O)₆ octahedra located on the 1a and 1b Wyckoff positions (0, 0, 0) and (0, 0, ½). The task of structure solution then reduces to determining the orientation of these octahedra and locating the sulfate tetrahedra [which must be close to (½, ½, ¼)] using simulated annealing methods, followed by a difference Fourier synthesis to locate the two interstitial water molecules we believe to be present.

The first stage was achieved using the parallel tempering algorithm in FOX, version 1.9.7.1 (Favre-Nicolin and Černý 2002, 2004) starting from the trial structure outlined above. In fact the initial model, including the estimated sulfate oxyanion location, gave fair agreement with the XRD data before running the optimisation. For the 8-hydrate, FOX was used to construct ideal NiO₆ octahedra with Ni‒O distances of 2.05 Å, and ideal SO₄ tetrahedra with S‒O distances of 1.48 Å; these were treated as rigid bodies throughout the solution process. In runs of ½ million trials each, the crystal structure was optimised against the X-ray powder diffraction data, consistently producing very similar arrangements of the polyhedra. Importantly, Fourier difference maps phased on these partial structures revealed two well-defined maxima per formula unit that seemed likely to correspond to the additional water molecules necessary to form the expected 8-hydrate. The structure with the lowest overall cost function was exported as a CIF file to form the basis for further analysis.

A set of unique (i.e., ordered) hydrogen atom locations were derived by examination of the nearest neighbours of each non-sulfate oxygen atom, these being positioned 0.98 Å along the shortest O···O vectors. An initial geometry relaxation of this trial structure in CASTEP then provided the most accurate starting position from which to begin a structural refinement using the experimental data.

The trial structure was refined against both the 260 K X-ray and 150 K neutron powder datasets simultaneously using GSAS/Expgui, on the assumption that the atomic fractional coordinates do not vary significantly in this temperature range. The joint refinement takes advantage of the larger coherent scattering cross section of sulfur to X-rays (compared with the equivalent cross section to neutrons) and the large coherent scattering cross section of deuterium to neutrons (with X-rays this is the weakest scatterer) to yield the optimum precision on the positions of all atoms in the crystal. Lattice parameters, phase fractions, background and peak-profile coefficients were allowed to refine independently for the two batches of data (due both to the different instrumental characteristics and the different temperatures), but the shifts in atom-fractional coordinates were constrained to be the same. At the start of the refinement comparatively loose bond distance restraints were applied to the O–D contacts (0.980 ± 0.005 Å) but these were switched off in the final cycles of the refinement. Structural parameters are given in Supplementary CIF data and selected bond distances and angles are reported in Table 2 for comparison with the DFT-derived values.

The structure (Fig. 5) consists of isolated Ni(H₂O)₆ octahedra on sites of $\bar {1}$ symmetry; the Ni1 octahedron, which occupies the 1a position, donates a hydrogen bond (via water molecule Ow2) to its neighbouring octahedron, situated on the 1b site via water molecule Ow5. This effectively creates H-bonded chains of Ni(H₂O)₆ octahedra running parallel to the c-axis at b = 0, which are exactly analogous with the H-bonded chains of octahedra running along the b-axis of the 9-hydrate (cf., Fig. 4). The sulfate tetrahedra occupy channels between the octahedral chains (sitting at c ≈ 0.2 and c ≈ 0.8). The two interstitial water molecules, Ow7 and Ow8, donate hydrogen bonds to the apical sulfate oxygens O3 and O4 to create a reticular motif in the a–b plane. The relationship between this sulfate–water net and the sulfate–water pentagonal ribbons in the 9-hydrate is shown in Fig. 6.

Table 2 Bond lengths and angles in the ionic polyhedra in NiSO₄·8(H/D)₂O and NiSO₄·9(H/D)₂O compared with the zero-pressure DFT geometry optimisations

Fig. 5

The asymmetric unit of NiSO₄·8H₂O and such other atoms as are necessary to complete the polyhedral representation. Symmetry codes: (i) − x, −y, −z; (ii) x, y − 1, z; (iii) − x, −y, 1 − z

Fig. 6

Depiction of the network formed by the hydrogen bonding between the interstitial water molecules and the sulfate tetrahedra in NiSO₄·8H₂O. Symmetry codes: (i) x + 1, y, z; (ii) x, y + 1, z; (iii) x + 1, y + 1, z; (iv) x − 1, y, z

The sulfate oxygens O1, O3 and O4 each accept three hydrogen bonds whilst O2 accepts only two. The effect of this is typically manifested in the S‒O bond lengths, those with the least number of H-bond connections tending to have the shortest S‒O length. Whilst this is evident from the DFT calculations (Table 2), the differences in S‒O bond lengths obtained experimentally show no such systematic variation.

The agreement between the DFT geometry optimisation (0 K) and the experimental structure refinement (150 K) is good. Only the calculated c-axis length differs from the experimental value by more than 1% and the overall difference in unit-cell volume is 1.3%. The DFT + U calculations yield S–O and Ni–O distances that are longer than the experimental values and so the polyhedral volumes are too great by 3–5%. This is not a deficiency of the spin-polarised calculations or the adopted value of U_eff, since the same differences were observed in MgSO₄·9H₂O (Fortes et al. 2017b). Further comparisons will be made in the context of the 9-hydrate structure in the following section.

Structure determination and completion (9-hydrate)

The structure of NiSO₄·9D₂O was refined using neutron powder diffraction data collected at 150 K using the published structure of the Mg-bearing analogue as a starting point. As with the octahydrate, bond distance restraints were applied in the early cycles of refinement and were subsequently turned off. Structural parameters are given in Supplementary CIF data and selected bond distances and angles are reported in Table 2 for comparison with the DFT-derived values. Since the structure is isotypic with MgSO₄·9D₂O, readers are referred to Fortes et al. (2017b) for a description of how the coordination polyhedra and interstitial water molecules are arranged. The following discussion will focus on comparisons with calculations and differences with the Mg analogue and with NiSO₄ octahydrate.

The sulfate tetrahedra in NiSO₄·9D₂O, NiSO₄·8D₂O and MgSO₄·9D₂O are identical (within errors) in volume, since each accepts the same overall number of hydrogen bonds. The M²⁺O₆ octahedra in the NiSO₄ cryohydrates are slightly smaller in volume than in the MgSO₄ analogue, but the deviations from perfectly regular octahedral geometry are very similar. In the two 9-hydrates, the M1 octahedral site is smaller than the M2 site and exhibits a larger bond-angle variance; this is reproduced in the DFT calculations for both the Mg and Ni species. Equally, the M2 site is elongated along the M²⁺–Ow5 axis (the H-bond acceptor) in both Mg and Ni species, whereas the M1 site is elongated along the M²⁺–Ow3 axis (perpendicular to the H-bond donor, Ow2). The signature of this is not clear in the NiSO₄·9D₂O structure refinement, but is present in the experimental MgSO₄·9D₂O refinement and in the NiSO₄·8D₂O structure as well as in all of the calculations.

The main structural elements and the overall packing of the 8-hydrate are thus found to be very similar indeed to the 9-hydrate.

Magnetic property measurements

The inverse molar susceptibility of a NiSO₄·9H₂O + ice Ih mixture over the range 2–240 K is shown in Fig. 7. At high temperatures the material exhibits the expected Curie–Weiss behaviour for a paramagnetic material with no evidence of magnetic ordering at lower temperatures; only the anomalous deviation due to devitrification at 225 K departs from this behaviour. Six separate data segments measured between 175 and 240 K in three different samples were fitted with a linear relation, 1/χ_m = (T − θ)/C, where θ is the Weiss constant and C is the Curie constant. From these, we obtain mean values and standard deviations of the fit parameters, θ = 13(3) K and C = 1.10(2) emu^− 1 mol Oe K^− 1. The latter is used to obtain the moment on the Ni²⁺ ion, 3.1(1) µ_B, which is slightly larger than the spin-only value (2.83 µ_B) and likely reflects an orbital contribution to the observed moment.

Fig. 7

Inverse molar susceptibility (emu^− 1 mol Oe) of the NiSO₄·9H₂O + ice Ih mixture as a function of temperature. The dashed red line represents a linear fit to the high-temperature data, following the Curie–Weiss law. The small anomaly highlighted at ~ 220 K is shown in greater detail in Fig. 3

Table 3 Unit-cell parameters and total electronic energy for the two NiSO₄ hydrates modelled with different spin configurations

The positive value of the Weiss constant is indicative of ferromagnetic coupling between neighbouring Ni²⁺ ions. Since the ions are coordinated by water, the interaction between them must inevitably be mediated through the hydrogen bond network. The Ni(H₂O)₆ octahedra are directly linked through Ow2–H2a···Ow5 to form 1D chains, so the most direct exchange pathway is across this hydrogen bridge. There are comparatively few examples in the literature of super-exchange coupling via hydrogen bonds. However, the available experimental and computational evidence points in general to weak antiferromagnetic coupling when the H-bonds are short, O···O ≈ 2.4 Å, becoming progressively weaker or becoming ferromagnetic for longer H-bonds, O···O > 2.8 Å (Desplanches et al. 2002; Ma et al. 2010; Bandeira and Le Guennic 2012; Cortijo et al. 2013). In NiSO₄·9H₂O the O···O separation is 2.985 Å, so it is not too surprising that we should find evidence of ferromagnetic coupling.

Watanabe (1962) measured the magnetic susceptibility of single-crystal and powder samples of NiSO₄·7H₂O and the tetragonal polymorph of NiSO₄·6H₂O. For comparison with our work, Watanabe reported θ_powder = − 0.3 K for the heptahydrate and + 0.4 K for the hexahydrate. In both of these salts there are also direct H-bonds between the Ni(H₂O)₆ coordination polyhedra, with O···O separations of 2.864 Å in NiSO₄·7H₂O (Ptasiewicz-Bak et al. 1997) and 2.790 Å in NiSO₄·6H₂O (Angel and Finger 1988). These are both substantially shorter than the interpolyhedral H-bond in NiSO₄·9H₂O, which may explain both the difference in magnitude and sign of the Weiss constant for the two lower hydrates. None of the hydrates with 6 < n < 7 exhibit any evidence of magnetic ordering at low temperature (Fisher et al. 1967, 1968a, b; Fisher and Hornung 1968; Stout and Hadley 1964; Stout et al. 1966), by contrast with anhydrous NiSO₄ which contains antiferromagnetic sheets with ferromagnetic coupling between the sheets (Frazer and Brown 1962).

DFT calculations reveal no significant difference in the total energy or lattice parameters for ferromagnetic or antiferromagnetic spin configurations in either NiSO₄·8H₂O or NiSO₄·9H₂O (Table 3). The calculated band gaps in the octahydrate and enneahydrate are 3.862 and 3.794 eV, respectively. For comparison with other work, we carried out a geometry relaxation and band structure calculation on NiSO₄·7H₂O, finding a band gap of 4.005 eV. This is lower than the value of Fang et al. (2015), who reported a band gap of 5.24 eV for the heptahydrate and 5.14/5.05 eV for the monoclinic/tetragonal polymorphs of the hexahydrate.

Behaviour on warming

The range of existence of the two new hydrates is comparatively small. The enneahydrate forms at 220 K on devitrification of the flash-frozen brine, and then exsolves one water molecule per formula unit between 245 and 250 K to form NiSO₄·8H₂O + ice Ih (Fig. 8). The octahydrate is itself unstable with respect to the heptahydrate and a slow progressive solid-state transformation of NiSO₄·8H₂O to NiSO₄·7H₂O + ice Ih occurs on warming above 250 K. A sudden change of all residual octahydrate to heptahydrate is then observed between 272 and 274 K, followed shortly afterwards by the onset of eutectic melting at ~ 276 K. The behaviour of NiSO₄·7H₂O at higher temperatures has been described elsewhere (Maneva et al. 1990).

Fig. 8

Neutron powder diffraction patterns collected on warming between 225 and 278 K showing the sequence of transitions from NiSO₄·9H₂O → NiSO₄·8H₂O → NiSO₄·7H₂O. The strongest Bragg peaks from water ice are marked near the top by asterisks; note that ice is not present in the last dataset at 278 K indicative of warming above the eutectic

These data correspond with the pure end-member nickel sulfate. Our previous work, done with a small Peltier-cooled X-ray stage, allowed us to achieve temperatures of ~ 255 K and we observed the octahydrate only in 90–100 atom % Ni samples at this temperature; lower concentrations of Ni²⁺ (between 40 and 90 atom %) resulted in the formation of the enneahydrate. In terms of the thermal stability, NiSO₄·9H₂O containing 10–60 atom % Mg is able to persist to at least 255 K, whereas more nickel-rich compositions are unstable and we observe the octahydrate instead at this temperature. The implication of this is that the temperature at which the enneahydrate breaks down to the octahydrate decreases with increasing nickel content. Further temperature-dependent studies on a range of compositions are required to establish this with certainty.

(Mg,Ni)SO ₄·9H ₂ O solid solutions

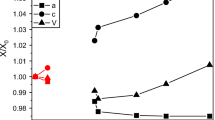
It was noted previously (Fortes et al. 2017b, their Supplementary Figure S2) that X-ray powder diffraction measurements on (Mg, Ni)SO₄·9H₂O solid solutions indicated some degree of site ordering in the crystal. All but three of our neutron powder datasets are suitable for refinement of site occupancies. Since these data are multiphase and dominated at short d-spacings by ice Bragg peaks, the accuracy of the site occupancies is limited but we nonetheless find that there is indeed a marked preference for Ni²⁺ to substitute for Mg²⁺ on the 2c sites at (0, 0, ½), as shown in Fig. 9; whilst these M2 octahedra are marginally larger than the M1 octahedral sites (by ~ 3%) they are considerably less distorted, indicating that crystal field stabilisation energy rather than cation radius is the main factor in determining the site substitution preference. This seems remarkable given the rather extreme disequilibrium nature of the synthesis and the improbability of achieving any intersite diffusional equilibrium at 150–200 K. Fitting a simple quadratic expression between the two end-member compositions (dashed lines in Fig. 9) gives a slowly varying site-distribution coefficient, K_D = [(Ni/Mg)_(2a)]/[(Ni/Mg)_(2c)] with a mean value of 7.6(6) from 0 to 60 atom % Ni²⁺; the minimum K_D = 7.1 occurs near 30 atom % Ni²⁺ and increases substantially at higher concentrations.

Fig. 9

Partitioning of Ni²⁺ between the two available sites in the (Mg,Ni)SO₄·9D₂O structure. Open grey and white symbols show the distribution of Ni²⁺ into the M1 and M2 sites as determined by refinement of neutron powder diffraction data collected from octahydrate-free specimens. The filled black symbols show the distribution obtained by refinement of a high-quality X-ray powder diffraction dataset on (Mg,Ni)SO₄·9H₂O

These values are closely comparable to the case of Ni²⁺ substitution in Mg₂SiO₄ olivine, where Ni²⁺ prefers the smaller and more distorted M1 site, with minimum K_D values in the region of 6–10 at intermediate compositions and higher values towards the Mg- or Ni-rich end-members (Rajamani et al. 1975; Bish 1981; Boström 1987; Ottonello et al. 1989; Tsukimura and Sasaki 2000; Henderson et al. 2001). Of itself, site ordering is not necessarily indicative of thermodynamically non-ideal solution behaviour. However, there is a small but significant positive excess volume of mixing manifested in the unit-cell refinements (Fig. 10; Table 4); this deviation from a linear relationship between the volumes of the end-members (Retger’s “law”) is indicative of a non-ideal solid solution.

Fig. 10

Unit cell parameters of (Mg,Ni)SO₄·9D₂O as a function Ni²⁺ dopant concentration (atom %) at 150 K. Solid lines are least-squares fits of Eq. (1); the plots underneath each parameter report the relative difference between the observed/model cell parameters and a linear mixing model (i.e., Vegard’s/Retger’s “law”)

Table 4 Cell parameters from neutron powder diffraction analysis of the MgSO₄·9D₂O–NiSO₄·9D₂O solid-solution series as a function of nickel content

Table 5 Parameters obtained by fitting of Eq. (1) to unit-cell parameters of (Mg, Ni)SO₄·9D₂O as a function of Ni content

Each of the cell parameters given in Table 4 has been fitted with an equation that describes the deviation from linearity (aka Vegard’s “law”) using a quadratic expression:

$$a=a_{{{\text{Mg}}}}^{{\text{0}}}(1 - X)+a_{{{\text{Ni}}}}^{{\text{0}}}(X)+\delta^{\prime} X{(1 - X)^2}+\delta^{\prime \prime} (1 - X){X^2},$$

(1)

where $a_{{{\text{Mg}}}}^{{\text{0}}}$ and $a_{{{\text{Ni}}}}^{{\text{0}}}$ are the cell parameters of the end-members, X is the Ni atom fraction and δ′ and δ″ characterise the deviation from linearity. Parameters from these fits are reported in Table 5 and are shown as solid lines in Fig. 10. The main contributor to the positive volume excess comes from the b-axis, which exhibits a substantial and asymmetric deviation from linearity as a function of composition, reaching a maximum of ~ 0.15% at 40 atom % Ni²⁺. Conversely, the a-axis exhibits a negative deviation from Vegard’s law whilst both c and β display trends that are statistically indistinguishable from linear. The extent to which this behaviour mimics the observations of Ni-doped olivine is remarkable. With replacement of Mg²⁺ by Ni²⁺ in olivine, the crystal’s b-axis displays an initial plateau or convex upward trend followed by a sharp decrease, exactly as seen in MgSO₄·9H₂O, whereas the a- and c-axes show very slight negative deviations from linearity (Matsui and Syono 1968; Rajamani 1975; Boström 1987; Vokurka and Rieder 1987; Hirschmann 1992; Chen et al. 1996; Henderson et al. 2001).

The model fits to the lattice parameters are used to determine the infinitesimal elastic strain tensor due to ionic substitution (e.g., Hazen et al. 2000); Fig. 11a shows a series of representations of the strain tensor (cf., Hashash et al. 2003). The eigenvalues and eigenvectors of these strain tensors, obtained by standard matrix decomposition methods, are the magnitudes and orientations of the principal strain directions (Fig. 11b).

Fig. 11

a Tensor representation of the substitutionally induced strain in (Mg,Ni)SO₄·9D₂O derived from the lattice parameters in Table 4. Drawn using WinTensor (Kaminski 2004). b Variation of the magnitude of the principal strains, and the angle between ε₁ and the c-axis, with composition

As expected, the main feature is a systematic increase in the magnitude of the negative strain parallel with the b-axis (ε₂), corresponding to shortening of the H-bonded octahedral chains due to substitution of Mg²⁺ with the smaller Ni²⁺ cation (Shannon 1976). Although ε₁ and ε₃ do not vary so substantially, there is large rotation of the strain tensor such that the angle between ε₁ and the c-axis changes from 66° to 23°. What this shows is that at low Ni dopant concentrations in MgSO₄·9H₂O, the largest contraction is in the spacing between adjacent H-bonded octahedral chains (i.e., roughly along the a-axis); at intermediate concentrations, shortening of these chains becomes prevalent; at high concentration, shortening of the gap between the sheets of octahedral chains is of a similar magnitude to that along the length of the chains.

Calculations of the strain due to substitution of Ni into the structure of MgSO₄·9H₂O, with the Ni distributed in various ways across the two available sites, produces good qualitative agreement with the observations. The absolute magnitudes of the distortions are much larger than observed experimentally, but the signs and relative magnitudes agree quite well.

For the a-axis, substituting Ni onto the M1 site produces a large positive deviation from Vegard’s law whilst substitution of Ni onto M2 results in a small negative deviation. For the b-axis, we observe the reverse; substitution of Ni onto M1 produces a negative deviation from Vegard’s law, whereas substitution onto the M2 site generates a large positive deviation. For the c-axis, the deviation from Vegard’s law produced by substitution of Ni is very small indeed (approximately ten times smaller than the maximum deviation in the b-axis) and does not vary at all according to the site preference of the cations. Similarly for β, the deviation is small (~ one-half that of the c-axis) but is slightly positive for Ni situated on M1 and slightly negative for Ni located on M2.

Using the geometry relaxations from the DFT calculations done for three different nickel distributions, we can obtain a rough estimate of the magnitude of the deviations corresponding with the experimentally observed case of 75% of the Ni ions being located on the M2 site. In this circumstance, the maximum deviations from linearity in the a- and b-axis are − 0.19 and + 0.43, respectively, compared with − 0.08 and + 0.15 observed experimentally. Hence the signs are correct, but the calculated magnitudes are too large by a factor of ~ 2–3. For the c-axis and for β, the DFT-calculated deviations from linearity are + 0.08 and − 0.05, respectively, compared with + 0.01 and − 0.01 experimentally. For the unit-cell volume, the calculated deviation from Vegard’s law is + 0.32, whereas the experimental value is + 0.08.

Overall, both the experimental and computational view is that the deviations from Vegard’s law produced by nickel substitution are confined entirely to the a–b plane, this being parallel with the octahedral sheets in the structure, with the largest effect being along the b-axis, the direction in which the octahedra are most directly connected by the Ow2–H2a···Ow5 hydrogen bond. It seems remarkable that distribution of dopants in these H-bonded octahedral chains should have such a dramatic effect: a crystal containing 50 atom % Ni where all of the Ni ions are on M1 has a b-axis that is 0.16 Å (1.3%) shorter than a crystal where those 50% of Ni ions are all on the M2 site. Whilst this may not appear to be a large reduction, it is more than twice as big as the change in the b-axis length in MgSO₄·9D₂O on cooling from 260 to 10 K and it is roughly equivalent to the change in b-axis length caused by the application of 600 MPa of hydrostatic pressure (Fortes et al. 2017b).

As noted earlier, the model used to describe the 50:50 distribution of Mg²⁺ and Ni²⁺ is not a very good analogue of the real crystal. Site disorder in the real crystal will act to dilute the effect of having Ni²⁺ located wholly on the M1 or M2 sites, reducing the deviations from Vegard’s law and providing a possible explanation for the difference between the experimental and computational lattice parameters as a function of composition.

DFT calculations also allow us to evaluate the relative energetic stability of the various ion configurations. As shown in Fig. 12, the configuration in which all Ni occupies the M1 site has an enthalpy (in the athermal limit) that is 3643.4 J mol^− 1 higher than the configuration where all Ni occupies the M2 site. The calculated enthalpy of the configuration in which the Ni ions are equally distributed over both sites has an enthalpy 1840.06 J mol^− 1 above the “all M2” reference state. Hence, in the athermal limit the variation is linear.

Fig. 12

Variation of Gibbs free energy as a function of the distribution of nickel between the M1 and M2 sites in NiSO₄·9H₂O. The open squares are the results of athermal DFT + U calculations and the dashed line depicts a linear variation through these points. Accounting for configurational entropy (Eqs. 2, 3) at higher temperatures results in the coloured curves

The effect of temperature is considered by calculation of the configurational entropy. For a two-site lattice, the configurational entropy, S_conf is related to the site occupancies by:

$${\text{~}}{S_{{\text{conf}}}}= - R\left( {{\upsilon _{{\text{M1}}}}\mathop \sum \nolimits^{} x_{i}^{{{\text{M1}}}}{\text{ln}}x_{i}^{{{\text{M1}}}}} \right) - R\left( {{\upsilon _{{\text{M2}}}}\mathop \sum \nolimits^{} x_{i}^{{{\text{M2}}}}{\text{ln}}x_{i}^{{{\text{M2}}}}} \right){\text{~,}}$$

(2)

where ${\upsilon _{{\text{M1}}}}$ and ${\upsilon _{{\text{M2}}}}$ are the number of moles of M1 and M2 sites per formula unit and $x_{i}^{{{\text{M1}}}}$, for example, is the fractional occupancy of species i on the M1 site. For the case of site ordering, where $x_{{{\text{Ni}}}}^{{{\text{M1}}}}=1,~\;x_{{{\text{Ni}}}}^{{{\text{M2}}}}=0$, and site anti-ordering, where $x_{{{\text{Ni}}}}^{{{\text{M1}}}}=0,~\;x_{{{\text{Ni}}}}^{{{\text{M2}}}}=1$, the total configurational entropy is zero. For the case of complete disorder across the two sites, S_conf reaches a minimum value of 5.762 J K^− 1 mol^− 1. The difference in free energy, ΔG, from the site anti-ordered crystal is:

$$\Delta G=\Delta H - T\Delta {S_{{\text{conf}}}}~.$$

(3)

Figure 12 shows the variations in ΔG for a range of temperatures; the energy minimum at 250 K corresponds to a distribution of ~ 83:17 for Ni on the M2:M1 sites, which agrees very well with the observed 75:25 distribution, despite the apparent lack of opportunity for equilibrium to be reached during the quench synthesis of our specimens. The substantial energetic preference for Ni to occupy the M2 is matched in similar calculations on both Zn- and Fe-doped analogues. For Fe²⁺ the athermal energy difference between M1 and M2 sites is considerably larger than the Ni species (7442.6 J mol^− 1) and for Zn²⁺ it is somewhat smaller (2745.0 J mol^− 1).

Concluding remarks

We have determined the structure of NiSO₄·8D₂O for the first time, including all hydrogen atom positions, using a combination of X-ray and neutron powder diffraction and we have refined the structure of NiSO₄·9D₂O using neutron powder data. Both contain virtually identical chains of directly H-bonded NiO₆ octahedra although other aspects of their framework (by virtue of the different number of interstitial water molecules) are not the same. Neither crystal is stable in aqueous solution, undergoing subsolidus transformations to the heptahydrate (morenosite) + ice prior to eutectic melting. Experimentally, there is evidence for weak ferromagnetic coupling in NiSO₄·9H₂O even though calculations show no differences in energy or structure for different spin configurations.

Isotypic enneahydrates of Mg-, Zn-, Fe- and Ni-sulfates have now been produced synthetically and may occur naturally in environments where aqueous solutions containing these solutes are frozen very quickly, such as in cryovolcanic vents on the surfaces of icy planetary bodies. Annealing between 250 and 270 K should also result in the formation of NiSO₄ octahydrate in these environments. Further work to characterise the vibrational spectra of these materials is required to aid their detection by remote sensing in such localities.