Thermophysical properties and phase diagrams in the system MgO–SiO₂–FeO at upper mantle and transition zone conditions derived from a multiple-Einstein method

Abstract

We applied a lattice vibrational technique, based on representing the vibrational density of states with multiple-Einstein frequencies, to determine consistency of data on thermophysical properties and phase diagrams in the system MgO–FeO–SiO₂. We present analyses of these data in the temperature range between 0 and 2000 K and pressure range between 0 and 20 GPa. The result is a database containing phases relevant to the Earth upper mantle and transition zone. We show that consistency of different datasets associated with the dissociation of the ringwoodite form of Fe₂SiO₄ depends on the crucible material that has been used to perform partitioning experiments between ringwoodite and ferropericlase, and that this results in different phase diagrams for FeSiO₃ and the post-spinel part of Mg₂SiO₄–Fe₂SiO₄. We show that the existence of a phase field coesite + ringwoodite in the phase diagram of FeSiO₃ is possible and that it might be used to fine-tune pressure scales. We demonstrate that the phase boundary between coesite and quartz is very sensitive to the low-temperature heat capacity of coesite and that heat capacity data of β-quartz are too large to be reconciled with the phase boundary between β-quartz and coesite. We compare our results with seismic data associated with the 410 km seismic discontinuity.

Introduction

Our work aims at developing a thermodynamic database for planetary materials, enhancing the interpretation of geophysical observations. In our previous paper, Jacobs et al. (2017), we showed a method suitable for constructing a small thermodynamic database for the system MgO–SiO₂, enabling the calculation of thermodynamic properties, sound velocities and phase diagrams in large ranges of pressure and temperature occurring in planetary interiors. Unlike conventional methods, such as those employing the Mie–Grüneisen–Debye (MGD) formalism, or those based on parameterizations of thermodynamic properties at 1 bar pressure, it includes the characteristic that vibrational density of states (VDoS), static properties and Grüneisen parameters predicted by ab initio techniques are incorporated in the formalism. We showed that this enhances better discrimination between the disparate experimental datasets relative to conventional methods, resulting in better constraints on Clapeyron slopes in phase diagrams. Our method includes deriving mechanical properties, such as the shear modulus, a requirement for comparing our calculations with seismic observations. Because the method combines the requirements of reliably representing available experimental data and computational efficiency, it enables development of large thermodynamic databases, necessary for extrapolating thermophysical properties to pressure–temperature regions not accessed by experimentation. Because FeO is the third abundant oxide material next to MgO and SiO₂ in planetary mantles, such as in Earth and Mars (McDonough and Sun 1995; Taylor 2013), it is obvious to extend the small database with iron endmembers of solid solution phases.

In the present paper we focus on the thermodynamic data of endmembers in the system FeO–SiO₂, with the ultimate goal to arrive at formulations for solid solution phases in the ternary system MgO–FeO–SiO₂, resulting in better approximations of thermodynamic properties of mantle materials. The endmembers in the system FeO–SiO₂ are coupled to those in the system MgO–SiO₂ because solid solutions are formed from them as exemplified in Fig. 1 for the polymorphs of Fe₂SiO₄ and Mg₂SiO₄. Because of that, our results obtained for endmembers in MgO–SiO₂ serve as constraints for the thermodynamic description of FeO–SiO₂.

Fig. 1

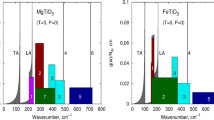
Left: phase diagram along the Mg₂SiO₄–Fe₂SiO₄ join including the solid solution phases olivine (ol), wadsleyite (wa), ringwoodite (ri) and ferropericlase (fp). St represents the stishovite form of SiO₂. Solid boundaries for ri + fp + st are based on experiments in rhenium capsules, whereas the dashed ones are based on experiments in iron capsules. Right: isobaric heat capacity of fayalite partitioned in physical effects contributing to isochoric heat capacity and the dilation term α²KVT

Contrasted to the system MgO–SiO₂, ab initio predictions of thermodynamic and mechanical properties are scant for endmembers in the system FeO–SiO₂, hampering a thermodynamic analysis. The main reason for this scantiness is that properties of iron endmembers are affected by combined electronic and magnetic effects inducing Schottky anomalies in the heat capacity, and in the small number of ab initio studies of this system these effects are not resolved in all detail. The consequence is that experimental heat capacities for iron endmembers are less well represented by ab initio predictions relative to those for the magnesium endmembers. Therefore, contrary to our previous analysis of MgO–SiO₂, the present one is challenged by less accurate or even unknown vibrational densities of states for most endmembers. Additionally, electronic effects have been established experimentally only sparsely for all iron endmembers, except for fayalite, which has been studied by Aronson et al. (2007). For these reasons, we regard our analysis as a preliminary one, which must be fine-tuned in the future when more experimental data concerning electronic effects and more accurate ab initio predictions become available. Notwithstanding these difficulties, we anticipate that our analysis may serve a guide for directing future experimental efforts.

Thermodynamic analyses of the system FeO–SiO₂ have been carried out by a number of investigators, such as by Stixrude and Lithgow-Bertelloni (2011) using a semi-empirical Mie–Grüneisen–Debye (MGD) formalism, and by Fabrichnaya et al. (2004), Holland and Powell (1998), Saxena (1996), and Fei et al. (1991) using empirical parameterization techniques. These analyses have in common that the low-pressure clinoferrosilite form of FeSiO₃ has been neglected and we shall include this polymorph in our analysis. We noticed that to arrive at a proper description of phase relations between the iron endmembers, it is mandatory to include in the analysis quartz and coesite, polymorphs of SiO₂, because it appeared that coesite might interfere with phase equilibria in the phase diagram of FeSiO₃.

For reasons of paper length, we have excluded the iron endmembers of the perovskite, post-perovskite, majorite and akimotoite phases. They will be discussed in a subsequent paper. Our main goal in the present paper is to find constraints for phase equilibria at conditions prevailing in the upper mantle and transition zone of the earth.

Theoretical background

The central equation from which we derive thermodynamic properties including the shear modulus is a semi-empirical expression for the Helmholtz energy, partitioned in static lattice, vibrational, electronic and magnetic effects:

$$A(T,V)={U^{{\text{ref}}}}+{U^{{\text{static}}}}(V)+{A^{{\text{vib}}}}(T,V)+{A^{{\text{cf-el}}}}(T)+{A^\lambda }(T).$$

(1)

The reference energy, U^ref in Eq. (1), is a constant, and adjusted such that available heats of formation of the substances are represented, such as for fayalite and orthoferrosilite. If the heat of formation of a substance is not available, this constant is determined by the location of phase boundaries. The second term represents the static lattice energy for a substance in which vibrational motions are absent. This contribution is determined by the equation of state for which we use Birch–Murnaghan expressions. Although a fictive contribution it can, in principle, be determined well by athermal ab initio methods. The third term in Eq. (1) is determined by vibrational motions. Mathematical expressions for these three terms are detailed by Jacobs et al. (2017).

It is well-known that iron atoms, octahedrally surrounded by oxygen atoms, split their fivefold degenerate energy levels into T_2g and E_g energy levels, which are split further due to spin–orbit coupling, such has been found for fayalite by Aronson et al. (2007). Figure 1 shows that this has a significant effect on the heat capacity. Aronson et al. (2007) and Jacobs and de Jong (2009) used a crystal-field expression via the partition function, Z, to express the Helmholtz energy contribution as:

$$Z=\frac{1}{{{g_1}}}\sum\limits_{{i=1}}^{m} {{g_i}\exp \left( { - \frac{{{\varepsilon _i}}}{{kT}}} \right)} ,$$

(2)

$${A^{{\text{cf-el}}}}= - kT\ln Z - \frac{1}{2}{\beta _{{\text{el}}}}\frac{{{n_{\text{a}}}}}{{{N_{\text{A}}}}}{\left( {\frac{V}{{{V_0}}}} \right)^{{\gamma _{{\text{el}}}}}}{T^2}.$$

(3)

Expression (3) is given per atom Fe and for one site, e.g., the M1 site in fayalite, n_a the number of atoms in a molecular formula and N_A Avogadro’s number. The m energy levels of one site are characterized by their energies, ε_i and degeneracies g_i. The first energy level is the ground state with ε₁ = 0. Equation (2) contains the factor 1/g₁ to constrain the entropy contribution to zero at zero temperature and zero pressure, commensurate with the third law of thermodynamics. Expressions for thermodynamic properties derived from the Helmholtz expression are detailed in Jacobs and de Jong (2009). Because the effect of volume on the energies, ε_i, is unknown experimentally for all iron endmembers, we assume that they have constant values. Therefore crystal-field contributions affect only Helmholtz energy, entropy and heat capacity. The last term in Eq. (3) denotes a free-electron gas contribution and it is used in an alternative analysis for taking into account that isochoric heat capacities at high temperature exceed the Dulong–Petit limit.

Aronson et al. (2007) found for fayalite, that the M1 site is mainly responsible for the Schottky anomaly, described by Eq. (3), and that the M2 site mainly contributes to the sharp critical lambda behavior in the heat capacity. The sharp critical phenomenon in the heat capacity is due to a change in ordering of the electronic spins, when fayalite changes from the antiferromagnetic state to the paramagnetic state and it cannot be represented by Eq. (3) alone. Jacobs and de Jong (2009) described it with an empirical expression for the Gibbs energy given by Hillert and Jarl (1979), frequently and successfully used in the Calphad community to model magnetic contributions to properties of metallic elements. This expression is an approximation of that deduced by Inden (1981) for the isobaric heat capacity. To have better consistency in Eq. (1) for the Helmholtz energy, we employ it for the isochoric heat capacity and write Inden’s (1981) expression as:

$$C_{{\text{V}}}^{\lambda }={a_1}\ln \left( {\frac{{1+{\tau ^m}}}{{1 - {\tau ^m}}}} \right)\,{n_{\text{a}}}R\ln (1+\beta )\,\quad\tau ={\raise0.7ex\hbox{$T$} \!\mathord{\left/ {\vphantom {T {{T_{\text{c}}}}}}\right.\kern-0pt}\!\lower0.7ex\hbox{${{T_{\text{c}}}}$}} \leq 1,$$

(4)

$$C_{{\text{V}}}^{\lambda }={a_2}\ln \left( {\frac{{{\tau ^n}+1}}{{{\tau ^n} - 1}}} \right)\,{n_{\text{a}}}R\ln (1+\beta )\,\quad\tau ={\raise0.7ex\hbox{$T$} \!\mathord{\left/ {\vphantom {T {{T_{\text{c}}}}}}\right.\kern-0pt}\!\lower0.7ex\hbox{${{T_{\text{c}}}}$}}>\,1.$$

(5)

In these expressions a₁, a₂, n > 1, m > 1 are constants, R denotes the gas constant, n_a the number of atoms in a molecular formula unit giving rise to a magnetic contribution (n_a= 2 for Fe₂SiO₄), β the average magnetic moment per atom and T_c the critical temperature. The expressions for heat capacity can be developed in Maclaurin series expansions, from which the Helmholtz energy is straightforwardly derived. To our knowledge the full expression has neither been published in the Calphad community, nor by Inden (1981). Therefore we express it below:

$${A^\lambda }(T)={n_{\text{a}}} \cdot g(\tau ) \cdot RT\ln (1+\beta ),$$

(6)

$$\begin{aligned} g(\tau \le 1) & = - \frac{{2a_{1} }}{m}\sum\limits_{{j = 0}}^{\infty } {\frac{{\tau ^{{(2j + 1)m}} - \tau ^{{ - 1}} }}{{(2j + 1)^{2} \left[ {(2j + 1)m + 1} \right]}}} - \tau ^{{ - 1}} \\ & \quad + \frac{{2a_{2} }}{n}\sum\limits_{{j = 0}}^{\infty } {\frac{{\tau ^{{ - 1}} }}{{(2j + 1)^{2} \left[ { - (2j + 1)n + 1} \right]}}} , \\ \end{aligned}$$

(7)

$$g(\tau>1)= - 1+\frac{{2{a_2}}}{n}\sum\limits_{{j=0}}^{\infty } {\frac{{{\tau ^{ - (2j+1)n}}}}{{{{(2j+1)}^2}\left[ { - (2j+1)n+1} \right]}}} .$$

(8)

The expressions given by Hillert and Jarl (1979) are in the Calphad community mostly used with only 3 or 4 terms in the series expansion, e.g., in Chen and Sundman (2001) for Fe, Ni and Co. Because critical phenomena in iron silicates occur at low temperatures, for which adiabatic or PPMS (physical properties measurement system designed by quantum design) calorimetric data are available, extra terms are necessary to represent these accurate data. For this reason we adhere to Inden’s (1981) original formulation rather than to the approximate formulation of Hillert and Jarl (1979). In “online resource appendix A” we show that constants a₁ and a₂ are expressed in n, m and a property p denoting the ratio of the magnetic energy above the critical temperature and the total magnetic transformation energy. In “online resource appendix A” other thermodynamic properties are given, derived from Eq. (6).

Equation (1) assumes that all physical effects can be treated independently. However, it may be anticipated that a VDoS predicted by ab initio methods including electronic and magnetic effects differs from the one in which these effects are neglected. For metallic elements, such as Al and Pt we have shown in Jacobs et al. (2013) that the independent treatment of physical effects is quite successful in representing experimental thermodynamic data. Because the effect of including electronic and magnetic effects on thermodynamic properties in ab initio predictions for iron silicates is still unresolved in all details, we assume the independent partitioning of physical contributions in Eq. (1) a useful working hypothesis.

We treat quartz in our analysis. We follow Holland and Powell (1998) to use the tricritical Landau-Lifshitz (1980) formalism to describe the thermodynamic properties of the α- and β form. This formalism is based on the Gibbs energy rather than the Helmholtz energy, and it is expressed as:

$${G^{{\text{total}}}}(P,T)=G(P,T)+{G^{{\text{Landau}}}}(P,T).$$

(9)

The first term on the right-hand side of this equation is determined by the Helmholtz energy formalism of Eq. (1) and applies to the high-temperature β-form, for which G^Landau = 0. The Landau contribution to the Gibbs energy is expressed in an order parameter, Q, and in the tricritical case we follow Carpenter (1992) by writing:

$${G^{{\text{Landau}}}}(P,T)=\frac{1}{2}{a_{\text{L}}}\,(T - {T_{\text{c}}}(P))\,{Q^2}+\frac{1}{6}\,c\,{Q^6}.$$

(10)

In Eq. (10), T_c(P) represents the critical temperatures along the phase boundary between the α (low-temperature) and β (high-temperature) form of quartz. Because the phase boundary is nearly linear, we express it in the inverse of its Clapeyron slope, h, as:

$${T_c}(P)={T_c}(P=0)+h \times P.$$

(11)

The order parameter is obtained from the equilibrium condition (∂G^Landau/∂Q)_P,T = 0 and the characteristic that Q = 1 at T = 0. Expressing c in a_L and T_c(P) the Gibbs energy contribution and order parameter are written as:

$${G^{{\text{Landau}}}}(P,T)=\frac{1}{2}{a_{\text{L}}}\,\left\{ {(T - {T_c}(P))\,{Q^2}+\frac{1}{3}{T_c}(P)\,{Q^6}} \right\},$$

(12)

$${Q^4}=\frac{{{T_c}(P) - T}}{{{T_c}(P)}}.$$

(13)

Because the Clapeyron slope of the phase boundary is known, the Landau contribution contains only one fitting parameter a_L. Expressions for thermodynamic properties derived from the Gibbs energy contribution are included in “online resource appendix A”. From the appendix it follows that the Landau contribution to entropy at zero Kelvin equals − 0.5a_L, where a_L is a positive value. Because the vibrational contribution is zero at this temperature the total entropy is a negative value, and therefore the third law of thermodynamics is violated. To correct for this situation, we add a value of + 0.5a_L to S^Landau (P,T) and − 0.5a_LT to G^Landau(P,T) in Eq. (9). This correction affects entropy and Gibbs energy of both the α- and the β-form of quartz. Therefore at zero Kelvin, the entropy of the unstable disordered phase (β-quartz) has a positive remnant entropy, whereas the stable ordered phase (α-quartz) has zero entropy.

Results

Figure 2 shows that phase equilibria in the systems FeSiO₃, Fe₂SiO₄ and SiO₂ are related to each other by fayalite, ringwoodite and stishovite. The stishovite polymorph of SiO₂ relates these phase equilibria to coesite and quartz and to phases in the system MgO–SiO₂. Additional relations to the system MgO–SiO₂ are available through experimental data on the exchange of iron and magnesium atoms between solid solution phases. This exchange is mainly determined by the Gibbs energy of the magnesium and iron endmembers of the solid solution phases in P–T space, and to a smaller extent by their mixing properties. Because our main interest is to elucidate the coupling between thermophysical properties and phase equilibria at conditions present in the upper mantle and transition zone of the Earth, our work is restricted to phases in the solid state. This is also the reason that we have neglected tridymite and cristobalite in the system SiO₂. However, coesite and quartz are included to better constrain thermophysical properties of fayalite and orthoferrosilite, and indirectly those of other phases such as HP- and LP-clinoferrosilite. To keep the description consistent with that for the endmembers in the system MgO–SiO₂ obtained in our previous work, we used 60 Einstein frequencies in the VDoS of each substance. The model parameters of the eight endmembers are given in Tables 1, 2 and 3 and fractions needed for their VDoS in “online resource Table 1”. The model parameters were derived from experimental data given in “online resource Table 2”. The resulting database for the iron endmembers was subsequently cloned to a database in which the endmembers contain 30 frequencies in the VDoS, using a method described in our previous paper, Jacobs et al. (2017). A text file containing the database is available on website http://www.geo.uu.nl/~jacobs/Downloads. Software for calculating the VDoS and thermophysical properties of endmembers using this database can be found there as well.

Fig. 2

Upper-left: phase diagram of Fe₂SiO₄. The dashed curve labeled (Fab) is taken from Fabrichnaya et al. (2004). The dashed line labeled (Kat) denotes the phase boundary by Katsura et al. (1998). The liquidus has been taken from Akimoto et al. (1967). Upper-right: phase diagram of FeSiO₃. Labels (Fab), (Kat), (Liq) have the same meaning as in the plot for Fe₂SiO₄. Solid triangles denote a calculation by Hugh-Jones et al. (1994). The grey area denotes the lens-shaped Ri + Coe field that appears when the Fa = Ri boundary in the system Fe₂SiO₄ is moved by − 0.21 GPa. Lower-left: phase diagram of SiO₂ without tridymite and cristobalite. The Debye model is taken from Stixrude and Lithgow-Bertelloni (2011). The dashed curve labeled (H) has been calculated by an analysis representing the ambient entropy by Hemingway et al. (1998) for coesite. The dashed liquidus has been taken from Gasparik (2003). Symbols for coesite = stishovite: cross: Zhang et al. (1996), inverse triangle: Zhang et al. (1993), diamond: Suito (1977), triangle: Yagi and Akimoto (1976), square: Akimoto and Syono (1969). Symbols for quartz = coesite: circle: Hemingway et al. (1998), asterisk: Bose and Ganguly (1995), cross: Bohlen and Boettcher (1982), inverse triangle: Mirwald and Massone (1980), triangle: Boyd et al. (1960). Lower-right: isobaric and isochoric heat capacity of fayalite with physical contributions shown in the inset

Table 1 Model parameters of FeO and polymorphs of Fe₂SiO₄, FeSiO₃ and SiO₂

Table 2 Model parameters for vibrational, magnetic, and electronic contributions

Table 3 Crystal-field energies (E) with their degeneracies (g)

Jacobs et al. (2017) showed that for most magnesium endmembers intrinsic anharmonicity is present in the lattice vibrations. Although no experimental data are available for iron endmembers on anharmonicity, through Raman and/or infrared spectroscopic experimental data, we anticipate that it is present in their lattice vibrations. This is supported by the characteristic that analyses in the quasi-harmonic approximation fail to represent phase boundaries, and as shown in Fig. 2 for fayalite, the heat capacity data at high temperature. However, the large high-temperature heat capacities generally occurring in iron endmembers might also be explained by the presence of electronic effects alone. For that reason, we show two analyses in Table 2, in which either intrinsic anharmonicity is introduced combined with no free-electron gas contribution [β^el = 0 in Eq. (3)] or in which the quasi-harmonic approximation is used combined with a free-electron gas contribution (β^el > 0) in the crystal-field expression. For both analyses given in Tables 1, 2 and 3, Online resource Table 1 the same VDoS, static properties and crystal-field properties are used. The results of both analyses appear to be insignificantly different with respect to experimental data. Therefore our analyses are unable to discriminate which effect is responsible for high temperature heat capacity. A combination of both effects is also possible.

We treated the endmember of ferropericlase, FeO, as a stoichiometric compound for the following reasons. It is well-known that wüstite Fe_yO (in which y is a variable between 0.85 and 0.95 at 1 bar) has a complicated structure, involving the ions Fe²⁺, Fe³⁺ and vacancies (Jacobsen et al. 2002). It could be anticipated that the properties of ferropericlase are well described by applying an ionic sublattice model that includes these constituents, such as has been achieved by Fabrichnaya et al. (2004). The application of their ionic sublattice model involves introducing fictive endmembers for which thermophysical properties are impossible to measure directly. Figure 2 shows, that incorporating these fictive endmembers into such a model, thereby expanding the model parameter space, is apparently not a guarantee to represent the phase boundary between ringwoodite, stishovite and FeO in the phase diagrams of Fe₂SiO₄ and FeSiO₃. Because we consider our work preliminary due to the absence of a VDoS predicted by ab initio for most iron endmembers, we attempted to circumvent the problem of introducing a larger amount of model parameters for fictive endmembers employing an ionic sublattice model for ferropericlase. Instead, we noticed that by treating wüstite as stoichiometric FeO, thermophysical properties for materials in the lower and upper mantle are represented surprisingly well. A possible reason for this might be appreciated by considering approximate overall Earth mantle compositions, e.g., pyrolytic or chondritic. Along a mantle P–T path, which is usually approximated by an isentropic path above about 6 GPa, the first formation of ferropericlase in equilibrium phase assemblages starts to occur at pressures above about 20 GPa. Calculations of phase equilibria for these overall mantle compositions along such paths, performed with present-day thermodynamic databases, indicate that the iron composition in ferropericlase never exceeds 30 mol% at lower and upper mantle conditions. Additionally, according to the observations of Jacobsen et al. (2002), Srečec et al. (1987), Simons (1980) and Rosenhauer et al. (1976) the Fe³⁺ content in ferropericlase decreases with increasing MgO content. From their work it follows that ferropericlase in phase assemblages at mantle conditions contain Fe³⁺/(Fe²⁺ + Fe³⁺) ratios smaller than 3.5%. Moreover, Simons (1980) and Fei and Saxena (1986) concluded that wüstite approaches the stoichiometric composition at pressures above 10 GPa. More recently McCammon (1993) showed that Fe_yO approaches the composition Fe_0.98O at pressures above 10 GPa. Therefore, we anticipate that phase equilibria and thermophysical properties for ferropericlase, can be represented reasonably well by treating wüstite as stoichiometric FeO at upper and lower mantle conditions. Our results might be improved by taking into consideration the effect of Fe³⁺, especially important for industrial applications, or in mineral physics at conditions prevailing in the Earth’s crust and asthenosphere. Because our main target is to represent thermophysical properties of materials at upper mantle and transition zone conditions, we postpone including this effect and will use our present results as constraints at a later stage of our database development.

Details of the optimization

The model parameters were obtained by applying a nonlinear least-squares optimization technique, described by Jacobs et al. (2017). Because systematic errors are present in experimental data, such as is for instance the case for the heat capacity of fayalite depicted in Fig. 2, we refrained from a global optimization of all available data. Instead, a multitude of optimizations was performed for each substance separately to elucidate which datasets from different sources are consistent with each other. After having obtained values for model parameters for each substance they were fine-tuned using phase diagram data and magnesium–iron exchange data between different solid solution phases. In “online resource appendix B”, we detail results of analyses for each substance separately. The most important findings are given here and in the subsequent sections.

Only for fayalite, ringwoodite, coesite and quartz a VDoS predicted by ab initio techniques is available, which constrains the frequencies at zero Kelvin and zero pressure. To arrive at a description representing low-temperature heat capacity of iron endmembers, larger shifts in the VDoS are required compared to those for magnesium endmembers. For the three polymorphs of FeSiO₃ no VDoS is available. However, use can be made of the property that the VDoS of these endmembers is similar to that of their magnesium counter endmembers, with the difference that frequencies of vibrational modes involving iron atoms are shifted to lower frequencies, as has been demonstrated by Yu et al. (2013) for Fe₂SiO₄. The iron endmembers are characterized by larger heat capacities than their magnesium counter end members due to electronic effects and/or intrinsic anharmonicity. For instance, Fig. 2 illustrates that from the calorimetric measurements of Benisek et al. (2012) it follows that isochoric heat capacity of fayalite crosses the Dulong–Petit limit, 174.6 J/K/mol. The sum of vibrational and crystal-field electronic contributions to isochoric heat capacity crosses the Dulong–Petit limit at about 680 K, much lower than is the case for forsterite, about 1700 K. Figure 3 shows that if the data of Benisek et al. (2012) are correct, the slope of the phase boundary between fayalite and ringwoodite constrains the heat capacity of ringwoodite to values larger than those determined by Watanabe et al. (1982). Isochoric heat capacity crosses the Dulong–Petit limit at about 750 K, whereas that of the magnesium counter endmember does not cross it.

Fig. 3

Upper-left: heat capacity of ringwoodite. The inset shows physical contributions to isochoric heat capacity. The horizontal dashed line represents the Dulong–Petit value. Upper-right: isobaric heat capacity of orthoferrosilite with physical contributions to isochoric heat capacity in the inset. The Debye model has been taken from Stixrude and Lithgow-Bertelloni (2011). Lower-left: heat capacity of coesite. Dashed curve, labeled (H), results from an alternative analysis representing the entropy determined by Hemingway et al. (1998) and Holm et al. (1967); it corresponds to the dashed curve, also labeled (H), in the phase diagram of SiO₂ in Fig. 2. Experimental data of Hemmingway et al. (1998) above 850 K were extrapolated. Lower-right: heat capacity of quartz. The Debye model is taken from Stixrude and Lithgow-Bertelloni (2011). Dashed curves were calculated with clones containing one (1E) and two (2E) Einstein frequencies in the VDoS

Table 4 Enthalpy of formation, and enthalpy differences in kJ/mol for reactions at 1 bar pressure in the system FeO–SiO₂

Table 5 Ambient entropy values, in J K^− 1 mol^− 1, calculated with different database clones

Only the crystal-field description of fayalite is robust. For all other iron endmembers no data for energy levels with their associated degeneracies are available, except for orthopyroxene (Mg_0.8Fe_0.2)SiO₃ determined by Victor et al. (2001), which from our analysis appears to be similar to that of orthoferrosilite. From the analyses it became clear that some trade-off is present between the energy levels in the crystal-field contribution, the VDoS and anharmonicity and in the analysis not including intrinsic anharmonicity the electronic coefficient, β^el. Only low energy levels in the crystal-field expression, giving rise to heat capacity contributions at temperatures in the vicinity of the critical points, can be established unambiguously. For that reason a multitude of possible expressions for the crystal-field energy levels with their degeneracies have been carried out to establish heat capacities, such as for ringwoodite and orthoferrosilite depicted in Fig. 3. Although there is some arbitrariness in the crystal-field model parameters, it became clear that thermodynamic properties and phase diagrams resulting from these analyses are robust. Because of the different possible descriptions for the crystal-field contributions, and associated anharmonicity parameters or electronic coefficients, it is difficult to assign robust uncertainties in the model parameters. For that reason, we consider uncertainties in the coefficients in Tables 1, 2 and 3 estimates. They are based on varying a specific model parameter in a way such that the sum of squares changes outside its uncertainty range determined by the uncertainties in experimental properties.

Thermochemical data

Because thermodynamic databases of Fabrichnaya et al. (2004) and Stixrude and Lithgow-Bertelloni (2011) are frequently used in geophysics, and to illustrate advances that are made with our method, we compare results obtained from these databases with our own results in Tables 4 and 5. Table 4 demonstrates that our small database, just as that of Fabrichnaya et al. (2004), results in a representation of heat of formation data to within experimental uncertainty. The exception is possibly the heat of formation of FeO, although it must be remarked that the value given by JANAF is an estimate based on assumptions on the heat capacity of FeO and its melting point. Our value and that derived from the database of Fabrichnaya et al. (2004) is closer to the JANAF value for wüstite, Fe_0.947O, rather than to that of stoichiometric FeO. Because heat capacity, in the entire range of the measurements, is cumbersome to represent by a Debye model, it is evident that the database of Stixrude and Lithgow-Bertelloni (2011) does not offer the possibility to include experimental heat of formation data and values for entropy at standard conditions. However, models based on the Debye formalism can be constrained by enthalpy difference data. For instance, enthalpy differences between fayalite and ringwoodite obtained by using this database, or our own, are better consistent with experimental values than those obtained with the database of Fabrichnaya et al. (2004). Table 5, however, shows that our database results in values for ambient entropy of ringwoodite representing the experimental value of Yong et al. (2007), whereas the other two databases deviate significantly from that value.

For the heat capacity of coesite, shown in Fig. 3, three datasets determined by adiabatic calorimetry are available constraining the value for ambient entropy. The datasets of Hemingway et al. (1998) and Holm et al. (1967) are consistent with each other and result in the same value for ambient entropy. Using these two datasets in our analyses results in the dashed heat capacity curve labeled (H) in Fig. 3. However, using these datasets invariably leads to a negative value for the Clapeyron slope of the boundary between coesite and quartz at temperatures below 1000 K, indicated by the curve labeled (H) in the phase diagram of SiO₂ in Fig. 2. The reason for this behavior is that the entropy–pressure curves of coesite and quartz intersect at pressures below the phase boundary, resulting in an entropy value for coesite larger than that of quartz at P–T conditions on the phase boundary, whereas its volume is smaller than that of quartz. Figure 3 shows that heat capacity of quartz is accurately represented. To arrive at the experimentally derived value for ambient entropy requires imposing the third law correction to entropy as stated in section “Theoretical background”. Neglecting this correction, + 0.5a_L, definitely results in entropy smaller than that of coesite. Because thermal expansivity and volume for both polymorphs are quite accurately represented in pressure–temperature space, such as shown for quartz in Fig. 4, the only way to avoid the intersection of the entropy–pressure curves is to assume a smaller value for ambient entropy of coesite. For that reason, we have constrained our model for coesite by heat capacity data of Atake et al. (2000). Although Fig. 3 shows that the differences between heat capacity curves derived from the datasets of Atake et al. (2000) and Hemingway et al. (1998) are small, the smaller value for ambient entropy of the former is sufficient to arrive at a phase boundary between coesite and quartz with a positive Clapeyron slope, representing all experimental datasets. The resulting enthalpy difference between coesite and quartz at room temperature is in that case in agreement with all experimental values in Table 4 with the exception of that established by Holm et al. (1967). At high temperatures the enthalpy difference is in accordance with the value experimented by Akaogi and Navrotsky (1984) and Akaogi et al. (1995). Enthalpy difference values between coesite and stishovite and those between quartz and stishovite represent experimental values of Akaogi and Navrotsky et al. (1984) and Akaogi (1995) to within experimental uncertainty.

Fig. 4

Upper-left: volume of quartz at 1 bar. Solid curve represents our calculations. The dashed curves labeled (Fab) and (Mao) were calculated from the databases of Fabrichnaya et al. (2004) and Mao et al. (2001). The inset represents adiabatic bulk modulus at 1 bar and solid squares are data of Kammer et al. (1948). Upper-right: volume of α-quartz and coesite. The dashed curves labeled (Fab) were calculated with the database of Fabrichnaya et al. (2004). Lower-left: adiabatic bulk and shear modulus of olivine calculated at compositions 10 and 12.5 mol% Fe₂SiO₄. Properties at 12.5 mol% were calculated at 300 K, 1000 K, 1500 K and 1700 K. Lower-right: volume–temperature behavior of orthopyroxene for different compositions indicated by the mole fraction numbers close to the volume axis

The database of Fabrichnaya et al. (2004) produces, just as ours, a phase boundary between coesite and quartz that is in accordance with the experimental data in Fig. 2, but Fig. 4 shows that their parameterizations are kept too simple to represent volume data for quartz and coesite. This also applies to the database for SiO₂ constructed by Mao et al. (2001), who used the same parameterization method as Fabrichnaya et al. (2004). Therefore thermo chemical data and the location of the phase boundary between coesite and quartz are better constrained by thermophysical properties resulting from our own description.

Figure 3 shows for quartz that a Debye model is characterized by problems with the heat capacity. This typical behavior of heat capacity can be simulated using our own method, by employing a small number of Einstein frequencies in the VDoS, using a process to clone a multiple-Einstein description, discussed by Jacobs et al. (2017). This process is characterized by setting a P–T condition for which entropy and enthalpy of the substance must be identical relative to the original description having many Einstein frequencies in the VDoS. We have chosen 1 bar and 1000 K. Figure 3 illustrates that the curve calculated by the Debye model is quite similar to that calculated by a model in which the VDoS is represented by a single Einstein frequency. Increasing the number of Einstein frequencies in the VDoS using the clone process, results in models that converge towards the experimental data, such as shown for a 2-Einstein model. The difference with the Debye model is that the process of cloning our description into a single-Einstein one, results in an accurate representation of the phase boundary between coesite and quartz, and even the volume properties of the two polymorphs. Table 5 shows that heat capacity and ambient entropy values of both coesite and quartz cannot be represented well when the number of Einstein frequencies is too small.

Although the experimental values in Tables 4 and 5 are represented satisfactorily, we were not able to achieve an unambiguous description for β-quartz, such that its high-temperature heat capacity is represented to within experimental uncertainty. Figure 3 shows that our analysis results in heat capacity values, about 2% smaller relative to the drop calorimetric data of Richet et al. (1982). Representing these data, to within experimental uncertainty, requires implementing dispersion in Grüneisen, mode-q, and anharmonicity parameters in at least three frequency ranges. Because no constraints could be set on these parameters due to the lack of experimental spectroscopic data, considerable trade-off is present in obtaining values for them by using just macroscopic thermodynamic properties in our analysis. Although the model parameters vary significantly, in these aside analyses, the resulting Clapeyron slope of the phase boundary between β-quartz and coesite is invariably and significantly too large as depicted by the curve labeled (R) in Fig. 2. The simplest description representing the heat capacity of β-quartz, monodisperse in Grüneisen parameters, using the parameters in Tables 1, 2 and 3, Online resource Table 1, is achieved by adding an artificial contribution to the Helmholtz energy for which Eq. (32) in “online resource appendix B” is suitable, by setting h = 6181 K, s = − 1.513, f = − 1, g = − 0.5. In that case the heat content measurements of Richet et al. (1982) are represented to within 0.4% and average deviation of 0.26%, which is close to the experimental uncertainty of 0.2–0.3%. Heat capacity data of Richet et al. (1982) are represented with an average deviation of 0.25%. An aside analysis using a first-order Landau method slightly improves the description for the heat content measurements, and results in a transition enthalpy between α- and β-quartz of only 175 J/mol. Also in that case, the artificial function is needed to represent the heat capacity of β-quartz. Just as for the tricritical Landau method the Clapeyron slope of the phase boundary between β-quartz and coesite, 1.99 MPa/K, is too large compared to the experimental values of Mirwald and Massone (1980), 1.34 ± 0.15 MPa/K and Boyd et al. (1960), 1.12 ± 0.15 MPa/K. The introduction of a more negative anharmonicity parameter for coesite to represent better the Clapeyron slope above 1600 K, has the effect that the phase boundary tends towards curve (H) in Fig. 2. Because coesite becomes more stable in that case, the additional effect is that the ringwoodite + coesite phase field in the FeSiO₃ phase diagram of Fig. 2 extends to temperatures below 1400 K, incommensurate with the data of Akimoto and Syono (1970). Because a first-order Landau model does not result in a significant improvement of our description and because we cannot find reasons for the inconsistency in heat capacity of β-quartz, we adhere to the simpler tricritical Landau model in Tables 1, 2 and 3, Online resource Table 1 without the introduction of an artificial contribution to its Helmholtz energy. In that case, the phase boundary between coesite and quartz is represented well, whereas the heat capacity of β-quartz is not represented well.

Constraints by solid solution phases

The system FeO–SiO₂ is coupled to the system MgO–SiO₂ by the solid solutions olivine, wadsleyite, ringwoodite, orthopyroxene, LP(HP)-clinopyroxene and ferropericlase. Therefore, the established model parameters for the iron endmembers can be used to constrain properties of the solid solutions and vice versa. Figure 4 shows that for olivine new experimental data measured by Mao et al. (2015) and ab initio predictions by Núñez-Valdez et al. (2013) became available for bulk- and shear modulus. Because results of these investigations are consistent with each other, we reappraised our own description for forsterite, by implementing a smaller pressure derivative of bulk modulus. Our new description for forsterite does not significantly affect the representation of thermophysical, thermochemical and phase diagram data that we used in our previous work, but the new data in Fig. 4 are better represented in that case.

Some remarks about selecting data in our analysis are necessary. For the description of excess volume of olivine we used, just as in Jacobs and de Jong (2009), experimental data obtained by Schwab and Küstner (1977) for synthetic (Mg_1−xFe_x)₂SiO₄ olivine mixtures, which cover the complete composition range. These investigators showed that natural olivines have larger volumes than synthetic ones, resulting in larger excess volumes for the solid solutions. For that reason our calculated room-temperature V–P–x isotherms are about 0.20% below those of Nestola et al. (2011), obtained by experiments on four natural olivine mixtures. However, their data could be represented to within experimental uncertainty by imposing an excess volume that is twice as large as indicated in Table 6. In our thermodynamic formulation of the volume of solid solutions, excess volume does not affect bulk modulus significantly. The effect of increasing excess volume by a factor of two is less than 0.1% on bulk modulus at the largest composition x = 0.38 measured by Nestola et al. (2011). Therefore bulk moduli of natural and synthetic olivines do not differ significantly, and the representation depicted in Fig. 4 also applies to natural olivines. For that reason we have additionally compared in “online resource Table 2” our results as V(P)/V(P = 0) with the experimentally derived values. Applying excess volume derived from natural olivines affects excess energy. To arrive at the phase diagram, insignificantly different from that shown in Fig. 1, requires an adjustment of the excess energy coefficient to W_U= 3.37 ± 0.45 kJ/mol, a value 0.7 times smaller than given in Table 6, and slightly smaller than the experimental value of 5.3 ± 1.7 kJ/mol of Kojitani and Akaogi (1994). In that case excess Gibbs energy established by Nafziger and Muan (1967) is not represented, and would require negative excess entropy, with a coefficient of W_S = − 0.94 J/K/mol, which falls in the range 0.6 ± 1.5 J/K/mol established by Kojitani and Akaogi (1994), and in the range − 1.6 ± 1.7 J/K/mol determined by Dachs and Geiger (2007). The exercise above, demonstrates that slightly more accurate excess enthalpy data are required to convincingly demonstrate if volume data for natural olivines may serve as constraints for excess properties. In our work we prefer as much as possible the data for synthetic samples.

Table 6 Excess energy, entropy, and volume for the solid solutions olivine, wadsleyite, ringwoodite, ferropericlase and orthopyroxene

The Gibbs energy in P–T space of orthoferrosilite is coupled to those of fayalite and quartz by the phase boundary between these phases, and additionally to the exchange of Mg and Fe atoms between olivine and orthopyroxene. Volume properties of orthoferrosilite are accurately constrained with available experimental data in “online resource Table 2”. That is also the case for orthopyroxene, demonstrated in Fig. 4. Because heat capacity of orthoferrosilite, shown in Fig. 2, is quite well constrained by experimental data, data for Mg–Fe partitioning between olivine and orthopyroxene were suitable for determining heat of formation of orthoferrosilite and excess properties of orthopyroxene. Our results, shown in Fig. 5, indicate that mixing of Mg and Fe atoms over the two sites M1 and M2 in orthopyroxene occurs in a nearly ideal manner, whereas the volume data depicted in Fig. 4 require a negative excess volume that is about equal but opposite in sign compared to that of olivine. Our results for Mg–Fe partitioning between olivine and orthopyroxene are not significantly different from those derived from the database of Fabrichnaya et al. (2004), but deviate from those obtained by Stixrude and Lithgow-Bertelloni (2011).

Fig. 5

Upper-left: Mg–Fe partitioning between olivine and orthopyroxene. Upper-right: heat capacity and volume of stoichiometric FeO. Labels (Re) and (Fe) denote analyses in which Mg–Fe partitioning between ringwoodite and ferropericlase is based on experiments carried out in rhenium or Iron capsules. Lower-left: Mg–Fe element partitioning between ringwoodite and ferropericlase. Labels (Re) and (Fe) denote analyses based on experiments performed in rhenium or iron capsules

In our previous work, we have constrained volume of the anhydrous wadsleyite form of Mg₂SiO₄ by recent V–T data of Trots et al. (2012) and V–P data of Holl et al. (2008). Volumes of the last dataset show a significantly smaller pressure derivative of bulk modulus compared to the data of Hazen et al. (2000). Therefore our description cannot be brought into accordance with presently available V–P–x data for the anhydrous solid solution, except for those of Fei et al. (1992) who measured the room-temperature isotherm of (Mg_0.84Fe_0.16)₂SiO₄. Bulk modulus has been constrained by data of Sinogeikin et al. (2003) who showed that this property does not change significantly with iron composition. These data are consistent with recent data of Wang et al. (2014) and ab initio calculations of Núñez-Valdez et al. (2013). The data of Sinogeikin et al. (2003) in P–T–x space and Wang et al. (2014) for (Mg_0.925Fe_0.075)₂SiO₄ enabled constraining shear modulus of this virtual endmember of Fe₂SiO₄ in P–T–x space.

“Online resource Table 2” shows that our analysis represents volume expansivity of ringwoodite solid solutions determined by Ming et al. (1992) to within experimental uncertainty. We could not make a proper comparison of V–P measurements of the solid solution due to the lack of X-ray measurements, except for those of Hazen (1993). Because ambient volume of Mg₂SiO₄ resulting from their investigation is about 0.3% larger than all datasets for this anhydrous form that we used in our previous work, the measurements are possibly affected by hydration effects. That also holds for their ringwoodite solid solution data for compositions up to x = 0.8. However, “online resource Table 2” shows that V–P measurements of the iron endmember are sufficient to represent bulk and shear modulus of the solid solution for Mg-rich compositions. We assumed that excess volume is not present in ringwoodite, which is supported by our result that the calorimetrically determined value for excess enthalpy is sufficient to represent the olivine–ringwoodite phase boundaries, shown in Fig. 1. Additionally, it has been shown by Frost et al. (2001), who studied the Mg, Fe partitioning between ringwoodite and ferropericlase, that excess Gibbs energy of ringwoodite is independent of pressure and temperature.

For the wadsleyite solid solution we used the phase diagram data depicted in Fig. 1 to establish excess properties, with the assumption that no excess volume is present. Table 6 shows that excess energies of olivine, wadsleyite and ringwoodite are quite similar and that they can be described with a simple regular solution model.

Thermophysical properties related to volume of endmember FeO are mainly based on those of the solid solution ferropericlase, detailed in “online resource appendix B”, and further discussed in the next section.

Phase diagrams

In “online resource appendix B” we showed for FeO that high-temperature heat capacity of Grønvold et al. (1993) depicted in Fig. 5 is consistent with the phase boundary between ringwoodite and FeO + stishovite determined by Matsuzaka et al. (2000), illustrated in the phase diagrams of Fe₂SiO₄ and FeSiO₃ in Fig. 2. Matsuzaka et al. (2000) measured the partitioning of Mg and Fe between the solid solution phases of ringwoodite and ferropericlase in rhenium capsules, from which they derived the excess Gibbs energy of ferropericlase. When we use their excess Gibbs energy for ferropericlase in combination with our results for ringwoodite, we arrive at the solid Mg–Fe partitioning curve depicted in Fig. 5, which represents their data and those of Frost et al. (2001), also obtained with rhenium capsules, in an excellent way. The phase boundaries that result from our calculation of the three-phase field ringwoodite + ferropericlase + stishovite at 1673 K, shown in Fig. 1, represent those of Matsuzaka et al. (2000) to within experimental uncertainty, whereas at 1873 K the three-phase field determined by Frost et al. (2001) is represented to within 0.35 GPa.

The non-triviality that arises in our analysis is that the experimentally determined Mg–Fe partitioning between ringwoodite and ferropericlase depends on the crucible material that was involved in performing the experiments, as has been shown in a detailed investigation by Frost et al. (2001), and illustrated in Fig. 5. Frost et al. (2001) showed that the use of rhenium or tantalum capsules in the experiments leads to larger amounts of Fe³⁺ in ferropericlase relative to the use of iron or molybdenum capsules, and consequently to a different Mg–Fe partitioning. This is a crucial finding, because their argument that the upper mantle contains only small amounts of Fe³⁺, referring to an investigation of O’Neill et al. (1993) on peridotite xenoliths, may lead to different phase diagrams. Frost et al.’s (2001) Mg–Fe partitioning curve, established with iron capsules, is given by the lower dashed one in Fig. 5, and is in accordance with measurements of Fei et al. (1991), performed with molybdenum capsules. We can represent this curve in two ways. The first possibility is by changing only the reference energy of FeO such that the phase boundary between ringwoodite and FeO+ stishovite is parallel to the phase boundary determined by Matsuzaka et al. (2000) at pressures 1.25 GPa higher. Because in that case the boundaries of Katsura et al. (1998) and Matsuzaka et al. (2000) are both mismatched, we preferred an alternative. It should be noticed that the phase boundary determined by Matsuzaka et al. (2000) has not been measured by a direct method. It resulted from their experimental data combined with a thermodynamic calculation based on parameterizations of selected thermodynamic properties. Katsura et al. (1998) measurements were obtained by a direct method. Their results are likely to be more accurate than preceding direct measurements, because by employing iron chloride as a catalyst the problem of the sluggishness of the reaction, which hampered earlier measurements, was avoided to a large extent. We arrive at their phase boundary, which has a zero Clapeyron slope, by making adjustments in the reference energy and electronic coefficient of FeO, which is given as the alternative description denoted by FeO⁽¹⁾ in Tables 1 and 2. By this change the Mg–Fe partitioning between ringwoodite and ferropericlase measured by Frost et al. (2001) in iron capsules is accurately represented. Additionally the heat capacity data by JANAF for FeO, instead of those of Grønvold et al. (1993), are accurately represented. In that case the boundaries of the three-phase field ringwoodite + ferropericlase + stishovite along the Mg₂SiO₄–Fe₂SiO₄ join, calculated at 1673 K and 1873 K, necessarily deviate from those determined by Matsuzaka et al. (2000) and Frost et al. (2001), respectively. Whereas Fig. 1 demonstrates that the deviations at 1673 K from the data of Matsuzaka et al. (2000) are not very significant, those at 1873 K with the diagram of Frost et al. (2001) become about ≤ 1 GPa rather than ≤ 0.35 GPa.

Our results are significantly different from the earlier assessments of Fabrichnaya et al. (2004) and Stixrude and Lithgow-Bertelloni (2011). Fabrichnaya et al. (2004) preferred the heat capacity of Grønvold et al. (1993) and Mg–Fe partitioning data of Ito and Takahashi (1989) obtained with tantalum capsules to derive the boundary between ringwoodite and FeO+ stishovite with a large negative Clapeyron slope. Stixrude and Lithgow-Bertelloni (2011) prefer the phase boundary of Matsuzaka et al. (2000) and Mg–Fe partitioning of Frost et al. (2001), obtained with Fe capsules, thereby arriving at a heat capacity of FeO about 6% below that of JANAF. Representing the Mg–Fe partitioning performed in tantalum capsules with our method would result in a phase boundary about 2 GPa below and parallel to that of Matsuzaka et al. (2000), provided that the heat capacity of FeO is between that of JANAF and Grønvold et al. (1993). The large negative Clapeyron slope obtained by Fabrichnaya et al. (2004) cannot be reproduced.

Although better explaining the source of the difference in established phase boundaries, heat capacity of FeO and Mg–Fe partitioning data relative to the two earlier assessments, some critical notes must be made on our results. “Online resource Fig. 1” shows that remarkable differences are found in experimentally established bulk moduli of ferropericlase, which indicates that an alternative description for FeO is possible. One explanation for the trend in bulk modulus is that it might show a sharp increase with composition beyond 90 mol% Fe, analogously to what has been established by McCammon (1993) and Zhang (2000) for Fe_yO, when y increases beyond about 0.9. Another explanation is offered by Jacobsen et al. (2002), who classified their samples as being non-stoichiometric and ‘more’ stoichiometric depending on the Fe³⁺ content. For the ‘more’ stoichiometric samples, characterized by x_FeO < 0.24 and ratios Fe³⁺/ΣFe < 0.02, they found a linear relation of bulk modulus with composition having a positive slope that extrapolates to the ambient value 182 ± 10 GPa for the bulk modulus of FeO, favorably in accordance with more recently established experimental results for x_FeO > 0.9. This compositional trend is also in accordance with ab initio results of Wu et al. (2013), who showed that (Mg_0.8125Fe_0.1875)O has a larger bulk modulus than MgO. In Tables 1 and 2, we show results of two alternative analyses, denoted as FeO^(2,3) in which we assumed an ambient bulk modulus of 182 GPa, instead of 155 GPa, for FeO. Also in this particular case we find the same consistency, as described above, between high-temperature heat capacity of FeO, Mg–Fe partitioning between ringwoodite and ferropericlase and the phase boundary between ringwoodite and FeO+ stishovite. V–P–T data of ferropericlase for x_FeO ≤ 0.4 in “online resource Table 2” are represented with similar accuracy, due to the use of a smaller pressure derivative of bulk modulus for FeO in these descriptions. We did not attempt to represent V–P–T data above 40 mol% iron because ambient volume resulting from these experiments deviate significantly from the line connecting the volumes of the two endmembers. Representing these data challenges the construction of a proper defect model, such as an ionic sub lattice model, which explains the apparent excess volume above this iron content and the behavior of bulk modulus as function of Fe²⁺, Fe³⁺ and vacancy concentration. These models require site fractions of the ionic species including vacancies, and to constrain model parameters properly requires accurate values for them when future V–P–T–x measurements are performed.

Fig. 6

Sound velocities and density along isentropic paths with foot temperatures between 1420 K and 1553 K. Line width illustrates the range of potential temperatures. The solid black curve represents a pyrolytic composition 38.04 mol% SiO₂, 55.38 mol% MgO, 6.58 mol% FeO taken from Saxena (1996). The solid red curve represents an olivine composition with the same iron composition. The dashed blue curve represents a composition in MgO–SiO₂, 38.04 mol% SiO₂, 61.96 mol% MgO

Turning to the ringwoodite endmember Fe₂SiO₄, Fig. 2 might give the impression that our phase boundary between fayalite and ringwoodite could be improved relative to the most recent in situ data of Ono et al. (2013) by moving it by − 0.38 GPa to lower pressures. We show here that this boundary is intimately linked to the location of a lens-shaped ringwoodite + coesite field that shows up in the phase diagram of FeSiO₃, and therefore this association could perhaps be used in the future to fine-tune pressure scales, provided that sufficient data are available. There are two possibilities to represent accurately Ono et al. (2013) boundary. Either ringwoodite should be stabilized by − 1473 J/mol, or fayalite should be destabilized by + 1473 J/mol relative to our present result. The effect of the first possibility is that a lens-shaped phase field ringwoodite + coesite with a width of about 1 GPa becomes stable in the phase diagram of FeSiO₃, at temperatures above 812 K. This is incommensurate with the data of Akimoto and Syono (1970), who found either HPclinoferrosilite or the assemblage ringwoodite + stishovite stable for temperatures up to 1473 K. Additionally, the 1-bar enthalpy difference at 986 K between fayalite and ringwoodite becomes 1474 J/mol, outside the uncertainty range of the measurement of Navrotsky et al. (1979), indicated in Table 4. Staying to within the uncertainty of Navrotsky et al.’s (1979) data, allows stabilizing ringwoodite by − 828 J/mol, producing the lens depicted in Fig. 2. To keep this field absent in the phase diagram of FeSiO₃, ringwoodite can only be stabilized by − 500 J/mol, which has the effect that the ringwoodite–fayalite boundary is lowered by only − 0.13 GPa relative to our present result. The appearance of the lens in FeSiO₃ is also the reason that we could not represent the data of Akimoto et al. (1967) above 1500 K, depicted in Fig. 2 in the phase diagram of Fe₂SiO₄. The second possibility is to destabilize fayalite. To keep the 1-bar enthalpy difference to within the uncertainty of Navrotksy et al.’s (1979) data, and additionally the heat of formation of fayalite to within experimental uncertainty, allows destabilizing fayalite by about 828–900 J/mol, which has the effect that the fayalite–ringwoodite boundary is lowered by − 0.23 GPa. Additionally the phase boundary between fayalite + quartz and orthoferrosilite is moved to pressures − 0.28 GPa below our present result, which is twice the difference between the boundaries determined by Bohlen et al. (1980) and Smith (1971). Stabilizing quartz or destabilizing orthoferrosilite to keep this boundary at the same location results in the same effect as the first possibility for changing the fayalite–ringwoodite boundary, that the ringwoodite + coesite field becomes stable at temperatures below 1473 K. Our present result represents the boundary of Bohlen et al. (1980), which is the lowest in pressure relative to previous measurements and the conclusion is that we can change the fayalite–ringwoodite boundary by only − 0.13 GPa, leaving a difference of 0.25 GPa relative to Ono et al.’s (2013) data points. This value is about the same as the distance between the boundaries determined by Akimoto and Syono (1970) and Ono et al. (2013) for fayalite–ringwoodite, which indicates that differences in pressure scales are of the order of 0.3 GPa. Fine-tuning pressure scales is therefore not an easy task, but perhaps use can be made of the location of the ringwoodite + coesite field in FeSiO₃, which might have escaped detection in Akimoto’s and Syono (1970) experiments. If this field is not present the gold scale of Dorogokupets and Dewaele (2007) that has been used by Ono et al. (2013) might be fine-tuned by 0.3 GPa in the low-pressure range between 4 and 6 GPa. The outline above also holds true if the fayalite–ringwoodite boundary is calibrated to other gold pressure scales, such as has been established by Dorogokupets and Oganov (2007), Fei et al. (2007) and Dorogokupets et al. (2015), because they are consistent to within 2% in pressure relative to the scale of Dorogokupets and Dewaele (2007). Therefore an experimental check for the presence of coesite in the phase diagram of FeSiO₃ is necessary.

Application: comparing our results with seismic velocities

To put our results into a geophysical perspective, we compare in Fig. 6 sound velocities calculated along isentropes with seismically derived velocities. This comparison can only be exploratory here because our small database does not include the more complicated mineralogy of the Earth mantle, in which at least phases containing calcium and aluminium are present, such as garnet. Nevertheless, such a comparison may be related to similar effects from variation in the major element components of our three component system. It is customary to approximate the Earth’s geotherm at depths larger than the asthenosphere (≈ 180 km) with an isentrope. For shallower depths this approximation does not hold and therefore we make the comparison for pressures larger than about 6 GPa. Moreover, our database does not include the solid solutions of perovskite, majorite and akimotoite, which limits the comparison to pressures up to about 22 GPa. Based on petrological studies (Mercier and Carter 1975; McKenzie and Bickle 1988) we have chosen isentropes with foot temperatures (apparent temperature at 1 bar) between 1420 K and 1553 K. Figure 6 shows for three overall mantle compositions that density calculated for a pyrolytic and olivine composition along these isentropes represents better the seismically derived data of PREM and AK135 relative to compositions that do not contain iron. Although density is represented reasonably well by a pyrolytic composition this is less the case for sound velocities. These are slightly underestimated in the olivine + HPclinopyroxene field, between 7 and 13 GPa, and slightly overestimated in phase fields above 13 GPa. This is also reflected in density and sound velocity contrasts at pressures where olivine transforms to wadsleyite, near 13 GPa, associated with the 410 km seismic discontinuity. For the calculation of the contrast in a property, p, we followed Núñez et al. (2013) by using the expression Δp = 200% × (p₂ − p₁)/(p₁ + p₂). For the iron free and the olivine composition, p₂ represents properties of wadsleyite and p₁ those of olivine. For the pyrolytic composition, p₂ represents properties of the stable assemblage wadsleyite + HPclinopyroxene and p₁ those of olivine + HP clinopyroxene. Using the model parameters in Tables 1, 2 and 3, Online resource Table 1, we find for the olivine composition, contrasts of density, longitudinal, bulk and transverse sound velocities denoted as (Δρ, ΔV_P, ΔV_B, ΔV_S) of (6.0 ± 0.1%, 9.6 ± 0.4%, 8.6 ± 0.35%, 11.0 ± 0.5%), respectively. For the pyrolytic composition these contrasts are significantly smaller, (4.3 ± 0.1%, 6.9 ± 0.6%, 5.9 ± 0.4%, 8.3 ± 1.1%), because olivine and wadsleyite are mixed with HPclinopyroxene. We showed in “online resource appendix B” that for HPclinopyroxene shear modulus is not determined well, due to the absence of experimental data for the iron endmember, and for that reason it is difficult to assess the uncertainties in V_P and V_S. Uncertainties in these velocities were based on a tentative uncertainty of 20 GPa (28%) in the shear modulus of HPclinoferrosilite. Constraining uncertainties of sound velocities better, thus calls for new elasticity measurements on HPclinoferrosilite or HPclinopyroxene. Nevertheless, our values for velocity contrasts given above are larger than those established from the two seismic models plotted in Fig. 6. For the AK135 seismic model these contrasts are (5.7%, 3.6%, 3.2%, 4.2%) and for PREM (5.0%, 2.5%, 2.0%, 3.4%). Our 3-component approximation of the pyrolytic composition is based on that given by Saxena (1996), who obtained it by eliminating Al, Ca, Na and K from Ringwood’s (1975) pyrolytic composition. It is characterized by amounts of about 72 vol% olivine and 28 vol% pyroxene at ambient conditions, which is larger than the 60 vol% olivine generally accepted (Ringwood 1975). Increasing the amount of pyroxene decreases the sound velocity contrasts. However, an amount of about 50% olivine is required to reach contrasts in sound velocities of about 5%, which is still larger than those established from seismic models, calling for an extension of our simple mineralogy.

We have further investigated the discriminating power of the seismically derived data shown in Fig. 6, for other aspects of our mineral physics model. To this end we have constructed an alternative database for the endmembers of the 3-component system, using a simplified VDoS with a single Einstein frequency, in a similar way as described earlier for quartz. Just as for the MgO–SiO₂ system described by Jacobs et al. (2017), the phase diagrams in the system FeO–SiO₂ differ insignificantly from those derived from the original database. That also holds for phase diagrams formed from solid solutions, such as depicted in Fig. 1, and moreover for the isentropes shown in Fig. 6. In contrast to this, just as for quartz, heat capacities, ambient entropies and heat of formation differ significantly from those calculated from the original database. For instance for forsterite and fayalite, ambient entropies differ by about 9%. On the other hand, volume properties, such as bulk modulus and thermal expansion do not differ significantly. From that, we conclude that a successful representation of seismic data by a model that includes all relevant phases is not a guarantee that thermodynamic properties of these phases are correctly described in the complete P–T range. This is an important conclusion relevant for application of databases in dynamical models for thermal convection in planetary mantles where, for example, specific heat plays an important role.

Conclusions

We showed that heat capacity can be delineated well in physical contributions. However, due to the lack of experimental data for crystal-field energy levels, and the lack of accurate ab initio predictions for vibrational densities of state, it was not possible to establish values for these energy levels and a VDoS in a robust way for most iron endmembers as was possible for fayalite. However, macroscopic thermodynamic properties could be established to within experimental uncertainties, with a number of exceptions. For the fayalite and ringwoodite form of Fe₂SiO₄ we found that heat capacity data above room temperature, determined by Watanabe (1982), are too small to be reconciled with the Clapeyron slope of the phase boundary between these forms. These DSC data are represented well by the database of Fabrichnaya et al. (2004) and the more recent one by Holland et al. (2013), because the employed empirical parameterizations are less suitable to constrain high-temperature heat capacity by simultaneously using low-temperature heat capacity data. The underestimation of heat capacity established by DSC, and the incorporation of it in these databases, also occurred for the magnesium wadsleyite and ringwoodite forms as shown by Jacobs et al. (2017) and independently by Dorogokupets et al. (2015), who also used a vibrational formalism. Therefore, we recommend re-measuring heat capacity of Fe₂SiO₄ ringwoodite by using the same method as has been employed by Kojitani et al. (2012) for the magnesium counter endmember or to assist the measurements by drop calorimetry as has been done by Benisek et al. (2012).

We showed that low-temperature heat capacity of coesite determined by Atake et al. (2000) is better consistent with the phase boundary between coesite and α-quartz than that determined by Hemingway et al. (1998) and Holm et al. (1967). Measured values for the heat capacity of β-quartz are too large to be reconciled with the phase boundary between coesite and β-quartz.

Our analysis reveals that Mg–Fe partitioning between ringwoodite and ferropericlase performed in rhenium capsules is consistent with heat capacity determined by Grønvold et al. (1993) for FeO and the phase boundary between Fe₂SiO₄ (ringwoodite) and FeO+ stishovite determined by Matsuzaka et al. (2000), having a negative Clapeyron slope. In that case the phase boundaries associated with the three-phase field formed by ringwoodite, ferropericlase and stishovite along the join Mg₂SiO₄–Fe₂SiO₄ represent those determined by Matsuzaka et al. (2000) at 1673 K and Frost et al. (2001) at 1873 K. On the other hand, Mg–Fe partitioning between ringwoodite and ferropericlase established in iron or molybdenum capsules is consistent with heat capacity of FeO given by JANAF and the phase boundary between Fe₂SiO₄ (ringwoodite) and FeO+ stishovite determined by Katsura et al. (1998), having a zero Clapeyron slope. In that case our calculated three-phase field formed by ringwoodite, ferropericlase and stishovite necessarily deviates from those determined by Matsuzaka et al. (2000) and Frost et al. (2001), and is more likely to be correct if the Earth’s mantle contains small amounts of Fe³⁺. This conclusion appears to be independent of the value for ambient bulk modulus that is assumed for stoichiometric FeO. To represent V–P–T data of ferropericlase for iron contents smaller than 40 mol% FeO, assuming an ambient bulk modulus of about 180 GPa, results in a pressure derivative of 3.00, smaller than is generally found in the literature, with the exception of the work of Wicks et al. (2015) who found 2.79 ± 0.09.

We showed that representing better the phase boundary between fayalite and ringwoodite determined by Ono et al. (2013) results in a lens-shaped phase field ringwoodite + coesite in the phase diagram of FeSiO₃, incommensurate with the measurements of Akimoto and Syono (1970). The difference between our calculated boundary between fayalite and ringwoodite and that established by Ono et al. (2013) in the phase diagram of Fe₂SiO₄ indicates that either a pressure scale effect is present, or that coesite has been overlooked in the measurements of the boundary between HPclinoferrosilite and ringwoodite + stishovite in the phase diagram of FeSiO₃. This might offer a possibility to fine-tune pressure scales below 10 GPa.

Our results are significantly different from those resulting from earlier databases, such as those of Fabrichnaya et al. (2004) and Stixrude et al. (2011). We found that models based on parameterizations of 1-bar properties by Fabrichnaya et al. (2004) and Mao et al. (2001) are kept too simple and do not represent experimental data, such as demonstrated for quartz and coesite. We demonstrated for quartz and coesite that these methods do not facilitate using low-temperature heat capacity to constrain high-temperature heat capacity. We showed that Debye models, just as single Einstein models, do not adequately represent heat capacity data in the complete temperature range, and that they cannot be constrained by data on heat of formation and ambient entropy.

We showed that for making a better comparison between calculated sound velocities and seismically derived ones new elasticity measurements are required in P–T space for orthoferrosilite and HPclinoferrosilite. Additionally, elasticity measurements above room temperature are required for coesite and for ferropericlase.

We showed that a successful representation of seismic data, by a model that includes all relevant phases, is not a guarantee that thermodynamic properties of these phases are correctly described. This impacts application of databases in dynamical models for thermal convection in planetary mantles where, for example, specific heat plays an important role.