Shear modulus, heat capacity, viscosity and structural relaxation time of Na₂O–Al₂O₃–SiO₂ and Na₂O–Fe₂O₃–Al₂O₃–SiO₂ melts

Abstract

The configurational heat capacity, shear modulus and shear viscosity of a series of Na₂O–Fe₂O₃–Al₂O₃–SiO₂ melts have been determined as a function of composition. A change in composition dependence of each of the physical properties is observed as Na₂O/(Na₂O + Al₂O₃) is decreased, and the peralkaline melts become peraluminous and a new charge-balanced Al-structure appears in the melts. Of special interest are the frequency dependent (1 mHz–1 Hz) measurements of the shear modulus. These forced oscillation measurements determine the lifetimes of Si–O bonds and Na–O bonds in the melt. The lifetime of the Al–O bonds could not, however, be resolved from the mechanical spectrum. Therefore, it appears that the lifetime of Al–O bonds in these melts is similar to that of Si–O bonds with the Al–O relaxation peak being subsumed by the Si–O relaxation peak. The appearance of a new Al-structure in the peraluminous melts also cannot be resolved from the mechanical spectra, although a change in elastic shear modulus is determined as a function of composition. The structural shear-relaxation time of some of these melts is not that which is predicted by the Maxwell equation, but up to 1.5 orders of magnitude faster. Although the configurational heat capacity, density and shear modulus of the melts show a change in trend as a function of composition at the boundary between peralkaline and peraluminous, the deviation in relaxation time from the Maxwell equation occurs in the peralkaline regime. The measured relaxation times for both the very peralkaline melts and the peraluminous melts are identical with the calculated Maxwell relaxation time. As the Maxwell equation was created to describe the timescale of flow of a mono-structure material, a deviation from the prediction would indicate that the structure of the melt is too complex to be described by this simple flow equation. One possibility is that Al-rich channels form and then disappear with decreasing Si/Al, and that the flow is dominated by the lifetime of Si–O bonds in the Al-poor peralkaline melts, and by the lifetime of Al–O bonds in the relatively Si-poor peralkaline and peraluminous melts with a complex flow mechanism occurring in the mid-compositions. This anomalous deviation from the calculated relaxation time appears to be independent of the change in structure expected to occur at the peralkaline/peraluminous boundary due to the lack of charge-balancing cations for the Al-tetrahedra.

Introduction

It has long been appreciated that the structure of peraluminous (Na₂O < Al₂O₃) Na₂O–Al₂O₃–SiO₂ melts must be different from that of peralkaline (Na₂O > Al₂O₃) melts as there are no longer enough Na⁺ to act as charge-balancers for the Al³⁺ in tetrahedral co-ordination (e.g. Lacy 1963; Toplis et al. 1997a, b; Mysen and Toplis 2007). The corollary is that compositional trends in the physical and thermodynamical properties (i.e. viscosity, thermal expansion, shear modulus, configurational heat capacity) of peraluminous melts must be different from those of peralkaline composition melts. A number of studies of the rheology and density of aluminosilicate melts have indeed shown that there is a change in the trend as a function of composition as the melts investigated change from peralkaline to peraluminous (e.g. Day and Rindone 1962a; Riebling 1966; Taylor and Rindone 1970; Hunold and Brückner 1980; Toplis et al. 1997a, b; Webb et al. 2004, 2007; Giordano et al. 2006). Therefore, it is clear that the extrapolation of physical and thermodynamic data across the composition divide will lead to increasing errors in predictions of the behaviour of multicomponent melts and magmas of differing compositions.

The structure of peralkaline sodium-aluminosilicate melts has been investigated by NMR studies, which have found that Na⁺ prefers to form non-bridging oxygens bonded to Si⁴⁺, and also acts as a charge-balancer for the tetrahedrally co-ordinated Al³⁺ (e.g. Mysen 1987; Allwardt et al. 2003). Mysen et al. (2003) concluded from their ²⁹Si NMR and Raman spectroscopic study on peralkaline glasses that the dominant fraction (>70%) of Al³⁺ resides in fully polymerised Q⁴ units.

Lacy (1963) discussed the various possible structures of peraluminous melts in terms of geometry and energy and concluded that tri-clusters of two Si⁴⁺-tetrahedra and one Al³⁺-tetrahedron sharing one apical oxygen was the most probable structure for the Al³⁺ tetrahedra without a Na⁺ charge-balancer. The existence of AlSi₂O_5.5 tri-clusters has not been confirmed by NMR measurements; however, the peak for such a triple bond to oxygen is expected to lie under the NMR signal for Si–O–Si bonds (Kubicki and Toplis 2002). Higher co-ordinated Al³⁺ has, however, been observed in Na₂O-Al₂O₃-SiO₂ melts and glasses (e.g. Stebbins et al. 2000, 2008). The occurrence of ^VAl³⁺ is viewed as an indication that Na₂O–Al₂O₃–SiO₂ melts flow not only by the creation of ^VSi⁴⁺ (as observed by Stebbins 1991; Stebbins and McMillan 1993) but also by a similar mechanism for the tetrahedral Al³⁺ in the melt (Stebbins et al. 2000).

Taylor and Rindone (1970), Hunold and Brückner (1980) and Toplis et al. (1997a, b) have observed a maximum in viscosity as a function of composition at Na–Al for Na₂O–Al₂O₃–SiO₂ melts with constant mol% SiO₂ content. The dramatic increase in the viscosity of the peralkaline melts as Na/Al is reduced is attributed to the decrease in the number of non-bridging oxygens being formed (Toplis et al. 1997a) with the small decrease in viscosity in the peraluminous melts accompanying a further decrease in Na/Al being attributed to the increase in the number of tri-clusters.

Maxwell (1867) calculated that there was a simple relationship between shear viscosity and the structural relaxation time of a liquid:

$$ \tau_{\text{M}} = {\frac{{\eta_{0} }}{{G_{\infty } }}} $$

(1)

for η ₀—long timescale relaxed Newtonian viscosity, G _∞—short timescale unrelaxed elastic shear modulus which is taken to be 10 GPa (Dingwell and Webb 1989). This relationship has been found to apply in general to silicate melts (e.g. Rivers and Carmichael 1987; Dingwell and Webb 1990; Webb 1992; Stebbins 1995). The Maxwell relaxation time is the timescale on which the slowest part of the melt structure moves, and is therefore the glass transition, or the α-relaxation (Brawer 1985). This slowest moving part of a silicate melt structure has been shown to be the lifetime of the Si–O bonds in the melt (e.g. Stebbins 1991, 1995).

In order to relate melt structure to flow mechanisms and to physical properties, the lifetimes of not only the Si–O but also the Na–O and Al–O bonds as well as more complex structural units (e.g. the AlSi₂–O bonds in tri-clusters) need be measured. This can be done via a range of techniques which include NMR spectroscopy (e.g. Stebbins 1991; Stebbins and McMillan 1993; Stebbins and Xu 1997; Stebbins et al. 2001); diffusion measurements (e.g. Liu et al. 1988) and mechanical spectroscopy (e.g. Day and Rindone 1962b; Mills 1974; Webb 1992). As discussed by Day and Rindone (1962b), the mechanical relaxation of each type of bond within a melt can be investigated by mechanical spectroscopy. They further pointed out the similarity it activation energy for their low-temperature relaxation and the electrical conductivity of Na₂O–Al₂O₃–SiO₂ melts; and thus identified their low temperature relaxation as the motion of Na⁺ in the melt. Steinkamp et al. (1967) also associated the low temperature mechanical relaxation peak with the diffusivity of Na⁺ in Na₂O–SiO₂ melts. The conclusions of the studies of Day and Rindone (1962b) and Steinkamp et al. (1967) have been confirmed by the modelling of Maass and Peibst (2006).

The NMR data of Gruener et al. (2001) for CaO–Al₂O₃–SiO₂ melts show that the lifetime of Si–O and Al–O bonds are identical at high temperatures in the 10⁻⁹–10⁻¹¹ s relaxation time range (10⁻¹ < η < 10² Pa s), with the relaxation time for viscous deformation being eight orders of magnitude slower than the Ca²⁺ motion in the region of the glass transition temperature (10⁸–10¹³ Pa s). Diffusion data (e.g. Dingwell and Webb 1990) show that the Al–O bonds have shorter lifetimes than the Si–O bonds in the vicinity of the glass transition temperature (see Fig. 1), and thus the lifetime of these bonds is (by definition, as they are the second slowest) the β-relaxation. Similarly, diffusion data show that the Na–O bond is the shortest lived and therefore its lifetime is the γ-relaxation in Na₂O–Al₂O₃–SiO₂ melts in the vicinity of the glass transition temperature. As shown in Fig. 1, the lifetime of Al–O bonds in the 10¹² Pa s viscosity range is expected to be shorter than that of the Si–O bonds; and identical with that of Si–O bonds at lower viscosities (higher temperatures). The lifetime of AlSi₂–O bonds is unknown; but is expected to be in the vicinity of that of Al–O and Si–O bonds.

Fig. 1

Relaxation timescales of Na, Ca and Al movement in silicate melts calculated from diffusivity data together with the viscosity and structural (Si–O) relaxation time for the melt. The dashed lines indicate the expected trend changes with decreasing viscosity (increasing temperature). The relaxation timescales are labelled α, β and γ for the slowest to fastest relaxation. Redrawn after Dingwell and Webb (1990)

Mechanical spectroscopy, or forced oscillation, involves the determination of energy loss of a stress wave at the frequency (time⁻¹ = 2πf—for frequency f) at which part of the material structure moves. In the case of metals and ceramics this may be the diffusion of atoms (e.g. Chakraborty 1995; Brady 1995). In the case of silicate melts it is the lifetime (inverse angular frequency—ω = 2πf) of Si–O bonds (Stebbins 1991, 1995) and therefore the diffusion of Si and O atoms as well as the diffusion of Na and K atoms (Day and Rindone 1962b) can be determined by mechanical spectroscopy.

In this study the changes in lifetime of the Si–O, and Al–O bonds and the rate at which Na ions move through Na₂O–Al₂O₃–SiO₂ and Na₂O–Fe₂O₃–Al₂O₃–SiO₂ melts are measured via forced oscillation techniques. Three energy loss peaks are expected in the mechanical spectra: one for the lifetime of Si–O bonds (associated with the diffusivity of Si and O), one for the lifetime of Al–O bonds (associated with the diffusivity of Al) and one for the Na–O bonds (associated with the diffusivity of Na). As peralkaline and peraluminous melts have different structures, it is to be expected that the distribution of lifetimes of Si–O and Al–O bonds as well as the diffusion rate of Na is different in the two composition extremes. The presence of Fe³⁺–O and Fe²⁺–O bonds is expected to broaden the energy loss peaks associated with the Al–O and Na–O energy loss, respectively, as these bonds are expected to have lifetimes slightly different (~±0.5 log₁₀ units) from the Al–O and Na–O bonds. The thermodynamic properties of these melts are investigated through determination of the configurational heat capacity and entropy with the density and shear modulus of the glasses also being determined. The question posed here is whether there are changes in C ^conf _p trend as a function of composition, which can be associated with the known changes in trend of the viscosity and density data. The Na₂O–Al₂O₃–SiO₂ melts were chosen as a simple series of melts, which illustrate the changes in physical properties as a function of the change in structural units with composition. The addition of iron to these compositions introduces a second tetrahedrally co-ordinated trivalent cation, as well as a divalent network modifier into the range of structures existing in the melt. These iron-bearing melts thus have a more complex range of structures than the simple Na₂O–Al₂O₃–SiO₂ melts.

Experimental techniques

Samples

The glasses NAS42–NAS100 and NAFS41–NAFS60 were made from oxide and carbonate powders that were decarbonated at 800°C and then melted in air at temperatures from 1,350 to 1,650°C in Pt₉₀Rh₁₀ crucibles in a MoSi₂ furnace. The melts were homogenised by stirring with a Pt-stirrer for up to 12 h. The stirring also removed bubbles from the viscous peraluminous (Al > Na) compositions. The compositions of the final melts were determined by microprobe analysis (see Table 1). The Fe²⁺ was determined by titration with KMnO₄. The parameter γ = (Na₂O + FeO)/(Na₂O + FeO + Fe₂O₃ + Al₂O₃) which describes the difference between peralkaline (γ > 0.5) and peraluminous (γ < 0.5) melt compositions is in mole fractions.

Table 1 Glass compositions in wt% and mol%

Density

The densities of the glasses at room temperature were determined by immersion in ethanol using the Archimedean technique:

$$ \rho_{\text{sample}} = {\frac{{\rho_{\text{e}} w_{\text{air}} }}{{w_{\text{air}} - w_{\text{e}} }}} $$

(2)

for ρ _e—density of the ethanol, w _air—weight of the sample in air, and w _e—weight of the sample in ethanol. A single crystal of Al₂O₃, with a density of 3.982 g cm⁻³ (Ohno et al. 1986) was used as an internal standard for the measurements. The density of ethanol as a function of temperature was taken from the table of Sartorius (2004).

Viscosity

The viscosity of the melts was measured by the micro-penetration technique. The samples used are 8 mm cylinders of melt, 3 mm thick. The faces of the cylinders are ground parallel to each other and the face which is used for the viscosity measurements is polished with 1 μm jewellers’ rouge. Viscosity η is measured from the rate at which a 1 mm radius single crystal sphere of Al₂O₃ is pushed into the surface of the melt using a force F;

$$ \eta = {\frac{0.1875 F\;t}{{r^{0.5} l^{1.5} }}} $$

(3)

for r—radius of sphere, t—time, l—indent distance (Pocklington 1940). At high viscosity conditions (e.g. 10¹¹ Pa s), the sample is held at temperature for at least 1 h in order to allow the melt structure to equilibrate with respect to the applied temperature, before the force is applied. The timescale of structural equilibration is calculated from the Maxwell equation (Eq. 1), assuming G _∞ ~10 GPa (Dingwell and Webb 1990). Upon application of the force, the indent rate of the corundum sphere is measured in a melt structure that has not relaxed with respect to the applied stress for the first ~10 τ _M. This is taken into account in the data analysis and the unrelaxed data are not included in the calculation of viscosity.

Shear modulus

The shear moduli of the glasses were measured at room temperature using the ultrasonic Pulse Echo Overlap Method (see Truell et al. 1969). A pulse of high-frequency waves (here f = 5 MHz) is sent into the sample via a 5 mm diameter quartz piezo-electric transducer which is glued to the sample. The echo pattern of the multiple reflected pulses is recorded and the wave speed through the sample is determined by measuring the time between successive echoes. The error associated in choosing the correct part of the pulsed signal results in at most ±0.6 GPa in the calculated elastic shear modulus. The lengths of the samples were between 2.1 and 3.7 mm.

Differential scanning calorimetry

The heat capacity of the glasses and melts was measured to η ~10⁹ Pa s in a Netzsch DSC 404C with argon used as the gas environment in the calorimeter. The heat capacity of the ~55 mg samples of powdered glass was measured against that of an empty crucible. The DSC was calibrated by determining the heat flow from a solid pellet (55.305 ± 0.005 mg) of polycrystalline Al₂O₃ and the heat capacity data of Robie et al. (1978). The heat flow from the crushed glasses was determined at heating rates of 10, 15, 20 and 25 K min⁻¹. Each melt was previously cooled from above T _g [η ~10⁹ Pa s] at the same rate as the subsequent heating-rate in the cycle. On the basis of repeated measurements using different calibration runs, the error in the glass and liquid heat capacity is ≤3%. Measurements were not performed to lower viscosities (higher temperatures) as the viscous deformation of the sample at lower viscosities results in a change in sample/crucible contact geometry and an apparent large decrease in the heat capacity.

Mechanical spectroscopy

Forced oscillation shear deformation is based on the principle of torsion of a fixed cylindrical rod. Here a torque is applied and the resulting deformation (angle of twist) of the rod is measured. In these measurements, the stress σ, and strain ε are determined as a function of frequency from 1 mHz to 1 Hz, and the real–G′(ω)—and imaginary—G″(ω)—components of the shear modulus are calculated from these measurements [G*(ω) = G′(ω) + iG″(ω)]. The real component of modulus is a measure of the stored energy, while the imaginary component is a measure of the energy loss in the melt. A peak in the loss modulus as a function of frequency indicates the motion of part of the melt structure on that frequency (or time⁻¹). As viscosity is a function of stress and strain-rate, the viscosity can be calculated from the frequency-dependent shear modulus (Webb 1991):

$$ \eta^{*} (\omega ) = {\frac{{G^{*} (\omega )}}{{{\text{i}}\,\omega }}} = \eta^{\prime}\left( \omega \right) - {\text{i}}\,\eta^{\prime\prime}(\omega ) $$

(4)

where ω = 2πf. The frequency-dependent shear modulus and viscosity are determined by applying a sinusoidal torque to a cylindrical sample which is fixed at one end, and measuring the angle of twist φ (in radians) at a position L along the length of the sample. The shear modulus of the cylinder can then be calculated for the applied stress σ, and the measured strain, ε:

$$ G^{*} (\omega ) = {\frac{\sigma }{\varepsilon }} = {\frac{{2\tau_{\varphi } /\pi r^{3} }}{\varphi r/L}} = {\frac{{2\tau_{\varphi } L}}{{\pi r^{4} \varphi }}}; $$

(5)

as can the shear viscosity:

$$ \eta^{*} \left( \omega \right) \, = \, {\frac{\sigma }{{\dot{\varepsilon }}}} \, = {\frac{{2\tau_{\varphi } L}}{{\pi r^{4} \dot{\varphi }}}}. $$

(6)

for τ _φ —applied torque, r—radius of the cylinder, and φ—angle of twist measured a length L from the fixed end of the rod (Riley et al. 1999; Sass et al. 1996).

Shear modulus of torsion rods

The torsion apparatus (see Fig. 2) was tested by measuring the shear modulus of a long rod of polycrystalline Al₂O₃ (Al23 Degussit^®). This rod is 8 mm in diameter and fixed at one end. The shear modulus of the alumina rod was determined by static measurements in which a torque τ _φ up to 0.5 Nm was applied.

Fig. 2

Schematic of the torsion apparatus with furnace

The angle of twist of the Al₂O₃ rod is measured from the motion of 10 cm long aluminium arms attached to the rod 66 mm (channel 1) and 480 mm (channel 2) above the fixed end. Fe-plates are attached to these Al arms and move between pairs of inductive transducers. The circuits connecting the pairs of inductive transducers delete sway in the rod and only measure twist of the rod. For the ±1 mm and ±2 mm air-gaps at channels 1 and 2; there is a linear relationship between transducer voltage and angle of twist. The maximum displacement between the air gaps is equivalent to φ = 0.01 rad and 0.02 rad, and ε ₁ ~6 × 10⁻⁴; and ε ₂ ~2 × 10⁻⁴, respectively. Measurements occur over much smaller φ values, with ε ₁, ε ₂ < 10⁻⁵.

The shear modulus of the Al₂O₃ rod was determined at channels 1 and 2 as a function of temperature up to 1,000°C in a Pt-wound, water-cooled furnace (see Webb 1992). The elastic shear modulus of the Al₂O₃ rod determined at room temperature from channel 1 is 162.6 ± 0.1 and 161.3 ± 0.1 GPa for channel 2. Straight line fits to the temperature dependent shear modulus data give apparent dG _∞/dT values of −5.9 ± 0.2 and −11.8 ± 0.2 MPa K⁻¹ for channels 1 and 2, respectively. The room temperature shear modulus measured here is in good agreement with the literature data for the shear modulus of polycrystalline Al₂O₃ calculated from single crystal data to be 162.5–163.2 GPa (Ahrens 1995). Goto et al. (1989) measured the shear modulus of single crystal Al₂O₃ from room temperature to 1,000°C and found dG _∞/dT = −24 MPa K⁻¹. The channel 1 shear modulus shows a temperature dependence despite the rod being outside the furnace. This is because the lower part of the rod heats up as the furnace temperature increases. The shear modulus obtained at channel 2 is for a rod that is outside the furnace at the top and bottom, and sits within a temperature gradient within the furnace. As most of the torsion measurements were conducted in the temperature range 450–800°C, a temperature independent value of $G_{{{\text{Al}}_{2} {\text{O}}_{3} }} = 160\,{\text{GPa}}$ was chosen for the analysis of the data. As the melts have a much lower shear modulus G _melt ~30 GPa, than the alumina rods, this assumption introduces an error of at most ±1 GPa in the calculated melt shear modulus.

Once the static calibration has been performed the frequency dependence of shear modulus can be determined by applying a sinusoidal torque via the “stress wing” and measuring the resulting sinusoidal deformation. This deformation is described by:

$$ y = a + bt + c\,\sin \,(\omega t + \delta ), $$

(7)

for: a, b—drift parameters, c—amplitude of the sinusoid (in V), δ—shift of the sinusoid from starting time (in radians), t—time (in s), ω—angular frequency (ω = 2πf). At 1,000°C the phase delay δ for the alumina rod is the same for both channels; showing that the alumina rod displays elastic behaviour over the entire the temperature range.

Shear modulus of melts

The shear modulus of the silicate melts were determined by melting a ~30 mm long, 8 mm diameter melt cylinder to an upper and lower Al₂O₃ torsion rod to produce a compound sample. As it was difficult to achieve a good bond between the Na₂O–Al₂O₃–SiO₂ melts and the Al₂O₃ torsion rods, a thin film (<0.3 mm) of 80 mol% SiO₂ rhyolite melt is used as a ‘glue’. This melt is allowed to react with the Al₂O₃ rod and the sample is then melted onto the rhyolite at the ends of the two torsion rod to produce a good contact between the melt and the torque rod (see Webb 1992). The viscosity of this glue is equal to, or greater than (by up to 6 orders of magnitude) that of the investigated melts at all temperatures, with the greatest difference occurring for melts with γ > 0.5. Thus, if the presence of this glue affects the measured stress/strain data it would be to produce a maximum in the imaginary part of the shear modulus accompanied by a non-zero value of the real part of the shear modulus at negative log₁₀ ωτ _M values. This would lead to a broadening of the imaginary part of the shear modulus curve as a function of log₁₀ ωτ for the melts as γ increases and the difference in relaxation time between the glue and the melt increases. As discussed later, no broadening of the imaginary peak is observed. The presence of this thin film of highly viscous melt is calculated in the worst case to introduce an error of ~1 GPa into the calculated shear modulus of the melt. Thus the measured shear moduli have an error of ±1.5 GPa due to the use of a temperature independent shear modulus for the torsion rods, and the use of a glue between the sample and the torsion rods. The temperature profile of the furnace was measured using a Type-S thermocouple. The melt sample sits within a 40 mm long region of constant temperature ±3°C.

The deformation analysis for the compound torsion rod (Al₂O₃ + melt + Al₂O₃) as a function of frequency was made in the same manner as for the simple alumina rod. Based upon the earlier calibrations, the voltage from the transducers at channel 1 gives the applied stress, and the voltage at channel 2 gives the deformation of the compound torsion rod. The time delay—Δδ—between the applied stress and the resulting strain can also be calculated by fitting Eq. 7 to the stress and strain sinusoids. The angle of twist of the compound rod must be separated into the components due to the twist of the lower elastic alumina rod, the viscoelastic melt and the upper elastic alumina rod. This gives the angle of twist of the melt—from which the strain in the melt can be determined; and γ—the phase delay between the applied stress and the deformation of the melt. The complex shear modulus can be determined from the stress, strain and phase delay measurements by:

$$ G^{*}_{\text{melt}} (\omega ) = G(\omega )_{\text{melt}} { \cos }(\gamma ) \, + {\text{i}}\;G(\omega )_{\text{melt}} { \sin }(\gamma ) $$

(8)

for

$$ G^{*}_{\text{melt}} (\omega ) = \, {\frac{{\sigma_{\text{applied}} }}{{\varepsilon_{\text{melt}} }}} \, = {\frac{{2\tau_{\varphi } L_{\text{melt}} }}{{\pi r^{4} \varphi_{\text{melt}} }}}. $$

(9)

Results

Density

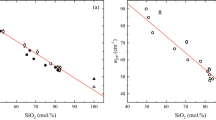
The densities of the glasses (see Table 2) as a function of composition are shown in Fig. 3. Density decreases as network-modifying Na⁺ is removed from the peralkaline glass; and begins to increase as charge-balancing Na⁺ is removed from the peraluminous glass. The curve drawn through the present data is simply a guide for the eye. Both Hunold and Brückner (1980) and Webb et al. (2007) determined the density of 67 mol% SiO₂ Na₂O–Al₂O₃–SiO₂ glasses. A minimum in density is observed in both of these studies at γ ~0.5. The ±0.01 g cm⁻³ difference between the densities of the 67 mol% SiO₂ glasses may be due to small variations in SiO₂ content; or to differences in cooling rate. The present glasses were cooled at 10°C min⁻¹ (between 1,650–700 and 550–25°C) and 1°C min⁻¹ (between 700–550°C) in order to avoid stress build up and cracking of the glasses; while those of Webb et al. (2007) were cooled at 5 and 10°C min⁻¹. Thus the glasses do not have the same fictive temperatures; but a density minimum is observed in all cases as the melt composition changes from peralkaline to peraluminous, and there is no longer enough Na⁺ to charge-balance all of the Al³⁺ in tetrahedral co-ordination. Similarly, a minimum is observed in density of the Fe-bearing glass compositions at the peraluminous/peralkaline boundary.

Table 2 Densities of the glasses at room temperature

Fig. 3

Measured densities of the glasses as a function of composition; together with curves describing the density of Na₂O–Al₂O₃–SiO₂ glasses of the same composition measured by Hunold and Brückner (1980) and Webb et al. (2007)

Figure 4 shows molar volume of the glasses as a function of the composition parameter γ. These data show that the Na and Al units take up different volumes in peraluminous and peralkaline melts; the trend line is a guide for the eye; it was chosen to break the trend at γ ~0.5, based on the density observations; a constant value of molar volume was chosen for the peraluminous melts based on the trends seen previously in the viscosity data by Hunold and Brückner (1980) and Toplis et al. (1997a, b). Both the density and volume data can be corrected from their known fictive temperature to a common temperature. Assuming a volume thermal expansion of 10⁻⁵ K⁻¹ (Bansal and Doremus 1986), this gives a 0.1% change in density and volume per 100°C. As there is a ~400°C decrease in the T ²⁰_f values with increasing γ, this would lead to a gradual increase in density (decrease in molar volume) of 0.4% with decreasing γ if all of the density data were recalculated to a common low temperature. This correction is twice the estimated error in the density and volume measurements, but does not change the observed trends in density and molar volume as a function of the composition parameter γ.

Fig. 4

Molar volume of the glasses at room temperature. The line is drawn as a guide to the eye, with the change in slope chosen to occur at γ ~0.5 due to the change in trend observed in the density data, and the expected new structural unit occurring in peraluminous melts as γ decreases below 0.5. The dashed line describes the data of Hunold and Brückner (1980) and Webb et al. (2007)

Viscosity

The micro-penetration viscosity data is plotted as a function of inverse temperature in Fig. 5 and listed in Table 3. The viscosity data has been fit by an Arrhenian curve:

$$ \log_{10} \,\eta = A + {\frac{{B \times 10^{4} }}{T}} $$

(10)

for viscosity η in Pa s and T in K. The A and B parameters are given in Table 4. The glass transition temperatures T ¹²_g (temperature at which η = 10¹² Pa s) are shown as a function of composition in Fig. 6 (see also Table 4). The T ¹²_g values for the Na₂O–Al₂O₃–SiO₂ melts show a change in trend as a function of composition on the peraluminous side of the composition range (γ ~0.475). The errors in the T ¹²_g values for the iron-bearing melts are too large to determine the composition at which the trend-change occurs. This change in trend as a function of Na/Al has been discussed previously by Toplis et al. (1997a, b) and Webb et al. (2004) in terms of the structural changes and the presence of tri-clusters in the melts with decreasing Na/Al ratio, and also in terms of the changes in flow mechanism accompanying such changes in melt structure.

Fig. 5

Log₁₀ viscosity for the Na₂O–Al₂O₃–SiO₂ and Na₂O–FeO–Fe₂O₃–Al₂O₃–SiO₂ melts as a function of inverse temperature. NAFS41 has less Fe₂O₃ than the other iron-bearing melts and therefore does not follow the viscosity/temperature trend

Table 3 Micro-penetration and torsion viscosity data for the Na₂O–Al₂O₃–SiO₂ melts and the Fe-bearing Na₂O–Al₂O₃–SiO₂ melts as a function of temperature

Table 4 Fits of the Arrhenian equation (Eq. 10) to the viscosity data, together with γ = (Na₂O + FeO)/(Na₂O + Al₂O₃ + FeO + Fe₂O₃); and T ¹²_g , the temperature at which η = 10¹² Pa s; and T ²⁰_f —the fictive temperature calculated from the scanning calorimetry data for a cooling- and heating-rate of 20 K min⁻¹

Fig. 6

A plot of T ¹²_g as a function of composition. The trend lines are a guide for the eye. Given the relatively large errors in the calculated T ¹²_g for the Fe-bearing melts, the trend line drawn through the data were chosen to have the same shape as the line through the Na₂O–Al₂O₃–SiO₂ data

Ultrasonics

The shear modulus determined from the pulse-echo-overlap measurements and the density of the glasses are shown in Table 2 and Fig. 7. The shear modulus trend as a function of composition is similar to that seen for viscosity and molar volume, with a change in slope at γ ~0.5.

Fig. 7

The calculated elastic shear modulus from the ultrasonic measurements (small symbols) and the torsion measurements (large symbols) for the iron-free (open symbols) and iron-bearing (filled symbols) glasses as a function of composition. The lines are a guide for the eye

Calorimetry

Figure 8 illustrates the heat capacity data as a function of temperature for all of the melts for a 20 K min⁻¹ cooling- and heating-rate. The configurational heat capacity of the liquid is calculated by fitting the Maier–Kelley equation;

$$ C_{\text{pg}} = a + bT + cT^{ - 2} $$

(11)

(Maier and Kelley 1932) with temperature in K, to the glassy heat capacity from 200°C to the temperature at which the onset of the glass transition peak occurs. This Maier–Kelly curve is then extrapolated to the maximum temperature at which heat capacity was measured. The configurational heat capacity is then calculated as the difference between the measured temperature independent liquid heat capacity and the extrapolated glass heat capacity. The resulting C ^conf _p values are plotted in Fig. 9 as a function of composition for the iron-free and iron-bearing melts and shown in Table 2, together with the liquid and extrapolated glassy heat capacity data—C _pl and C _pg. The C ^conf _p , C _pl and C _pg for the present NAS48 melt are 9.02, 92.58 and 83.57 J mol⁻¹ K⁻¹, respectively; in comparison with the values determined by Richet and Bottinga (1984) for a melt of similar composition of 8.48, 93.17 and 84.69 J mol⁻¹ K⁻¹.

Fig. 8

The heat capacity for a the Na₂O-Al₂O₃-SiO₂ melts, and b the iron-bearing melts as a function of temperature. A cooling and heating rate of 20 K min⁻¹ was used

Fig. 9

C ^conf _p for the iron-free (open symbols) and iron-bearing (filled symbols) melts as a function of composition. The straight line fits to the data are for γ ≥ 0.5 and γ ≤ 0.5. The data are compared with the measurements of Webb (2008) for Na₂O–Al₂O₃–SiO₂ melts—small grey circles

The fictive temperature of each melt was determined from the heat capacity data using the method described by Moynihan et al. (1976) and DeBolt et al. (1976) (see also Webb 2008). The fictive temperatures for 20 K min⁻¹ cooling- and heating-rate are listed in Table 4. There is a linear relationship between T ²⁰_f and T ¹²_g , with T ²⁰_f  = 22.6 + 0.96 T ¹²_g for the Na₂O–Al₂O₃–SiO₂ melts and T ²⁰_f  = −9.6 + 1.01 T ¹²_g , for the iron-bearing melts.

Torsion

The frequency dependent deformation data were obtained from 300–1,000°C. Figure 10 shows the real and imaginary shear modulus of two of the melts as a function of angular frequency (2πf = ω) times Maxwell relaxation time (τ _M) (see also Falenty 2007). The relaxation time is calculated at each temperature from the Maxwell equation (Eq. 1)—determined from the micro-penetration viscosity measurements, and elastic (infinite frequency) shear modulus G _∞ which is taken to be the shear modulus at 1 Hz at the lowest temperature of measurement. These shear modulus data are listed in Table 2 together with the room temperature ultrasonic data on the same composition glasses. Plotting data from different temperatures on the same ωτ _M curve uses the principle of “thermorheological simplicity” which assumes that the structure and mechanism of flow in these melts does not change over the temperature interval of the measurements (e.g. Narayanaswamy 1988).

Fig. 10

Real (solid symbols) and imaginary (hollow symbols) components of the shear modulus of melts NAS42 and NAFS49 as a function of log₁₀ ωτ _M The dashed lines are the model of Herzfeld and Litovitz (1959) for a melt with a single structural unit

Herzfeld and Litovitz (1959) developed a general equation to describe the frequency dependence of the shear modulus of a material independent of its structure;

$$ G^{*} (\omega ) = {\frac{{G_{\infty } \omega^{2} \tau^{2} }}{{1 + \omega^{2} \tau^{2} }}} + {\text{i}}{\frac{{G_{\infty } \omega \tau }}{{1 + \omega^{2} \tau^{2} }}} $$

(12)

where τ is the structural relaxation time. The dashed lines in Fig. 10 are the real and imaginary shear modulus expected from the theory of Herzfeld and Litovitz (1959). As can be seen, none of the present data is adequately described by this equation. The solid lines are fits to the data based on the assumption that there is a distribution of relaxation times. Instead of assuming a distribution, the data have been fit by a summation of Eq. 12:

$$ G^{*} (\omega \tau ) = \sum\limits_{x = - 8.5}^{1.5} {G^{*}_{x} } (\omega \tau \times 10^{x} ) $$

(13)

with steps of 0.5 in the x value. This is the same analysis as was used in the study of the structural relaxation of a rhyolite composition melt by Webb (1992) with steps of 0.8 in the x value. The real and imaginary parts of the data have been fit separately. The parameters of the fit are given in Table 5. Figure 11 illustrates the relaxation time on which the data are centred (the “x”-term which has the largest G _real or G _im value) as the log₁₀ difference from the Maxwell relaxation time; these values are given in Table 5. The α-relaxation of melts with γ ~0.5 is up to 30 times faster than calculated from the Maxwell relaxation equation.

Table 5 The parameters of the fits of Eq. 13 for the melts

Fig. 11

Deviation of relaxation from the Maxwell relaxation time as a function of composition for both the real (small symbols) and imaginary (large symbols) data: a and d α-relaxation of Na₂O–Al₂O₃–SiO₂ melts as a function of γ and S/T; b and e α-relaxation of Na₂O–Fe₂O₃–Al₂O₃–SiO₂ melts as a function of γ and S/T; c β-relaxation for all melts—as a function of γ. The curves describing the α-relaxation data are the best fit Gaussian curve to the Na₂O–Al₂O₃–SiO₂ data. There is too much scatter in the Na₂O–Fe₂O₃–Al₂O₃–SiO₂ data to allow such a fit. The data of Webb (1992) for a rhyolite composition melt are the filled diamond in b and e. The data of Bagdassarov et al. (1993) for iron-free haplogranitic melts are the open diamond in a and d

An analysis of the shear modulus curve shapes found that the width of the α-imaginary peak is similar for all the melt compositions, with the FWHM ranging from 1.13 to 2.68 with no clear compositional dependence. However, the position of the α-imaginary peak moves from being centred on log₁₀ ωτ _M = 0, to being centred on a timescale ~1.5 orders of magnitude smaller. Such fast relaxation has never been measured before in a silicate melt. The data of Mills (1974), Bagdassarov et al. (1993) and Webb (1992) all have the α-peak determined by mechanical spectroscopy centred on log₁₀ ωτ _M = 0 ± 0.5.

The shear moduli measured by ultrasonic methods at room temperature are ~3.5 GPa higher than the moduli determined by torsion methods. As there is, in general, a 500°C temperature difference between the ultrasonic and torsion data, an average temperature dependence of the shear modulus of all the melts of ~−7 MPa K⁻¹ is calculated. Literature values of the temperature dependence of the shear modulus of silicate glasses range from −3 to −11 MPa K⁻¹ (Bass 1995).

Two peaks are observed in the imaginary component of the shear modulus of the Na₂O–Al₂O₃–SiO₂ melts. Both peaks are accompanied by an increase in the real part of the shear modulus. The peak which occurs at the lowest frequencies is the α-relaxation and caused by the loss of energy to the motion of Si and O ions in the melt (Dingwell and Webb 1990)—the glass transition—which results in the change in shear modulus from 0 to ~35 GPa. The second relaxation peak occurs up to 7.5 orders of magnitude faster than the α-peak and is accompanied by a 2–3 GPa increase in the real part of the modulus (see Fig. 10). There are two energy loss processes other than that associated with the life-time of Si–O bonds expected in these melts—the motion of Al³⁺ ions (lifetime of Al–O bonds) and the motion of Na⁺ ions (lifetimes of Na–O bonds).

As seen in Fig. 12, the maximum in the imaginary part of the shear modulus of NAS100 is centred on log₁₀ ωτ _M = 0. The data are compared to the data of Mills (1974) on the same composition at the same deformation frequencies. Here, a G _∞ of 27.5 GPa was determined. Mills (1974) determined G _∞ = 15 GPa for the same melt composition (see Table 2). The room-temperature shear modulus for this melt composition determined by ultrasonic methods is 29.9 GPa, with 24.1 GPa presented in the compilation of Ahrens (1995). There is good agreement between the present torsion data and that determined by ultrasonic techniques—for a dG _∞/dT = −6 MPa K⁻¹. A dG _∞/dT of −24 to −40 MPa K⁻¹ is needed to bring Mills’ high temperature shear modulus into agreement with the literature data or the present ultrasonic data. The dG _∞/dT values of −7.6 and −10.6 MPa K⁻¹ are found in the literature for 30 and 35 mol% Na₂O–SiO₂ glasses (Bansal and Doremus 1986).

Fig. 12

Frequency dependent real (solid symbols) and imaginary (hollow symbols) components of the shear modulus of 0.33Na₂O–0.67SiO₂ (sample NAS100). The dashed line is the data of Mills (1974) on the same composition

The greatest difficulty in designing a torsion experiment is the rigidity of the connection between the torsion rods and the sample. If there is slippage at this connection, low shear modulus values are measured. The high elastic shear modulus determined here by torsion and ultrasonic methods indicates that the low values of elastic shear modulus determined by Mills (1974) are due possibly to slippage at the connections between sample and torsion rod. In his experiments, Mills (1974) used clamps between torsion rod and 50 mm long sample. These clamps sat inside his furnace. Mills determined the correct value of shear modulus for SiO₂ melt (~30 GPa in comparison with the 31.2 GPa value in the compilation of Bass 1995) as this melt was measured as a long cylinder which was held by clamps outside the furnace. Both the present data and that of Mills (1974) have the imaginary peak centred on log₁₀ ωτ _M = 0 for the NS100 melt.

Viscosity

Viscosity is also calculated from the torsion data as:

$$ \eta^{*} (\omega ) = {\frac{{G^{*} (\omega )}}{{{\text{i}}\,\omega }}} $$

(14)

(Webb 1992). As an example, the viscosity of the melts NAS47 and 48 is shown in Fig. 13 as a function of frequency at each temperature. The Newtonian viscosity is given by the low-frequency frequency-independent part of the viscosity curve and is calculated at each temperature from the average of the frequency independent data; or where there are not enough data, the Newtonian viscosity is taken to be the lowest frequency datum. Each of these viscosity data is plotted in Fig. 14 (and shown in Table 3) as a function of inverse temperature, together with the viscosity data from the micro-penetration measurements. The agreement between viscosities determined in the micro-penetration and torsion experiments supports the robustness of the torsion data. As the viscosities agree, the temperature calibrations of the two furnaces are correct, and there is no slippage at the torsion rod/melt interface—as also shown from the general agreement between the torsion and the ultrasonic shear modulus values. The agreement between viscosity determined using these two techniques also supports the shift in relaxation times to shorter values than the Maxwell relaxation time being real and not due to errors in measurements or temperature. As the lowest frequency of the torsion measurements is 1 mHz, the highest viscosity expected to be accurately determined is ~10¹³ Pa s. Allowing for the distribution in relaxation times; all viscosities >10¹⁵ Pa s are not relaxed and therefore slightly lower than the relaxed viscosity. As shown in Fig. 10, higher temperature data are not available as the measured shear modulus is zero for the range of frequencies available with the torsion device.

Fig. 13

Frequency dependent viscosity of NAS47 and 48 for a range of temperatures. The grey lines mark the value of the frequency-independent viscosity

Fig. 14

Viscosity determined from torsion measurements for the a Na₂O–Al₂O₃–SiO₂ and b the Na₂O–FeO–Fe₂O₃–Al₂O₃–SiO₂ melts. The straight lines are the Arrhenian fits to the micro-penetration viscosity data. The dashed lines are the extrapolations of the micro-penetration data

Discussion

Each of the physical properties investigated here shows a change in trend at the γ ~0.5 composition. These changes in trend as a function of composition indicate that there is a change in the structural units occurring in the melt with changing composition. The molar volume, T ¹²_g (and T ²⁰_f ) and shear modulus data all follow the same trend, with an almost constant value for the peraluminous melts and glasses and a decreasing value as the melt or glass becomes increasingly peralkaline. Both density and C ^conf _p show a minimum value at γ ~0.5; no clear trend change is seen in C _pl, however.

Heat capacity

The heat capacity data can be combined with the viscosity data to calculate the configurational entropy S _conf(T _g) of the melts, using the equation of Richet et al. (1986);

$$ { \log }_{ 1 0} \,\eta = A_{\text{e}} + {\frac{{B_{\text{e}} }}{{{ \ln }\, 1 0\left[ {S_{\text{conf}} (T_{\text{g}} ) + \int_{{T_{\text{g}} }}^{T} {{\frac{{C_{p}^{\text{conf}} }}{T}}{\text{d}}T} } \right]T}}} $$

(15)

where A _e is either found from fits to the viscosity data or is taken to be the composition independent constant −2.6 ± 1 log₁₀ Pa s, determined by Toplis (1998). At T _g, the integral of C ^conf _p /T is zero and thus the B _e and S _conf(T _g) terms can be calculated from viscosity data as a function of temperature. The calculation of B _e and S _conf(T _g) have been performed with A _e = −2.6, as there is no low viscosity data to constrain the value of A _e. The calculated B _e and S _conf(T _g ) as shown in Table 2 and Fig. 15. Straight line fits to the data show that a general increase in S _conf(T _g) with increasing peraluminosity is observed for both iron-free and iron-bearing melts; but no clear trend change as a function of composition is seen. No clear trend change is seen in B _e as a function of composition, simply a general increase that mirrors the S _conf(T _g) data. The determination of the A _e term presents problems if only high viscosity data are available. In the few cases where both low viscosity (10⁻¹–10⁴ Pa s) concentric cylinder and high viscosity (10⁸–10¹³ Pa s) micro-penetration or parallel plate data exist, it is possible to determine the A _e term. This term has been calculated by Russell et al. (2003) by fitting the Vogel–Fulcher–Tamman and the Adam–Gibbs equation to a large series of viscosity data and found to be A _VFT = −4.3 ± 0.7 log₁₀ Pa s, and A _AG = −3.2 ± 0.7 log₁₀ Pa s. Giordano et al. (2006) found a preferred value of −4.07 in their study of viscosity; and suggested that the minimum possible value of A _e should be −4.5; based on theories of kinetic rate processes in melts. Toplis (1998) in his summary of Adam-Gibbs parameters found A _e to be −2.6 ± 1.0 log₁₀ Pa s. The A _e value of Toplis (1998) is used in the present study. Use of a different A _e value produces the same trends in B _e and S _conf(T _g) but the parameters have slightly different absolute values [If a value of −4.5 is used for the term A _e, instead of the −2.6 employed here, the calculated B _e and S _conf(T _g) terms increase linearly by a factor of ~1.5.].

Fig. 15

Calculated S _conf(T _g) and B _e for the iron-free (open symbols) and iron-bearing (filled symbols) melts. Straight lines have been fit to the data—black and grey, respectively

C ^conf _p is a measure of the energy needed for rearrangement of the structural units in the melt (e.g. Richet and Toplis 2001). Thus, the least amount of energy is required for a melt in which there are (theoretically) no non-bridging oxygens and no tri-clusters. The amount of energy needed to rearrange the melt structure increases as the number of NBOs increases and also as the number of tri-clusters (or other new Al³⁺-structure increases). S_conf(T_g) is a measure of the number of different structural units within the melt and appears to increase as the melt composition changes from Al-free peralkaline to Al-rich peraluminous compositions. The B_e term which is a measure of the size of the smallest re-arranging structural unit (e.g. Richet and Toplis 2001) increases with increasing S_conf(T_g). This suggests that as the composition is changed from peralkaline to peraluminous, the number of different structural units increases as does the size of these units.

Torsion and mechanical spectra

Of the three peaks expected in the imaginary part of the torsion spectrum, only two are seen. The second, fast, β-structural relaxation is assumed to be associated with the diffusion of Na⁺ in the melt. This fast relaxation peak has been observed in previous studies (e.g. Day and Rindone 1962b). This is the first study to observe both the α and β peaks in Na₂O–Al₂O₃–SiO₂ melts in the same experiment.

The compilation of diffusivity data in Fig. 1 illustrates schematically that the diffusion rate of Na⁺ approaches that of Si and O in silicate melts at high temperature (low viscosities). At high viscosity (~10¹² Pa s) however, the diffusion rate of Na⁺ is ~12 orders of magnitude faster than that of Si and O for a Na₂O–Al₂O₃–SiO₂ composition melt; while the diffusion rate of Al³⁺ is ~5 orders of magnitude faster than that of Si and O. Mungall et al. (1998) determined the diffusion rate of Al³⁺ and Na⁺ in a Na₂O–K₂O–Al₂O₃–SiO₂–H₂O melt. A straight line extrapolation of their data in inverse temperature space, together with a rescaling using the Eyring equation to calculate the structural relaxation time τ _M = η₀/G _∞ = kT/DλG _∞, gives a ~7 orders of magnitude difference between the lifetime of a Na–O bond and a Si–O bond at the present viscosities. This supports the assumption that the fast relaxation seen in our measurements is due to Na⁺ diffusion. A close look at the log ωτ _M value at which this second peak occurs for each melt composition shows that the peak moves to slower times (~2 log₁₀ unit difference between samples NAS42 and 53) with increasing Al-content (see Fig. 11c). This is in agreement with the calculations of Kargl and Meyer (2004) who showed that with increasing Al₂O₃ content the β-relaxation peak (Na⁺) moves to slower times: closer to the α-relaxation peak.

The attenuation peak associated with the motion of Al³⁺ in the melt is not observed in the torsion data. It is assumed that the peak for Al motion will occur between the Si and the Na peaks in frequency space. The data of Mungall et al. (1998) however suggest that the diffusivity of Al in the present viscosity range should be very similar to that of Si and O if not slower (this observation would therefore imply that the glass transition, which is defined by the longest-lived bond lifetime, is a function of the Al–O bonds in aluminium-rich melts). Thus the absence of an observable Al-peak suggests that the Al–O bond lifetimes which were sought in this study are buried in the peak due to the Si–O bond lifetimes.

Without a clear Al–O peak, the effect of the presence of tri-clusters cannot be identified. As there is no clear trend observed in the FWHM of the imaginary peak in the shear modulus data, there can be no discussion about increasing or decreasing distributions of relaxation times associated with increasing numbers of Al–O bonds or AlSi₂–O bonds as a function of peralkalinity/peraluminosity.

Inspection of the frequency dependence of the shear modulus data however, shows that the curves for the different compositions are centred on different ωτ _M values. Figure 11 a, b illustrates the ωτ _M at which G _im is centred (see Table 5) as a function of γ. Some of the melts relax up to 30 times faster than predicted by the Maxwell equation. Previous studies of relaxation in silicate melts have found that the α-relaxation occurs within ±0.5 log₁₀ units (a factor of 3) of ωτ _M = 1 (e.g. Mills 1974; Webb 1992; Bagdassarov et al. 1993). The relaxation spectra from torsion experiments of Webb (1992—rhyolite composition) and Bagdassarov et al. (et al. (1993)—haplogranitic compositions) on aluminosilicate melts with γ ranging from 0.48 to 0.52 are centred on log₁₀ ωτ _M = 0. The imaginary peaks for all of the present melts within this γ range are centred on log₁₀ ωτ _M = + 0.5 to +1.5, suggesting that the γ parameter is not the relevant structural measure to describe the relaxation time trend.

An alternative measure of “structure” is Al/Si (e.g. Mysen 1999). Here, this ratio is calculated as the number of Si-tetrahedra (S) per number of Si + Al tetrahedra in the melt (T). The shift of the relaxation from ωτ _M is shown as a function of Si/T in Fig. 11. The data of Webb (1992) and Bagdassarov (1993) are for relatively SiO₂-rich melts with Si/T ~0.85, and therefore fit into the trend of deviation from ωτ _M as a function of Si/T. Thus it would appear that the observed deviation from the Maxwell relaxation time may be due to a change in flow mechanism as a function of Si/T and not to the presence of tri-clusters. This suggests that two different effects are being observed in these different experiments. The physical properties reported here in their relaxed (viscosity, C ^conf _p ) or unrelaxed (elastic modulus, density) conditions show a trend change as a function of composition at γ ~0.5. These changes in trend can be associated with the introduction of a new structural unit whose occurrence is controlled by the Na/Al. The relaxation time data do not appear to be sensitive to the appearance of a new structural unit. The relaxation time does however appear to be sensitive to changes in the flow mechanism of the melt which occur as a function of Si/Al.

The Maxwell relationship was developed for a gas with a single type of structural unit. It has been shown to work well in the investigation of almost all silicate melts which have been studied previously. Here, the Maxwell relationship does not successfully predict the relaxation times of the melts with γ ~0.5. These melts are also those with Si/T ~0.65 and are the most silica-poor melts that have been investigated by torsion techniques to date. The deviation of the melt relaxation to times faster than τ _M could be explained in terms of the melt structure changing from being dominated by the network forming Si (whose relaxation can be described by the Maxwell equation), to a mixture of Si and Al tetrahedra (which is too complex to be described by the Maxwell equation) to a melt structure whose flow is dominated by the making and breaking of Al–O bonds (whose relaxation can be described by the Maxwell equation). On this basis one would expect the deviation from the Maxwell behaviour to occur for Si/T ~0.5. This deviation, however, occurs for Si/T ~0.65 suggesting that there are further changes occurring in the melt structure and flow mechanism. One possibility is that there are clusters of Si–O bonds surrounded by volumes (or channels) of Al–O bonding melt occurring before the Si=Al condition occurs. This structural model is analogous to that proposed by Bockris et al. (1956) for M₂O–SiO₂ melts and by Greaves (2000) and Kargl and Meyer (2004) for Al-poor Na₂O–Al₂O₃–SiO₂ melts. In these studies the existence and effect on physical properties of Na-rich channels within the melt were discussed and modelled.

Attenuation

The energy loss due to the relaxation of parts of the melt structure can also be analysed in terms of the quality factor Q ⁻¹(ω) where

$$ Q^{ - 1} (\omega ) = {\frac{G''(\omega )}{G'(\omega )}} $$

(16)

(O’Connell and Budiansky 1978; Johnston and Toksöz 1981; Webb and Jackson 2003). Figure 16 shows Q ⁻¹(ω) for melt NAS48 as a function of inverse temperature. Two straight line trends can be seen in this plot—one associated with the slowest relaxing part of the melt structure; and one associated with the ~7.5 orders of magnitude faster relaxation. The two regions have been fit separately by the equation

$$ Q^{ - 1} (\omega ) = Q_{0}^{ - 1} \omega^{ - \alpha } \exp \left( { - {\frac{\alpha \,E}{R\,T}}} \right) $$

(17)

(Webb and Jackson 2003). The parameters of the fits to the data are given in Table 4. As shown in Fig. 17, the activation energy for the α-relaxation of the melt is in good agreement with the activation energy for viscous flow determined from the micro-penetration measurements in these melts—as is expected. The average activation energy for the faster motion is ~126 kJ mol⁻¹. The activation energy for Na diffusion in silicate melts is 50–100 kJ mol⁻¹ (Bansal and Doremus 1986). This is in agreement with the second energy loss peak being for the diffusion of Na⁺ in the melt.

Fig. 16

The attenuation data for the α and β attenuation peaks of the melt NAS48. The lines are the fits calculated using Eq. 17

Fig. 17

Plot of the activation energy determined from the attenuation data and the torsional viscosity against the activation energy from micro-penetration viscosity data

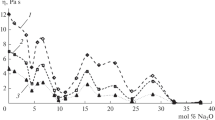
The parameter α in Eq. 17 is found for both the α- and the β-relaxation peak and listed in Table 4; and shown in Fig. 18. The curves in Fig. 18 are a guide for the eye, with the trend change chosen to occur at γ ~0.5 in view of all of the other physical property and parameter changes occurring at this composition.

Fig. 18

The α-parameter from Eq. 17 for the Na₂O–Al₂O₃–SiO₂ and the iron-bearing Na₂O–Al₂O₃–SiO₂ melts

Summary

It is assumed here that the viscous flow in these melts is identified in the torsion measurements as the α-relaxation. In Fig. 17 the activation energy for viscous flow determined by torsion is compared to the activation energy determined from the attenuation data as a function of activation energy from viscosity (micro-penetration technique). The data should plot on a straight line with slope = 1.

The C ^conf _p , G, ρ, η data all show a trend change as a function of composition in Na₂O–(Fe₂O₃)–Al₂O₃–SiO₂ melts at Na₂O(+FeO)–Al₂O₃(+Fe₂O₃), for constant SiO₂ content. This change in physical property trend can be associated with the change in structural units which must occur with decreasing [Na₂O + FeO]/[Al₂O₃ + Fe₂O₃] when there are no longer enough monovalent or divalent atoms (Na⁺, Fe²⁺) to charge balance all of the tetrahedrally co-ordinated trivalent atoms (Al³⁺, Fe³⁺).

The expected Al–O relaxation peak does not appear in the torsion spectra. The diffusion data in the literature suggest that the timescale of Al diffusion is close to that of Si and O diffusion at the temperature and viscosity conditions of the torsion measurements. Thus it appears that the Al–O peak is part of the Si–O peak. The width of the Si–O peak for the imaginary part of the modulus, however, does not change as the Si/T ratio decreases.

The elastic shear modulus and the viscosity data obtained from the torsion measurements are in agreement with the ultrasonic and micro-penetration data, respectively. It can be seen from the frequency dependence of the shear modulus, however, that the glass transition does not occur at the ωτ _M = 1 condition for all melts as expected from Maxwell theory. This is in contrast to all of the literature data which show that the α peak in the imaginary part of the shear modulus is centred on ωτ _M ~1 (−0.5 < log₁₀ ωτ < 0.2; see Mills 1974; Webb 1991; Bagdassarov et al. 1993). These melts are in the composition range γ ~0.5, and Si/T ~0.85.

Recently, Stebbins et al. (2001; 2008) and Neuville et al. (2006) have discussed that the ^VSi and ^VAl found to exist in silicate glasses could be involved in the flow process of melts. The Maxwell relationship was created for an ideal material in which all of the atoms involved in the flow process are identical. In an Al-free melt in which the flow process is controlled by Si–O bond lifetimes, the conditions are the same as those of the Maxwell equation. In melts with increasing amounts of Al, there are two different structural units dominating flow, and the assumptions built into the Maxwell equation no longer apply to the flow process of the melt. The result is that the Maxwell equation no longer accurately calculates the relaxation time. This deviation from the Maxwell relaxation time is not associated with the appearance of a new structural unit in the melt which is a function of Na/Al. It is associated with the timescale of the flow mechanism in the melt which appears to be a function of Si/Al.

It is to be expected that the deviation from the Maxwell equation should occur in the Si–Al compositional range, and not at the Si–2Al composition. This suggests the possibility of a more complicated relationship for flow and structure than simply Si–O and Al–O bonds. One could have melts in which clusters of unrelaxed Si–O melt is surrounded by Al–O bonds similar to the Na-rich channels occurring in Al-poor melts which disappear with increasing Al content. Such a structure consisting of Si–O clusters surrounded by Al–O bonds is similar to the iceberg type structure proposed by Bockris et al. (1956).