Abstract
The heterogeneity of resource availability shapes animal movements at different spatio-temporal scales. Given that movements at various scales are assumed to be linked, the space use of temperate ungulates within seasonal ranges (winter, summer) should be related to their movement patterns at the annual scale. In this study, we aimed to evaluate the level of stationarity of moose (Alces alces) within their seasonal ranges and to link annual movement patterns to within-season space use. We analysed the ranging behaviour of 32 moose fitted with GPS collars from two study areas in Eastern Poland, where at the annual scale a fraction of individuals migrate between summer and winter ranges (partial migration). Our results revealed that moose stationarity within seasonal home ranges expressed remarkable variation. The probability of moose stationarity within seasonal ranges was significantly higher (by 23%), and the mean home range size tended to be lower (9.7 km2) among individuals that seasonally migrated than among non-migratory moose (14.3 km2). In addition, we found that (i) in summer, moose were significantly more stationary (by 19%) and exhibited a smaller mean home range size than in winter (9.0 and 15.9 km2, respectively) and (ii) the mean seasonal home range size of males (19.6 km2) was remarkably greater than that of females (9.6 km2). Given the significant link between annual and seasonal scales of animal movements, any environmental change (e.g. climate warming) affecting an animal’s annual movement strategy could alter within-season animal space use and presumably individual fitness.
Significance statement
To maximize their fitness, animals adjust their movements to deal with variations in resource distribution in the landscape. The scale of spatio-temporal variation causes different types of migratory behaviours, ranging from year-round stationarity to migration, when individuals establish spatially separated seasonal ranges. Studies on ungulates suggest that the stability and the size of seasonal home ranges can be linked to annual movement behaviour. Using the locations of GPS-tracked moose, we demonstrate in this study that migratory individuals were more prone to establishing stable seasonal home ranges (especially in summer) than moose that occupied the same area throughout the year. Moreover, stable seasonal home ranges were remarkably smaller in summer than in winter, which may suggest a season-specific spatial distribution and a renewability of moose forage. Our results show a clear link between different temporal scales of animal movements.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Animal movement is driven by an individual’s intrinsic motivation to move, its ability to move as well as a broad set of extrinsic factors (Nathan et al. 2008). Among external factors, the highest importance is assigned to foraging availability, but access to water (Gaylard et al. 2003), weather conditions (Borowik et al. 2020a), predation risk (Mitchell and Lima 2002; Forrester et al. 2015) and human disturbance (Preisler and Wisdom 2006; Haidt et al. 2018) are additional predictors of animal movement. According to the marginal value theorem (Charnov 1976), in environments where food occurs in clumps or patches, animals, when looking for food resources, choose the most beneficiary patch types. Animals are expected to leave specific patch when the energetic benefit of foraging in it drops below the average value of other available patches. When food resources have a high regenerative potential, animals, based on their cognitive abilities, can repeatedly utilize the same foraging patches, leading to the establishment of stable home ranges (stationary behaviour; Benhamou 2014; Bracis et al. 2015). Stationarity, however, is a scale-dependent concept (Benhamou 2014). For a given data series, animal movements can be classified as stationary at a specific temporal scale, but at finer scales a mixture of stationary and non-stationary periods can be observed (multiphasic movements). For example, an animal’s movement can be considered stationary at the seasonal scale, while at finer scales, the seasonal tracking period can be divided into several stationary and non-stationary phases (Johnson et al. 2002; Börger et al. 2008; Benhamou 2014; Couriot et al. 2018).
Indeed, scale-dependent stationarity has been indicated, among others, in ungulates from seasonal environments, where natural resources tend to be spatially aggregated and animals move between resource aggregates (patches). As a result, a series of subseasonal stationary (functional home ranges) and non-stationary phases has been observed (e.g. Niger buffalo Ictiobus niger, Benhamou 2014; roe deer Capreolus capreolus, Couriot et al. 2018; sable antelope Hippotragus niger, Owen-Smith et al. 2010; elk Cervus elaphus manitobensis, Fryxell et al. 2008). Stationary phases correspond to frequent, short intrapatch movements and a high path tortuosity, while (rarer) non-stationary periods relate to interpatch movements of lower sinuosity (Barraquand and Benhamou 2008; Fryxell et al. 2008; Benhamou 2014). Moreover, in temperate latitudes, ungulate movement can change seasonally as animals utilize different food resources and habitat patches in summer and winter. Hence, even in the same area, resource distribution can express different levels of heterogeneity across seasons. High habitat patchiness, which has been observed in winter, restricts foraging activity to small, discrete forage aggregates and prompts animals to move between foraging areas (Johnson et al. 2002; van Beest et al. 2010). In addition, the greater ability of forage regeneration in summer results in more frequent revisits of previously utilized patches and thus the emergence of smaller and more stable home ranges (Börger et al. 2008; Owen-Smith et al. 2010). Nevertheless, in many ungulate populations, part of individuals seasonally migrate (partial migration) to cope with heterogeneity in resource distribution at this scale, allowing them to establish seasonal home ranges in more homogeneous landscapes (Chapman et al. 2011).
Whereas ungulate movements at the annual scale have received considerable attention (Mysterud 1999; Mueller et al. 2011; Naidoo et al. 2012; Singh et al. 2012; Cagnacci et al. 2016; Peters et al. 2017; Borowik et al. 2020b), only a few surveys focusing on within-seasonal movements have been conducted (Fryxell et al. 2008; Owen-Smith et al. 2010; Couriot et al. 2018). Knowledge of animal movements at lower spatio-temporal scales is of considerable importance for species management and conservation strategies, because small-scale movements can greatly affect individual fitness components. For example, Couriot et al. (2018) have demonstrated significant differences in the level of seasonal stationarity for roe deer inhabiting sharply contrasting environments across Europe and have suggested that such a phenomenon may be widespread among populations of other ungulates.
In this study we sought to evaluate the level of stationarity of seasonal home ranges in moose (Alces alces) from populations in Eastern Poland and relate it to movement strategies at annual scale. We chose moose as a model species, as in Eastern Poland moose populations are composed of resident and migratory individuals and their movement strategies are related to habitat patchiness; i.e., lower habitat patchiness is associated with the predominance of migrating individuals, while in more patchy landscapes, resident moose dominate (Borowik et al. 2020b). In addition, food resources differ seasonally; thus, animals utilize different habitat patches in winter (coniferous forests) from summer (wetlands; Czernik et al. 2013; Kuijper et al. 2016). We used the GPS locations of 32 moose collected in 2012–2018 to classify individual yearly movements and assess within-season stationarity and home range sizes. We hypothesized that the stationarity of seasonal home ranges would be dependent on movement at the annual scale, as seasonal migration can allow an animal to better adjust to seasonal changes in the heterogeneity of resource distribution at this scale (Noonberg et al. 2007). Therefore, we predicted that individuals that migrate between winter and summer ranges should have a higher probability of being a resident within seasonal home ranges and have a smaller seasonal home range size compared with non-migrating moose. Second, we expected that the probability of an animal being stationary within seasonal ranges and seasonal home ranges would be greater in winter than in summer, because in the latter, food resources are renewable and less dispersed across the landscape, stimulating repeated visits to the same food patches (Owen-Smith et al. 2010; Couriot et al. 2018).
Materials and methods
Study area
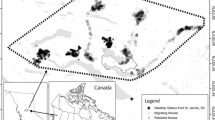
The study area was located in Eastern Poland at the southern range of species distribution in Europe and included two study sites, being the core areas of moose in Poland (Fig. 1). The northern study site (22° 35′ E, 53° 26′ N) included the southern part of the Biebrza National Park and neighbouring forest districts (hereafter Biebrza), while the southern study site (23° 8′ E, 51° 26′ N) encompassed the Polesie National Park and surrounding forest districts (hereafter Polesie; Fig. 1). The Biebrza is a large marshland of the Biebrza river valley, surrounded by elevated areas with coniferous forests (mainly Scots pine Pinus sylvestris). The Polesie study site is a mosaic of wetland and forest habitats with numerous oligotrophic lakes. In both areas, wetlands are overgrown with sedge, sedge-moss and reed communities as well as willow (Salix sp.) bushes. In forests, the most common are pine, black alder (Alnus glutinosa) and downy birch (Betula pubescens). Besides moose, the ungulate guild is represented by red deer (Cervus elaphus), roe deer and wild boar (Sus scrofa; Wawrzyniak et al. 2010; Borowik et al. 2013). In both areas, wolves (Canis lupus) preyed upon moose, although they constitute only a relatively small proportion of the latter’s diet (Jędrzejewski et al. 2012). Moose are not hunted in Poland due to a ban imposed in 2001, while the hunting of other ungulates is allowed (Raczyński and Ratkiewicz 2011; Borowik et al. 2018).
Movement data
We used GPS tracking data of adult moose (≥ 2 years) from the Biebrza (2012–2017; 12 females and 10 males) and Polesie study sites (2013–2018; 9 females and 1 male). Animals were immobilized with etorphine (Arnemo et al. 2003) injected via a pneumatic dart gun (Dan-Inject) and then fitted with Ecotone Telemetry GPS-GSM collars. The collaring took place in winter (January–March; see also Borowik et al. 2020b). No animal suffered during anaesthesia, and we did not observe any negative impact of the collaring on animal behaviour and survival. The GPS collars were set to send animal positions registered every hour. We screened the GPS data for positional outliers (location errors) and removed them from the final databases. We classified a location as an outlier when the step length exceeded 15 km for a 1-h interval. It was not possible to record data blind because our study involved focal animals in the field.
Data analyses
Annual movement patterns
We classified the annual patterns of moose behaviour into migrant and non-migrant categories using the net squared displacement (NSD) method. NSD is a squared straight-line distance between the predefined starting position of an individual within its starting range and every subsequent position (Turchin, 1988; Bunnefeld et al. 2011). At the beginning we extracted one location per day (first position acquired in a given day) and divided the moose tracking data into 80 yearly subsets of 365 (366) locations (Biebrza, n = 57; Polesie, n = 23; from 1 to 5 yearly subsets per individual), starting on 15 February. We chose this date because it corresponded to the time when all individuals remained in their winter ranges (time preceding migratory movements). Then, with the help of the ‘migrateR’ package (R environment; Spitz et al. 2017), we generated 70 NSD plots of the annual movement patterns of individual moose. Finally, we visually inspected these plots and classified moose movements based on the temporal distribution of the NSD scores (Fig. 2). We considered an individual a migrant when the NSD plot presented clearly temporally separate clouds of points representing winter and summer ranges and the animal spent at least 21 days in a spatially separate summer range (Supplementary file 1, Fig. S1A). The plot of non-migratory moose, in turn, presented a single cloud of points, i.e. the winter and summer NSD scores expressed a temporal overlap (Supplementary file 1, Fig. S1A). We did not observe any nomadic behaviours, while moose dispersal was noted only once, thus we excluded this particular moose from further analyses (Fig. 2).
Seasonal movement patterns and home range size
We divided the annual tracking data sets into winter and summer subsets, applying different criteria for seasonally migrating and non-migrating animals. For migrants, summer was the period that started from arrival at the summer range until the start of the rutting period (28 August), while winter corresponded to the time spent by moose in the winter range, i.e. from arrival at the winter range (autumn) until departure to summer range (spring). In migratory individuals, locations from migration periods were not included in the estimation either of summer or winter ranges. We also decided to remove the rutting period from the analyses to obtain comparable home range size estimates for both sexes. Males during the rut exhibited increased movement (Supplementary file 1, Fig. S2) and often made ‘exploratory sallies’ beyond their summer range that could have led to the incorrect classification of male movement behaviours during summer. As we found a clear autumnal peak in moose movement corresponding to the rutting period, we assumed that the beginning of the rut was the time when males’ mean daily movement started exponentially increasing (28 August). We calculated the daily movements of the studied males as the sum of the distances between daily locations. For non-migrants, summer was the period delimited by the median date of the spring migration midpoint estimated for migratory individuals (21 April) and the start of the rutting period (28 August), while winter was the period between the median date of the autumn migration midpoint (17 October) until 21 April (Borowik et al. 2020b). Migration start, midpoint and end dates were estimated based on the curve parameters fitted to the NSD data of migratory individuals with the ‘MigrateR’ package (R environment; Spitz et al. 2017). To sum up, in migrants, the summer time series of locations ranged over the period of 43–181 days (mean = 124.9 days) and winter over 79–268 days (mean = 141.6 days), while in non-migrants, the summer time series spread over 129 days and winter over 186–187 days.
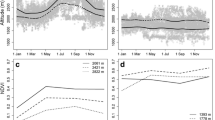
We classified the movement behaviour of moose and calculated the seasonal home range size with the application of the ‘ctmm’ package (R environment; Calabrese et al. 2016). For each seasonal tracking subset (both migratory and non-migratory individuals), we visualized the autocorrelation structure in moose locations by generating a variogram presenting estimated semi-variance plotted against time lags for half of the data set’s duration (Supplementary file 1, Fig. S1B). We visually inspected all variograms (n = 158) to classify the movement behaviour of moose into stationary or non-stationary movements. We assumed moose to be stationary in a given season when the variogram, estimated for the corresponding tracking data, presented semi-variance reaching a clear asymptote across the considered time lags. Non-stationary individuals were moose whose semi-variance did not reach an asymptote (Fig. 3; Supplementary file 1, Fig S1B; Fleming et al. 2015; Noonan et al. 2019). Stationary moose, then, were individuals that occupied the range uniformly throughout the season, whereas non-stationary individuals tended to utilize different parts of the range over time (temporal range shift; Calabrese et al. 2016). The estimated movement behaviour of moose within seasonal home ranges (stationary vs non-stationary) was weakly related to the number of locations used for semi-variance calculation (Spearman’s rank correlation = − 0.14, n = 158, P = 0.09).
Empirical variograms representing autocorrelation structure in seasonal (summer and winter) tracking data of moose. For stationary moose, semi-variance function expressed an asymptotic behaviour (upper panel), while for non-stationary individuals, an asymptote was not reached at any of the considered time lags (lower panel). Semi-variance represents the average square distance travelled by moose over a specific period of time. Maximum semi-variance ranged from 0.05 to 23 km2. Maximum time-lag ranged from 0.9 to 4.5 months
For each seasonal data set, we estimated the seasonal home range size of moose via 95% autocorrelated kernel density estimation (AKDE; Fleming et al. 2015). This up-to-date and powerful method allows the estimation of home range sizes with accurate confidence intervals from autocorrelated data sets without the need to coarsen the sampling rate or stratify across individuals (Laver and Kelly 2008; Fleming et al. 2015). On the basis of the shape of the empirical variogram, the initial guesstimated parameters of the prototype model were estimated using the ctmm.guess function. Subsequently, this prototype model served for calculating an optimal movement model (fitted via maximum likelihood and ranked based on AICc) and individual home ranges (akde function, Fleming et al. 2015; Calabrese et al. 2016). An optimal bandwidth differed between seasonal tracking subsets because it was dependent on movement behaviour through the autocorrelation function — the higher autocorrelation the larger optimal bandwidth. The estimated seasonal home range sizes of stationary moose were weakly associated with the number of locations used for range estimation (Spearman’s rank correlation = 0.09, n = 105, P = 0.37).
Statistical analyses
To delineate the association between males’ daily movement and the day of the year, we applied a generalized additive model (GAM; Wood 2020) with a gamma error structure. We set males’ daily movement as a response variable and the day of the year as an explanatory variable. The day of the year was fitted with a non-parametric spline, allowing the modelling of non-linear relationships between response and explanatory variables (Wood 2017). In addition, we used a cyclic smoother, forcing the model to assume the same value of response at both extremes of the explanatory variable (e.g. male daily movement was assumed to be the same in days 1 and 365 (366); see Wood 2017). As we estimated males’ daily movement on the basis of moose GPS fixes collected by repeated sampling of the same individuals over five years, we added the moose identification number (ID) and the year as categorical random factors to GAM as penalized regression terms (Wood 2017).
We tested differences in the probability of moose stationarity within seasons between migratory and non-migratory individuals, seasons (winters vs summer) and sex using a generalized linear mixed model (GLMM 1) with a binomial error structure (R environment: ‘lme4’ package, glmer function; Bates et al. 2015). We set moose within seasonal stationarity (1, stationary; 0, non-stationary) as a response variable, while the explanatory variables included yearly movement type, season and sex. For individuals that were indicated as being stationary within seasonal home ranges based on an inspection of the variograms, we used a generalized linear mixed model with gamma error structure (GLMM 2) to test the differences in the seasonal home range sizes between migratory and non-migratory individuals, seasons (winters vs summer) and sex. Here, we set seasonal home range size as a response variable and yearly movement type, season and sex as explanatory variables. In both GLMMs, we added the moose identification number (ID) and the year as random factors, because we classified the movement behaviour of moose on the basis of their GPS locations, collected by repeating sampling of the same individuals over multiple years. For both GLMMs, we created a set of competing models, which were ranked using the Akaike information criterion (AIC) with the second-order correction for a small sample size (AICc) (Burnham and Anderson 2002). All models close to the top model (lowest AICc), having ΔAIC ≤ 2, were considered to have substantial empirical support. All statistical analyses were done in R (R Core Team 2020).
Results
According to the NSD method, 49% of the yearly subsets (NSD plots) represented migratory individuals, 50% non-migratory moose and 1% dispersers (Biebrza: migratory—65%, non-migratory—35%; Polesie: migratory—8%, non-migratory—88%, dispersers—4%). Within the analysed seasons, stationary behaviour (the semi-variance reached an asymptote on the variogram plot) was attributed to 75% of the summer tracking subsets and 58% of the winter subsets (Figs. 3 and 4; Supplementary file 1, Table S1). The AIC-based ranking of models, which tested the association between the probability of the seasonal stationarity of moose and their annual movement strategy, season and sex, confirmed the highest support for the model including movement strategy and season among its explanatory variables (GLMM 1; Table 1A). The probability of moose being stationary was significantly greater (by 23%) for individuals that seasonally migrated between winter and summer ranges than for non-migratory individuals (P = 0.03) and was higher by 19% in summer than in winter (P = 0.02; Table 2A; Fig. 5).
Home range size (autocorrelated kernel density estimation, AKDE 95% ± 95% CI) of moose in Eastern Poland from 2012 to 2017. The colour of the dots and squares represent the classification of individuals’ movements within their seasonal ranges. Black dots and squares denote stationary individuals; white dots and squares indicate non-stationary individuals. Only the home range sizes of stationary individuals were used in the analyses
Predicted probability (mean ± 95% confidence intervals) of seasonal stationarity of moose depending on individual annual movement strategy and season (results of GLMM 1; Table 2A)
The evaluation of the models, which tested the association between the seasonal home range size of moose and their annual movement strategy, season and sex, indicated that within ΔAICc ≤ 2 two top-ranked models received comparable support (GLMM 2; Table 1B). Hence, we treated both models as best models and reported the parameter estimates for the top-ranked model, including all considered explanatory variables (Table 2B). The seasonal home range size tended to be significantly associated with the annual movement strategy (P = 0.09): individuals with spatially separated seasonal home ranges had smaller seasonal home ranges than non-migratory moose (9.7 and 14.3 km2, respectively) (Figs. 4 and 6). The seasonal home range size of moose was significantly greater in winter (15.9 km2) than in summer (9.0 km2; P < 0.001), and males had a considerably larger seasonal home range size (19.6 km2) than females (9.6 km2; P = 0.01; Table 2B, Figs. 4 and 6; Supplementary file 1, Table S1).
Predicted moose home range size (mean ± 95% confidence intervals) depending on individual annual movement strategy, season and sex (results of GLMM 2; Table 2B)
Discussion
The results indicated that the majority of individuals from the studied populations established stable seasonal home ranges, while a fraction of the individuals expressed non-stationary behaviours. Migratory moose had a higher probability of seasonal stationarity, as has also been found for roe deer (Couriot et al. 2018). Moreover, their home ranges were smaller compared with non-migrants. Large-scale movements allow migratory individuals to find and select more optimal habitats with more uniformly distributed food supplies and to adjust to seasonal changes of food resources at the yearly scale (van Moorter et al. 2013). In our study sites, as in other populations worldwide (Baskin and Danell 2003; Schwartz et al. 2007), moose feed on different plant species and utilize various habitat patches in winter and summer (Borkowska and Konopko 1994; Czernik et al. 2013). Therefore, the home ranges of non-migratory individuals should include food patches that provide forage both in summer and in winter, while the seasonal ranges of migratory moose in the majority consist of seasonally specific habitat types, i.e. forests in winter ranges and wetlands in summer ranges (Borowik et al. 2018, 2020b). As a consequence, non-migratory individuals within seasonal ranges may be forced to move more and occupy larger ranges to obtain preferable food items compared with migrants, which may utilize less dispersed food resources. Indeed, the spatio-temporal distribution and availability of food resources are among the most important determinants of home range sizes in ungulates (McNab 1963; Tufto et al. 1996; Relyea et al. 2002; van Beest et al. 2011).
In line with our prediction, in summer, moose were more stationary, and their home ranges were smaller than in winter. This may be related to differences in the heterogeneity of forage distribution and their regeneration capacity in both seasons. In winter, moose in Poland forage predominantly on twigs and barks of young forest successional stages (especially pine plantations; Borkowska and Konopko 1994; Czernik et al. 2013). This forage type, however, regenerates only after a few months, during the growing season (spring–summer; Kilpeläinen et al. 2006; Mäkinen et al. 2018), while summer forage can partly regrow within the same growing season (Tuomi et al. 1994). Hence, in summer, moose can more often revisit the same forage patches. Furthermore, in the study area, the patches of young pine plantations are spatially isolated by older pine stands of much lower forage availability, which causes a high spatial dispersal of forage patches in winter. This may restrict foraging activity to small, discrete patches and promote multi-range tactics (Benhamou 2014; Couriot et al. 2018). By contrast, in summer, willow bushes and aquatic vegetation are relatively abundant and less spatially dispersed, potentially resulting in more uniform range utilization (Johnson et al. 2002).
Finally, we observed larger seasonal home ranges among males than females. This could stem from sexual dimorphisms, as larger males, due to their greater energy needs and nutritional demands, are expected to have higher spatial requirements than females (Mysterud et al. 2001; Kamler et al. 2003; Ofstad et al. 2016). The larger home range sizes of males can also be linked to the contrasting dispersal of preferred forage patches, because both sexes utilize slightly different habitats within their home ranges (Nikula et al. 2004). Nevertheless, other factors such as mobility, rearing of the young or predator avoidance can additionally contribute to sex-specific differences in home range size (Cederlund and Sand 1994; Dussault et al. 2005).
Our results are likely to show the differences in the stability of seasonal home ranges and indicate the linkage between two different scales of movement behaviours among moose. We have explained the movement patterns we observed in terms of spatio-temporal variation in resource distribution and ability of resources to regenerate. Future research, however, should be directed at measuring variables that would accurately index forage abundance and distribution at meaningful spatio-temporal scales and link movements at these scales with animal fitness components. This can be a very challenging task, because animals can respond to environmental variation at a very fine scale and available metrics may prove too coarse to efficiently track these changes (Couriot et al. 2018). Interestingly, we have also demonstrated a high intra-individual variation of space use patterns in moose inhabiting the same landscapes, which may indicate that beyond environmental factors, individual personality can be involved in movement tactics and foraging decisions (Borowik et al. 2020b; Ranc et al. 2020). Despite increasing research on animal personality (Dingemanse et al. 2012), ungulates’ individual-level choices of movement strategies are still poorly studied and need further exploration (Found and Clair 2019). Finally, given the significant link between annual and seasonal scales of animal movements, any environmental change (e.g. climate change, habitat destruction; Wilcove and Wikelski 2008) affecting an animal’s annual movement strategy could alter its within-season space use and presumably individual fitness.
Data availability
The data set used and/or analysed during the current study are available in Open Forest Data repository (https://doi.org/10.48370/OFD/T463HH).
Code availability
Not applicable.
References
Arnemo JM, Kreeger TJ, Soverti T (2003) Chemical immobilization of free-ranging moose. Alces 39:243–253
Barraquand F, Benhamou S (2008) Animal movements in heterogeneous landscapes: identifying profitable places and homogeneous movement bouts. Ecology 89:3336–3348
Baskin L, Danell K (2003) Ecology of ungulates: a handbook of species in Eastern Europe and Northern and Central Asia. Springer Verlag, Berlin
Bates D, Maechler M, Bolker B, Walker S (2015) Fitting linear mix effects models using lme4. J Stat Softw 67:1–48
Benhamou S (2014) Of scales and stationarity in animal movements. Ecol Lett 17:261–272
Börger L, Dalziel BD, Fryxell JM (2008) Are there general mechanisms of animal home range behaviour? A review and prospects for future research. Ecol Lett 11:637–650
Borkowska A, Konopko A (1994) Moose browsing on pine and willow in the Biebrza Valley, Poland. Acta Theriol 39:73–82
Borowik T, Cornulier T, Jędrzejewska B (2013) Environmental factors shaping ungulate abundances in Poland. Acta Theriol 58:403–413
Borowik T, Ratkiewicz M, Maślanko W, Duda N, Rode P, Kowalczyk R (2018) Living on the edge: predicted impact of renewed hunting on moose in national parks in Poland. Basic and Appl Ecol 30:87–95
Borowik T, Ratkiewicz M, Maślanko W, Duda N, Kowalczyk R (2020a) Too hot to handle: summer space use shift in a cold-adapted ungulate at the edge of its range. Landscape Ecol 35:1341–1351
Borowik T, Ratkiewicz M, Maślanko W, Duda N, Kowalczyk R (2020) The level of habitat patchiness influences movement strategy of moose in Eastern Poland. PLoS ONE 15:e0230521
Bracis C, Gurarie E, van Moorter B, Goodwin RA (2015) Memory effects on movement behavior in animal foraging. PLoS ONE 10:e0136057
Bunnefeld N, Börger L, van Moorter B, Rolandsen CM, Dettki H, Solberg EJ, Ericsson G (2011) A model-driven approach to quantify migration patterns: individual, regional and yearly differences. J Anim Ecol 80:466–476
Burnham KP, Anderson DR (2002) Model selection and multi-model inference. Springer Verlag, Berlin, A practical information-theoretic approach
Cagnacci F, Focardi S, Ghisla A et al (2016) How many routes lead to migration? Comparison of methods to assess and characterise migratory movements. J Anim Ecol 85:54–68
Calabrese JM, Fleming CH, Gurarie, (2016) ctmm: an r package for analyzing animal relocation data as a continuous-time stochastic process. Methods Ecol Evol 7:1124–1132
Cederlund G, Sand H (1994) Home-range size in relation to age and sex in moose. J Mammal 75:1005–1012
Chapman BB, Brönmark C, Nilsson JÅ, Hansson LA (2011) The ecology and evolution of partial migration. Oikos 120:1764–1775
Charnov EL (1976) Optimal foraging, the marginal value theorem. Theor Popul Biol 9:129–136
Core Team (2020) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria, http://www.R-project.org. Accessed 04 10 2020
Couriot O, Hewison AJM, Saïd S et al (2018) Truly sedentary? The multi-range tactic as a response to resource heterogeneity and unpredictability in a large herbivore. Oecologia 187:47–60
Czernik M, Świsłocka M, Duda N, Czajkowska M, Ratkiewicz M (2013) Fast and efficient DNA-based method for winter diet analysis from stools of three cervids: moose, red deer and roe deer. Acta Theriol 58:379–386
Dingemanse NJ, Dochtermann NA, Nakagawa S (2012) Defining behavioural syndromes and the role of ‘syndrome deviation’ in understanding their evolution. Behav Ecol Sociobiol 66:1543–1548
Dussault C, Courtois R, Ouellet JP, Girard I (2005) Space use of moose in relation to food availability. Can J Zool 83:1431–1437
Fleming CH, Fagan WF, Mueller T, Olson KA, Leimgruber P, Calabrese JM (2015) Rigorous home range estimation with movement data: a new autocorrelated kernel density estimator. Ecology 96:1182–1188
Forrester TD, Casady DS, Wittmer HU (2015) Home sweet home: fitness consequences of site familiarity in female black-tailed deer. Behav Ecol Sociobiol 69:603–612
Found R, St Clair CC (2019) Influence of personality on ungulate migration and management. Front Ecol Evol 7:438
Fryxell JM, Sinclair ARE (1988) Causes and consequences of migration by large herbivores. Trends Ecol Evol 3:237–241
Fryxell JM, Hazell M, Börger L, Dalziel BD, Haydon DT, Morales JM, McIntosh T, Rosatte RC (2008) Multiple movement modes by large herbivores at multiple spatiotemporal scales. P Natl Acad Sci USA 105:19114–19119
Gaylard A, Owen-Smith N, Redfern J (2003) Surface water availability: implications for heterogeneity and ecosystem processes. In: du Toit JT, Rogers KH, Biggs HC (eds) The Kruger experience: ecology and management of savanna heterogeneity. Island Press, Washington DC, pp 171–188
Haidt A, Kamiński T, Borowik T, Kowalczyk R (2018) Human and the beast – flight and aggressive responses of European bison to human disturbance. PLoS ONE 13:e0200635
Jędrzejewski W, Niedziałkowska M, Hayward MW et al (2012) Prey choice and diet of wolves related to ungulate communities and wolf subpopulations in Poland. J Mammal 93:1480–1492
Johnson CJ, Parker KL, Heard DC, Gillingham MP (2002) Movement parameters of ungulates and scale-specific responses to the environment. J Anim Ecol 71:225–235
Kamler JF, Jędrzejewski W, Jędrzejewska B (2008) Home ranges of red deer in European old-growth forest. Am Midl Nat 159:75–82
Kilpeläinen A, Peltola H, Rouvinen I, Kellomäki S (2006) Dynamics of daily height growth in Scots pine trees at elevated temperature and CO2. Trees 20:16–27
Kuijper DPJ, Devriendt K, Borman M, Van Diggelen R (2016) Do moose redistribute nutrients in low-productive fen systems? Agr Ecosyst Environ 234:40–47
Laver PN, Kelly MJ (2008) A critical review of home range studies. J Wildlife Manage 72:290–298
Mäkinen H, Jyske T, Nöjd P (2018) Dynamics of diameter and height increment of Norway spruce and Scots pine in southern Finland. Ann Forest Sci 75:28
McNab BK (1963) Bioenergetics and determination of home range size. Am Nat 894:133–140
Mitchell WA, Lima SL (2002) Predator-prey shell games: large-scale movement and its implications for decision-making by prey. Oikos 99:249–259
Mueller T, Fagan WF (2008) Search and navigation in dynamic environments - from individual behaviors to population distributions. Oikos 117:654–664
Mueller T, Olson KA, Dressler G, Leimgruber P, Fuller TK, Nicolson C, Navaro AJ, Bolgeri MJ, Wattles D, DeStefano S (2011) How landscape dynamics link individual to population-level movement patterns: a multispecies comparison of ungulate relocation data. Global Ecol Biogeogr 20:683–694
Mysterud A (1999) Seasonal migration pattern and home range of roe deer (Capreolus capreolus) in an altitudinal gradient in southern Norway. J Zool 247:479–486
Mysterud A, Pérez-Barbería FJ, Gordon IJ (2001) The effect of season, sex and feeding style on home range area versus body mass scaling in temperate ruminants. Oecologia 127:30–39
Naidoo R, Du Preez P, Stuart-Hill G, Jago M, Wegmann M (2012) Home on the range: factors explaining partial migration of African buffalo in a tropical environment. PLoS ONE 7:e36527
Nathan R, Getz WM, Revilla E, Holyoak M, Kadmon R, Saltz D, Smouse PE (2008) A movement ecology paradigm for unifying organismal movement research. P Natl Acad Sci USA 105:19052–19059
Nikula A, Heikkinen S, Helle E (2004) Habitat selection of adult moose Alces alces at two spatial scales in central Finland. Wildlife Biol 10:121–135
Noonan MJ, Tucker MA, Fleming CH et al (2019) A comprehensive analysis of autocorrelation and bias in home range estimation. Ecol Monogr 89:e01344
Noonberg EG, Newman LA, Lewis M, Crabtree RL, Potapov AB (2007) Sequential decision making in a variable environment: modeling elk movement in Yellowstone National Park as a dynamic game. Theor Popul Biol 71:182–195
Ofstad EG, Herfindal I, Solberg EJ, Sæther BE (2016) Home ranges, habitat and body mass: simple correlates of home range size in ungulates. Proc R Soc B 283:20161234
Owen-Smith N, Fryxell JM, Merrill EH (2010) Foraging theory upscaled: the behavioural ecology of herbivore movement. Phil Trans R Soc B 365:2267–2278
Peters W, Hebblewhite M, Mysterud A et al (2017) Migration in geographic and ecological space by a large herbivore. Ecol Monogr 87:297–320
Preisler HK, Wisdom MJ (2006) Statistical methods for analysing responses of wildlife to human disturbance. J Appl Ecol 43:164–172
Raczyński J, Ratkiewicz M (2011) The functioning of the moose population in Poland. Ann Warsaw Univ Life Sci – SGGW. Anim Sci 50:51–56
Ranc N, Moorcroft PR, Hansen KW, Ossi F, Sforna T, Ferraro E, Brugnoli A, Cagnacci F (2020) Preference and familiarity mediate spatial responses of a large herbivore to experimental manipulation of resource availability. Sci Rep 10:11946
Relyea RA, Lawrence RK, Demarias S (2000) Home range of desert mule deer: testing the body size and habitat productivity hypotheses. J Wildlife Manage 64:146–153
Schwartz CC, Franzmann AW, McCabe RE (2007) Ecology and management of the North American moose, 2nd edn. University Press of Colorado, Boulder
Singh NJ, Börger L, Dettki H, Bunnefeld N, Ericsson G (2012) From migration to nomadism: movement variability in a northern ungulate across its latitudinal range. Ecol Appl 22:2007–2020
Spitz DB, Hebblewhite M, Stephenson TR (2017) “MigrateR”: extending model-driven methods for classifying and quantifying animal movement behavior. Ecography 40:788–799
Tufto J, Andersen R, Linnell J (1996) Habitat use and ecological correlates of home-range size in a small cervid: the roe deer. J Anim Ecol 65:715–724
Tuomi J, Nilsson P, Astrom M (1994) Plant compensatory responses: bud dormancy as an adaptation to herbivory. Ecology 75:1429–1436
Turchin P (1988) Quantitative analysis of movement. Sinauer Associates
van Beest FM, Mysterud A, Loe LE, Milner JM (2010) Forage quantity, quality and depletion as scale-dependent mechanisms driving habitat selection of a large browsing herbivore. J Anim Ecol 79:910–922
van Beest FM, Rivrud IM, Loe LE, Milner JM, Mysterud A (2011) What determines variation in home range size across spatiotemporal scales in a large browsing herbivore? J Anim Ecol 80:771–785
van Moorter B, Bunnefeld N, Panzacchi M, Rolandsen CM, Solberg EJ, Sæther BE (2013) Understanding scales of movement: animals ride waves and ripples of environmental change. J Anim Ecol 82:770–780
Wawrzyniak P, Jędrzejewski W, Jędrzejewska B, Borowik T (2010) Ungulates and their management in Poland. In: Apollonio M, Andersen R, Putman R (eds) European ungulates and their management in the 21st century. Cambridge University Press, Cambridge, pp 223–242
Wilcove DS, Wikelski M (2008) Going, going, gone: is animal migration disappearing? PLoS Biol 6:e188
Wood SN (2017) Generalized additive models: an introduction with R, 2nd edn. Chapman and Hall/CRC, Boca Raton, FL
Wood SN (2020) mgcv (R package version 1.8-33), https://CRAN.R-project.org/package=mgcv. Accessed 04 10 2020
Acknowledgements
We are grateful to the authorities of the Biebrza and Polesie National Parks, as well as the Knyszyn, Rajgród, Parczew, Sobibór and Włodawa forest districts and P. Rode (University of Białystok), Tomasz Kamiński and Roman Kozak (Mammal Research Institute PAS) for help in moose immobilisation and collaring. We also would like to thank Michał Żmihorski for his advice in data analyses. We are grateful to prof. Marco Apollonio and second anonymous reviewer whose remarks substantially improved the paper.
Funding
This study was funded by the Polish Ministry of Science and Higher Education of Poland, project no. NN3042809940 (National Science Centre, NCN; Poland) granted to M. Ratkiewicz and under subsidy for maintaining the research potential of the Faculty of Biology, University of Bialystok (for moose in the Biebrza National Park) and the budget of the University of Life Sciences in Lublin (for moose in the Polesie National Park).
Author information
Authors and Affiliations
Contributions
TB, RK and MR formulated the idea. RK, WM, ND and MR conducted fieldwork. WM, ND and MR collected data. TB developed methodology, made statistical analyses and wrote the manuscript with assistance from MR and RK.
Corresponding author
Ethics declarations
Ethics approval
Ethics approval for this study was waived by the State Ethics Committee for Animal Experimentation in Białystok and Lublin, reference numbers: Białystok—10/2010, 57/2011; Lublin—15/2011, 2/2013, 92/2015. All applicable international, national, and/or institutional guidelines for the use of animals were followed.
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Conflict of interest
The authors declare no competing interests.
Additional information
Communicated by K. Eva Ruckstuhl
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Borowik, T., Kowalczyk, R., Maślanko, W. et al. Annual movement strategy predicts within-season space use by moose. Behav Ecol Sociobiol 75, 119 (2021). https://doi.org/10.1007/s00265-021-03059-4
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00265-021-03059-4