Abstract
In mammals, when females are clumped in space, male access to receptive females is usually determined by a dominance hierarchy based on fighting ability. In polygynandrous primates, as opposed to most mammalian species, the strength of the relationship between male social status and reproductive success varies greatly. It has been proposed that the degree to which paternity is determined by male rank decreases with increasing female reproductive synchrony. The priority-of-access model (PoA) predicts male reproductive success based on female synchrony and male dominance rank. To date, most tests of the PoA using paternity data involved nonseasonally breeding species. Here, we examine whether the PoA explains the relatively low reproductive skew in relation to dominance rank reported in the rhesus macaque, a strictly seasonal species. We collected behavioral, genetic, and hormonal data on one group of the free-ranging population on Cayo Santiago (Puerto Rico) for 2 years. The PoA correctly predicted the steepness of male reproductive skew, but not its relationship to male dominance: the most successful sire, fathering one third of the infants, was high but not top ranking. In contrast, mating success was not significantly skewed, suggesting that other mechanisms than social status contributed to male reproductive success. Dominance may be less important for paternity in rhesus macaques than in other primate species because it is reached through queuing rather than contest, leading to alpha males not necessarily being the strongest or most attractive male. More work is needed to fully elucidate the mechanisms determining paternity in rhesus macaques.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In mammals, when sexually receptive females are clumped in space, male access to females is mainly determined by male dominance status (Darwin 1871; Altmann 1962). In most animal species, dominance rank is largely based on fighting abilities, and thus, should give high-ranking males a mating and reproductive advantage over low-ranking ones, both through mechanisms of male–male competition and/or female mate choice for superior males (Clutton-Brock and Harvey 1976; Andersson 1994; Clutton-Brock and McAuliffe 2009). Interestingly, while this scenario seems to apply for the majority of mammals (Dewsbury 1982; Ellis 1995), primates deviate from this general pattern by showing an unusually high degree of variability in male reproductive skew (e.g., van Noordwijk and van Schaik 2004).
In many primate species living in multimale–multifemale groups, the reproductive advantage of the alpha male is pronounced (e.g., savannah baboons, Papio cynocephalus, Alberts et al. 2003, 2006; mandrills, Mandrillus sphinx, Setchell et al. 2005; long-tailed macaques, Macaca fascicularis, Engelhardt et al. 2006). In a considerable number of primate species, however, the link between dominance rank and male reproductive success is weak or even absent (reviewed in Cowlishaw and Dunbar 1991; Ellis 1995; Rodriguez-Llanes et al. 2009). Across the primate order, this leads to levels of alpha male paternity ranging from 100% to 0% (e.g., van Noordwijk and van Schaik 2004; Kutsukake and Nunn 2006). The causes of this extreme variation in male reproductive skew and the reasons why alpha males sometimes fail to gain high reproductive success are still poorly understood, emphasizing the need for more empirical data on the proximate mechanisms underlying paternity outcome in primate males.
Comparative studies and meta-analyses have shown that one of the main factors influencing the relationship between male dominance rank and reproductive success is the number of females per group simultaneously undergoing ovarian activity (hereafter, female synchrony) (Paul 1997, 2004; Kutsukake and Nunn 2006; Ostner et al. 2008). Indeed, when several females are simultaneously sexually receptive (i.e., mating), alpha males are not able to mate guard all of them and thus, low-ranking males get the opportunity to mate and reproduce as well (Emlen and Oring 1977). The degree of female synchrony in a group depends on the number of females per group and on the species' degree of breeding seasonality (Paul 1997, 2004; Kutsukake and Nunn 2006; Ostner et al. 2008).
The priority-of-access model (hereafter, PoA model) (Altmann 1962) is commonly used to quantify the influence of degree of female synchrony on male reproductive skew in primates (cf. Kutsukake and Nunn 2006), although it has been also been tested in, to our knowledge, two other mammalian species (e.g., reindeers, Rangifer tarandus, Hirotani 1994; spotted hyenas, Crocuta crocuta, Engh et al. 2002). This model predicts that each group male can only monopolize access to one female at a time so that the rank of the lowest ranking male able to mate with a female on a given day is equal to the number of females simultaneously receptive. Since the model assumes that access to females directly translates into male reproductive success, it makes predictions about male reproductive success in a given group based on their rank and on the number of females simultaneously sexually receptive. To date, however, the predictions of the PoA model concerning the distribution of paternity have only been thoroughly tested in a few species, and mainly in non-strictly seasonally breeding ones (savannah baboons, Hausfater 1975; Alberts et al. 2003, 2006; chacma baboons, Papio ursinus, Weingrill et al. 2003; mandrills, Setchell et al. 2005; chimpanzees, Pan troglodytes, Boesch et al. 2006; Wroblewski et al. 2009). These studies showed a significant positive association between predicted and actual reproductive success, overall supporting the model's predictions. However, the reproductive success of the highest ranking males was slightly overestimated by the model, suggesting that other factors then the degree of female synchrony may be at play in preventing the alpha male to monopolize all the fertilizations predicted.
One possible explanation for the overestimation of the alpha males' success could be that high-ranking males are more limited in time and energy needed for mate guarding than acknowledged by the PoA model (Alberts et al. 2006; Boesch et al. 2006; Engelhardt et al. 2006; reviewed in Port and Kappeler 2010; see also Engelhardt et al. 2006). If this is true, the discrepancy between the predicted and the actual observed reproductive success of high-ranking males should be even more pronounced in strictly seasonally breeding species in which the degree of female synchrony is high. Therefore, these primate species are the ideal model to test the validity of the PoA model.
To date, studies testing the PoA model in strictly seasonally breeding primates are still scarce and those that have been carried out so far only used indirect measures of (1) reproductive success (e.g., mating success instead of genetic paternity data) and of (2) female reproductive stage (e.g., female mating activity instead of hormonal data to determine timing of the female fertile phase) (rhesus macaques, Macaca mulatta, Chapais 1983; Japanese macaques, Macaca fuscata, Hayakawa 2007; Barbary macaques, Macaca sylvanus, Bissonnette et al. 2011). In these studies, it was again shown that the PoA model overall correctly predicts male access to females at the behavioral level, but overestimates access by the highest ranking males and underestimates that of low-ranking ones (Chapais 1983; Bissonnette et al. 2011). However, since male mating success might be a poor predictor of reproductive success in primates (Ellis 1995; Soltis 2004; e.g., Brauch et al. 2007), studies using genetic paternity data are needed to fully test the PoA model in seasonal breeders.
In the present study, we investigated whether and to what extent the degree of female synchrony influences the relationship between dominance and reproductive success in male rhesus macaques using genetic paternity assignment and assessing female cycle synchrony through measurements of (1) female behavioral receptivity and (2) female sex hormones. The rhesus macaque is an ideal model for this study because it is strictly seasonal in its reproduction and characterized by the formation of large groups containing several adult females (Lindburg 1983; Seth and Seth 1986; Southwick et al. 1996; Hoffman et al. 2008). Furthermore, it is known for its relatively low correlation between male dominance rank and male reproductive success based on paternity data (Berard et al. 1993; Smith 1994; Bercovitch and Nürnberg 1997; Widdig et al. 2004). In our study, we used a three-pronged approach. First, we determined female synchrony and calculated male mating/reproductive success as predicted by the PoA model (predicted success). We then tested the accuracy of the PoA model by comparing predicted success to (1) observed mating access (mating success) and (2) genetically determined paternity outcome (reproductive success). The study was carried out over two consecutive years on one group of the free-ranging population of Cayo Santiago, Puerto Rico. Here, we tested the accuracy of the PoA model for a seasonally breeding primate species combining behavioral observations with genetic and hormonal data.
Method
Study site and subjects
The study was conducted during two consecutive mating seasons (end of March to mid-September), 2006 and 2007, on one of the six social troops (group V) of the free-ranging population of rhesus macaques living on Cayo Santiago (associated with the Caribbean Primate Research Center, CPRC), a 16-ha island off the coast of Puerto Rico (see Rawlins and Kessler 1986 for details on population). The study group was composed of 21–23 adult parous females (6–24 years old), four to nine subadult nulliparous females (3–5 years old), 17–25 adult males (≥4 years old), and 39–41 immature individuals across years, which falls in the range of group size and sex ratio encountered in natural habitat in this species (reviewed in Fooden 2000; Ménard 2004). All parous females but two reproduced during the study period. None of the subadult nulliparous females reproduced in 2006, while four out of nine did in 2007. Behavioral and hormonal data were collected only on adult parous females. During the study, parous females gave birth to 31 infants (17 in 2006, 14 in 2007), but 3 died in their first few days of life (1 in 2006, 2 in 2007), before they could be sampled for genetic paternity analysis (see below). Consequently, the analyses presented here concern 28 conceptive cycles of 19 females (16 for 2006, 12 for 2007).
Behavioral data collection and definitions
Behavioral data were collected by CD and three field assistants from 0700 to 1430 hours (opening hours of the site), 5–6 days a week, for a total of 1,045 contact hours with the group (498 h in 2006, 547 h in 2007). During the peak of the mating season, four to six people monitored sexual activity in the group every day. All parous females showed a cyclic pattern of sexual receptivity during the mating season, even those who did not conceive, and some went through a period of sexual activity during pregnancy. All occurrence of mating activity (mount, mount series, ejaculations), presence of sperm plugs in the female vagina, and instances of male–female proximity were recorded (Altmann 1974; Martin and Bateson 1986). In addition, 30-min focal continuous sampling was collected on receptive females every 1–3 days. Male–male agonistic interactions (fear grin, stare, displacement, spontaneous retreat, rush towards, run away, chase, stare, avoid, bites) were noted ad libitum throughout the study (2006–2007) and during all-day continuous sampling on males between August and September 2006 in order to determine the male dominance hierarchy (see below) (Altmann 1974; Martin and Bateson 1986).
A female was considered receptive if she was seen engaged in mating activity (mating series, ejaculatory mounts) or with a sperm plug in her vagina (Dixson 1998). The period of sexual receptivity (hereafter receptive period) should not be confused with the more precise period of fertility (fertile phase, see definition below). Sexual receptivity follows a cyclic pattern and each receptive period were defined as a continuous period of mating activity surrounded by periods lacking mating activity, although 1–2 days lacking observed mating activity was included into the receptive period when mating continued afterwards. Only mounts with penetration and pelvic thrusts were considered as mating. Since rhesus macaques are multiple mounters, two observed mounts were considered part of the same mount series if they took place ≤30 min apart from each other, unless an ejaculation pause or a new sperm plug was observed (based on mating series lasting 1–56 min; Manson 1996). Mere presence of a sperm plug was not used as an indicator that mating took place with a specific male if the mating itself was not observed.
Male dominance hierarchy
Rhesus males' dominance relationships are rather stable over time, with new immigrants entering the group at the bottom of the hierarchy and queuing for dominance with rare direct dyadic aggression (Bercovitch 1992b; Berard 1999). A total of 483 male–male agonistic interactions were collected (280 in 2006, 203 in 2007). All adult and subadult males who synchronized their movements with group V at some point during the 2-year study period were considered as members of the group (30 in 2006, 27 in 2007, leading to a total of 37 different males), even those who did not regularly interact with other group members. However, agonistic data were available only for the males who resided in the group for ≥40 consecutive days. As a result, 20 males were included in the hierarchy each year, leading to a total of 27 different males across years. Since rhesus males of Cayo Santiago can start reproducing at 3.8 years old (Bercovitch et al. 2003), only the three subadult males (3–5 years old; Bercovitch et al. 2003) who engaged in agonistic conflicts with adult males and formed consorts with parous females were included in the hierarchy (see McMillan 1989; Bercovitch 1992a). This includes two natal males. No adult natal males resided in the group during the study.
The dominance hierarchy was established in two steps. First, we established the dominance order of core males of the group, i.e., the 19 resident males who were already in the group at the beginning of the study and/or those who resided in the group during both mating seasons (including the two natal males), using all the dyadic agonistic interactions involving two of those males collected in the 2 years (average number of interactions per male, 44.8; range 20–82). Next, to include the immigrant males who resided in the group only in one of the two mating seasons (five in 2006, eight in 2007), we established two dominance orders separately for each mating season, using all the data available for the 2 years involving males who resided in the group during the same mating season (2006: average number of interactions per male 43.1, range 11–84; 2007: average 30.7, range 3–73). Two resident males of the group left between the two mating seasons and came back during the second one. Those males were considered as core males only for the first mating season and as new immigrant males for the second year because our observation revealed that they had to queue for rank again (C. Dubuc, personal observation).
We used the program SOCPROG 2.4 (http://myweb.dal.ca/hwhitehe/social.htm) to generate the rank order and to calculate the Landau index of linearity (Whitehead 2009a, b). In order to account for unknown relationships for some dyads, we used the de Vries' “I&SI” method minimizing inconsistencies and corrected Landau index, h′ (de Vries 1995, 1998; Whitehead 2009a, b). A linear hierarchical order was generated for the core males (h′ = 0.457, p < 0.001), as well as for all males in each of the mating seasons (2006, h′ = 0.383, p < 0.001; 2007, h′ = 0.381, p = 0.012). Males were divided into three categories: high-ranking (ranks 1–6), middle-ranking (ranks 7–12), and low-ranking males (ranks 13–20). In both years, high- and middle-ranking positions were occupied by core males (2006, ranks 1–17; 2007, ranks 1–12), while low-ranking positions were mostly occupied by new immigrant males, most of which were peripheral to the group. Both subadult natal males occupied high-ranking positions: the first occupied rank 4 in 2006 and ranks 1–2 in 2007 (see below) and the other, the rank 6, in 2007.
The alpha male of the group had occupied his position already for at least 2 years at the beginning of the study (i.e., since 2004; Gerald et al. unpublished data). Towards the end of the 2007 mating season, however, he was outranked by the male occupying the beta position that year, a subadult natal male, during a decisive interaction witnessed by CD (see also Brent et al. 2011). The new rank order between these two males was stable over time and maintained the following mating season (Maria Rahkovskaya, personal communication). Because two females conceived after the overthrow, measures of success (reproductive and mating success) in 2007 were calculated according to the respective dominance rank held by these males during times of conception.
Determination of paternity
Genetic paternity analysis was carried out by LM using the genotypic data previously available (methods detailed in Nürnberg et al. 1998), in addition to newly generated data for group V individuals. Biological samples (hair, blood, and tissue samples) were collected during the annual trapping season (mid-January to mid-March) 2007–2009 for all infants born during the study period and still alive during trapping. Because a genetic database for the rhesus macaque population of Cayo Santiago was implemented in 1992 and was continuously updated thereafter, we only sampled mothers and potential sires (see definition below) for which DNA was lacking or insufficient beforehand.
Genomic DNA was extracted using the DNEasy Blood & Tissue Kit (Qiagen Inc., Valencia, CA, USA) and amplified at 12–15 autosomal microsatellite loci (mean ± SD = 13.5 ± 1.5). These included 13 of the 19 loci previously used in the existing genetic database and two loci newly incorporated in order to improve the power of analyses (Muniz and Widdig, unpublished data). All loci were in Hardy–Weinberg equilibrium and had a mean ± SD of 8.27 ± 3.24 alleles. The mean observed heterozygosity across loci was 0.74 ± 0.06 (Cervus 3.0; Kalinowski et al. 2007). Maternity derived from long-term field observations was first confirmed using genotypic data for all group V mother–infant pairs and this information was subsequently used in paternity analyses. Males considered as potential sires were all males in the entire population older than 1,250 days of age (based on youngest age at reproduction; Bercovitch et al. 2003) and present on the island at least 200 days before the actual birth of a given infant (based on mean ± SD gestation length of 166.5 ± 7.4; Silk et al. 1993).
Paternity was determined for all 28 infants with an available sample using a combination of exclusion and likelihood analyses as follows. All paternity assignment was supported at the 95% confidence level by the maximum likelihood method calculated by CERVUS 3.0 (Kalinowski et al. 2007). In 24 cases, all males were excluded on at least two loci, with the exception of the assigned sire, who matched the offspring–mother pair at all loci. In three other cases, a sire was assigned with zero mismatches with the offspring, but one or more candidate sires could only be excluded at one locus. For the remaining case, only one male of the island had a single genetic mismatch with the offspring. We are nevertheless convinced that the assigned sire is the actual father of this infant because (1) more than 98% of potential sires in the population, including all potential sires in group V, have been included in the analysis, greatly decreasing the chances of misassignment due to unsampled sires, and (2) all other sampled potential sires were excluded at three or more loci. A potential explanation for the mismatch could be a “null” allele (Callen et al. 1993) due to mutation, given that the mother, the offspring, and the sire were homozygous at the mismatching locus. All genotyped infants were sired by group V members.
Calculation of predicted success
Calculation of predicted success (mating and reproductive success) based on female synchrony was restricted to the conceptive cycles. In this respect, all receptive periods of parous females were used in analyses, including those taking place after conception. Since nulliparous females receive little attention from adult males (C. Dubuc, personal observation; see also Dixson 1998; Setchell and Wickings 2006), they were not included in this analysis.
The PoA model predicts that the rank of the lowest ranking male who can have access to a female is equal to the number of females simultaneously receptive (i.e., sexually active) on a given day (rank 1, alpha male). Because we used the entire receptive period instead of the fertile phase, we avoided overestimating female synchrony by calculating overall female synchrony during receptive periods of the mating season rather than considering specific numbers of females receptive on given days. Hence, for each conceptive cycle, we calculated the average daily number of receptive parous females and rounded this value to the closest integer. For each conceptive cycle, all males whose rank was equal or lower than this value were being attributed a probability of access to the female; the probability was set at one divided by the average daily number of receptive parous females. For example, for an average degree of female synchrony of five during the conceptive cycle of a given female, a probability of access to the female of 1/5 was attributed to all males ranked 1–5 and a probability of 0 to all other males. The predicted success of each male was calculated as the sum of the probability of access to the female for all studied conceptive cycles (e.g., Chapais 1983; Wroblewski et al. 2009; Bissonnette et al. 2011). Predicted success is used to describe both predicted mating success and predicted reproductive success, as the PoA model assumes that mating success determines directly reproductive success.
Calculation of male mating success
In order to compare whether males' access to receptive females followed the predictions of the PoA model, we calculated mating success as follows. For all the mating partners a female had during the receptive period of her conceptive cycle, mating success of each mating partner was calculated as the number of mating series a male was involved in divided by the total number of mating series the female was involved in. Overall mating success of each male was calculated as the sum of all mating successes calculated for this male as described above.
Evaluation of male reproductive skew
We used three methods to compare the reproductive skew among group males between the three measures of success (predicted success, mating success, and reproductive success). First, we investigated the relationship between dominance rank and the three measures of success. Second, we calculated the proportion of paternity secured by the alpha male (α-male concentration) for each measure (van Noordwijk and van Schaik 2004; see also Kutsukake and Nunn 2006; Ostner et al. 2008). We followed van Noordwijk and van Schaik (2004), considering paternity concentration to be (1) high if the alpha male sired more than 50% of the infants, (2) middle if the alpha male sired less than 50% but was the most successful sire of the group, and (3) low if the alpha male was not the most successful sire. Third, we calculated the deviation from a random distribution with Nonac's binomial skew index, or B index (Nonacs 2000, 2003), which allowed us to investigate male skew independently of male dominance hierarchy. The B index allows to test whether the skew is significantly different from a random distribution (i.e., B significantly >0). The B index was calculated using the program Skew Calculator 2003 (http://www.eeb.ucla.edu/Faculty/Nonacs/shareware.htm). Where applicable, values were rounded to the nearest integer because the program cannot handle decimals. The advantage of this skew index is that it allows us to consider the number of days males resided in the group during the mating season as well as to combine the two observation years.
Male success in relation to current female synchrony
As an alternative way to investigate whether, as predicted by the PoA model, males other than the alpha should be able to sire an offspring when the degree of female synchrony is high, we tested the association between the average daily number of receptive parous females during each conceptive cycles (see above) and (1) the sire's rank and (2) the average rank of the mating partners females had.
Hormonal data and interpretation
For determination of timing of ovulation and the fertile phase in our study females, we collected fecal samples directly after defecation and discarded those that were contaminated with urine. The fecal boluses were homogenized and placed 0.5–2 g in individual polypropylene tubes. The samples were kept on ice until we returned to the field station at the end of the observation day, where they were stored at −20°C. Samples were shipped on dry ice to the endocrine lab of the German Primate Center where samples were analyzed for progestogen metabolites by CD using a validated enzyme immunoassay (see Dubuc et al. 2009).
Details on the estimation of the timing of the ovulation window can be found in Dubuc et al. (2009). In short, assessment of ovulation time was based on the significant postovulatory rise of progestogen levels. Taking into account the time lag that occurs between ovulation and rise in progesterone levels in the blood as well as between excretion of progesterone into the blood and excretion of its metabolites into the feces, we considered the ovulation window to have occurred on days -2/-3 relative to the defined fecal progestogen rise (day 0). To account for sperm life span in the female tract (Behboodi et al. 1991; Wilcox et al. 1995), we defined a 5-day fertile phase including the ovulation window and the three preceding days. We considered that the fertile phase could be established with enough reliability only if the gap between the progestogen rise and the previous sample comprised 3 days or less (Dubuc et al. 2009). The fertile phase could be established reliably enough for 10 conceptive cycles in nine females, 4 in 2006 and 6 in 2007.
We used the hormonal profiles (i.e., maintenance of high progestogen levels until the end of the mating season) to identify the conceptive cycle for 22 of the 28 conceptive cycles included in this study (11 in 2006, 11 in 2007). For the remaining 6 cycles for which we did not have reliable hormonal data, the conception cycle was identified by backdating from the date of birth (CPRC database) using an average gestation length of 166.5 days (Silk et al. 1993).
Limiting analyses to the fertile phase
In order to take into account the possibility that the method we use may result in overestimations of predicted success and mating success of middle- and low-ranking males because the entire receptive period was considered instead of the fertile phase only, analyses were repeated for the subsample of cycles for which the fertile phase could be established. This time, predicted success was calculated by considering the average degree of female synchrony during the fertile phase and reproductive success was calculated only for the 10 resulting offspring. Mating success was calculated by considering only those males who had access to females during the fertile phase.
Statistical analyses
Generalized linear mixed models (GLMM) fit by Laplace approximation for Poisson distributed data were used to investigate whether the degree of female synchrony influences the relationship between dominance rank and reproductive success in the males. Male ID and year were included as random factors in the model. We also included in the model the number of days males spent in the group per mating season. Assumption for lack of over dispersion was respected for all analyses. GLMMs were performed with the R v. 2.6.0 statistical package for Windows (R Development Core Team 2010) using the library “lme4” (Bates and Maechler 2010), and Spearman correlation tests were conducted in PAWS 18.0 (SPSS Inc.). The level of significance was set at p < 0.05 for all statistical tests.
Results
Female synchrony and number of mating partners
In both study years, mating was observed from the end of March to mid-September. During this period, an average of 66.5 receptive periods (2006, 61; 2007, 72) were observed in 22–23 females, including an average of 8.5 postconception receptive periods (2006, 7; 2007, 10). On average, 4.0 females (2006, mean ± SD, 4.9 ± 2.5; 2007, 3.4 ± 2.3) were simultaneously receptive on a given day during the conception cycle, with a maximal number of 10 females. During their conceptive cycles, females had on average 3.2 ± 1.5 observed mating partners, including 2.5 ± 1.2 during their fertile phase.
Predicted skew
Based on female synchrony on our data set, the PoA model predicted an intermediate level of mating and reproductive skew in the studied group (Table 1). Specifically, male success (mating or reproductive success) was predicted to be significantly skewed (B = 0.0545, p = 0.002), the association between dominance rank and success was predicted to be strong (Z = −5.053, N = 40, p < 0.001), and the alpha male was predicted to be the most successful sire, fathering a fourth of all infants (2006, 26.3%; 2007, 26.3%). Male success was predicted to be almost limited to high-ranking males (2006, 97.5%; 2007, 100%; Fig. 1a).
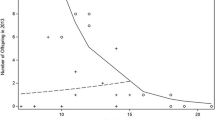
Comparison of the predictions of the PoA model (predicted RS) with males' reproductive success (RS, i.e., number of infants sired) and mating success (MS, proportion of access to females). a Comparison of the three measures in relation to male dominance rank for the entire data set (N = 28 cycles). b Comparison of the three measures if only the fertile phase of the conceptive cycles are considered (N = 10 cycles). Only offspring of parous females are included (males ranked 8, 9, and 10 each fertilized one nulliparous female in 2007). Every data point is the average measure between the two males who occupied the given rank position each year. Data are presented as mean + SEM in order to illustrate the highest value obtained per rank
Mating skew
There was a significant positive association between dominance rank and observed mating success (Z = −3.785, N = 40, p < 0.001; Table 1). However, in contrast to what would have been expected in case of an intermediate skew in favor of the alpha male, he was not the most successful male with regard to mating (Fig. 1a). Additionally, mating skew was low among males, with the distribution of mating not being significantly different from random (B = 0.0017, p = 0.528), showing that many males were able to mate with females. Mating success was nevertheless highest among high-ranking and some middle-ranking males (ranks 1–10; Fig. 1a). A similar mating pattern emerged when only male access to females during the fertile phase was considered (Fig. 1b). Predicted success was significantly positively associated with mating success (Z = 3.507, N = 40, p < 0.001).
Reproductive skew
Out of the 20 males present in the group, only 8 produced offspring. Altogether male reproductive skew was intermediate (B = 0.0837, p = 0.005) with one male in both years siring one third of infants (2006, 31.5%; 41.7%) and 75% of infants being sired by four males only (Fig. 2). Mating success was significantly positively associated with reproductive success (Z = 3.673, N = 40, p < 0.001; Fig. 1a).
Reproductive success was also significantly associated with dominance rank (Z = −2.772, N = 40, p = 0.006), with number of infants sired increasing as male rank increases. However, when years were considered separately, there was a significant association in 2006 (Spearman rank test; r s = −0.596, N = 20, p = 0.006), but not in 2007 (r s = −0.214, N = 20, p = 0.365). Although high-ranking males sired most of the offspring (2006, 68.8%; 2007, 50%; Fig. 1a), contrary to the prediction of the PoA model, the alpha male was not the most successful sire, fathering only a low proportion of infants (mean 6.25%; Table 1, Fig. 1a). Nevertheless, the most successful male, siring a third of all infants, was a high-ranking male in both years (rank 3 in both years; different IDs). Also in contrast to the predicted skew, middle-ranking males obtained an important share of paternity (2006, 25%; 2007, 41.7%). In fact, some middle-ranking males obtained a share similar to or even higher than that of the alpha male. Finally, and in each year, one low-ranking male (rank 18 and 20) reproduced (2006, 6.25%; 2007, 8.33%), including a new immigrant. A similar pattern of male reproductive success emerges if only fertile phases are considered (Fig. 1b).
Thus, the PoA model did not precisely predict male reproductive success in our study group, as it overestimated success of high-ranking males, specifically that of the alpha male, and underestimated success of middle- and low-ranking males. Nevertheless, overall, the predicted success was significantly positively associated with reproductive success (Z = 3.131, N = 40, p = 0.002; Fig. 1a). An even stronger association between predicted and reproductive success was however obtained when data were analyzed independent of dominance rank, i.e., classifying males based on the number of infants sired instead of rank (Z = 6.406, N = 40, p < 0.001; Fig. 2).
Male success in relation to current female synchrony
We did not find any significant relationship between average female synchrony during the conceptive cycle and the sire's rank (Z = −1.184, N = 28, p = 0.236; Fig. 3) or the average rank of male sexual partners that the females had (Z = 0.827, N = 28, p = 0.408). High- and middle-ranking males were able to reproduce when female synchrony was above or below the average (see above). Low-ranking males, in contrast, reproduced when female synchrony was around the average. Middle- and low-ranking males thus mated with and fertilized females independently of the respective degree of female synchrony, i.e., even when female synchrony was low.
Discussion
In this study, we tested whether the predictions of the PoA model can explain the distribution of male reproductive success in a seasonally breeding primate species, the rhesus macaque. Our results show that the PoA model is not a good predictor of paternity distribution among group males in this species. Although it predicted the general degree of skew of paternity distribution well, it poorly predicted its relationship with male dominance rank. Therefore, it seems that the application of the PoA model may be limited in seasonally breeding species in regard to paternity distribution.
Several studies have shown that male reproductive skew in relation to dominance rank is low in rhesus macaques (Berard et al. 1993; Smith 1994; Nürnberg et al. 1998; Widdig et al. 2004). Our genetic results are in line with these observations showing (1) that the alpha male was not the most successful sire, (2) that middle- and low-ranking males sired a substantial amount of offspring, and (3) that a significant correlation between dominance rank and reproductive success occurred only in one of the two study years (see also Smith 1994). In contrast to this finding, however, the PoA model based on the degree of female synchrony observed in our study group predicted an intermediate level of reproductive skew in relation to dominance rank among group males (cf. van Noordwijk and van Schaik 2004). In detail, the model predicted a strong correlation between dominance rank and reproductive success, with the alpha male being the most successful sire of the group, fathering a fourth of the infants, and only high-ranking males obtaining a share in paternity. The discrepancy between observed and predicted reproductive skew thus strongly suggests that female reproductive synchrony alone is not sufficient to explain the low reproductive skew in relation to dominance rank observed in rhesus macaques.
One factor that may have led to a reproductive skew in relation to dominance rank lower than predicted may be that mating success of high-ranking males was lower than predicted by the PoA model. In fact, mating access to females was much less steeply correlated to rank than predicted, similar to what has been observed in previous studies carried out on rhesus macaques (Chapais 1983; see also Berard et al. 1993). Therefore, the PoA model not only overestimated reproductive success of high-ranking males in our study, but also their mating access to females, while it underestimated that of middle- and low-ranking males. We found the same discrepancy between observed and predicted mating success even in our subset of cycles in which we focused on the fertile phase only (the restricted period of the female cycle when mating can actually lead to conception), although high-ranking males should concentrate their mating efforts to this period in order to increase reproductive success (see Engelhardt et al. 2006; Heistermann et al. 2008). These observations suggest that high-ranking males were more limited in their ability to monopolize access to receptive females than would have been expected taking only female cycle synchrony into account, even during their fertile phase.
There are different, non-mutually exclusive explanations for the discrepancy between observed and predicted mating success. Firstly, it may be that the PoA model underestimates the importance of female mate choice on males' access to females. In rhesus macaques, females are able to resist mating with consortship partners and to actively solicit low-ranking males more than high-ranking ones (Chapais 1983; Manson 1992, 1997; Bercovitch 1997). More specifically, rhesus females appear to lose attraction towards males with long tenure (Bercovitch 1997; Berard 1999; but see Manson 1995), and to resist mating with related males (Manson and Perry 1993). Since in our group the two males who occupied the alpha position in the two study years were a long-term resident and a natal male, female preference is likely to have played a significant role in mating distribution in our study. The idea that female mate choice may be important for male reproductive success in rhesus macaques is supported by a the fact that males of this species develop a red sexual skin coloration during the mating season, which seems to be regulated by testosterone levels (Baulu 1976; Rhodes et al. 1997) and appears to attract female attention (Waitt et al. 2003), suggesting that male facial color may have evolved under pressures of sexual selection signaling male quality to females. Another possible explanation for why in our study highest ranking males monopolized access to females less often than expected could be that the PoA model overestimated the number of females a male is able to mate guard successively by underestimating the time and energetic demands of mate guarding, as has been suggested for other primates (e.g., savannah baboons, Alberts et al. 2003, 2006; long-tailed macaques, Engelhardt et al. 2006; chimpanzees, Boesch et al. 2006). Mate guarding is considered to entail high costs in terms of reduced feeding time and attention paid to the female (Matsubara 2003; Alberts et al. 2006). Given that the mating season lasts over 6 months in rhesus macaques, energetic condition of males may have limited male ability to monopolize access to females in addition to cycle synchrony. Accordingly, it has been shown that sires lose considerable amount of fat reserve over the mating season in rhesus macaques (Bercovitch and Nürnberg 1996). As a final note, in some species, such as in savannah baboons (e.g., Bercovitch 1992b) and Barbary macaques (e.g., Bissonnette et al. 2011), it has been shown that top-ranking males can lose control over mating because of individual or collective harassment by low-ranking males. No such behavior is observed in rhesus macaques though (C. Dubuc, personal observation; Bercovitch 1992b), and hence, harassment is unlikely to have contributed to the top-ranking males' reduced access to females in our group of rhesus macaques.
Whatever the reasons for the observed reduced mating skew may be in rhesus macaques, the skew itself still does not fully explain the observed pattern of paternity distribution in our study group. Whereas mating success was significantly correlated with dominance rank, reproductive success was not. Furthermore, when the dominance rank was not taken into account, paternity distribution followed an intermediate skew with the most successful sire being high but not top ranking. The fact that male reproductive success is skewed towards high-ranking males others than the alpha male has been shown for another much larger group on Cayo Santiago over several consecutive years (Widdig et al. 2002, 2004), suggesting that this phenomenon is common in this population. Interestingly, these patterns of skew appear to be identical regardless of the number of males in the group. Collectively, these results suggest that more factors than male social status alone play an important role for determining paternity outcome in this species.
A potential reason for the discrepancy between mating and reproductive success may be that at least some paternities were determined on the post-copulatory level. The low degree of female monopolization observed should have allowed sperm of different males to still compete within the female reproductive tract and for paternity to depend on individual sperm quality or quantity, as well as on female cryptic choice (Reeder 2003; Birkhead and Kappeler 2004). Such post-copulatory mechanisms would be even further facilitated if females were not systematically mate guarded during the precise timing of the fertile phase of their conceptive cycles, as suggested by our results. The idea that sperm competition may be important for male reproductive success in rhesus macaques is supported by the fact that rhesus macaque males have large testes in relation to body size (gonadosomatic index) (Bercovitch 1992b; Bercovitch and Rodriguez 1993; Harcourt et al. 1995; Møller et al. 2009) suggesting that they are under selective pressures to invest into sperm production. In such a scenario, top-ranking males of our group may have had a decreased chance of siring offspring since they are not in their prime (i.e., one post-prime male and one subadult male). Indeed, sperm quality (e.g., humans, Sloter et al. 2006), ejaculatory rate (Phoenix and Chambers 1988; McMillan 1989), and testosterone levels (Schwartz and Kemnitz 1992) are all known to be highest at prime age in male primates (see Bercovitch and Harvey 2004).
A phenomenon still unexplained is the reduced capacity of high-ranking males to monopolize receptive females in our group. A potential explanation may that, in rhesus macaques, there is a negative feedback loop between female monopolization potential and the payoff of reaching top rank through contest, which can be described as follows. Whenever the alpha male position may not guarantee a share of paternity large enough to compensate the risks of injuries or expulsion from the group received through direct challenges for reaching this position, male–male contest for dominance can be expected to be reduced (van Noordwijk and van Schaik 2004). In primates, this phenomenon seems to be particularly common in seasonally breeding species forming large groups (van Noordwijk and van Schaik 2004). Whereas in several primate species, males contest for rank, leading to high-ranking males being usually strong young prime males, in rhesus macaques, males mainly reach dominance through succession or queuing (Berard 1999): males slowly increase in rank as the males who dominate them die or leave the group. The hypothesis that male–male contest is of reduced importance in rhesus macaques is not only supported by behavioral observations (reviewed in Bercovitch 1992b; Berard 1999), but also by the fact that sexual dimorphism in body weight and canine size is relatively low compared to other cercopithecine species (Plavcan and van Schaik 1992; Plavcan 2004; Singh and Sinha 2004). Given that dominance is thus not determined by fighting ability but by residency length, the alpha male (1) is most likely to be highly familiar to females, (2) is not necessarily the group's strongest male, and (3) can be outside of his prime (Berard 1999; van Noordwijk and van Schaik 2004). If the top-ranking males are not the strongest, fittest, and most attractive males of the group, their ability to monopolize access to females and to secure fertilization may be limited. Consequently, the strength of the correlation between rank and mating/reproductive success would be even lower than predicted by the PoA model, potentially even further decreasing the benefits for males to contest high-ranking males.
Support of this negative feedback loop also comes from Japanese macaques. In this other seasonally breeding species forming large groups, males also queue for dominance (reviewed in Berard 1999), and dominance is reported to play only a little role in male reproductive success, and in female mate preference (Inoue 1995; Soltis et al. 1997, 1999; reviewed in Takahata et al. 1999; Soltis 2004). Such negative feedback loops most likely apply to non-primate species as well. In spotted hyenas, one of the rare mammal species in which males queue for dominance, the most successful sires were also reported to be high- but not top-ranking males (Engh et al. 2002). In contrast, such a negative feedback loop is not expected to occur in species in which dominance is reached through contest, e.g., nonseasonally breeding species, because high-ranking males should be the group's strongest males (van Noordwijk and van Schaik 2004). In line with this assumption, alpha males in species following this pattern are reported to fertilize more females than predicted based on their access to females (e.g., savannah baboons, Alberts et al. 2003, 2006; long-tailed macaques, van Noordwijk and van Schaik 2001; Engelhardt et al 2006), suggesting that they gained additional advantages over other males (e.g., at the level of female mate choice and sperm competition). Such an increase in paternity concentration may even create a positive feedback loop between the importance of rank for male reproductive success and the value of male contest for rank. Further work will be needed to test this hypothesis and to investigate under which conditions in terms of seasonality and group size we would find the switching point between positive and negative feedback loops in primates and other species living in multimale groups.
In conclusion, our results show that dominance plays a weaker role for male reproductive success in rhesus macaques than predicted by the PoA model. It appears that the model (1) overestimated the highest ranking males' ability to mate guard females and (2) underestimated the importance of female mate choice and male alternative reproductive strategies on paternity distribution. The fact that dominance is not reached through contest in this species is likely to play an important role in this respect because it may lead to alpha males not necessarily being the strongest, fittest, or most attractive male of the group. Further studies looking into the proximate mechanisms leading to male reproductive success in rhesus macaques will be needed to fully understand the pattern of paternity distribution in this species.
References
Alberts SC, Buchan JC, Altmann J (2006) Sexual selection in wild baboons: from mating opportunities to paternity success. Anim Behav 72:1177–1196
Alberts SC, Watts HE, Altmann J (2003) Queuing and queue-jumping: long-term patterns of reproductive skew in male savannah baboons, Papio cynocephalus. Anim Behav 65:821–840
Altmann J (1974) Observational study of behaviour: sampling methods. Behaviour 49:227–267
Altmann SA (1962) A field study of the sociobiology of rhesus monkeys, Macaca mulatta. Ann N Y Acad Sci 102:338–435
Andersson M (1994) Sexual selection. Princeton University Press, Princeton
Bates D, Maechler M (2010) lme4: linear mixed-effects models using S4 classes. R package version 0.999375-34 http://CRAN.R-project.org/package=lme4. Accessed 10 March 2011
Baulu J (1976) Seasonal sex skin coloration and hormonal fluctuations in free-ranging and captive monkeys. Horm Behav 7:481–494
Behboodi E, Katz DF, Samuels SJ, Tell L, Hendrickx AG, Lasley BL (1991) The use of a urinary estrone conjugate assay for detection of optimal mating time in the cynomologus macaque (Macaca fascicularis). J Med Primatol 20:229–234
Berard JD (1999) A four-year study of the association between male dominance rank, residency status, and reproductive activity in rhesus macaques (Macaca mulatta). Primates 40:159–175
Berard JD, Nuernberg P, Epplen JT, Schmidtke J (1993) Male rank, reproductive behavior, and reproductive success in free-ranging rhesus macaques. Primates 34:481–489
Bercovitch F, Harvey NC (2004) Reproductive life history. In: Thierry B, Singh M, Kaumanns W (eds) Macaque societies: a model for the study of social organization. Cambridge University Press, Cambridge, pp 61–79
Bercovitch FB (1992a) Re-examining the relationship between rank and reproduction in male primates. Anim Behav 44:1168–1170
Bercovitch FB (1992b) Sperm competition, reproductive tactics, and paternity in savanna baboons and rhesus macaques. In: Martin RD, Dixson AF, Wickings EJ (eds) Paternity in primates: genetic tests and theories. Karger, Basel, pp 225–237
Bercovitch FB (1997) Reproductive strategies of rhesus macaques. Primates 38:247–263
Bercovitch FB, Nürnberg P (1996) Socioendocrine and morphological correlates of paternity in rhesus macaques (Macaca mulatta). J Reprod Fertil 107:59–68
Bercovitch FB, Nürnberg P (1997) Genetic determination of paternity and variation in male reproductive success in two populations of rhesus macaques. Electrophoresis 18:1701–1705
Bercovitch FB, Rodriguez JF (1993) Testis size, epididymis weight, and sperm competition in rhesus macaques. Am J Primatol 30:163–168
Bercovitch FB, Widdig A, Trefilov A, Kessler MJ, Berard JD, Schmidtke J, Nuernberg P, Krawczak M (2003) A longitudinal study of age-specific reproductive output and body condition among male rhesus macaques, Macaca mulatta. Naturwissenschaften 90:309–312
Birkhead T, Kappeler PM (2004) Post-copulatory sexual selection in birds and primates. In: Kappeler PM, van Schaik CP (eds) Sexual selection in primates: new and comparative perspectives. Cambridge University Press, New York, pp 151–171
Bissonnette A, Bischofberger N, van Schaik C (2011) Mating skew in Barbary macaque males: the role of female mating synchrony, female behavior, and male–male coalitions. Behav Ecol Sociobiol 65:167–182
Boesch C, Kohou G, Nene H, Vigilant L (2006) Male competition and paternity in wild chimpanzees of the Tai forest. Am J Phys Anthropol 130:103–115
Brauch K, Pfefferle D, Hodges K, Möhle U, Fischer J, Heistermann M (2007) Female sexual behavior and sexual swelling size as potential cues for males to discern the female fertile phase in free-ranging Barbary macaques (Macaca sylvanus) of Gibraltar. Horm Behav 52:375–383
Brent LJN, Semple S, Dubuc C, Heistermann M, MacLarnon A (2011) Social capital and physiological stress levels in adult female rhesus macaques. Physiol Behav 102:76–83
Callen DF, Thompson AD, Shen Y, Phillips HA, Richards R, Mulley JC, Sutherland GR (1993) Incidence and origin of “null” alleles in the (AC)n microsatellite markers. Am J Hum Genet 52:922–927
Chapais B (1983) Reproductive activity in relation to male dominance and the likelihood of ovulation in rhesus monkeys. Behav Ecol Sociobiol 12:215–228
Clutton-Brock TH, Harvey PH (1976) Evolutionary rules and primate societies. In: Bateson PPG, Hinde RA (eds) Growing points in ethology. Cambridge University Press, Cambridge, pp 195–237
Clutton-Brock TH, McAuliffe K (2009) Female mate choice in mammals. Q Rev Biol 84:3–27
Cowlishaw G, Dunbar RIM (1991) Dominance rank and mating success in male primates. Anim Behav 41:1045–1056
Darwin C (1871) The descent of man and selection in relation to sex. J. Murray, London
de Vries H (1995) An improved test of linearity in dominance hierarchies containing unknown or tied relationships. Anim Behav 50:1375–1389
de Vries H (1998) Finding a dominance order most consistent with a linear hierarchy: a new procedure and review. Anim Behav 55:827–843
Dewsbury DA (1982) Dominance rank, copulatory behavior, and differential reproduction. Q Rev Biol 57:135–159
Dixson AF (1998) Primate sexuality: comparative studies of the prosimians, monkeys, apes, and human beings. Oxford University Press, Oxford
Dubuc C, Brent LJN, Accamando AK, Gerald MS, MacLarnon A, Semple S, Heistermann M, Engelhardt A (2009) Sexual skin color contains information about the timing of the fertile phase in free-ranging Macaca mulatta. Int J Primatol 30:777–789
Ellis L (1995) Dominance and reproductive success among nonhuman animals: a cross-species comparison. Ethol Sociobiol 16:257–333
Emlen ST, Oring LW (1977) Ecology, sexual selection, and the evolution of mating systems. Science 197:215–223
Engelhardt A, Heistermann M, Hodges JK, Nuernberg P, Niemitz C (2006) Determinants of male reproductive success in wild long-tailed macaques (Macaca fascicularis)—male monopolisation, female mate choice or post-copulatory mechanisms? Behav Ecol Sociobiol 59:740–752
Engh AL, Funk SM, Van Horn RC, Scribner KT, Bruford MW, Libants S, Szykman M, Smale L, Holekampa KE (2002) Reproductive skew among males in a female-dominated mammalian society. Behav Ecol 13:193–200
Fooden J (2000) Systematic review of the rhesus macaque, Macaca mulatta (Zimmermann, 1780). Fieldiana: Zool 96:1–180
Harcourt AH, Purvis A, Liles L (1995) Sperm competition: mating system, not breeding system, affects testes size of primates. Funct Ecol 9:468–476
Hausfater G (1975) Dominance and reproduction in baboons (Papio cynocephalus): quantitative analysis. Contrib Primatol 7:2–150
Hayakawa S (2007) Female defensibility in small troops of Japanese macaques vis-a-vis nontroop males and copulation on the periphery of the troop. Int J Primatol 28:73–96
Heistermann M, Brauch K, Moehle U, Pfefferle D, Dittami J, Hodges K (2008) Female ovarian cycle phase affects the timing of male sexual activity in free-ranging Barbary macaques (Macaca sylvanus) of Gibraltar. Am J Primatol 70:44–53
Hirotani A (1994) Dominance rank, copulatory behaviour and estimated reproductive success in male reindeer. Anim Behav 48:929–936
Hoffman CL, Ruiz-Lambides AV, Davila E, Maldonado E, Gerald MS, Maestripieri D (2008) Sex differences in survival costs of reproduction in a promiscuous primate. Behav Ecol Sociobiol 62:1711–1718
Inoue M (1995) Application of paternity discrimination by DNA polymorphism to the analysis of the social behavior of primates. Hum Evol 10:53–62
Kalinowski ST, Taper ML, Marshall TC (2007) Revising how the computer program CERVUS accommodates genotyping error increases success in paternity assignment. Mol Ecol 16:1099–1106
Kutsukake N, Nunn CL (2006) Comparative tests of reproductive skew in male primates: the roles of demographic factors and incomplete control. Behav Ecol Sociobiol 60:695–706
Lindburg DG (1983) Mating behavior and estrus in the Indian rhesus monkey. In: Seth PK (ed) Perspectives in primate ecology. Today & Tomorrow's Printers and Publishers, New Delhi, pp 45–61
Manson JH (1992) Measuring female mate choice in Cayo Santiago rhesus macaques. Anim Behav 44:405–416
Manson JH (1995) Do female rhesus macaques choose novel males? Am J Primatol 37:285–296
Manson JH (1996) Male dominance and mount series duration in Cayo Santiago rhesus macaques. Anim Behav 51:1219–1231
Manson JH (1997) Primate consortships: a critical review. Curr Anthropol 38:353–374
Manson JH, Perry SE (1993) Inbreeding avoidance in rhesus macaques: whose choice? Am J Phys Anthropol 90:285–288
Martin P, Bateson P (1986) Measuring behaviour: an introductory guide. Cambridge University Press, Cambridge
Matsubara M (2003) Costs of mate guarding and opportunistic mating among wild male Japanese macaques. Int J Primatol 24:1057–1075
McMillan CA (1989) Male age, dominance, and mating success among rhesus macaques. Am J Phys Anthropol 80:83–89
Ménard N (2004) Do ecological factors explain variation in social organization? In: Thierry B, Singh M, Kaumanns W (eds) Macaque societies: a model for the study of social organization. Cambridge University Press, New York, pp 237–262
Møller AP, Mousseau TA, Rudolfsen G, Balbontín J, Marzal A, Hermosell I, De Lope F (2009) Senescent sperm performance in old male birds. J Evol Biol 22:334–344
Nonacs P (2000) Measuring and using skew in the study of social behavior and evolution. Am Nat 156:577–589
Nonacs P (2003) Measuring the reliability of skew indices: is there one best index? Anim Behav 65:615–627
Nürnberg P, Sauermann U, Kayser M, Lanfer C, Manns E, Widdig A, Berard J, Bercovitch FB, Kessler M, Schmidtke J, Krawczak M (1998) Paternity assessment in rhesus macaques (Macaca mulatta): multilocus DNA fingerprinting and PCR marker typing. Am J Primatol 44:1–18
Ostner J, Nunn CL, Schuelke O (2008) Female reproductive synchrony predicts skewed paternity across primates. Behav Ecol Sociobiol 19:1150–1158
Paul A (1997) Breeding seasonality affects the association between dominance and reproductive success in non-human male primates. Folia Primatol (Basel) 68:344–349
Paul A (2004) Dominance and paternity. In: Thierry B, Singh M, Kaumanns W (eds) Macaque societies: a model for the study of social organization. Cambridge University Press, New York, pp 131–134
Phoenix CH, Chambers KC (1988) Old age and sexual exhaustion in male rhesus macaques. Physiol Behav 44:157–163
Plavcan JM (2004) Sexual selection, measures of sexual selection, and sexual dimorphism in primates. In: Kappeler PM, van Schaik CP (eds) Sexual selection in primates: new and comparative perspectives. Cambridge University Press, New York, pp 230–252
Plavcan JM, van Schaik CP (1992) Intrasexual competition and canine dimorphism in anthropoid primates. Am J Phys Anthropol 87:461–477
Port M, Kappeler PM (2010) The utility of reproductive skew models in the study of male primates, a critical evaluation. Evol Anthropol 19:46–56
R Development Core Team (2010) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna
Rawlins RG, Kessler MJ (1986) The history of the Cayo Santiago colony. In: Rawlins RG, Kessler MJ (eds) The Cayo Santiago macaques: history, behavior and biology. State University of New York Press, Albany, pp 13–45
Reeder DM (2003) The potential for cryptic female choice in primates: behavioral, anatomical, and physiological considerations. In: Jones CB (ed) Sexual selection and reproductive competition in primates: new perspectives and directions. American Society of Primatologists, Norman, pp 255–303
Rhodes L, Argersinger ME, Gantert LT, Friscino BH, Hom G, Pikounis B, Hess DL, Rhodes WL (1997) Effects of administration of testosterone, dihydrotestosterone, oestrogen and fadrozole, and aromatase inhibitor, on sex skin colour in intact male rhesus macaques. J Reprod Fertil 111:51–57
Rodriguez-Llanes JM, Verbeke G, Finlayson C (2009) Reproductive benefits of high social status in male macaques (Macaca). Anim Behav 78:643–649
Schwartz SM, Kemnitz JW (1992) Age- and gender-related changes in body size, adiposity, and endocrine and metabolic parameters in free-ranging rhesus macaques. Am J Primatol 89:109–121
Setchell JM, Charpentier M, Wickings J (2005) Mate guarding and paternity in mandrills: factors influencing alpha male monopoly. Anim Behav 70:1105–1120
Setchell JM, Wickings EJ (2006) Mate choice in male mandrills (Mandrillus sphinx). Ethol Sociobiol 112:91–99
Seth PK, Seth S (1986) Ecology and behavior of rhesus monkeys in India. In: Else JG, Lee PC (eds) Primate ecology and conservation, vol 2. Cambridge University Press, Cambridge, pp 192–305
Silk J, Short J, Roberts J, Kusnitz J (1993) Gestation length in rhesus macaques (Macaca mulatta). Int J Primatol 14:95–104
Singh M, Sinha A (2004) Life-history traits: ecological adaptations or phylogenetic relics? In: Thierry B, Singh M, Kaumanns W (eds) Macaque societies: a model for the study of social organization. Cambridge University Press, New York, pp 80–83
Sloter E, Schmid TE, Marchett F, Eskenazi B, Nath J, Wyrobek AJ (2006) Quantitative effects of male age on sperm motion. Hum Reprod 21:2868–2875
Smith DG (1994) Male dominance and reproductive success in a captive group of rhesus macaques (Macaca mulatta). Behaviour 129:225–242
Soltis J (2004) Mating systems. In: Thierry B, Singh M, Kaumanns W (eds) Macaque societies: a model for the study of social organization. Cambridge University Press, New York, pp 135–151
Soltis J, Mitsunaga F, Shimizu K, Nozaki M, Yanagihara Y, Domingo-Roura X, Takenaka O (1997) Sexual selection in Japanese macaques II: female mate choice and male–male competition. Anim Behav 54:737–746
Soltis J, Mitsunaga F, Shizumi K, Yanagihara Y, Nozaki M (1999) Female mating strategy in an enclosed group of Japanese macaques. Am J Primatol 47:263–278
Southwick CH, Yongzu Z, Haisheng J, Zhenhe L, Wenyuan Q (1996) Population ecology of rhesus macaques in tropical and temperate habitats in China. In: Fa JE, Lindburg DG (eds) Evolution and ecology of macaque societies. Cambridge University Press, Cambridge, pp 95–105
Takahata Y, Huffman MA, Suzuki S, Koyama N, Yamagiwa J (1999) Why dominants do not consistently attain high mating and reproductive success: a review of longitudinal Japanese macaque studies. Primates 40:143–158
van Noordwijk MA, van Schaik CP (2001) Career moves: transfer and rank challenge decisions by male long-tailed macaques. Behaviour 138:359–395
van Noordwijk MA, van Schaik CP (2004) Sexual selection and the careers of primate males: paternity concentration, dominance-acquisition tactics and transfer decisions. In: Kappeler PM, van Schaik CP (eds) Sexual selection in primates: new and comparative perspectives. Cambridge University Press, Cambridge, pp 208–229
Waitt C, Little AC, Wolfensohn S, Honess P, Brown AP, Buchanan-Smith HM, Perrett DI (2003) Evidence from rhesus macaques suggests that male coloration plays a role in female primate mate choice. Proceedings of the Royal Society of London B270:S144-S146
Weingrill T, Lycett JE, Barrett L, Hill RA, Henzi SP (2003) Male consortship behaviour in chacma baboons: the role of demographic factors and female conceptive probabilities. Behaviour 140:405–427
Whitehead H (2009a) Programs for analyzing social structure. SOCPROG Users' Manual
Whitehead H (2009b) SOCPROG programs: analyzing animal social structures. Behav Ecol Sociobiol 63:765–778
Widdig A, Bercovitch FB, Streich WJ, Sauermann U, Nuernberg P, Krawczak M (2004) A longitudinal analysis of reproductive skew in male rhesus macaques. Proceedings of the Royal Society of London B271:819–826
Widdig A, Nuernberg P, Krawczak M, Streich WJ, Bercovitch F (2002) Affiliation and aggression among adult female rhesus macaques: a genetic analysis of paternal cohorts. Behaviour 139:371–391
Wilcox AJ, Weinberg CR, Baird DD (1995) Timing of sexual intercourse in relation to ovulation. N Engl J Med 333:1517–1522
Wroblewski EE, Murray CM, Keele BF, Schumacher-Stankey JC, Hahn BH, Pusey AE (2009) Male dominance rank and reproductive success in chimpanzees, Pan troglodytes schweinfurthii. Anim Behav 77:873–885
Acknowledgments
We thank the CRPC for permission to conduct this study on Cayo Santiago, and CPRC employees, especially Edgar Avila and Julio Resto, for their assistance during field work. Particular thanks go to Véronique Martel, Camille Guillier, Giulia Sirianni, Julie Cascio, Claude Richer, Edith Hovington, Isabelle Benoît, François Bourgault, Doreen Hess, and Akie Yanagi for assisting in data and sample collection; and Sven Schreiter, Sara Hermann, Andrea Heistermann, and Jutta Hagedorn for the laboratory assistance. Linda Vigilant kindly provided laboratory access and advice. We also thank Michael Krawczak and Olaf Junge for access to a management program of genetic data (FINDSIRE), Lauren Brent for sharing valuable observation and samples, and Melissa Gerald and Maria Rahkovskaya for sharing their male dominance hierarchy. Finally, Bernard Chapais provided fruitful discussions, and Roger Mundry assisted in statistical analyses. Two anonymous referees provided helpful comments on an earlier version of the manuscript. This project was funded by SSHRC (to CD), Université de Montréal (to CD), DFG (grant No. WI 1808/3-1 to AW; and grant No. EN 719/2-1 to AE), NSERC (to Bernard Chapais), and the German Initative of Excellence. This publication was made possible by Grant Number CM-5 P40 RR003640-20 from the National Center for Research Resources (NCRR), a component of the National Institutes of Health (NIH). Its contents are solely the responsibility of the authors and do not necessarily represent the official views of NCRR or NIH. The investigation was approved by the IACUC of the University of Puerto Rico, Medical Sciences Campus (protocol No. 9400106).
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by M. Charpentier
Antje Engelhardt and Anja Widdig equally contributed.
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Dubuc, C., Muniz, L., Heistermann, M. et al. Testing the priority-of-access model in a seasonally breeding primate species. Behav Ecol Sociobiol 65, 1615–1627 (2011). https://doi.org/10.1007/s00265-011-1172-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00265-011-1172-8