Abstract
Theory states that an optimal forager should exploit a patch so long as its harvest rate of resources from the patch exceeds its energetic, predation, and missed opportunity costs for foraging. However, for many foragers, predation is not the only source of danger they face while foraging. Foragers also face the risk of injuring themselves. To test whether risk of injury gives rise to a foraging cost, we offered red foxes pairs of depletable resource patches in which they experienced diminishing returns. The resource patches were identical in all respects, save for the risk of injury. In response, the foxes exploited the safe patches more intensively. They foraged for a longer time and also removed more food (i.e., had lower giving up densities) in the safe patches compared to the risky patches. Although they never sustained injury, video footage revealed that the foxes used greater care while foraging from the risky patches and removed food at a slower rate. Furthermore, an increase in their hunger state led foxes to allocate more time to foraging from the risky patches, thereby exposing themselves to higher risks. Our results suggest that foxes treat risk of injury as a foraging cost and use time allocation and daring—the willingness to risk injury—as tools for managing their risk of injury while foraging. This is the first study, to our knowledge, which explicitly tests and shows that risk of injury is indeed a foraging cost. While nearly all foragers may face an injury cost of foraging, we suggest that this cost will be largest and most important for predators.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Patch use by foraging animals is typically affected by multiple inputs. These include harvest rates of resources, energetic costs of exploiting the patch, costs arising from interference and aggression, and costs arising from the risk of predation. An individual's patch use behavior is often the outcome of conflicting demands arising from trade-offs of food and safety (e.g., Brown 1992; Brown and Kotler 2004). These behaviors have far-reaching consequences for populations and communities via their effects on resource availabilities, competitive interactions, encounter rates with predators, and predator–prey interactions (e.g., Kotler and Brown 1988, 1999; Kotler and Blaustein 1995).
Theory states that an optimal forager should exploit a patch so long as its harvest rate (H) of resources from the patch exceeds its energetic (C), predation (P), and missed opportunity costs (MOC) for foraging in that patch (i.e., H = C + P + MOC; Charnov 1976; Brown 1988, 1992). Typically, predictions from such a model are couched in terms of quitting harvest rates and tested by examining the effect of various factors on the amount of food left in the patch after exploitation, i.e., the giving up density (GUD). Extensive experimental evidence exists showing that these factors affect GUDs, as theory suggests (e.g., Brown and Kotler 2004).
For many foragers, however, predation is not the only source of danger they face while foraging. Foragers may also face the risk of injuring themselves. For herbivores, plants may be defended by many kinds of chemical and/or mechanical traits (Karban and Baldwin 1997; Gomez and Zamora 2002), and some plants even evolve mutualistic relationships with animal species such as ants to protect them from herbivory (Janzen 1966). For predators, a prey may possess dangerous defensive weapons or toxic compounds. An injury need not be a serious one in order to have a strong affect on a predator's fitness. For predators that rely on peak performance to catch their prey, even a minor injury can be life-threatening, as an injured predator may starve to death while healing (Brown and Kotler 2004).
We suggest that for a forager pursuing dangerous prey, there is a cost of foraging that arises from the risk of injury. An injury may not only reduce the foraging ability of the forager (i.e., lower harvest rates) but may also, in extreme cases, kill the forager outright. Thus, a forager facing such risks of injury should take them into consideration and require greater compensations. In this sense, the risk of injury should be similar to the risk of predation: It gives rise to foraging costs. Hence, the risk of injury cost can either be added to costs of foraging or even replace the cost of predation when top predators that prey on the forager in question are absent or rare, i.e., H = C + P + MOC becomes either H = C + P + RI + MOC or H = C + RI + MOC, where RI represents the risk of injury cost. Hence, the forager's behavior should reflect a trade-off between energy gain from prey items and the possibility of suffering injury while pursuing them (Gilchrist et al. 1998).
The cost of predation is directly affected by the marginal value of energy, and the response to predation risk will depend on the state of the forager (Brown 1992; Kotler 1997). In the same manner, the cost of injury for a forager should depend on its state, and this should have a substantial effect on its foraging strategy.
As the forager grows hungrier, the marginal value of energy associated with the prey items increases and with it the fitness rewards of energy gain. Thus, hungry foragers are expected to be more willing to risk injury for energy gain than foragers in good state. That is, they should be more daring.
Although several studies have dealt with the risks foragers encounter while feeding (e.g., Juanes and Hartwick 1990; Cognil et al. 2002; Dietl 2003), a direct experimental test of the hypothesis that the risk of injury is a foraging cost is lacking. To this end, we quantified the patch use behavior of captive red foxes (Vulpes vulpes) presented with depletable artificial food patches that differed in their potential risk of injury. We predict that if foragers treat risk of injury as a foraging cost, they should show a preference for foraging in the safe food patch (i.e., lower GUDs and higher harvest rates). We also predict that foragers in better physical state should take fewer risks when foraging and leave patches at higher food densities.
Materials and methods
Study species
Red foxes are the most common carnivores in the Middle East (Mendelssohn and Yom-Tov 1999). In Israel, they are solitary, mainly nocturnal, and territorial. Mean body mass and body length are 3.10 kg and 58 cm for males and 3.04 kg and 57 cm for females (Mendelssohn and Yom-Tov 1999). Red foxes feed mainly on rodents (Bekoff 1975), but also on a variety of other food sources including insects, birds, reptiles, hares, fruits, and human waste (Mendelssohn and Yom-Tov 1999).
Experimental design
Patch use experiment
The experiments were conducted using three adult red foxes housed individually in separate 3 × 3-m enclosures at the Sede Boqer Campus of Ben-Gurion University located in the Negev Desert highlands, Israel between February and April 2007. The foxes were either trapped from the wild (one male) or obtained from a zoo (one male and one female).
To quantify the foraging behavior of the foxes, we presented food to individual foxes in artificial food patches and measured their GUDs while exploiting these patches. A food patch consisted of a deep bucket (17 l) filled with 12 l of sand into which 130 g ± 0.2 g of dog food pellets were mixed (the foxes' daily requirement on average). Each pellet was approximately 1 × 0.5 × 0.5 cm in size with average mass of 0.3 g. Experimental evidence confirmed that foxes experience diminishing returns while foraging in similar patches (Mukherjee et al. 2009; also see below), and thus, differences in GUDs should reflect differences in costs of foraging or harvest rates. We presented food patches to each fox two patches at a time. The buckets were placed into 30-cm diameter holes cut into a 130 × 55-cm wooden platform raised 30 cm above the floor of the enclosure on a wooden frame. In order to extract food from these patches, the foxes had to climb onto and stand on the table-like platform.
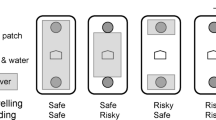
For each pair of food patches, one served as the safe patch and the other as the risky patch. To create a risk of injury that was serious enough to cause the foxes to forage carefully, but not so severe as to cause actual harm, we placed short 1.5-cm-long nails at roughly 2-cm intervals, with their sharp ends pointing up, in a 55 × 55-cm area at one end of the platform. The assay patch was placed right in the middle of this area. In addition, we also threaded two strands of stiff, flat razor wire, each of 2.5 m long, coiled inside the food patch and anchored to the bottom of the bucket. Finally, we placed two short lengths of razor wire crosswise across the mouth of the bucket. This final design of the risky patch was achieved after several observational and feeding trials. Due to the inherent nature of this experimental design, we decided to run the experiment with a small sample size of foxes. In order to ensure the safety of the animals, we monitored the foxes closely in the days following experimental sessions. The foxes never showed any signs of injury or abnormal behavior throughout the entire duration of the experiment.
The safe patch had a similar setup, but we instead drove the nails into the surface of the wooden platform surrounding the bucket in the standard way such that their flat heads stuck out of the wood and formed an irregular surface upon which the fox could stand without noticeable discomfort. Inside the food patch, we coiled two 2.5-m-long strands of smooth wire (2.2-mm diameter) and added two smooth, short wires across the mouth. Every night, we rotated the orientation of the platforms to alternate the location of the risky and safe patches to control for any possible side preference that the foxes might have had. Each fox had free access to one such pair of patches for an entire night (approximately 11 h). In the morning, we sifted the sand and weighed the remaining food in the patches to obtain the GUD of the patch.
We manipulated the state of the foxes as follows. (1) Foxes that were offered supplemental food in a separate plate, in addition to the food patches, were considered not hungry. (2) Foxes that last received food 24 h prior to the beginning of the experiment were considered hungry. (3) Foxes that last received food only 48 h prior to the beginning of the experiment were considered very hungry. We ran three complete three-night rounds so that each fox experienced each state three times (nine times in total). On any given night of the experiment, each state was represented by one fox, and in any given round, each fox experienced all three state treatments. The order of the treatments was randomized across foxes, nights, and rounds using a Latin square. We used a general linear mixed model to check for the effects of the riskiness of the patch, the state of the fox, and the fox identity on the GUDs.
Harvest rate curves
Harvest rate curves can be used to investigate the forager's intake rate of resources at different stages of its foraging bout. Comparing between different harvest rate curves constructed for various resource patches can reveal changes in the foraging strategies of the foragers (Ovadia et al. 2001). Harvest rate curves have been used to investigate the foraging behavior of mammalian granivores (i.e., Kotler and Brown 1990; Brown et al. 1994; Smith 1995) and herbivores (i.e., Gross et al. 1993).
As we will show below, foxes leave different GUDs in safe versus risky patches. This raised the question of whether they employ more careful tactics or time allocation in arriving at the GUD. To help reveal how foxes deal with safe and risky resource patches, we constructed foraging curves (food harvested per unit time) for a captive red fox by presenting it with artificial food patches and filming it foraging using an infrared camera.
We simultaneously presented the fox with two artificial food patches that differed in their risk of injury in the manner described above. We presented the food patches to the fox for different time periods (10 min–12 h). The order of treatments was randomized, and each exposure time was repeated twice. At the end of a foraging session, we collected the GUDs from each patch.
We recorded the foraging sessions using an “X Nite IR Board Cam” infrared camera attached to the wall of the enclosure and connected to a Mitsubishi HS-MS11V video recorder. We later watched the recordings of the foraging sessions and measured the time that the fox spent foraging in each of the patches using two stopwatches.
We tested for the effects of only two state treatments, hungry and very hungry. The hungry treatment was carried out in April 2007. During this period, we recorded 19 foraging sessions. During the very hungry treatment, which took place between the months of June and August 2007, we recorded 17 foraging sessions. In order to not cause any damage to the very hungry fox, we allowed the fox recovery time of a few days between days of starvations. During these recovery days, the fox received extra food. We note that the hungry treatments and the very hungry treatments were conducted in different months. However, as both time periods did not overlap with the breeding season of the red foxes in Israel and as in the Negev Desert the months of April as well as the summer months are dry, the main dissimilarity between the experimental periods is that the summer months are warmer. We strongly believe that the warmer climate should have no effect on the reaction of the fox to risk of injury, but this possible confounding effect should be noted nevertheless.
This research was carried out under permit 2006/26606 from the Israel Nature Protection Authority. No foxes were injured in the course of the experiments.
The statistical analyses for the patch use experiment were done using Statistica 8.0 (StatSoft, Inc., Tulsa, OK, USA) statistical software. The statistical analyses for the harvest rate curve construction were done using SPSS 14.0 (SPSS Inc, Chicago, IL, USA) statistical software.
Results
Patch use experiment
Foxes show concordance in how they rank the various combinations of riskiness and internal state. When we ranked the different combinations of patch types and states for each fox and compared them among the foxes, we found concordance among the different individual foxes (Friedman randomized blocks, χ 2 = 0.667, df = 2, p = 0.717). Thus, the foxes all responded to the experimental treatments in a highly uniform way despite variation between the foxes in the amounts of food they consumed and in their foraging abilities. This result gives us confidence that despite the low number of foxes used in this experiment, due to ethical and technical reasons, any significant effects revealed in the experiments are not a reflection of any idiosyncrasies of our experimental animals.
The foxes left significantly greater amounts of food in the risky patch type (one-tailed general linear mixed model with fox identity as a random factor: MS = 20,215, F 1,2 = 14.07, p = 0.03; Fig. 1). Thus, risk of injury affects GUDs and is treated as a cost of foraging by foxes. State also affected the amount of food foxes left in resource patches (MS = 5,755, F 2,4 = 19.16, p < 0.001; Fig. 1). Hungrier foxes exploited food patches more thoroughly and left lower GUDs. Thus, state affects the injury cost of foraging in foxes.
The amount of food left in the patches (GUD) in grams as a factor of the state of the foxes (X-axis) and the riskiness of the patch (safe—white, risky—dark gray). Numbers at the bottom of the bars represent the sample size, error bars represent one standard error, and letter associated with bars represent Tukey's honestly significant difference grouping between state treatments
Harvest rate curves
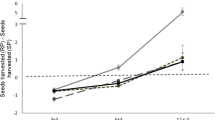
The fox was able to harvest food more quickly (higher harvest rate) in the safe patch than in the risky patch (Fig. 2). The fox's harvest rate curves, i.e., the cumulative weight of food harvested as a function of time spent searching in the patch, for both the risky and the safe patches in both hunger states are well described using quadratic regressions (hungry—safe: y = 0.051x–7.9 × 10−6 x 2, R 2 = 0.988, F 2,19 = 683.70, p < 0.0001; hungry—risky: y = 0.045x–8.8 × 10−6 x 2, R 2 = 0.994, F 2,19 = 1,328.23, p < 0.0001; very hungry—safe: y = 0.038x–4.1 × 10−6 x 2, R 2 = 0.990, F 2,17 = 729.51, p < 0.0001; very hungry—risky: y = 0.033x–3.4 × 10−6 x 2, R 2 = 0.982, F 2,15 = 355.32, p < 0.0001; Fig. 2). Although in all of the above cases linear regressions could also be used to describe the data, the F of improvement between the linear and quadratic regressions is significant (p < 0.0001 in all of the cases); thus, the quadratic regressions offer significantly better fits to the data. The fit to the quadratic regression demonstrates that the fox experiences diminishing returns to harvest with time spent in the patch.
The regression coefficients (time and time2) are significant, as well as the interactions between the coefficients with both the type of the patch and the state of the fox (Table 1). Thus, the type of the patch and the state of the fox have significant effects on both the slopes of the regressions and their curvatures, i.e., the fox harvested food more slowly from the risky patch and when it was hungrier (see below).
In both hunger states, the fox spent significantly more time foraging in the safe patch than in the risky patch (paired t test, hungry: t 15 = −3.171, p = 0.006; very hungry: t 13 = −3.039, p = 0.01) and ate significantly more food in the safe patch (paired t test, hungry: t 15 = −3.418, p = 0.004; very hungry: t 13 = −5.194, p < 0.001).
The harvest rate curves allow us to derive estimates of the quitting harvest rates for the different treatments. To do so, we take the derivatives of the quadratic equations for the harvest rate curves from Fig. 2 and plug in the appropriate GUD. This yields quitting harvest rates for a hungry fox of 0.0497 and 0.0433 g/s for safe and risky patches, respectively, and for a very hungry fox of 0.0374 and 0.0324 g/s, respectively. Thus, quitting harvest rates were lower in the risky patches and when the fox was very hungry. Also, the difference in quitting harvest rates between risky and safe patches was approximately 30% greater when the fox was hungry compared to when it was very hungry.
Discussion
A forager should abandon a depletable food patch when the benefits derived from its present harvest rate no longer exceed the costs of foraging in the patch (Brown 1988; Brown et al. 1997). Consequently, foragers should demand higher harvest rates from resource patches with higher foraging costs and quit them at higher quitting harvest rates and giving up densities. We presented foxes with identical food patches in terms of their metabolic, predation, and missed opportunity costs, but with different risks of injury. Thus, the differences in the GUDs between the patches must be attributed to the differences in the risk of injury between the patches.
Our results show that foxes leave higher GUDs in resource patches with higher risk of injury than they do in safer patches. This result strongly suggests that foragers treat risk of injury as a foraging cost. Foxes also leave higher GUDs when they are less hungry. These state-dependent changes in the foxes' foraging strategies may have come about via two main pathways: (1) As the forager grows hungrier, its missed opportunities cost of foraging decreases because acquiring food becomes a more valuable activity for it, and it spends more time foraging. (2) The cost of injury for a forager is a product of the injury risk and the marginal rate of substitution of energy for injury (MRSei). MRSei is the quotient of two components: survivor's fitness and the marginal value of energy (∂F/∂e; Brown 1992; Kotler 1997). Thus, hungrier foragers (higher marginal value of energy) are expected to take higher risks and be willing to spend more time foraging in risky patches. Our results demonstrate that foxes treat the foraging cost arising from the risk of injury in a similar manner to which other foragers treat the foraging cost arising from the risk of predation. Hence, an optimally foraging animal should forage in a patch as long as its harvest rate exceeds the sum of its metabolic, predation, missed opportunities, and injury costs associated with foraging in that patch.
The riskiness of the patch affected both the slopes of the harvest rate curves and their curvatures. The different shapes of the curves can reveal information about the foraging tactics of the fox. The slopes of the gain curves in the safe patches were steeper, i.e., the rate of food gain was higher in these patches. As both food patches contained an identical initial amount of food mixed thoroughly throughout the patch, the change in the rate of food gain between the patches has to be a result of differences in the fox's foraging behavior while exploiting them. A slower intake rate could reflect a more cautious approach to the patch that would increase the time spent searching for and extracting food from the patch. Our video footage supports the notion that the fox approached the risky patches with much more care than the safe patches. Thus, the increase in foraging costs in the risky patch is likely due to elevated searching and handling time in that patch, i.e., the fox reduced its intake rate in order to decrease the chances of injuring itself. As an injury could reduce the future intake rate of the fox, such behavior might reflect a trade-off between long-term and short-term intake rates.
The state of the fox also affected its harvest rate. When the fox was very hungry, the slopes of the curves were overall gentler, at least compared to the fox exploiting the safer patch when it was less hungry. This at first may appear to be somewhat counterintuitive, as a hungrier animal can be expected to forage more rapidly and less carefully and thus have a higher rate of food consumption. We believe that the slower overall intake rate of the very hungry fox is due to more thorough patch exploitation by the fox. Because of its higher marginal value of energy when very hungry, the fox chose a lower GUD and therefore spent substantially more time foraging in each patch (Fig. 2). That is, we recorded many more data points for the very hungry fox at especially long foraging times. These times were associated with low harvest rates due to extensive patch depletion by that time. When averaging overall rate, these points lower the average. Furthermore, the approximately equal numbers of points for the hungry and very hungry treatments are spread differently. Those for the hungry state tend to be bunched at times less than 20 min; those for the very hungry state are much more evenly spread across the entire range of observations. Thus, we have a better rendering of the shape of the harvest rate curve for the very hungry treatment, and it is weighted more heavily for the lower harvest rates incurred at long foraging times. In fact, for the first 20 min of patch exploitation while the fox removed the easy-to-get food items on top, there is little difference in harvest rate for any patch and condition. Any differences there are more statistical than biologically meaningful.
There were no significant interactions between the effects of the patch type and the state of the fox on its harvest rate curves when only three-way interactions are included. Thus, the riskiness of the patch and the fox's state have an additive effect on the fox behavior. Interestingly, when we include the four-way interaction of risk × state × time × time2, it is significant, but then neither the lower order interactions nor the main effects are. Four-way interactions can be extremely difficult to interpret, so we say with great caution that this may offer support for the interaction of state and risk in determining the curvature of the harvest rate curves in a manner consistent with the use of daring, i.e., stronger separation between the curves when the fox is very hungry.
Most foragers are likely to face both risks—predation and injury—at the same time. However, they may differ in the relative weights of the different foraging costs. Top predators may be especially susceptible to risk of injury. Predators must pursue, capture, and kill others in order to eat, and in so doing, they may hurt themselves. In extreme cases, predators may actually be killed by their intended victims, as may happen when African lions attack buffalo (Mangani 1962; Beyers 1964) or wolves attack moose (Mech 1966). Thus, for top predators, which are often assumed to be free of predation costs, the heightened chances of risk of injury may be their main foraging cost, equivalent to the predation cost of their prey.
Just as prey individuals manage risk of predation, using behavioral tools of time allocation and vigilance (Brown 1999; Bouskila 2001), predators too should manage their own risks while foraging. To this end, predators may have several behavioral tools at their disposal such as: (1) selecting for prey size and type (e.g., Rutten et al. 2006); (2) using time allocation to decide how long to hunt in a certain area and how long to pursue a prey item; and (3) varying their degree of daring. Daring can be defined as the willingness of the animal to risk injury. A more daring predator is likely to be more lethal (higher capture rate), but also may suffer a higher risk of injury while foraging. The willingness of the predator to take these risks may strongly depend on its energetic state. Predators may use any or all of these behavioral tools to maximize their expected fitness while facing a trade-off between energy reward and the risk of injury they face while foraging (Gilchrist et al. 1998; Brown and Kotler 2004; Rutten et al. 2006).
In our experiment, the fox used the behavioral tools of both time allocation and daring for managing its risk of injury. It spent more time foraging in the safe patches even though it was exposed to both types of patches for exactly the same amount of time. Also, despite its apparent discomfort (personal observation) and the risk of injuring itself, the fox increased the amount of time foraging in the risky patch when it was hungrier. This willingness to risk injury could be regarded as daring behavior. The fox was willing to stay longer in the risky patch in order to increase his energetic gain. Daring behavior, while risky, may increase the lethality of a predator (e.g., an owl increasing its diving speed, a bird eating a butterfly despite its warning colors, etc). This, in turn, may cause a change in the prey behavior and in the long run may even have an effect on the evolution of certain prey species (Sherratt 2003).
References
Bekoff M (1975) Social behavior and ecology of African Canidae: a review. In: Fox MW (ed) The wild canids. Van Nostrand Reinhold, New York, pp 120–142
Bouskila A (2001) A habitat selection game for interactions between rodents and their predators. Ann Zool Fenn 38:55–70
Brown JS (1988) Patch use as an indicator of habitat preference, predation risk, and competition. Behav Ecol Sociobiol 22:37–47
Brown JS (1992) Patch use under predation risk. I. Models and predictions. Ann Zool Fenn 29:301–309
Brown JS (1999) Vigilance, patch use and habitat selection: foraging under predation risk. Evol Ecol Res 1:49–71
Brown JS, Kotler BP (2004) Hazardous duty pay and the foraging cost of predation. Ecol Lett 7:999–1014
Brown JS, Kotler BP, Valone TJ (1994) Foraging under predation—a comparison of energetic and predation costs in rodent communities of the Negev and Sonoran deserts. Aust J Ecol 42:435–448
Brown JS, Kotler BP, Mitchell WA (1997) Competition between birds and mammals: a comparison of giving-up densities between crested larks and gerbils. Evol Ecol 11:757–771
Charnov EL (1976) Optimal foraging: the marginal value theorem. Theor Popul Biol 9:129–136
Cogni R, Freitas AVL, Filho BFA (2002) Influence of prey size on predation success by Zelus longipes L. (Het., Reduviidae). J Appl Entomol 126:74–78
Beyers CP de L (1964) Lion vs buffalo. Animal 5:220–221
Dietl GP (2003) Interaction strength between a predator and dangerous prey: Sinistrofulgur predation on Mercenaria. J Exp Mar Biol Ecol 289:287–301
Gilchrist HG, Gaston AJ, Smith JNM (1998) Wind and prey nest sites as foraging constraints on an avian predator, the glaucous gull. Ecology 79:2403–2414
Gomez JM, Zamora R (2002) Thorns as induced mechanical defense in a long-lived shrub (Hormathophylla spinosa, Cruciferae). Ecology 83:885–890
Gross JE, Shipley LA, Hobbs NT, Sparinger DE, Wundur BA (1993) Functional-response of herbivores in food-concentrated patches—tests of a mechanistic model. Ecology 74:778–791
Janzen DH (1966) Co-evolution of mutualism between ants and acacias in Central America. Evolution 120:249–275
Juanes F, Hartwick EB (1990) Prey size selection in Dungeness crabs: the effect of claw damage. Ecology 71:744–758
Karban R, Baldwin IT (1997) Induced responses to herbivory. Chicago University Press, Chicago, IL, USA
Kotler BP (1997) Patch use by gerbils in a risky environment: manipulating food and safety to test four models. Oikos 78:274–282
Kotler BP, Blaustein L (1995) Titrating food and safety in a heterogeneous environment: when are the risky and safe patches of equal value? Oikos 74:251–258
Kotler BP, Brown JS (1988) Environmental heterogeneity and the coexistence of desert rodents. Ann Rev Ecol Syst 19:281–307
Kotler BP, Brown JS (1990) Rates of seed harvest by two species of gerbilline rodents. J Mammal 71:591–596
Kotler BP, Brown JS (1999) Mechanisms of coexistence of optimal foragers as determinants of local abundances and distributions of desert granivores. J Mammal 80:361–374
Mangani B (1962) Buffalo kills lion. Afr Wildl 16:27
Mech LD (1966) The wolves of Isle Royale. Fauna of the national parks of the United States. Fauna Series 7, National Park Service, Washington, DC
Mendelssohn H, Yom-Tov Y (1999) Fauna Palestina, Mammalia of Israel. The Israel Academy of Sciences and Humanities
Mukherjee S, Zelcer M, Kotler BP (2009) Patch use in time and space by a mesopredator in a risky world. Oecologia 159:661–668
Ovadia O, Ziv Y, Abramsky Z, Pinshow B, Kotler BP (2001) Harvest rates and foraging strategies in Negev Desert gerbils. Behav Ecol 12:219–226
Rutten AL, Oosterbeek K, Ens BJ, Verhulst S (2006) Optimal foraging on perilous prey: risk of bill damage reduces optimal prey size in oystercatchers. Behav Ecol 17:297–302
Sherratt TN (2003) State-dependent risk-taking by predators in systems with defended prey. Oikos 103:93–100
Smith RJ (1995) Harvest rates and escape speeds in two coexisting species of montane ground squirrels. J Mammal 76:189–195
Acknowledgments
We thank Arnon Lotem and Ron Elazari-Volcani for helping us obtain the foxes for this research. We are grateful for the insights and suggestions provided by David Saltz and Ofer Ovadia. This research was carried out under permit 2006/26606 from the Israel Nature Protection Authority. This is publication number 646 of the Mitrani Department of Desert Ecology.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by P. Bednekoff
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License ( https://creativecommons.org/licenses/by-nc/2.0 ), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Berger-Tal, O., Mukherjee, S., Kotler, B.P. et al. Look before you leap: is risk of injury a foraging cost?. Behav Ecol Sociobiol 63, 1821–1827 (2009). https://doi.org/10.1007/s00265-009-0809-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00265-009-0809-3